雷达对地成像技术多向演化趋势与规律分析

杨建宇

doi:10.12000/JR19099

雷达对地成像技术多向演化趋势与规律分析

DOI: 10.12000/JR19099

杨建宇^,

电子科技大学成都 611731

基金项目: 国家自然科学基金重点项目(60632020)，国家自然科学基金面上项目(61771113, 61671117)

详细信息

作者简介:
杨建宇(1963–)，电子科技大学教授，博士生导师，校科技委主任，国务院学位委员会信息与通信工程学科评议组成员，中国电子学会雷达分会副主任委员。主要研究方向为雷达前视成像、实孔径超分辨成像、双多基合成孔径雷达成像。获国家出版基金资助出版专著1部。获省部级奖6项、国家技术发明二等奖2项。E-mail: jyyang@uestc.edu.cn

通讯作者:
杨建宇 jyyang@uestc.edu.cn

¹ 严格意义上属于伪彩色，文中为表述方便，简称为彩色。² 中国科学院电子学研究所提供。
³图8中的层析SAR是指多航过层析SAR。
⁴图16中层析SAR指单航过层析SAR，例如图15所对应的成像方式。
⁵这里采用视线横向分辨和视线纵向分辨的表述方式，而未采用方位分辨和距离分辨的表述方式，是为了便于从透镜成像的角度来类比合成孔径成像的原理。
⁶为绘图标识方便，显著放大了波长和转角。例如，3 cm波长，0.3 m分辨，转角仅2.86°; θ在10°以内，sin θ/2≈θ/2，误差小于0.13%。
中图分类号: TN95
计量
- 文章访问数: 6599
- HTML全文浏览量: 2179
- PDF下载量: 859
- 被引次数: 4
出版历程
- 收稿日期: 2019-11-19
- 修回日期: 2019-12-20
- 网络出版日期: 2019-12-01

Multi-directional Evolution Trend and Law Analysis of Radar Ground Imaging Technology（in English）

YANG Jianyu^,

University of Electronic Science and Technology of China, Chengdu 611731, China

Funds: The Key Program of the National Natural Science Foundation of China (60632020), The General Program of The National Natural Science Foundation of China (61771113, 61671117)

More Information

Corresponding author: YANG Jianyu, jyyang@uestc.edu.cn

摘要

摘要:
该文从成像结果表征、孔径流形、信号通道、系统形态、观测方向、处理方法、实现机理、目标识别等方面剖析了雷达对地成像技术的多向演化态势，并试图从宏观的视角和大的时间尺度，分析和认识雷达对地成像技术发展的内外因素和发展规律，推演预测未来发展方向，以期为把握雷达对地成像技术发展的时代脉络和宏观趋势、契合需求和引领创新、推动发展和促进应用，提供另类的观察视角和思维方式。
- 雷达成像 /
- 宏观趋势 /
- 影响因素 /
- 发展规律
Abstract:
This paper analyzes the multi-directional evolution of radar ground imaging technology from the aspects of the representation of imaging results, aperture manifolds, signal channels, system morphologies, observation directions, processing methods, realization mechanisms, and target recognition. Attempts are made to analyze and understand the internal and external factors as well as the development law of radar ground imaging technology from a macroscopic perspective over a long time scale, and to predict the direction of future development. Alternative observation perspective and thinking method are proposed with a view to advance the understanding of the times veins and macro trends of radar ground imaging technology, meet practical needs, lead innovation efforts, and promote development and applications.
- Radar imaging /
- Macro trend /
- Influencing factors /
- Development law

HTML全文

1. 引言

双基星载合成孔径雷达(Synthetic Aperture Radar, SAR)利用信号收发平台的分置，能够同时获取不同视角的观测数据，在测绘、干涉测量、地面目标识别、自然灾害监测等领域^[1,2]具有重要的应用价值。以Tandem-L为代表的新一代双基星载SAR系统应用多通道、数字波束形成(Digital Beam Forming, DBF)等技术，实现方位向高分辨率和距离向宽测绘带SAR(High Resolution Wide Swath SAR, HRWS-SAR)成像，系统的成像能力得到显著改善^[3,4]。

HRWS-SAR系统在方位向采用多通道采样降低系统的脉冲重复频率(Pulse Recurrence Frequency, PRF)，在不降低方位分辨率的前提下实现系统的宽测绘带成像。HRWS-SAR系统进行成像处理时，若方位向信号为均匀采样可直接采用传统SAR成像处理方法，而受载星平台轨迹约束及应用场景的限制，方位向的非均匀采样更为普遍^[5]，因而对方位向信号进行重构以获得其均匀采样信号或多普勒谱是HRWS-SAR系统成像处理的一项关键技术。单基星载HRWS-SAR系统的方位向信号重构得到了广泛而深入的研究^[6–17]。重排算法^[6]和插值算法^[7]是两种典型的时域重构算法。重排算法依据接收信号的方位向位置将各通道信号重新排列，只能在特定的PRF得到方位向信号的均匀采样。插值算法则依据文献[7]所提出的周期性非均匀采样信号重构公式通过时域插值得到方位向信号的均匀采样，该算法运算复杂度高且精度依赖于插值核的长度。Krieger等依据广义采样定理提出矩阵求逆算法^[8,9]，该算法通过线性方程求解从混叠的多通道信号中重构出无模糊的多普勒谱。该算法不需要协方差矩阵等先验信息且易于实现，但在重叠采样时该算法无法进行信号重构，接近重叠采样时重构性能也较差。文献[10–13]则采用不同的方法对矩阵求逆算法进行改进，实现重叠采样附近的高性能信号重构。文献[14,15]基于统一的信号模型，选取不同代价函数进行优化，提出了多种自适应波束形成(DBF)算法：正交投影算法、信号最大化算法、最大化信号模糊噪声比算法、最小均方误差算法等。与矩阵求逆算法相比，DBF类算法运算复杂度较高，并假定各通道的噪声为高斯白噪声且相互独立。文献[16]则对方位向信号重构算法的性能进行了仿真对比分析。文献[17]采用NUFFT直接重构方位向非均匀采样信号的多普勒频谱。

上述方位向信号重构方法理论上均能推广到双基星载HRWS-SAR系统。考虑到矩阵求逆算法易于实现且研究较为广泛，本文研究该算法在双基HRWS-SAR系统中的实现。本文首先将方位照射时间内时变的发射接收距离比近似为一个常数，推导了双基星载HRWS-SAR系统与某个单基系统在方位向多信道间传递函数上的等效性，从而构建了双基星载HRWS-SAR系统的方位向信号模型。而后，提出了适用于一般双基构型星载HRWS-SAR系统方位向信号重构的矩阵求逆算法，并给出了信噪比缩放因子及方位模糊比这两个重构性能指标的计算公式。最后，通过对几种典型双基构型的星载HRWS-SAR系统进行方位向信号重构仿真，验证了矩阵求逆算法在一般双基构型星载HRWS-SAR系统中的适用性。

2. 双基星载HRWS-SAR系统的方位向信号模型

为保持双基星载HRWS-SAR系统对地面的持续观测，收发平台应置于同一轨道(顺飞模式)或高度相同的平行轨道(平飞模式)。图1给出了一般构型双基星载HRWS-SAR系统的信号收发几何。发射天线和接收天线的最短距离分别为r_T0, r_R0，接收天线共有M个通道，RX_equ为方位向信号重构后的等效接收通道，通道i到等效接收通道RX_equ的方位向距离为 $\Delta {x_i}$ , t_fd为发射天线和接收天线的零多普勒时间差。

图 1 双基星载HRWS-SAR系统的双基构型

Figure 1. Bistatic configuration of bistatic spaceborne HRWS-SAR

下载: 全尺寸图片幻灯片

不失一般性，假定点目标P在t=0时刻位于接收天线的零多普勒面，容易得到t时刻点P在接收通道i的收发距离和 $R\left( t \right)$ 计算公式为：

$\begin{aligned} R\left( t \right) =& \sqrt {r_{{\rm{T}}0}^2 + {{\left( {vt - v{t_{{\rm{fd}}}}} \right)}^2}} \\ & + \sqrt {r_{{\rm{R}}0}^2 + {{\left( {vt - \Delta {x_i}} \right)}^2}} \end{aligned}$

(1)

忽略天线方向图的影响，接收通道i的冲激响应函数可表示为：

$\begin{aligned} {h_i}\left( t \right) = & \exp \left( { - {\rm j}\frac{{2{{π}} }}{\lambda }R\left( t \right)} \right) \\ = & \exp \Biggr( { - {\rm j}\frac{{2{{π}} }}{\lambda }\biggr( {\sqrt {r_{{\rm{T}}0}^2 + {{\left( {vt - v{t_{{\rm{fd}}}}} \right)}^2}}}} \\ & { {\left.+ {\sqrt {r_{{\rm{R}}0}^2 + {{\left( {vt - \Delta {x_i}} \right)}^2}} } \right)} \Biggr)} \end{aligned}$

(2)

2.1 单基星载HRWS-SAR系统的方位向信号模型

单基星载HRWS-SAR系统可视为r_T0=r_R0=r₀, t_fd=0，发射天线为等效接收通道的特殊情况。由式(2)可得此时接收通道i的冲激响应为：

$\begin{aligned} {\tilde h_i}\left( t \right) = & \exp \Biggr( { - {\rm j}\frac{{2{{π}} }}{\lambda }\biggr( {\sqrt {r_0^2 + {{\left( {vt} \right)}^2}}}} \\ & + {{\sqrt {r_0^2 + {{\left( {vt - \Delta {x_i}} \right)}^2}} } \biggr)} \Biggr) \end{aligned}$

(3)

令此时单基单通道SAR的冲激响应函数为 ${\tilde h_{{\rm{mono}}}}\left( t \right)$ , ${\tilde h_{{\rm{mono}}}}\left( t \right)$ 可由式(4)表示。

${\tilde h_{{\rm{mono}}}}\left( t \right) = \exp \left( { - {\rm j}\frac{{4{{π}} }}{\lambda }\sqrt {r_0^2 + {{\left( {vt} \right)}^2}} } \right)$

(4)

文献[9]对 ${\tilde h_{{\rm{mono}}}}\left( t \right)$ 及 ${\tilde h_i}\left( t \right)$ 的泰勒级数展开进行2阶相位近似处理，可得

$\left\{ \begin{aligned} &{{\tilde h}_{{\rm{mono}}}}\left( t \right) \approx \exp \left( { - {\rm j}\frac{{4{{π}} }}{\lambda }{r_0}} \right) \cdot \exp \left( { - {\rm j}\frac{{2{{π}} {v^2}{t^2}}}{{\lambda {r_0}}}} \right)\\ &{{\tilde h}_i}\left( t \right) \approx \exp \left( { - {\rm j}\frac{{4{{π}} }}{\lambda }{r_0}} \right) \cdot \exp \left( { - {\rm j}\frac{{{{π}} \Delta x_i^2}}{{2\lambda {r_0}}}} \right) \\ & \quad\quad\quad\ \cdot \exp \left( { - {\rm j}\frac{{2{{π}} {v^2}{{\left( {t - \displaystyle\frac{{\Delta {x_i}}}{{2v}}} \right)}^2}}}{{\lambda {r_0}}}} \right) \end{aligned} \right.\quad$

(5)

因而 ${\tilde h_{{\rm{mono}}}}\left( t \right)$ 与 ${\tilde h_i}\left( t \right)$ 间存在式(6)所示的关系，其中 $*$ 为卷积运算。

${\tilde h_i}\left( t \right) \!=\! \exp \left( { \!- {\rm j}\!\frac{{{{π}} \Delta x_i^2}}{{2\lambda {r_0}}}} \right) \!\cdot\! \delta \left( {t \!-\! \frac{{\Delta {x_i}}}{{2v}}} \right)\! *\! {\tilde h_{{\rm{mono}}}}\left( t \right)$

(6)

将式(6)进行Fourier变换，可得单基单通道SAR与接收通道i的系统函数关系：

$\begin{aligned} {\tilde H_i}\left( f \right) = & \exp \left( { - {\rm j}\frac{{{{π}} \Delta x_i^2}}{{2\lambda {r_0}}}} \right) \cdot \exp \left( { - {\rm j}2{{π}} \frac{{\Delta {x_i}}}{{2v}}f} \right) \\ &\cdot {\tilde H_{{\rm{mono}}}}\left( f \right) \end{aligned}$

(7)

单基单通道SAR到接收通道i的传递函数 ${\tilde G_i}\left( f \right)$ 为：

${\tilde G_i}\left( f \right) = \exp \left( { - {\rm j}\frac{{{{π}} \Delta x_i^2}}{{2\lambda {r_0}}}} \right) \cdot \exp \left( { - {\rm j}2{{π}} \frac{{\Delta {x_i}}}{{2v}}f} \right)$

(8)

基于上述分析，单基星载HRWS-SAR系统的方位向信号生成模型可由图2进行描述。方位向各通道信号在时域为单基单通道SAR信号经对应的相位偏移和时间延迟的结果，而在多普勒域为单基单通道SAR信号与对应的常数相位因子和线性相位因子相乘后的结果。PRF小于多普勒带宽时，方位向各通道信号为时域上的欠采样，将导致多普勒域的频谱混叠。

图 2 单基星载HRWS-SAR系统的方位向信号生成模型

Figure 2. Azimuth signal generating model in monostatic spaceborne HRWS-SAR

下载: 全尺寸图片幻灯片

2.2 双基星载HRWS-SAR系统的方位向信号模型

一般双基构型的星载HRWS-SAR系统中r_T0≠r_R0, t_fd≠0，不能通过对h_mono及h_i的泰勒级数展开进行2阶相位近似处理得到与式(6)、式(7)相似的表达式。本节将对式(2)进一步处理，推导一般双基构型星载HRWS-SAR系统中 ${h_{{\rm{mono}}}}\left( t \right)$ 及 ${h_i}\left( t \right)$ 的关系，进而构建其方位向信号生成模型。

引入点目标P的收发距离比函数 $C\left( t \right) =$ $\displaystyle\frac{{\sqrt {r_{{\rm{T}}0}^2 + {{\left( {vt - v{t_{{\rm{fd}}}}} \right)}^2}} }}{{\sqrt {r_{{\rm{R}}0}^2 + {{\left( {vt} \right)}^2}} }}$ ，式(2)等价于：

$\begin{aligned} {h_i}\left( t \right) = & \exp \Biggr( { - {\rm j}\frac{{2{{π}} }}{\lambda }\biggr( {C\left( t \right)\sqrt {r_{{\rm{R}}0}^2 + {{\left( {vt} \right)}^2}}}} \\ & + {{\sqrt {r_{{\rm{R}}0}^2 + {{\left( {vt - \Delta {x_i}} \right)}^2}} } \biggr)} \Biggr) \end{aligned}$

(9)

等效接收通道RX_equ的冲激响应函数为：

$\begin{aligned} & {h_{{\rm{mono}}}}\left( t \right) \\ & \quad =\exp \Biggr( { - {\rm j}\frac{{2{{π}} }}{\lambda }\left( {\left( {C\left( t \right) + 1} \right)\sqrt {r_{{\rm{R}}0}^2 + {{\left( {vt} \right)}^2}} } \right)} \Biggr)\quad\ \end{aligned}$

(10)

对式(9)、式(10)的泰勒级数展开进行2阶相位近似处理，可得：

$\left\{ \begin{aligned} &{h_i}\left( t \right) \approx \exp \left( { - {\rm j}\frac{{2{{π}} }}{\lambda }\left( {C\left( t \right) + 1} \right){r_{{\rm{R}}0}}} \right) \\ & \quad\quad\quad\ \cdot \exp \left( { - {\rm j}\frac{{{π}} }{{\lambda {r_{{\rm{R}}0}}}} \cdot \frac{{C\left( t \right)\Delta x_i^2}}{{C\left( t \right) + 1}}} \right) \\ & \quad\quad\quad\ \cdot \exp \Biggr( { - {\rm j}\frac{{{π}} }{{\lambda {r_{{\rm{R}}0}}}} \cdot \Big( {C^{} \left( t \right) + 1} \Big) }\\ & \quad\quad\quad\ {\cdot {v^2}{{\left( {t - \frac{{\Delta {x_i}}}{{\left( {C\left( t \right) + 1} \right)v}}} \right)}^2}} \Biggr)\\ & {h_{{\rm{mono}}}}\left( t \right) \approx \exp \left( { - {\rm j}\frac{{2{{π}} }}{\lambda }\left( {C\left( t \right) + 1} \right){r_{{\rm{R}}0}}} \right) \\ & \quad\quad\quad\quad\ \cdot \exp \left( { - {\rm j}\frac{{{π}} }{{\lambda {r_{{\rm{R}}0}}}} \cdot \left( {C\left( t \right) + 1} \right) \cdot {v^2}{t^2}} \right) \end{aligned} \right.$

(11)

在目标照射时间T_a内， $C\left( t \right)$ 的变化极小，用波束中心穿越时刻的取值C₀予以近似。容易得到接收通道i与等效接收通道RX_equ的冲激响应关系为：

$\begin{aligned} {h_i}\left( t \right) = & \exp \left( { - {\rm j}\frac{{{π}} }{{\lambda {r_{{\rm{R}}0}}}} \cdot \frac{{{C_0}\Delta x_i^2}}{{{C_0} + 1}}} \right) \\ & \ \cdot \delta \left( {t - \frac{{\Delta {x_i}}}{{\left( {{C_0} + 1} \right)v}}} \right) * {h_{{\rm{mono}}}}\left( t \right) \end{aligned}$

(12)

式(12)进行Fourier变换，可得等效接收通道RX_equ与接收通道i的系统函数关系：

$\begin{aligned} {H_i}\left( f \right) = & \exp \left( { - {\rm j}\frac{{{π}} }{{\lambda {r_{{\rm{R}}0}}}} \cdot \frac{{{C_0}\Delta x_i^2}}{{{C_0} + 1}}} \right) \\ & \cdot \exp \left( { - {\rm j}2{{π}} \frac{{\Delta {x_i}}}{{\left( {{C_0} + 1} \right)v}}f} \right) \cdot {H_{{\rm{mono}}}}\left( f \right) \end{aligned}$

(13)

等效接收通道RX_equ到接收通道i的传递函数为：

$\begin{aligned} {G_i}\left( f \right) = & \exp \left( { - {\rm j}\frac{{{π}} }{{\lambda {r_{{\rm{R}}0}}}} \cdot \frac{{{C_0}\Delta x_i^2}}{{{C_0} + 1}}} \right) \\ & \cdot \exp \left( { - {\rm j}2{{π}} \frac{{\Delta {x_i}}}{{\left( {{C_0} + 1} \right)v}}f} \right) \end{aligned}$

(14)

考察式(8)、式(14)，传递函数 ${G_i}\left( f \right)$ 与 ${\tilde G_i}\left( f \right)$ 可视为f及 $\Delta {x_i}$ 的二元函数，并存在如下关系：

${G_i}\left( {f,\Delta {x_i}} \right) = {\tilde G_i}\left( {f,\frac{2}{{\left( {{C_0} + 1} \right)}}\Delta {x_i}} \right)$

(15)

式(15)表明双基星载HRWS-SAR系统的方位向信号的生成模型可等效为一单基系统模型，只需将图2中的 $\Delta {x_i}$ 替换为 $2/{{\left( {{C_0} + 1} \right)}}\Delta {x_i}$ 即可予以描述，C₀=1时，双基系统退化为单基系统。

2.3 C(t)近似为C₀的合理性

式(12)、式(13)、式(14)是在 $C\left( t \right)$ 近似为C₀的基础上推导的结果，显然存在近似误差。上述近似误差进行理论上的严格定量分析非常复杂，然而可以从上述表达式中得到简单的定性结果。以式(14)为例，由于在双基星载HRWS-SAR系统中 $\Delta x_i^2 \ll {r_{{\rm{R}}0}}$ ，从而 $\exp \left( { - {\rm j}\displaystyle\frac{{{π}} }{{\lambda {r_{{\rm{R}}0}}}} \cdot \displaystyle\frac{{C\left( t \right)\Delta x_i^2}}{{C\left( t \right) + 1}}} \right)$ 可视为常数1。指数项 $\exp \left( { - {\rm j}2{{π}} \displaystyle\frac{{\Delta {x_i}}}{{\left( {{C_0} + 1} \right)v}}f} \right)$ 的相位近似误差约为 $\Delta \varphi \approx 2{{π}} \left| {\displaystyle\frac{{C\left( t \right) - {C_0}}}{{{C_0} + 1}}} \right| \cdot \left| {\displaystyle\frac{{\Delta {x_i}}}{{\left( {C\left( t \right) + 1} \right)v}}f} \right|$ ，在多普勒带宽B_fd范围内，令接收通道的长度为L_R, $\mathop {\max }\limits_{i = 1,2, \cdot \cdot \cdot ,M} \left| {\Delta {x_i}} \right|\! =\! \alpha {L_{\rm{R}}}$ ，则 $\left| {\displaystyle\frac{{\Delta {x_i}}}{{\left( {C\left( t \right) + 1} \right)v}}f} \right|\!<$ $\left| {\displaystyle\frac{{\alpha {L_a}}}{{\left( {C\left( t \right) + 1} \right)v}}{B_{{\rm{fd}}}}} \right| \approx 0.886\alpha$ 。受天线最小尺寸的限制，L_R不能过小即 $\alpha$ 不会太大，可合理假定 $\alpha$ 在10¹数量级。记 $\varepsilon \left( t \right) \!=\! \left| {\displaystyle\frac{{C\left( t \right) - {C_0}}}{{{C_0} + 1}}} \right|$ ，仿真分析表明 $\mathop {\max }\limits_{t \in \left( { - \frac{{{T_a}}}{2},\frac{{{T_a}}}{2}} \right)} \left( {\varepsilon \left( t \right)} \right)$ 一般不超过10^–3量级，因而 $\Delta \varphi$ 在 $2{{π}} \cdot {10^{ - 2}}$ 量级，为一极小相位。上述分析表明可以忽略式(14)的近似误差，即C₀是 $C\left( t \right)$ 的合理近似。

3. 方位向信号重构的矩阵求逆算法

文献[8]给出了单基HRWS-SAR系统方位向信号重构的矩阵求逆算法，由于双基HRWS-SAR系统在方位向信号模型上与单基系统的等效性，矩阵求逆算法在双基系统同样适用。

3.1 双基HRWS-SAR系统的矩阵求逆算法

矩阵求逆算法的理论依据是广义采样定理。在双基HRWS-SAR系统中，通过发射到接收通道i的传递函数，能够得到单基单通道SAR的信号 $S\left( f \right) = U\left( f \right) \cdot H\left( f \right)$ 在接收通道i的表达式 ${S_i}\left( f \right) =$ ${G_i}\left( f \right) \cdot S\left( f \right)$ 。对于方位向有M个通道的系统，在无重叠采样的情况下，可以得到 $S\left( f \right)$ 的M种独立表达，且采样率均为PRF。根据广义采样定理，能够恢复带宽最高为 $M \cdot {\rm{PRF}}$ 的信号 $S\left( f \right)$ 。

矩阵求逆算法主要包括3个步骤：

首先，构造系统的传递函数矩阵 ${{G}}\left( f \right)$ 及响应矩阵 ${\tilde{{S}}}\left( f \right)$ ：

${{G}}\left( f \right) = \left( {\begin{array}{*{20}{c}} {{G_1}\left( f \right)} & {{G_1}\left( {f + {\rm{PRF}}} \right)} & ·\!·\!· & {{G_1}\left( {f + \left( {M - 1} \right) \cdot {\rm{PRF}}} \right)}\\ {{G_2}\left( f \right)} & {{G_2}\left( {f + {\rm{PRF}}} \right)} & ·\!·\!· & {{G_2}\left( {f + \left( {M - 1} \right) \cdot {\rm{PRF}}} \right)}\\ \vdots & \vdots & \ddots & \vdots \\ {{G_M}\left( f \right)} & {{G_M}\left( {f + {\rm{PRF}}} \right)} & ·\!·\!· & {{G_M}\left( {f + \left( {M - 1} \right) \cdot {\rm{PRF}}} \right)} \end{array}} \right)$

(16)

${\tilde{{S}}}\left( f \right) = {\Big( {{S_1}\left( f \right),{S_2}\left( f \right), \cdots ,{S_M}\left( f \right)} \Big)^{\rm{T}}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\,\,$

(17)

然后，对 ${{G}}\left( f \right)$ 进行求逆运算，得到信号重构矩阵 ${{P}}\left( f \right)$ ：

${{P}}\left( f \right) = \left( {\begin{array}{*{20}{c}} {{P_1}\left( f \right)} & {{P_2}\left( f \right)} & ·\!·\!· & {{P_M}\left( f \right)}\\ {{P_1}\left( {f + {\rm{PRF}}} \right)} & {{P_2}\left( {f + {\rm{PRF}}} \right)} & ·\!·\!· & {{P_M}\left( {f + {\rm{PRF}}} \right)}\\ \vdots & \vdots & \ddots & \vdots \\ {{P_1}\left( {f + \left( {M - 1} \right) \cdot {\rm{PRF}}} \right)} & {{P_2}\left( {f + \left( {M - 1} \right) \cdot {\rm{PRF}}} \right)} & ·\!·\!· & {{P_M}\left( {f + \left( {M - 1} \right) \cdot {\rm{PRF}}} \right)} \end{array}} \right)$

(18)

最后，利用公式 ${{P}}\left( f \right) \cdot {{S}}\left( f \right) = {\big( {S\left( f \right),S\left( {f + } \right.$ ${ {\left. {{\rm{PRF}}} \right), ·\!·\!· ,S\left( {f + \left( {M - 1} \right) \cdot {\rm{PRF}}} \right)} \big)^{\rm{T}}}$ 即可重构出方位向信号的多普勒频谱。矩阵求逆算法进行方位向重构的原理框图及物理实现原理可参看文献[8]。

3.2 矩阵求逆算法的重构性能

星载HRWS-SAR系统的单通道信号带宽为PRF，采用矩阵求逆算法重构后的方位向信号带宽为 $M \cdot {\rm{PRF}}$ ，因而方位向信号重构必然影响到信噪比和方位模糊比这两个重要的SAR系统性能指标。

3.2.1 信噪比缩放因子文献[8]定义信噪比缩放因子表征方位向重构对信噪比的影响，其定义式及计算公式为：

${\varPhi _{{\rm{bf}}}} \!=\! \frac{{{\rm{SN}}{{\rm{R}}_{{\rm{in}}}}/{\rm{SN}}{{\rm{R}}_{{\rm{out}}}}}}{{\left( {{\rm{SN}}{{\rm{R}}_{{\rm{in}}}}/{\rm{SN}}{{\rm{R}}_{{\rm{out}}}}} \right)\left| {_{{\rm{PR}}{{\rm{F}}_{{\rm{uni}}}}}} \right.}} \!=\! \frac{{\displaystyle\sum\limits_{j = 1}^M {{\mathop{\rm E}\nolimits} \left( {{{\left| {{P_j}\left( f \right)} \right|}^2}} \right)} }}{N}$

(19)

其中，SNR_in, SNR_out为方位向信号重构前后的信噪比，PRF_uni表示方位向均匀采样时的PRF, ${P_j}\left( f \right)$ 对应于式(18)中的第j行，为作用于接收通道j的重构函数， ${\mathop{\rm E}\nolimits} \left( \cdot \right)$ 为求期望运算。 ${\varPhi _{{\rm{bf}}}}$ 表征了SNR_in与SNR_out的比值随PRF的变化规律。由式(19)可知，越小的 ${\varPhi _{{\rm{bf}}}}$ 意味着更多的信噪比改善。

${\varPhi _{{\rm{bf}}}}$ 还可以通过式(20)进行计算：

${\varPhi _{{\rm{bf}}}} = \frac{{\displaystyle\sum\limits_{j = 1}^M {{\lambda _j}\left( f \right)} }}{N}$

(20)

其中， ${\lambda _j}\left( f \right)$ 为矩阵 ${{P}}\left( f \right) \cdot {{{P}}^{\rm{H}}}\left( f \right)$ 的特征值， ${{{P}}^{\rm{H}}}\left( f \right)$ 为 $\, {{P}}\left( f \right)$ 的共轭转置。

3.2.2 方位模糊比文献[8]详细推导了单基HRWS-SAR系统的方位模糊比(AASR)计算公式，与之类似可推导出双基HRWS-SAR系统的AASR计算公式，可概括为如下4个计算式：

$\begin{aligned} \\ {e_k}\left( f \right) = & {A_k}\left( f \right)\sum\limits_m^{} {\sum\limits_{j = 1}^M {{G_j}\left( {f + k \cdot {\rm{PRF}}} \right)} } \\ \text{} & \ \cdot {P_j}\left( {f + m \cdot {\rm{PRF}}} \right) \end{aligned}$

(21)

$\begin{aligned} {e_\Sigma }\left( f \right) = & \sum\limits_{k = - \infty ,k \ne 0}^\infty {{e_k}\left( f \right)} \\ = & \sum\limits_{k = - \infty ,k \ne 0}^\infty {\Biggr( {{A_k}\left( f \right)\sum\limits_m^{} {\sum\limits_{j = 1}^M {{G_j}\left( {f + k \cdot {\rm{PRF}}} \right)} } }} \\ \text{ } & {\cdot {P_j}\big( {f + m \cdot {\rm{PRF}}}\big)}\Biggr) \end{aligned}\quad\quad$

(22)

${p_{\rm{s}}} = {\rm{E}}\left( {{{\Big| {A\left( f \right) \cdot {\rm{rect}}\left( {f/{{I}}} \right)} \Big|}^2}} \right)\quad\quad\quad\quad\quad\quad\quad \$

(23)

${\rm{AASR}} = \frac{{{\rm{E}}\left( {{{\left| {{e_\Sigma }\left( f \right)} \right|}^2}} \right)}}{{{p_{\rm{s}}}}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\$

(24)

$A\left( f \right)$ 为发射天线和接收通道合成的天线方向图，双基系统中t_c≠0时 $A\left( f \right) \ne A\left( { - f} \right)$ ，这是导致双基系统AASR计算公式不同于单基系统的根本原因。 ${A_k}\left( f \right)$ 为区间 $\left[ { - {\rm{PRF}}/{2}{\rm{,}}\ {\rm{PRF}}/{2}} \right] + k \cdot {\rm{PRF}}$ 上的 $A\left( f \right)$ , ${e_k}\left( f \right)$ 为区间 $\left[ { - {\rm{PRF}}/{2}{\rm{,}}\ {\rm{PRF}}/{2}} \right] + k \cdot {\rm{PRF}}$ 内的信号产生的方位模糊信号，I为区间 $\left[ - M \right.$ $\left. \cdot {{\rm{PRF}}/{2}}{\rm{,}}{M \cdot {\rm{PRF}}/{2}} \right]$ , p_s为信号能量。上式中m的取值规则为：k>0时， $\max \left( {M - k + 1,1} \right) \le m \le N$ ; k<0时， $1 \le m \le - k$ 。

4. 仿真分析

本节对几种典型的双基构型星载HRWS-SAR系统进行方位向信号重构进行仿真，验证矩阵求逆算法的正确性，并分析算法的重构性能。表1列出了系统的方位向系统参数，对于单基系统容易计算出多普勒带宽B_fd=5.61 kHz，照射时间T_a=1.05 s。

表 1 双基星载HRWS-SAR系统的方位向系统参数

Table 1. Azimuth parameters in bistatic spaceborne HRWS-SAR

参数	数值
发射天线方位尺寸(m)	2.4
接收通道方位尺寸(m)	2.4
接收通道数目	5
轨道高度(km)	600
接收天线最短距离(km)	700
方位向速度(m/s)	7600
载波波长(cm)	3.1

下载: 导出CSV

| 显示表格

表2列出了7种典型的双基构型。表2中采用发射天线和接收天线的零多普勒时间差t_fd与轨道距离L对双基构型进行表征：t_fd=0时系统工作在平飞模式，L=0时系统工作在顺飞模式，L<0时发射天线位于测绘带近端，反之L>0时接收天线位于测绘带近端，构型Ⅰ中t_fd=0且L=0退化为单基系统。

表 2 双基星载HRWS-SAR系统的7种双基构型

Table 2. Seven configurations for bistatic spaceborne HRWS-SAR

构型编号	t_fd (s)	L (km)
Ⅰ	0	0
Ⅱ	1	0
Ⅲ	10	0
Ⅳ	0	10
Ⅴ	0	100
Ⅵ	0	–10
Ⅶ	0	–100

下载: 导出CSV

| 显示表格

4.1 C₀对C(t)的近似性能

将 $C\left( t \right)$ 近似为C₀是构建双基星载HRWS-SAR系统方位向信号模型及建立矩阵求逆算法的关键步骤，该近似的合理性直接影响到模型及算法的正确性，第3.3小节定性分析了该近似的合理性，本节结合具体的仿真条件予以验证。图3给出了各双基构型下在照射时间范围内的 $C\left( t \right)$ 及 $\varepsilon \!\left( t \right)$ 的变化曲线，图3中对近似误差相对较大的构型Ⅱ、构型Ⅲ采用蓝色线标注，其他构型使用红色线。图3(a)中各双基构型下 $C\left( t \right)$ 曲线近似为直线，直观地的反映出 $C\left( t \right)$ 近似为常数；而图3(b)、图3(c)表明 $\varepsilon \left( t \right)$ 在各双基构型下均小于10^–3，验证了C₀为 $C\left( t \right)$ 的合理近似。图3也表明出目标照射时间T_a及收发天线的零多普勒时间差t_fd是影响 $\varepsilon\! \left( t \right)$ 的主要因素， $\mathop {\max }\limits_t \left( {\varepsilon \left( t \right)} \right)$ 的取值与T_a及t_fd的取值呈正相关性。

图 3 照射时间T_a范围内的

$C\left( t \right)$ 及

$\varepsilon \! \left( t \right)$ 变化曲线

Figure 3.

$C\left( t \right)$ and

$\varepsilon \! \left( t \right)$ variation curve in irradiation time T_a

下载: 全尺寸图片幻灯片

4.2 方位向信号重构结果

各接收通道的信噪比设置为20 dB，取PRF=2.0 kHz，对图1所示的点目标P方位向信号重构过程进行仿真，其结果如图4和图5所示。

图 4 构型Ⅰ方位向信号重构前后的成像结果

Figure 4. Unreconstructed and reconstructed azimuth signal Doppler spectrum for bistatic configuration Ⅰ

下载: 全尺寸图片幻灯片

图 5 方位向信号重构后的成像结果

Figure 5. Imaging for reconstructed azimuth signal Doppler spectrum

下载: 全尺寸图片幻灯片

图4(a)、图4(b)中，由于PRF小于多普勒带宽B_fd，单个接收通道的多普勒频谱有严重的混叠现象，图4(c)则表明采用矩阵求逆算法进行方位向信号重构消除了多普勒频谱中的混叠现象。图4(c)及图5给出了各双基构型下的方位向信号重构后的成像结果，验证了矩阵求逆算法对一般双基构型的适用性，同时也表明重构性能受双基构型的影响，尤其是构型Ⅴ、Ⅶ与其他构型性能差异较为明显。

4.3 方位向信号重构性能

将PRF设置在区间1.4 kHz≤PRF≤2.8 kHz，采用表1的系统参数和表2的双基构型，利用式(20)、式(24)可以得到方位向信号的重构性能曲线，如图6所示。为了便于图6的分析，首先计算各双基构型下的C₀及典型PRF值，计算结果为表3，其中PRF_uni为均匀采样时的PRF值，PRF_rep1及PRF_rep2为PRF范围内出现重叠采样的两个PRF值。构型Ⅰ的PRF_uni, PRF_rep1和PRF_rep2在图6中予以标注。

图 6 方位向信号重构性能曲线

Figure 6. Azimuth signal reconstruction performance curve

下载: 全尺寸图片幻灯片

表 3 C₀及典型PRF值

Table 3. C₀ and typical PRF

构型编号	C₀	PRF_uni (kHz)	PRF_rep1 (kHz)	PRF_rep2 (kHz)
Ⅰ	1.0000	2.533	1.583	2.111
Ⅱ	1.0001	2.533	1.583	2.111
Ⅲ	1.0059	2.540	1.588	2.117
Ⅳ	0.9927	2.524	1.577	2.103
Ⅴ	0.9345	2.450	1.531	2.041
Ⅵ	1.0074	2.542	1.589	2.118
Ⅶ	1.0805	2.635	1.647	2.196

下载: 导出CSV

| 显示表格

对比图6和表3，可得到如下结论：

(1) 均匀采样时PRF=PRF_uni，方位向信号的重构性能达到局部最优；重叠采样时PRF=PRF_rep，信噪比缩放因子趋向于无穷大，矩阵求逆算法将不能实现信号重构；PRF位于PRF_rep附近时，矩阵求逆算法的性能急剧下降。从矩阵理论的观点分析，PRF=PRF_rep时，传递函数 ${{G}}\left( f \right)$ 为非满秩矩阵，因而 ${{G}}\left( f \right)$ 及重构矩阵 ${{P}}\left( f \right)$ 的条件数为无穷大，此时信噪比缩放因子 ${\varPhi _{{\rm{bf}}}}$ 也为无穷大，从而无法完成方位向信号的重构。PRF趋于PRF_rep时，重构矩阵 ${{P}}\left( f \right)$ 的条件数急剧增大，方位向信号的重构性能也急剧下降。

(2) C₀值的差异直接导致同一PRF时方位向信号重构性能差异。与其他构型相比构型Ⅴ、Ⅶ的C₀值差异较大因而构性能差异也大，与图5的结论相一致。根本原因在于与双基HRWS-SAR系统等效的单基系统，通道间的方位向距离为 $2/{{\left( {{C_0} + 1} \right)}}$ $\cdot \Delta {x_i}$ , C₀的取值直接影响到方位向采样的均匀性，进而影响到矩阵求逆算法的重构性能。

5. 结束语

本文通过分析单基与双基星载HRWS-SAR系统的方位向信号模型，给出了适用于一般双基构型星载HRWS-SAR系统方位向信号重构的矩阵求逆算法，并使用信噪比缩放因子及方位模糊比两个指标分析了该算法的重构性能。本文的分析方法对其他方位向信号重构算法推广到双基星载HRWS-SAR系统具有借鉴意义。双基星载HRWS-SAR系统方位向信号重构的工程应用中，需改进矩阵求逆算法以改善重叠采样附近的重构性能。

图 1 GF-3星载全极化SAR图像^[11]

Figure 1. GF-3 spaceborne fully polarized SAR image^[11]

下载: 全尺寸图片幻灯片

图 2 用色彩表征视向形变量的SAR图像^[13]

Figure 2. SAR image with color representation of line-of-sight deformation^[13]

下载: 全尺寸图片幻灯片

图 3 用颜色表征地物散射方向性的SAR图像^[14]

Figure 3. SAR image with color representation of ground scattering directivity^[14]

下载: 全尺寸图片幻灯片

图 4 干涉SAR成像原理及维苏威火山成像结果^[16]

Figure 4. InSAR imaging principle and imaging result of Vesuvius volcano^[16]

下载: 全尺寸图片幻灯片

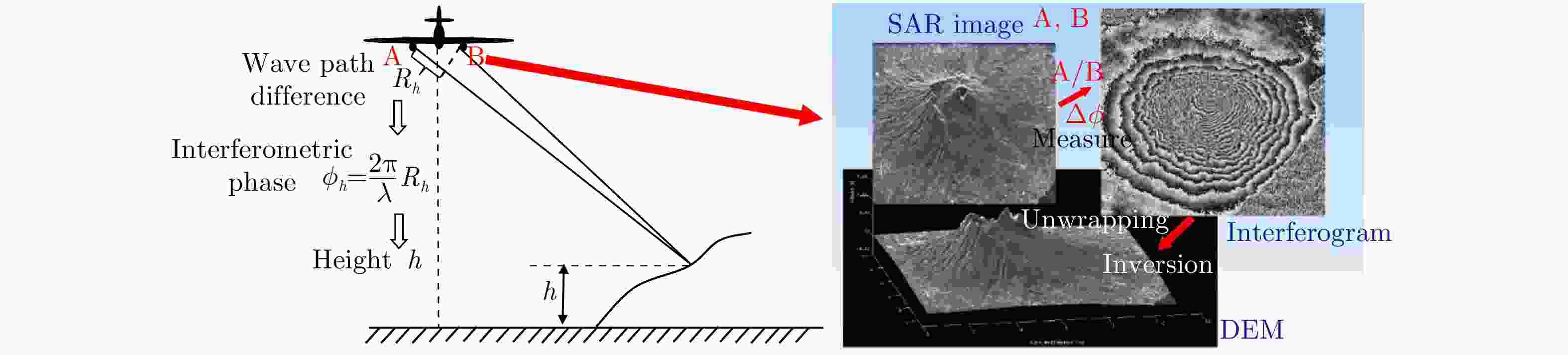
图 5 极化干涉SAR原理与地物三维成像结果^[17]

Figure 5. Principle of Pol-InSAR and three-dimensional imaging result

下载: 全尺寸图片幻灯片

图 6 圣地亚国家实验室的视频SAR成像结果^[19]

Figure 6. Video SAR imaging results of Sandia national laboratories^[19]

下载: 全尺寸图片幻灯片

图 7 不同频段地物SAR图像差异的直观理解

Figure 7. Intuitive understanding of the differences between the SAR images of the ground objects in different frequency bands

下载: 全尺寸图片幻灯片

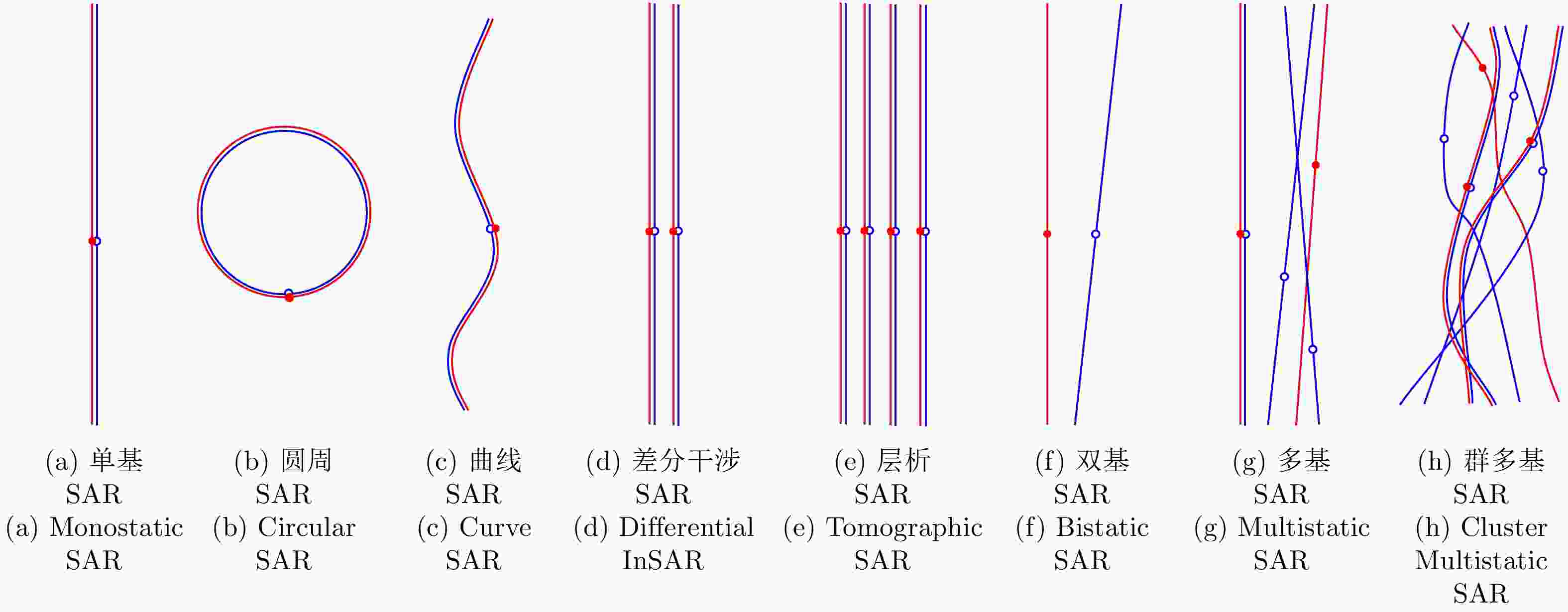
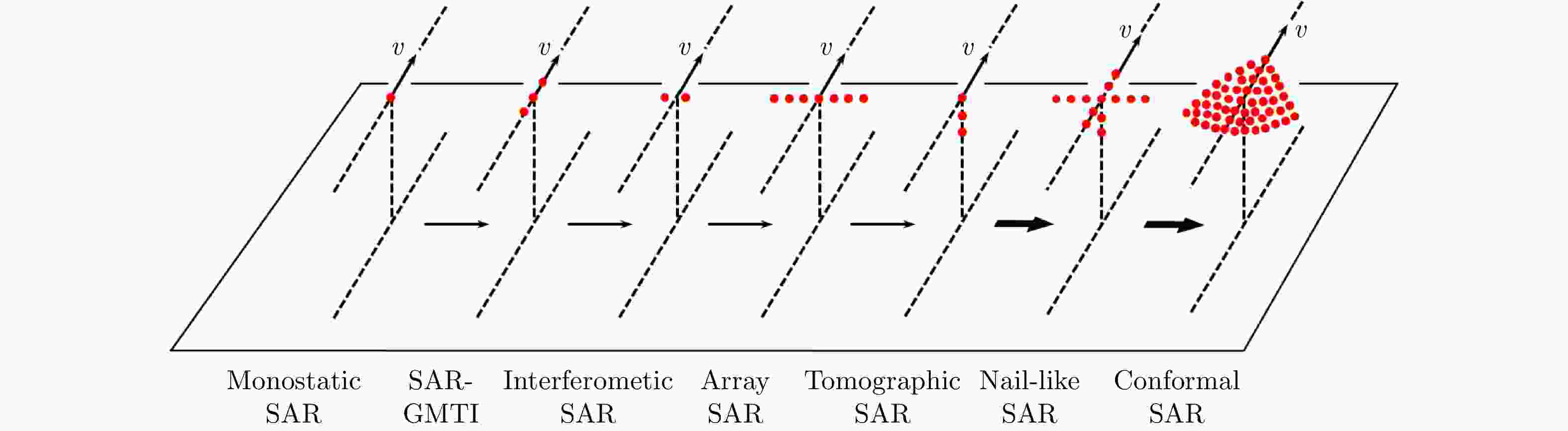
图 8 孔径流形的演变^②

Figure 8. Evolution of the aperture manifold

下载: 全尺寸图片幻灯片

图 9 圆周SAR与条带SAR成像结果对比^[23]

Figure 9. Comparison of imaging results of circular SAR and stripmap SAR^[23]

下载: 全尺寸图片幻灯片

图 10 圆周SAR试验情况^[24]

Figure 10. Experiment of circular SAR^[24]

下载: 全尺寸图片幻灯片

图 11 复杂机动轨迹SAR的示意图

Figure 11. Schematic diagrams of complex maneuvering SAR

下载: 全尺寸图片幻灯片

图 12 多航过层析SAR

Figure 12. Multi-pass tomographic SAR

下载: 全尺寸图片幻灯片

图 13 单平台多通道SAR示意图

Figure 13. Diagrams of single platform multi-channel SAR

下载: 全尺寸图片幻灯片

图 14 立体分布地物的三维成像^[38]

Figure 14. Three-dimensional imaging of stereo distributed ground objects^[38]

下载: 全尺寸图片幻灯片

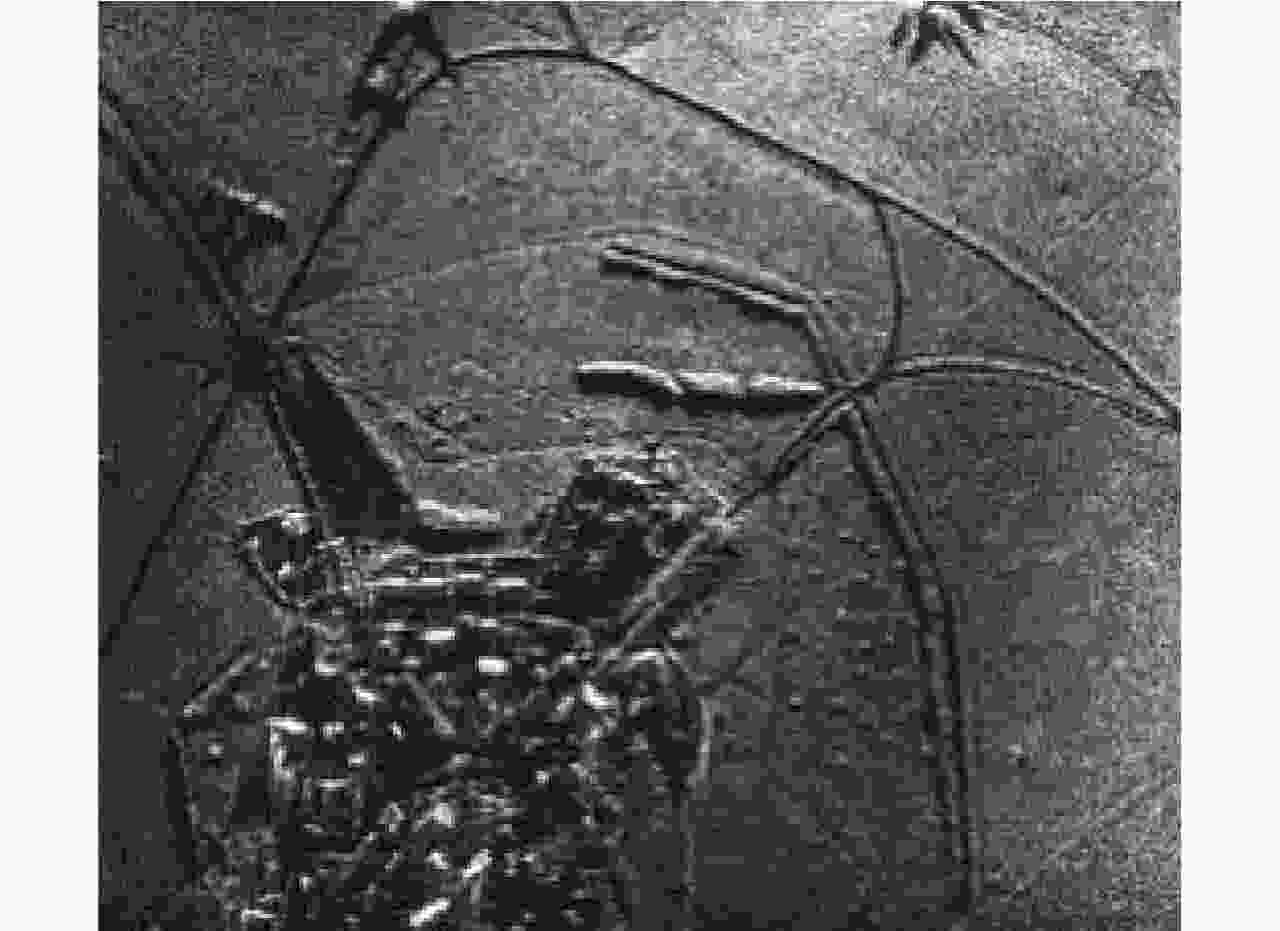
图 15 建筑群的三维成像^[25]

Figure 15. Three-dimensional imaging of buildings

下载: 全尺寸图片幻灯片

图 16 多通道SAR演进图^③

Figure 16. Multi-channel SAR evolution map

下载: 全尺寸图片幻灯片

图 17 双多基地SAR系统形态

Figure 17. Morphology of Bistatic/Multistatic SAR

下载: 全尺寸图片幻灯片

图 18 单双基SAR图像明暗关系差异^[47]

Figure 18. Difference in light-dark relationship between monostatic and bistatic SAR images^[47]

下载: 全尺寸图片幻灯片

图 19 聚束式双基SAR试验^[48]

Figure 19. Experiment of spotlight bistatic SAR^[48]

下载: 全尺寸图片幻灯片

图 20 机载双基侧视SAR试验^[49]

Figure 20. Experiment of airborne bistatic side-looking SAR^[49]

下载: 全尺寸图片幻灯片

图 21 星机双基侧视SAR试验^[50]

Figure 21. Experiment of spaceborne/airborne bistatic side-looking SAR^[50]

下载: 全尺寸图片幻灯片

图 22 国内首幅机载双基侧视SAR图像^[51]

Figure 22. The first airborne bistatic side-looking SAR image in China^[51]

下载: 全尺寸图片幻灯片

图 23 外辐射源双基SAR试验^[52]

Figure 23. Experiment of passive bistatic SAR^[52]

下载: 全尺寸图片幻灯片

图 24 机载双基前视SAR图像^[61]

Figure 24. Airborne bistatic forward-looking SAR image^[61]

下载: 全尺寸图片幻灯片

图 25 星机双基地后视SAR试验^[63]

Figure 25. Experiment of spaceborne/airborne bistatic backward-looking SAR^[63]

下载: 全尺寸图片幻灯片

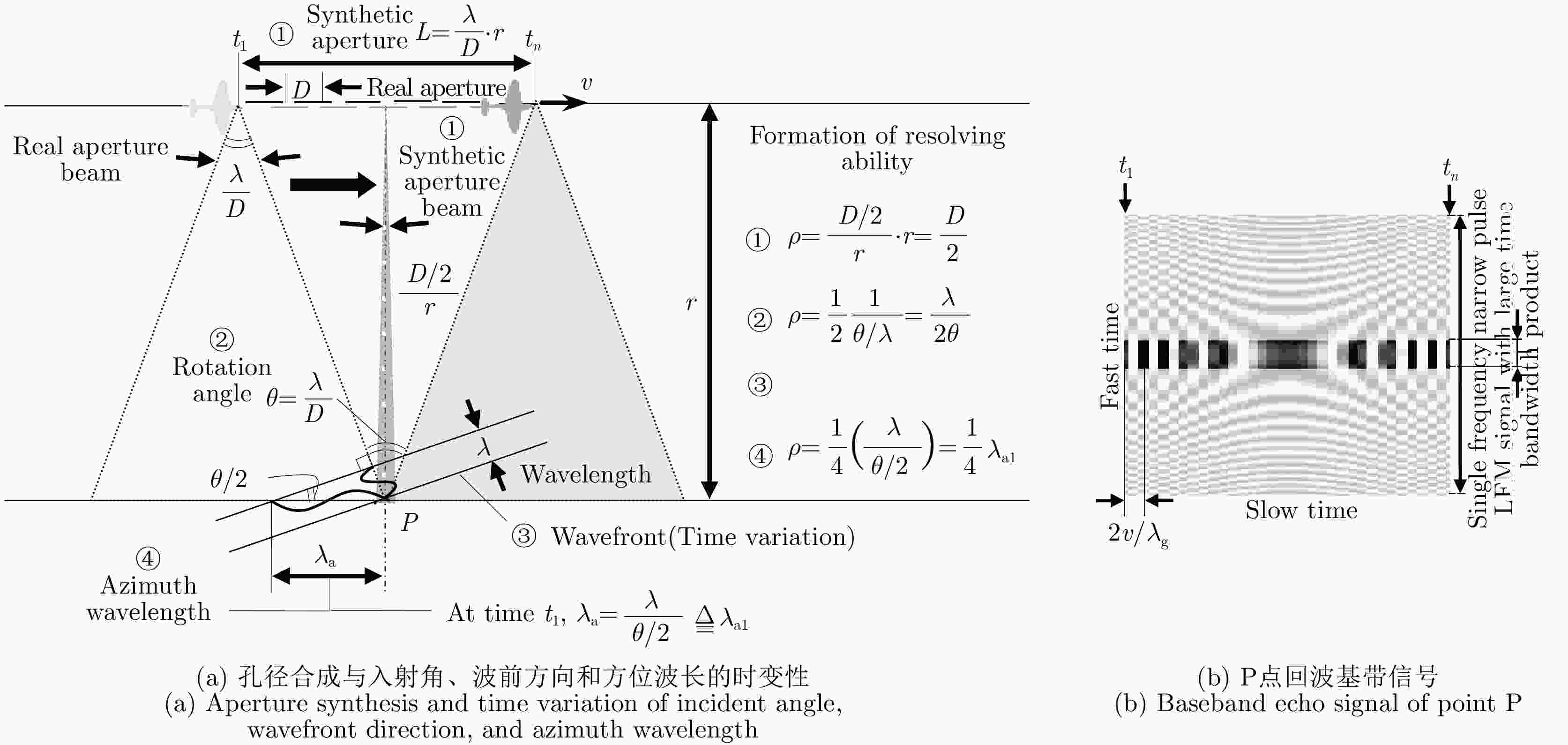
图 26 合成孔径原理的4种不同解释^⑤

Figure 26. Four different interpretations of synthetic aperture principle

下载: 全尺寸图片幻灯片

图 27 扫描波束锐化技术的交汇船只分辨试验^[82]

Figure 27. Resolving ships experiment of scanning beam sharpening^[82]

下载: 全尺寸图片幻灯片

图 28 扫描波束锐化技术的面目标成像试验^[82]

Figure 28. Surface target imaging experiment of scanning beam sharpening^[82]

下载: 全尺寸图片幻灯片

图 29 电磁涡旋成像的可行性验证^[96]

Figure 29. Feasibility verification of electromagnetic vortex imaging^[96]

下载: 全尺寸图片幻灯片

图 30 支撑成长识别能力的主要机制

Figure 30. The main mechanisms that support growth recognition

下载: 全尺寸图片幻灯片

图 31 雷达对地成像技术发展的外部因素

Figure 31. External influencing factors for the development of radar ground imaging technology

下载: 全尺寸图片幻灯片

图 32 雷达对地成像技术发展的内部因素

Figure 32. Internal influencing factors for the development of radar ground imaging technology

下载: 全尺寸图片幻灯片

参考文献(106)

[1]	吴一戎, 朱敏慧. 合成孔径雷达技术的发展现状与趋势[J]. 遥感技术与应用, 2000, 15(2): 121–123. doi: 10.3969/j.issn.1004-0323.2000.02.012 WU Yirong and ZHU Minhui. The developing status and trends of synthetic aperture radar[J]. Remote Sensing Technology and Application, 2000, 15(2): 121–123. doi: 10.3969/j.issn.1004-0323.2000.02.012
[2]	MOREIRA A, PRATS-IRAOLA P, YOUNIS M, KRIEGER G, HAJNSEK I, and PAPATHANASSIOU K P. A tutorial on synthetic aperture radar[J]. IEEE Geoscience and Remote Sensing Magazine, 2013, 1(1): 6–43. doi: 10.1109/MGRS.2013.2248301
[3]	魏钟铨. 合成孔径雷达卫星[M]. 北京: 科学出版社, 2001. WEI Zhongquan. Synthetic Aperture Radar Satellite[M]. Beijing: Science Press, 2001.
[4]	杨建宇. 雷达技术发展规律和宏观趋势分析[J]. 雷达学报, 2012, 1(1): 19–27. doi: 10.3724/SP.J.1300.2012.20010 YANG Jianyu. Development laws and macro trends analysis of radar technology[J]. Journal of Radars, 2012, 1(1): 19–27. doi: 10.3724/SP.J.1300.2012.20010
[5]	TURKAR V, DEO R, RAO Y S, MOHAN S, and DAS A. Classification accuracy of multi-frequency and multi-polarization SAR images for various land covers[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(3): 936–941. doi: 10.1109/JSTARS.2012.2192915
[6]	JIN Yaqiu and XU Feng. Polarimetric Scattering and SAR Information Retrieval[M]. Singapore: John Wiley & Sons Singapore Pte. Ltd., 2013.
[7]	董庆, 郭华东, 王长林. 多波段多极化合成孔径雷达的海洋学应用[J]. 地球科学进展, 2001, 16(1): 93–97. doi: 10.3321/j.issn:1001-8166.2001.01.017 DONG Qing, GUO Huadong, and WANG Changlin. Oceanographic survey of multi-band and multi-polarization synthetic aperture radar[J]. Advance in Earth Sciences, 2001, 16(1): 93–97. doi: 10.3321/j.issn:1001-8166.2001.01.017
[8]	王雪松. 雷达极化技术研究现状与展望[J]. 雷达学报, 2016, 5(2): 119–131. doi: 10.12000/JR16039 WANG Xuesong. Status and prospects of radar polarimetry techniques[J]. Journal of Radars, 2016, 5(2): 119–131. doi: 10.12000/JR16039
[9]	SUN Jili, YU Weidong, and DENG Yunkai. The SAR payload design and performance for the GF-3 mission[J]. Sensors, 2017, 17(10): 2419. doi: 10.3390/s17102419
[10]	宋国栋, 李建新, 张金平, 高铁. 新型双极化波导缝隙天线研究[J]. 现代雷达, 2010, 32(12): 67–71. doi: 10.3969/j.issn.1004-7859.2010.12.015 SONG Guodong, LI Jianxin, ZHANG Jinping, and GAO Tie. A study on the novel waveguide slotted antenna with dual-polarization[J]. Modern Radar, 2010, 32(12): 67–71. doi: 10.3969/j.issn.1004-7859.2010.12.015
[11]	WANG Yu, YU Weidong, and WANG Chunle. A hierarchical extension of a multiple-component scattering model with unitary transformation of the coherency matrix[J]. Remote Sensing Letters, 2019, 10(11): 1047–1056. doi: 10.1080/2150704X.2019.1646933
[12]	WANG Jili, YU Weidong, DENG Yunkai, WANG R, WANG Yingjie, ZHANG Heng, and ZHENG Mingjie. Demonstration of time-series InSAR processing in Beijing using a small stack of gaofen-3 differential interferograms[J]. Journal of Sensors, 2019, 2019: 4204580.
[13]	王超, 张红, 刘智, 陈锁忠, 闾国年. 苏州地区地面沉降的星载合成孔径雷达差分干涉测量监测[J]. 自然科学进展, 2002, 12(6): 621–624. doi: 10.3321/j.issn:1002-008X.2002.06.012 WANG Chao, ZHANG Hong, LIU Zhi, CHEN Suozhong, and LÜ Guonian. Differential interferometry and monitoring of ground subsidence by satellite-borne synthetic aperture radar in Suzhou[J]. Progress in Natural Science, 2002, 12(6): 621–624. doi: 10.3321/j.issn:1002-008X.2002.06.012
[14]	TENG Fei, HONG Wen, LIN Yun, HAN Bing, WANG Yanping, SHEN Wenjie, and FENG Shanshan. An anisotropic scattering analysis method based on likelihood ratio using circular Sar Data[C]. 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Janpan, 2019: 477–480.
[15]	FERRETTI A, MONTI-GUARNIERI A, PRATI C, ROCCA F, and MASSONET D InSAR principles: Guidelines for SAR interferometry processing and interpretation[R]. ESA TM-19, 2007.
[16]	JONES H G and VAUGHAN R A. Remote Sensing of Vegetation: Principles, Techniques, and Applications[M]. Oxford: Oxford University Press, 2010.
[17]	PAPATHANASSIOU K P and CLOUDE S R. Single-baseline polarimetric SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(11): 2352–2363. doi: 10.1109/36.964971
[18]	DAMINI A, BALAJI B, PARRY C, and MANTLE V. A videoSAR mode for the x-band wideband experimental airborne radar[C]. The SPIE 7699, Algorithms for Synthetic Aperture Radar Imagery XVⅡ, Orlando, USA, 2010: 76990E.
[19]	Sandia National Laboratories: Infrared-VideoSAR comparison[EB/OL]. https://www.sandia.gov/radar/video/index.html, 2019.
[20]	胡睿智. 视频合成孔径雷达成像理论与关键技术研究[D]. [博士论文], 电子科技大学, 2018. HU Ruizhi. Research on imaging theory and key technology of video synthetic aperture radar[D]. [Ph.D. dissertation], University of Electronic Science and Technology of China, 2018.
[21]	ROSA R A S, FERNANDES D, NOGUEIRA J B, and WIMMER C. Automatic change detection in multitemporal X- and P-band SAR images using Gram-Schmidt process[C]. 2015 IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy, 2015: 2797–2800.
[22]	杨建宇. 双基合成孔径雷达[M]. 北京: 国防工业出版社, 2017. YANG Jianyu. Bistatic Synthetic Aperture Radar[M]. Beijing: National Defense Industry Press, 2017.
[23]	洪文. 圆迹SAR成像技术研究进展[J]. 雷达学报, 2012, 1(2): 124–135. doi: 10.3724/SP.J.1300.2012.20046 HONG Wen. Progress in circular SAR imaging technique[J]. Journal of Radars, 2012, 1(2): 124–135. doi: 10.3724/SP.J.1300.2012.20046
[24]	CHEN Leping, AN Daoxiang, and HUANG Xiaotao. A backprojection-based imaging for circular synthetic aperture radar[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(8): 3547–3555. doi: 10.1109/JSTARS.2017.2683497
[25]	丁赤飚, 仇晓兰, 徐丰, 梁兴东, 焦泽坤, 张福博. 合成孔径雷达三维成像——从层析、阵列到微波视觉[J]. 雷达学报, 2019, 8(6): 693–709. doi: 10.12000/JR19090 DING Chibiao, QIU Xiaolan, XU Feng, LIANG Xingdong, JIAO Zekun, and ZHANG Fubo. Synthetic aperture radar three-dimensional imaging——from TomoSAR and array InSAR to microwave vision[J]. Journal of Radars, 2019, 8(6): 693–709. doi: 10.12000/JR19090
[26]	孙龙, 邬伯才, 沈明星, 江凯, 鲁加国. 机载UWB数字阵列SAR系统技术研究[J]. 雷达科学与技术, 2017, 15(2): 171–177, 184. doi: 10.3969/j.issn.1672-2337.2017.02.011 SUN Long, WU Bocai, SHEN Mingxing, JIANG Kai, and LU Jiaguo. Research on UWB airborne digital array SAR technology[J]. Radar Science and Technology, 2017, 15(2): 171–177, 184. doi: 10.3969/j.issn.1672-2337.2017.02.011
[27]	代大海, 邢世其, 王玺, 庞礡. 数字阵列合成孔径雷达[M]. 北京: 国防工业出版社, 2017. DAI Dahai, XING Shiqi, WANG Xi, and PANG Bo. Digital Array Synthetic Aperture Radar[M]. Beijing: National Defense Industry Press, 2017.
[28]	ZHANG Jiajia, SUN Guangcai, XING Mengdao, BAO Zheng, and FANG Zhou. An efficient signal reconstruction algorithm for stepped frequency MIMO-SAR in the spotlight and sliding spotlight modes[J]. International Journal of Antennas and Propagation, 2014, 2014: 329340.
[29]	雷万明, 许道宝, 余慧, 刘颖. 距离向DBF-SAR自适应SCORE处理研究[J]. 现代雷达, 2019, 41(9): 37–40. LEI Wanming, XU Daobao, YU Hui, and LIU Ying. A study on adaptive SCORE processing for range DBF-SAR[J]. Modern Radar, 2019, 41(9): 37–40.
[30]	CERUTTI-MAORI D, KLARE J, BRENNER A R, and ENDER J H G. Wide-area traffic monitoring with the SAR/GMTI system PAMIR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(10): 3019–3030. doi: 10.1109/TGRS.2008.923026
[31]	WEIß M, PETERS O, and ENDER J. First flight trials with ARTINO[C]. The 7th European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2008: 187–190.
[32]	雷万明, 赵敬亮. 大带宽高分辨力多通道SAR频谱重构[J]. 宇航学报, 2011, 32(10): 2210–2215. doi: 10.3873/j.issn.1000-1328.2011.10.018 LEI Wanming and ZHAO Jingliang. Doppler signal reconstruction of multichannel wide bandwidth SAR with high resolution[J]. Journal of Astronautics, 2011, 32(10): 2210–2215. doi: 10.3873/j.issn.1000-1328.2011.10.018
[33]	WU Youming, YU Ze, XIAO Peng, and LI Chunsheng. Suppression of azimuth ambiguities in spaceborne SAR images using spectral selection and extrapolation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(10): 6134–6147.
[34]	洪文, 王彦平, 林赟, 谭维贤, 吴一戎. 新体制SAR三维成像技术研究进展[J]. 雷达学报, 2018, 7(6): 633–654. doi: 10.12000/JR18109 HONG Wen, WANG Yanping, LIN Yun, TAN Weixian, and WU Yirong. Research progress on three-dimensional SAR imaging technique[J]. Journal of Radars, 2018, 7(6): 633–654. doi: 10.12000/JR18109
[35]	MAHAFZA B R and SAJJADI M. Three-dimensional SAR imaging using linear array in transverse motion[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(1): 499–510. doi: 10.1109/7.481296
[36]	WEIB M and ENDER J H G. A 3D imaging radar for small unmanned airplanes - ARTINO[C]. The European Radar Conference, Paris, Frend, 2005: 209–212.
[37]	SHI Jun, PENG Zuoyong, REN Congyue, FAN Ling, and ZHANG Xiaoling. DEM estimation for LASAR based on variational model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(2): 978–995. doi: 10.1109/TGRS.2016.2617402
[38]	SHI Jun, ZHANG Xiaoling, YANG Jianyu, et al. APC trajectory design for “One-Active” linear-array three-dimensional imaging SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(3): 1470–1486. doi: 10.1109/TGRS.2009.2031430
[39]	SHI Jun, ZHANG Xiaoling, YANG Jianyu, and WANG Yinbo. Surface-tracing-based LASAR 3-D imaging method via Multiresolution approximation[J].IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(11): 3719–3730. doi: 10.1109/TGRS.2008.2001170
[40]	ZHANG Siqian, DONG Ganggang, and KUANG Gangyao. Matrix completion for downward-looking 3-D SAR imaging with a random sparse linear array[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(4): 1994–2006. doi: 10.1109/TGRS.2017.2771826
[41]	ZHANG Siqian, ZHU Yutao, DONG Ganggang, and KUANG Gangyao. Truncated SVD-based compressive sensing for downward-looking three-dimensional SAR imaging with uniform/nonuniform linear array[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(9): 1853–1857. doi: 10.1109/LGRS.2015.2431254
[42]	ZHANG Siqian, DONG Ganggang, and KUANG Gangyao. Superresolution downward-looking linear array three-dimensional SAR imaging based on two-dimensional compressive sensing[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(6): 2184–2196. doi: 10.1109/JSTARS.2016.2549548
[43]	LI Hang, LIANG Xingdong, ZHANG Fubo, DING Chibiao, and Wu Yirong. A novel 3-D reconstruction approach based on group sparsity of array InSAR[J]. Scientia Sinica Informationis, 2018, 48(8): 1051–1064. doi: 10.1360/N112017-00023
[44]	李杭, 梁兴东, 张福博, 吴一戎. 基于高斯混合聚类的阵列干涉SAR三维成像[J]. 雷达学报, 2017, 6(6): 630–639. doi: 10.12000/JR17020 LI Hang, LIANG Xingdong, ZHANG Fubo, and WU Yirong. 3D imaging for array InSAR based on Gaussian mixture model clustering[J]. Journal of Radars, 2017, 6(6): 630–639. doi: 10.12000/JR17020
[45]	LOPEZ-DEKKER P, MALLORQUI J J, SERRA-MORALES P, and SANZ-MARCOS J. Phase synchronization and doppler centroid estimation in fixed receiver Bistatic SAR systems[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(11): 3459–3471. doi: 10.1109/TGRS.2008.923322
[46]	HE Zhihua, HE Feng, CHEN Junli, HUANG Haifeng, and LIANG Diannong. Phase synchronization processing method for alternating bistatic mode in distributed SAR[J]. Journal of Systems Engineering and Electronics, 2013, 24(3): 410–416. doi: 10.1109/JSEE.2013.00049
[47]	YOCKY D A, WAHL D E, and JAKOWATZ C V. Bistatic SAR: Imagery & image products[R]. SAND2014-18346, 2014.
[48]	YATES G, HOME A M, BLAKE A P, and MIDDLETON R. Bistatic SAR image formation[J]. IEE Proceedings - Radar,Sonar and Navigation, 2006, 153(3): 208–213. doi: 10.1049/ip-rsn:20045091
[49]	WALTERSCHEID I, ENDER J H G, BRENNER A R, and LOFFELD O. Bistatic SAR processing and experiments[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(10): 2710–2717. doi: 10.1109/TGRS.2006.881848
[50]	RODRIGUEZ-CASSOLA M, BAUMGARTNER S V, KRIEGER G, and MOREIRA A. Bistatic TerraSAR-X/F-SAR spaceborne-airborne SAR experiment: Description, data processing, and results[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(2): 781–794. doi: 10.1109/TGRS.2009.2029984
[51]	XIAN Li, XIONG Jintao, HUANG Yulin, and YANG Jianyu. Research on airborne bistatic SAR squint imaging mode algorithm and experiment data processing[C]. The 2007 1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, China, 2007: 618–621.
[52]	ULANDER L M H, FRÖLIND P O, GUSTAVSSON A, RAGNARSSON R, and STENSTRÖM G. VHF/UHF bistatic and passive SAR ground imaging[C]. Proceedings of 2015 IEEE Radar Conference, Arlington, USA, 2015: 669–673.
[53]	WU Junjie, SUN Zhichao, LI Zhongyu, HUANG Yulin, YANG Jianyu, and LIU Zhe. Focusing translational variant Bistatic forward-looking SAR using keystone transform and extended nonlinear chirp scaling[J]. Remote Sensing, 2016, 8(10): 840. doi: 10.3390/rs8100840
[54]	PU Wei, WU Junjie, HUANG Yulin, LI Wenchao, SUN Zhichao, YANG Jianyu, and YANG Haiguang. Motion Errors and compensation for bistatic forward-looking SAR with cubic-order processing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(12): 6940–6957. doi: 10.1109/TGRS.2016.2592536
[55]	WALTERSCHEID I and PAPKE B. Bistatic forward-looking SAR imaging of a runway using a compact receiver on board an ultralight aircraft[C]. The 2013 14th International Radar Symposium, Dresden, Germany, 2013: 461–466.
[56]	HU Cheng, ZENG Tao, LONG Teng, and YANG Chun. Forward-looking bistatic SAR range migration alogrithm[C]. The 2006 CIE International Conference on Radar, Shanghai, China, 2006: 1–4.
[57]	WU Junjie, LI Zhongyu, HUANG Yulin, YANG Jianyu, YANG Haiguang, and LIU Qinghuo. Focusing bistatic forward-looking SAR with stationary transmitter based on keystone transform and nonlinear chirp scaling[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(1): 148–152. doi: 10.1109/LGRS.2013.2250904
[58]	QIU Xiaolan, HU Donghui, and DING Chibiao. Some reflections on bistatic SAR of forward-looking configuration[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(4): 735–739. doi: 10.1109/LGRS.2008.2004506
[59]	WU Junjie, YANG Jianyu, HUANG Yulin, YANG Haiguang, and WANG Haocheng. Bistatic forward-looking SAR: Theory and challenges[C]. The 2009 IEEE Radar Conference, Pasadena, USA, 2009: 1–4.
[60]	LI Wenchao, YANG Jianyu, HUANG Yulin, and WU Junjie. A geometry-based doppler centroid estimator for bistatic forward-looking SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(3): 388–392. doi: 10.1109/LGRS.2011.2170151
[61]	YANG Jianyu, HUANG Yulin, YANG Haiguang, WU Junjie, LI Wenchao, LI Zhongyu, and YANG Xiaobo. A first experiment of airborne bistatic forward-looking SAR - Preliminary results[C]. 2013 IEEE International Geoscience and Remote Sensing Symposium, Melbourne, Australia, 2013: 4202–4204.
[62]	PU Wei, WU Junjie, HUANG Yulin, DU Ke, LI Wenchao, YANG Jianyu, and YANG Haiguang. A rise-dimensional modeling and estimation method for flight trajectory error in Bistatic forward-looking SAR[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(11): 5001–5015.
[63]	ESPETER T, WALTERSCHEID I, KLARE J, BRENNER A R, and ENDER J H G. Bistatic forward-looking SAR: Results of a spaceborne-airborne experiment[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(4): 765–768. doi: 10.1109/LGRS.2011.2108635
[64]	MCCORKLE. Focusing of synthetic aperture ultra wideband data[C]. IEEE 1991 International Conference on Systems Engineering, Dayton, USA, 1991: 1–5.
[65]	刘吉英. 压缩感知理论及在成像中的应用[D]. [博士论文], 国防科学技术大学, 2010. LIU Jiying. Theory of compressed sensing and its application in imaging[D]. [Ph.D. dissertation], National University of Defense Technology, 2010.
[66]	BARANIUK R and STEEGHS P. Compressive radar imaging[C]. 2007 IEEE Radar Conference, Boston, USA, 2007: 128–133.
[67]	吴一戎, 洪文, 张冰尘. 稀疏微波成像导论[M]. 北京: 科学出版社, 2018. WU Yirong, HONG Wen, and ZHANG Bingchen. Introduction to Sparse Microwave Imaging[M]. Beijing: Science Press, 2018.
[68]	ZHANG Bingchen, HONG Wen, and WU Yirong. Sparse microwave imaging: Principles and applications[J]. Science China Information Sciences, 2012, 55(8): 1722–1754. doi: 10.1007/s11432-012-4633-4
[69]	BECK A and TEBOULLE M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183–202. doi: 10.1137/080716542
[70]	KAMILOV U S, RANGAN S, FLETCHER A K, and UNSER M. Approximate message passing with consistent parameter estimation and applications to sparse learning[J]. IEEE Transactions on Information Theory, 2014, 60(5): 2969–2985. doi: 10.1109/TIT.2014.2309005
[71]	吴一戎, 洪文, 张冰尘, 蒋成龙, 张柘, 赵曜. 稀疏微波成像研究进展(科普类)[J]. 雷达学报, 2014, 3(4): 383–396. doi: 10.3724/SP.J.1300.2014.14105 WU Yirong, HONG Wen, ZHANG Bingchen, JIANG Chenglong, ZHANG Zhe, and ZHAO Yao. Current developments of sparse microwave imaging[J]. Journal of Radars, 2014, 3(4): 383–396. doi: 10.3724/SP.J.1300.2014.14105
[72]	杨东. 星载稀疏成像及动目标检测处理方法研究[D]. [博士论文], 西安电子科技大学, 2015. YANG Dong. Sparse signal processing techniques of spaceborne SAR imaging and moving target detection[D]. [Ph.D. dissertation], Xidian University, 2015.
[73]	ZHU Xiaoxiang and BAMLER R. Demonstration of super-resolution for tomographic SAR imaging in urban environment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(8): 3150–3157. doi: 10.1109/TGRS.2011.2177843
[74]	韦顺军. 线阵三维合成孔径雷达稀疏成像技术研究[D]. [博士论文], 电子科技大学, 2013. WEI Shunjun. Research on linear array three-dimensional synthetic apertureradar sparse imaging technology[D]. [Ph.D. dissertation], University of Electronic Science and Technology of China, 2013.
[75]	张磊. 高分辨SAR/ISAR成像及误差补偿技术研究[D]. [博士论文], 西安电子科技大学, 2012. ZHANG Lei. Study on high resolution SAR/ISAR imaging and error correction[D]. [Ph.D. dissertation], Xidian University, 2012.
[76]	ZHU Daiyin, LI Yong, YU Xiang, ZHANG Wei, and ZHU Zhaoda. Compressed ISAR autofocusing: Experimental results[C]. 2012 IEEE Radar Conference, Atlanta, USA, 2012: 425–430.
[77]	DAVIDSON G W, CUMMING I G, and ITO M R. A chirp scaling approach for processing squint mode SAR data[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(1): 121–133. doi: 10.1109/7.481254
[78]	SUN Guangcai, JIANG Xiuwei, XING Mengdao, QIAO Zhijun, WU Yirong, and BAO Zheng. Focus improvement of highly squinted data based on azimuth nonlinear scaling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2308–2322. doi: 10.1109/TGRS.2010.2102040
[79]	AN Daoxiang, HUANG Xiaotao, JIN Tian, and ZHOU Zhimin. Extended nonlinear chirp scaling algorithm for high-resolution highly squint SAR data focusing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(9): 3595–3609. doi: 10.1109/TGRS.2012.2183606
[80]	毛士艺, 李少洪, 黄永红, 陈远知. 机载PD雷达DBS实时成像研究[J]. 电子学报, 2000, 28(3): 32–34. doi: 10.3321/j.issn:0372-2112.2000.03.009 MAO Shiyi, LI Shaohong, HUANG Yonghong, and CHEN Yuanzhi. Study of real-time image by DBS on airborne PD radar[J]. Acta Electronica Sinica, 2000, 28(3): 32–34. doi: 10.3321/j.issn:0372-2112.2000.03.009
[81]	CUMMING I G and WONG F H. Digital Processing of Synthetic Aperture Radar Data[M]. Boston: Artech House, 2005.
[82]	ZHANG Yongchao, ZHANG Yin, LI Wenchao, HUANG Yulin, and YANG Jianyu. Super-resolution surface mapping for scanning radar: Inverse filtering based on the fast iterative adaptive approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(1): 127–144. doi: 10.1109/TGRS.2017.2743263
[83]	徐浩. 基于空间谱理论和时空两维随机辐射场的雷达成像研究[D]. [博士论文], 中国科学技术大学, 2011. XU Hao. The radar imaging based on space spectrum and temporal-spatial stochastic radiation field[D]. [Ph.D. dissertation], University of Science and Technology of China, 2011.
[84]	何学智. 微波凝视关联成像的信息处理方法与仿真[D]. [博士论文], 中国科学技术大学, 2013. HE Xuezhi. The information processing methods and simulations in microwave staring correlated imaging[D]. [Ph.D. dissertation], University of Science and Technology of China, 2013.
[85]	丁义元, 杨建宇, 张卫华, 黄顺吉. 改进实孔径雷达角分辨力的广义逆滤波方法[J]. 电子学报, 1993, 21(9): 15–19. doi: 10.3321/j.issn:0372-2112.1993.09.003 DING Yiyuan, YANG Jianyu, ZHANG Weihua, and HUANG Shunji. Improvement of angular resolution of real aperture radar via generalized inverse filtering[J]. Acta Electronica Sinica, 1993, 21(9): 15–19. doi: 10.3321/j.issn:0372-2112.1993.09.003
[86]	ZHANG Yongchao, LI Wenchao, ZHANG Yin, HUANG Yulin, and YANG Jianyu. A fast iterative adaptive approach for scanning radar angular superresolution[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(11): 5336–5345.
[87]	YIN Zhang, ZHANG Qiping, LI Changlin, ZHANG Yongchao, HUANG Yulin, and YANG Jianyu. Sea-surface target angular superresolution in forward-looking radar imaging based on maximum a posteriori algorithm[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(8): 2822–2834. doi: 10.1109/JSTARS.2019.2918189
[88]	MAO Deqing, ZHANG Yin, ZHANG Yongchao, HUANG Yulin, and YANG Jianyu. Realization of airborne forward-looking radar super-resolution algorithm based on GPU frame[C]. The 2016 CIE International Conference on Radar, Guangzhou, China, 2016: 1–5.
[89]	LAVERY M P J, SPEIRITS F C, BARNETT S M, and PADGETT M J. Detection of a spinning object using light’s orbital angular momentum[J]. Science, 2013, 341(6145): 537–540. doi: 10.1126/science.1239936
[90]	TAMAGNONE M, CRAEYE C, and PERRUISSEAU-CARRIER J. Comment on ‘Encoding many channels on the same frequency through radio vorticity: First experimental test’[J]. New Journal of Physics, 2012, 14(3): 118001.
[91]	THIDÉ B, THEN H, SJÖHOLM J, PALMER K, BERGMAN J, CAROZZI T D, ISTOMIN Y N, IBRAGIMOV N H, and KHAMITOVA R. Utilization of photon orbital angular momentum in the low-frequency radio domain[J]. Physical Review Letters, 2007, 99(8): 087701. doi: 10.1103/PhysRevLett.99.087701
[92]	LIU Kang, CHENG Yongqiang, YANG Zhaocheng, WANG Hongqiang, QIN Yuliang, and LI Xiang. Orbital-angular-momentum-based electromagnetic vortex imaging[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14: 711–714. doi: 10.1109/LAWP.2014.2376970
[93]	LIU Kang, LIU Hongyan, QIN Yuliang, CHENG Yongqiang, WANG Shunan, LI Xiang, and WANG Hongqiang. Generation of OAM beams using phased array in the microwave band[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(9): 3850–3857. doi: 10.1109/TAP.2016.2589960
[94]	YUAN Tiezhu, CHENG Yongqiang, WANG Hongqiang, and QIN Yuliang. Mode characteristics of vortical radio wave generated by circular phased array: Theoretical and experimental results[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(2): 688–695. doi: 10.1109/TAP.2016.2635620
[95]	刘红彦. 面向雷达成像的涡旋电磁波产生方法研究[D]. [硕士论文], 国防科学技术大学, 2016. LIU Hongyan. Research on the generation of vortex electromagnetic waves for radar imaging[D]. [Master dissertation], National University of Defense Technology, 2016.
[96]	LIU Kang, CHENG Yongqiang, GAO Yue, LI Xiang, QIN Yuliang, and WANG Hongqiang. Super-resolution radar imaging based on experimental OAM beams[J]. Applied Physics Letters, 2017, 110(16): 164102. doi: 10.1063/1.4981253
[97]	袁铁柱. 涡旋电磁波在雷达成像中的应用研究[D]. [博士论文], 国防科学技术大学, 2017. YUAN Tiezhu. Research on radar imaging using electromagnetic vortex wave[D]. [Ph.D. dissertation], National University of Defense Technology, 2017.
[98]	HUANG Yulin, PEI Jifang, YANG Jianyu, WANG Bing, and LIU Xian. Neighborhood geometric center scaling embedding for SAR ATR[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(1): 180–192. doi: 10.1109/TAES.2013.110769
[99]	WANG Bing, HUANG Yulin, YANG Jianyu, and WU Junjie. A feature extraction method for Synthetic Aperture Radar (SAR) automatic target recognition based on maximum interclass distance[J].Science China Technological Sciences, 2011, 54(9): 2520. doi: 10.1007/s11431-011-4430-0
[100]	DANG Sihang, CAO Zongjie, CUI Zongyong, PI Yiming, and LIU Nengyuan. Open set incremental learning for automatic target recognition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(7): 4445–4456. doi: 10.1109/TGRS.2019.2891266
[101]	PEI Jifang, HUANG Yulin, SUN Zhichao, YANG Jianyu, and YEO Tatsoon. Multiview synthetic aperture radar automatic target recognition optimization: Modeling and implementation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(11): 6425–6439. doi: 10.1109/TGRS.2018.2838593
[102]	PEI Jifang, HUANG Yulin, HUO Weibo, ZHANG Yin, YANG Jianyu, and YEO Tatsoon. SAR automatic target recognition based on multiview deep learning framework[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(4): 2196–2210. doi: 10.1109/TGRS.2017.2776357
[103]	CUI Zongyong, QUAN Hongbin, CAO Zongjie, XU Shengping, DING Chunmei, and WU Junjie. SAR target CFAR detection via GPU parallel operation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(12): 4884–4894. doi: 10.1109/JSTARS.2018.2879082
[104]	HUO Weibo, HUANG Yulin, PEI Jifang, LIU Xiaojia, and YANG Jianyu. Virtual SAR target image generation and similarity[C]. The 2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 2016: 914–917.
[105]	HUO Weibo, HUANG Yulin, PEI Jifang, ZHANG Yin, and YANG Jianyu. A new SAR image simulation method for sea-ship scene[C]. 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 2018: 721–724.
[106]	ZHU Jiehao, ZHOU Jianjiang, and XIA Weijie. High resolution radar cross section imaging based on complex target backscattering simulation[C]. The 2008 8th International Symposium on Antennas, Propagation and EM Theory, Kunming, China, 2008: 577–580.

施引文献

期刊类型引用(1)
1. 叶恺，禹卫东，王伟. 基于矩阵束方法的星载MEB SAR俯仰向DBF处理方法. 电子与信息学报. 2018(11): 2659-2666 . 百度学术
其他类型引用(3)

资源附件(0)

访问统计

图(32)

计量

文章访问数: 6599
HTML全文浏览量: 2179
PDF下载量: 859
被引次数: 4

1. 引言
2. 双基星载HRWS-SAR系统的方位向信号模型
2.1 单基星载HRWS-SAR系统的方位向信号模型
2.2 双基星载HRWS-SAR系统的方位向信号模型
2.3 C(t)近似为C0的合理性
3. 方位向信号重构的矩阵求逆算法
3.1 双基HRWS-SAR系统的矩阵求逆算法
3.2 矩阵求逆算法的重构性能
4. 仿真分析
4.1 C0对C(t)的近似性能
4.2 方位向信号重构结果
4.3 方位向信号重构性能
5. 结束语

1. 引言
2. 双基星载HRWS-SAR系统的方位向信号模型
2.1 单基星载HRWS-SAR系统的方位向信号模型
2.2 双基星载HRWS-SAR系统的方位向信号模型
2.3 C(t)近似为C₀的合理性
3. 方位向信号重构的矩阵求逆算法
3.1 双基HRWS-SAR系统的矩阵求逆算法
3.2 矩阵求逆算法的重构性能
4. 仿真分析
4.1 C₀对C(t)的近似性能
4.2 方位向信号重构结果
4.3 方位向信号重构性能
5. 结束语

参考文献(106)

施引文献

资源附件(0)

访问统计

雷达对地成像技术多向演化趋势与规律分析

DOI: 10.12000/JR19099

通讯作者:
杨建宇 jyyang@uestc.edu.cn

计量

Multi-directional Evolution Trend and Law Analysis of Radar Ground Imaging Technology（in English）

Corresponding author: YANG Jianyu, jyyang@uestc.edu.cn

1. 引言

2. 双基星载HRWS-SAR系统的方位向信号模型

2.1 单基星载HRWS-SAR系统的方位向信号模型

2.2 双基星载HRWS-SAR系统的方位向信号模型

2.3 C(t)近似为C₀的合理性

3. 方位向信号重构的矩阵求逆算法

3.1 双基HRWS-SAR系统的矩阵求逆算法

3.2 矩阵求逆算法的重构性能

4. 仿真分析

4.1 C₀对C(t)的近似性能

4.2 方位向信号重构结果

4.3 方位向信号重构性能

5. 结束语

期刊类型引用(1)

其他类型引用(3)

计量

目录

1. 引言

2. 双基星载HRWS-SAR系统的方位向信号模型

2.1 单基星载HRWS-SAR系统的方位向信号模型

2.2 双基星载HRWS-SAR系统的方位向信号模型

2.3 C(t)近似为C₀的合理性

3. 方位向信号重构的矩阵求逆算法

3.1 双基HRWS-SAR系统的矩阵求逆算法

3.2 矩阵求逆算法的重构性能

4. 仿真分析

4.1 C₀对C(t)的近似性能

4.2 方位向信号重构结果

4.3 方位向信号重构性能

5. 结束语

期刊介绍

联系我们

雷达对地成像技术多向演化趋势与规律分析

DOI: 10.12000/JR19099

通讯作者: 杨建宇 jyyang@uestc.edu.cn

计量

出版历程

Multi-directional Evolution Trend and Law Analysis of Radar Ground Imaging Technology（in English）

Corresponding author: YANG Jianyu, jyyang@uestc.edu.cn

1. 引言

2. 双基星载HRWS-SAR系统的方位向信号 模型

2.1 单基星载HRWS-SAR系统的方位向信号模型

2.2 双基星载HRWS-SAR系统的方位向信号模型

2.3 C(t)近似为C0的合理性

3. 方位向信号重构的矩阵求逆算法

3.1 双基HRWS-SAR系统的矩阵求逆算法

3.2 矩阵求逆算法的重构性能

4. 仿真分析

4.1 C0对C(t)的近似性能

4.2 方位向信号重构结果

4.3 方位向信号重构性能

5. 结束语

期刊类型引用(1)

其他类型引用(3)

计量

出版历程

目录

1. 引言

2. 双基星载HRWS-SAR系统的方位向信号 模型

2.1 单基星载HRWS-SAR系统的方位向信号模型

2.2 双基星载HRWS-SAR系统的方位向信号模型

2.3 C(t)近似为C0的合理性

3. 方位向信号重构的矩阵求逆算法

3.1 双基HRWS-SAR系统的矩阵求逆算法

3.2 矩阵求逆算法的重构性能

4. 仿真分析

4.1 C0对C(t)的近似性能

4.2 方位向信号重构结果

4.3 方位向信号重构性能

5. 结束语

期刊介绍

联系我们

通讯作者:
杨建宇 jyyang@uestc.edu.cn

2. 双基星载HRWS-SAR系统的方位向信号模型

2.3 C(t)近似为C₀的合理性

4.1 C₀对C(t)的近似性能

2. 双基星载HRWS-SAR系统的方位向信号模型

2.3 C(t)近似为C₀的合理性

4.1 C₀对C(t)的近似性能