基于极化轴比参数的圆极化波发射误差分析方法

陈诗强; 洪文

doi:10.12000/JR19063

基于极化轴比参数的圆极化波发射误差分析方法

DOI: 10.12000/JR19063

陈诗强,
洪文^,

空间信息处理与应用系统技术重点实验室北京 100190
中国科学院空天信息创新研究院北京 100190
中国科学院大学北京 100049

基金项目: 国家自然科学基金(61431018)

详细信息

作者简介:
陈诗强(1990–)，男，中国科学院电子学研究所在读博士生，研究方向为混合极化系统误差分析及相关应用研究。E-mail: chenshiqiang13@mails.ucas.ac.cn

洪　文(1968–)，女，中国科学院电子学研究所研究员，博士生导师，研究方向为极化/极化干涉SAR处理及应用、三维SAR信号处理、圆迹SAR信号处理以及稀疏微波成像技术等。E-mail: whong@mail.ie.ac.cn

通讯作者:
洪文 whong@mail.ie.ac.cn

责任主编：陈思伟 Corresponding Editor: CHEN Siwei
中图分类号: TN95
计量
- 文章访问数: 3240
- HTML全文浏览量: 1266
- PDF下载量: 479
- 被引次数: 0
出版历程
- 收稿日期: 2019-06-27
- 修回日期: 2019-09-04
- 网络出版日期: 2020-04-01

Analysis on the Transmit Distortion of the Circular Polarized Wave Based on the Axial Ratio Parameter

CHEN Shiqiang,
HONG Wen^,

Key Laboratory of Technology in Geospatial Information Processing and Application System, Beijing 100190, China
Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100190, China
University of Chinese Academy of Sciences, Beijing 100049, China

Funds: The National Natural Science Foundation of China (61431018)

More Information

Corresponding author: HONG Wen, whong@mail.ie.ac.cn

摘要

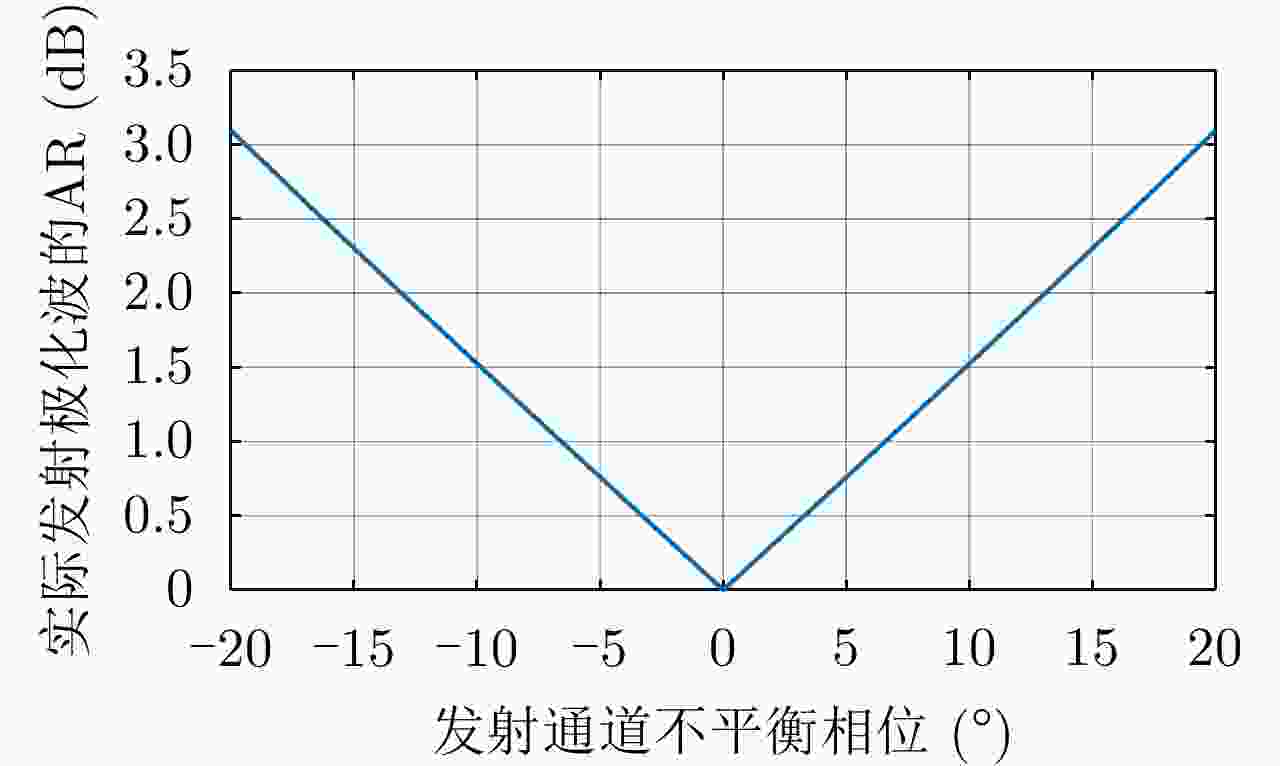
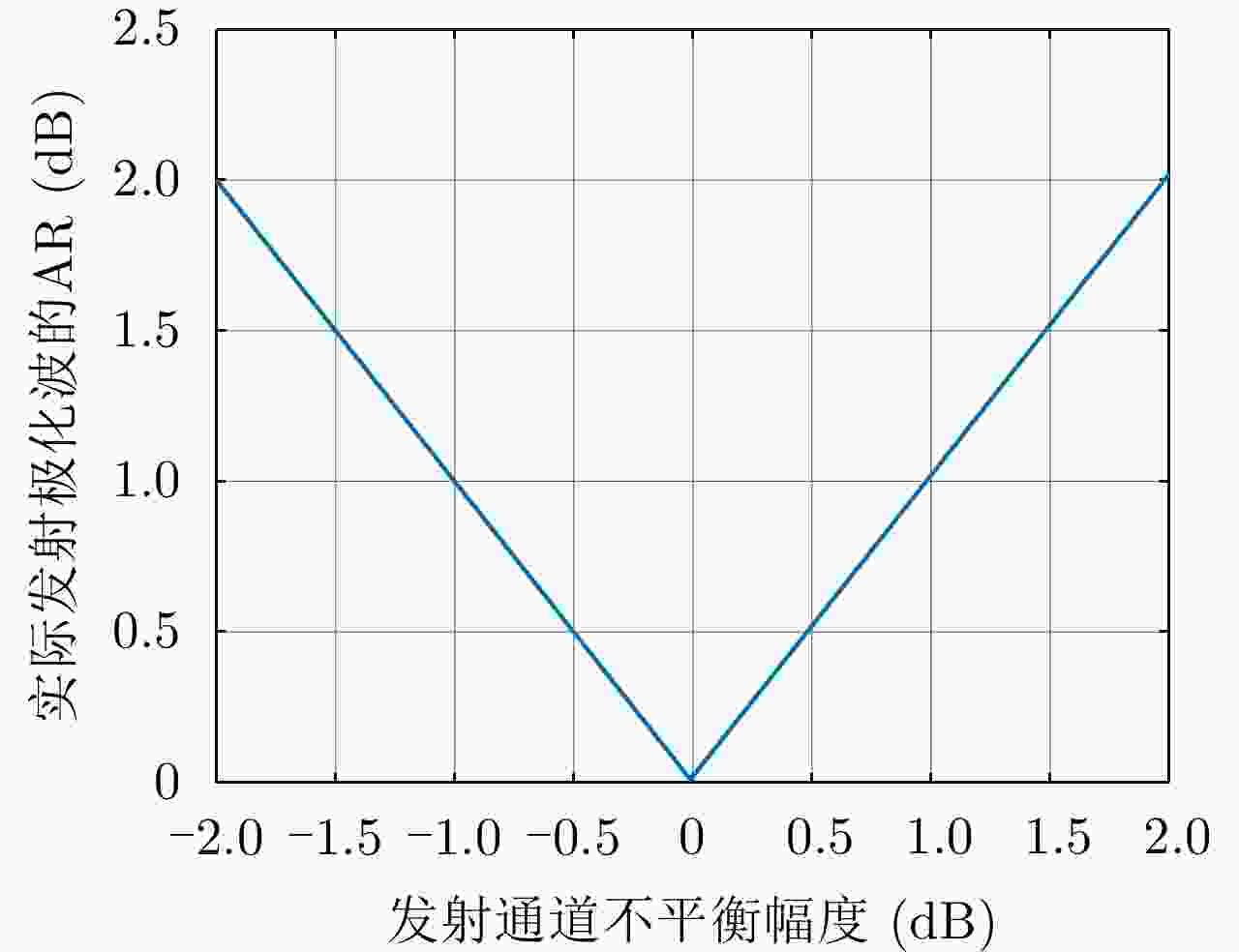
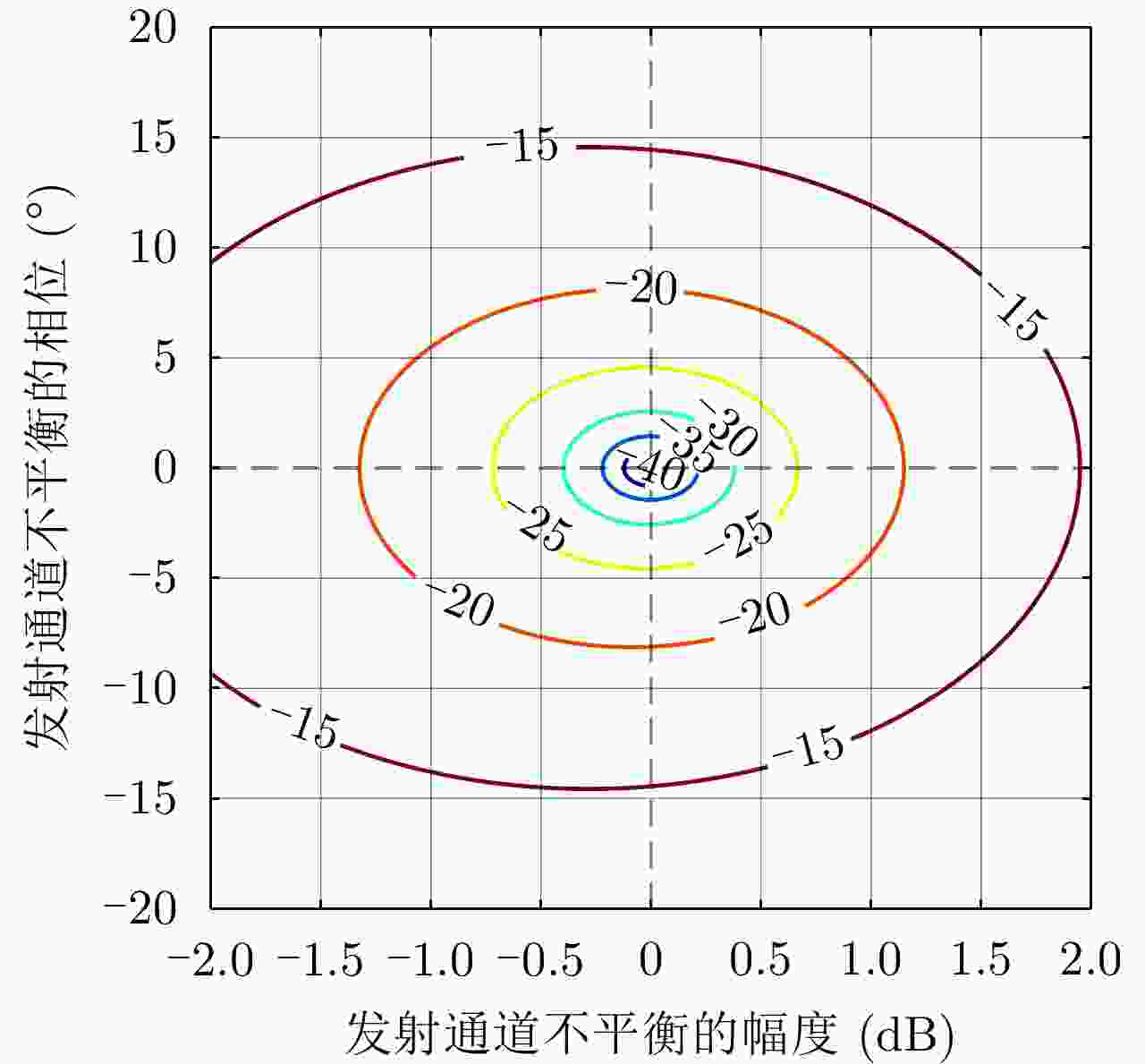
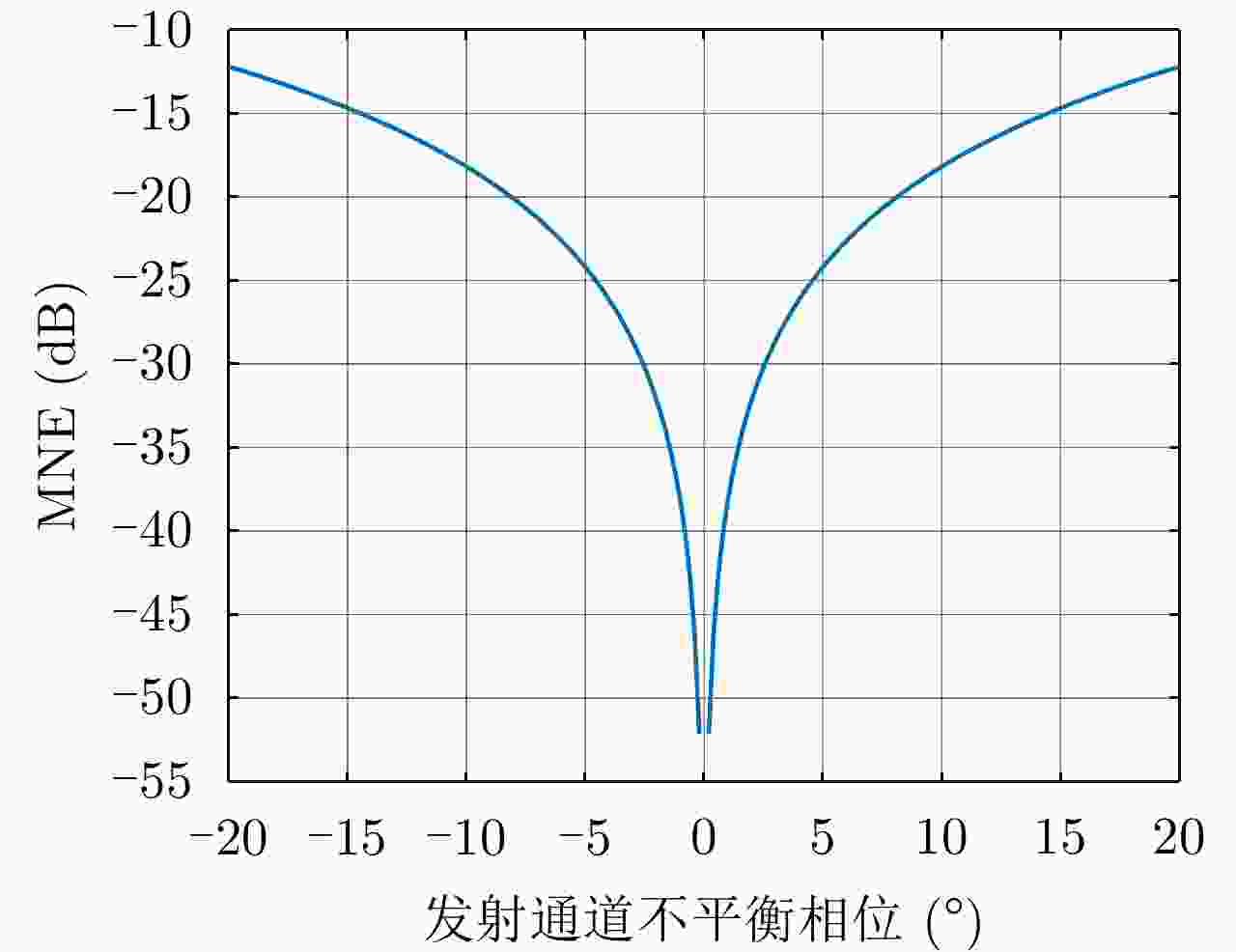
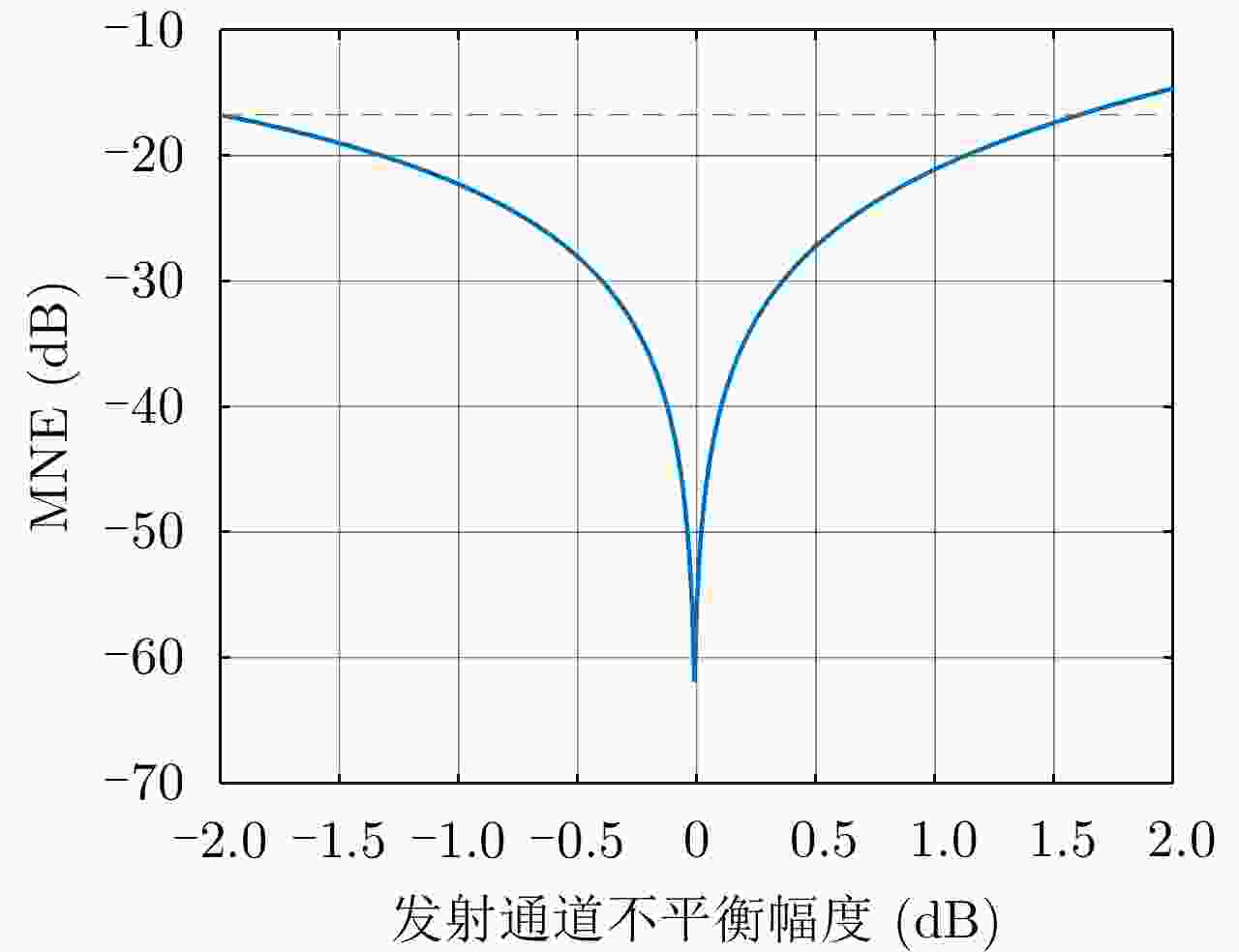
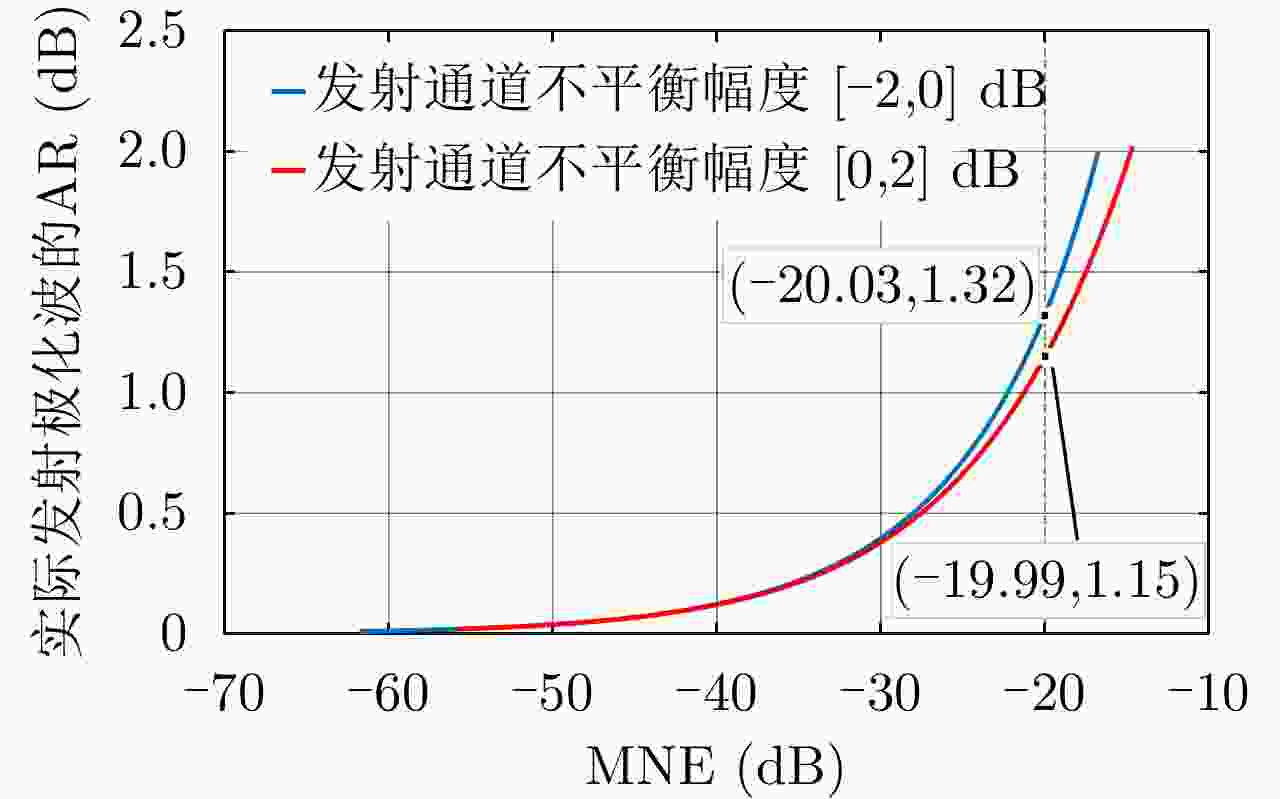
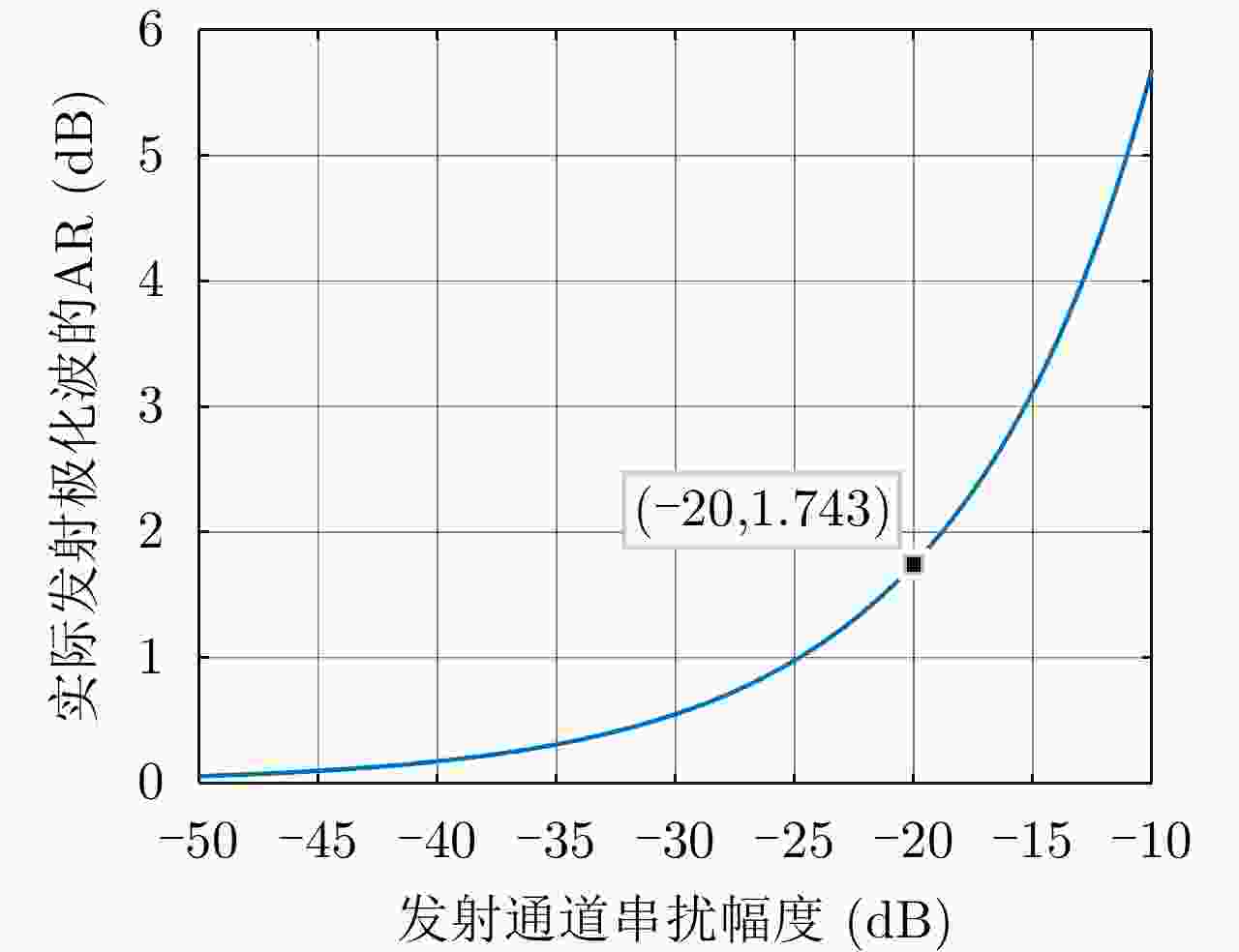
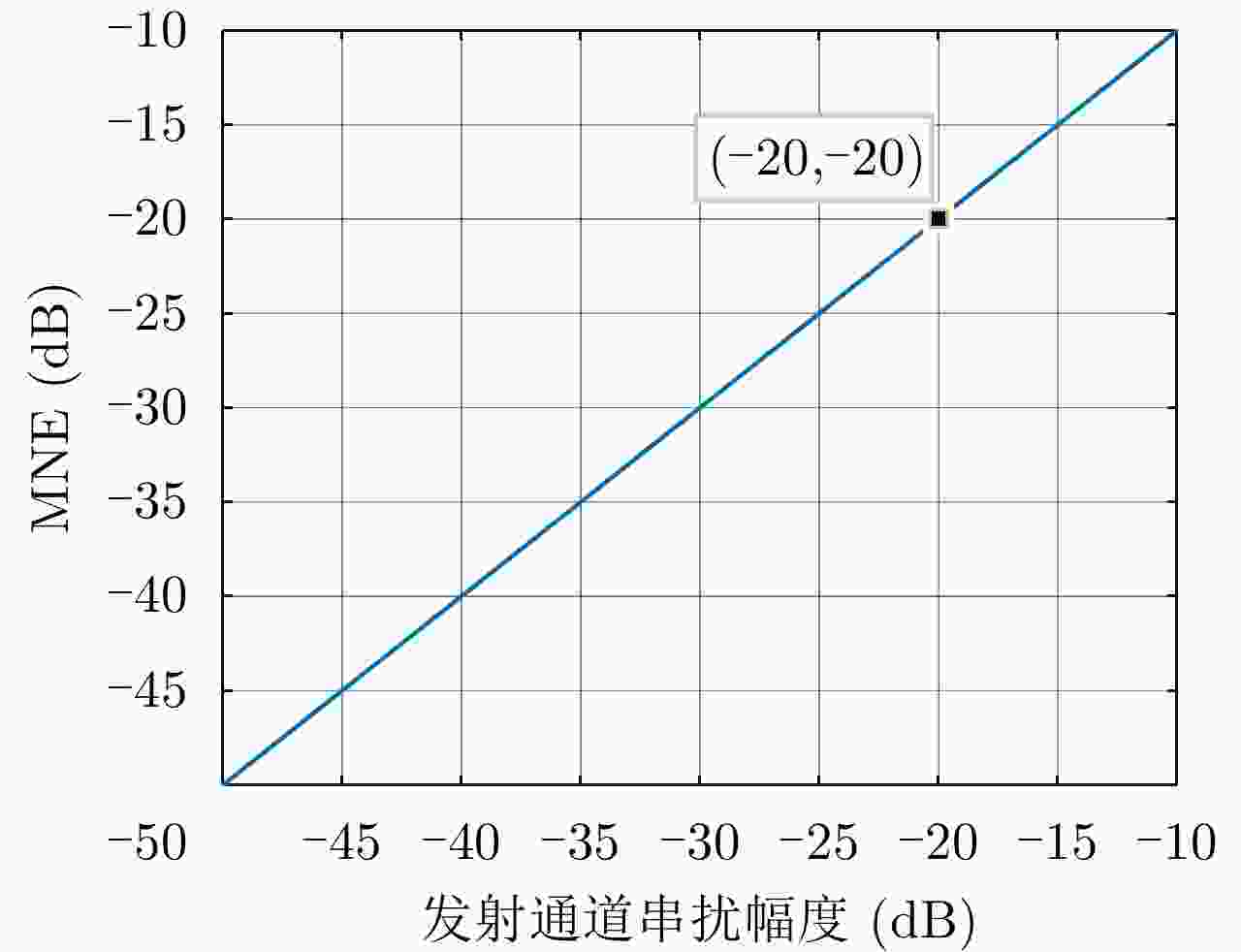
摘要: 简缩极化(CP)模式是一种新型双极化模式。在实际工程应用中，包括简缩极化模式在内的所有双极化模式均无法直接通过外定标的方法补偿发射误差。因而有必要对发射误差所带来的影响进行详细分析。针对极化SAR系统，目前已有学者提出使用误差的最大归一化误差(MNE)参数对极化SAR系统的极化质量做分析评估。该文针对发射圆极化波的简缩极化模式提出了一种基于实际发射极化波极化轴比(AR)参数的发射误差分析方法。首先，通过仿真分析不同发射误差源对AR参数的影响，与此同时还展示了相同发射误差源影响下的MNE参数；通过分析对比，总结了AR参数相对MNE参数的3个优点；最后，使用高分三号卫星的实际测量误差数据与圆极化发射波实验系统的实测数据验证了该文提出的发射误差评估方法的有效性。
- 极化SAR /
- 简缩极化 /
- 极化轴比 /
- 发射误差 /
- 最大归一化误差
Abstract: Compact Polarimetric (CP) mode is a new dual-pol mode introduced in the last decade. The main current CP mode transmits circular polarized waves. Data in the form of Stokes parameters obtained by this mode has rotational invariance. In real engineering applications, transmit distortions in all dual-pol modes, including the CP mode, cannot be directly compensated with external calibration methods. Therefore, it is necessary to analysis the influences caused by transmit distortions. Until now, the Maximum Normalized Error (MNE) parameter has already been proposed by existing researches to analyze polarimetric quality of the Polarimetric SAR (PolSAR) system. This paper has proposed an analysis method to analysis the influence of transmit distortions in polarimetric modes with circular polarimetric wave in transmission, based on the Axial Ratio (AR) parameter of real transmitted wave. Firstly, this paper has analyzed the influence of different transmit distortion sources to AR parameter with simulations. Meanwhile, this part has also demonstrated the influence of same distortion sources to the MNE parameter. Through comparison of this two results, this paper has concluded three advantages of the AR parameter over the MNE parameter. At last, the effectiveness of the proposed evaluation method has been verified using real measured GF-3 distortion data and test data obtained by experimental system, which transmit circular polarized waves.
- Polarimetric SAR (PolSAR) /
- Compact Polarimetry (CP) /
- Axial Ratio (AR) /
- Transmit distortion /
- Maximum Normalized Error (MNE)

HTML全文

图 1 极化椭圆

Figure 1. The polarization ellipse

下载: 全尺寸图片幻灯片

图 2 发射通道不平衡的幅度与相位对实际发射极化波AR的影响

Figure 2. The influence of transmit channel imbalance’s amplitude and phase to AR of actually transmitted polarized wave

下载: 全尺寸图片幻灯片

图 3 发射通道不平衡的幅度等于0 dB时，相位对实际发射极化波AR的影响

Figure 3. The influence of transmit channel imbalance’s phase, when it’s amplitude equals 0 dB, to AR of actually transmitted polarized wave

下载: 全尺寸图片幻灯片

图 4 发射通道不平衡的相位等于0°时，幅度对实际发射极化波AR的影响

Figure 4. The influence of transmit channel imbalance’s amplitude, when it’s phase equals 0°, to AR of actuallytransmitted polarized wave

下载: 全尺寸图片幻灯片

图 5 发射通道不平衡幅度与相位变化共同引起的MNE

Figure 5. MNE caused by the amplitude and phase of transmit channel imbalance

下载: 全尺寸图片幻灯片

图 6 发射通道不平衡的幅度为0 dB时，相位变化引起的MNE

Figure 6. MNE caused by the phase of transmit channel imbalance when it’s amplitude equals 0 dB

下载: 全尺寸图片幻灯片

图 7 发射通道不平衡的相位为0°时，幅度变化引起的MNE

Figure 7. MNE caused by the amplitude of transmit channelimbalance when it’s phase equals 0°

下载: 全尺寸图片幻灯片

图 8 通道不平衡的相位等于0°，幅度为变量时，MNE与实际发射极化波AR之间的关系图

Figure 8. The relationship between MNE and AR of actually transmitted polarized wave when transmit channel imbalance’s phase equals 0° and amplitude changes

下载: 全尺寸图片幻灯片

图 9 通道不平衡的相位等于0 dB，相位为变量时，MNE与实际发射极化波AR之间的关系图

Figure 9. The relationship between MNE and AR of actually transmitted polarized wave when transmit channel imbalance’s amplitude equals 0 dB and phase changes

下载: 全尺寸图片幻灯片

图 10 发射通道串扰相位为0°时，串扰幅度对实际发射极化波AR的影响

Figure 10. The influence of transmit crosstalk’s amplitude, when it’s phase distortion equals 0°, to AR of actuallytransmitted polarized wave

下载: 全尺寸图片幻灯片

图 11 发射通道串扰幅度等于–20 dB时，串扰相位对实际发射极化波AR的影响

Figure 11. The influence of transmit crosstalk’s phase, when it’s amplitude distortion equals –20 dB, to AR of actually transmitted polarized wave

下载: 全尺寸图片幻灯片

图 12 发射通道串扰相位等于0°时，串扰幅度引起的MNE

Figure 12. MNE of transmit crosstalk’s amplitude, when crosstalk’s phase equals 0°

下载: 全尺寸图片幻灯片

图 13 发射通道串扰幅度等于–20 dB时，串扰相位引起的MNE

Figure 13. MNE of transmit crosstalk’s phase, when crosstalk’s amplitude equals –20 dB

下载: 全尺寸图片幻灯片

图 14 两路发射通道间的相位差、幅度比(dB差)与AR参数之间的关系

Figure 14. Relationship between the difference of phase, the ratio of amplitude (difference in dB) of two transmit channelsand the AR parameter

下载: 全尺寸图片幻灯片

表 1 高分三号在轨定标试验的实测发射误差与对应的AR与MNE参数

Table 1. Measured transmit distortion of GF-3 on-orbit calibration experiment and corresponding AR and MNE parameters

实验时间	T11	T12	T21	T22	AR (dB)	MNE (dB)
2016.09.08	1.0∠0.0°	0.0149∠–45.2715°	0.0040∠168.4078°	0.9133∠19.3436°	3.0751	–12.4789
2016.09.19	1.0∠0.0°	0.0152∠–92.6368°	0.0026∠–49.6355°	0.8752∠8.6810°	1.8590	–17.4527
2017.07.11	1.0∠0.0°	0.0126∠–69.1254°	0.0042∠–177.2737°	0.9431∠10.4461°	1.7046	–17.4304
2017.07.16	1.0∠0.0°	0.0131∠–54.6146°	0.0032∠–178.2101°	0.9382∠11.0117°	0.6557	–26.6122

下载: 导出CSV

表 2 第1次发射通道部分测试结果

Table 2. Partial measured results of the first transmit channel test

编号	调幅设置(dB)	调相设置(°)	x通道幅度(dB)	x通道相位(°)	y通道幅度(dB)	y通道相位(°)	幅度比(dB)	相位差(°)	AR参数(dB)
1	2.5	5.625	–13.3275	–40.4487	–13.4555	–132.3204	0.1281	91.8717	0.3114
2	2.5	185.625	–13.3081	139.3082	–13.4567	–132.3170	0.1486	–88.3748	0.2878
3	3.0	11.250	–13.5909	–45.1950	–13.4556	–132.3143	–0.1353	87.1193	0.4574
4	3.0	191.250	–13.5295	134.5363	–13.4578	–132.3216	–0.0717	–93.1422	0.4819

下载: 导出CSV

表 3 第2次发射通道部分测试结果

Table 3. Partial measured results of the second transmit channel test

编号	调幅设置(dB)	调相设置(°)	x通道幅度(dB)	x通道相位(°)	y通道幅度(dB)	y通道相位(°)	幅度比(dB)	相位差(°)	AR参数(dB)
1	2.5	5.625	–13.3411	–39.9068	–13.4518	–131.8972	0.1106	91.9904	0.3214
2	2.5	185.625	–13.3186	139.9906	–13.4539	–131.8965	0.1353	–88.1129	0.3165
3	3.0	11.250	–13.6044	–44.5745	–13.4533	–131.8974	–0.1511	87.3299	0.4332
4	3.0	191.250	–13.5426	135.2489	–13.4533	–131.8920	–0.0894	–92.8591	0.4427

下载: 导出CSV

参考文献(22)

[1]	MOREIRA A, PRATS-IRAOLA P, YOUNIS M, et al. A tutorial on synthetic aperture radar[J]. IEEE Geoscience and Remote Sensing Magazine, 2013, 1(1): 6–43. doi: 10.1109/MGRS.2013.2248301
[2]	CHEN Siwei, LI Yongzhen, WANG Xuesong, et al. Modeling and interpretation of scattering mechanisms in polarimetric synthetic aperture radar: Advances and perspectives[J]. IEEE Signal Processing Magazine, 2014, 31(4): 79–89. doi: 10.1109/MSP.2014.2312099
[3]	CHARBONNEAU F J, BRISCO B, RANEY R K, et al. Compact polarimetry overview and applications assessment[J]. Canadian Journal of Remote Sensing, 2010, 36(Suppl 2): S298–S315. doi: 10.5589/M10-062
[4]	SOUYRIS J C, IMBO P, FJØRTOFT R, et al. Compact polarimetry based on symmetry properties of geophysical media: The $\pi $ /4 mode[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(3): 634–646. doi: 10.1109/TGRS.2004.842486
[5]	STACY N and PREISS M. Compact polarimetric analysis of X-band SAR data[C]. The 6th European Conference on Synthetic Aperture Radar, Dresden, Germany, 2006.
[6]	RANEY R K. Hybrid-polarity SAR architecture[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3397–3404. doi: 10.1109/TGRS.2007.895883
[7]	洪文. 基于混合极化架构的极化SAR: 原理与应用(中英文)[J]. 雷达学报, 2016, 5(6): 559–595. doi: 10.12000/JR16074 HONG Wen. Hybrid-polarity architecture based polarimetric SAR: Principles and applications (in Chinese and in English)[J]. Journal of Radars, 2016, 5(6): 559–595. doi: 10.12000/JR16074
[8]	RANEY R K. Comparing compact and quadrature polarimetric SAR performance[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(6): 861–864. doi: 10.1109/LGRS.2016.2550863
[9]	RANEY R K, SPUDIS P D, BUSSEY B, et al. The lunar mini-RF radars: Hybrid polarimetric architecture and initial results[J]. Proceedings of the IEEE, 2011, 99(5): 808–823. doi: 10.1109/JPROC.2010.2084970
[10]	MISRA T and KIRANKUMAR A S. RISAT-1: Configuration and performance evaluation[C]. 2014 XXXIth URSI General Assembly and Scientific Symposium, Beijing, China, 2014: 1–4. doi: 10.1109/URSIGASS.2014.6929612.
[11]	KANKAKU Y, OSAWA Y, SUZUKI S, et al. The overview of the L-band SAR onboard ALOS-2[C]. The Progress in Electromagnetics Research Symposium, Moscow, Russia, 2009: 735–738.
[12]	TOUZI R and CHARBONNEAU F. Requirements on the calibration of hybrid-compact SAR[C]. 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, Canada, 2014: 1109–1112. doi: 10.1109/IGARSS.2014.6946623
[13]	THOMPSON A A. Overview of the RADARSAT constellation mission[J]. Canadian Journal of Remote Sensing, 2015, 41(5): 401–407. doi: 10.1080/07038992.2015.1104633
[14]	WANG Yanting, AINSWORTH T L, and LEE J S. Assessment of system polarization quality for polarimetric SAR imagery and target decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(5): 1755–1771. doi: 10.1109/TGRS.2010.2087342
[15]	GUO Shenglong, ZHANG Jingjing, LI Yang, et al. Effects of polarization distortion at transmission and faraday rotation on compact polarimetric SAR system and H/ $\bar \alpha $ decomposition[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(8): 1700–1704. doi: 10.1109/LGRS.2015.2420116
[16]	LEE J S and POTTIER E. Polarimetric Radar Imaging: From Basics to Applications[M]. Boca Raton: CRC press, 2009.
[17]	陈琳, 张晶晶, 李洋, 等. 单发双收SAR系统通用极化定标算法[J]. 雷达学报, 2012, 1(3): 323–328. doi: 10.3724/SP.J.1300.2012.20062 CHEN Lin, ZHANG Jingjing, LI Yang, et al. General calibration algorithm for single-transmitting-dual-receiving polarimetric SAR system[J]. Journal of Radars, 2012, 1(3): 323–328. doi: 10.3724/SP.J.1300.2012.20062
[18]	JIANG Sha, QIU Xiaolan, HAN Bing, et al. Error source analysis and correction of GF-3 polarimetric data[J]. Remote Sensing, 2018, 10(11): 1685. doi: 10.3390/rs10111685
[19]	WRIGHT P A, QUEGAN S, WHEADON N S, et al. Faraday rotation effects on L-band spaceborne SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(12): 2735–2744. doi: 10.1109/TGRS.2003.815399
[20]	FREEMAN A and SAATCHI S S. On the detection of faraday rotation in linearly polarized L-band SAR backscatter signatures[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(8): 1607–1616. doi: 10.1109/TGRS.2004.830163
[21]	LIANG Weibin, JIA Zengzeng, QIU Xiaolan, et al. Polarimetric calibration of the GaoFen-3 mission using active radar calibrators and the applicable conditions of system model for radar polarimeters[J]. Remote Sensing, 2019, 11(2): 176. doi: 10.3390/rs11020176
[22]	MCKERRACHER P L, JENSEN J R, SEQUEIRA H B, et al. Mini-RF calibration, a unique approach to on-orbit synthetic aperture radar system calibration[C]. The 41st Lunar and Planetary Science Conference, The Woodlands, USA, 2010: 2352.