一种用于准单站配置的步进频探地雷达建模方法

张经纬; 刘新; 叶盛波; 方广有

doi:10.12000/JR18096

一种用于准单站配置的步进频探地雷达建模方法

doi: 10.12000/JR18096

张经纬^1,2,3,
刘新^1,2,3,
叶盛波^2,3,
方广有^2,3, ,

①.
中国科学院大学北京 100049
②.
中国科学院电子学研究所北京 100190
③.
中国科学院电磁辐射与探测技术重点实验室北京 100190

基金项目: 中国科学院面上基金(CXJJ-17-M140)，国家重点研发计划(2017YFF0107700)

详细信息

作者简介:
张经纬(1992–)，男，湖北荆州人，中国科学院电子学研究所博士研究生，主要研究方向为探地雷达系统建模及探地雷达信号处理，目前已发表多篇期刊论文及国际会议论文

刘　新(1992–)，男，山东新泰人，中国科学院电子学研究所博士研究生，主要研究方向为伪随机编码雷达系统设计及其在穿墙成像中的应用

叶盛波(1985–)，男，湖北黄陂人，现为中国科学院电子学研究所副研究员，主要研究方向为超宽带探地雷达系统设计，目前发表多篇论文

方广有(1963–)，男，河南人，现为中国科学院电子学研究所研究员，主要研究方向为超宽带雷达成像技术、微波成像新方法和技术、超宽带电磁场理论及工程应用，目前发表多篇高质量论文

通讯作者:
方广有 gyfang@mail.ie.ac.cn

中图分类号: TN958
计量
- 文章访问数: 1945
- HTML全文浏览量: 774
- PDF下载量: 176
- 被引次数: 0
出版历程
- 收稿日期: 2018-11-04
- 修回日期: 2018-11-28
- 网络出版日期: 2019-08-28

A Modeling Method for Quasi-monostatic Stepped Frequency Ground Penetrating Radar

ZHANG Jingwei^1,2,3,
LIU Xin^1,2,3,
YE Shengbo^2,3,
FANG Guangyou^{2,3
, ,}

①.
University of Chinese Academy of Sciences, Beijing 100049, China
②.
Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China
③.
Key Laboratory of Electromagnetic Radiation and Sensing Technology, Chinese Academy of Sciences, Beijing 100190, China

Funds: Chinese Academy of Sciences Innovation Fund Grant (CXJJ-17-M140), The National Key R&D Program of China (2017YFF0107700)

More Information

Corresponding author: FANG Guangyou, gyfang@mail.ie.ac.cn

摘要

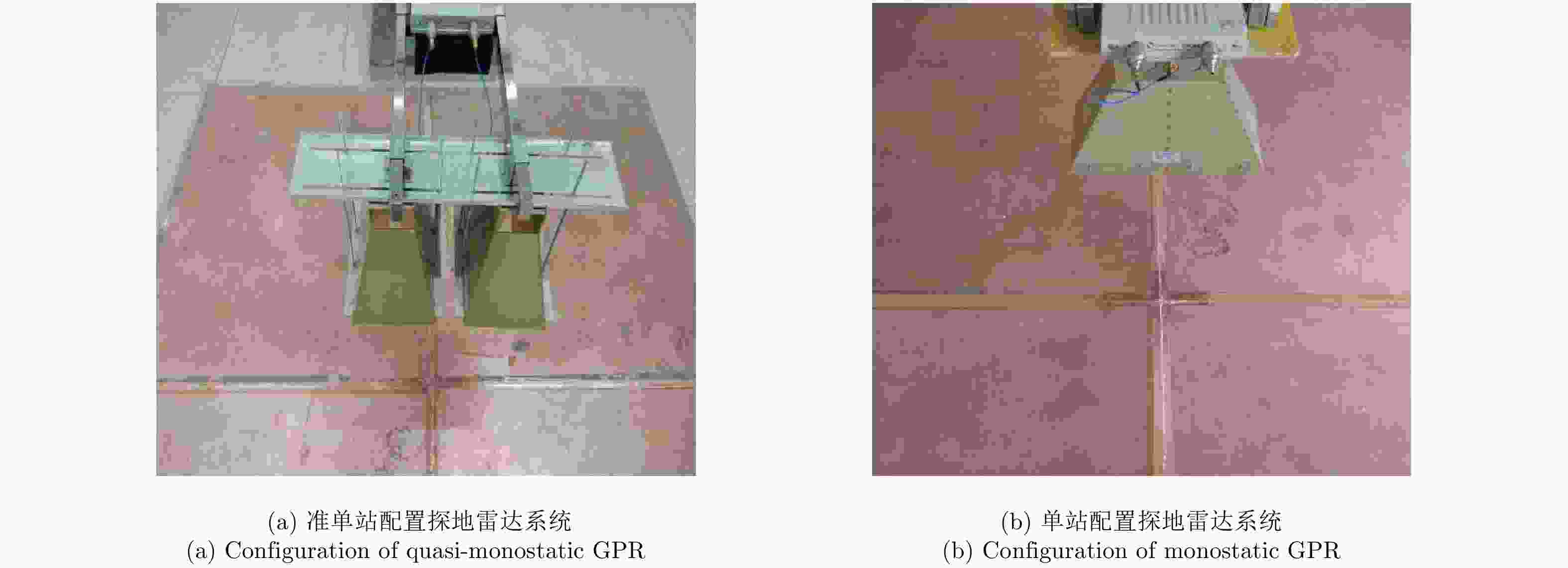
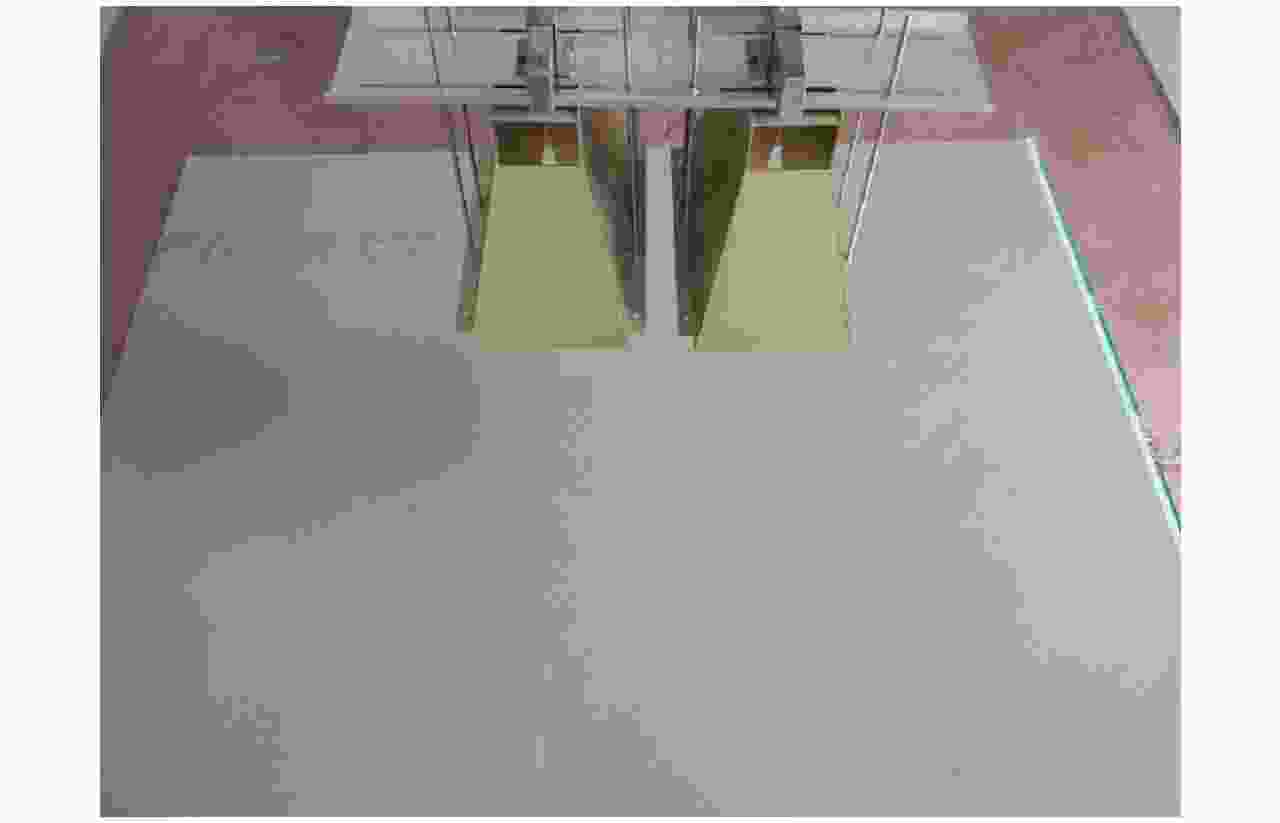
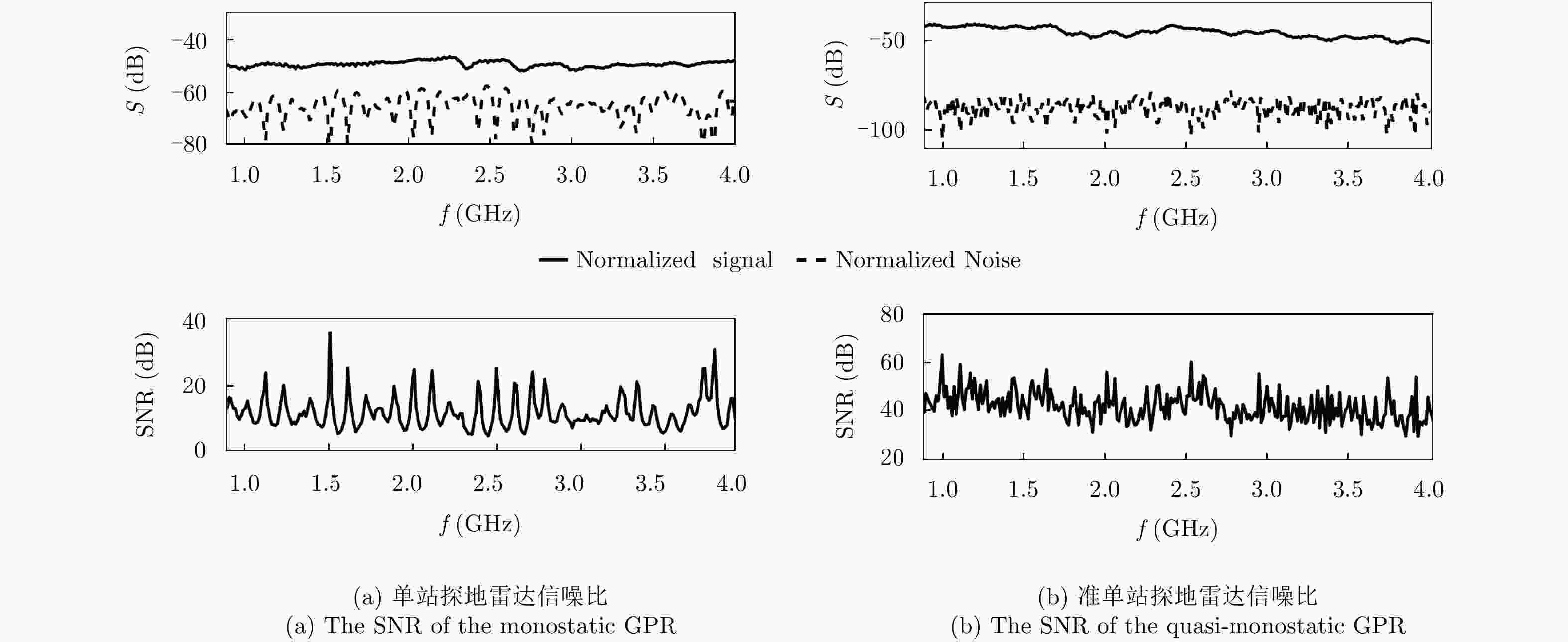
摘要: 探地雷达是一种被广泛使用的无损检测技术。利用探地雷达对分层媒质进行全波反演时，构建精确的探地雷达正演模型具有十分重要的意义。该文提出一种可用于准单站配置的步进频探地雷达的建模方法。在该模型中，探地雷达系统及其与分层媒质间的相互作用被表示成线性方程，天线对雷达信号的影响被表示为只与频率有关的传输函数。为验证模型准确性，该文在实验室条件下搭建了准单站配置的步进频探地雷达系统，并对已知厚度的石膏板和木板的雷达测量信号进行全波反演。反演结果表明：石膏板和木板的厚度估计误差均不超过0.3 mm，验证了所提出的正演模型具有高准确度。利用石膏板和木板搭建分层模型，该文进一步比较了准单站配置和单站配置步进频探地雷达系统对介电常数差异较小的分层媒质的反演性能。实验结果表明：准单站配置探地雷达能获得更精确的反演参数。通过对分界面反射信号的信噪比估计可知，准单站配置比单站配置探地雷达系统能获得高出约10 dB的信噪比，因此具有更好的反演性能。
- 正演模型 /
- 步进频探地雷达 /
- 准单站配置 /
- 信噪比 /
- 全波反演
Abstract: Ground Penetrating Radar (GPR) is a widely used non-destructive testing tool. Constructing an appropriate forward model is crucial for GPR to perform a full-waveform inversion of layered media. In this paper, a forward model for the quasi-monostatic Stepped-Frequency GPR (SFGPR) is proposed. In the model, the GPR and its interaction with the layered medium are represented as a linear equation in which the effects of the antennas are represented by a set of frequency-dependent transfer functions. To verify the accuracy of the proposed model, the authors constructed a quasi-monostatic SFGPR in a laboratory condition and performed a full-waveform inversion of the measurement signals of plasterboard and woodblock with known thickness. In the inversion results, the thickness estimation errors of the plasterboard and woodblock are not more than 0.3 mm, indicating that the proposed forward model has a very high accuracy. The inversion performances of the quasi-monostatic and monostatic SFGPR are further compared for the layered medium constructed with plasterboard and woodblock, which has a small permittivity difference. The results show that the quasi-monostatic SFGPR can obtain more accurate inversion parameters. By estimating the Signal to Noise Ratio (SNR) of the reflected signal from the interface, it is found that the SNR obtained by the quasi-monostatic configuration is 10 dB higher than that of the monostatic; therefore, the quasi-monostatic GPR has the better inversion performance.
- Forward model /
- Stepped-Frequency Ground Penetrating Radar (SFGPR) /
- Quasi mono-static /
- Signal to Noise Ratio (SNR) /
- Full-waveform inversion

HTML全文

图 1 准单站探地雷达建模框图

Figure 1. Modeling diagram for the quasi-monostatic ground penetrating radar

下载: 全尺寸图片幻灯片

图 2 准单站配置和单站配置探地雷达系统

Figure 2. Configurations of quasi-monostatic and monostatic GPR

下载: 全尺寸图片幻灯片

图 3 简化模型和原始模型建模误差

Figure 3. Fitting errors of the simplified model and original model

下载: 全尺寸图片幻灯片

图 4 利用厚度已知的石膏板验证准单站探地雷达模型的精度

Figure 4. Validating the accuracy of the quasi-monostatic model with the thickness-known plasterboard

下载: 全尺寸图片幻灯片

图 5 石膏板与木板的实测波形与仿真波形的对比

Figure 5. Comparison of the measured and simulated signal for plasterboard and woodblock

下载: 全尺寸图片幻灯片

图 6 分界面反射信号的计算模型

Figure 6. Models used to calculate the reflections on the interface

下载: 全尺寸图片幻灯片

图 7 单站配置探地雷达和准单站配置探地雷达的信噪比对比

Figure 7. The comparison of the SNR between the monostatic and quasi-monostatic GPR

下载: 全尺寸图片幻灯片

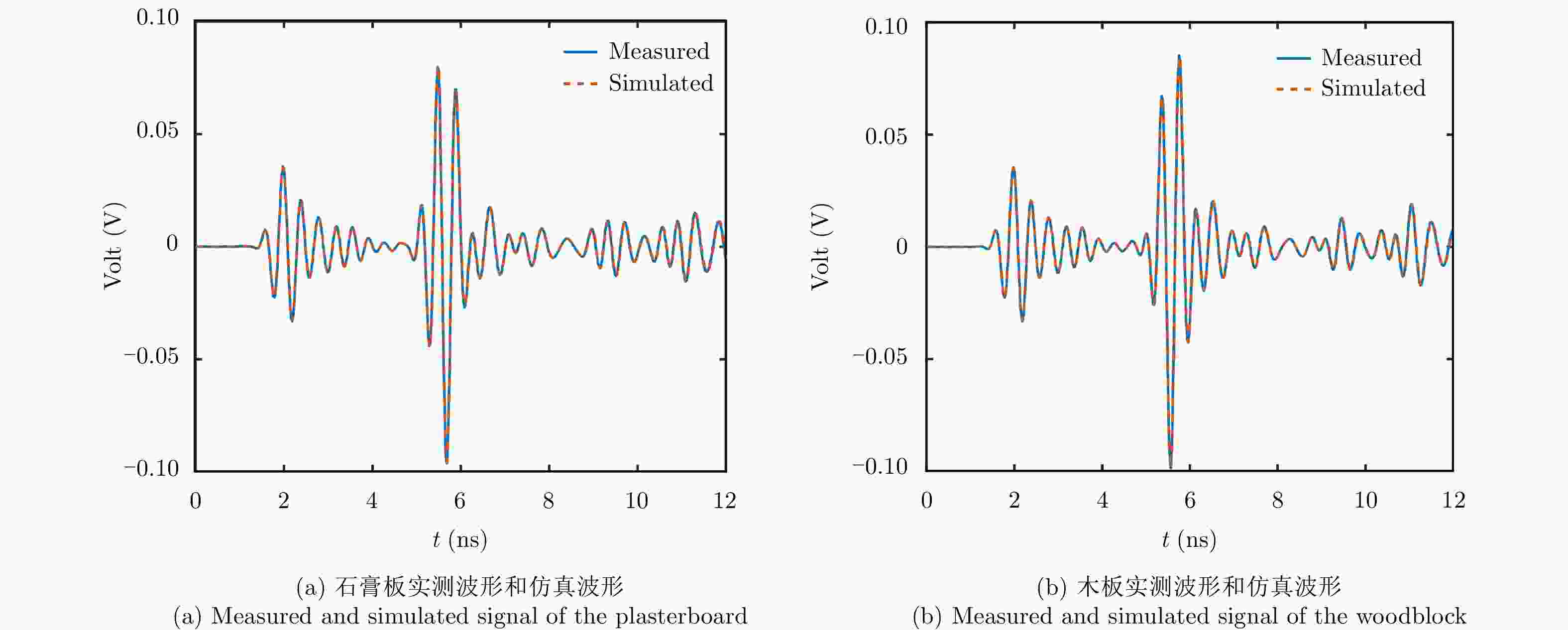
表 1 准单站探地雷达石膏板反演结果

Table 1. Inversion results of the plasterboard with the quasi-monostatic GPR

高度(mm)	反演相对介电常数	反演厚度(mm)	厚度估计误差(mm)
534.3	2.32	28.7	0.3
522.5	2.33	28.3	0.1
515.3	2.32	28.6	0.2

下载: 导出CSV

表 2 准单站探地雷达木板反演结果

Table 2. Inversion results of the woodblock with quasi-monostatic GPR

高度(mm)	反演相对介电常数	反演厚度(mm)	厚度估计误差(mm)
531.5	2.72	19.2	0.2
523.2	2.73	18.8	0.2
512.4	2.74	18.7	0.3

下载: 导出CSV

表 3 简化模型对石膏板的反演结果

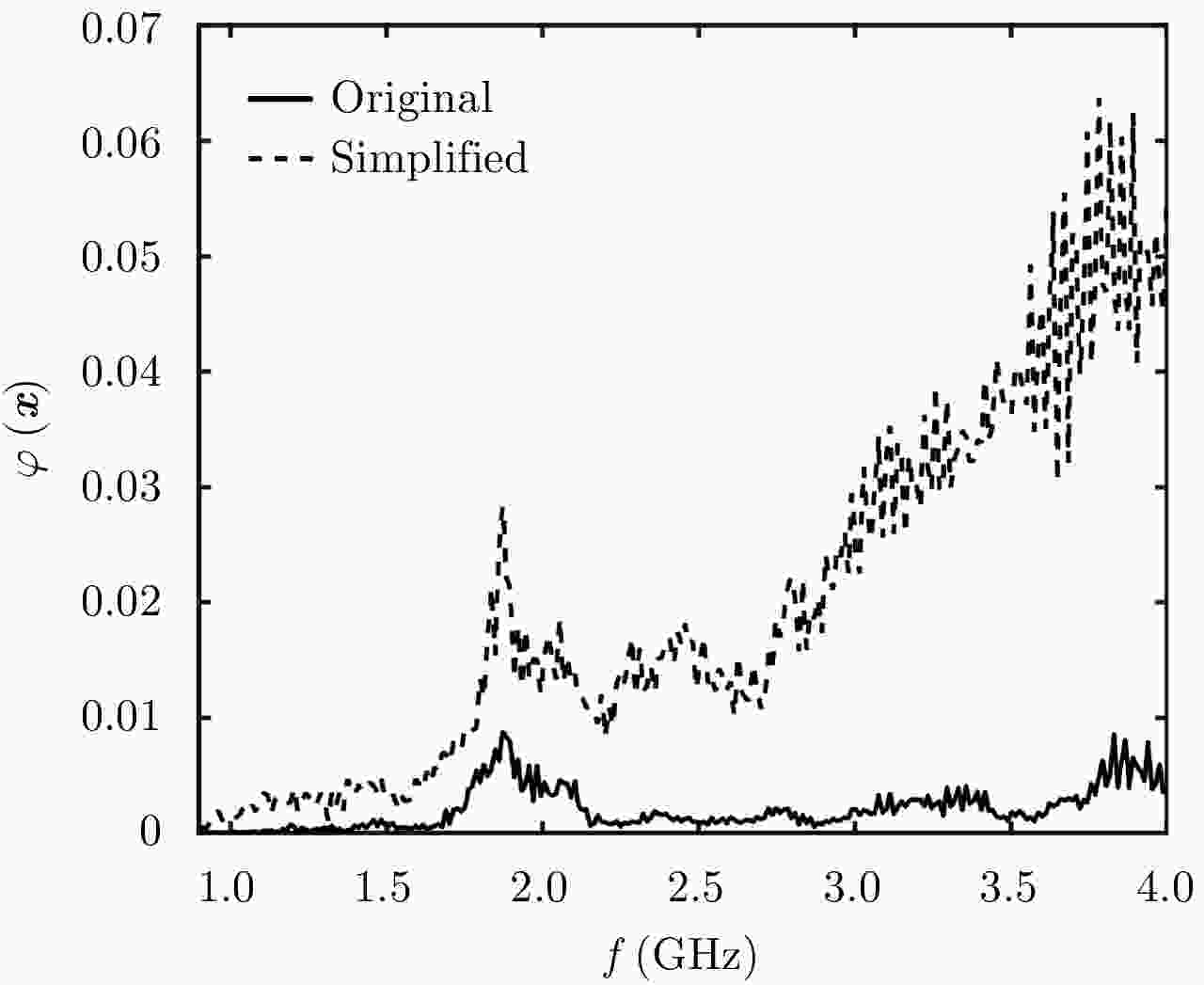
Table 3. Inversion results of the plasterboard with simplified model

高度(mm)	反演相对介电常数	反演厚度(mm)	厚度估计误差(mm)
533.8	2.43	28.0	0.4
522.0	2.45	27.6	0.8
514.7	2.44	27.9	0.5

下载: 导出CSV

表 4 准单站配置雷达3层结构反演结果

Table 4. Inversion results of the three-layer structure with quasi-monostatic GPR

天线高度 (mm)	反演石膏板介电常数	石膏板反演厚度 (mm)	石膏板厚度误差 (mm)	反演木板介电常数	木板反演厚度 (mm)	木板厚度误差 (mm)
532.2	2.34	28.1	0.3	2.71	19.5	0.5
524.2	2.32	28.8	0.4	2.72	19.4	0.4
510.3	2.31	28.9	0.5	2.75	18.5	0.5

下载: 导出CSV

表 5 单站配置雷达3层结构反演结果

Table 5. Inversion results of the three-layer structure with monostatic GPR

天线高度 (mm)	反演石膏板介电常数	石膏板反演厚度 (mm)	石膏板厚度误差 (mm)	反演木板介电常数	木板反演厚度 (mm)	木板厚度误差 (mm)
535.3	2.31	27.8	0.6	2.63	20.1	1.1
525.2	2.30	28.9	0.5	2.78	18.1	0.9
513.3	2.33	27.7	0.7	2.65	19.8	0.8

下载: 导出CSV

参考文献(13)

[1]	刘澜波, 钱荣毅. 探地雷达: 浅表地球物理科学技术中的重要工具[J]. 地球物理学报, 2015, 58(8): 2606–2617. doi: 10.6038/cjg20150802 LIU Lan-bo and QIAN Rong-yi. Ground penetrating radar: A critical tool in near-surface geophysics[J]. Chinese Journal of Geophysics, 2015, 58(8): 2606–2617. doi: 10.6038/cjg20150802
[2]	ZHANG J W, YE S B, YI L, et al. A Hybrid method applied to improve the efficiency of full-waveform inversion for pavement characterization[J]. Sensors, 2018, 18(9): 2916. doi: 10.3390/s18092916
[3]	KLĘSK P, KAPRUZIAK M, and OLECH B. Statistical moments calculated via integral images in application to landmine detection from Ground Penetrating Radar 3D scans[J]. Pattern Analysis and Applications, 2018, 21(3): 671–684. doi: 10.1007/s10044-016-0592-5
[4]	DEIANA R, LEUCCI G, and MARTORANA R. New perspectives on geophysics for archaeology: A special issue[J]. Surveys in Geophysics, 2018, 39(6): 1035–1038. doi: 10.1007/s10712-018-9500-4
[5]	LAHOUAR S and AL-QADI I L. Automatic detection of multiple pavement layers from GPR data[J]. NDT & E International, 2008, 41(2): 69–81. doi: 10.1016/j.ndteint.2007.09.001
[6]	LAMBOT S, SLOB E C, VAN DEN BOSCH I, et al. Modeling of ground-penetrating radar for accurate characterization of subsurface electric properties[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(11): 2555–2568. doi: 10.1109/TGRS.2004.834800
[7]	WARREN C and GIANNOPOULOS A. Creating finite-difference time-domain models of commercial ground-penetrating radar antennas using Taguchi’s optimization method[J]. Geophysics, 2011, 76(2): G37–G47. doi: 10.1190/1.3548506
[8]	HYUN S Y, KIM S Y, and KIM Y S. An equivalent feed model for the FDTD analysis of antennas driven through a ground plane by coaxial lines[J]. IEEE Transactions on Antennas and Propagation, 2009, 57(1): 161–167. doi: 10.1109/TAP.2008.2009650
[9]	VENKATARAYALU N V, GAN Y B, LEE R, et al. Application of hybrid FETD-FDTD method in the modeling and analysis of antennas[J]. IEEE Transactions on Antennas and Propagation, 2008, 56(9): 3068–3072. doi: 10.1109/TAP.2008.928809
[10]	ALKHALIFEH K, HISLOP G, OZDEMIR N A, et al. Efficient MoM simulation of 3-D antennas in the vicinity of the ground[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(12): 5335–5344. doi: 10.1109/TAP.2016.2618482
[11]	GENTILI G G and SPAGNOLINI U. Electromagnetic inversion in monostatic ground penetrating radar: TEM horn calibration and application[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(4): 1936–1946. doi: 10.1109/36.851775
[12]	LAMBOT S, SLOB E, and VEREECKEN H. Fast evaluation of zero-offset green’s function for layered media with application to ground-penetrating radar[J]. Geophysical Research Letters, 2007, 34(21): L21405. doi: 10.1029/2007GL031459
[13]	The data sheet of the portable VNA[OL]. http://www.c-oppermountaintech.com/products/12/S5048/.