超宽带雷达建筑物结构稀疏成像

金添; 宋勇平

doi:10.12000/JR18031

超宽带雷达建筑物结构稀疏成像

DOI: 10.12000/JR18031

金添^,,
宋勇平

国防科技大学电子科学学院长沙 410073

基金项目: 国家自然科学基金（61271441，61372161）

详细信息

作者简介:
金　添(1980–)，男，国防科学技术大学，教授，博士生导师，主要从事隐蔽目标雷达成像与检测识别、新型微波传感器机理与系统实现等方面的研究工作。2009年获全国优秀博士学位论文奖，2010年入选教育部“新世纪优秀人才支持计划”，2014年获国际无线电科学联盟青年科学家奖。承担国家自然科学基金、武器装备探索等多项课题，获省部级科技进步一等奖1项、二等奖2项。“信号处理与系统”国家精品课程和资源共享课主讲教师，信号处理系列课程国家级教学团队主要成员。已发表论文100余篇，获授权国家发明专利5项，出版专著3部、译著1部、教材1部。E-mail: tianjin@nudt.edu.cn

通讯作者:
金添 tianjin@nudt.edu.cn

计量
- 文章访问数: 2651
- HTML全文浏览量: 997
- PDF下载量: 444
- 被引次数: 0
出版历程
- 收稿日期: 2018-04-08
- 修回日期: 2018-05-22
- 网络出版日期: 2018-06-28

Sparse Imaging of Building Layouts in Ultra-wideband Radar

Jin Tian^,,
Song Yongping

College of Electronic Science, National University of Defense Technology, Changsha 410073, China

Funds: The National Natural Science Foundation of China (61271441, 61372161)

摘要

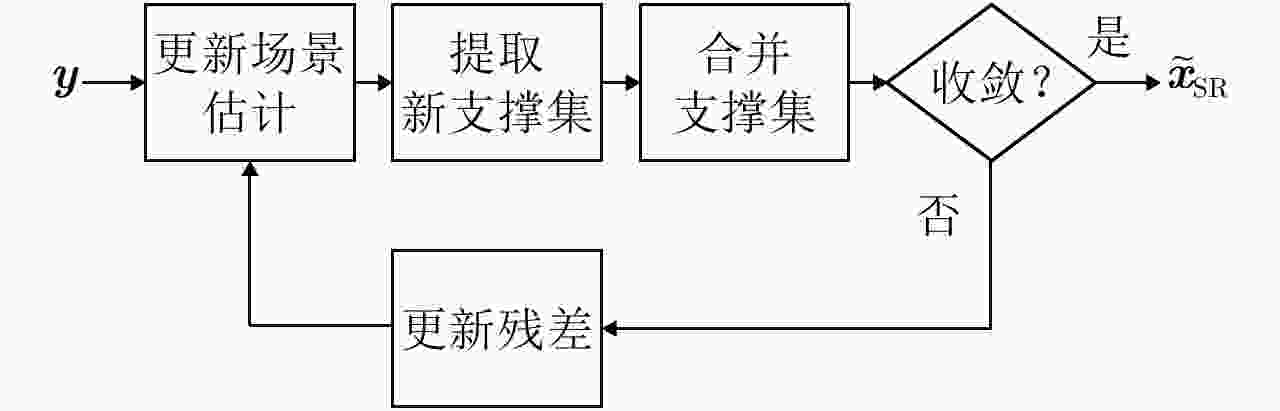
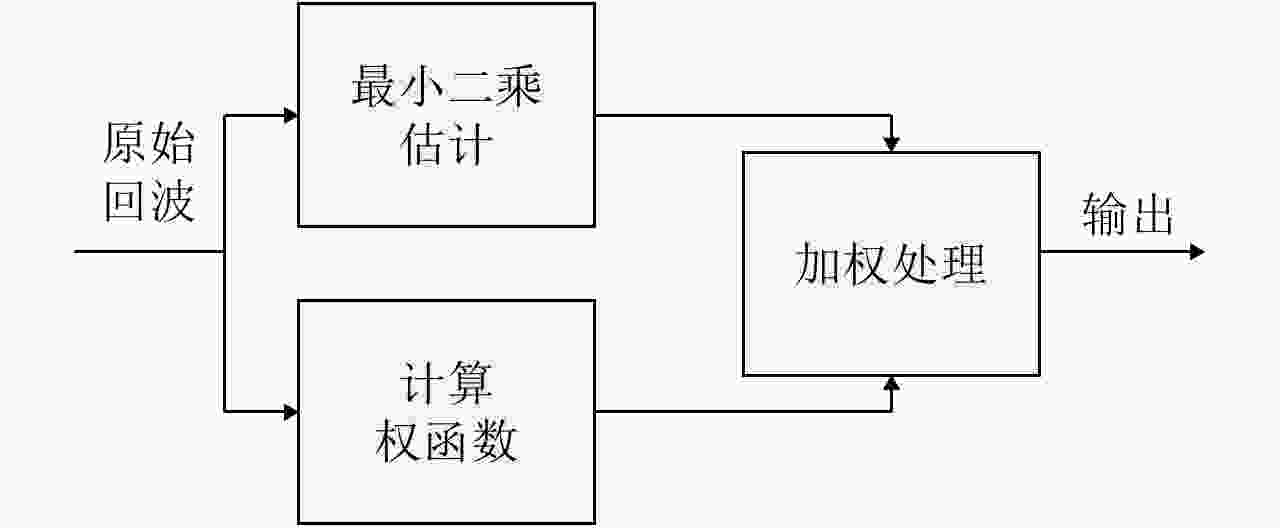
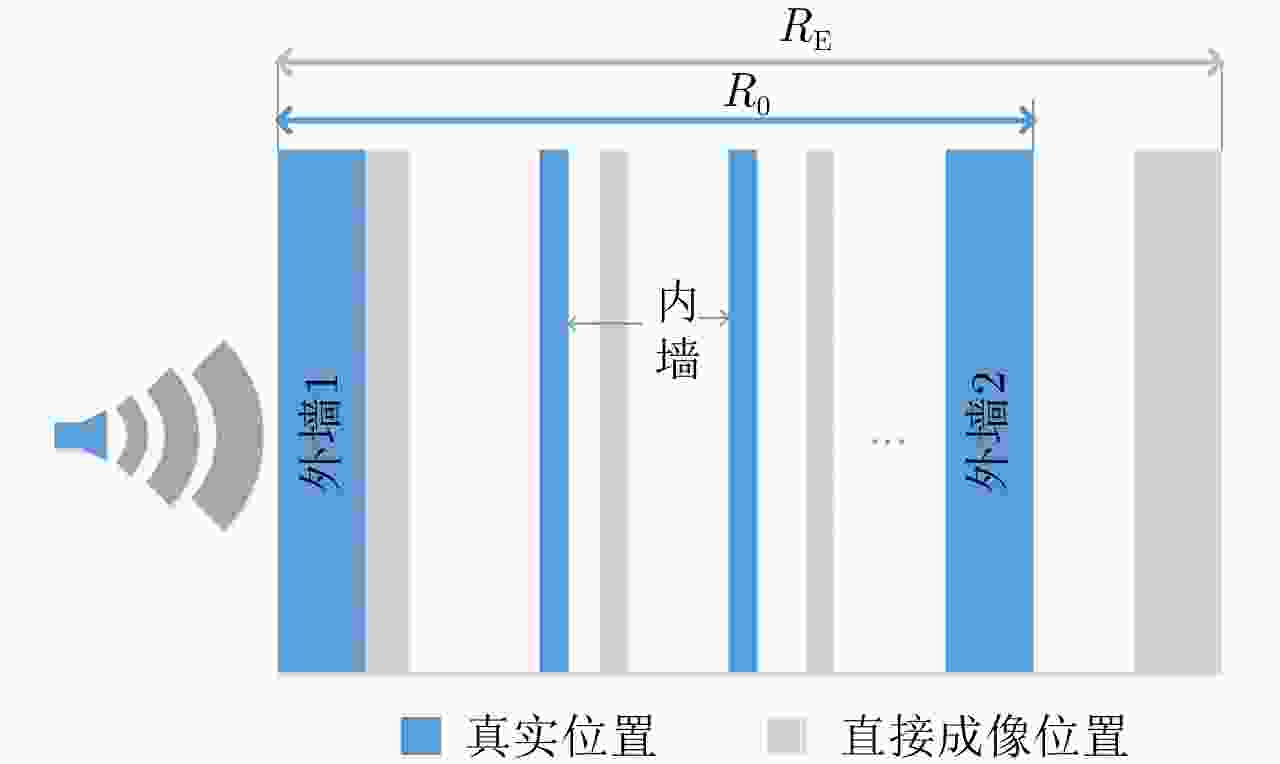
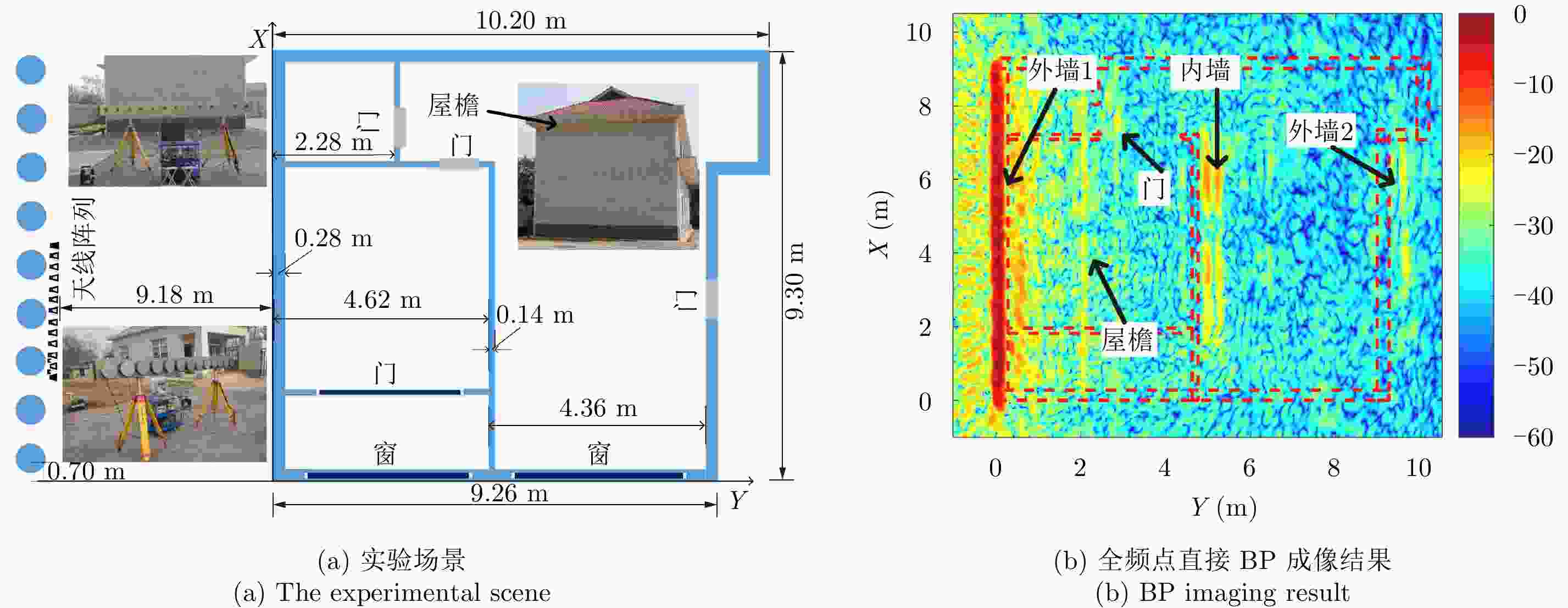
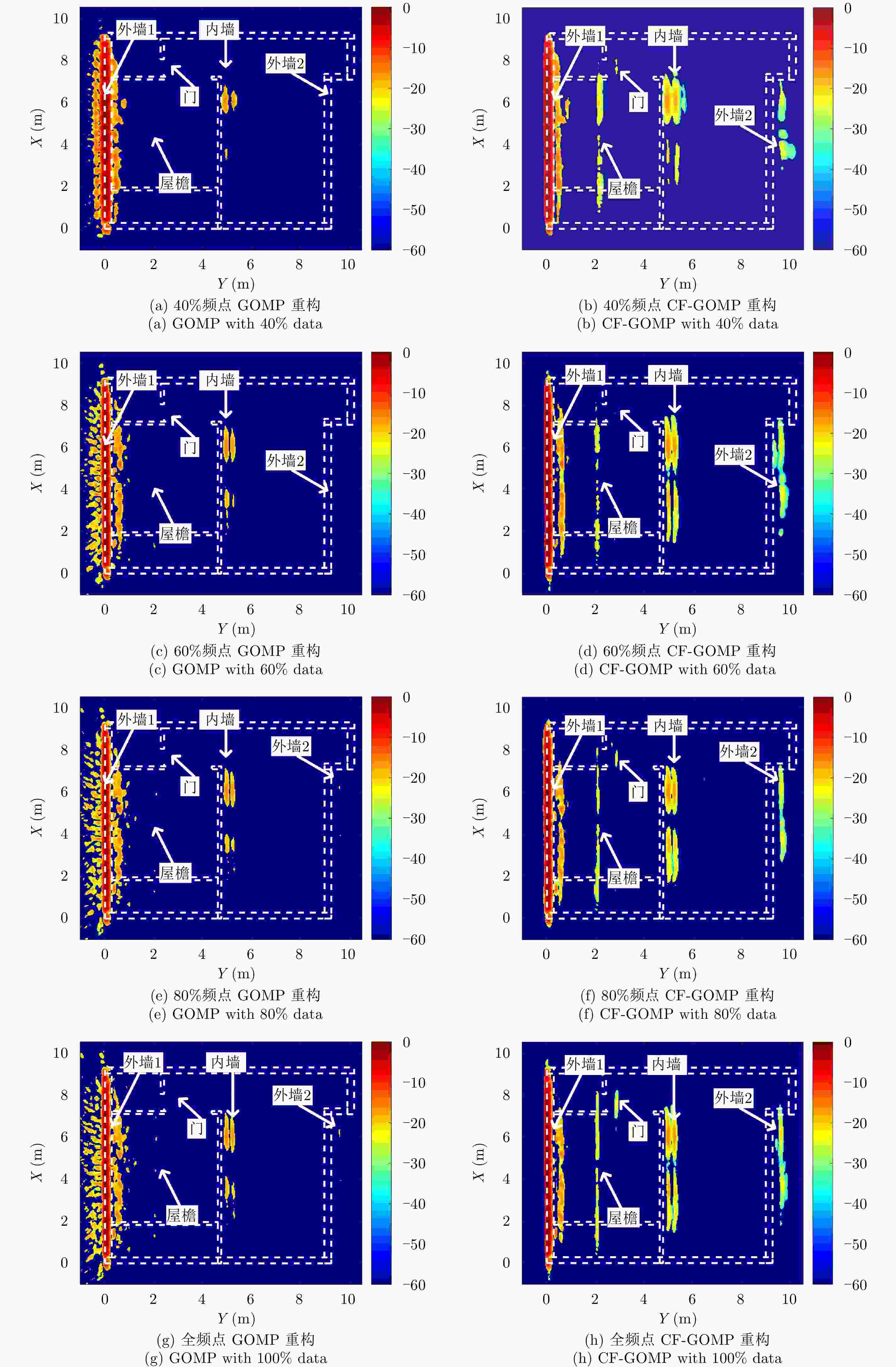
摘要: 超宽带雷达具备穿透墙体获得建筑物内部结构布局的能力，为建筑物内人员探测定位提供更丰富的信息。传统成像常存在较为严重的旁瓣，而且墙后目标成像位置也会受墙体影响而产生偏移。为提高成像质量，稀疏重构技术被引入穿墙成像领域，但传统方法对弱散射目标的重构概率较低。该文提出结合相干因子(Coherence Factor, CF)加权的稀疏重构方法，在稀疏重构提取支撑集的过程中，利用CF增强成像的结果来提高支撑集原子的正确性，降低稀疏重构过程中强散射目标旁瓣的影响，最终提高场景中弱散射目标的重构概率。同时建立了多层墙体位置校正模型，将场景校正放到稀疏重构之后进行，从而以较低的计算复杂度降低墙体定位误差。实测数据处理结果表明，相比于传统的稀疏成像方法，相同的数抽取比例下，该文提出的方法能够有效提高场景中弱散射目标重构概率，并将建筑物内部墙体定位误差降低至10 cm以内。
- 超宽带雷达 /
- 穿墙成像 /
- 稀疏重构 /
- 建筑物结构
Abstract: Ultra-WideBand (UWB) radar can reconstruct the layout of a building, providing rich information for detecting and locating humans in buildings. Traditional imaging methods suffer from serious sidelobes and location displacement of behind-the-wall target because of the influence of walls. Sparse recovery is introduced into the field of through-the-wall imaging to improve the imaging quality. However, the reconstruction probability of weak scattering targets is low in traditional methods. In this study, the combination of sparse recovery method and Coherence Factor (CF) weighting is proposed to improve the reconstruction probability of weak scattering targets inside a room. The quasi-establishment of the support set can be improved during sparse imaging by reducing the effect of the sidelobes of strong scattering targets with CF, ultimately enhancing the robustness of the sparse imaging of the building layout. A location correction model for multiple walls after sparse imaging is established, based on which the locating error of walls can be reduced with a low amount of calculation. The results of the measured data reveal that compared with the traditional generalized orthogonal matching pursuit method, the proposed methods can improve the reconstruction probability of weak scattering targets and reduce the locating error of the inner layouts of buildings to less than 10 cm.
- Ultra-WideBand (UWB) radar /
- Through-the-wall imaging /
- Sparse recovery /
- Building layout

HTML全文

图 1 MIMO雷达成像模型

Figure 1. MIMO radar image model

下载: 全尺寸图片幻灯片

图 2 贪婪法的一般流程

Figure 2. The general flow of greed methods

下载: 全尺寸图片幻灯片

图 3 CF处理过程

Figure 3. The procedure of CF

下载: 全尺寸图片幻灯片

图 4 多层墙体结构的建筑物成像示意图

Figure 4. The schematic of building layout imaging with multi-layer wall

下载: 全尺寸图片幻灯片

图 5 实验场景与全频点直接BP成像结果

Figure 5. The experimental scene and BP imaging result

下载: 全尺寸图片幻灯片

图 6 不同数据比例下GOMP与CF-GOMP重构结果对比

Figure 6. Comparison of GOMP and CF-GOMP reconstruction results under different data ratios

下载: 全尺寸图片幻灯片

图 7 校正前后全频点CF-GOMP重构结果中建筑物结构在y 轴上的分布对比

Figure 7. Comparison of the distribution of building structures on the y axis before (the blue dot line) and after (the red solid line) correction in CF-GOMP reconstruction with 100% data

下载: 全尺寸图片幻灯片

图 8 校正后的全频点CF-GOMP重构结果

Figure 8. Corrected CF-GOMP reconstruction result with 100% data

下载: 全尺寸图片幻灯片

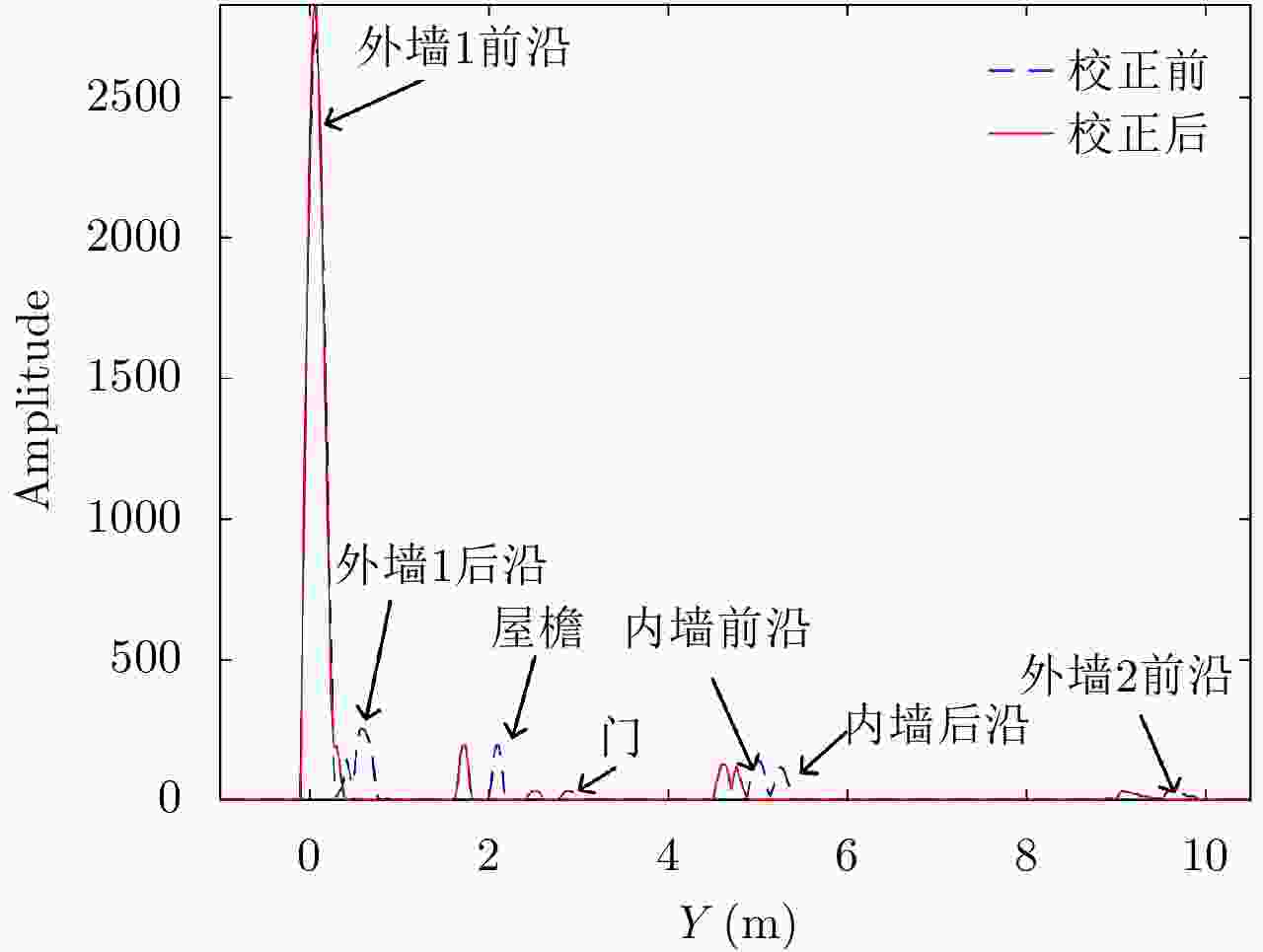
表 1 各墙体校正前后y方向位置对比

Table 1. The position contrast on y axis before and after correction of each wall

结构名称	校正前位置(m)	真实位置(m)	校正后位置(m)	校正前误差(m)	校正后误差(m)
外墙1后沿	0.614	0.280	0.297	0.334	0.017
内墙前沿	5.024	4.620	4.591	0.404	–0.029
内墙后沿	5.254	4.760	4.793	0.494	0.033
外墙2前沿	9.491	8.980	9.059	0.511	0.079

下载: 导出CSV

参考文献(19)

[1]	Amin M. Compressive Sensing for Urban Radar[M]. Boca Raton, FL: CRC Press, 2015: 49–86.
[2]	Chen B, Jin T, Lu B Y, et al. Building interior layout reconstruction from through-the-wall radar image using MST-based method[J]. EURASIP Journal on Advances in Signal Processing, 2014, 2014: 31. DOI: 10.1186/1687-6180-2014-31
[3]	胡俊. 远距离超宽带穿墙雷达人体目标成像关键技术研究[D]. [博士论文], 国防科学技术大学, 2014: 33–57. Hu Jun. Study of human target imaging with long-range ultra-wideband through-wall imaging radar[D]. [Ph.D. dissertation], National University of Defense Technology, 2014: 33–57.
[4]	Anwar N S N and Abdullah M Z. Sidelobe suppression featuring the phase coherence factor in 3-D through-the-wall radar imaging[J]. Radioengineering, 2016, 25(4): 730–740. DOI: 10.13164/re.2016.0730
[5]	Burkholder R J and Browne K E. Coherence factor enhancement of through-wall radar images[J]. IEEE Antennas and Wireless Propagation Letters, 2010, 9: 842–845. DOI: 10.1109/LAWP.2010.2069078
[6]	吴一戎, 洪文, 张冰尘, 等. 稀疏微波成像研究进展(科普类)[J]. 雷达学报, 2014, 3(4): 383–395. DOI: 10.3724/SP.J.1300.2014.14105 Wu Yi-Rong, Hong Wen, Zhang Bing-chen, et al. Current developments of sparse microwave imaging[J]. Journal of Radars, 2014, 3(4): 383–395. DOI: 10.3724/SP.J.1300.2014.14105
[7]	刘记红, 徐少坤, 高勋章, 等. 压缩感知雷达成像技术综述[J]. 信号处理, 2011, 27(2): 251–260. DOI: 10.3969/j.issn.1003-0530.2011.02.016 Liu Ji-hong, Xu Shao-kun, Gao Xun-zhang, et al. A review of radar imaging technique based on compressed sensing[J]. Signal Processing, 2011, 27(2): 251–260. DOI: 10.3969/j.issn.1003-0530.2011.02.016
[8]	李少东, 杨军, 陈文峰, 等. 基于压缩感知理论的雷达成像技术与应用研究进展[J]. 电子与信息学报, 2016, 38(2): 495–508. DOI: 10.1109/JEIT150874 Li Shao-dong, Yang Jun, Chen Wen-feng, et al. Overview of radar imaging technique and application based on compressive sensing theory[J]. Journal of Electronics&Information Technology, 2016, 38(2): 495–508. DOI: 10.1109/JEIT150874
[9]	顾福飞, 池龙, 张群, 等. 基于压缩感知的稀疏阵列MIMO雷达成像方法[J]. 电子与信息学报, 2011, 33(10): 2452–2457. DOI: 10.3724/SP.J.1146.2011.00287 Gu Fu-fei, Chi Long, Zhang Qun, et al. An imaging method for MIMO radar with sparse array based on compressed sensing[J]. Journal of Electronics&Information Technology, 2011, 33(10): 2452–2457. DOI: 10.3724/SP.J.1146.2011.00287
[10]	Carmi A Y, Mihaylova L S, and Godsill S J. Compressed Sensing & Sparse Filtering[M]. Heidelberg: Springer, 2014: 396–461.
[11]	Eldar Y C and Kutyniok G. Compressed Sensing: Theory and Applications[M]. Cambridge: Cambridge University Press, 2012: 348–393.
[12]	孙洪, 张智林, 余磊. 从稀疏到结构化稀疏: 贝叶斯方法[J]. 信号处理, 2012, 28(6): 759–773. DOI: 10.3969/j.issn.1003-0530.2012.06.001 Sun Hong, Zhang Zhi-lin, and Yu Lei. From sparsity to structured sparsity: Bayesian perspective[J]. Signal Processing, 2012, 28(6): 759–773. DOI: 10.3969/j.issn.1003-0530.2012.06.001
[13]	Wang J, Kwon S, and Shim B. Generalized orthogonal matching pursuit[J]. IEEE Transactions on Signal Processing, 2012, 60(12): 6202–6216. DOI: 10.1109/TSP.2012.2218810
[14]	杨俊刚. 利用稀疏信息的正则化雷达成像理论与方法研究[D]. [博士论文], 国防科学技术大学, 2013: 19–30. Yang Jun-gang. Research on sparsity-driven regularization radar imaging theory and method[D]. [Ph.D. dissertation], National University of Defense Technology, 2013: 19–30.
[15]	孙鑫. 超宽带穿墙雷达成像方法与技术研究[D]. [博士论文], 国防科学技术大学, 2015: 37–68. Sun Xin. Research on method and technique of ultra-wideband through-the-wall radar imaging[D]. [Ph.D. dissertation], National University of Defense Technology, 2015: 37–68.
[16]	Song Y P, Jin T, Lu B Y, et al. An extended virtual aperture imaging model for through-the-wall sensing and its environmental parameters estimation[J]. Radioengineering, 2014, 23(3): 842–851.
[17]	Jin T, Chen B, and Zhou Z M. Image-domain estimation of wall parameters for autofocusing of through-the-wall SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(3): 1836–1843. DOI: 10.1109/TGRS.2012.2206395
[18]	刘记红, 黎湘, 徐少坤, 等. 基于改进正交匹配追踪算法的压缩感知雷达成像方法[J]. 电子与信息学报, 2012, 34(6): 1344–1350. DOI: 10.3724/SP.J.1146.2011.01097 Liu Ji-hong, Li Xiang, Xu Shao-kun, et al. Compressed sensing radar imaging methods based on modified orthogonal matching pursuit algorithms[J]. Journal of Electronics&Information Technology, 2012, 34(6): 1344–1350. DOI: 10.3724/SP.J.1146.2011.01097
[19]	Fang J, Xu Z B, Zhang B C, et al. Fast compressed sensing SAR imaging based on approximated observation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(1): 352–363. DOI: 10.1109/JSTARS.2013.2263309