基于子空间正交的阵列干涉SAR系统相位中心位置定标方法

卜运成; 王宇; 张福博; 冀广宇; 陈龙永; 梁兴东

doi:10.12000/JR18007

基于子空间正交的阵列干涉SAR系统相位中心位置定标方法

DOI: 10.12000/JR18007

卜运成^1,2,3,,
王宇^1,2,3,,
张福博^1,2,,
冀广宇^1,2,3,,
陈龙永^1,2,3,,
梁兴东^1,2,3, ,

①.
中国科学院电子学研究所北京 100190
②.
微波成像技术国家级重点实验室北京 100190
③.
中国科学院大学北京 100049

基金项目: 国家部委基金

详细信息

作者简介:
卜运成(1991–)，男，湖南人，电子科技大学学士，中国科学院电子学研究所博士研究生，主要研究方向为多通道合成孔径雷达3维成像、阵列干涉合成孔径雷达系统定标。E-mail: buyuncheng13@mails.ucas.ac.cn

王宇：王宇(1976–)，男，博士，中国科学院电子学研究所副研究员，研究方向为机载合成孔径雷达定标和雷达信号处理。E-mail: wangyu@mail.ie.ac.cn

张福博(1988–)，男，河北人，博士，中国科学院电子学研究所助理研究员，研究方向为多通道合成孔径雷达3维成像。E-mail: zhangfubo8866@126.com

冀广宇(1988–)，男，辽宁人，中国科学技术大学学士，中国科学院电子学研究所博士研究生，研究方向为机载合成孔径雷达信号处理。E-mail: gyji@mail.ustc.edu.cn

陈龙永(1979–)，男，安徽人，中国科学院电子学研究所博士，研究员，研究方向为新概念雷达系统设计与实现。E-mail: lychen@mail.ie.ac.cn

梁兴东(1973–)，男，陕西人，北京理工大学博士，中国科学院电子学研究所研究员，研究方向为高分辨率合成孔径雷达系统、干涉合成孔径雷达、成像处理及应用、实时数字信号处理等。E-mail: xdliang@mail.ie.ac.cn

通讯作者:
梁兴东 xdliang@mail.ie.ac.cn

计量
- 文章访问数: 3149
- HTML全文浏览量: 622
- PDF下载量: 268
- 被引次数: 0
出版历程
- 收稿日期: 2018-01-25
- 修回日期: 2018-05-18
- 网络出版日期: 2018-06-28

Antenna Phase Center Calibration for Array InSAR System Based on Orthogonal Subspace

Bu Yuncheng^{1,2,3
,},
Wang Yu^{1,2,3
,},
Zhang Fubo^{1,2
,},
Ji Guangyu^{1,2,3
,},
Chen Longyong^{1,2,3
,},
Liang Xingdong^{1,2,3
, ,}

①.
Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China
②.
National Key Laboratory of Science and Technology on Microwave Imaging, Beijing 100190, China
③.
University of Chinese Academy of Sciences, Beijing 100049, China

Funds: The National Ministries Foundation

摘要

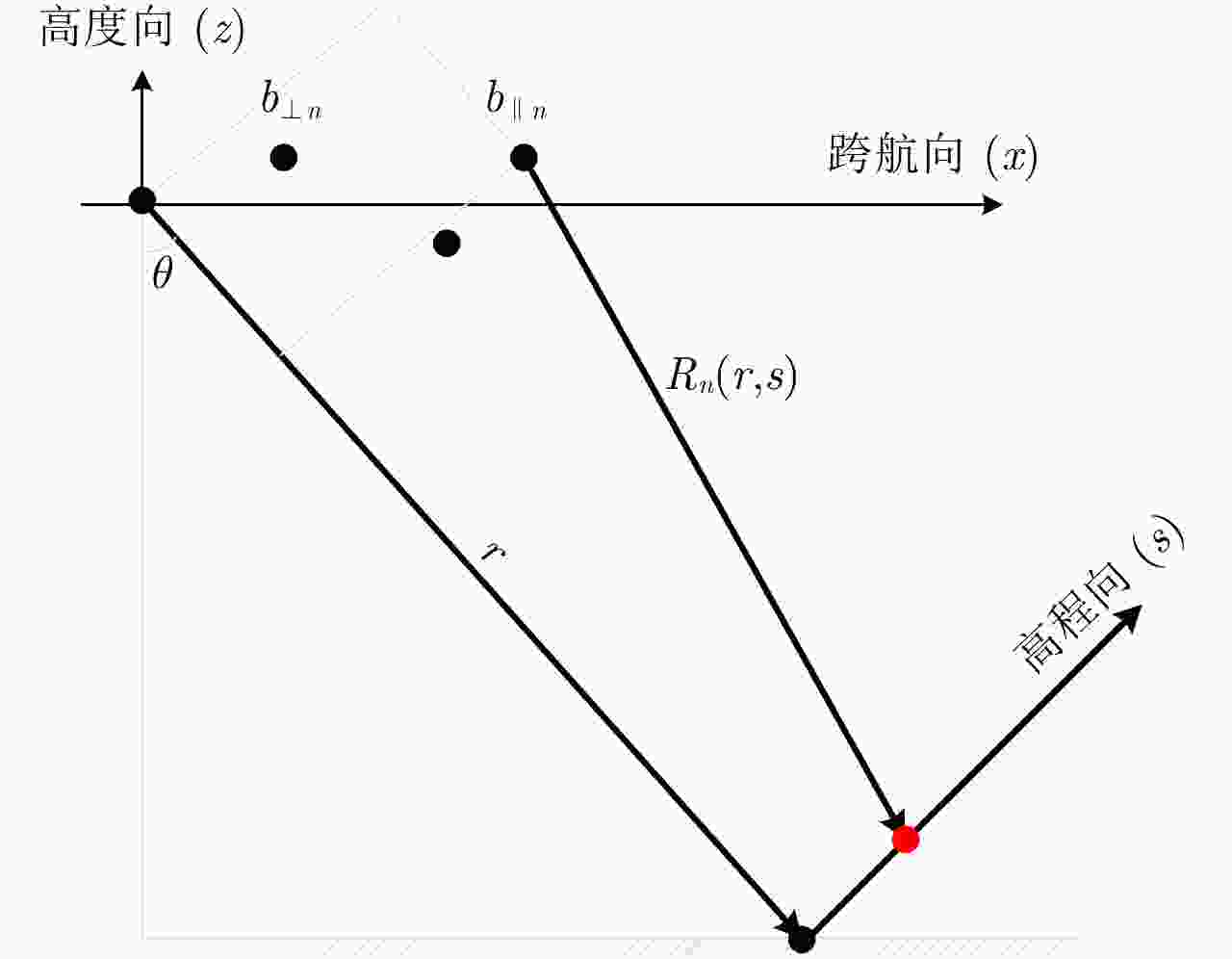
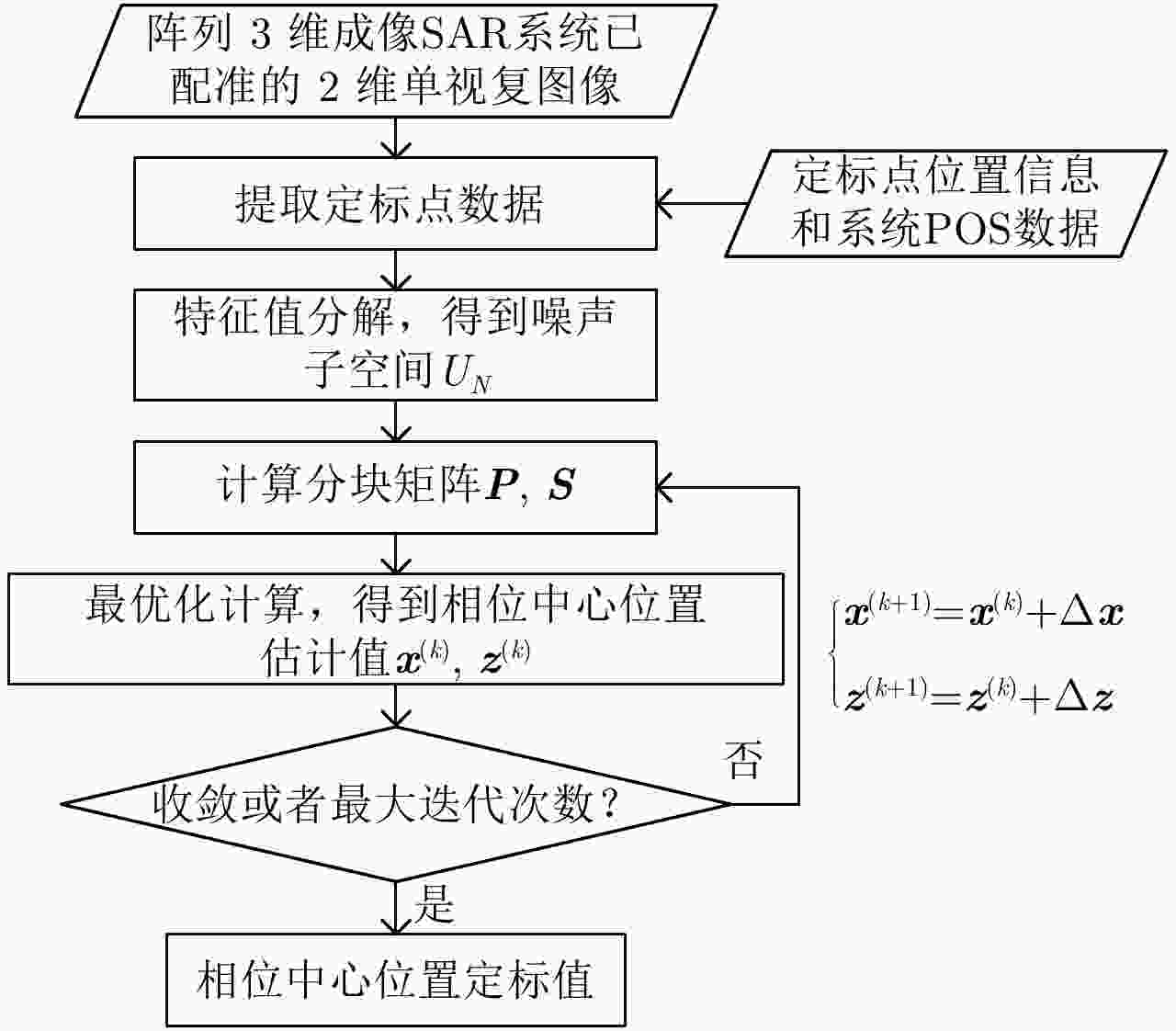
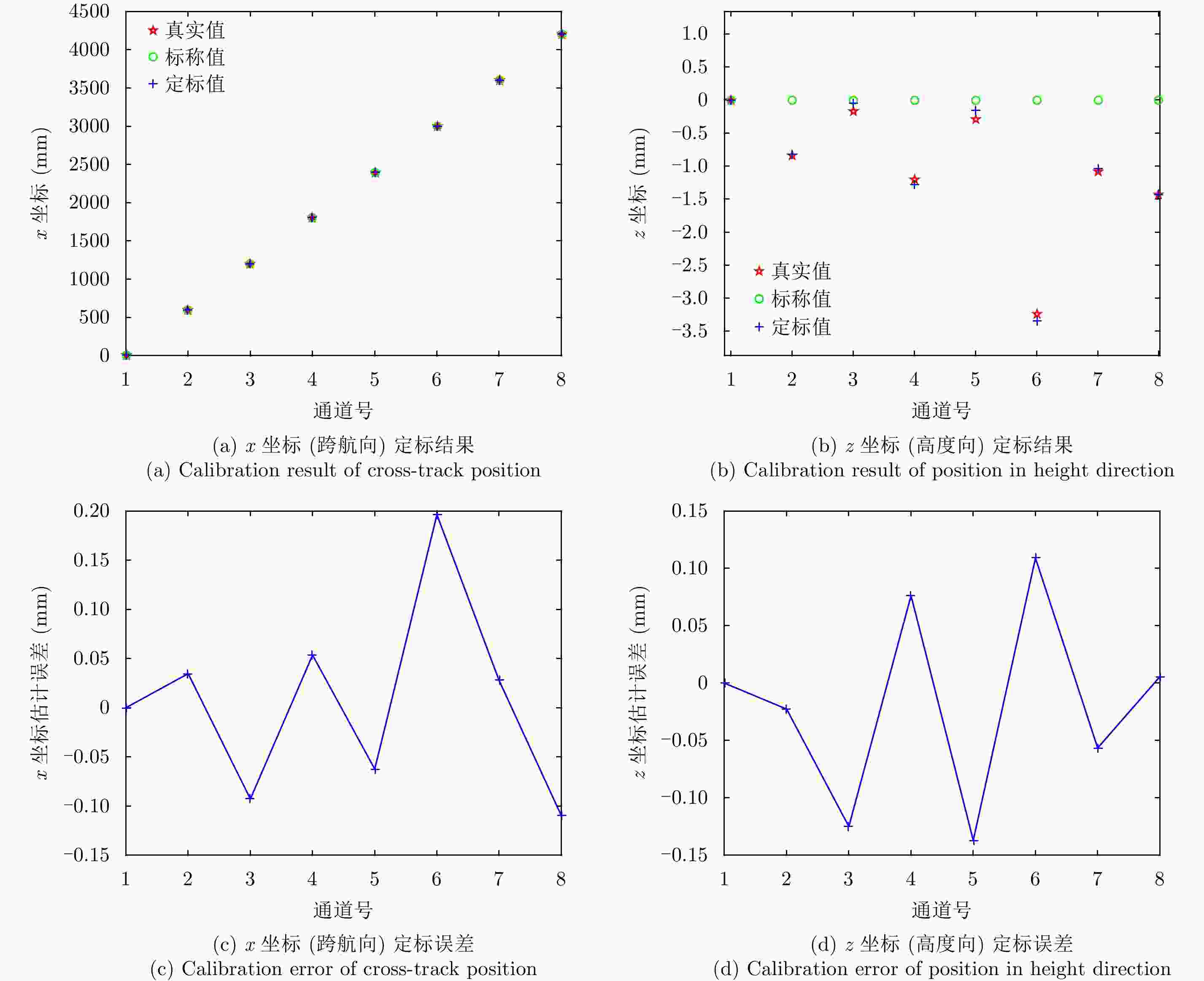
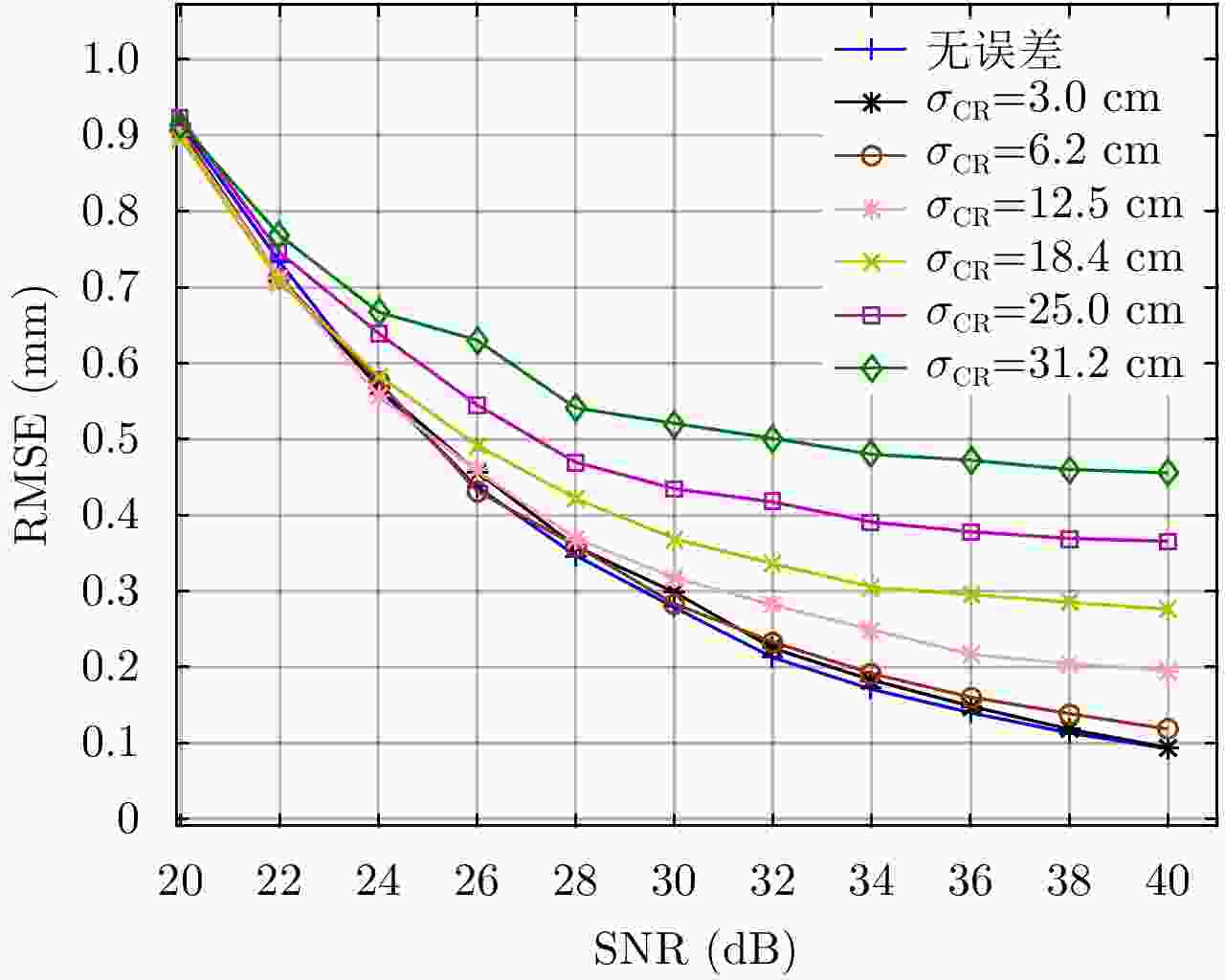
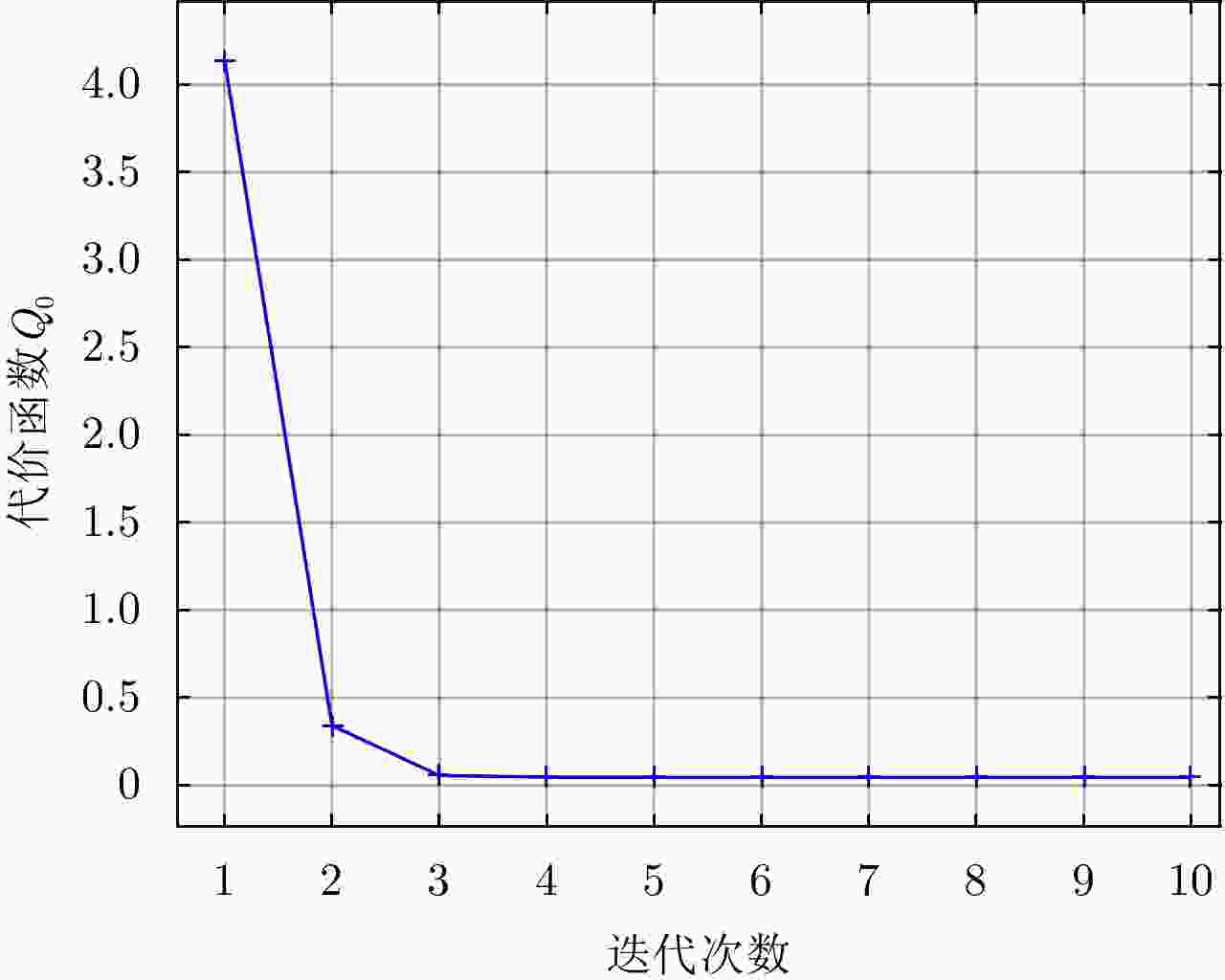
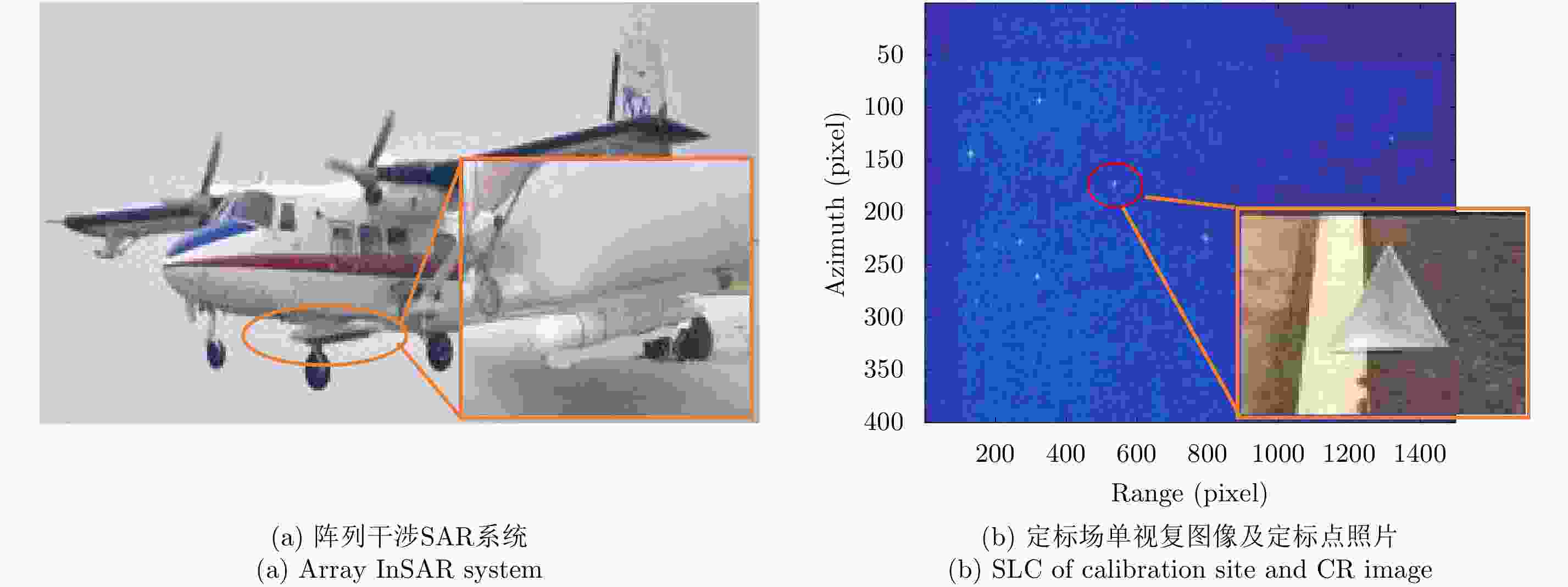
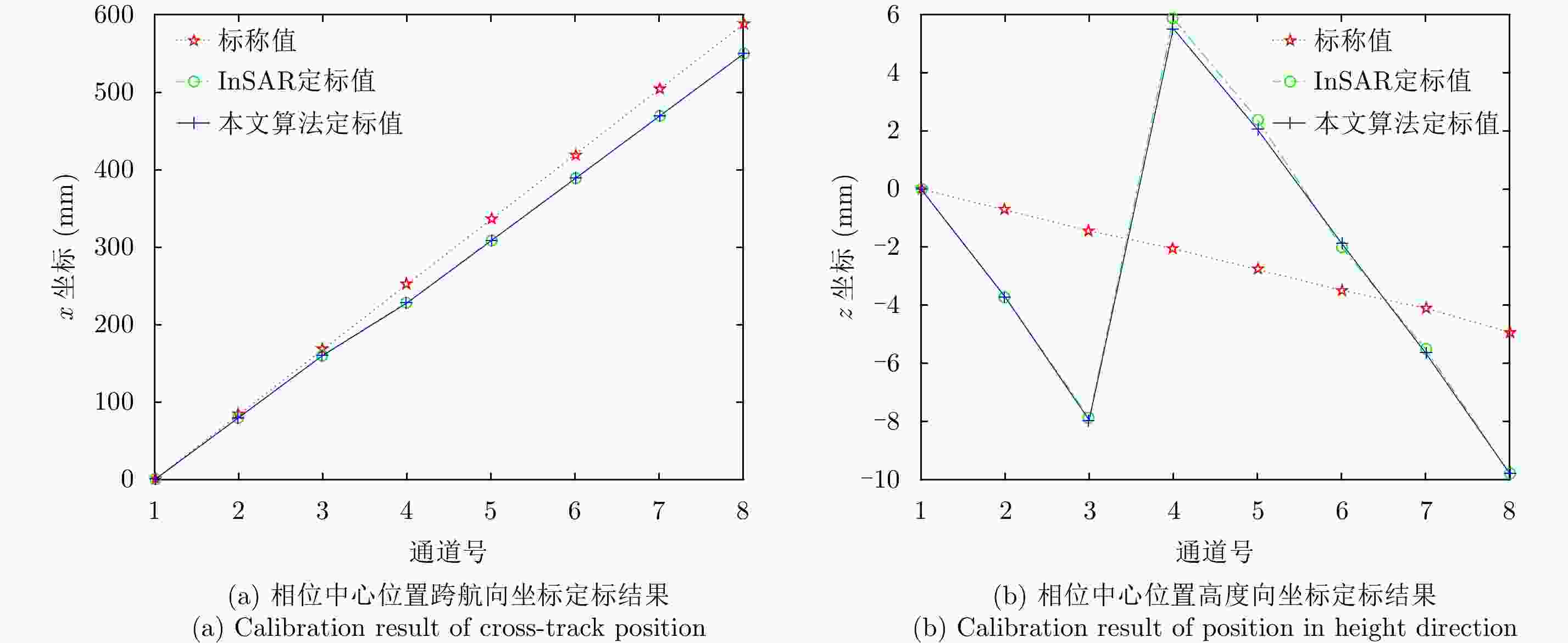
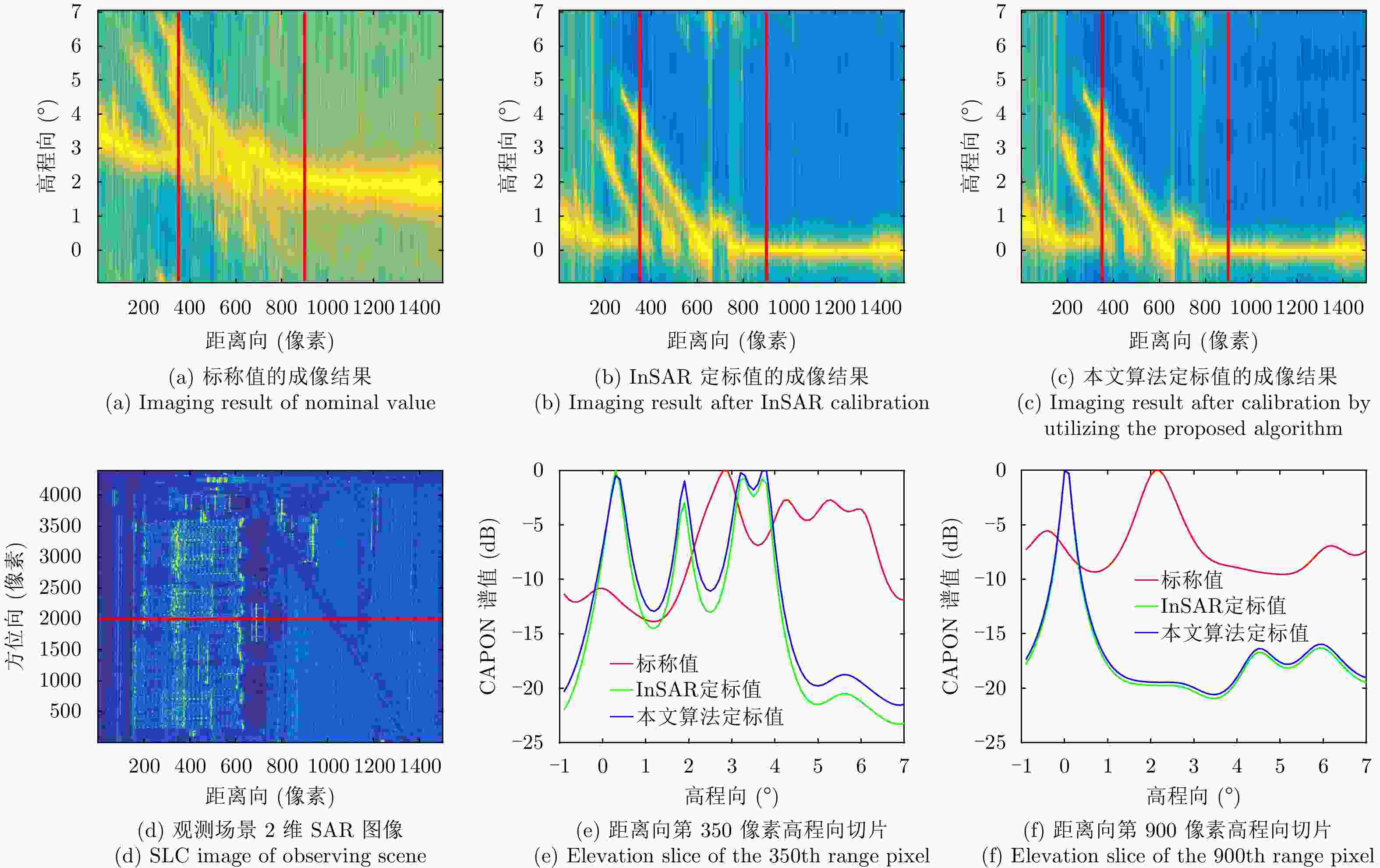
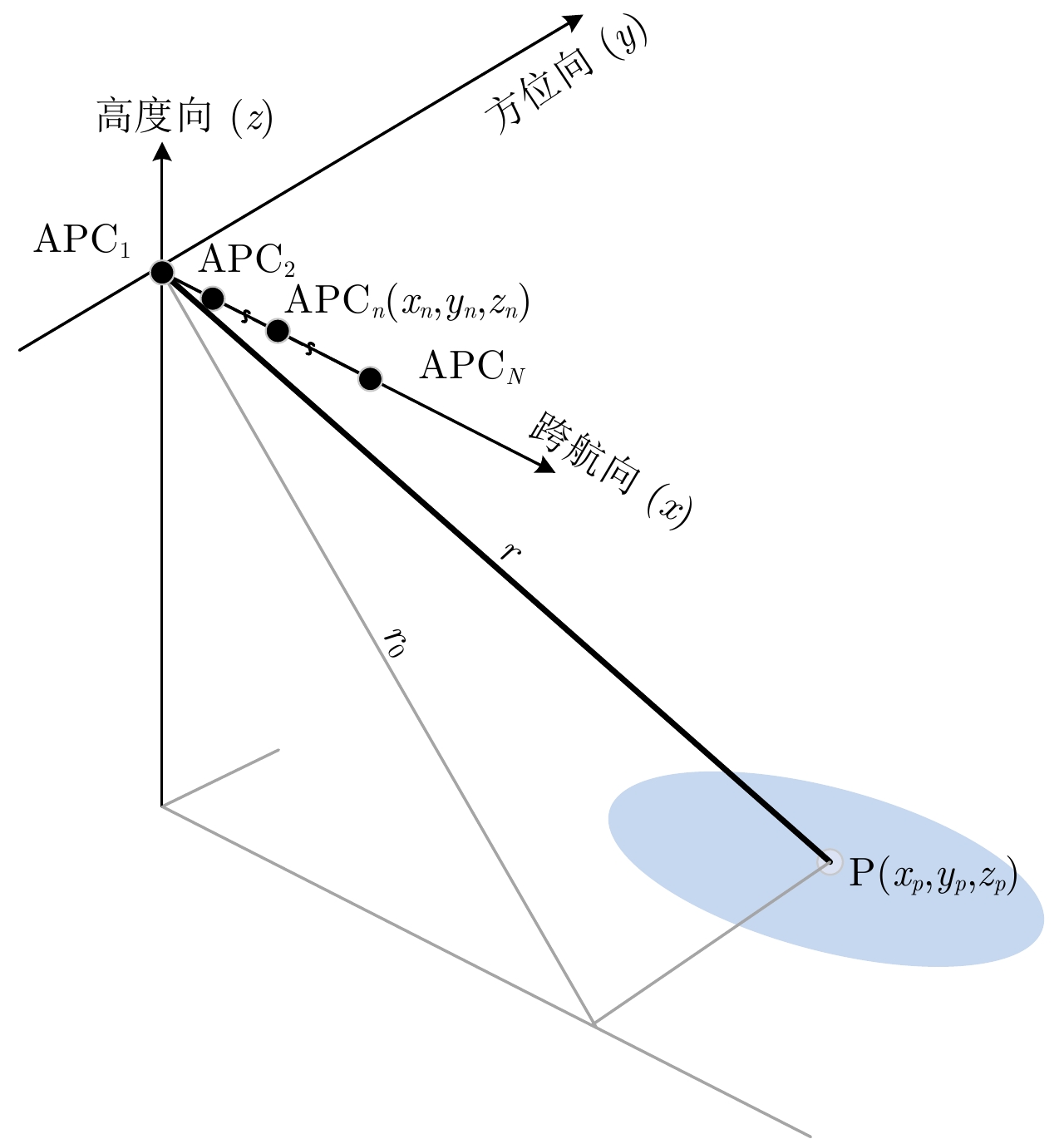
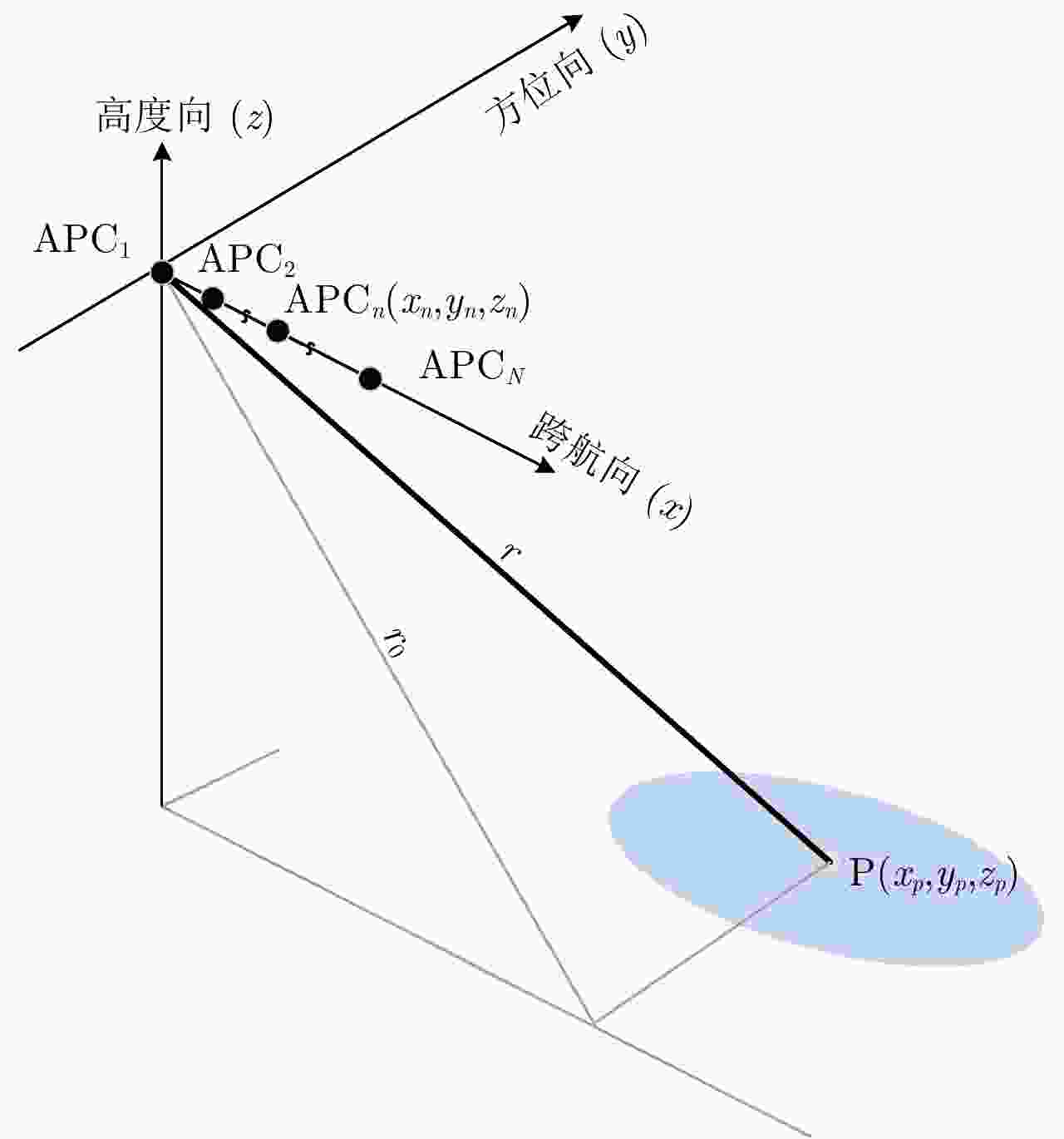
摘要: 阵列干涉合成孔径雷达(Synthetic Aperture Radar, SAR)系统采用距离脉冲压缩、方位合成孔径和高度实孔径的方式，能够获得观测场景的3维SAR图像。在实际系统中多个通道的天线相位中心位置信息通常难以精确获得，如果不进行定标而直接进行成像处理将会造成高度维成像质量降低。针对天线相位中心位置定标问题，该文分析了天线相位中心位置误差对高度维成像造成的影响，提出了一种基于子空间正交原理的相位中心位置定标方法。该方法利用2维SAR单视复图像中的定标点数据，通过特征值分解得到噪声子空间，利用子空间正交原理同时求解多个通道对应的天线相位中心位置。针对阵列干涉SAR系统应用，该文给出了相位中心位置定标处理流程，最后通过仿真和实际数据处理验证了定标方法的有效性。
- 3维成像 /
- 定标 /
- 阵列干涉SAR系统 /
- 相位中心位置 /
- 子空间正交
Abstract: The array InSAR system obtains a three-dimensional image of an observed scene using a combination of pulse compression and synthetic and real aperture techniques. However, Antenna Phase Center (APC) errors can occur within a practical array InSAR system, which thus degrades the imaging quality in a height direction. The aim of this paper is to improve calibration problems occurring with APC errors. The effect of APC errors is analyzed, and a calibration method based on the orthogonal subspace principle is proposed that utilizes SAR Single Look Complex (SLC) to obtain the noise subspace through eigenvalue decomposition. The subspace orthogonal principle is then used to solve the APC positions of multiple channels simultaneously. In addition, a calibration scheme for the APC position is presented for application with an array InSAR system. The effectiveness of the proposed calibration method is verified using simulations and experimental results.
- 3D imaging /
- Calibration /
- Array Interference Synthetic Aperture Radar (InSAR) system /
- Antenna Phase Center (APC) /
- Orthogonal subspace

HTML全文

图 1 阵列干涉SAR系统数据获取示意

Figure 1. Acquisition geometry of array 3D imaging SAR system

下载: 全尺寸图片幻灯片

图 2 正侧视零多普勒平面几何关系示意

Figure 2. Geometry in the zero Doppler plane

下载: 全尺寸图片幻灯片

图 3 相位中心位置定标流程图

Figure 3. Flow chart of APC calibration

下载: 全尺寸图片幻灯片

图 4 仿真数据的相位中心位置定标结果

Figure 4. Calibration results of APC position in simulation

下载: 全尺寸图片幻灯片

图 5 RMSE与信噪比的关系

Figure 5. RMSE as a function of SNR

下载: 全尺寸图片幻灯片

图 6 RMSE与定标点误差的关系

Figure 6. RMSE as a function of CR errors

下载: 全尺寸图片幻灯片

图 7 代价函数与迭代次数的关系

Figure 7. Cost function as a function of the number of iterations

下载: 全尺寸图片幻灯片

图 8 实验系统及定标场图像

Figure 8. The experiment system and calibration site

下载: 全尺寸图片幻灯片

图 9 实际数据相位中心位置定标结果

Figure 9. Calibration results of APC position in an airborne experiment

下载: 全尺寸图片幻灯片

图 10 实际数据验证实验

Figure 10. Real data experiments

下载: 全尺寸图片幻灯片

表 1 仿真实验中的系统参数

Table 1. System parameters of simulation data

参数名称	参数取值
工作频率	15 GHz (Ku-Band)
基线长度	4.2 m
带宽	500 MHz
PRF	2000 Hz
飞行相对高度	1000 m
飞行速度	60 m/s
方位向波束宽度	2°
距离向波束宽度	30°～60°
信噪比	30 dB

下载: 导出CSV

参考文献(25)

[1]	张红, 江凯, 王超, 等. SAR层析技术的研究与应用[J]. 遥感技术与应用, 2010, 25(2): 282–287 Zhang Hong, Jiang Kai, Wang Chao, et al. The current status of SAR tomography[J]. Remote Sensing Technology and Application, 2010, 25(2): 282–287
[2]	Zhang F B, Liang X D, Wu Y R, et al. 3D surface reconstruction of layover areas in continuous terrain for multi-baseline SAR interferometry using a curve model[J]. International Journal of Remote Sensing, 2015, 36(8): 2093–2112. DOI: 10.1080/01431161.2015.1030042
[3]	张福博, 梁兴东, 吴一戎. 一种基于地形驻点分割的多通道SAR三维重建方法[J]. 电子与信息学报, 2015, 37(10): 2287–2293. DOI: 10.11999/JEIT150244 Zhang Fu-bo, Liang Xing-dong, and Wu Yi-rong. 3-D reconstruction for multi-channel SAR interferometry using terrain stagnation point based division[J]. Journal of Electronics&Information Technology, 2015, 37(10): 2287–2293. DOI: 10.11999/JEIT150244
[4]	Zhu X X and Bamler R. Superresolving SAR tomography for multidimensional imaging of urban areas: Compressive sensing-based TomoSAR inversion[J]. IEEE Signal Processing Magazine, 2014, 31(4): 51–58. DOI: 10.1109/MSP.2014.2312098
[5]	Schmitt M, Shahzad M, and Zhu X X. Reconstruction of individual trees from multi-aspect TomoSAR data[J]. Remote Sensing of Environment, 2015, 165: 175–185. DOI: 10.1016/j.rse.2015.05.012
[6]	Tebaldini S and Ferro-Famil L. High resolution three-dimensional imaging of a snowpack from ground-based SAR data acquired at X and Ku band[C]. Proceedings of 2013 IEEE International Geoscience and Remote Sensing Symposium, Melbourne, VIC, Australia, 2015: 77–80.
[7]	Reigber A and Moreira A. First demonstration of airborne SAR tomography using multibaseline L-band data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2142–2152. DOI: 10.1109/36.868873
[8]	丁振宇, 谭维贤, 王彦平, 等. 基于波数域子孔径的机载三维SAR偏航角运动误差补偿[J]. 雷达学报, 2015, 4(4): 467–473. DOI: 10.12000/JR15016 Ding Zhen-yu, Tan Wei-xian, Wang Yan-ping, et al. Yaw angle error compensation for airborne 3-D SAR based on wavenumber-domain subblock[J]. Journal of Radars, 2015, 4(4): 467–473. DOI: 10.12000/JR15016
[9]	Tebaldini S and Guarnieri A M. On the role of phase stability in SAR multibaseline applications[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(7): 2953–2966. DOI: 10.1109/TGRS.2010.2043738
[10]	朱海洋, 洪峻, 明峰. 相位中心偏差对机载阵列天线下视3D-SAR成像影响分析[J]. 电子与信息学报, 2012, 34(4): 910–916. DOI: 10.3724/SP.J.1146.2011.00776 Zhu Hai-yang, Hong Jun, and Ming Feng. Analysis of impact of phase center variations in linear array antena downward-looking 3D-SAR imaging[J]. Journal of Electronics&Information Technology, 2012, 34(4): 910–916. DOI: 10.3724/SP.J.1146.2011.00776
[11]	朱海洋. 阵列下视3D-SAR相位中心定标方法研究[D]. [硕士论文], 中国科学院大学, 2012. Zhu Hai-yang. Study on phase center calibration methods of linear array downward-looking 3D-SAR[D]. [Master dissertation], University of Chinese Acedamy of Science, 2012.
[12]	韩阔业. 基于稀疏线阵的机载合成孔径雷达成像模型、方法与实验研究[D]. [博士论文], 中国科学院大学, 2015. Han Kuo-ye. Study on model, algorithm and experiment for airborne synthetic aperture radar imaging based on sparse linear array antennas[D]. [Ph.D. dissertation], University of Chinese Academy of Sciences, 2015.
[13]	Pardini M, Papathanassiou K, Bianco V, et al.. Phase calibration of multibaseline SAR data based on a minimum entropy criterion[C]. Proceedings of 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 2012: 5198–5201. DOI: 10.1109/IGARSS.2012.6352438.
[14]	Tebaldini S, Rocca F, d’Alessandro M M, et al. Phase calibration of airborne tomographic SAR data via phase center double localization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(3): 1775–1792. DOI: 10.1109/TGRS.2015.2488358
[15]	Fornaro G, Lombardini F, and Serafino F. Three-dimensional multipass SAR focusing: Experiments with long-term spaceborne data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 702–714. DOI: 10.1109/TGRS.2005.843567
[16]	Urasawa F, Yamada H, Yamaguchi Y, et al.. Fundamental study on multi-baseline SAR tomography by Pi-SAR-L2[C]. Proceedings of the URSI Asia-Pacific Radio Science Conference, Seoul, South Korea, 2016: 514–515. DOI: 10.1109/URSIAP-RASC.2016.7601342.
[17]	柳祥乐. 多基线层析成像合成孔径雷达研究[D]. [博士论文], 中国科学院电子学研究所, 2007. Liu Xiang-le. Study on multibaseline tomography synthetic aperture radar[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2007.
[18]	赵逸超, 朱宇涛, 粟毅, 等. 用于线阵三维SAR成像的二维快速ESPRIT算法[J]. 雷达学报, 2015, 4(5): 591–599. DOI: 10.12000/JR15065 Zhao Yi-chao, Zhu Yu-tao, Su Yi, et al. Two-dimensional fast ESPRIT algorithm for linear array SAR imaging[J]. Journal of Radars, 2015, 4(5): 591–599. DOI: 10.12000/JR15065
[19]	Zhu X X and Bamler R. Superresolving SAR tomography for multidimensional imaging of urban areas: Compressive sensing-based TomoSAR inversion[J]. IEEE Signal Processing Magazine, 2014, 31(4): 51–58. DOI: 10.1109/MSP.2014.2312098
[20]	Schmitt M and Stilla U. Compressive sensing based layover separation in airborne single-pass multi-baseline InSAR data[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(2): 313–317. DOI: 10.1109/LGRS.2012.2204230
[21]	李杭, 梁兴东, 张福博, 等. 基于高斯混合聚类的阵列干涉SAR三维成像[J]. 雷达学报, 2017, 6(6): 630–639. DOI: 10.12000/JR17020 Li Hang, Liang Xing-dong, Zhang Fu-bo, et al. 3D imaging for array InSAR based on Gaussian mixture model clustering[J]. Journal of Radars, 2017, 6(6): 630–639. DOI: 10.12000/JR17020
[22]	Stoica P and Nehorai A. MUSIC, maximum likelihood, and Cramer-Rao bound[J]. IEEE Transactions on Acoustics,Speech,and Signal Processing, 1989, 37(5): 720–741. DOI: 10.1109/29.17564
[23]	张福博. 阵列干涉SAR三维重建信号处理技术研究[D]. [博士论文], 中国科学院大学, 2015. Zhang Fu-bo. Research on signal processing of 3-D reconstruction in linear array Synthetic Aperture Radar interferometry[D]. [Ph.D. dissertation], University of Chinese Acedamy of Science, 2015.
[24]	Freeman A. SAR calibration: An overview[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(6): 1107–1121. DOI: 10.1109/36.193786
[25]	焦培南, 张忠治. 雷达环境与电波传播特性[M]. 北京: 电子工业出版社, 2007. Jiao Pei-nan and Zhang Zhong-zhi. Radio Environment and Radio Wave Propagation Characteristics[M]. Beijing: Publishing House of Electronics Industry, 2007.