一种新颖的星载SAR无线内定标方法研究

王沛; 孙慧峰; 禹卫东

doi:10.12000/JR18005

一种新颖的星载SAR无线内定标方法研究

DOI: 10.12000/JR18005 CSTR: 32380.14.JR18005

王沛^1,2, ,,
孙慧峰^1,,
禹卫东^1,

①.
中国科学院电子学研究所北京 100190
②.
中国科学院大学北京 100049

基金项目: 国家部委基金

详细信息

作者简介:
王沛：王沛(1977–)，男，陕西省西安市人，副研究员，硕士生导师。2005年在中国科学院大学获得通信与信息系统硕士学位，现为中国科学院电子学研究所副研究员。参与和负责我国多个重点星载、机载SAR工程型号项目的研制。主要研究方向为宽带信号产生技术、射频系统技术及SAR系统设计。E-mail: vanpei@163.com

孙慧峰(1979–)，男，中国科学院电子学研究所副研究员，硕士生导师。研究方向为星载合成孔径雷达天线技术。E-mail: sunemt@163.com

禹卫东(1969–)，男，中国科学院电子学研究所研究员，博士生导师。研究方向为合成孔径雷达信号处理技术。E-mail: ywd@mail.ie.ac.cn

通讯作者:
王沛 vanpei@163.com

计量
- 文章访问数: 2622
- HTML全文浏览量: 539
- PDF下载量: 349
- 被引次数: 10
出版历程
- 收稿日期: 2018-01-19
- 修回日期: 2018-06-11
- 网络出版日期: 2018-08-28

A Novel Wireless Internal Calibration Method of Spaceborne SAR

Wang Pei^{1,2
, ,},
Sun Huifeng^1
,,
Yu Weidong^1
,

①.
Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China
②.
University of Chinese Academy of Sciences, Beijing 100049, China

Funds: The National Ministries Foundation

摘要

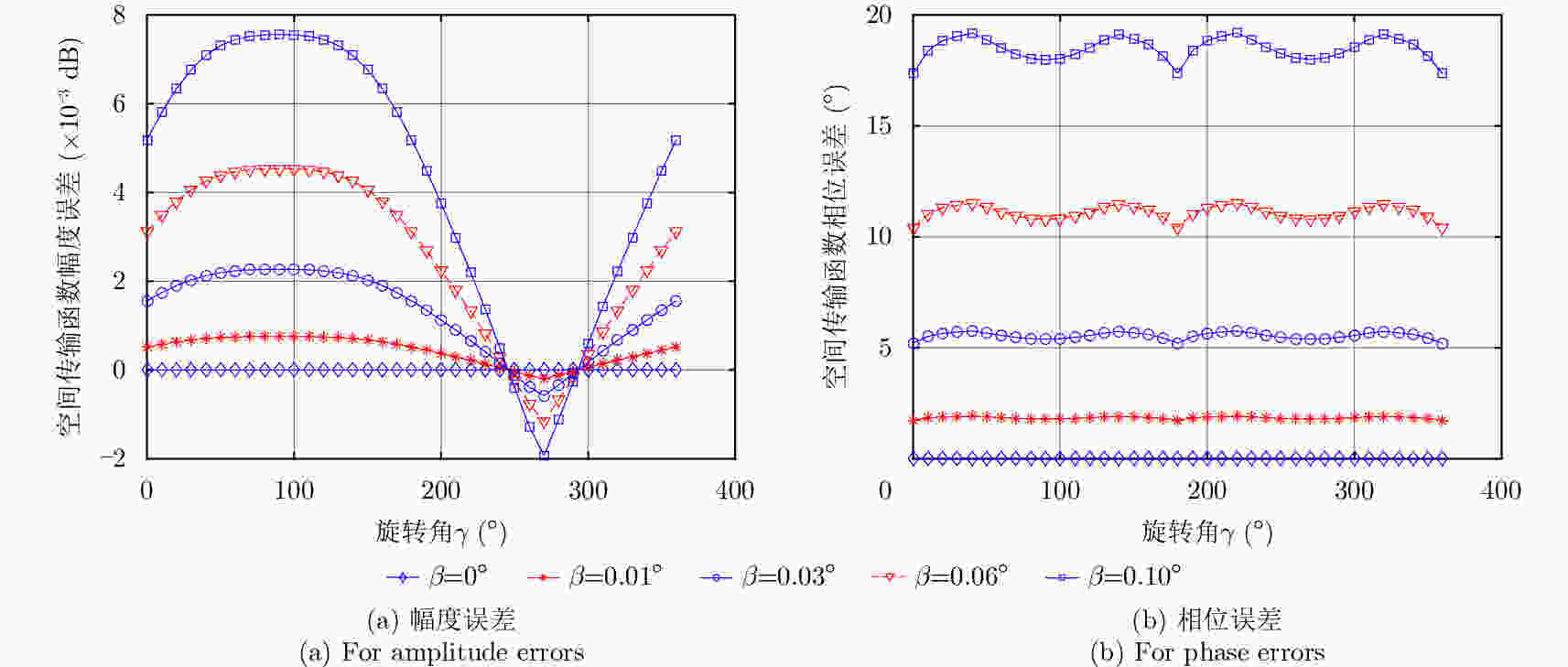
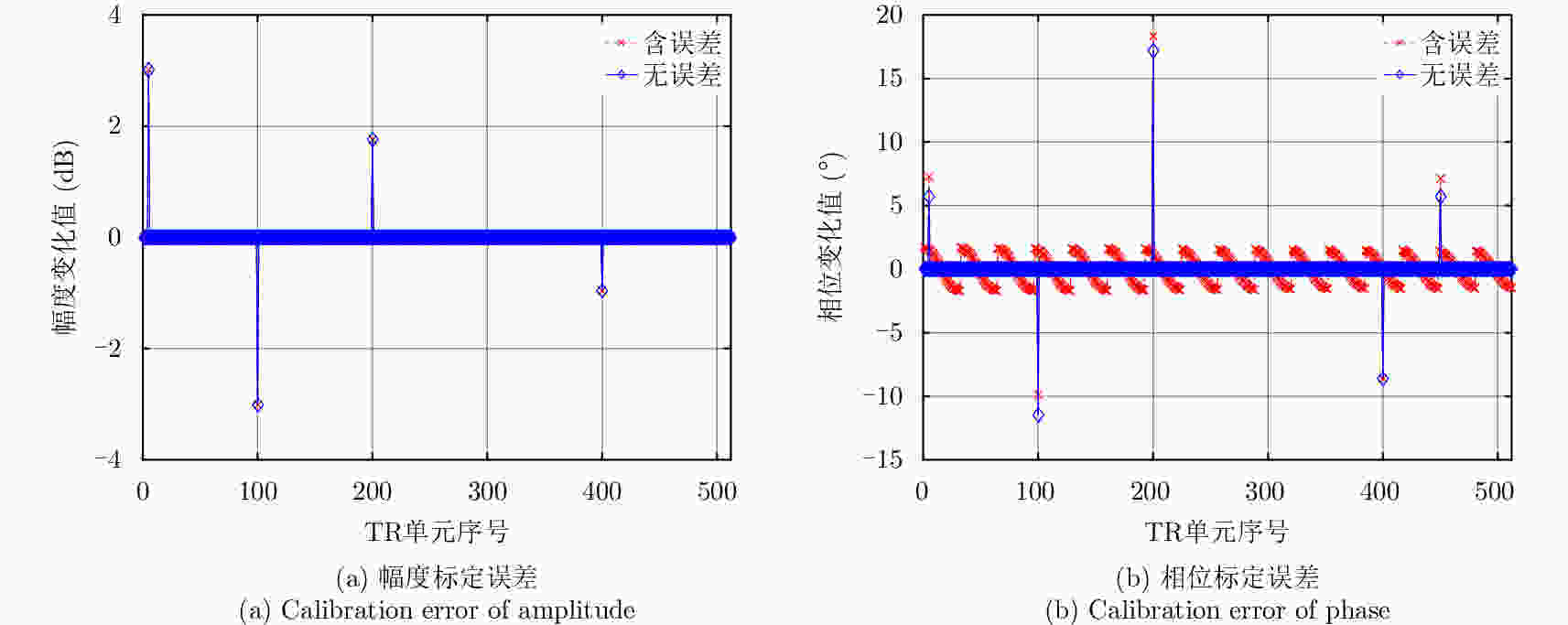
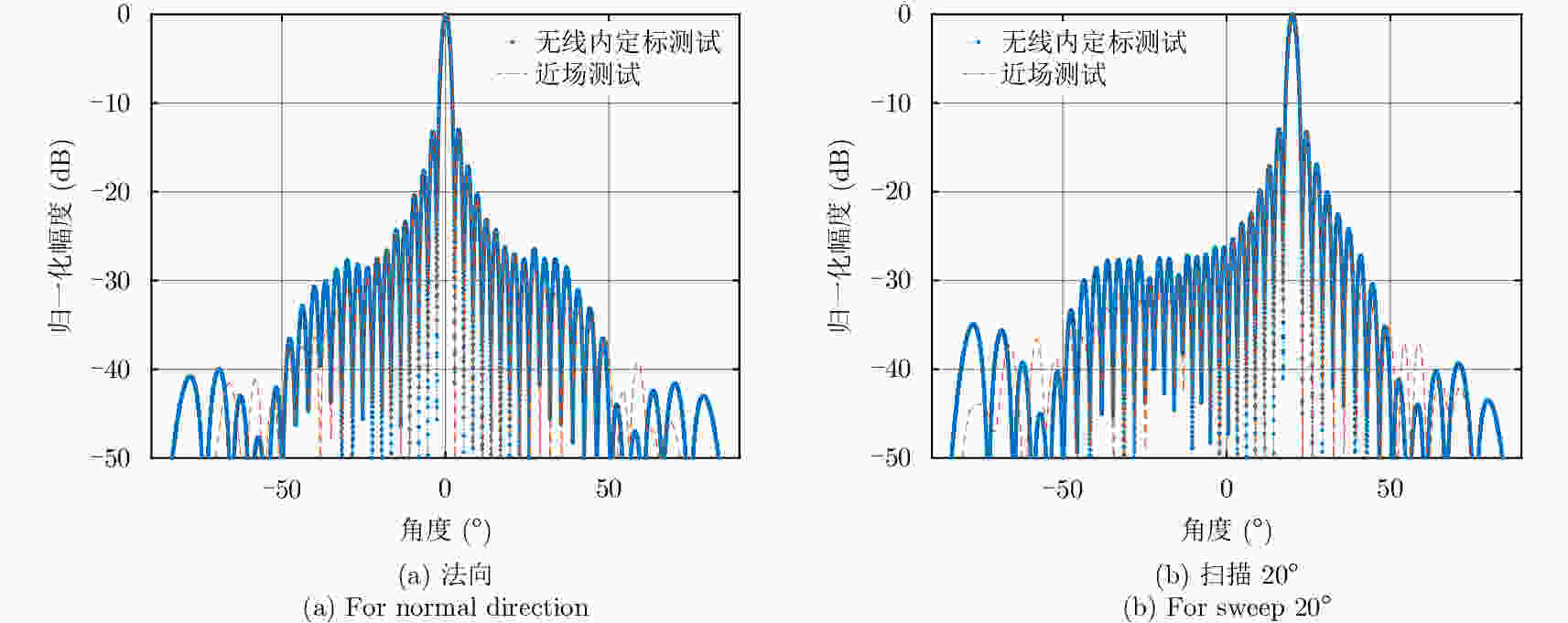
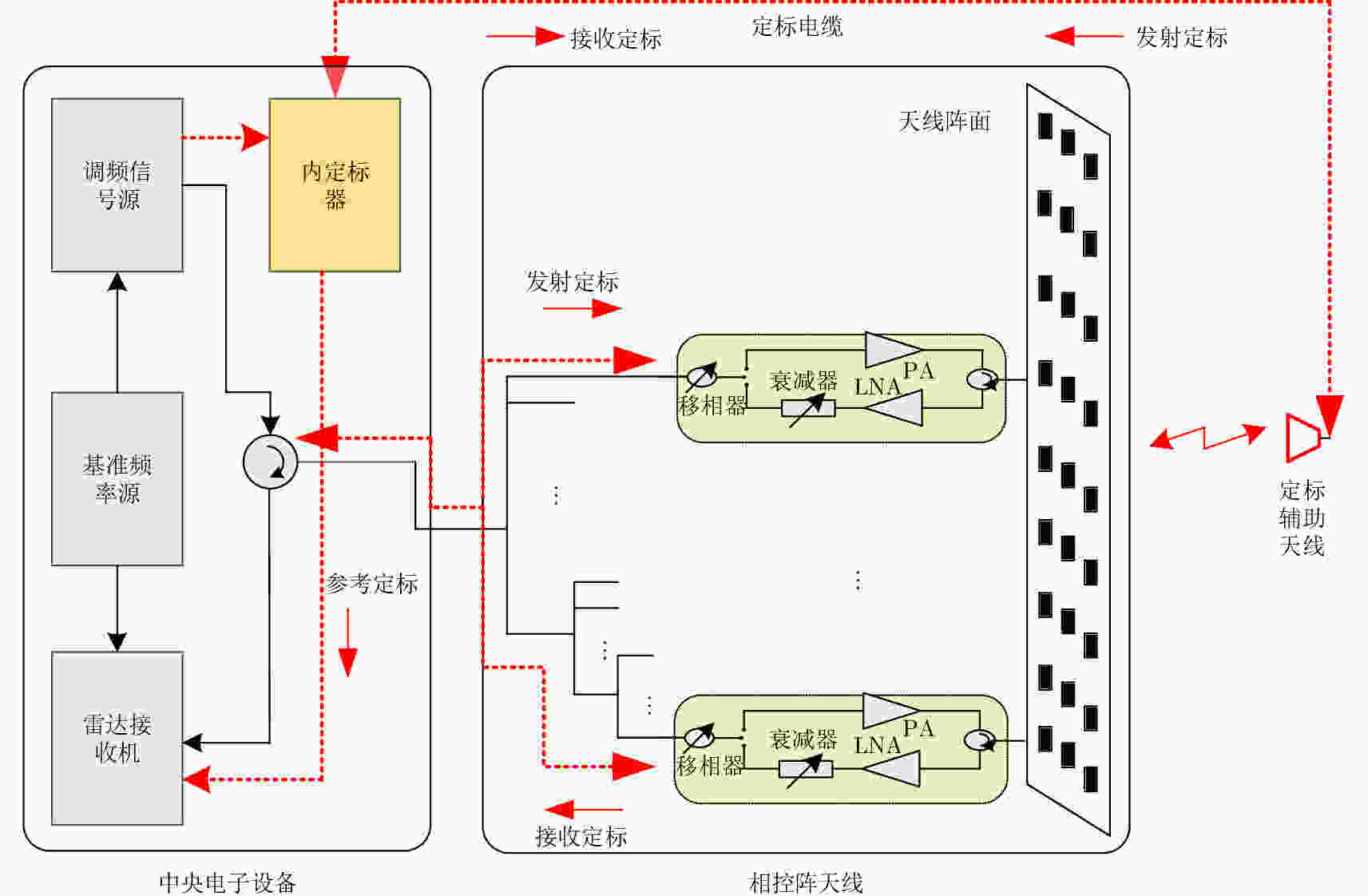
摘要: 内定标利用雷达系统内部设备和定标通路来测量系统各部分幅度和相位在成像过程中的相对变化，是保证雷达图像辐射精度的重要手段。该文针对传统有线内定标方案定标通路未覆盖相控阵天线TR输出端至无源阵面路径、定标网络庞大且自身误差控制难等不足，提出了一种新颖的利用辅助天线的无线内定标方法，给出了定标原理和分析模型，推导了SAR天线TR通道幅相特性和系统传递函数的标定方法，并在典型星载SAR系统参数下对标定误差进行了仿真分析，仿真结果表明，辅助天线支撑杆位置引起的TR通道幅度标定误差在10^–3 dB量级，可以忽略；引起相位标定误差与支撑杆位置偏差密切相关，可依据文中给出的仿真曲线得到。支持杆位置引起的系统传递函数幅度标定误差小于0.1 dB；引起的相位标定误差对支撑杆位置偏差不敏感。最后在实际相控阵天线上对无线内定标方法进行了验证，获取了TR通道幅相特性标定的实测结果，表明了该方案的可行性和有效性。
- 合成孔径雷达 /
- 内定标 /
- 无线传输 /
- 幅相误差 /
- 传递函数
Abstract: Internal calibration measures the changes in amplitude and phase of a system during imaging via the calibration loop built in Synthetic Aperture Radar (SAR). Internal calibration is also an important factor to improve the radiation accuracy of the radar. In this study, a novel wireless internal calibration method with auxiliary antenna is presented, considering that the traditional scheme is inefficient, as the calibration loop cannot cover the path from the TR (Transmitter-Receiver) output to the antenna radiator. The calibration loop also results in a complicated and heavy network. The principle and model of the new method is given, and the TR performance and system transfer function calibration approach are deduced. In addition, error analysis is conducted. The simulation results show that TR amplitude calibration errors caused by the rod of auxiliary antenna are at a 10^–3 dB level, and phase calibration errors are obtained from the simulation curve in the paper; transfer function amplitude calibration errors are less than 0.1 dB, and phase calibration errors are not sensitive to the bias of the rod. Finally, the simulation results based on typical parameters of spaceborne SAR and the individual TR calibration experiments confirm the availability and feasibility of this novel method.
- Synthetic Aperture Radar (SAR) /
- Internal calibration /
- Wireless transmission /
- Amplitude and phase error /
- Transfer function

HTML全文

图 2 星载SAR无线内定标原理

Figure 2. Diagram of wireless internal calibration in spaceborne SAR

下载: 全尺寸图片幻灯片

图 1 传统星载SAR内定标原理

Figure 1. Diagram of traditional internal calibration in spaceborne SAR

下载: 全尺寸图片幻灯片

图 3 无线内定标空间几何关系

Figure 3. Geometry of wireless internal calibration

下载: 全尺寸图片幻灯片

图 4 支撑杆的位置偏差示意

Figure 4. Bias of rod position

下载: 全尺寸图片幻灯片

图 5 位置误差引起的空间传输函数 $S\left( i \right)$ 的变化

Figure 5. $S\left( i \right)$ variation versus rod position errors

下载: 全尺寸图片幻灯片

图 6 TR通道幅相标定误差

Figure 6. Calibration errors of TR channel

下载: 全尺寸图片幻灯片

图 7 $\delta$ 函数幅相变化与位置误差关系

Figure 7. Variation of function $\delta$ versus rod position errors

下载: 全尺寸图片幻灯片

图 8 TR通道幅相特性

Figure 8. Calibration results of TR channel

下载: 全尺寸图片幻灯片

图 9 距离向接收方向图

Figure 9. Reception pattern in elevation

下载: 全尺寸图片幻灯片

表 1 TR通道幅相特性标定误差源

Table 1. Error sources of TR amplitude and phase calibration

误差项	误差代号	幅度(dB)	相位(°)
空间传输函数误差	$\Delta S\left( i \right)$	$\Delta {A_S}\left( i \right)$	$\Delta {\varphi _S}\left( i \right)$
移相器误差	$\Delta P\left( {i{\rm{,}}k} \right)$	$\Delta A\left( {i{\rm{,}}k} \right)$	$\Delta \varphi \left( {i{\rm{,}}k} \right)$

下载: 导出CSV

表 2 系统传递函数标定误差源

Table 2. Error sources of transfer function calibration

误差项		误差代号	幅度(dB)	相位(°)
定标电缆的误差		$\Delta {C_L}$	$\Delta {A_{{\rm{CL}}}}$	$\Delta {\varphi _{{\rm{CL}}}}$
内定标器误差	参考定标回路	$\Delta {\rm{C}}{{\rm{R}}_{\rm{1}}}$	$\Delta {A_{{\rm{CR1}}}}$	$\Delta {\varphi _{{\rm{CR1}}}}$
	发射定标回路	$\Delta {\rm{C}}{{\rm{R}}_{\rm{2}}}$	$\Delta {A_{{\rm{CR2}}}}$	$\Delta {\varphi _{{\rm{CR2}}}}$
	接收定标回路	$\Delta {\rm{C}}{{\rm{R}}_{\rm{3}}}$	$\Delta {A_{{\rm{CR3}}}}$	$\Delta {\varphi _{{\rm{CR3}}}}$
传输函数矢量和误差		$\Delta \delta = \Delta \left\{ {\sum\nolimits_{i = 1}^N {{S_C}\left( i \right)S\left( i \right)} } \right\}$	$\Delta {A_\delta }$	$\Delta {\varphi _\delta }$

下载: 导出CSV

表 3 仿真参数设置

Table 3. Parameters of simulation

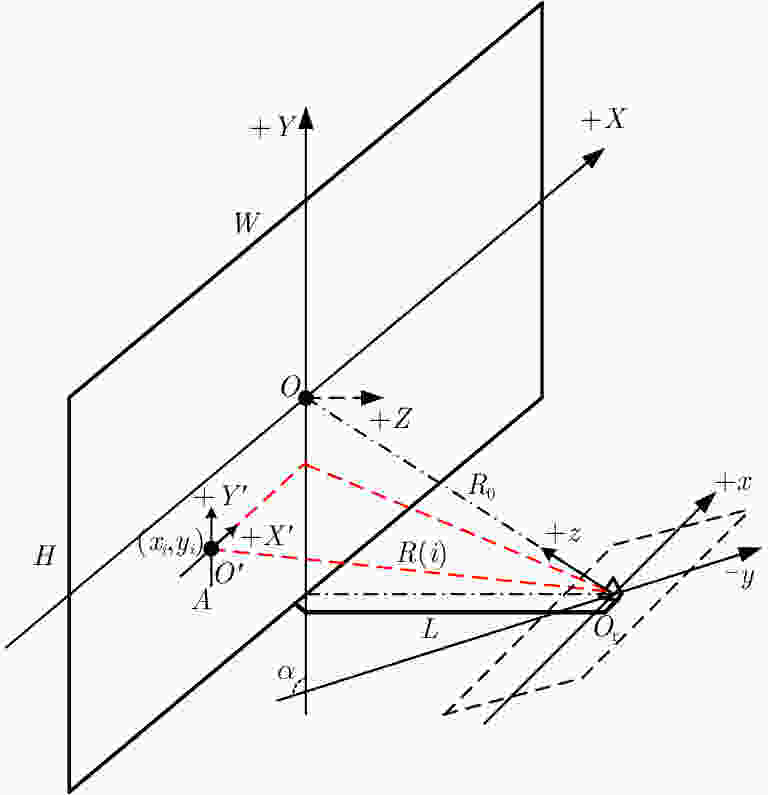
参数名称	参数代号	参数值
工作频段	f	X波段
天线长度	W	5 m
天线高度	H	1 m
支撑杆长度	L	1 m
方位向单元数	M	32
距离向单元数	N	16
支撑杆位置误差	$\beta$	0°～0.10°
支撑杆旋转角	$\gamma$	0°～360°
辅助天线形式	/	开口波导
辐射单元形式	/	波导缝隙
内定标器误差(幅度)	/	0.4 dB
内定标器误差(相位)	/	2.0°
定标电缆误差(幅度)	/	0.1 dB
定标电缆误差(相位)	/	1°

下载: 导出CSV

表 4 系统传递函数标定误差

Table 4. Errors of system transfer function calibration

支撑杆位置误差 $\beta$ (°)	传递函数标定误差
支撑杆位置误差 $\beta$ (°)	幅度(dB)	相位(°)
0	0.447	2.828
0.01	0.448	2.829
0.02	0.449	2.829
0.03	0.453	2.831
0.04	0.459	2.832
0.06	0.485	2.832
0.08	0.535	2.837
0.10	0.616	2.844

下载: 导出CSV

参考文献(19)

[1]	邓云凯, 赵凤军, 王宇. 星载SAR技术的发展趋势及应用浅析[J]. 雷达学报, 2012, 1(1): 1–10. DOI: 10.3724/SP.J.1300.2012.20015 Deng Yun-kai, Zhao Feng-jun, and Wang Yu. Brief analysis on the development and application of spaceborne SAR[J]. Journal of Radars, 2012, 1(1): 1–10. DOI: 10.3724/SP.J.1300.2012.20015
[2]	李春升, 王伟杰, 王鹏波, 等. 星载SAR技术的现状与发展趋势[J]. 电子与信息学报, 2016, 38(1): 229–240. DOI: 10.11999/JEIT151116 Li Chun-sheng, Wang Wei-jie, Wang Peng-bo, et al. Current situation and development trends of spaceborne SAR technology[J]. Journal of Electronics&Information Technology, 2016, 38(1): 229–240. DOI: 10.11999/JEIT151116
[3]	袁孝康. 星载合成孔径雷达导论[M]. 北京: 国防工业出版社, 2003 Yuan Xiao-kang. Introduce to the Spaceborne Sythetic Aperture Radar[M]. Beijing: National Defend Industry Press, 2003
[4]	杨汝良, 戴博伟, 谈璐璐, 等. 极化微波成像[M]. 北京: 国防工业出版社, 2017 Yang Ru-liang, Dai Bo-wei, Tan Lu-lu, et al.. Polarimetric Microwave Imaging[M]. Beijing: National Defend Industry Press, 2017
[5]	Brautigam B, Gonzalez J H, Schwerdt M, et al. TerraSAR-X instrument calibration results and extension for TanDEM-X[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(2): 702–715. DOI: 10.1109/TGRS.2009.2030673
[6]	Takahashi T, Nakamoto N, Ohtsuka M, et al. On-board calibration methods for mechanical distortions of satellite phased array antennas[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(3): 1362–1372. DOI: 10.1109/TAP.2011.2180303
[7]	Schwerdt M, Bachmann M, Schrank D, et al.. Precise calibration techniques for complex SAR systems based on active phased array antennas[C]. Proceedings of 2010 IEEE International Symposium on Phased Array Systems and Technology, Waltham, MA, USA, 2010: 695–699. DOI: 10.1109/ARRAY.2010.5613290
[8]	Schwerdt M, Hounam D, and Stangl M. Calibration concept for the TerraSAR-X instrument[C]. Proceedings of 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 2003, 7: 4509–4511. DOI: 10.1109/IGARSS.2003.1295563
[9]	Brautigam B, Schwerdt M, Bachmann M, et al.. Individual T/R module characterisation of the TerraSAR-X active phased array antenna by calibration pulse sequences with orthogonal codes[C]. Proceedings of 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 2007: 5202–5205. DOI: 10.1109/IGARSS.2007.4424034
[10]	Luscombe A P. Internal calibration of the radarsat synthetic aperture radar[C]. Proceedings of the 10th Annual International Symposium on Geoscience and Remote Sensing, College Park, Maryland, USA, 1990: 2325–2328. DOI: 10.1109/IGARSS.1990.689003
[11]	Schied E, Rostan F, Oestergaard A, et al.. The sentinel-1 C-SAR internal calibration[C]. Proceedings of the 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 2010: 1–3
[12]	Bast D. Parameters affecting orthogonal SAR transmit and receive module calibration[C]. Committee Earth Observation Satellites Synthetic Aperture Radar (CEOS SAR) Workshop, Ulm, Germany, 2004
[13]	Deng Y K, Zheng H F, Wang R, et al. Internal calibration for stepped-frequency chirp SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(6): 1105–1109. DOI: 10.1109/LGRS.2011.2157889
[14]	Shnitkin H. Rapid fast Fourier transform phase alignment of an electronically scanned antenna[C]. Proceedings of the 20th European Microwave Conference, Budapest, Hungary, 1990, 1: 247–251. DOI: 10.1109/EUMA.1990.336051
[15]	杨震, 杨汝良. HJ-1-C卫星SAR系统的内定标[J]. 雷达学报, 2014, 3(3): 314–319. DOI: 10.3724/SP.J.1300.2014.14028 Yang Zhen and Yang Ru-liang. Internal calibration of HJ-1-C satellite SAR system[J]. Journal of Radars, 2014, 3(3): 314–319. DOI: 10.3724/SP.J.1300.2014.14028
[16]	TIMES. Phase track full line brochure[EB/OL]. http://www.timesmicrowave.com/, 2016
[17]	张骏华. 导弹和运载火箭复合材料结构设计指南[M]. 北京: 宇航出版社, 1999: 1, 16 ZHANG Junhua. Structural design guid of composite material[M]. Beijing: Aerospace press, 1999: 1, 16
[18]	欧阳国恩, 许路, 刘成民, 等. 几种纤维的热膨胀系数实验测定[J]. 宇航材料工艺, 1988(4): 48–53, 32 OUYANG Enguo, XU Lu, Liu Chengmin, et al. Experimental determination for coefficients of thermal expansion of several fibers[J]. Aerospace Materials and Technology, 1988(4): 48–53, 32
[19]	薛丰廷, 汤心溢. 空间目标瞬态温度特性研究[J]. 激光与红外, 2008, 38(3): 223–225. DOI: 10.3969/j.issn.1001-5078.2008.03.009 Xue Feng-ting and Tang Xin-yi. Study on the transient temperature of the space target[J]. Laser&Infrared, 2008, 38(3): 223–225. DOI: 10.3969/j.issn.1001-5078.2008.03.009

施引文献

期刊类型引用(5)

1.	方迎潮，赵雪，陈文乐，王庆，吴森. Sentinel-1A影像在山区管道地表形变监测中的适用性评价指标构建. 科学技术与工程. 2024(18): 7639-7645 . 百度学术
2.	李东，侯西勇. 沿海低山丘陵区DEM提取及精度分析. 测绘通报. 2021(S1): 61-64 . 百度学术
3.	李伟华，张华春，张衡. 基于StereoSAR辅助的InSAR DEM重建方法研究. 现代雷达. 2020(01): 55-63 . 百度学术
4.	唐新明，李涛，高小明，陈乾福，张祥. 雷达卫星自动成图的精密干涉测量关键技术. 测绘学报. 2018(06): 730-740 . 百度学术
5.	陈立福，王思雨，袁志辉，王静，邢学敏，武鸿. 非线性ECS自配准成像算法中相位保持精度分析. 中国科学院大学学报. 2017(05): 640-646 . 百度学术