太赫兹波段碲化镉介电常数的理论与实验研究

孙旺; 李粮生; 张景; 殷红成

doi:10.12000/JR17096

太赫兹波段碲化镉介电常数的理论与实验研究

DOI: 10.12000/JR17096

电磁散射重点实验室北京 100854

基金项目: 国家自然科学基金(6149069502)

详细信息

作者简介:
孙　旺(1993–)，男，硕士研究生，研究方向为太赫兹波段材料的密度泛函方法

李粮生(1981–)，男，研究员，研究方向为太赫兹技术、量子技术和统计物理

张　景(1987–)，男，博士后，研究方向为太赫兹测量技术

殷红成(1967–)，男，研究员，博士生导师，主要研究方向为电磁散射、雷达目标特性、目标识别等

通讯作者:
李粮生 liliangshengbititp@163.com

中图分类号: TN952
计量
- 文章访问数: 2437
- HTML全文浏览量: 586
- PDF下载量: 475
- 被引次数: 0
出版历程
- 收稿日期: 2017-11-03
- 修回日期: 2018-01-21
- 网络出版日期: 2018-02-01

Theoretical and Experimental Study on the Permittivity of CdTe in the Terahertz Band

Science and Technology on Electromagnetic Scattering Laboratory, Beijing 100854, China

Funds: The National Natural Science Foundation of China (6149069502)

摘要

摘要: 该文采用密度泛函理论研究了闪锌矿型碲化镉的声子色散谱、特征向量及晶格振动频率，获得了碲化镉介电常数随频率变化的理论值。通过太赫兹时域光谱系统测量碲化镉单晶的介电常数，该实验结果与局域密度近似修正、广义梯度近似修正和广义梯度近似修正的计算结果吻合较好。最后，3种近似交换关联势的计算结果之间存在一定差异性，该差异性结果表明太赫兹波段碲化镉的介电常数由电子声子耦合所主导，但是横波和纵波声子频率敏感于电子密度分布。
- 碲化镉 /
- 介电常数 /
- 反射率 /
- 横/纵光学模 /
- 时域光谱
Abstract: The phonon dispersion spectrum, eigenvector, and lattice vibration frequency of cadmium telluride with a zinc blende structure have been investigated using the density functional theory, and the permittivity of cadmium telluride crystal is numerically calculated. The permittivity of the crystal is measured using the terahertz time-domain spectroscopy system. The experimental results are consistent with the theoretical calculations on the modified local density approximation, the general gradient approximation, and the modified general gradient approximation. Finally, the differences among the three approximate exchange correlation potentials indicate that in the terahertz region, the permittivity of cadmium telluride is dominantly contributed by the coupling between electron and phonon; however, the phonon frequencies of transverse wave and longitudinal wave were sensitive to electron density distribution.
- Cadmium telluride /
- Permittivity /
- Reflectivity /
- Transverse/longitudinal optical mode /
- Time domain spectroscopy

HTML全文

图 1 CdTe晶体结构：红球为Te原子，蓝球为Cd原子，绿色箭头表示晶体的主轴方向

Figure 1. The crystal structure of CdTe: The red spheres indicate Te atoms. The blue spheres indicate Cd atoms. The green arrow indicates the direction of crystal major axis

下载: 全尺寸图片幻灯片

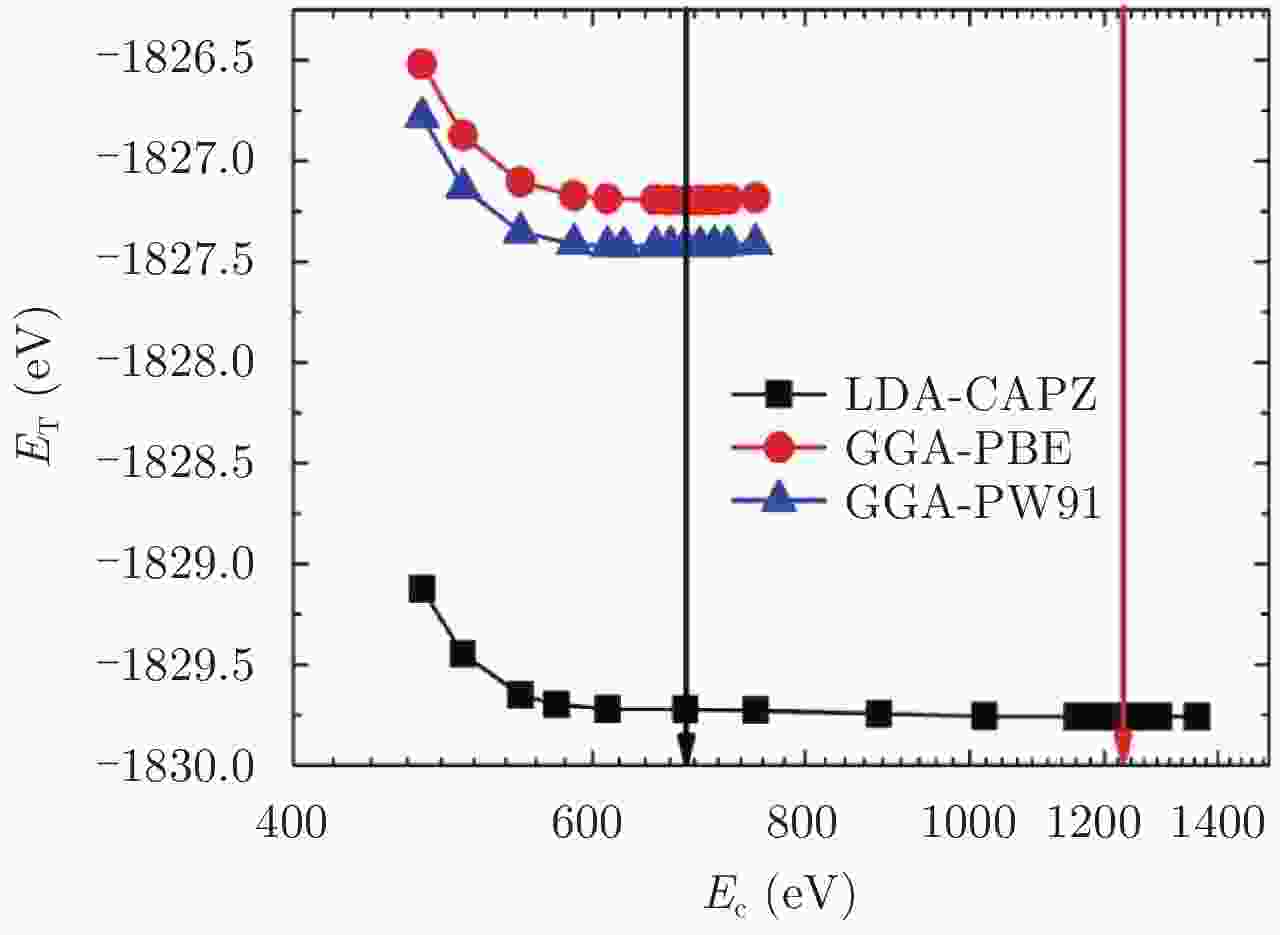
图 2 总能量与截断能的依赖关系。黑色箭头表示选取GGA的截断能位置 $E_{\rm{c}}^{{\rm{PBE/PW91}}}{\rm{ = }}680 \ {{\rm{eV}}} $ 。红色箭头表示选取LDA的截断能位置 $E_{\rm{c}}^{{\rm{LDA}}}{\rm{ = }}1225\ {{\rm{eV}}}$

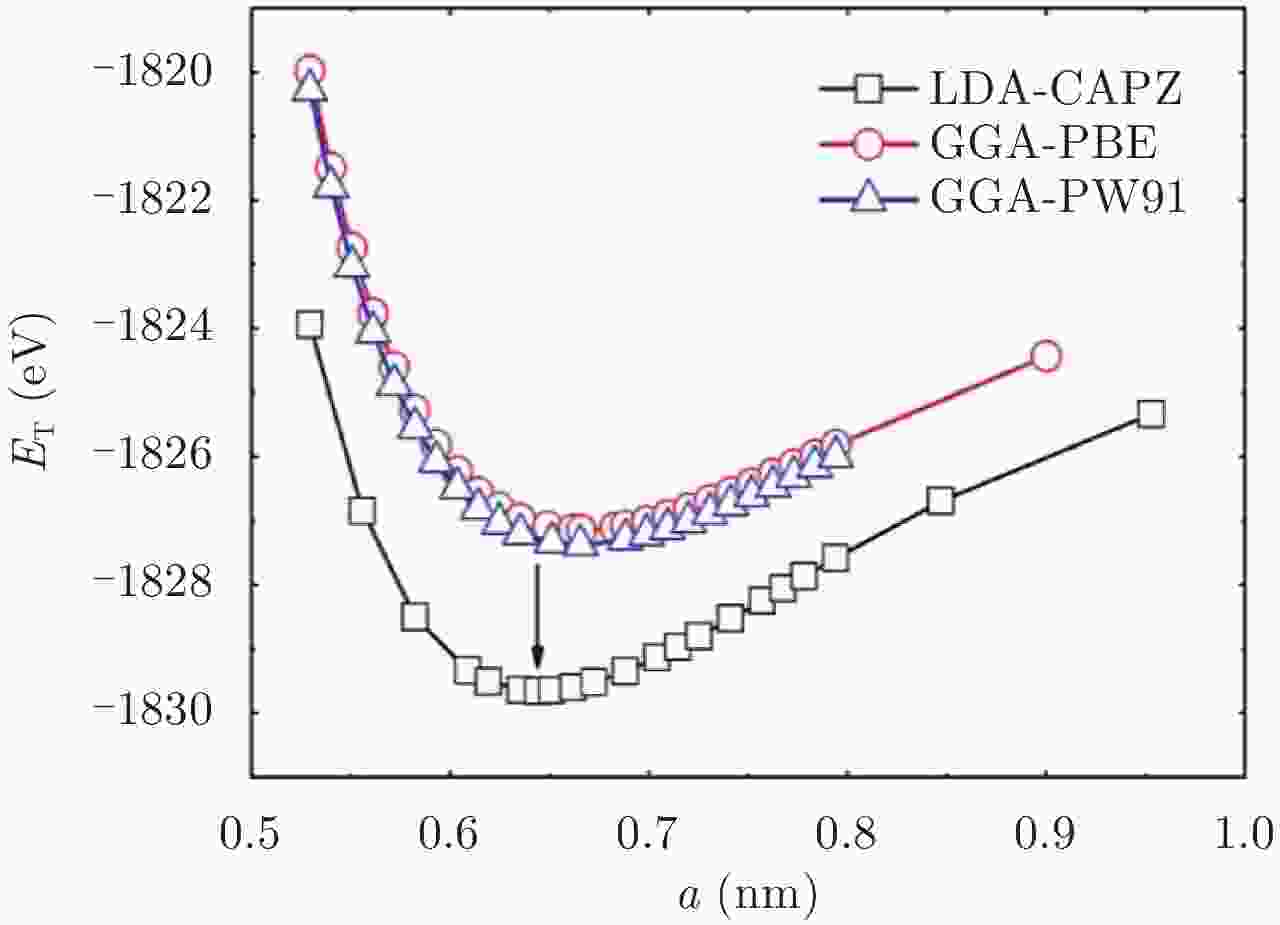
Figure 2. The total energy vs the cut-off energy. The black arrow indicates the value of GGA cut-off energy $E_{\rm{c}}^{{\rm{PBE/PW91}}}{\rm{ = }}680 \ {{\rm{eV}}} $ . The red arrow indicates the value of LDA cut-off energy $E_{\rm{c}}^{{\rm{LDA}}}{\rm{ = }}1225\ {\rm eV} $

下载: 全尺寸图片幻灯片

图 3 总能量随k-point数量的依赖关系。黑色箭头表示合适的k-point选择

Figure 3. The total energy as a function of k-point. Black arrows indicate the selected k-point

下载: 全尺寸图片幻灯片

图 4 LDA, GGA-PBE和GGA-PW91方法计算的总能量与尝试晶格常数a的依赖关系。黑色箭头表示LDA计算总能量最小值的位置 $a_{{\rm{LDA}}}^{{\rm{CA {^{\scriptsize{-}}} PZ}}} = 0.64424 \ {\rm{nm}}$

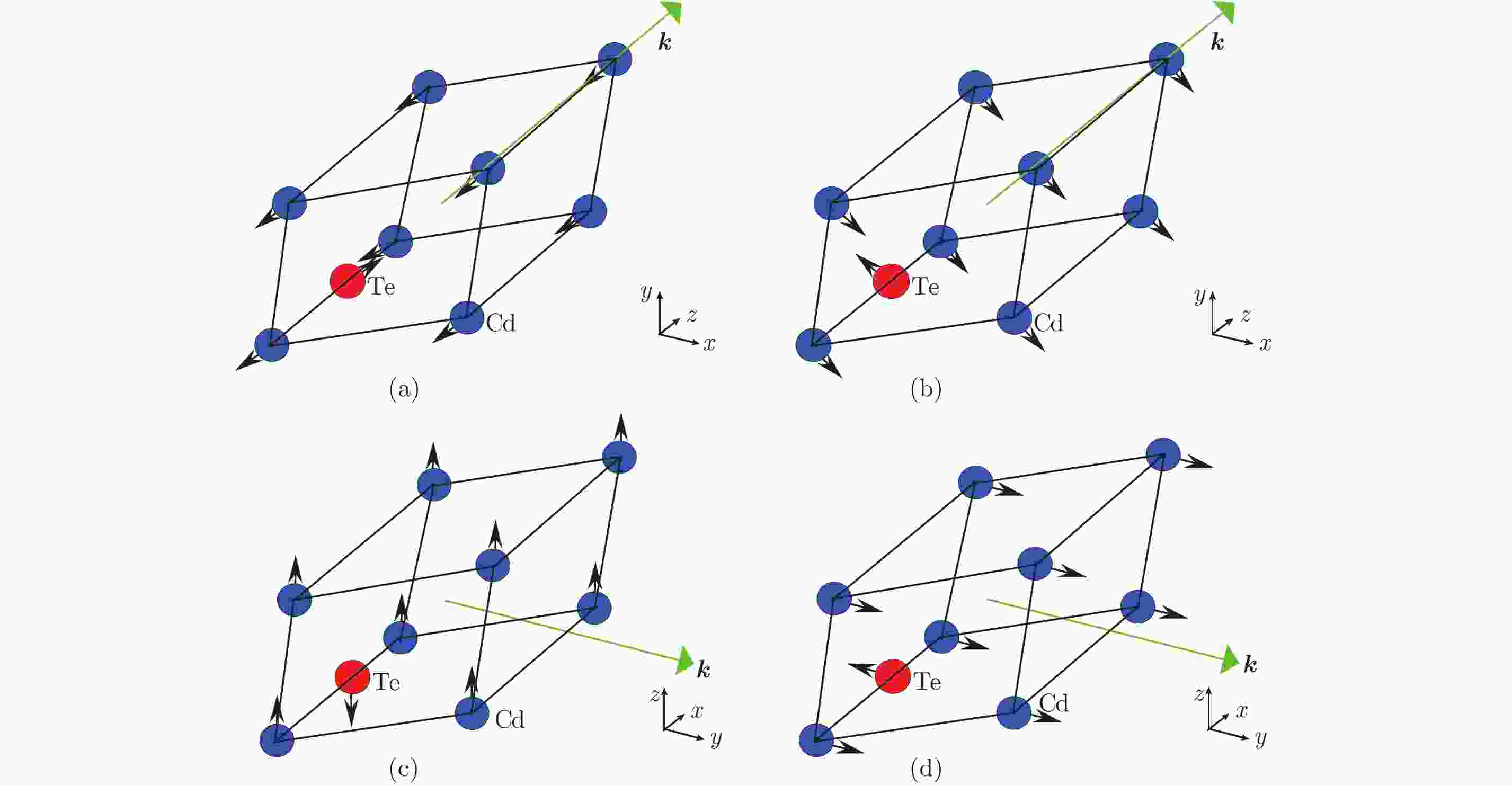
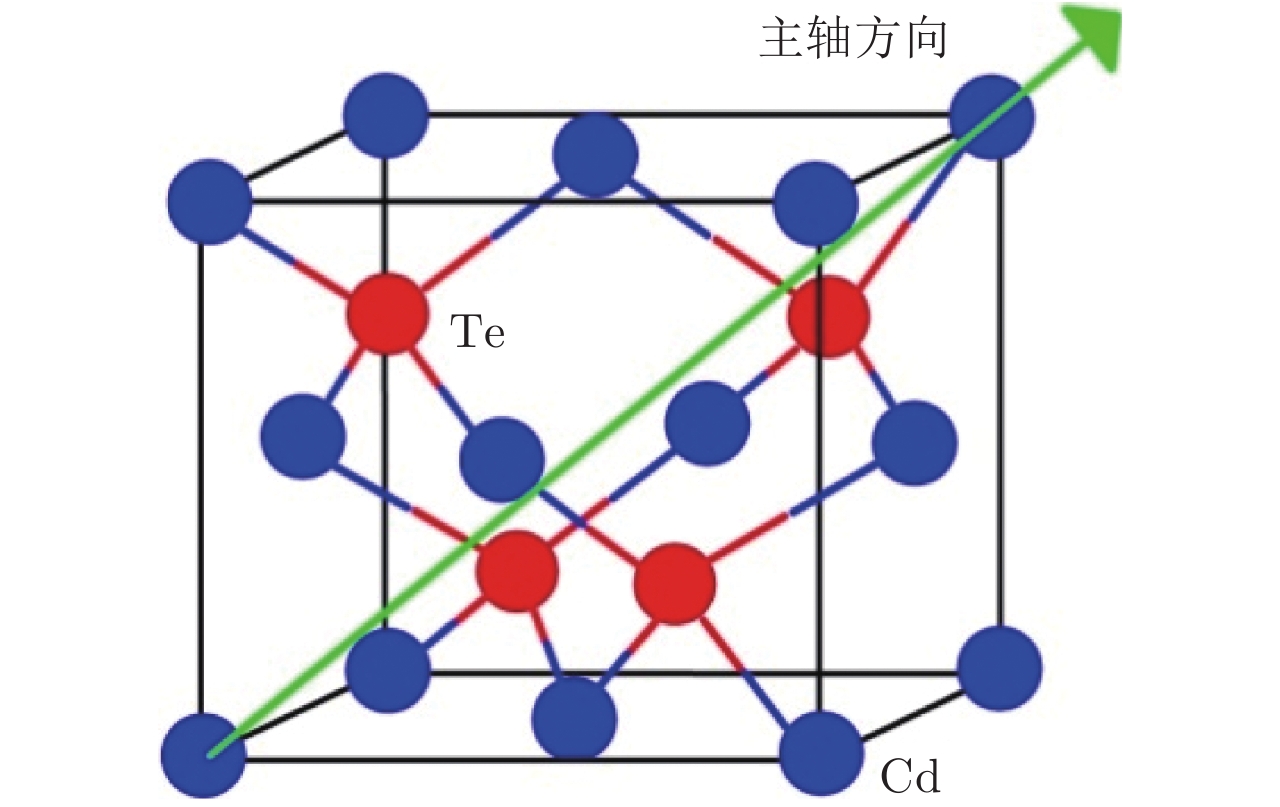
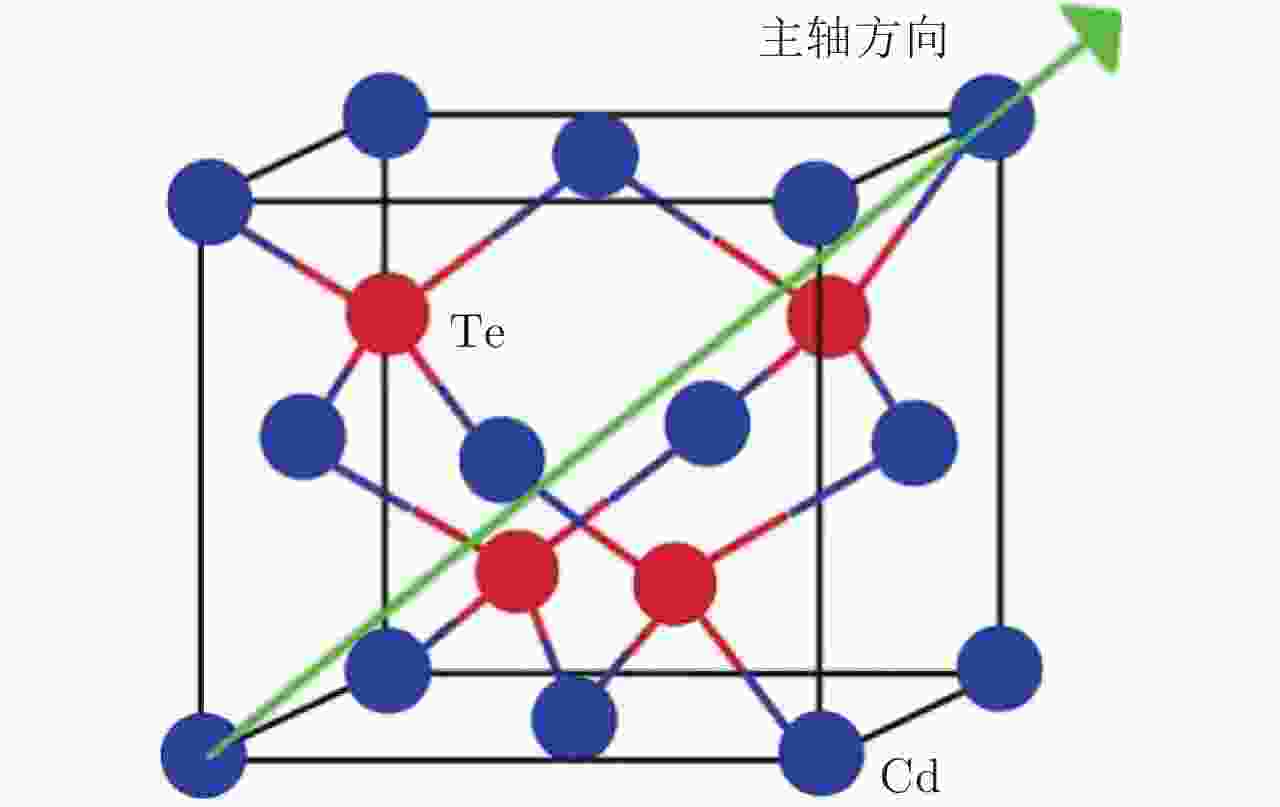
Figure 4. The total energy (calculated by LDA, GGA-PBE, and GGA-PW91 methods) vs the test lattice constant. The black arrow indicates the minimum of total energy, where $a_{{\rm{LDA}}}^{{\rm{CA {^{\scriptsize{-}}} PZ}}} = 0.64424 \ {\rm{nm}}$

下载: 全尺寸图片幻灯片

图 5 CdTe的声子色散谱，使用3种交换关联势为LDA, PBE, PW91

Figure 5. Phonon dispersions of CdTe with three exchange correlations LDA, PBE, PW91

下载: 全尺寸图片幻灯片

图 6 声子波矢方向与原子振动方向平行(a), (d)与垂直(b), (c)示意图。(a)和(b)中的声子波矢方向为CdTe主轴方向。(c)和(d)中的声子波矢方向为y轴方向。黑色箭头表示原子振动方向。绿色箭头表示声子传播方向

Figure 6. Schematic diagram: the phonon wave vectors are parallel (a), (d) and perpendicular (b), (c) to directions of atomic vibration. (a)-(b) the phonon wave vectors are parallel to the direction of CdTe principal axis. (c)-(d) The phonon wave vectors are parallel to the y-axis direction. Black arrows indicate the direction of atomic vibration. Green arrows indicate the direction of phonon propagation

下载: 全尺寸图片幻灯片

图 7 全空气太赫兹系统实验装置示意图。β-BBO为I型硼酸钡，PM为离轴抛物面镜，HV为高电压调制器，PMT为光电倍增管

Figure 7. Schematic diagram of full-air terahertz experimental system. β-BBO is type I barium borate, PM is an off-axis parabolic mirror, HV is a high-voltage modulator, and PMT is a photomultiplier tube

下载: 全尺寸图片幻灯片

图 8 理论计算与实验测量结果

Figure 8. The results of theoretical calculations and experimental measurements

下载: 全尺寸图片幻灯片

表 1 CdTe单晶材料： ${\text{ω} _{\text{LO}}}$ , ${\text{ω} _{\text{TO}}}$ , $\text{ε}$ (∞)和 $\text{γ} $ 理论和实验值

Table 1. CdTe single crystal: the theoretical and experimental values of ${\text{ω} _{{\text{LO}}}}$ , ${\text{ω} _{{\text{TO}}}}$ , $\text{ε}$ (∞) and $\text{γ} $

方法	光学声子横波模式 ${\omega _{{\rm{TO}}}}$ (THz)	光学声子纵波模式 ${\omega _{{\rm{LO}}}}$ (THz)	高频极限介电常数 $\varepsilon (\infty )$	碰撞频率 $\gamma $ (THz)	晶格常数 ${a_0}$ (nm)
LDA	4.402	5.111	7.55792	0.13	0.64424
GGA-PBE	4.518	5.301	6.62839	0.12	0.66594
GGA-PW91	4.533	5.309	6.72645	0.12	0.66541
实验值	4.25	5.01	6.93	0.125	0.64827^[33]

下载: 导出CSV

参考文献(33)

[1]	Lloyd-Hughes J and Jeon T I. A review of the terahertz conductivity of bulk and Nano-materials[J]. Journal of Infrared,Millimeter,and Terahertz Waves, 2012, 33(9): 871–925. DOI: 10.1007/s10762-012-9905-y.
[2]	程伟, 王迎新, 赵自然. 光电导太赫兹源新进展[J]. 激光与红外, 2011, 41(6): 597–604. DOI: 10.3969/j.issn.1001-5078.2011.06.001. Cheng Wei, Wang Ying-xin, and Zhao Zi-ran. New research progress of photoconductive terahertz source[J]. Laser&Infrared, 2011, 41(6): 597–604. DOI: 10.3969/j.issn.1001-5078.2011.06.001.
[3]	Withayachumnankul W, Png G M, Yin X X, et al. T-Ray sensing and imaging[J]. Proceedings of the IEEE, 2007, 95(8): 1528–1558. DOI: 10.1109/JPROC.2007.900325.
[4]	Scalari G, Maissen C, Turčinková D, et al. Ultrastrong coupling of the cyclotron transition of a 2D electron gas to a THz metamaterial[J]. Science, 2012, 335(6074): 1323–1326. DOI: 10.1126/science.1216022.
[5]	Stantchev R I, Sun B Q, Hornett S M, et al. Noninvasive, near-field terahertz imaging of hidden objects using a single-pixel detector[J]. Science Advances, 2016, 2(6): e1600190. DOI: 10.1126/sciadv.1600190.
[6]	Dengler R J, Cooper K B, Chattopadhyay G, et al.. 600 GHz imaging radar with 2 cm range resolution[C]. The IEEE/MTT-S International Microwave Symposium, Honolulu, HI, USA, 2007: 1371–1374.
[7]	Cooper K B, Dengler R J, Llombart N, et al. THz imaging radar for standoff personnel screening[J]. IEEE Transactions on Terahertz Science and Technology, 2011, 1(1): 169–182. DOI: 10.1109/TTHZ.2011.2159556.
[8]	Cooper K B, Dengler R J, Llombart N, et al. Penetrating 3-D imaging at 4- and 25-m range using a submillimeter-wave radar[J]. IEEE Transactions on Microwave Theory and Techniques, 2008, 56(12): 2771–2778. DOI: 10.1109/TMTT.2008.2007081.
[9]	Cooper K B, Dengler R J, Chattopadhyay G, et al. A high-resolution imaging radar at 580 GHz[J]. IEEE Microwave and Wireless Components Letters, 2008, 18(1): 64–66. DOI: 10.1109/LMWC.2007.912049.
[10]	Llombart N, Cooper K B, Dengler R J, et al. Confocal ellipsoidal reflector system for a mechanically scanned active terahertz imager[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(6): 1834–1841. DOI: 10.1109/TAP.2010.2046860.
[11]	Sheen D M, Hall T E, Severtsen R H, et al.. Standoff concealed weapon detection using a 350-GHz radar imaging system[C]. SPIE Passive Millimeter-Wave Imaging Technology XIII, Orlando, Florida, United States, 2010, 7670: 767008.
[12]	Sheen D M, McMakin D L, Hall T E, et al.. Active millimeter-wave standoff and portal imaging techniques for personnel screening[C]. 2009 IEEE Conference on Technologies for Homeland Security, Boston, MA, USA, 2009: 440–447.
[13]	Robertson D A, Marsh P N, Bolton D R, et al.. 340-GHz 3D radar imaging test bed with 10-Hz frame rate[C]. SPIE Passive and Active Millimeter-Wave Imaging XV, Baltimore, Maryland, 2012, 8362: 836206.
[14]	Wanke M C, Mangan M A, and Foltynowicz R J. Atmospheric propagation of THz radiation[R]. Albuquerque, NM, USA: Sandia National Laboratories, 2005: 2005–6389.
[15]	戴宁, 葛进, 胡淑红, 等. 太赫兹探测技术在遥感应用中的研究进展[J]. 中国电子科学研究院学报, 2009, 4(3): 232–237. DOI: 10.3969/j.issn.1673-5692.2009.03.002. Dai Ning, Ge Jin, Hu Shu-hong, et al. The development of the terahertz detection techniques in the applications of remote sensing[J]. Journal of CAEIT, 2009, 4(3): 232–237. DOI: 10.3969/j.issn.1673-5692.2009.03.002.
[16]	刘其军, 刘正堂, 冯丽萍, 等. 闪锌矿型CdTe电子结构和光学性质的第一性原理[J]. 中国科学院研究生院学报, 2009, 26(5): 615–620. Liu Qi-jun, Liu Zheng-tang, Feng Li-ping, et al. First-principle calculations of electronic structure and optical properties of Zinc blende CdTe[J]. Journal of the Graduate School of the Chinese Academy of Sciences, 2009, 26(5): 615–620.
[17]	孙立忠, 陈效双, 郭旭光, 等. CdTe和HgTe能带结构的第一性原理计算[J]. 红外与毫米波学报, 2004, 23(4): 271–275. DOI: 10.3321/j.issn:1001-9014.2004.04.007. Sun Li-zhong, Chen Xiao-shuang, Guo Xu-guang, et al. First principles calculation of the band structure of CdTe and HgTe[J]. Journal of Infrared and Millimeter Waves, 2004, 23(4): 271–275. DOI: 10.3321/j.issn:1001-9014.2004.04.007.
[18]	王琰, 侯延冰, 唐爱伟, 等. 不同稳定剂对水溶性CdTe纳米晶光学性质的影响[J]. 发光学报, 2008, 29(1): 171–175. Wang Yan, Hou Yan-bing, Tang Ai-wei, et al. Influence of different stabilizers on optical properties of water-soluble CdTe nanocrystals[J]. Chinese Journal of Luminescence, 2008, 29(1): 171–175.
[19]	Merad A E, Kanoun M B, Merad G, et al. Full-potential investigation of the electronic and optical properties of stressed CdTe and ZnTe[J]. Materials Chemistry and Physics, 2005, 92(2/3): 333–339. DOI: 10.1016/j.matchemphys.2004.10.031.
[20]	吴文智, 郑植仁, 金钦汉, 等. 水溶性CdTe量子点的三阶光学非线性极化特性[J]. 物理学报, 2008, 57(2): 1177–1182. DOI: 10.7498/aps.57.1177. Wu Wen-zhi, Zheng Zhi-ren, Jin Qin-han, et al. The property of third-order optical nonlinear susceptibility of water soluble CdTe quantum dots[J]. Acta Physica Sinica, 2008, 57(2): 1177–1182. DOI: 10.7498/aps.57.1177.
[21]	Vodopyanov L K. Optical studies of II–VI alloy lattice dynamics[J]. Journal of Alloys and Compounds, 2004, 371(1/2): 72–76. DOI: 10.1016/j.jallcom.2003.05.007.
[22]	Deligoz E, Colakoglu K, and Ciftci Y. Elastic, electronic, and lattice dynamical properties of CdS, CdSe, and CdTe[J]. Physica B:Condensed Matter, 2006, 373(1): 124–130. DOI: 10.1016/j.physb.2005.11.099.
[23]	Polit J, Sheregii E M, Cebulski J, et al. Phonon and vibrational spectra of hydrogenated CdTe[J]. Journal of Applied Physics, 2006, 100(1): 013521. DOI: 10.1063/1.2211368.
[24]	Robouch B V, Zajdel P, Kisiel A, et al. Analysis of the phonon line profile of hydrogenated CdTe[J]. Journal of Physics:Condensed Matter, 2008, 20(32): 325217. DOI: 10.1088/0953-8984/20/32/325217.
[25]	Stergiou V C, Kontos A G, and Raptis Y S. Anharmonic effects and Faust-Henry coefficient of CdTe in the vicinity of the energy gap[J]. Physical Review B, 2008, 77(23): 235201. DOI: 10.1103/PhysRevB.77.235201.
[26]	Tan J J, Ji G F, Chen X R, et al. The high-pressure phase transitions and vibrational properties of zinc-blende XTe (X=Zn, Cd, Hg): Performance of local-density-approximation density functional theory[J]. Computational Materials Science, 2010, 48(4): 796–801. DOI: 10.1016/j.commatsci.2010.03.037.
[27]	Ceperley D M and Alder B J. Ground state of the electron gas by a stochastic method[J].Physical Review Letters, 1980, 45(7): 566–569. DOI: 10.1103/PhysRevLett.45.566.
[28]	Perdew J P and Zunger A. Self-interaction correction to density-functional approximations for many-electron systems[J]. Physical Review B, 1981, 23(10): 5048–5079. DOI: 10.1103/PhysRevB.23.5048.
[29]	Perdew J P and Wang Y. Accurate and simple analytic representation of the electron-gas correlation energy[J]. Physical Review B, 1992, 45(23): 13244–13249. DOI: 10.1103/PhysRevB.45.13244.
[30]	Perdew J P, Burke K, and Ernzerhof M. Generalized gradient approximation made simple[J]. Physical Review Letters, 1996, 77(18): 3865–3868. DOI: 10.1103/PhysRevLett.77.3865.
[31]	黄昆, 韩汝琦. 固体物理[M]. 北京: 高等教育出版社, 1988: 104–111. Huang Kun and Han Ru-qi. Solid State Physics[M]. Beijing: Higher Education Press, 1988: 104–111.
[32]	Monkhorst H J and Pack J D. Special points for Brillonin-zone integrations[J]. Physical Revie B, 1976, 13(12): 5188–5192. DOI: 10.1103/PhysRevB.13.5188.
[33]	Rabadanov M K, Verin I A, Ivanov Y M, et al. Refinement of the atomic structure of CdTe single crystals[J]. Crystallography Reports, 2001, 46(4): 636–641. DOI: 10.1134/1.1387130.