作者中心
专家审稿
责编办公
编辑办公
A Sinusoidal Frequency Modulation Fourier-Bessel Transform and its Application to Micro-Doppler Feature Extraction
-
摘要: 针对微动目标特征提取问题，该文提出了一种正弦调频Fourier-Bessel变换(Sinusoidal Frequency Modulation Fourier-Bessel Transform, SFMFBT)，并基于SFMFBT提出了一种雷达目标微动频率的精确提取方法。首先给出了SFMFBT的定义，分析了变换的相关性质，并通过频率提取误差分析给出了一种修正方法，最后讨论了离散信号处理中的若干问题。相比于傅里叶-贝塞尔变换，SFMFBT将k分辨率参数引入Bessel函数基，克服了其对应频率不可细分的缺陷，并且通过误差分析提高了信号分解精度，从而将Bessel函数基引入特征提取领域，拓展了其应用范围。仿真结果表明该方法同样适用于微动群目标频率提取与回波分离重构，且在SNR>0 dB条件下具有较好的鲁棒性。
-
关键词:
- 微多普勒 /
- 特征提取 /
- 群目标 /
- 正弦调频Fourier-Bessel变换(SFMFBT)
Abstract: In this paper, a Sinusoidal Frequency Modulation Fourier-Bessel Transform (SFMFBT) is proposed for micro-Doppler (m-D) target feature extraction. Initially, the definition of SFMFBT is given, and then, some of its properties are analyzed. A method to reduce frequency extraction error is then introduced based on error analysis. Finally, some issues in the frequency extraction of discrete signals are discussed. After comparing with the values of Fourier-Bessel Transform (FBT), SFMFBT introduces the parameter k-resolution into the kernel function of FBT so that accuracy of the signal decomposition is distinctly improved. In addition, from the error analysis in SFMFBT, Bessel-based signal decomposition methods can be used for feature extraction, whose application scope is extended. Simulation results verify the effectiveness of the proposed method for a group m-D target and also verifies its robustness when SNR>0 dB. -
图 3 目标回波及各目标重构回波时频分析
Figure 3. Time-frequency analysis of the echo signal and the individual reconstructed signals
图 4 频率提取正确概率pe随SNR及k分辨率变化曲线
Figure 4. The curve of m-D frequency extraction probability pe in different SNR and k-resolution conditions
图 5 提取旋转频率NRMSE随旋转半径及SNR变化曲线
Figure 5. NRMSE curves with different rotation radius and SNR
表 1 微动频率提取结果
Table 1. The m-D frequency extraction result
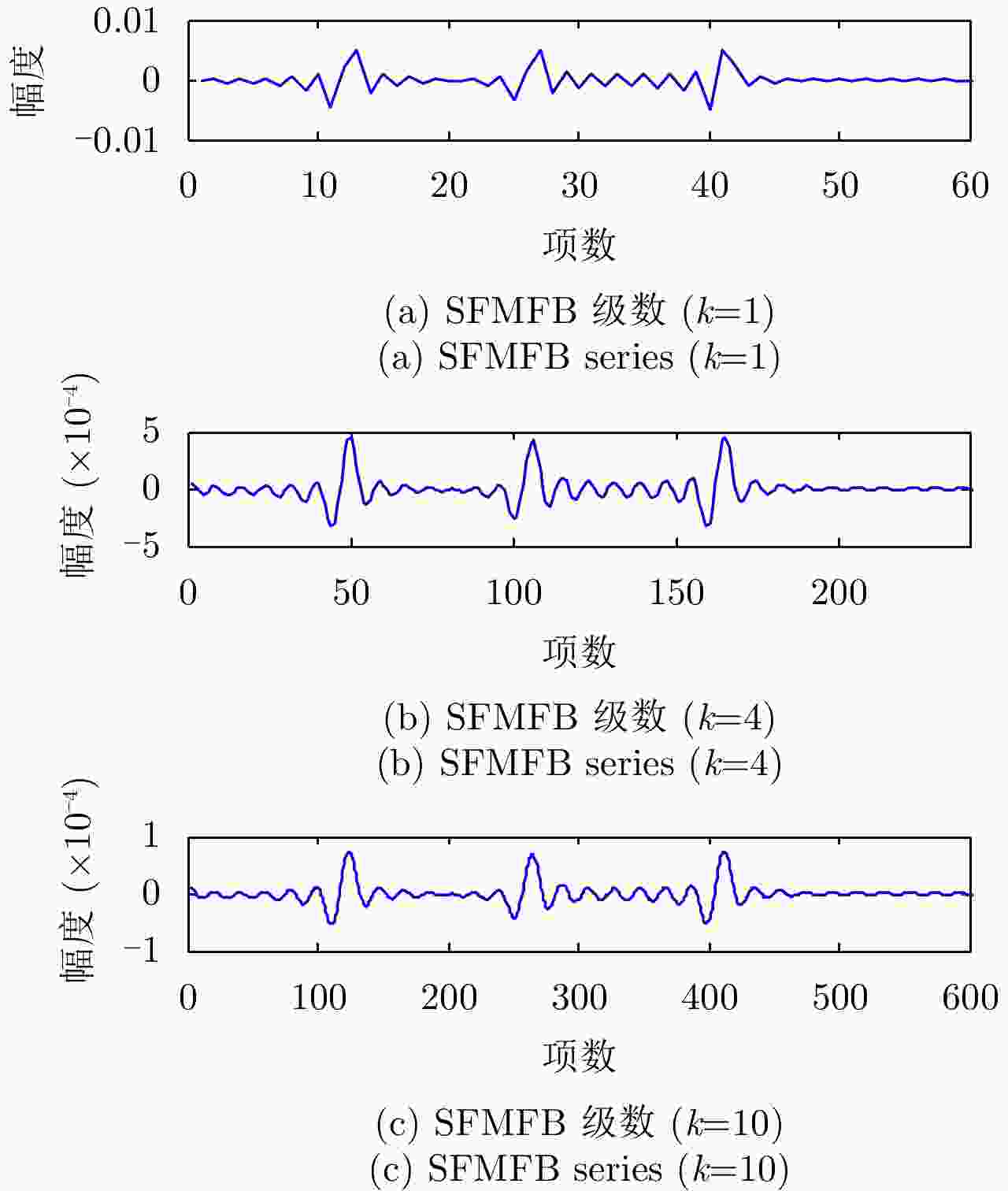
目标 k分辨率 最大值项数 初始频率(Hz) 修正频率(Hz) 绝对误差(Hz) 目标1 1 11 2.6878 2.7398 0.2602 4 50 3.1094 3.0254 0.0254 10 124 3.0938 3.0088 0.0088 目标2 1 25 6.1876 6.2381 0.2619 4 106 6.6094 6.5234 0.0234 10 264 6.5938 6.5083 0.0083 目标3 1 40 9.9376 9.9881 0.2119 4 165 10.2969 10.2089 0.0089 10 412 10.2938 10.2078 0.0078 
下载: 导出CSV
-
[1] Chen V C. Doppler signatures of radar backscattering from objects with micro-motions[J]. IET Signal Processing, 2008, 2(3): 291–300. DOI: 10.1049/iet-spr:20070137 [2] Tahmoush D. Review of micro-Doppler signatures[J]. IET Radar,Sonar&Navigation, 2015, 9(9): 1140–1146. [3] 陈小龙, 关键, 何友. 微多普勒理论在海面目标检测中的应用及展望[J]. 雷达学报, 2013, 2(1): 123–134. DOI: 10.3724/SP.J.1300.2013.20102Chen Xiao-long, Guan Jian, and He You. Applications and prospect of micro-motion theory in the detection of sea surface target[J]. Journal of Radars, 2013, 2(1): 123–134. DOI: 10.3724/SP.J.1300.2013.20102 [4] 赵双, 鲁卫红, 冯存前, 等. 基于窄带雷达网的弹道目标三维进动特征提取[J]. 雷达学报, 2017, 6(1): 98–105. DOI: 10.12000/JR15129Zhao Shuang, Lu Weihong, Feng Cunqian, et al. Three-dimensional precession feature extraction of ballistic targets based on narrowband radar network[J]. Journal of Radars, 2017, 6(1): 98–105. DOI: 10.12000/JR15129 [5] 韩勋, 杜兰, 刘宏伟, 等. 基于时频分布的空间锥体目标微动形式分类[J]. 系统工程与电子技术, 2013, 35(4): 684–691Han Xun, Du Lan, Liu Hong-wei, et al. Classification of micro-motion form of space cone-shaped objects based on time-frequency distribution[J]. Systems Engineering and Electronics, 2013, 35(4): 684–691 [6] Shui Peng-lang, Bao Zheng, and Su Hong-tao. Nonparametric detection of FM signals using time-frequency ridge energy[J]. IEEE Transactions on Signal Processing, 2008, 56(5): 1749–1760. DOI: 10.1109/TSP.2007.909322 [7] 陈小龙, 刘宁波, 王国庆, 等. 基于高斯短时分数阶Fourier变换的海面微动目标检测方法[J]. 电子学报, 2014, 42(5): 971–977Chen Xiao-long, Liu Ning-bo, Wang Guo-qing, et al. Gaussian short-time fractional Fourier transform based detection algorithm of target with micro-motion at sea[J]. Acta Electronica Sinica, 2014, 42(5): 971–977 [8] Chen Xiaolong, Guan Jian, Bao Zhonghua, et al. Detection and extraction of target with micromotion in spiky sea clutter via short-time fractional Fourier transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(2): 1002–1018. DOI: 10.1109/TGRS.2013.2246574 [9] Li K, Liu Y, Huo K, et al. Estimation of micro-motion parameters based on cyclostationary analysis[J]. IET Signal Processing, 2010, 4(3): 218–223. DOI: 10.1049/iet-spr.2009.0044 [10] Orović I, Stankovic S, and Thayaparan T. Time-frequency-based instantaneous frequency estimation of sparse signals from incomplete set of samples[J]. IET Signal Processing, 2014, 8(3): 239–245. DOI: 10.1049/iet-spr.2013.0354 [11] Luo Ying, Zhou Liang, Lin Yong-zhao, et al.. Micro-Doppler extraction of frequency-stepped chirp signal based on the Hough transform[C]. Proceedings of the 8th International Symposium on Antennas, Propagation and EM Theory, Kunming, China, 2008: 408–411. [12] Zhang Qun, Yeo T S, Tan H S, et al. Imaging of a moving target with rotating parts based on the Hough transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 291–299. DOI: 10.1109/TGRS.2007.907105 [13] Peng Bo, Wei Xizhang, Deng Bin, et al. A sinusoidal frequency modulation Fourier transform for radar-based vehicle vibration estimation[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(9): 2188–2199. DOI: 10.1109/TIM.2014.2308031 [14] 杨陈, 池龙, 张群, 等. 正弦调频傅里叶变换的自旋微动群目标分辨[J]. 空军工程大学学报(自然科学版), 2016, 17(3): 51–56. DOI: 10.3969/j.issn.1009-3516.2016.03.010Yang Chen, Chi Long, Zhang Qun, et al. Resolution of group targets with spinning micro motion based on sinusoidal frequency modulation Fourier transform[J]. Journal of Air Force Engineering University(Natural Science Edition) , 2016, 17(3): 51–56. DOI: 10.3969/j.issn.1009-3516.2016.03.010 [15] Suresh P, Thayaparan T, and Venkataramaniah K. Fourier-Bessel transform and time-frequency-based approach for detecting manoeuvring air target in sea-clutter[J]. IET Radar,Sonar&Navigation, 2015, 9(5): 481–491. [16] Suresh P, Thayaparan T, Obulesu T, et al. Extracting micro-Doppler radar signatures from rotating targets using Fourier-Bessel transform and time-frequency analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3204–3210. DOI: 10.1109/TGRS.2013.2271706 [17] 张群, 何其芳, 罗迎. 基于贝塞尔函数基信号分解的微动群目标特征提取方法[J]. 电子与信息学报, 2016, 38(12): 3056–3062. DOI: 10.11999/JEIT161036Zhang Qun, He Qifang, and Luo Ying. Micro-Doppler feature extraction of group targets using signal decomposition based on Bessel function basis[J]. Journal of Electronics&Information Technology, 2016, 38(12): 3056–3062. DOI: 10.11999/JEIT161036 [18] Spiegel M R, Lipschutz S L, and Liu J. Mathematical Handbook of Formulas and Tables[M]. Third Edition, New York: Academic Press Co., 2009. [19] McLachlan N W. Bessel Functions for Engineers[M]. Oxford, England: Clarendon Press, 1955. [20] Mathematical Handbook[M]. Athens, Abbrev. State: ESPI Publishing, 2007. -
图(6) / 表(1)
计量
- 文章访问数: 3143
- HTML全文浏览量: 802
- PDF下载量: 434
- 被引次数: 0
