Range-angle Decoupled Transmit Beamforming with Frequency Diverse Array (in English)
DOI: 10.12000/JR16113 cstr: 32380.14.JR16113
-
摘要:
常规频率分集雷达(FDA)在发射阵元采用均匀的频率间隔,从而可以形成距离-角度耦合的波束方向图。但是该方向图在多个距离上均形成多峰值波束,当干扰位于任一波束最大指向的距离时,将会带来信干噪比损失。针对上述问题,该文通过分析波束形成的表达式,从原理上提出一个关于频率分集雷达阵列配置的基本原则,能够在指定的距离角度范围内,形成单峰值的波束方向图。几种特例和仿真结果均证明了该原则的有效性。
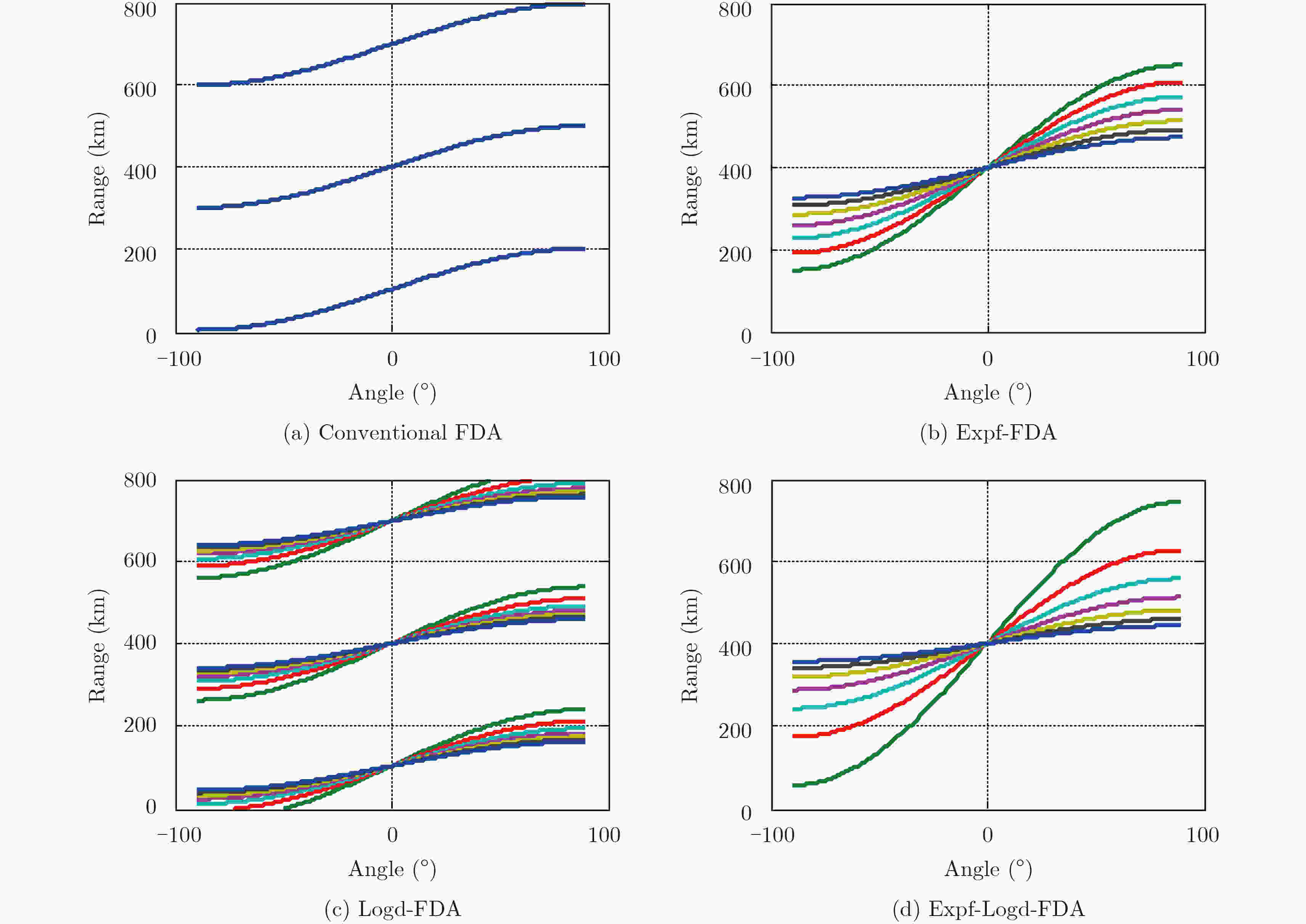
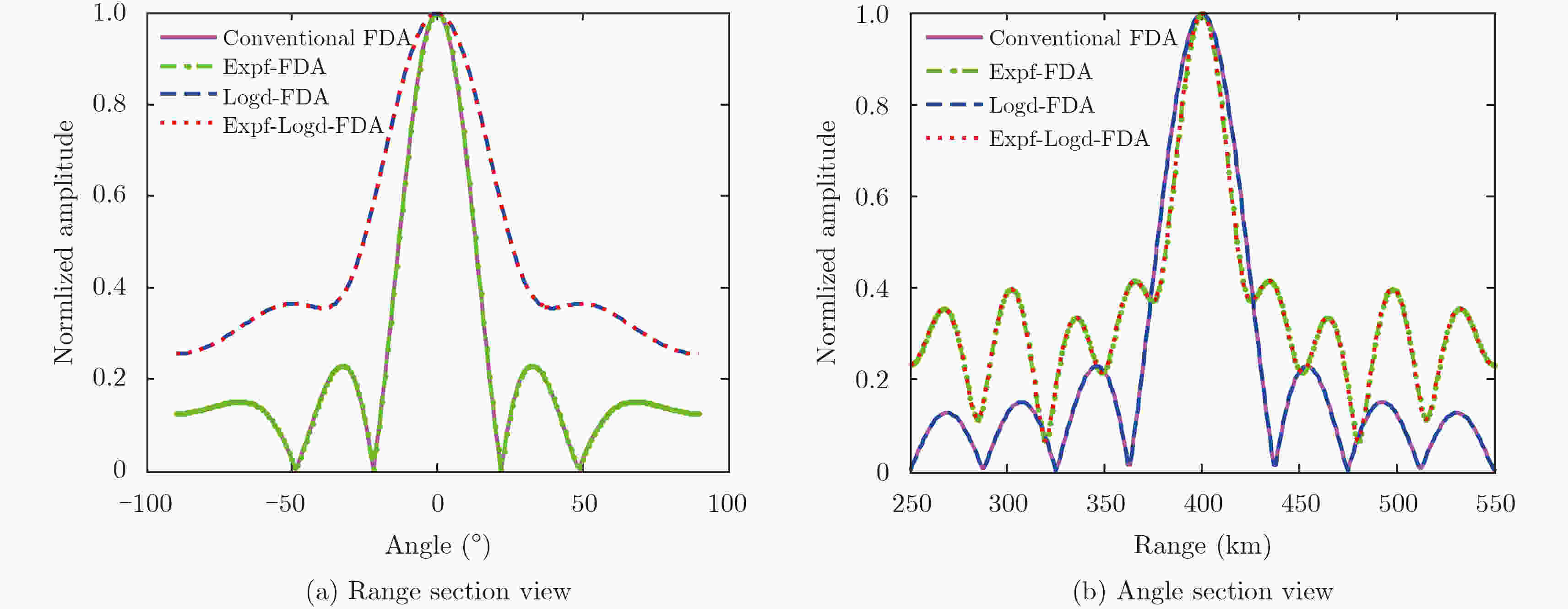
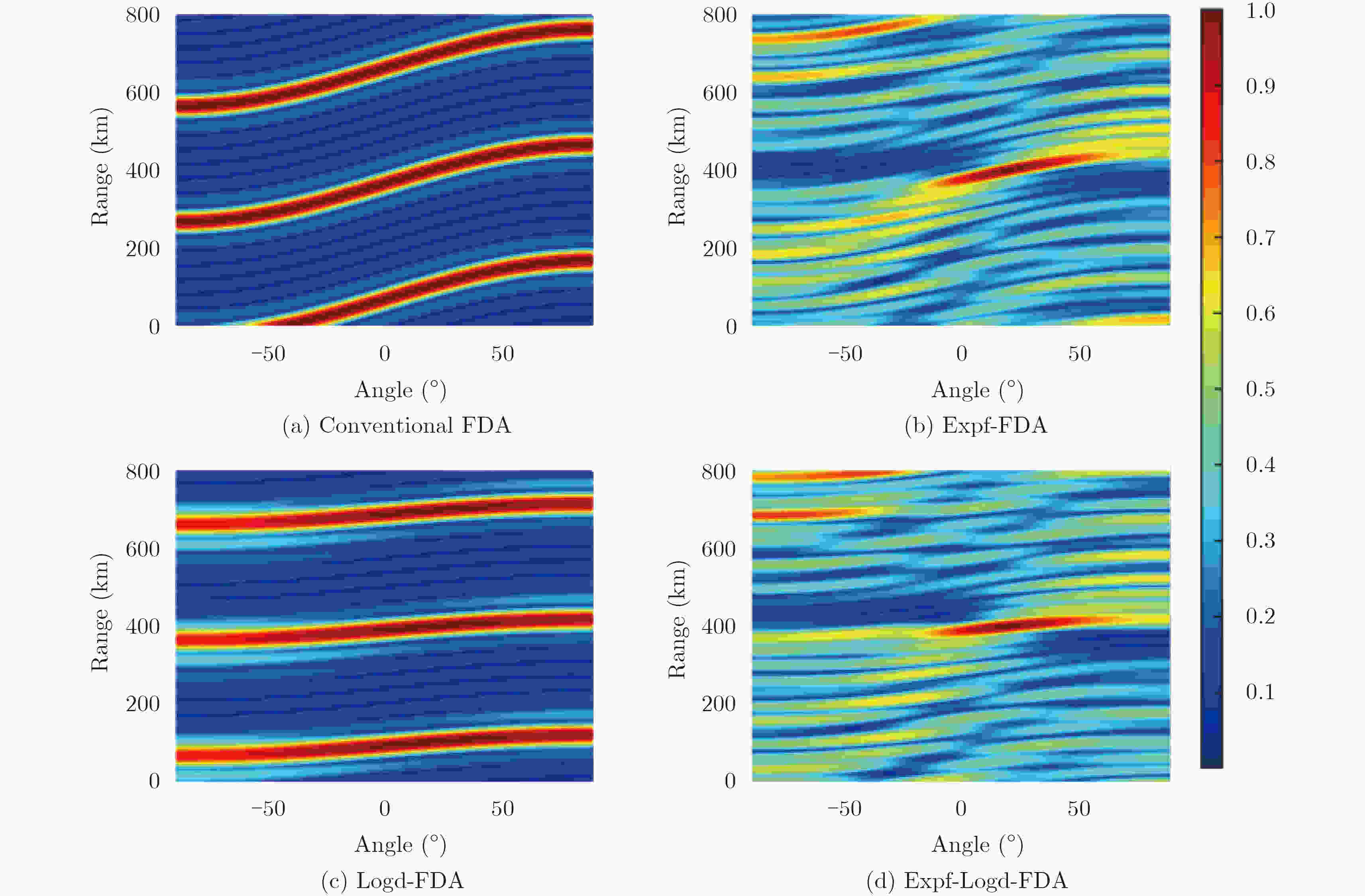
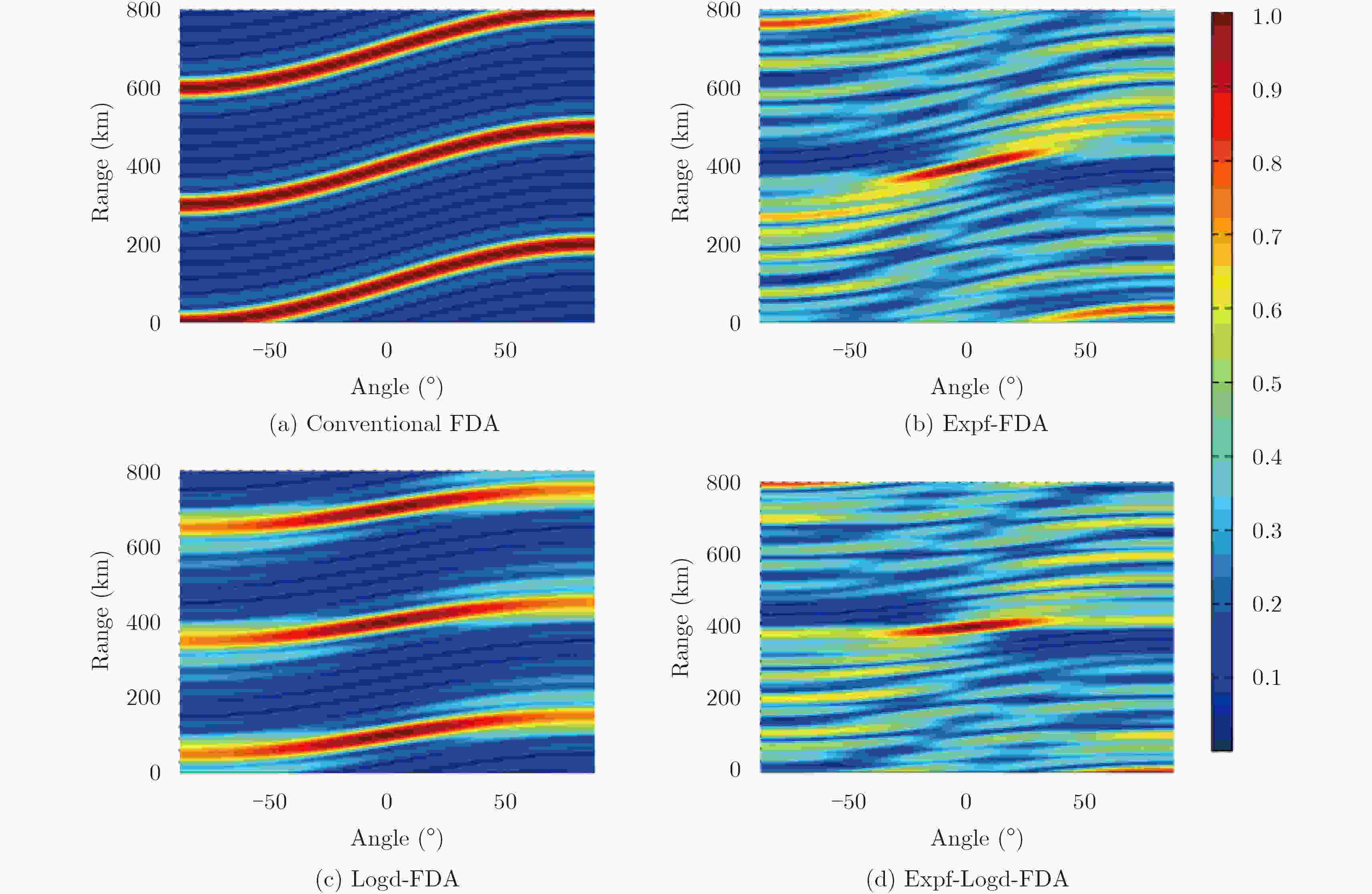
Abstract:It has been shown that Frequency Diverse Arrays (FDA) exhibit a range-angle dependent beam steering feature by employing a uniform frequency increment across the array elements. However, this beam pattern generates maxima at multiple range values, possibly leading to loss of signal-to-interference-plus-noise ratio when the interferences are located at any of the maxima. Herein, we prove that the beam pattern of FDA is range-periodic and propose the basic criteria for the FDA configuration to decouple the range and angle. In an illuminated space, a single-maximum beam pattern can be obtained by configuring the frequency increment between the elements. Specific examples have been discussed herein, and the simulation results verify the proposed theory.
-
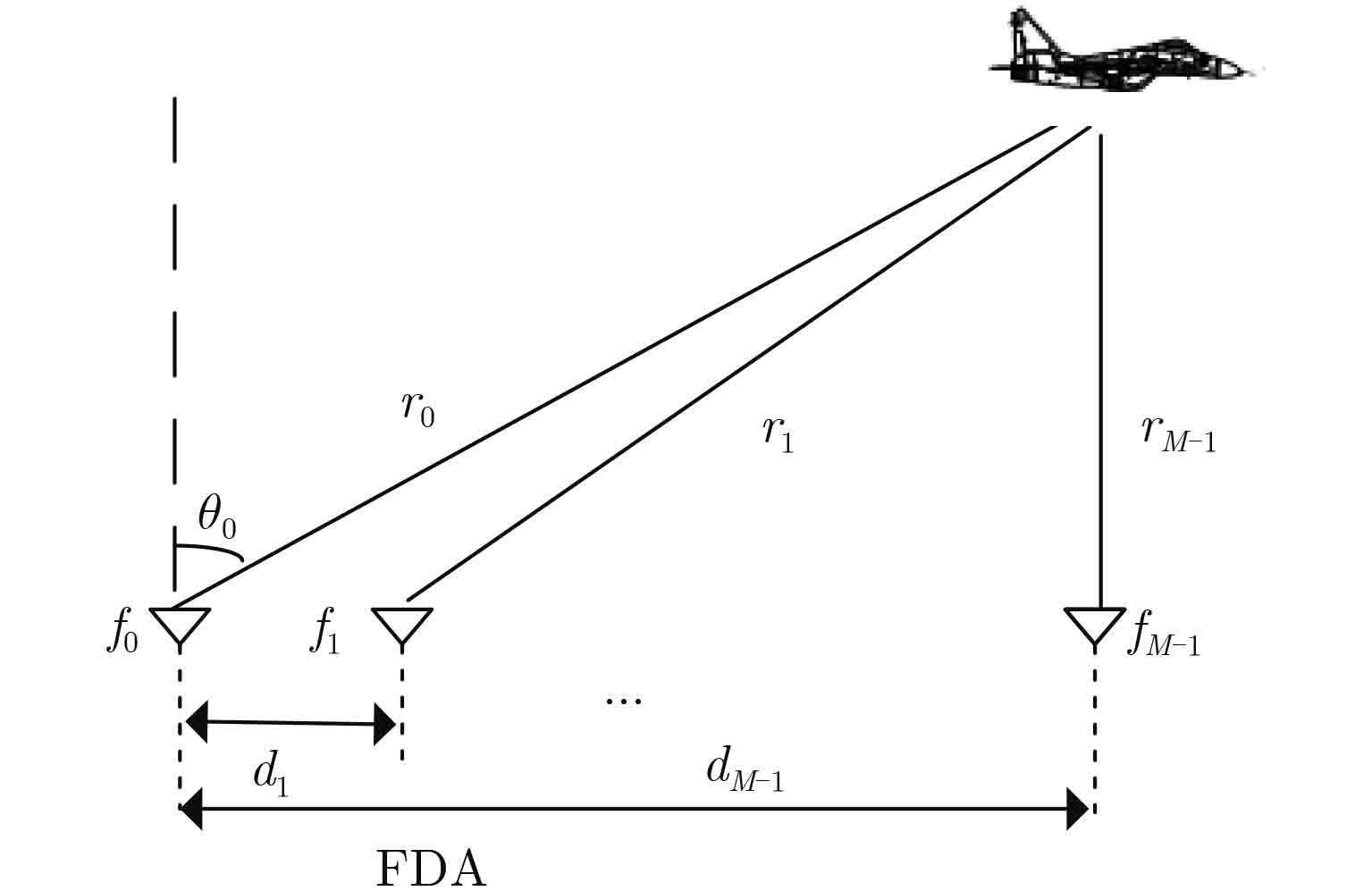
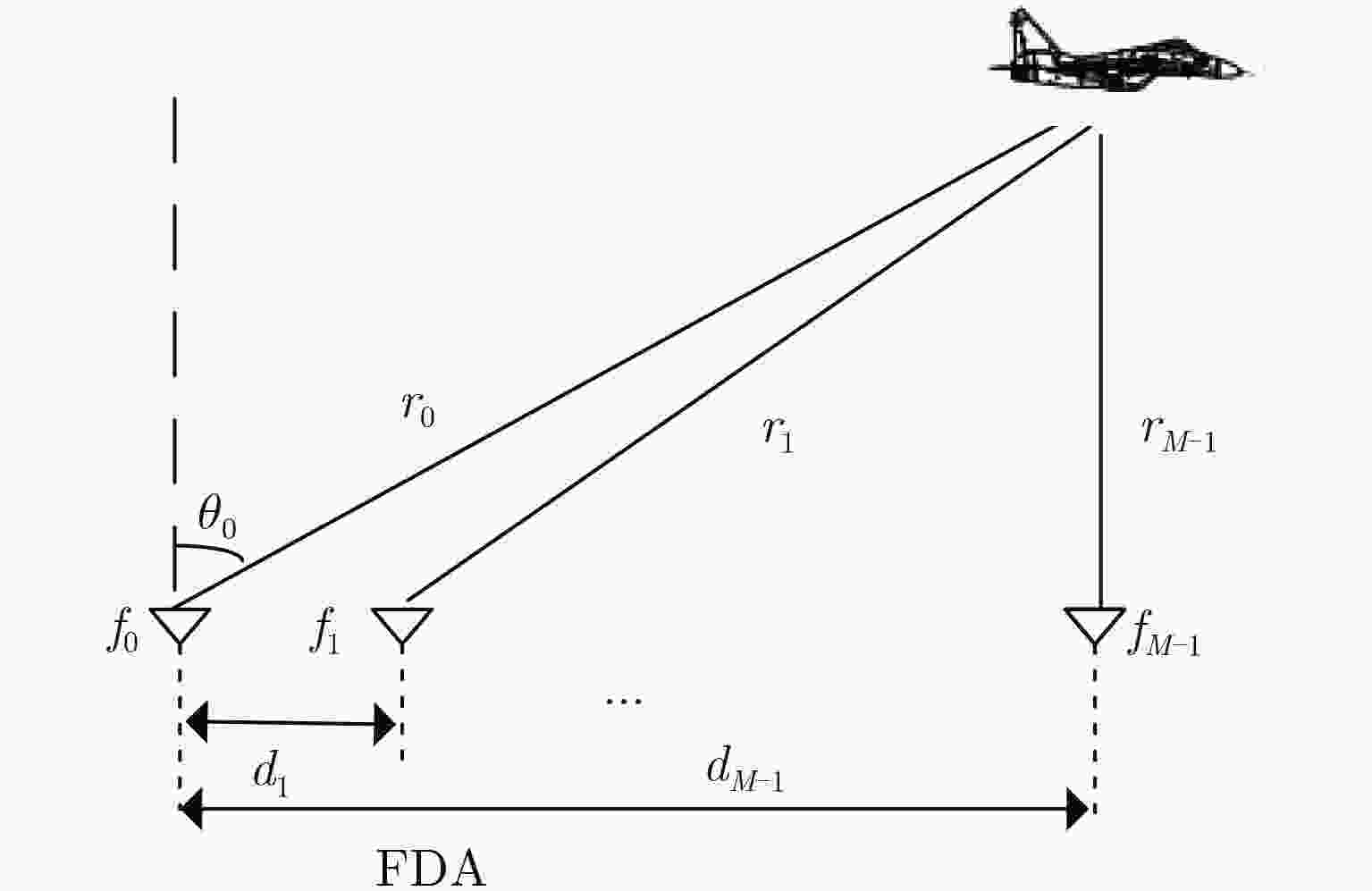
Table 1. Parameters for simulations
Parameter Value Parameter Value Element number M 8 d 0.1 m Reference frequency f0 1 GHz b 1.4 {\Delta}f 1 kHz Desired point
( \theta_0, r0)(0°, 400 km) -
[1] Antonik P, Wicks M C, and Griffiths H D. Range dependent beamforming using element level waveform diversity[C]. International Waveform Diversity Design Conference, Las Vegas, NV, USA, Jan. 2006: 22–27. [2] Secmen M, Demir S, and Hizal A. Frequency diverse array antenna with periodic time modulated pattern in range and angle[C]. IEEE Radar Conference, Boston, MA, USA, Apr. 2007: 427–430. [3] Antonik P, Wicks M C, and Griffiths H D. Multi-mission, multi-mode waveform diversity[C]. IEEE Radar Conference, Verona, NY, USA, Apr. 2006: 580–582. [4] Zhuang L and Liu X Z. Precisely beam steering for frequency diverse arrays based on frequency offset selection[C]. International Radar Conference, Bordeaux, France, Oct. 2009: 1–4. [5] Chen Y G, Li Y T, and Wu Y H. Research on the linear frequency diverse array performance[C]. IEEE International Conference on Signal Processing, Beijing, China, Oct. 2010: 2324–2327. [6] Sammartino P F, Backer C J, Griffiths H D. Frequency diverse MIMO techniques for radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 201–222. DOI: 10.1109/TAES.2013.6404099 [7] Xu J W, Liao G S, and Zhu S Q. Receive beamforming of frequency diverse array radar systems[C]. 31th URSI General Assembly and Scientific Symposium (URSIGASS), Beijing, China, Aug. 2014: 1–5. [8] Wang W Q. Range-angle dependent transmit beampattern synthesis for linear frequency diverse arrays[J]. IEEE Transactions on Antennas Propagation, 2014, 61(8): 4073–4081. [9] Khan W, Qureshi I M. Frequency diverse array radar with time dependent frequency offset[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13: 758–761. DOI: 10.1109/LAWP.2014.2315215 [10] Wang W Q, So H C, Shao H. Nonuniform frequency diverse array for range-angle imaging of targets[J].IEEE Sensors Journal, 2014, 14(8): 2469–2476. DOI: 10.1109/JSEN.2014.2304720 [11] Khan W, Qureshi I M, Saeed S. Frequency diverse array radarwith logarithmically increasing frequency offset[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14: 499–502. DOI: 10.1109/LAWP.2014.2368977 [12] Xu Y H, Shi X W, Xu J W. Range-angle-dependent beamforming of pulsed frequency diverse array[J]. IEEE Transactions on Antennas Propagation, 2015, 63(7): 3262–2367. DOI: 10.1109/TAP.2015.2423698 [13] Gao K, Wang W Q. Decoupled frequency diverse array range-angle-dependent beampattern synthesis using non-linearly increasing frequency offsets[J]. IET Microwaves,Antennas&Propagation, 2016, 10(8): 880–884. [14] Gao K, Wang W Q. Transmit beamspace design for multi-carrier frequency diverse array sensor[J]. IEEE Sensors Journal, 2016, 16(14): 5709–5714. DOI: 10.1109/JSEN.2016.2573379 [15] Shao H, Dai J, Xiong J. Dot-shaped range-angle beampattern synthesis for frequency diverse array[J]. IEEE Antennas and Wireless Propagation(published online) , 2016. DOI: 10.1109/LAWP.2016.2527818 [16] Schmidt R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas Propagation, 1986, 34(1): 276–280. -



 作者中心
作者中心 专家审稿
专家审稿 责编办公
责编办公 编辑办公
编辑办公
 下载:
下载: