- Home
- Articles & Issues
-
Data
- Dataset of Radar Detecting Sea
- SAR Dataset
- SARGroundObjectsTypes
- SARMV3D
- AIRSAT Constellation SAR Land Cover Classification Dataset
- 3DRIED
- UWB-HA4D
- LLS-LFMCWR
- FAIR-CSAR
- MSAR
- SDD-SAR
- FUSAR
- SpaceborneSAR3Dimaging
- Sea-land Segmentation
- SAR Multi-domain Ship Detection Dataset
- SAR-Airport
- Hilly and mountainous farmland time-series SAR and ground quadrat dataset
- SAR images for interference detection and suppression
- HP-SAR Evaluation & Analytical Dataset
- GDHuiYan-ATRNet
- Multi-System Maritime Low Observable Target Dataset
- DatasetinthePaper
- DatasetintheCompetition
- Report
- Course
- About
- Publish
- Editorial Board
- Chinese
Article Navigation >
Journal of Radars
>
2026
> Proofreading [3rd]
| Citation: | TAN Zhuohang, CHEN Zeyu, TANG Haojie, et al. Fast structured sparse millimeter-wave 3D SAR imaging based on low-rank and smooth matrix completion[J]. Journal of Radars, in press. doi: 10.12000/JR25267 |
Fast Structured Sparse Millimeter-wave 3D SAR Imaging Based on Low-rank and Smooth Matrix Completion
DOI: 10.12000/JR25267 CSTR: 32380.14.JR25267
More Information-
Abstract
The millimeter-Wave (mmWave) radar is widely used in security screening, nondestructive testing, and through-the-wall imaging due to its compact size, high resolution, and strong penetration capability. High-resolution mmWave radar imaging typically requires synthetic aperture emulation, which involves dense two-dimensional spatial sampling via structured scanning on a mechanical platform. However, this process is time-consuming in practical applications. Therefore, many existing studies have focused on reconstructing echo data under sparse sampling conditions for imaging. However, most existing sparse recovery methods assume uniformly random sparse sampling or involve high computational complexity, making them difficult to apply in practical Synthetic Aperture Radar (SAR) imaging systems. This paper proposes a fast, structured sparse, mmWave three-Dimensional (3D) SAR imaging algorithm based on low-rank and smooth Matrix Completion (MC) to address this problem. First, the global low-rank property and local smoothness prior of echo data are analyzed within the framework of near-field mmWave SAR imaging theory. Our analysis demonstrated that structured sparse SAR data arising from missing entire rows or columns in practical scanning can be recovered. Building on this, an MC model incorporating low-rank and smoothness constraints was constructed. This MC model jointly regularizes with nuclear norm and total variation and can be solved efficiently using the Alternating Direction Method of Multipliers (ADMM). Finally, the performance of the proposed algorithm was validated through multiple simulation runs and real-world experiments. Experimental results showed that, using only 20%–30% of randomly sampled rows or columns of echo data, the proposed algorithm can achieve fast data recovery and high-resolution 3D imaging within tens of seconds. -

-
References
[1] 温鑫, 黄培康, 年丰, 等. 主动式毫米波近距离圆柱扫描三维成像系统[J]. 系统工程与电子技术, 2014, 36(6): 1044–1049. doi: 10.3969/j.issn.1001-506X.2014.06.05.WEN Xin, HUANG Peikang, NIAN Feng, et al. Active millimeter-wave near-field cylindrical scanning three-dimensional imaging system[J]. Systems Engineering and Electronics, 2014, 36(6): 1044–1049. doi: 10.3969/j.issn.1001-506X.2014.06.05.[2] 谢朋飞, 张磊, 吴振华. 融合ω-K和BP算法的圆柱扫描毫米波三维成像算法[J]. 雷达学报, 2018, 7(3): 387–394. doi: 10.12000/JR17112.XIE Pengfei, ZHANG Lei, and WU Zhenhua. A three-dimensional imaging algorithm fusion with ω-K and BP algorithm for millimeter-wave cylindrical scanning[J]. Journal of Radars, 2018, 7(3): 387–394. doi: 10.12000/JR17112.[3] WINGREN N and SJÖBERG D. Nondestructive testing using mm-wave sparse imaging verified for singly curved composite panels[J]. IEEE Transactions on Antennas and Propagation, 2023, 71(1): 1185–1189. doi: 10.1109/TAP.2022.3211341.[4] GAO Yuan and ZOUGHI R. Millimeter wave reflectometry and imaging for noninvasive diagnosis of skin burn injuries[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(1): 77–84. doi: 10.1109/TIM.2016.2620778.[5] LIAO Jiancheng, ZENG Xiaolu, YANG Xiaopeng, et al. MIMO through-the-wall radar 3-D imaging using propagation compensation and coherence factor[J]. IEEE Transactions on Aerospace and Electronic Systems, 2025, 61(6): 17213–17226. doi: 10.1109/TAES.2025.3602758.[6] YANIK M E and TORLAK M. Near-field 2-D SAR imaging by millimeter-wave radar for concealed item detection[C]. 2019 IEEE Radio and Wireless Symposium, Orlando, USA, 2019: 1–4. doi: 10.1109/RWS.2019.8714552.[7] 刘可, 朱泽政, 于军, 等. 基于互质阵列孔洞分析的稀疏阵列设计方法[J]. 电子与信息学报, 2022, 44(1): 372–379. doi: 10.11999/JEIT201024.LIU Ke, ZHU Zezheng, YU Jun, et al. Sparse array design methods based on hole analysis of the coprime array[J]. Journal of Electronics & Information Technology, 2022, 44(1): 372–379. doi: 10.11999/JEIT201024.[8] 邢孟道, 马鹏辉, 楼屹杉, 等. 合成孔径雷达快速后向投影算法综述[J]. 雷达学报(中英文), 2024, 13(1): 1–22. doi: 10.12000/JR23183.XING Mengdao, MA Penghui, LOU Yishan, et al. Review of fast back projection algorithms in synthetic aperture radar[J]. Journal of Radars, 2024, 13(1): 1–22. doi: 10.12000/JR23183.[9] SHEEN D M, MCMAKIN D L, and HALL T E. Three-dimensional millimeter-wave imaging for concealed weapon detection[J]. IEEE Transactions on Microwave Theory and Techniques, 2001, 49(9): 1581–1592. doi: 10.1109/22.942570.[10] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582.[11] ZHOU Zichen, WEI Shunjun, WANG Mou, et al. Comparison of MF and CS algorithm in 3-D near-field SAR imaging[C]. 2021 7th Asia-Pacific Conference on Synthetic Aperture Radar, Bali, Indonesia, 2021: 1–5. doi: 10.1109/APSAR52370.2021.9688546.[12] WANG Mou, WEI Shunjun, LIANG Jiadian, et al. RMIST-Net: Joint range migration and sparse reconstruction network for 3-D mmW imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5205117. doi: 10.1109/TGRS.2021.3068405.[13] CANDES E J and TAO T. The power of convex relaxation: Near-optimal matrix completion[J]. IEEE Transactions on Information Theory, 2010, 56(5): 2053–2080. doi: 10.1109/TIT.2010.2044061.[14] KESHAVAN R H, MONTANARI A, and OH S. Matrix completion from a few entries[J]. IEEE Transactions on Information Theory, 2010, 56(6): 2980–2998. doi: 10.1109/TIT.2010.2046205.[15] ZHANG Siqian, DONG Ganggang, and KUANG Gangyao. Matrix completion for downward-looking 3-D SAR imaging with a random sparse linear array[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(4): 1994–2006. doi: 10.1109/TGRS.2017.2771826.[16] PENG Yechao, SHENG Zhichao, and HE Guoqiang. Near-field low-storage SAR imaging with spatio-temporal sub-Nyquist samples[J]. IEEE Sensors Journal, 2024, 24(12): 19442–19453. doi: 10.1109/JSEN.2024.3393761.[17] MA Yuxin, HAI Yu, YANG Jianyu, et al. A near-field 3-D SAR imaging method with non-uniform sparse linear array based on matrix completion[C]. 2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 2022: 1664–1667. doi: 10.1109/IGARSS46834.2022.9883674.[18] CAI Jianfeng, CANDÈS E J, and SHEN Zuowei. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956–1982. doi: 10.1137/080738970.[19] 马宇欣, 海宇, 李中余, 等. 稀疏轨迹毫米波雷达三维高分辨成像算法[J]. 雷达学报, 2023, 12(5): 1000–1013. doi: 10.12000/JR23001.MA Yuxin, HAI Yu, LI Zhongyu, et al. 3D high-resolution imaging algorithm with sparse trajectory for millimeter-wave radar[J]. Journal of Radars, 2023, 12(5): 1000–1013. doi: 10.12000/JR23001.[20] CHEN Yuxin and CHI Yuejie. Robust spectral compressed sensing via structured matrix completion[J]. IEEE Transactions on Information Theory, 2014, 60(10): 6576–6601. doi: 10.1109/TIT.2014.2343623.[21] 胡循勇, 杨晓梅, 李昊怡, 等. 融合低秩和稀疏先验的结构性缺失图像修复[J]. 北京航空航天大学学报, 2022, 48(5): 855–862. doi: 10.13700/j.bh.1001-5965.2020.0663.HU Xunyong, YANG Xiaomei, LI Haoyi, et al. Structural missing image inpainting based on low rank and sparse prior[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(5): 855–862. doi: 10.13700/j.bh.1001-5965.2020.0663.[22] ZHENG Hang, SHI Zhiguo, ZHOU Chengwei, et al. Coarray tensor completion for DOA estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(5): 5472–5486. doi: 10.1109/TAES.2023.3263153.[23] BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends® in Machine Learning, 2011, 3(1): 1–122. doi: 10.1561/2200000016.[24] SHENG Haonan, WANG Zhiyong, SO H C, et al. Multi-matrix completion: A novel framework for structurally missing elements[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2026, 48(2): 1626–1640. doi: 10.1109/TPAMI.2025.3616607.[25] PAPAFITSOROS K, SCHÖNLIEB C B, and SENGUL B. Combined first and second order total variation inpainting using split Bregman[J]. Image Processing on Line, 2013, 3: 112–136. doi: 10.5201/ipol.2013.40.[26] BARTELS R H and STEWART G W. Algorithm 432[C2]: Solution of the matrix equation AX+XB=C [F4][J]. Communications of the ACM, 1972, 15(9): 820–826. doi: 10.1145/361573.361582. -
Proportional views

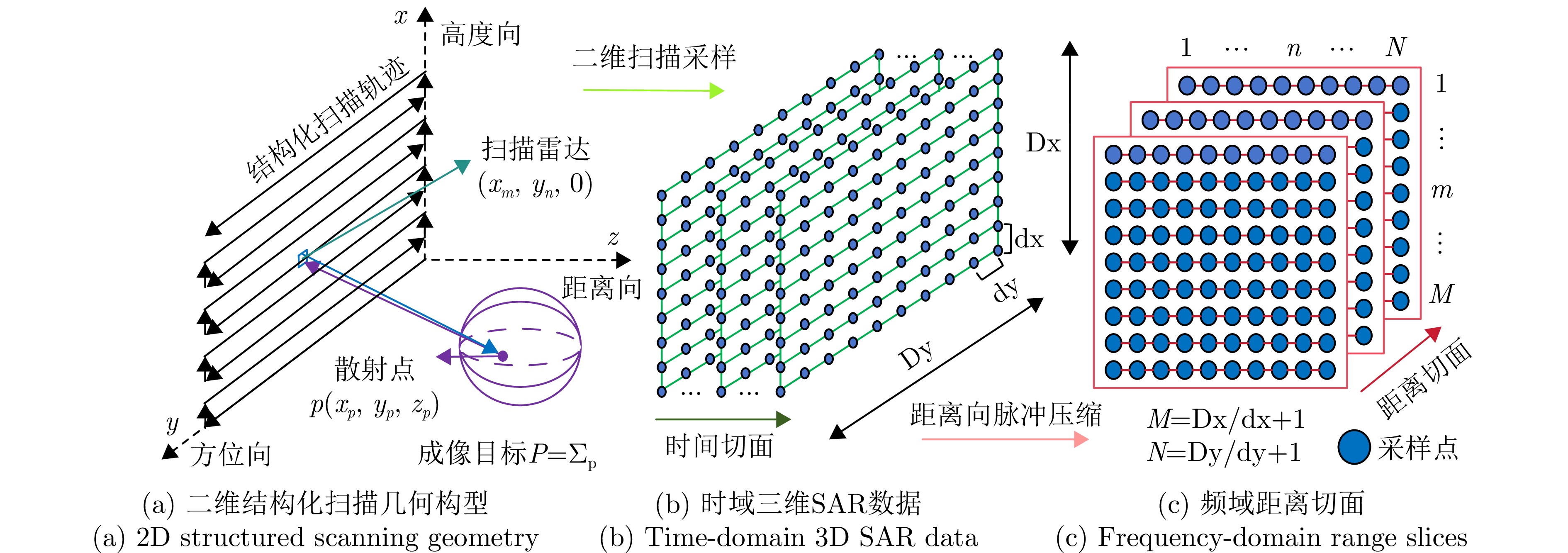
- Figure 1. Schematic diagram of mmWave SAR imaging geometry and signal slices
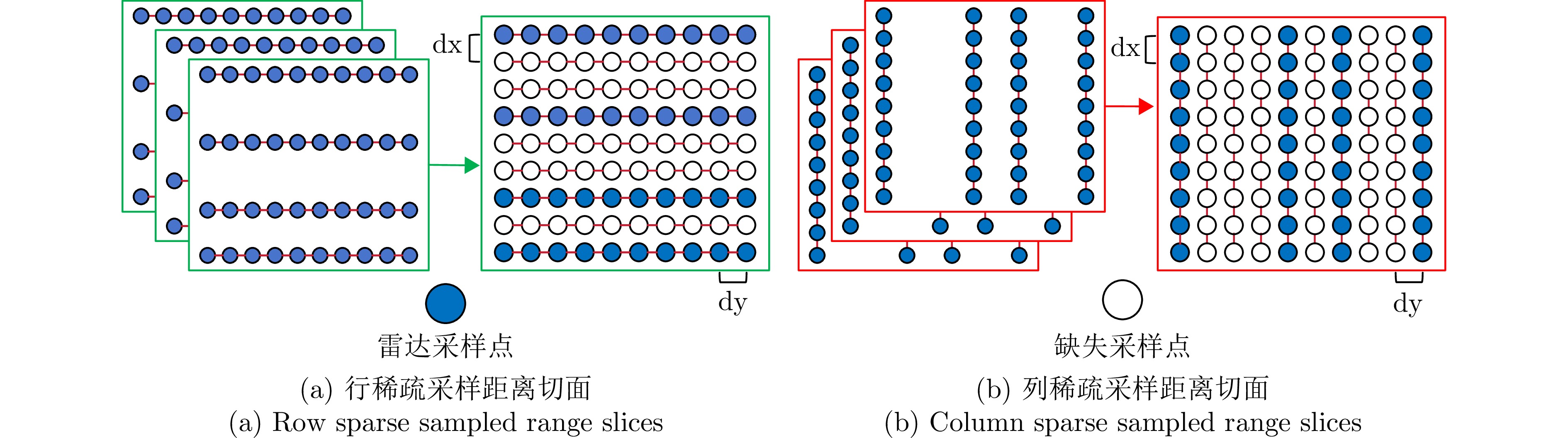
- Figure 2. Row or column sparse sampled range slices
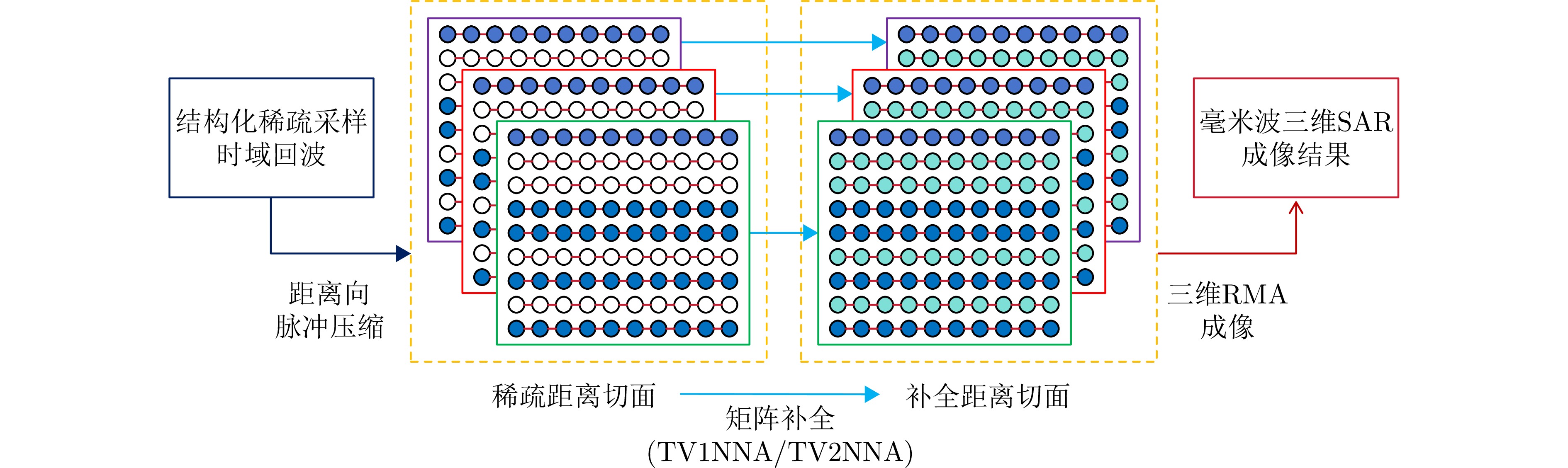
- Figure 3. Flowchart of fast structured sparse 3D SAR imaging
- Figure 4. 3D SAR imaging system physical prototype
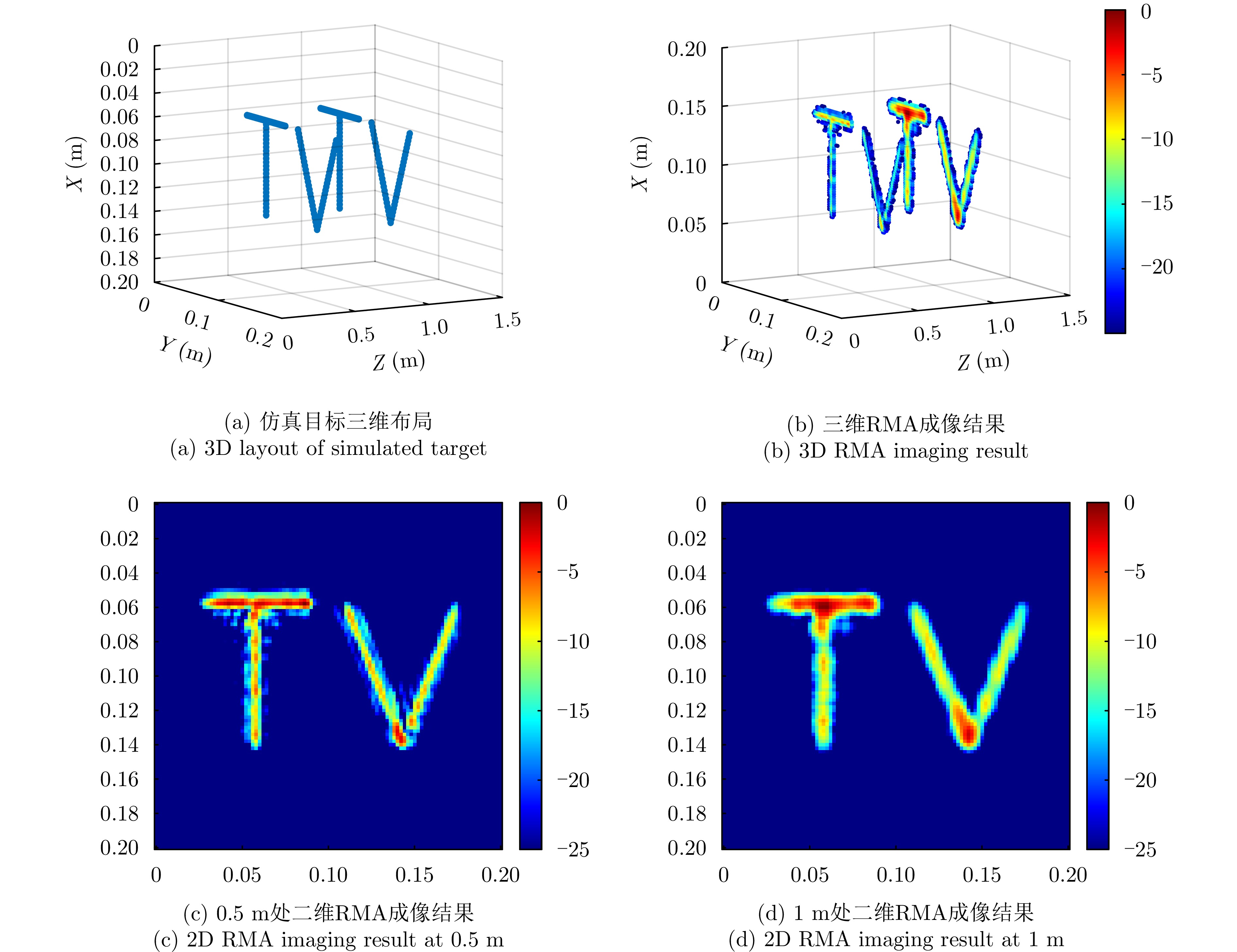
- Figure 5. 3D layout and RMA imaging results of simulated target
- Figure 6. Comparison of echo completion and imaging results by different algorithms under 20% row sparse sampling
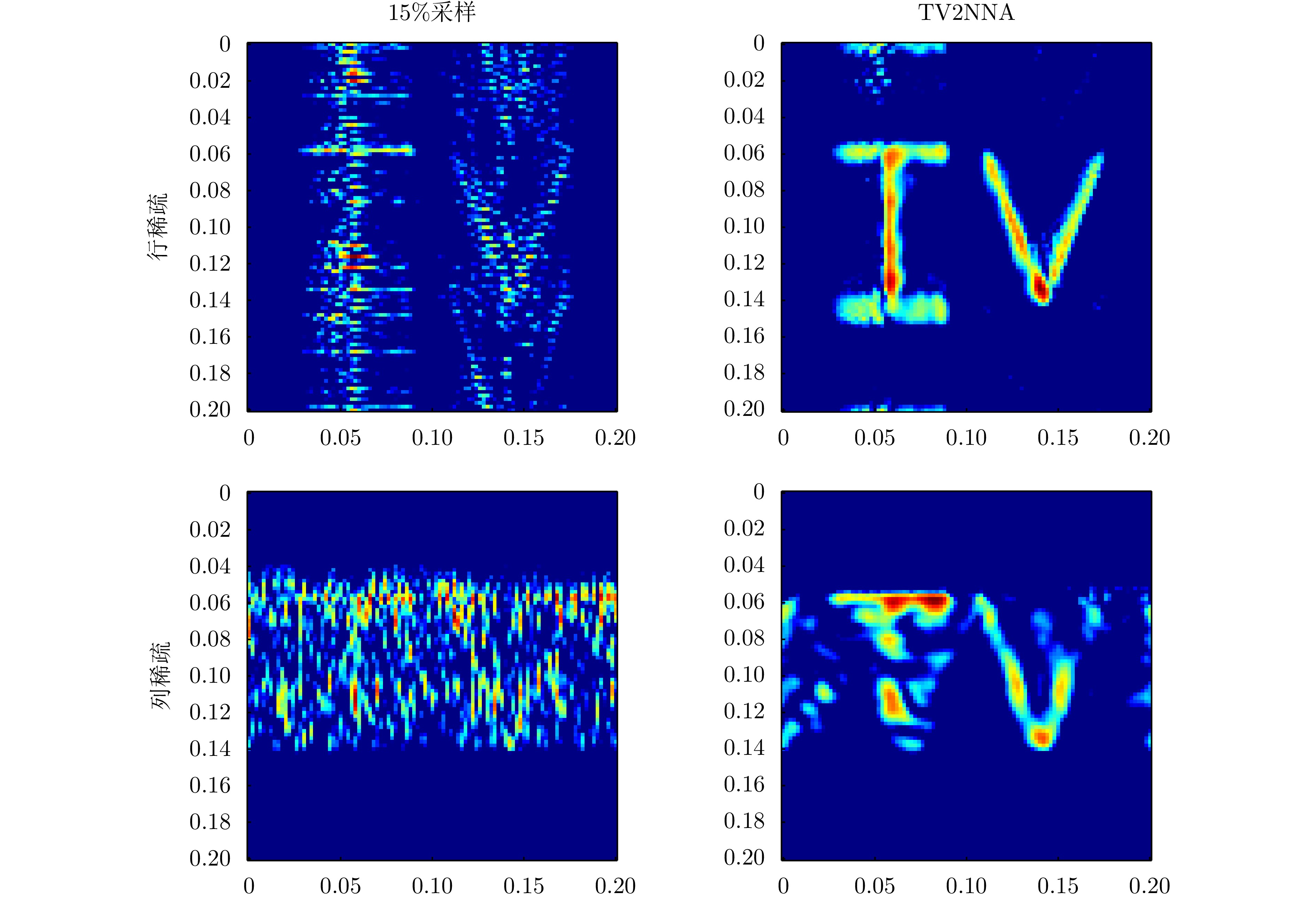
- Figure 7. Imaging results by TV2NNA under 15% row and column sparse sampling
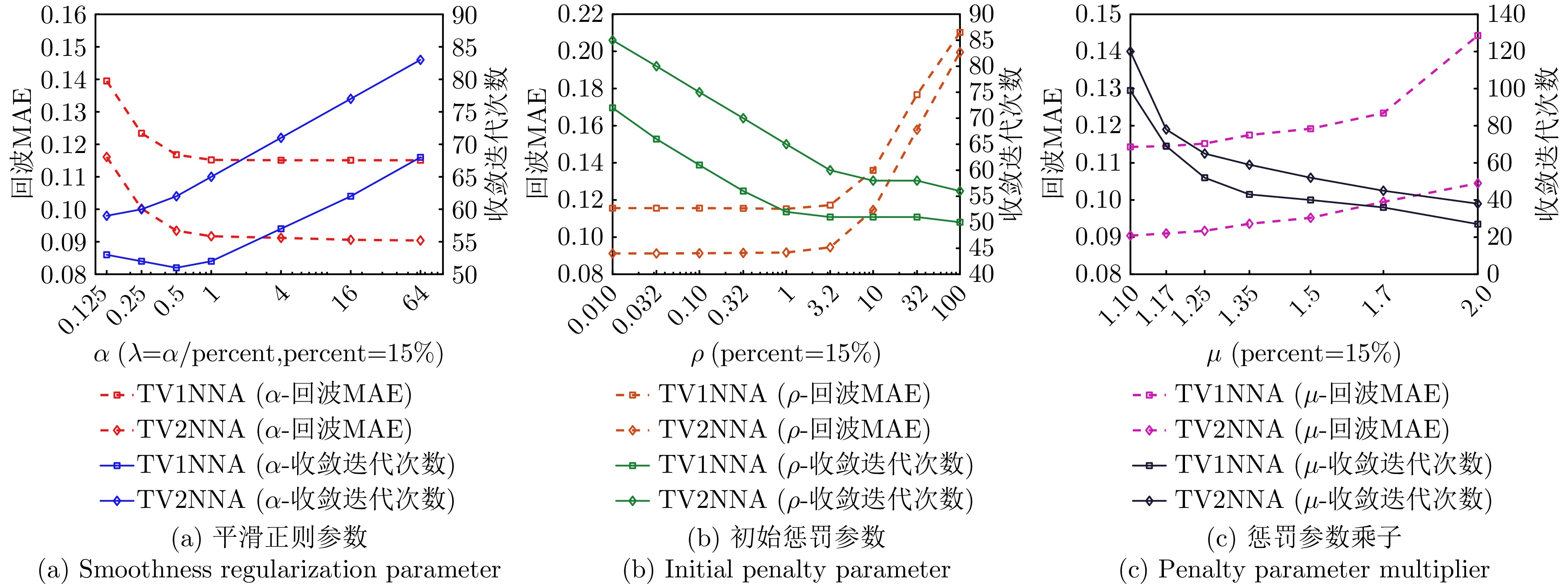
- Figure 8. Effect of parameter variations on algorithm performance and convergence speed
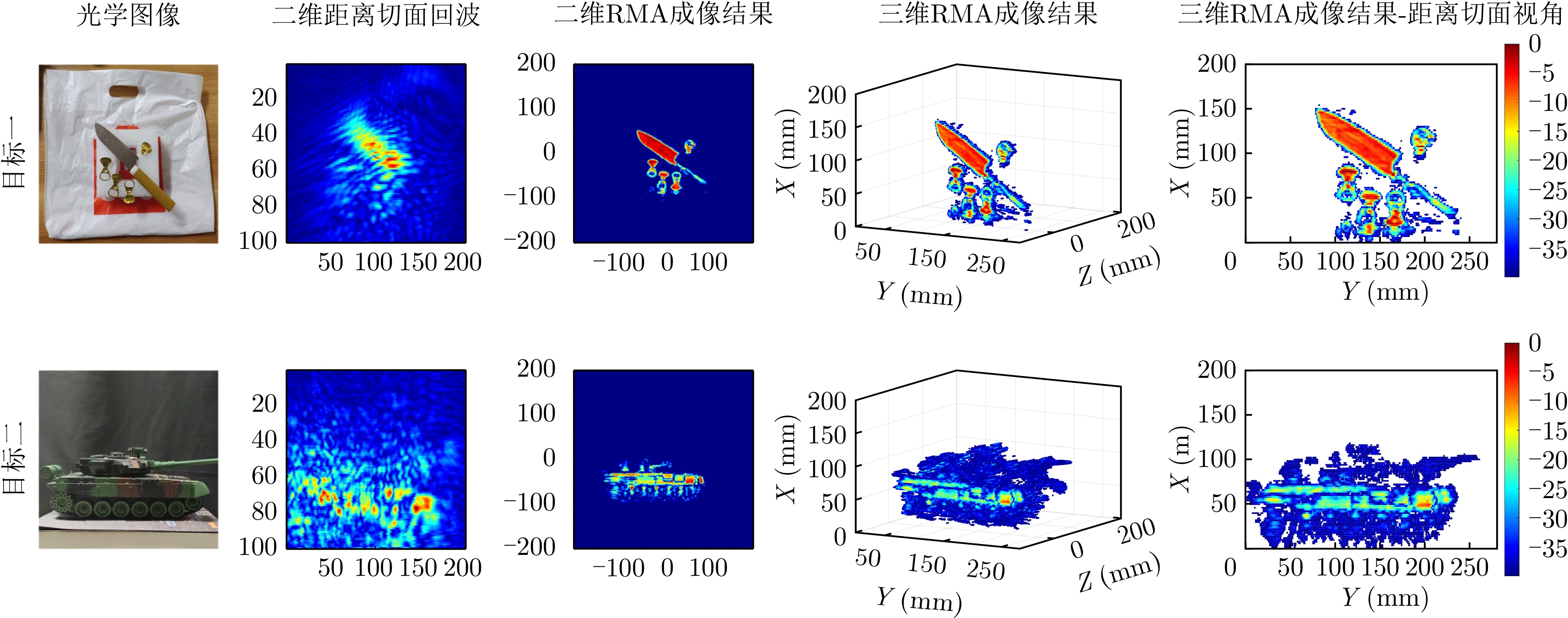
- Figure 9. Echoes and RMA imaging results of Target 1 and Target 2
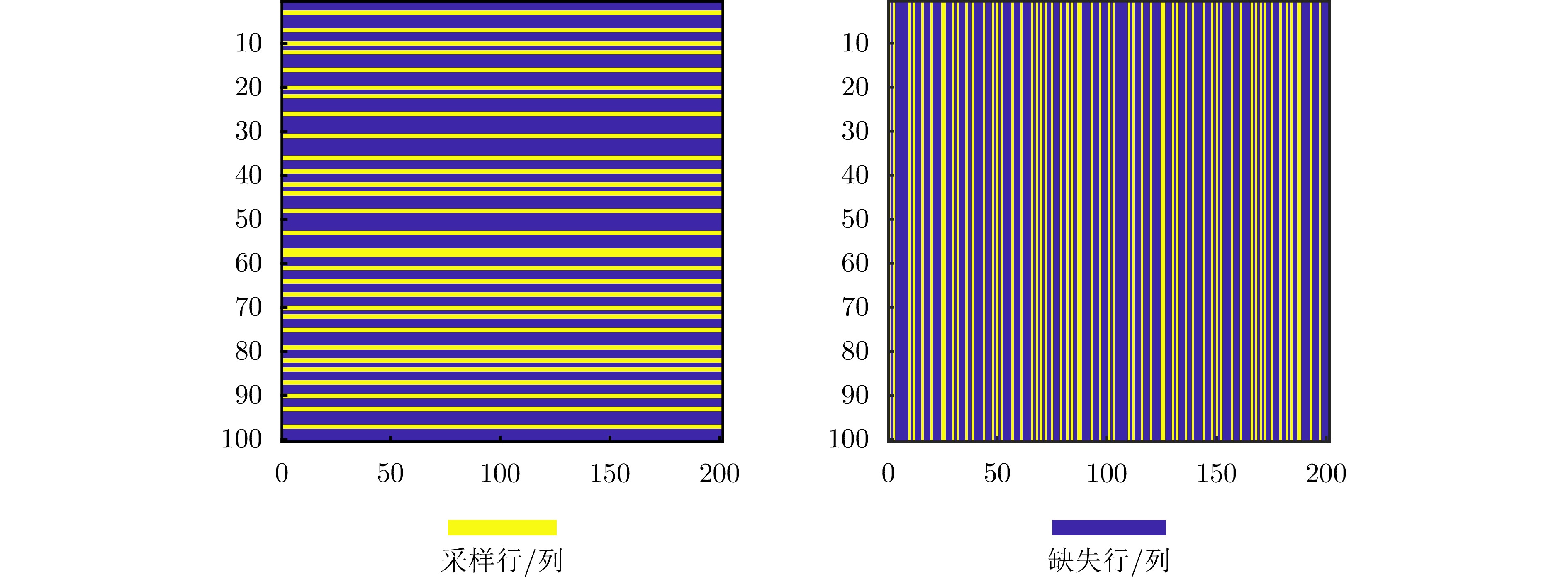
- Figure 10. 30% row and column sparse sampling pattern for Target 1 and Target 2
- Figure 11. Comparison of 3D SAR imaging results by different algorithms under 30% row and column sparse sampling
- Figure 12. Comparison of echo completion and imaging results by different algorithms under 20% row sparse sampling
- Figure 13. Comparison of echo completion and imaging results by different algorithms under 20% column sparse sampling
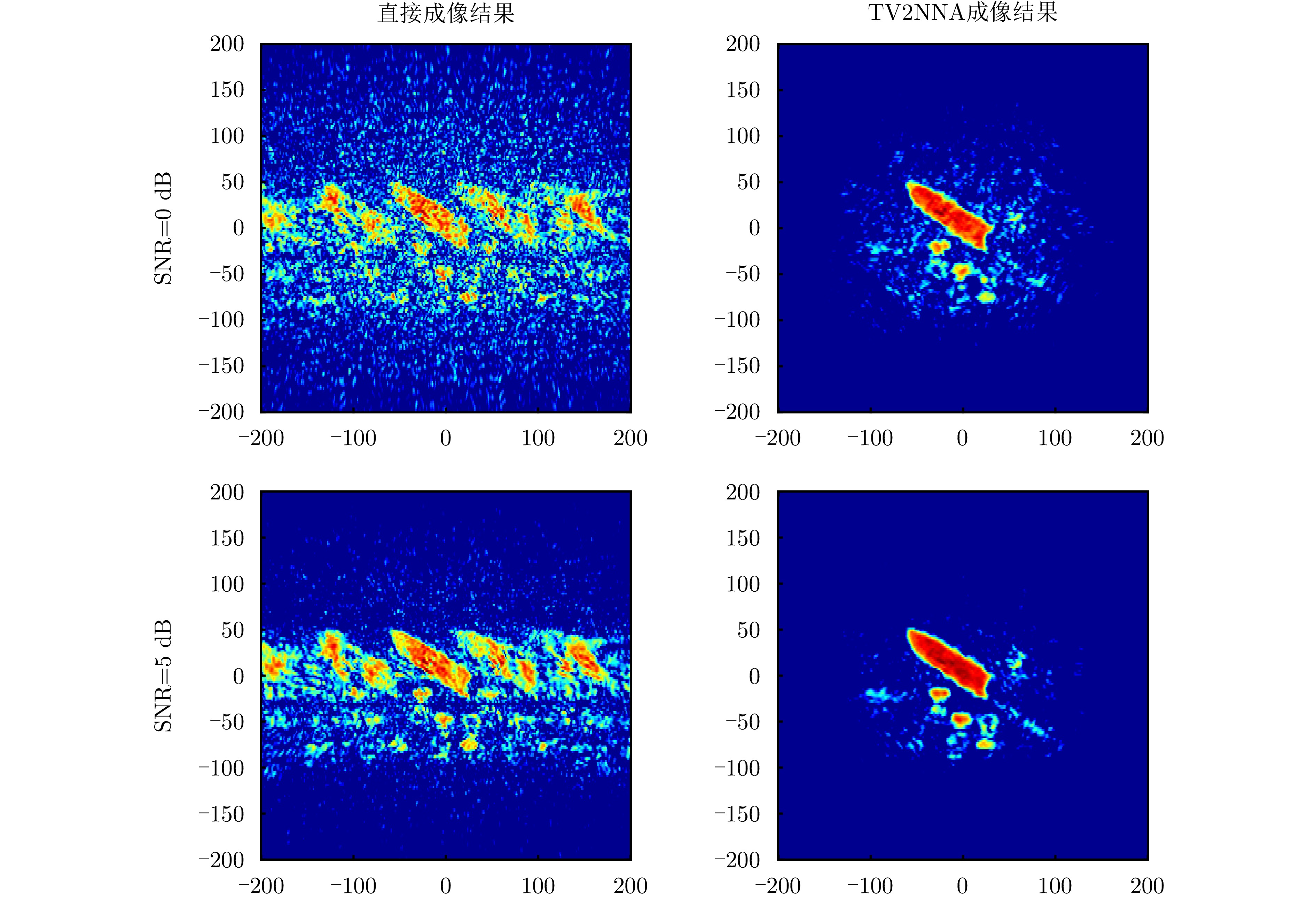
- Figure 14. Imaging results under different SNR
- Figure 15. Imaging results under uniform random sparse sampling
- Figure 16. Echo completion under extremely uniform column sparse sampling


 Submit Manuscript
Submit Manuscript Peer Review
Peer Review Editor Work
Editor Work




 DownLoad:
DownLoad: