Turn off MathJax
Article Contents
Article Navigation >  Journal of Radars  > 2025  > Online First
CUI Linfeng, WU Min, HAO Chengpeng, et al. Fast and gridless sparse recovery STAP method based on nonconvex relaxation of atomic norm[J]. Journal of Radars, 2025, 14(6): 1376–1392. doi: 10.12000/JR25125
Citation: CUI Linfeng, WU Min, HAO Chengpeng, et al. Fast and gridless sparse recovery STAP method based on nonconvex relaxation of atomic norm[J]. Journal of Radars, 2025, 14(6): 1376–1392. doi: 10.12000/JR25125
shu

Fast and Gridless Sparse Recovery STAP Method Based on Nonconvex Relaxation of Atomic Norm

DOI: 10.12000/JR25125 CSTR: 32380.14.JR25125
  • 1.

    Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China

  • 2.

    University of Chinese Academy of Sciences, Beijing 100049, China

  • 3.

    State Key Laboratory of Acoustics and Marine Information, Beijing 100049, China

Funds:  The National Natural Science Foundation of China (62371446, 62471463, 62001468), Youth Innovation Promotion Association, CAS (2023030)
More Information
  • Corresponding author: HAO Chengpeng, haochengp@mail.ioa.ac.cn
  • Received Date: 2025-07-18
  • Rev Recd Date: 2025-11-14
    • Available Online: 2025-11-16
    Abstract
  • Sparse Recovery-based Space-Time Adaptive Processing (SR-STAP) methods offer significant advantages in nonhomogeneous clutter environments owing to their minimal requirement for training samples. However, the performance of most existing SR-STAP methods is limited by the grid mismatch effect, which arises from the discretization of the space-time plane. To address this problem and enhance clutter suppression, this paper proposes a gridless SR-STAP method based on a nonconvex relaxation of atomic norm. The proposed method formulates a gridless sparse recovery model using atoms in the continuous domain, overcoming the grid mismatch effect inherent in traditional discrete dictionary-based methods. Furthermore, a nonconvex relaxation of atomic norm is employed, with optimization progress iteratively executed using a reweighting strategy, which effectively surpasses the resolution limit. In addition, to address the high computational complexity associated with solving semidefinite programming, a fast solution scheme based on an improved Alternating Direction Method of Multipliers (ADMM) is proposed. This scheme exploits the low-rank and block-Toeplitz properties of the clutter covariance matrix, reduces the algorithm’s complexity using an approximate positive semidefinite projection technique, and accelerates convergence with an adaptive penalty parameter based on hypergradient descent. Simulation results and real-measured data demonstrate that the proposed method achieves superior clutter suppression, robust target detection performance, and higher computational efficiency compared to existing SR-STAP methods.

     

    • FullText(HTML)
  • loading
    • References(39)
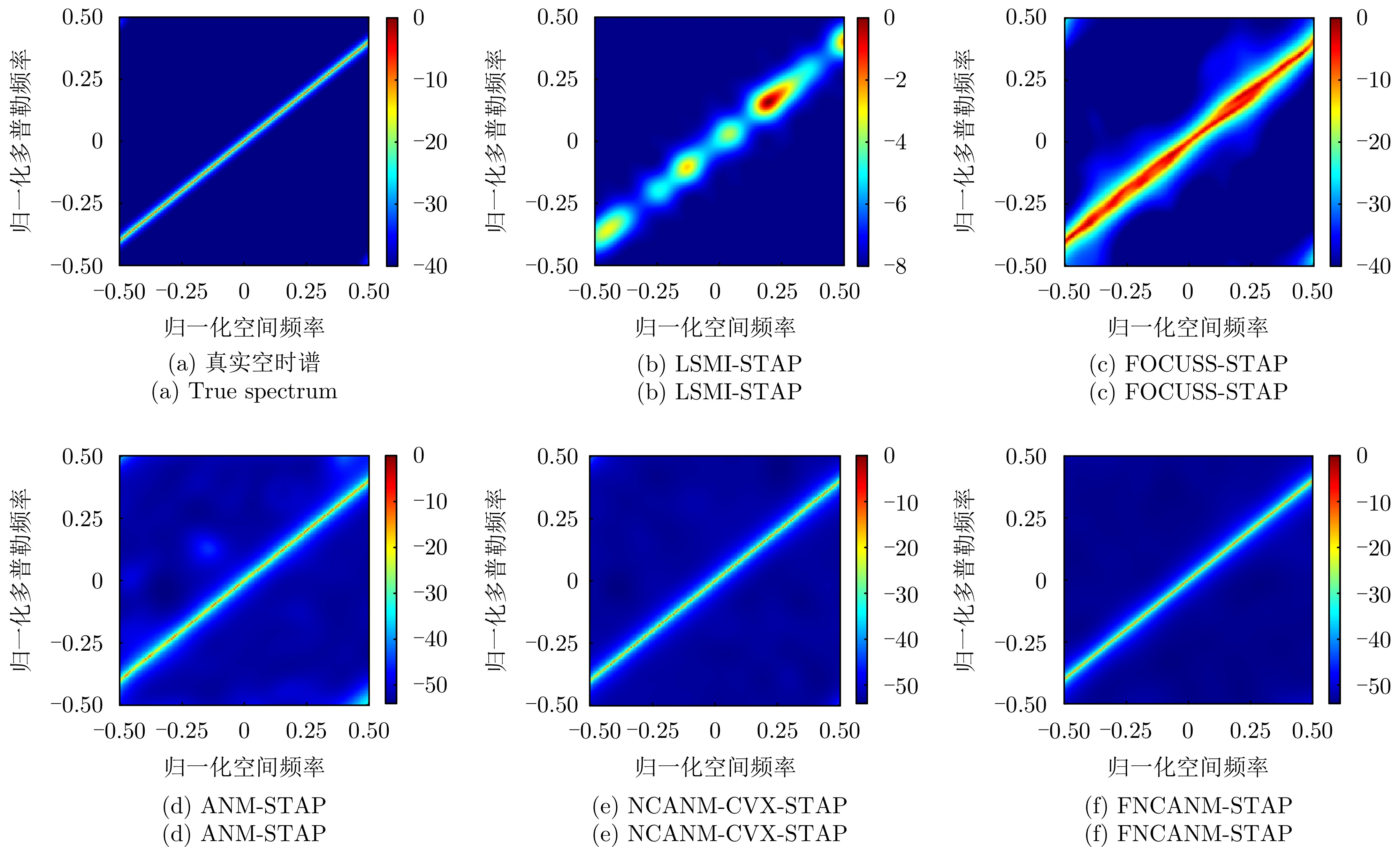
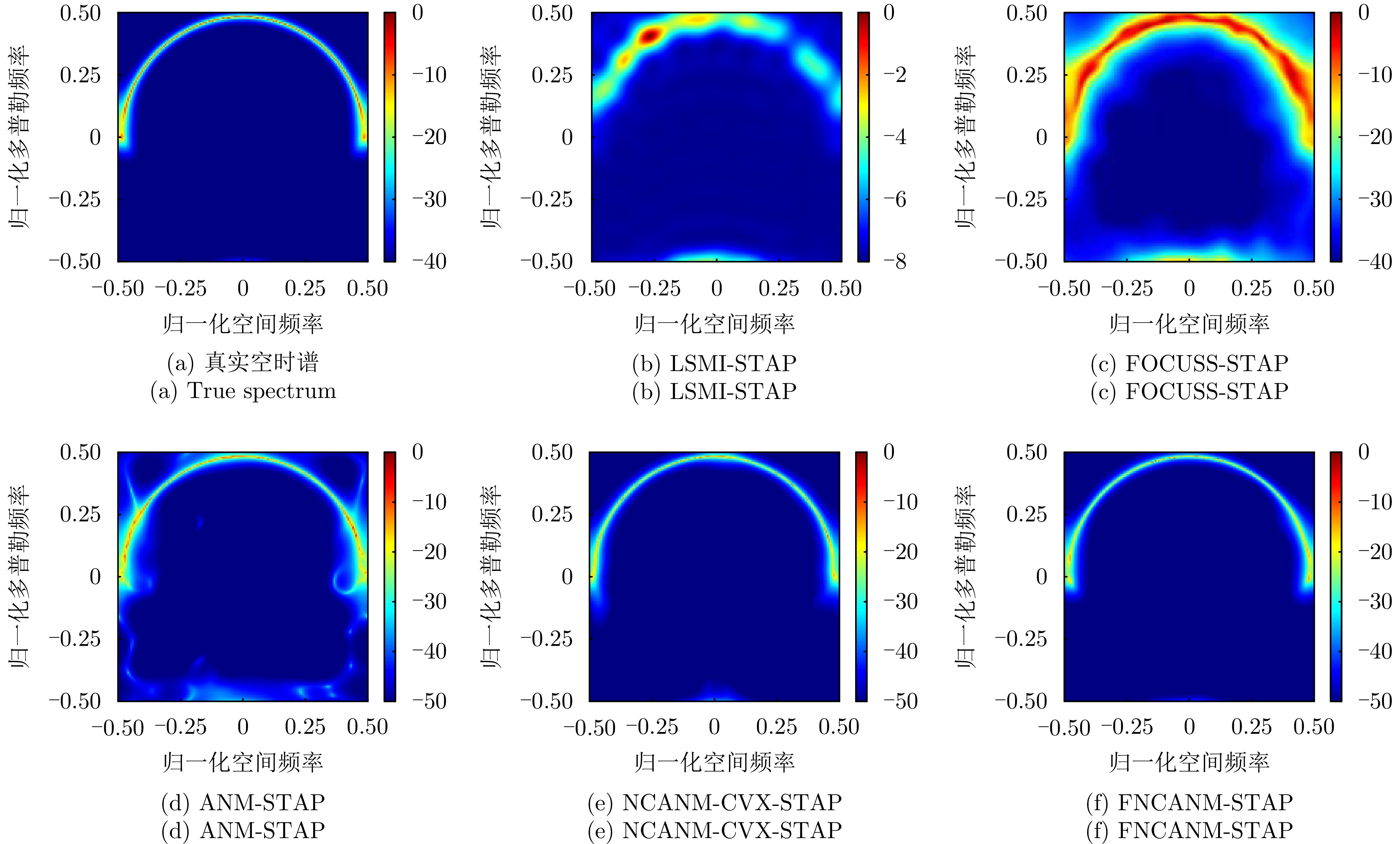
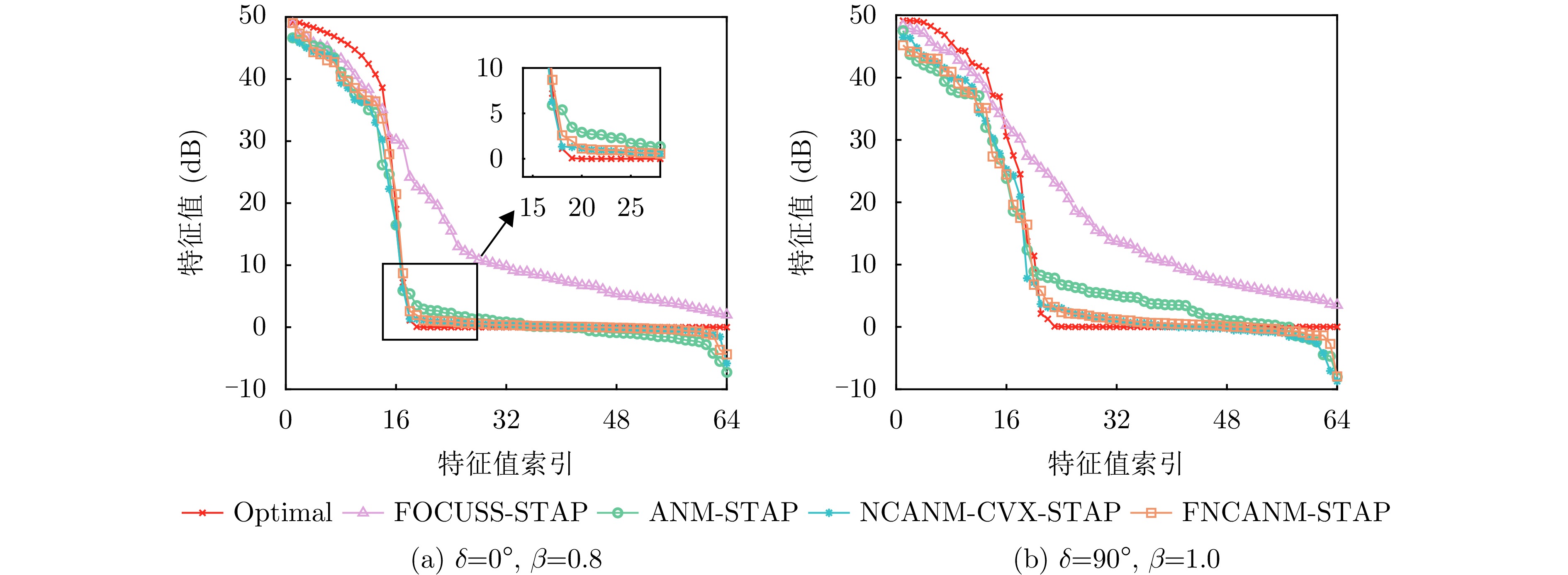
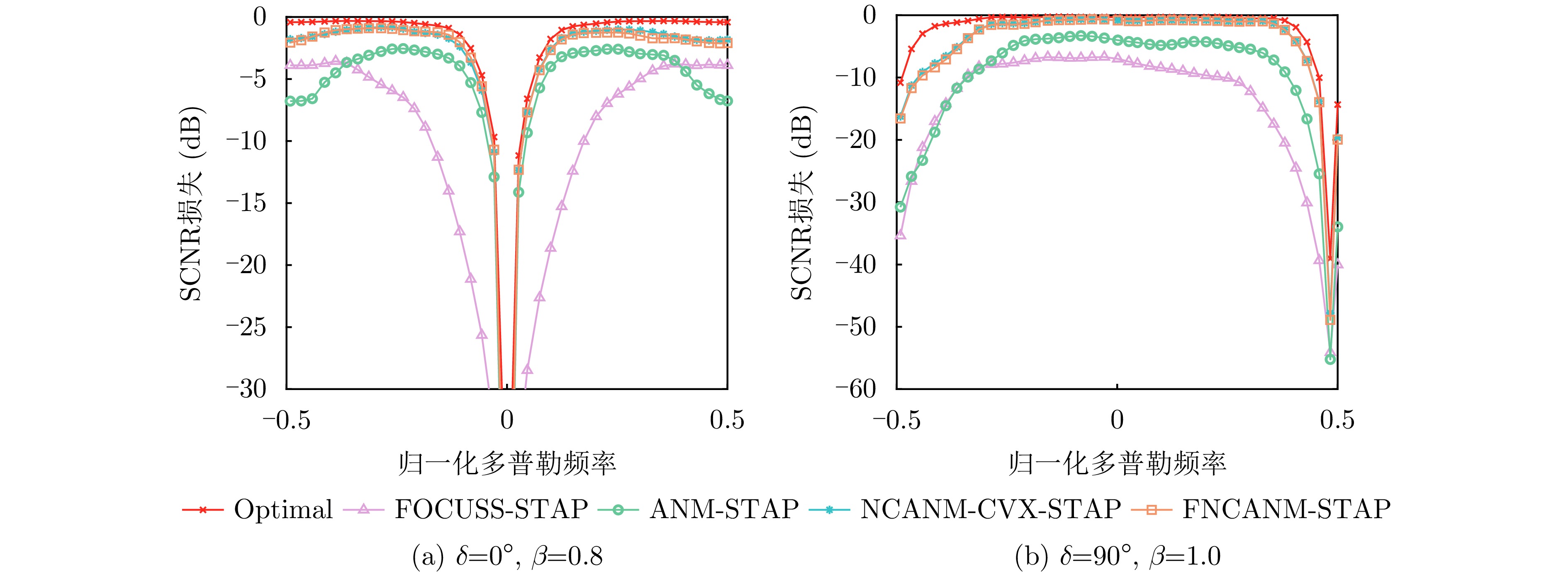
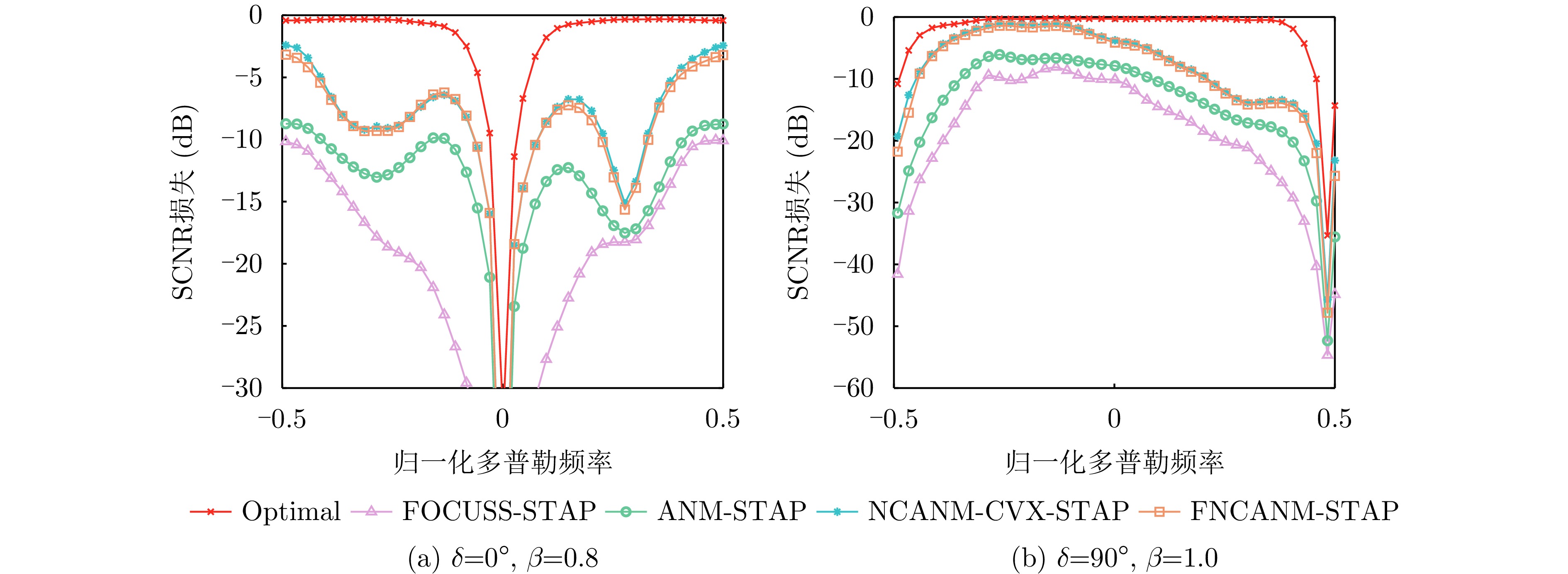
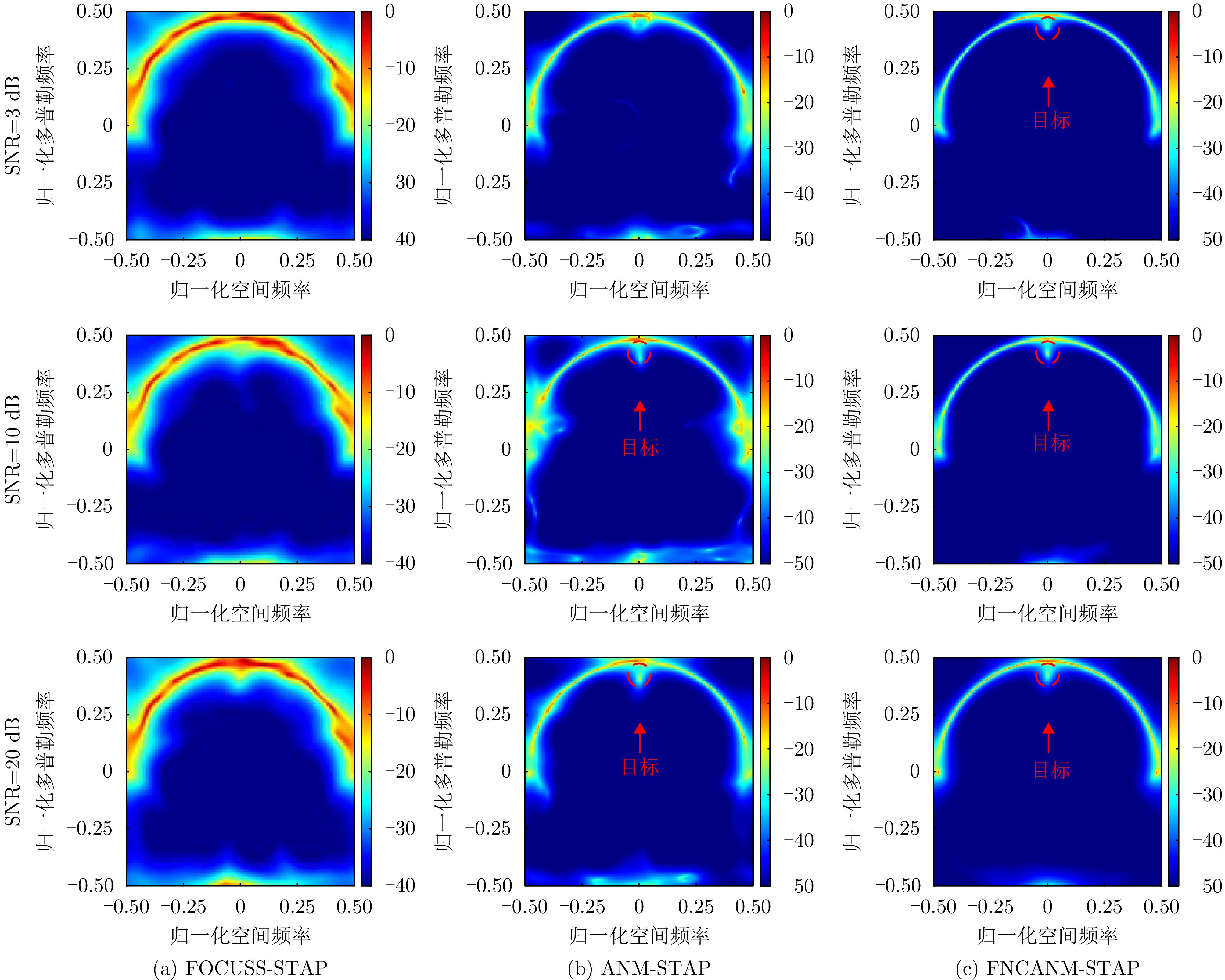
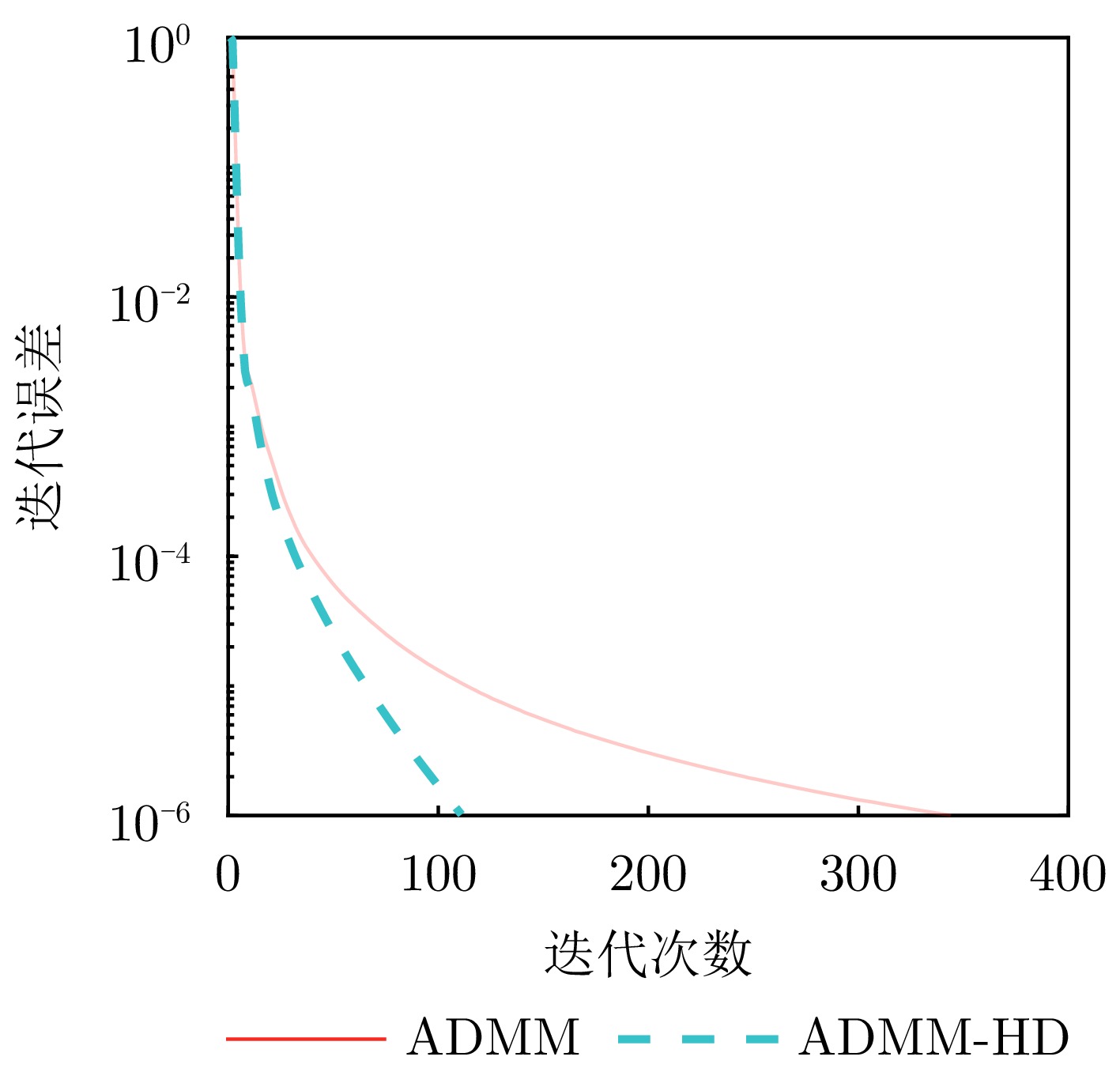
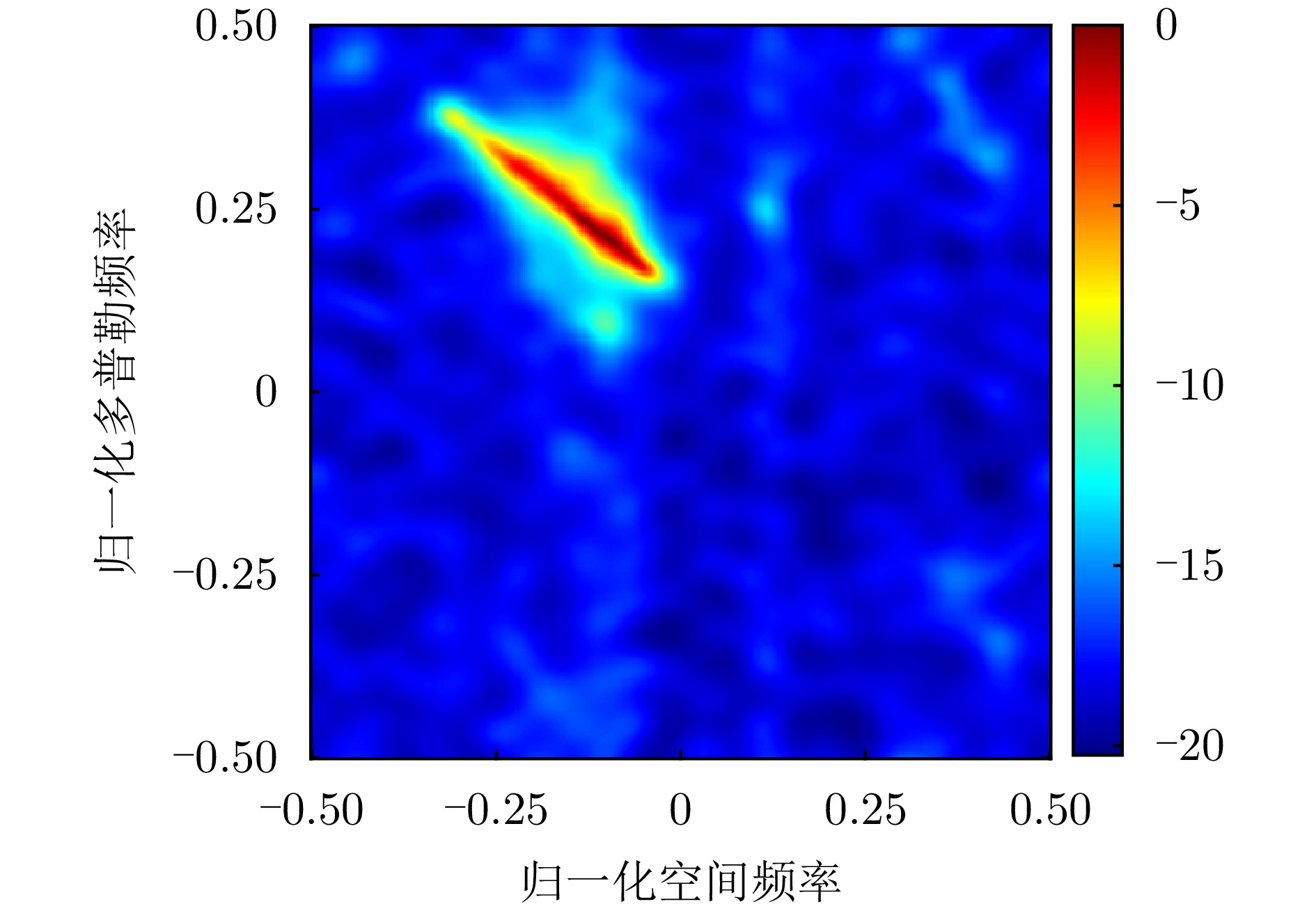
  • [1]
    谢文冲, 段克清, 王永良. 机载雷达空时自适应处理技术研究综述[J]. 雷达学报, 2017, 6(6): 575–586. doi: 10.12000/JR17073.

    XIE Wenchong, DUAN Keqing, and WANG Yongliang. Space time adaptive processing technique for airborne radar: An overview of its development and prospects[J]. Journal of Radars, 2017, 6(6): 575–586. doi: 10.12000/JR17073.
    [2]
    REED I S, MALLETT J D, and BRENNAN L E. Rapid convergence rate in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, AES-10(6): 853–863. doi: 10.1109/TAES.1974.307893.
    [3]
    KLEMM R. Comparison between monostatic and bistatic antenna configurations for STAP[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 596–608. doi: 10.1109/7.845248.
    [4]
    MELVIN W L. A STAP overview[J]. IEEE Aerospace and Electronic Systems Magazine, 2004, 19(1): 19–35. doi: 10.1109/MAES.2004.1263229.
    [5]
    KLEMM R. Adaptive airborne MTI: An auxiliary channel approach[J]. IEE Proceedings F (Communications, Radar and Signal Processing), 1987, 134(3): 269–276. doi: 10.1049/ip-f-1.1987.0054.
    [6]
    HAIMOVICH A M and BAR-NESS Y. An eigenanalysis interference canceler[J]. IEEE Transactions on Signal Processing, 1991, 39(1): 76–84. doi: 10.1109/78.80767.
    [7]
    MELVIN W L and SHOWMAN G A. An approach to knowledge-aided covariance estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(3): 1021–1042. doi: 10.1109/TAES.2006.248216.
    [8]
    PILLAI S U, LIM Y L, and GUERCI J R. Generalized forward/backward subaperture smoothing techniques for sample starved STAP[J]. IEEE Transactions on Signal Processing, 2000, 48(12): 3569–3574. doi: 10.1109/78.887049.
    [9]
    DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582.
    [10]
    MALLAT S G and ZHANG Zhifeng. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397–3415. doi: 10.1109/78.258082.
    [11]
    马泽强, 王希勤, 刘一民, 等. 基于稀疏恢复的空时二维自适应处理技术研究现状[J]. 雷达学报, 2014, 3(2): 217–228. doi: 10.3724/SP.J.1300.2014.14002.

    MA Zeqiang, WANG Xiqin, LIU Yimin, et al. An overview on sparse recovery-based STAP[J]. Journal of Radars, 2014, 3(2): 217–228. doi: 10.3724/SP.J.1300.2014.14002.
    [12]
    SUN Ke, MENG Huadong, WANG Yongliang, et al. Direct data domain STAP using sparse representation of clutter spectrum[J]. Signal Processing, 2011, 91(9): 2222–2236. doi: 10.1016/j.sigpro.2011.04.006.
    [13]
    DUAN Keqing, WANG Zetao, XIE Wenchong, et al. Sparsity-based STAP algorithm with multiple measurement vectors via sparse Bayesian learning strategy for airborne radar[J]. IET Signal Processing, 2017, 11(5): 544–553. doi: 10.1049/iet-spr.2016.0183.
    [14]
    BAI Gatai, TAO Ran, ZHAO Juan, et al. Parameter-searched OMP method for eliminating basis mismatch in space-time spectrum estimation[J]. Signal Processing, 2017, 138: 11–15. doi: 10.1016/j.sigpro.2017.03.003.
    [15]
    TANG Gongguo, BHASKAR B N, SHAH P, et al. Compressed sensing off the grid[J]. IEEE Transactions on Information Theory, 2013, 59(11): 7465–7490. doi: 10.1109/TIT.2013.2277451.
    [16]
    YANG Zai and XIE Lihua. On gridless sparse methods for line spectral estimation from complete and incomplete data[J]. IEEE Transactions on Signal Processing, 2015, 63(12): 3139–3153. doi: 10.1109/TSP.2015.2420541.
    [17]
    CANDÈS E J and FERNANDEZ-GRANDA C. Towards a mathematical theory of super-resolution[J]. Communications on Pure and Applied Mathematics, 2014, 67(6): 906–956. doi: 10.1002/cpa.21455.
    [18]
    LI Yuanxin and CHI Yuejie. Off-the-grid line spectrum denoising and estimation with multiple measurement vectors[J]. IEEE Transactions on Signal Processing, 2016, 64(5): 1257–1269. doi: 10.1109/TSP.2015.2496294.
    [19]
    FENG Weike, GUO Yiduo, ZHANG Yongshun, et al. Airborne radar space time adaptive processing based on atomic norm minimization[J]. Signal Processing, 2018, 148: 31–40. doi: 10.1016/j.sigpro.2018.02.008.
    [20]
    YANG Zai and XIE Lihua. Enhancing sparsity and resolution via reweighted atomic norm minimization[J]. IEEE Transactions on Signal Processing, 2016, 64(4): 995–1006. doi: 10.1109/TSP.2015.2493987.
    [21]
    WU Xiaohuan, ZHU Weiping, and YAN Jun. A high-resolution DOA estimation method with a family of nonconvex penalties[J]. IEEE Transactions on Vehicular Technology, 2018, 67(6): 4925–4938. doi: 10.1109/TVT.2018.2817638.
    [22]
    高一丁, 吴敏, 郝程鹏, 等. 无需信源数先验的快速稀疏增强DOA估计方法[J]. 海军航空大学学报, 2024, 39(5): 515–522. doi: 10.7682/j.issn.2097-1427.2024.05.001.

    GAO Yiding, WU Min, HAO Chengpeng, et al. Fast sparse enhanced DOA estimation method without source number priors[J]. Journal of Naval Aviation University, 2024, 39(5): 515–522. doi: 10.7682/j.issn.2097-1427.2024.05.001.
    [23]
    黎子皓, 吴敏, 郝程鹏, 等. 使用重加权原子范数最小化的稀疏可重构直线阵列设计[J]. 声学学报, 2023, 48(6): 1174–1188. doi: 10.12395/0371-0025.2022071.

    LI Zihao, WU Min, HAO Chengpeng, et al. Design of sparse reconfigurable array using reweighted atomic norm minimization[J]. Acta Acustica, 2023, 48(6): 1174–1188. doi: 10.12395/0371-0025.2022071.
    [24]
    LI Zhongyue and WANG Tong. ADMM-based low-complexity off-grid space-time adaptive processing methods[J]. IEEE Access, 2020, 8: 206646–206658. doi: 10.1109/ACCESS.2020.3037652.
    [25]
    HALKO N, MARTINSSON P G, and TROPP J A. Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions[J]. SIAM Review, 2011, 53(2): 217–288. doi: 10.1137/090771806.
    [26]
    CHANDRA K, XIE A, RAGAN-KELLEY J, et al. Gradient descent: The ultimate optimizer[C]. 36th International Conference on Neural Information Processing Systems, New Orleans, USA, 2022: 597.
    [27]
    CARLSON B D. Covariance matrix estimation errors and diagonal loading in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1988, 24(4): 397–401. doi: 10.1109/7.7181.
    [28]
    ZHOU Zhiyong and YU Jun. A new nonconvex sparse recovery method for compressive sensing[J]. Frontiers in Applied Mathematics and Statistics, 2019, 5: 14. doi: 10.3389/fams.2019.00014.
    [29]
    CHI Yuejie and FERREIRA DA COSTA M. Harnessing sparsity over the continuum: Atomic norm minimization for superresolution[J]. IEEE Signal Processing Magazine, 2020, 37(2): 39–57. doi: 10.1109/MSP.2019.2962209.
    [30]
    ECKSTEIN J and YAO Wang. Relative-error approximate versions of Douglas-Rachford splitting and special cases of the ADMM[J]. Mathematical Programming, 2018, 170(2): 417–444. doi: 10.1007/s10107-017-1160-5.
    [31]
    RONTSIS N, GOULART P, and NAKATSUKASA Y. Efficient semidefinite programming with approximate ADMM[J]. Journal of Optimization Theory and Applications, 2022, 192(1): 292–320. doi: 10.1007/s10957-021-01971-3.
    [32]
    YANG Zai, XIE Lihua, and STOICA P. Vandermonde decomposition of multilevel toeplitz matrices with application to multidimensional super-resolution[J]. IEEE Transactions on Information Theory, 2016, 62(6): 3685–3701. doi: 10.1109/TIT.2016.2553041.
    [33]
    BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends® in Machine Learning, 2010, 3(1): 1–122. doi: 10.1561/2200000016.
    [34]
    CHEN Tiancheng, MENG Yang, ZHOU Guoru, et al. An improved imaging method for highly-squinted SAR based on hyper-optimized admm[C]. 2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, USA, 2023: 4548–4551. doi: 10.1109/IGARSS52108.2023.10281842.
    [35]
    LIU Weijian, XIE Wenchong, LI Rongfeng, et al. Adaptive detectors in the Krylov subspace[J]. Science China Information Sciences, 2014, 57(10): 1–11. doi: 10.1007/s11432-014-5080-1.
    [36]
    BRENNAN L E and REED L S. Theory of adaptive radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 1973, AES-9(2): 237–252. doi: 10.1109/TAES.1973.309792.
    [37]
    ROBEY F C, FUHRMANN D R, KELLY E J, et al. A CFAR adaptive matched filter detector[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(1): 208–216. doi: 10.1109/7.135446.
    [38]
    TITI G W and MARSHALL D F. The ARPA/NAVY mountaintop program: Adaptive signal processing for airborne early warning radar[C]. 1996 IEEE International Conference on Acoustics, Speech, and Signal Processing Conference Proceedings, Atlanta, USA, 1996: 1165–1168. doi: 10.1109/ICASSP.1996.543572.
    [39]
    AUBRY A, DE MAIO A, PALLOTTA L, et al. Covariance matrix estimation via geometric barycenters and its application to radar training data selection[J]. IET Radar, Sonar & Navigation, 2013, 7(6): 600–614. doi: 10.1049/iet-rsn.2012.0190.
    • Relative Articles
    • Supplements(0)
    • Cited By
  • 加载中

Catalog

    通讯作者: 陈斌, bchen63@163.com
    • 1. 

      沈阳化工大学材料科学与工程学院 沈阳 110142

    1. 本站搜索
    2. 百度学术搜索
    3. 万方数据库搜索
    4. CNKI搜索
    Get Citation
    PDF
    XML
    Article views(74) PDF downloads(15) Cited by()
    Proportional views
    Related

    京ICP备20021838号-14   Supported by: Beijing Renhe Information Technology Co. Ltd     百度统计

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return