- Home
- Articles & Issues
-
Data
- Dataset of Radar Detecting Sea
- SAR Dataset
- SARGroundObjectsTypes
- SARMV3D
- AIRSAT Constellation SAR Land Cover Classification Dataset
- 3DRIED
- UWB-HA4D
- LLS-LFMCWR
- FAIR-CSAR
- MSAR
- SDD-SAR
- FUSAR
- SpaceborneSAR3Dimaging
- Sea-land Segmentation
- SAR Multi-domain Ship Detection Dataset
- SAR-Airport
- Hilly and mountainous farmland time-series SAR and ground quadrat dataset
- SAR images for interference detection and suppression
- HP-SAR Evaluation & Analytical Dataset
- GDHuiYan-ATRNet
- Multi-System Maritime Low Observable Target Dataset
- DatasetinthePaper
- DatasetintheCompetition
- Report
- Course
- About
- Publish
- Editorial Board
- Chinese
| Citation: | FU Jixiang, ZHANG Chao, XING Wenjie, et al. Fast space-variant phase error compensation and geometric correction for bistatic ISAR imaging using a modified Newton’s method[J]. Journal of Radars, 2025, 14(5): 1253–1275. doi: 10.12000/JR25052 |
Fast Space-variant Phase Error Compensation and Geometric Correction for Bistatic ISAR Imaging Using a Modified Newton’s Method
DOI: 10.12000/JR25052 CSTR: 32380.14.JR25052
More Information-
Abstract
Bistatic Inverse Synthetic Aperture Radar (Bi-ISAR) has garnered significant attention in the military and civilian domains due to its superior stealth and antijamming capabilities. However, the changing bistatic angle during Bi-ISAR imaging causes space-variant defocusing and geometric distortion in the resulting images, thereby severely compromising the accuracy of subsequent information extraction and target recognition. To address these issues, this study proposes a fast space-variant phase error compensation and geometric correction method for Bi-ISAR imaging based on a modified Newton’s method. This method uses the image entropy of the Bi-ISAR imaging result as the cost function and introduces space-variant coefficients and rotation parameters as optimization variables to formulate an optimization equation. By modifying the traditional Newton’s method to ensure the positive definiteness of the Hessian matrix, the cost function is guaranteed to be optimized along the descent direction in each iteration. Solving this optimization equation to minimize image entropy simultaneously estimates the rotation parameters, which are then used to construct a geometric correction function and calculate the scaling factor, that is, the actual size of each grid in the image, enabling geometric correction and scaling of the final imaging result. The proposed method simultaneously corrects space-variant phase errors and geometric distortion and operates in a data-driven manner, requiring only low initial image quality. Furthermore, due to the quadratic convergence property of Newton’s method, the proposed method offers higher computational efficiency compared with other methods. Finally, the effectiveness of the proposed method is validated through the processing and comparative analysis of the point target simulation, electromagnetic calculation, and ground real target experimental data. -

-
References
[1] 李俊颜, 杨青, 李中余, 等. 基于空变多普勒参数聚类的微波光子ISAR高精度成像方法[J]. 电子学报, 2024, 52(12): 3941–3956. doi: 10.12263/DZXB.20240442.LI Junyan, YANG Qing, LI Zhongyu, et al. High-precision microwave photonic ISAR imaging method based on spatially variant Doppler parameter clustering[J]. Acta Electronica Sinica, 2024, 52(12): 3941–3956. doi: 10.12263/DZXB.20240442.[2] 邢孟道, 谢意远, 高悦欣, 等. 电磁散射特征提取与成像识别算法综述[J]. 雷达学报, 2022, 11(6): 921–942. doi: 10.12000/JR22232.XING Mengdao, XIE Yiyuan, GAO Yuexin, et al. Electromagnetic scattering characteristic extraction and imaging recognition algorithm: A review[J]. Journal of Radars, 2022, 11(6): 921–942. doi: 10.12000/JR22232.[3] 符吉祥, 邢孟道, 徐丹, 等. 一种基于微波光子超高分辨雷达机翼振动参数估计方法[J]. 雷达学报, 2019, 8(2): 232–242. doi: 10.12000/JR19001.FU Jixiang, XING Mengdao, XU Dan, et al. Vibration-parameters estimation method for airplane wings based on microwave-photonics ultrahigh-resolution radar[J]. Journal of Radars, 2019, 8(2): 232–242. doi: 10.12000/JR19001.[4] 田彪, 刘洋, 呼鹏江, 等. 宽带逆合成孔径雷达高分辨成像技术综述[J]. 雷达学报, 2020, 9(5): 765–802. doi: 10.12000/JR20060.TIAN Biao, LIU Yang, HU Pengjiang, et al. Review of high-resolution imaging techniques of wideband inverse synthetic aperture radar[J]. Journal of Radars, 2020, 9(5): 765–802. doi: 10.12000/JR20060.[5] CHEN Hongmeng, LI Jun, ZHOU Rui, et al. Optimal Bi-ISAR imaging arc selection method with bistatic angle derivative constraint[C]. 2024 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Zhuhai, China, 2024: 1–4. doi: 10.1109/ICSIDP62679.2024.10869106.[6] JIANG Yicheng, WEI Jin, and LIU Zitao. Bistatic ISAR imaging and scaling algorithm based on the estimation of bistatic factor and effective rotation velocity[J]. IEEE Transactions on Aerospace and Electronic Systems, 2024, 60(6): 8522–8538. doi: 10.1109/TAES.2024.3432109.[7] CHEN Hongmeng, LI Jun, ZHOU Rui, et al. Focused bistatic ISAR imaging demonstration with nonparametric autofocusing[C]. IET International Radar Conference, Chongqing, China, 2023: 3370–3374. doi: 10.1049/icp.2024.1643.[8] DING Jiabao, LI Yachao, WANG Jiadong, et al. Integration of high-order motion compensation and 2-D scaling for maneuvering target bistatic ISAR imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2025, 63: 5205120. doi: 10.1109/TGRS.2025.3533881.[9] FU Jixiang, YANG Weichao, XUE Min, et al. A novel bistatic ISAR space-variant phase error compensation and geometric correction method based on entropy minimization[C]. IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 2024: 3536–3539. doi: 10.1109/IGARSS53475.2024.10641057.[10] DING Jiabao, WANG Jiadong, LI Yachao, et al. A spatial variant phase compensation algorithm for bistatic ISAR imaging of maneuvering targets based on optimal parameter estimation[C]. 2021 CIE International Conference on Radar, Haikou, China, 2021: 2087–2090. doi: 10.1109/Radar53847.2021.10027972.[11] QIAN Guangzhao and WANG Yong. Satellite-missile bistatic forward-looking SAR imaging of ship target via hybrid SAR-ISAR algorithm[C]. IET International Radar Conference, Chongqing, China, 2023: 2669–2674. doi: 10.1049/icp.2024.1510.[12] QIAN Guangzhao and WANG Yong. Monostatic-equivalent algorithm via Taylor expansion for BiSAR ship target imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5200919. doi: 10.1109/TGRS.2022.3233384.[13] 朱瀚神, 胡文华, 郭宝锋, 等. 双基地ISAR稀疏孔径机动目标MTRC补偿成像算法[J]. 系统工程与电子技术, 2023, 45(7): 2022–2030. doi: 10.12305/j.issn.1001-506X.2023.07.12.ZHU Hanshen, HU Wenhua, GUO Baofeng, et al. Bistatic ISAR sparse aperture maneuvering target MTRC compensation imaging algorithm[J]. Systems Engineering and Electronics, 2023, 45(7): 2022–2030. doi: 10.12305/j.issn.1001-506X.2023.07.12.[14] LI Rui, LUO Ying, ZHANG Qun, et al. Time-varying bistatic radar coincidence imaging for rotating targets[C]. IEEE 2nd International Conference on Electronic Information and Communication Technology, Harbin, China, 2019: 495–498. doi: 10.1109/ICEICT.2019.8846253.[15] 李中余, 桂亮, 海宇, 等. 基于变分模态分解与优选的超高分辨ISAR成像微多普勒抑制方法[J]. 雷达学报(中英文), 2024, 13(4): 852–865. doi: 10.12000/JR24043.LI Zhongyu, GUI Liang, HAI Yu, et al. Ultrahigh-resolution ISAR micro-Doppler suppression methodology based on variational mode decomposition and mode optimization[J]. Journal of Radars, 2024, 13(4): 852–865. doi: 10.12000/JR24043.[16] ZHANG Shuanghui, LIU Yongxiang, LI Xiang, et al. Fast ISAR cross-range scaling using modified newton method[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(3): 1355–1367. doi: 10.1109/TAES.2017.2785560.[17] 柴守刚, 陈卫东, 陈畅. 联合几何畸变校正及定标的B-ISAR稀疏成像算法[J]. 现代雷达, 2015, 37(1): 32–37. doi: 10.3969/j.issn.1004-7859.2015.01.008.CHAI Shougang, CHEN Weidong, and CHEN Chang. B-ISAR sparse imaging algorithm with geometric distortion correction and calibration[J]. Modern Radar, 2015, 37(1): 32–37. doi: 10.3969/j.issn.1004-7859.2015.01.008.[18] 史林, 郭宝锋, 马俊涛, 等. 基于图像旋转相关的空间目标ISAR等效旋转中心估计算法[J]. 电子与信息学报, 2019, 41(6): 1280–1286. doi: 10.11999/JEIT181086.SHI Lin, GUO Baofeng, MA Juntao, et al. Rotation center estimation algorithm for ISAR image of the space target based on image rotation and correlation[J]. Journal of Electronics & Information Technology, 2019, 41(6): 1280–1286. doi: 10.11999/JEIT181086.[19] AI Xiaofeng, HUANG Yan, ZHAO Feng, et al. Imaging of spinning targets via narrow-band T/R-R bistatic radars[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(2): 362–366. doi: 10.1109/LGRS.2012.2205893.[20] JIANG Yicheng, SUN Sibo, YEO T S, et al. Bistatic ISAR distortion and defocusing analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(3): 1168–1182. doi: 10.1109/TAES.2016.140028.[21] 夏靖远, 杨志雄, 周治兴, 等. 一种基于元学习的稀疏孔径ISAR成像算法[J]. 雷达学报, 2023, 12(4): 849–859. doi: 10.12000/JR23121.XIA Jingyuan, YANG Zhixiong, ZHOU Zhixing, et al. A metalearning-based sparse aperture ISAR imaging method[J]. Journal of Radars, 2023, 12(4): 849–859. doi: 10.12000/JR23121.[22] YUAN Zhengkun, WANG Junling, ZHAO Lizhi, et al. An MTRC-AHP compensation algorithm for Bi-ISAR imaging of space targets[J]. IEEE Sensors Journal, 2020, 20(5): 2356–2367. doi: 10.1109/JSEN.2019.2951735.[23] WANG Jiannan, MA Jingtao, HUANG Penghui, et al. Linear-geometry distortion correction for bistatic inverse synthetic aperture radar imaging based on deep learning model[C]. IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 2024: 11414–11417. doi: 10.1109/IGARSS53475.2024.10640941.[24] DING Jiabao, LI Yachao, WANG Jiadong, et al. Joint motion compensation and distortion correction for maneuvering target bistatic ISAR imaging based on parametric minimum entropy optimization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5118919. doi: 10.1109/TGRS.2022.3213579.[25] FU Jixiang, XING Mengdao, and AMIN M G. ISAR imaging motion compensation in low SNR environments using phase gradient and filtering techniques[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(6): 4296–4312. doi: 10.1109/TAES.2021.3098129.[26] KRAGH T J. Monotonic iterative algorithm for minimum-entropy autofocus[C]. Adaptive Sensor Array Processing Workshop, Lexington, USA, 2006: 1147–1159. -
Proportional views

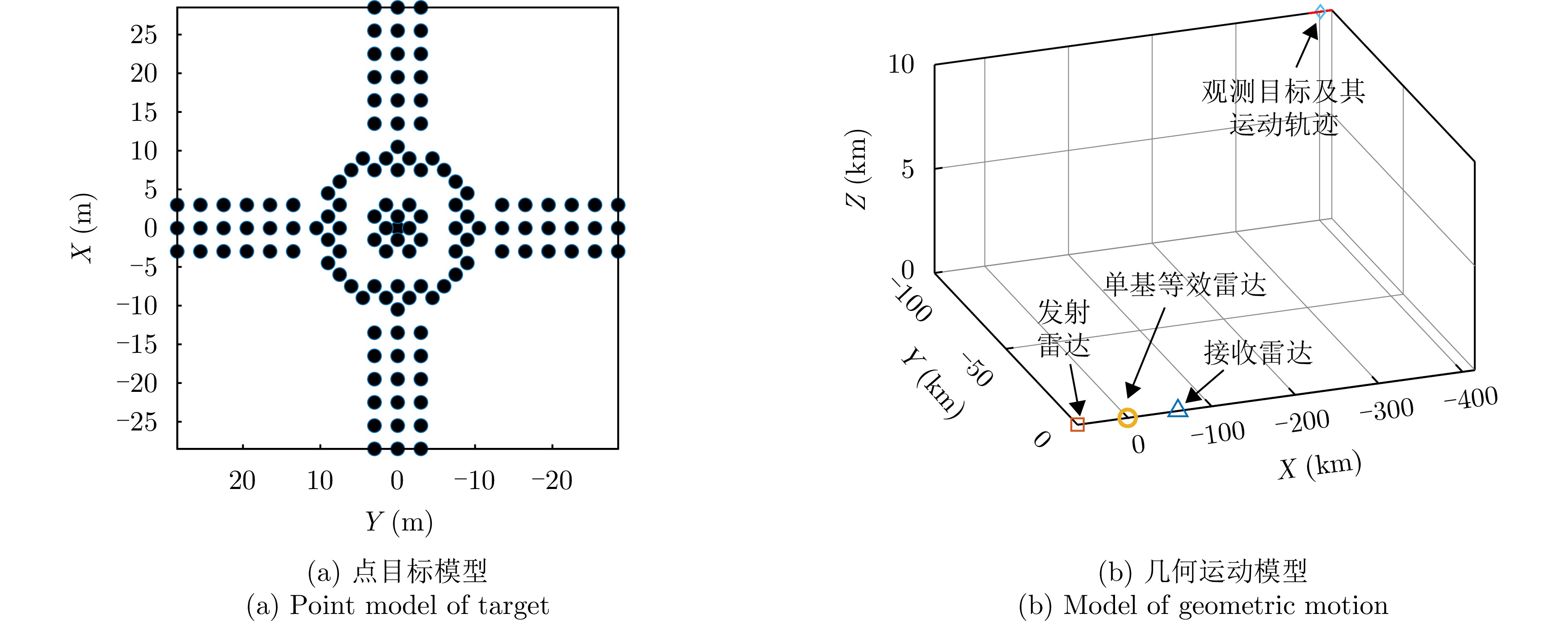
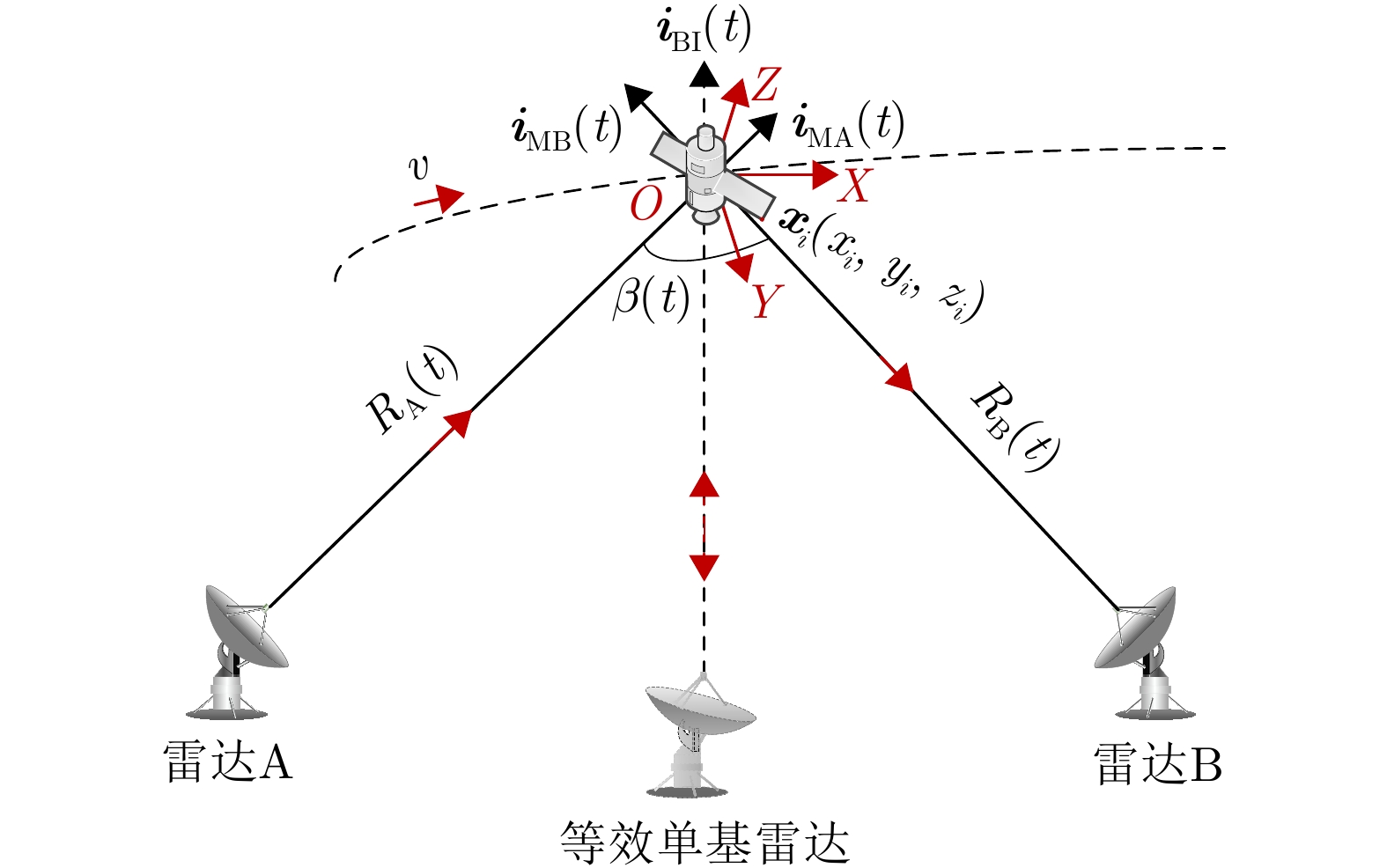
- Figure 1. Geometry model of Bistatic ISAR
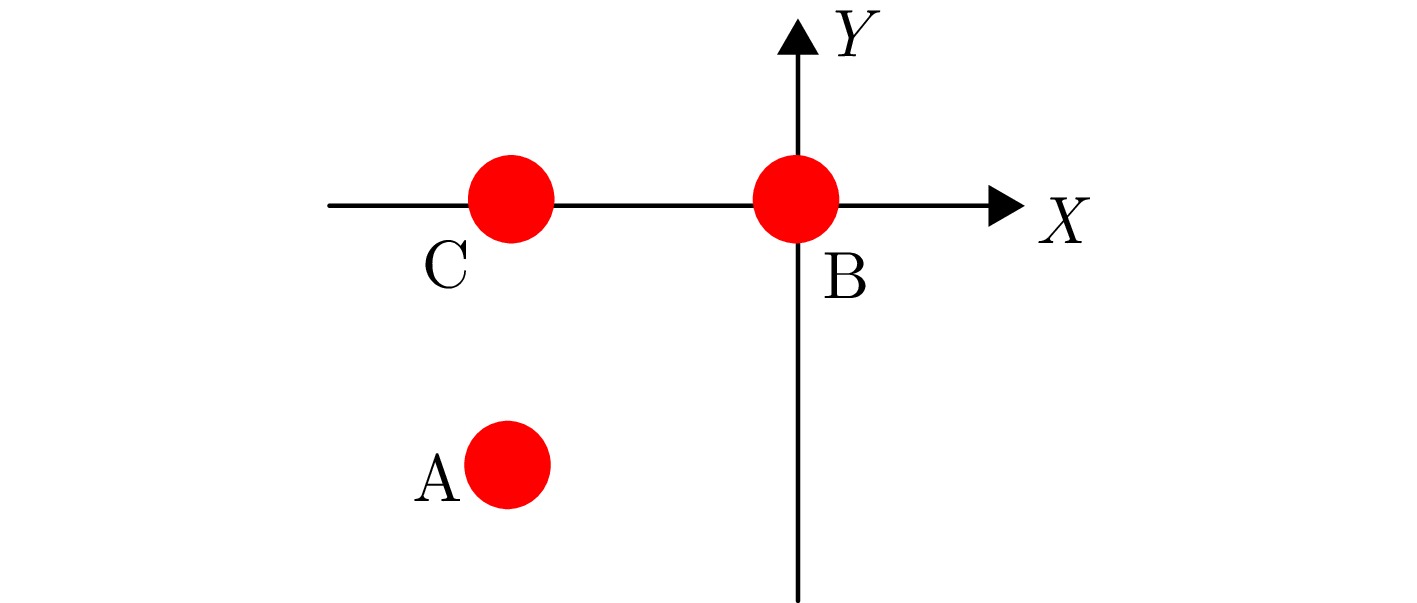
- Figure 2. Point target location diagram
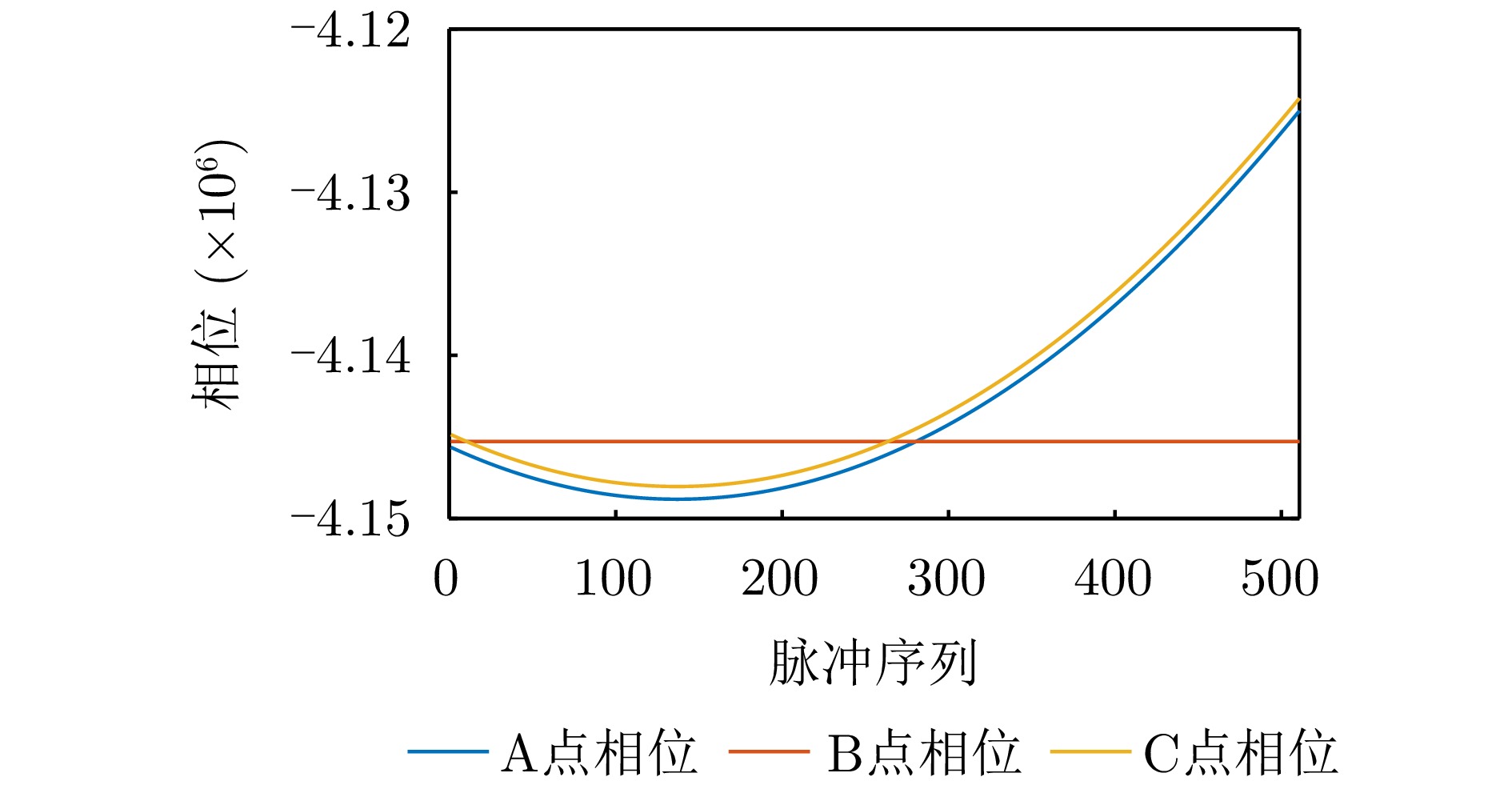
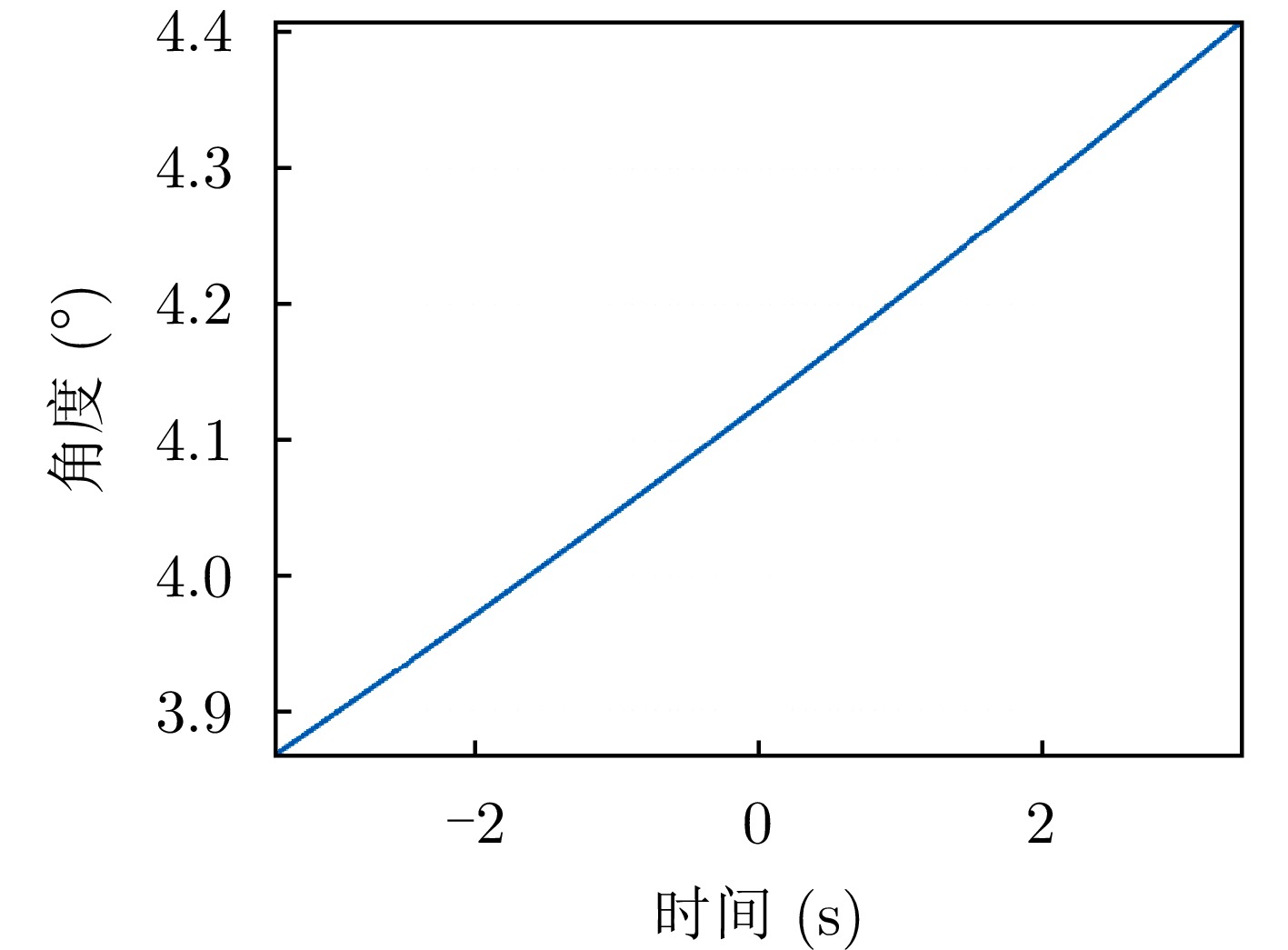
- Figure 3. Point target phase curve diagram
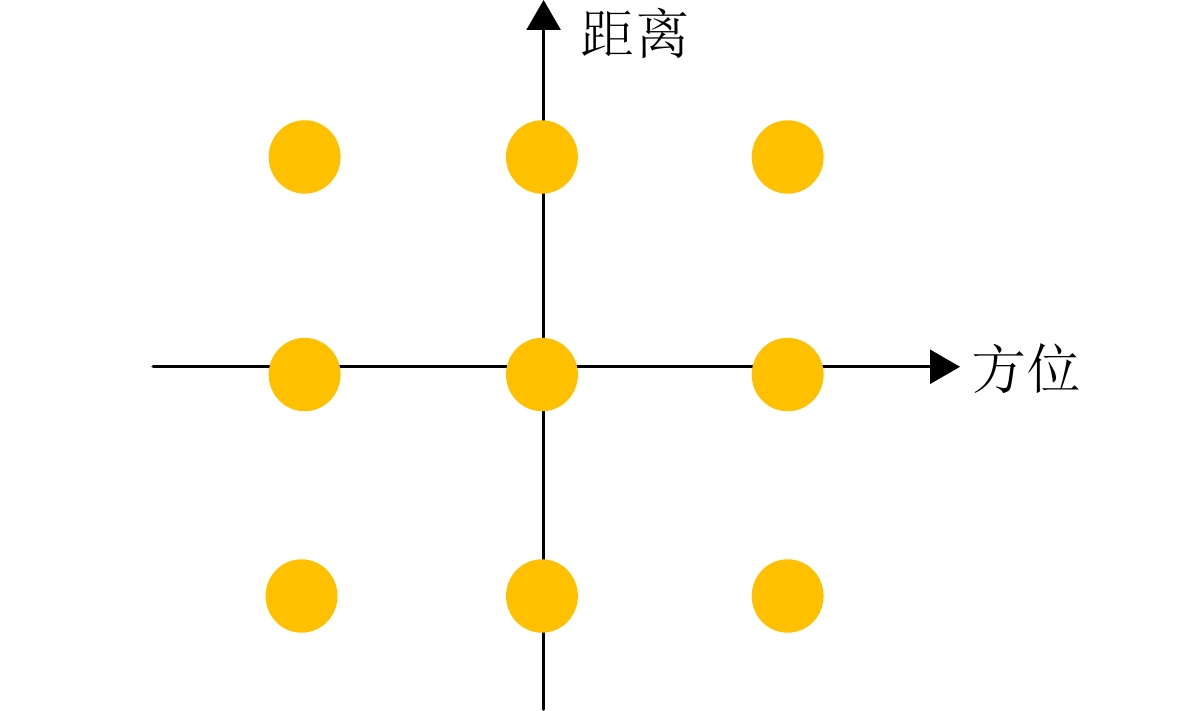
- Figure 4. Single base ISAR imaging diagram
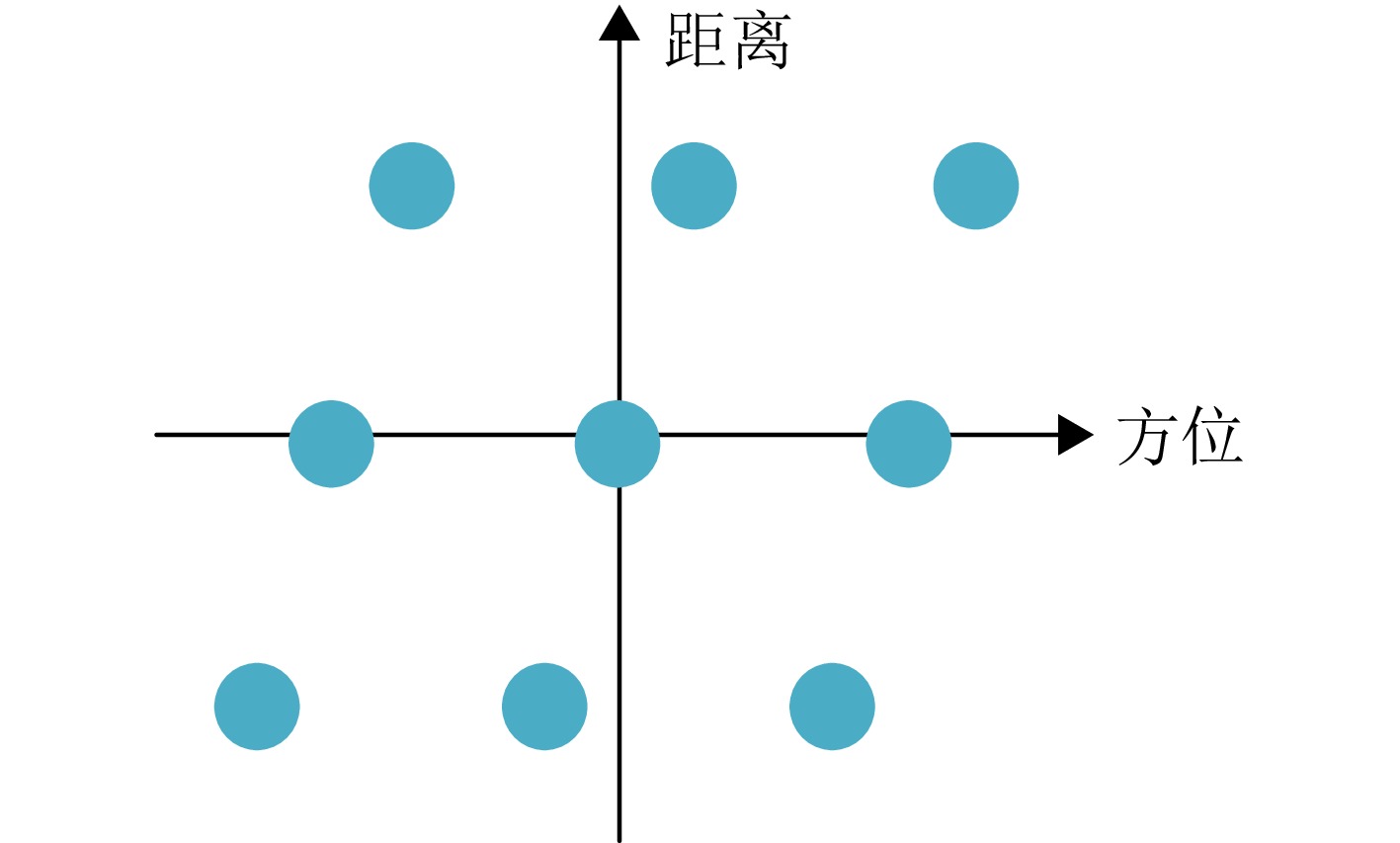
- Figure 5. Bistatic ISAR imaging diagram
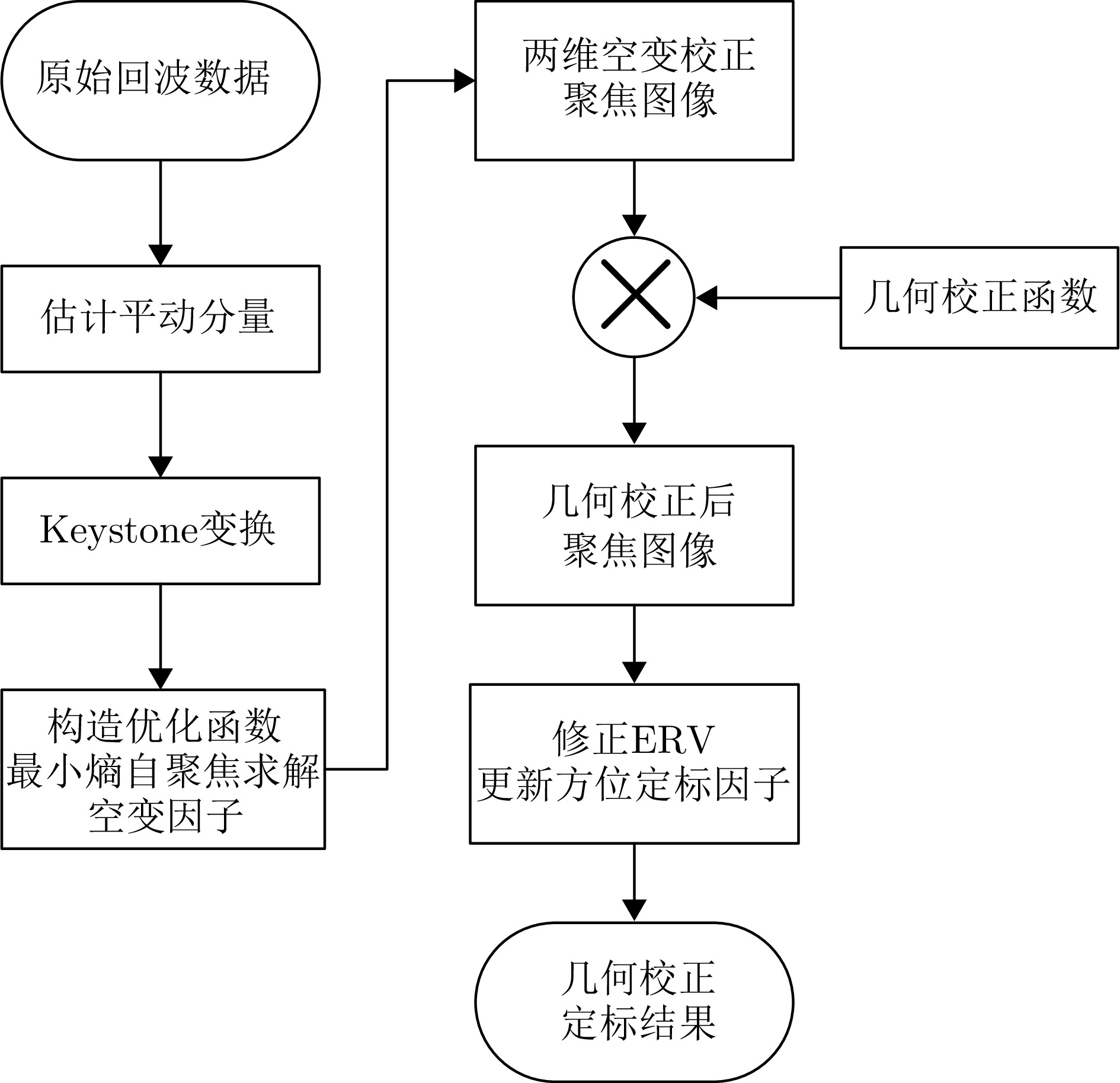
- Figure 6. Flowchart of two-dimensional spatial variation correction for Bi-ISAR based on modified Newton’s method
- Figure 7. Flow chart of space-variant phase error compensation and geometric correction image scaling for Bi-ISAR imaging based on modified Newton’s method
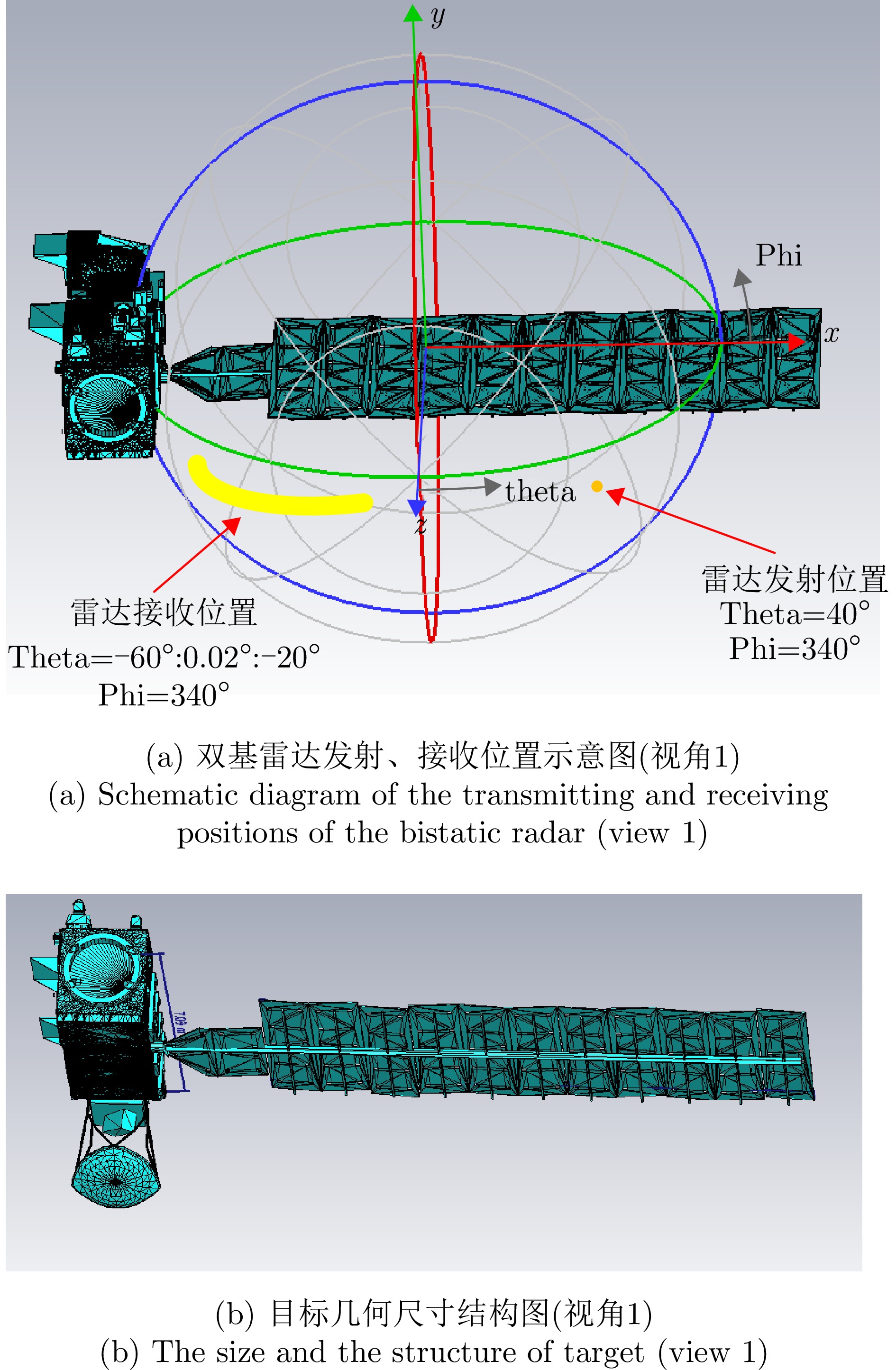
- Figure 8. The model of simulated target
- Figure 9. The changing trend of bistatic angle
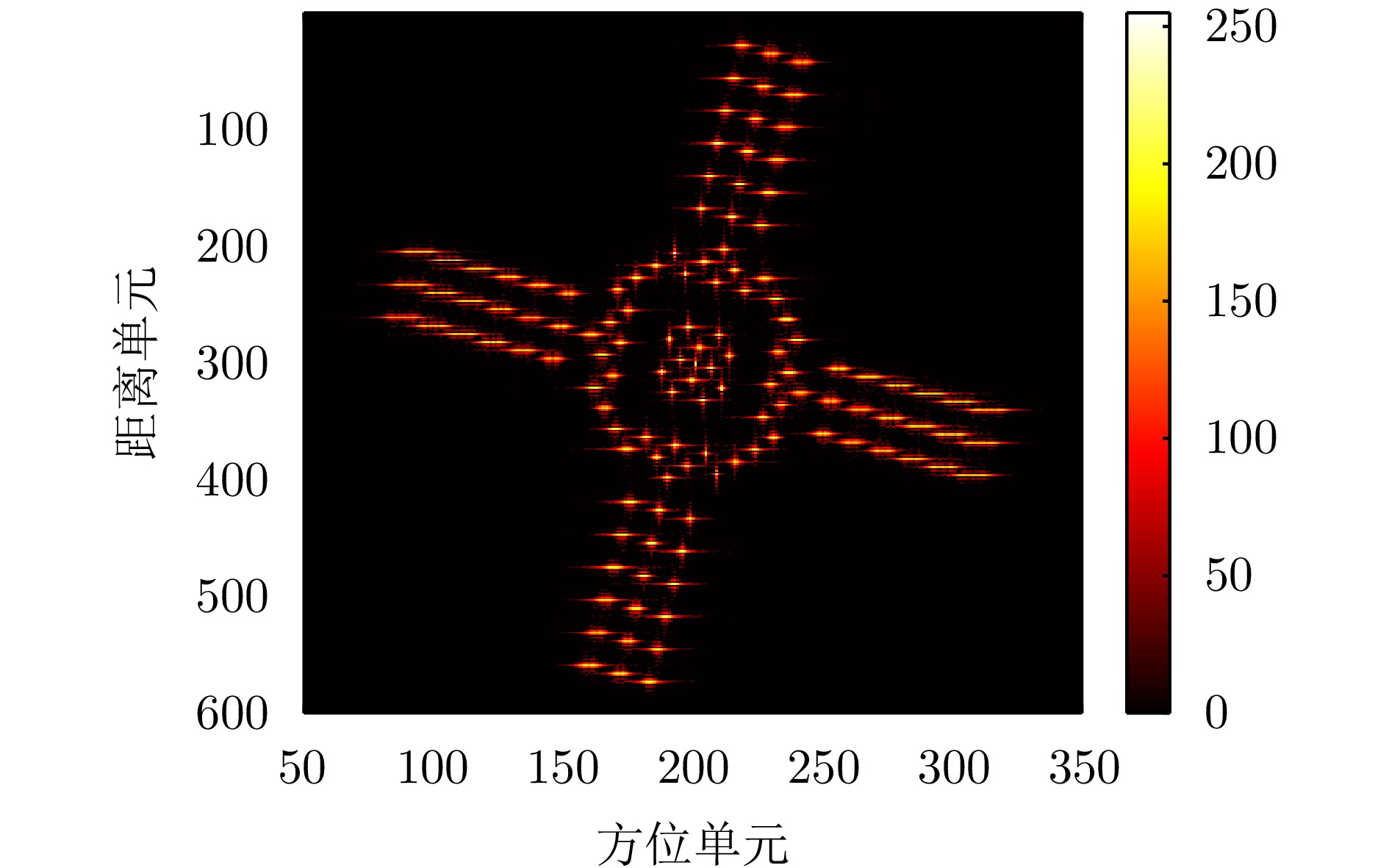
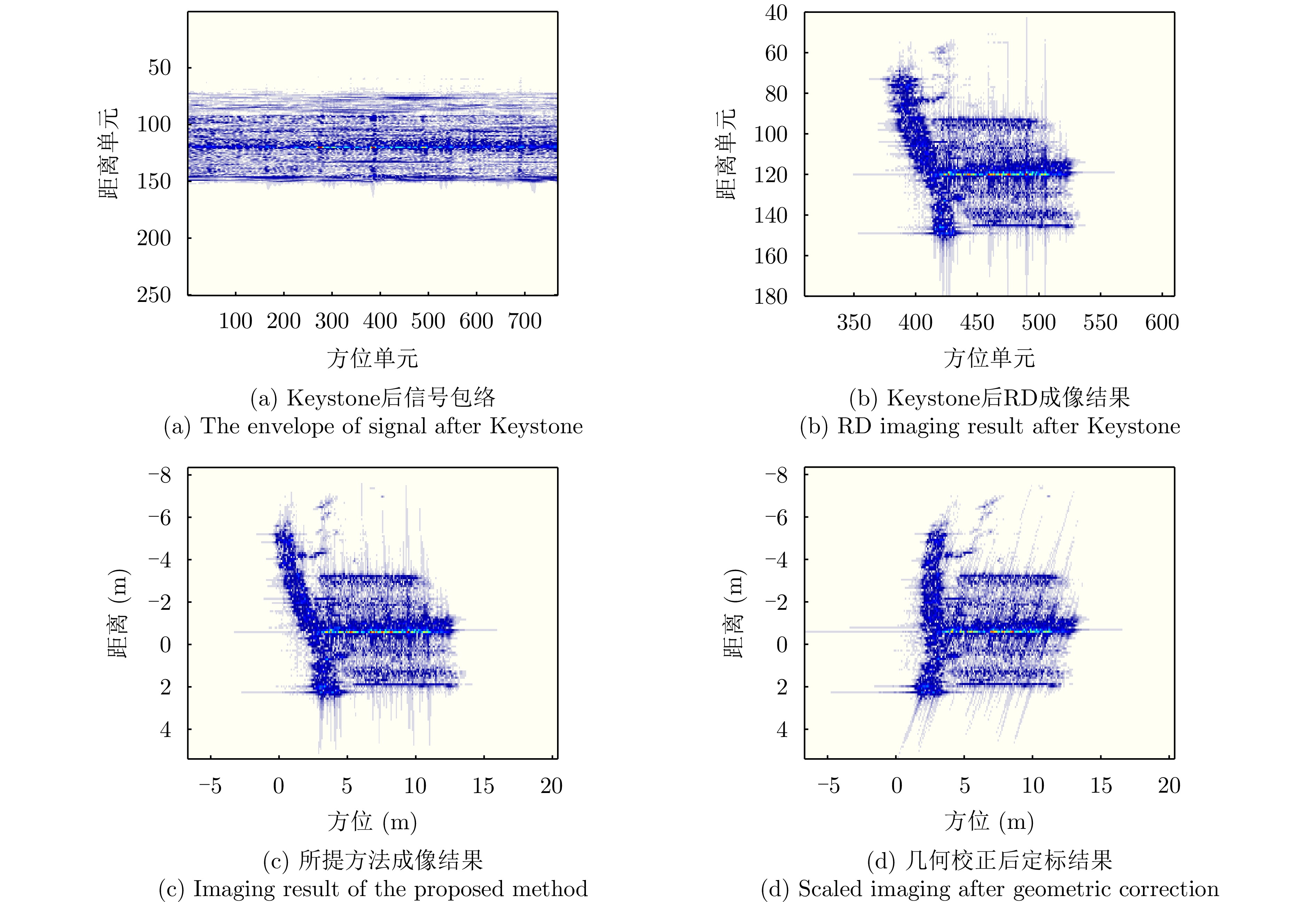
- Figure 10. Imaging result after Keystone transform
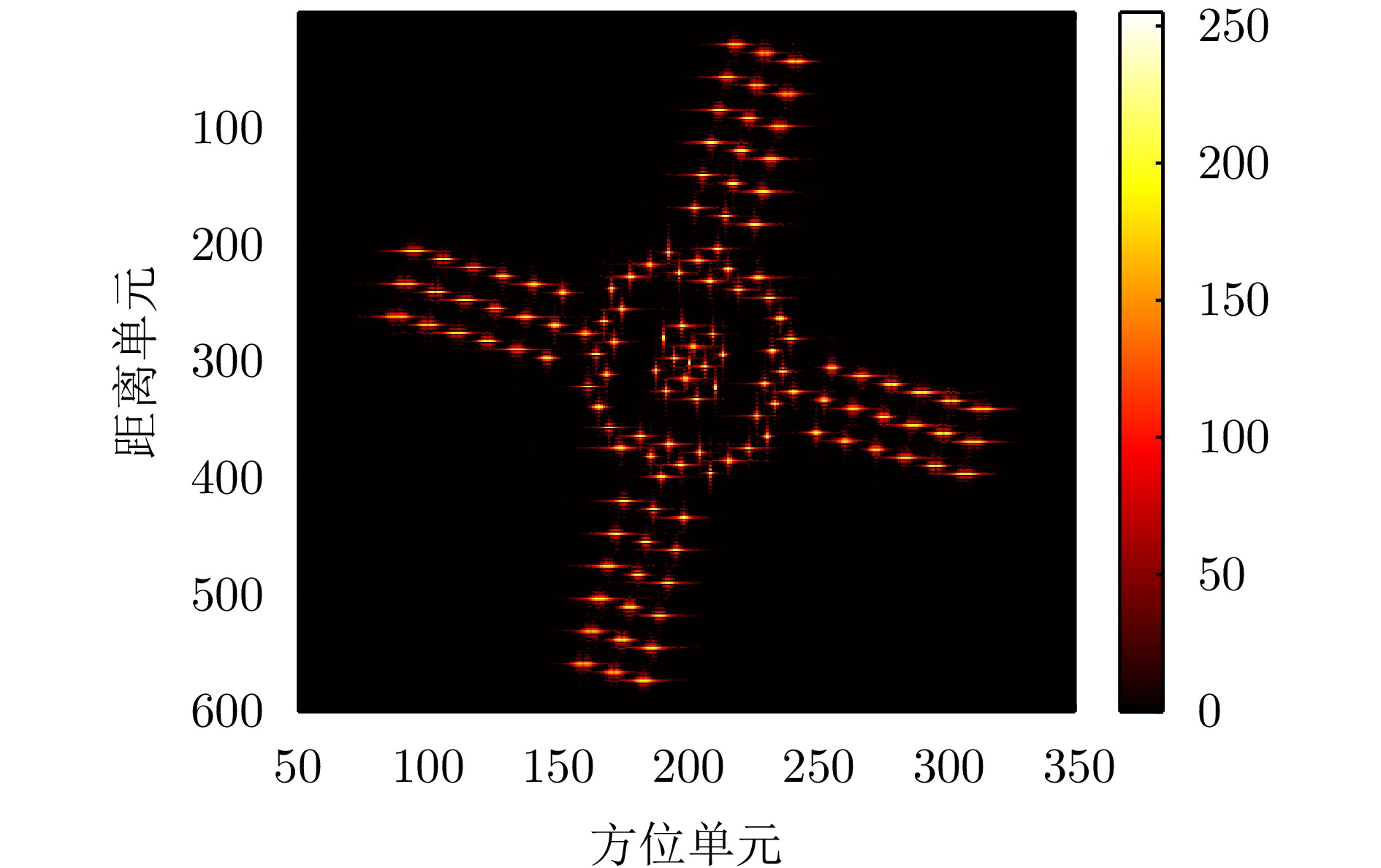
- Figure 11. Imaging results after initial parameter value compensation
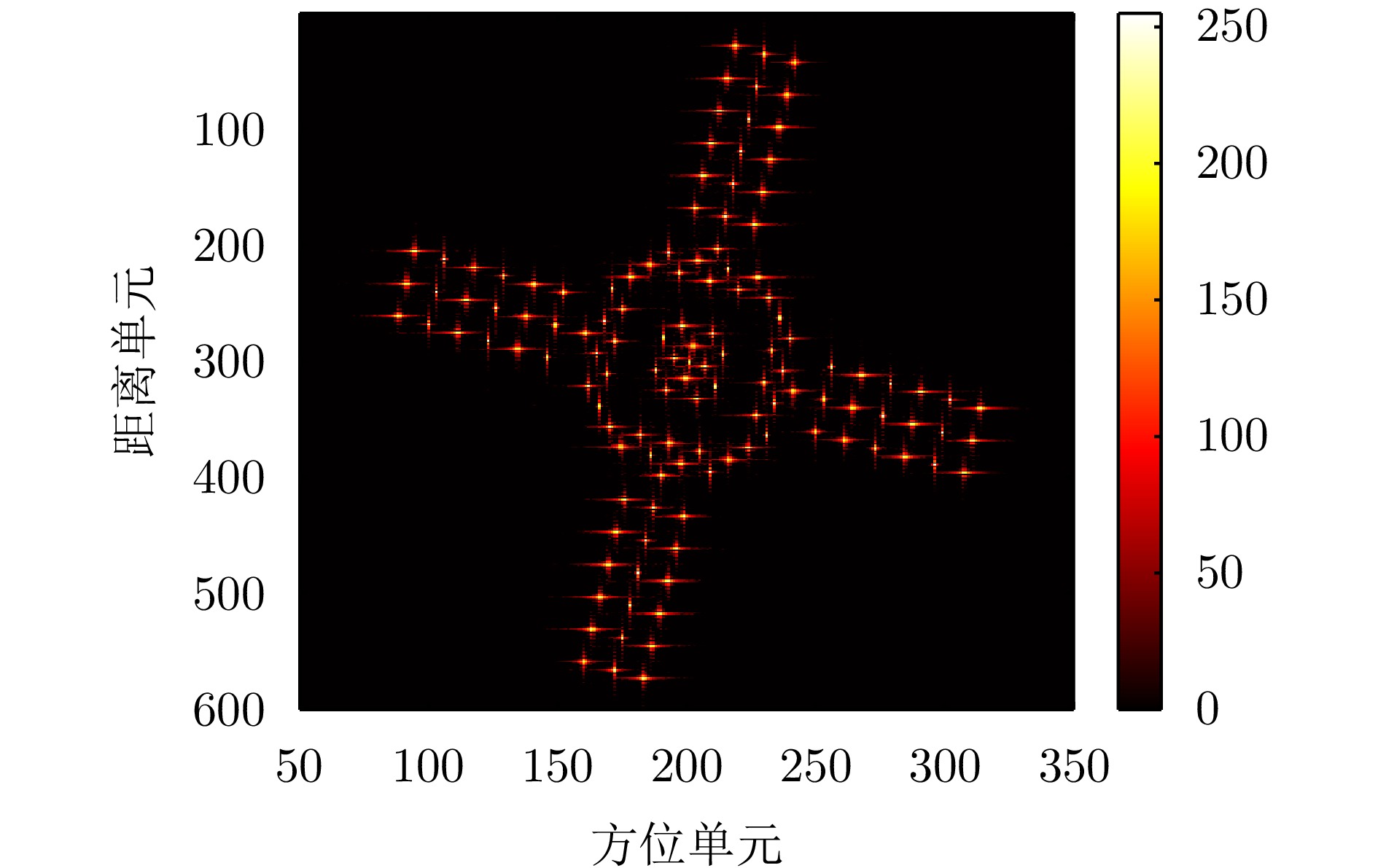
- Figure 12. Imaging result after 2D space-variant phase error compensation
- Figure 13. Imaging result after optimization
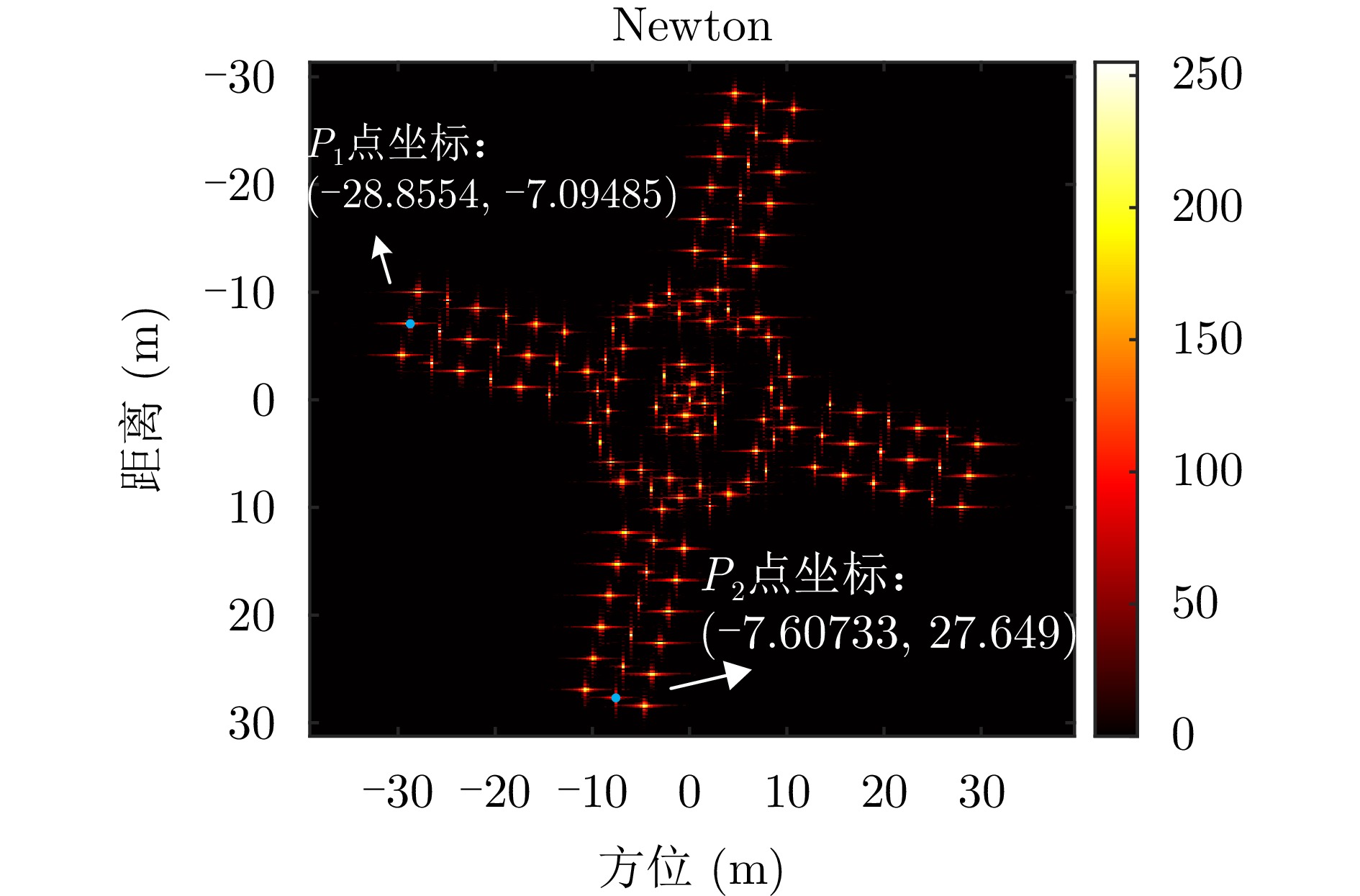
- Figure 14. Imaging result after geometric correction
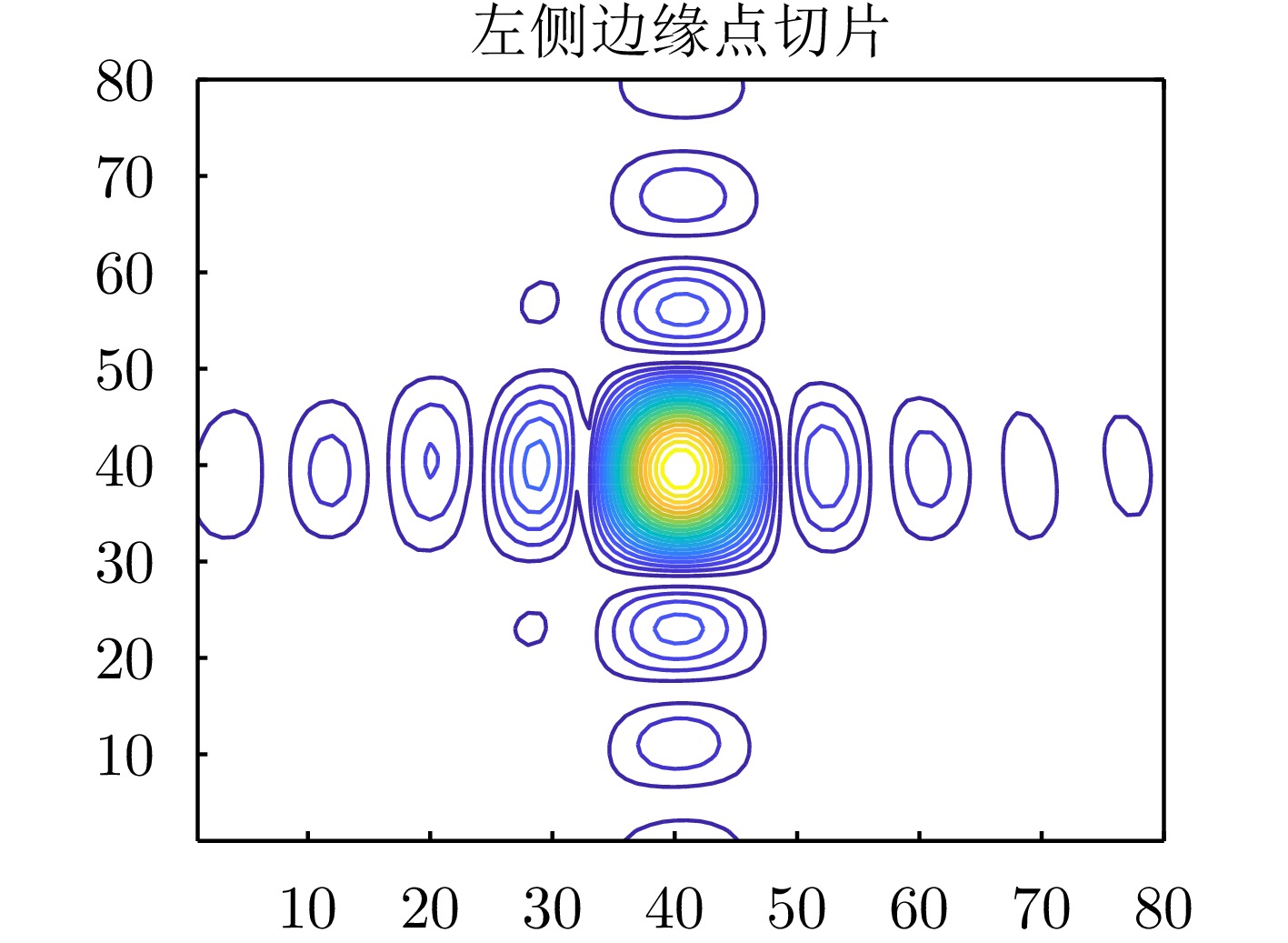
- Figure 15. Contour map of 8 times interpolated point P1 after compensation
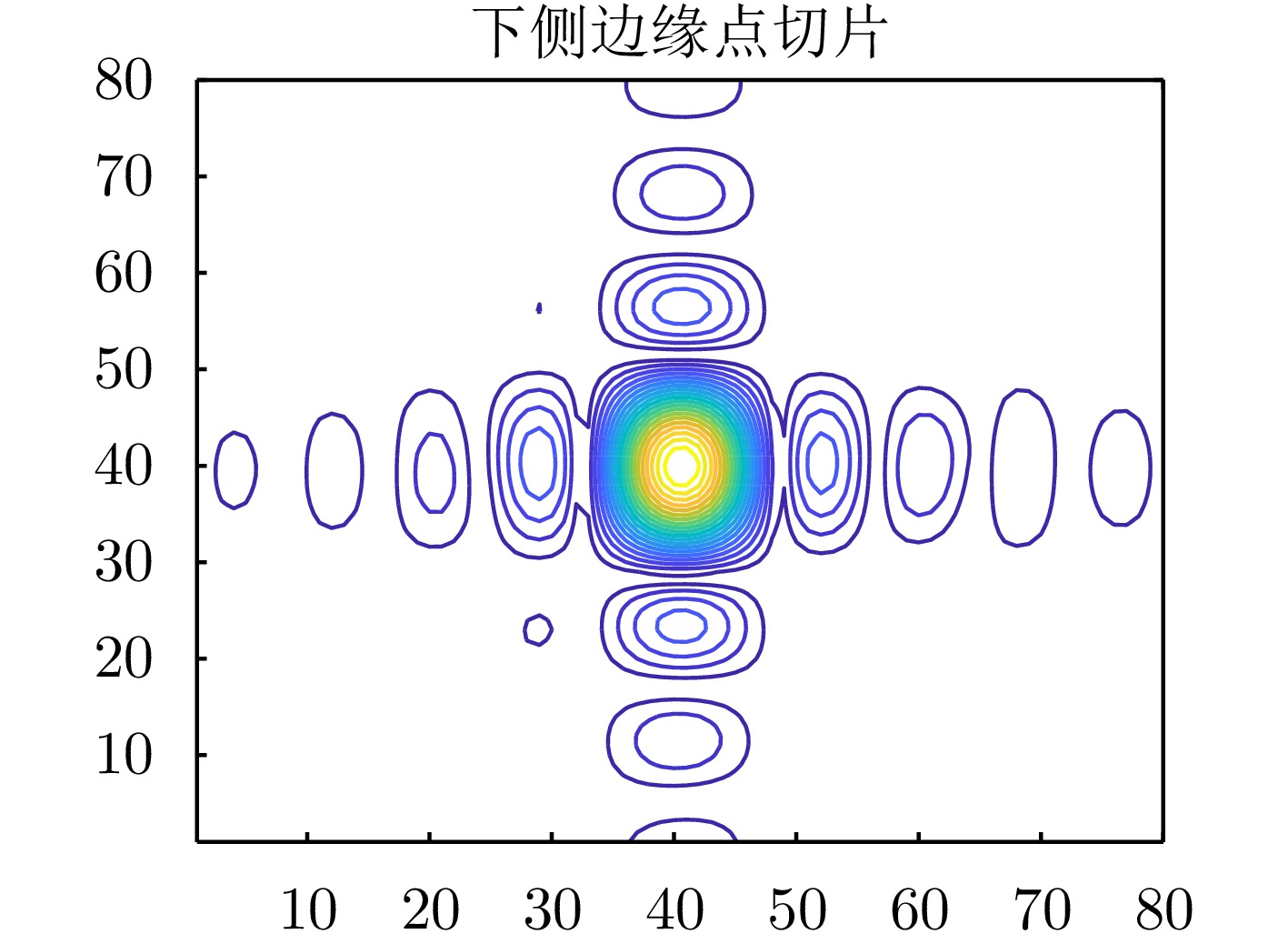
- Figure 16. Contour map of 8 times interpolated point P2 after compensation
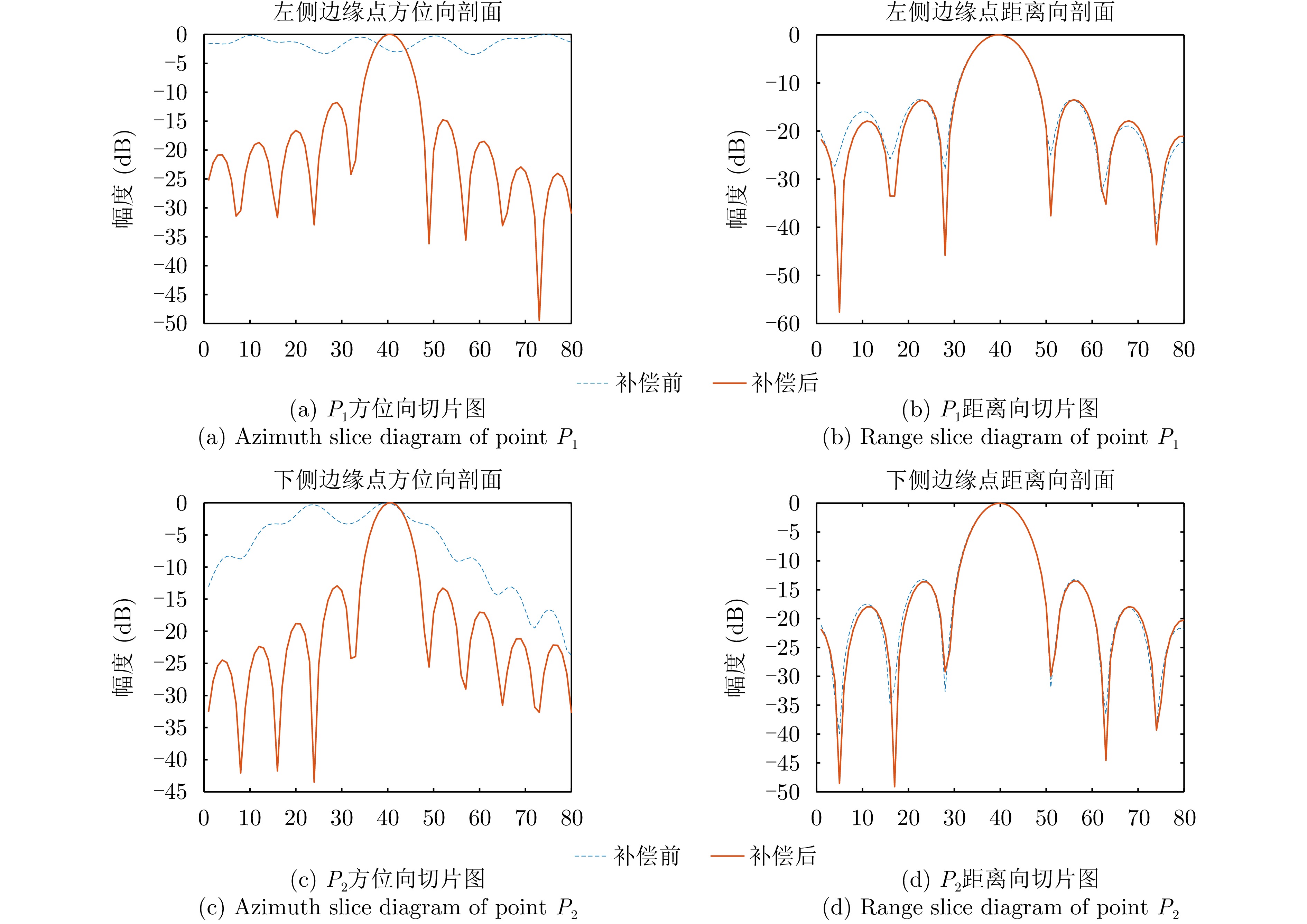
- Figure 17. Azimuth and Range slice diagram of points P1 and P2
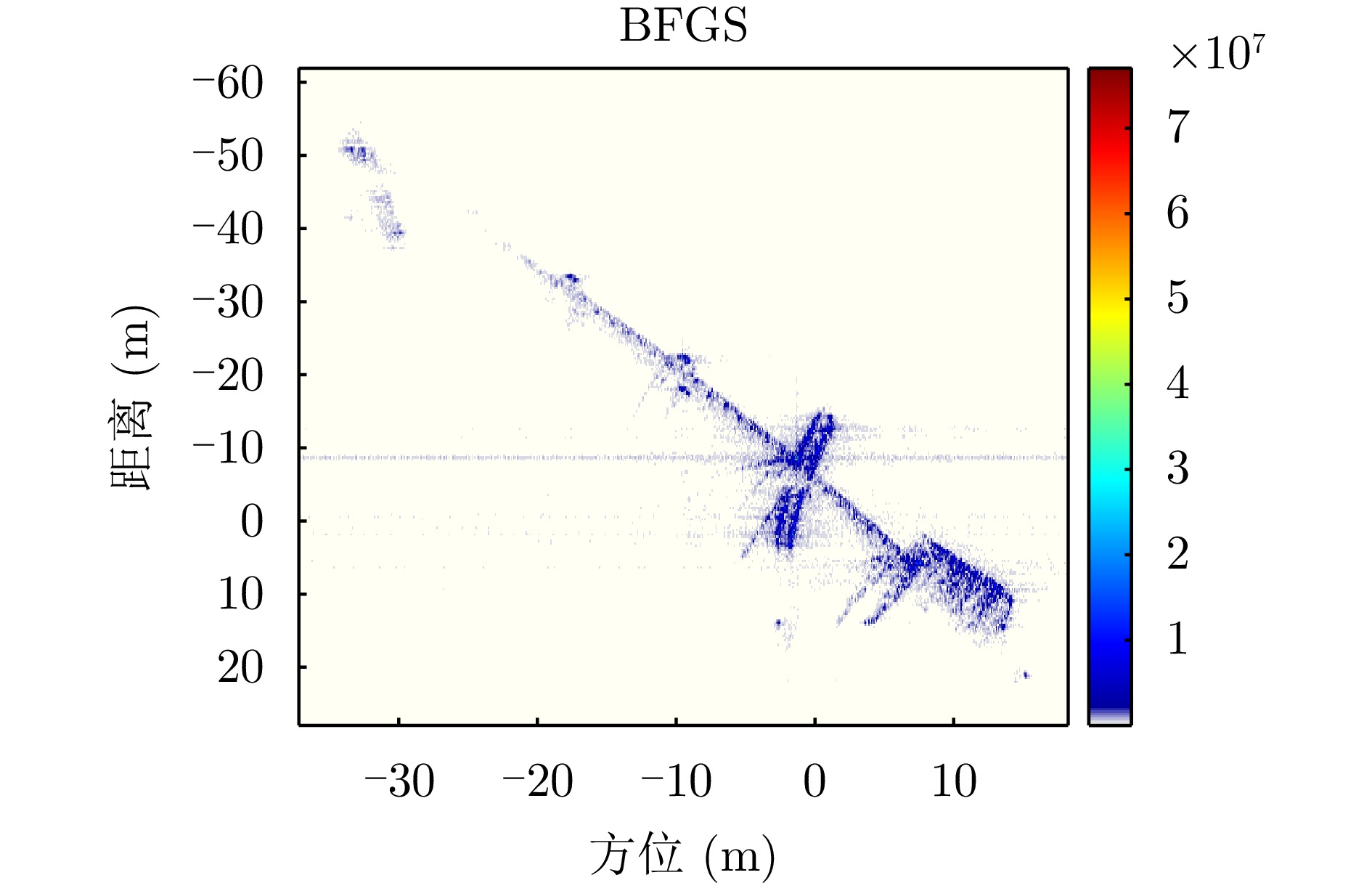
- Figure 18. Imaging result of the contrast method (BFGS)
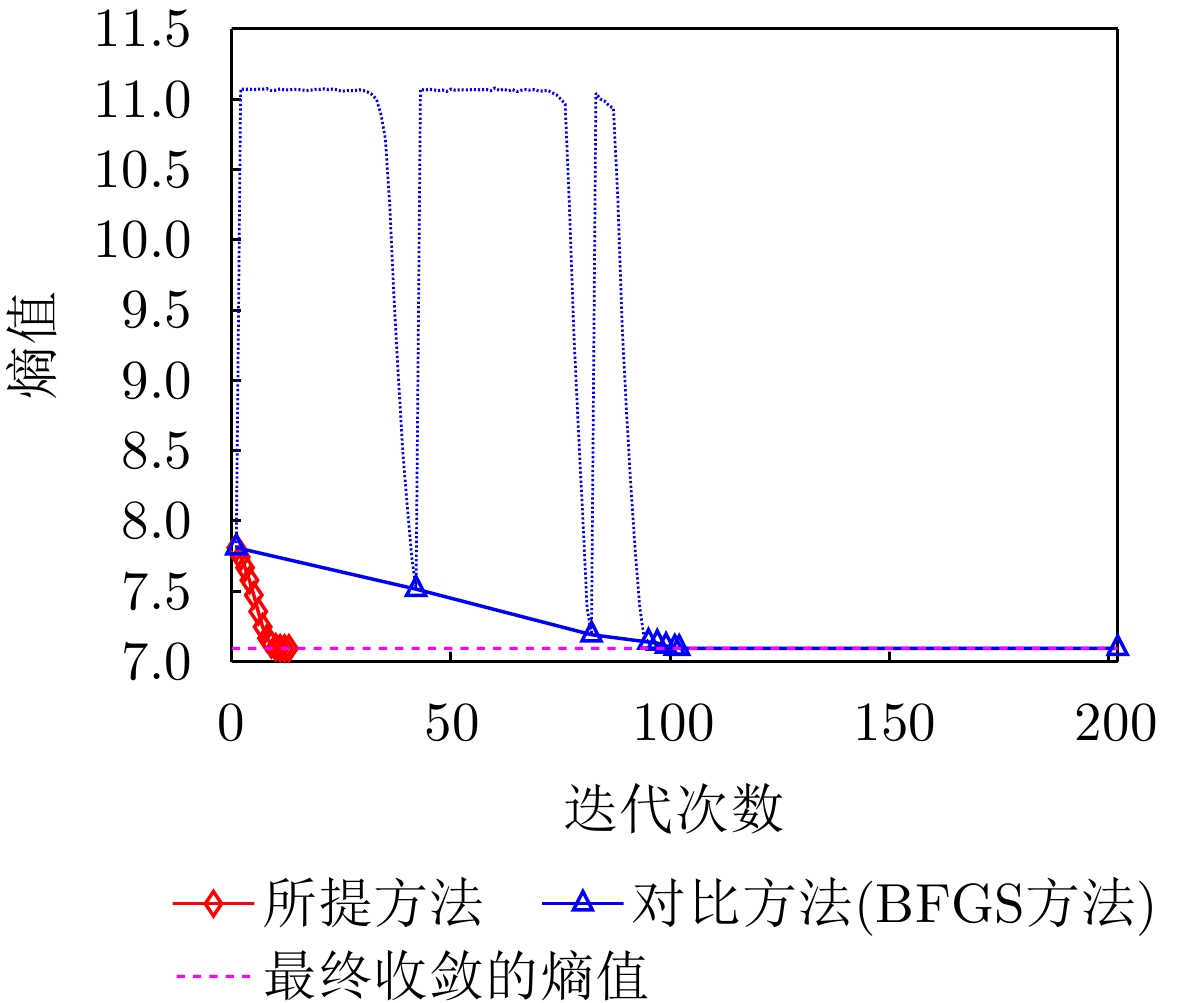
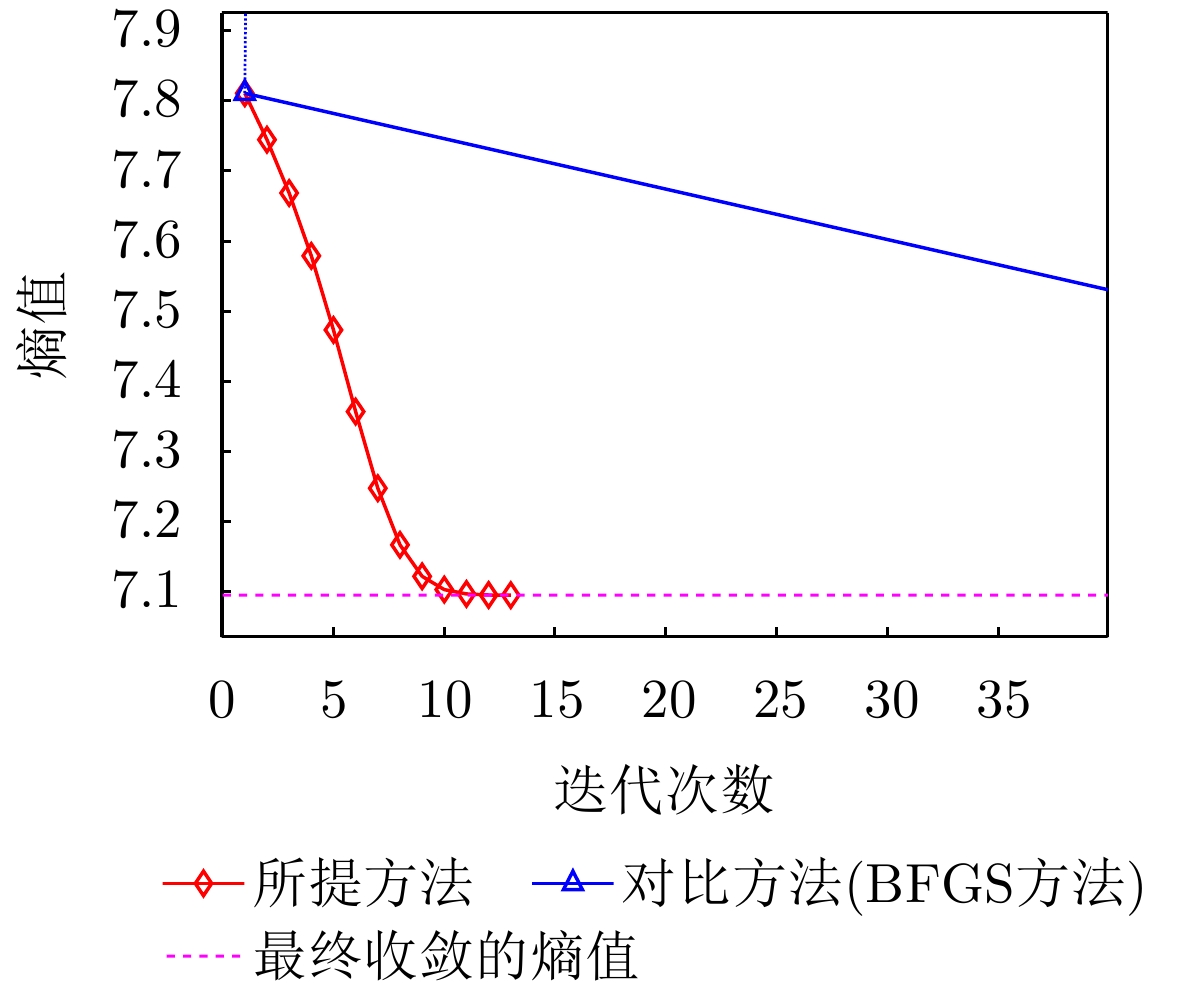
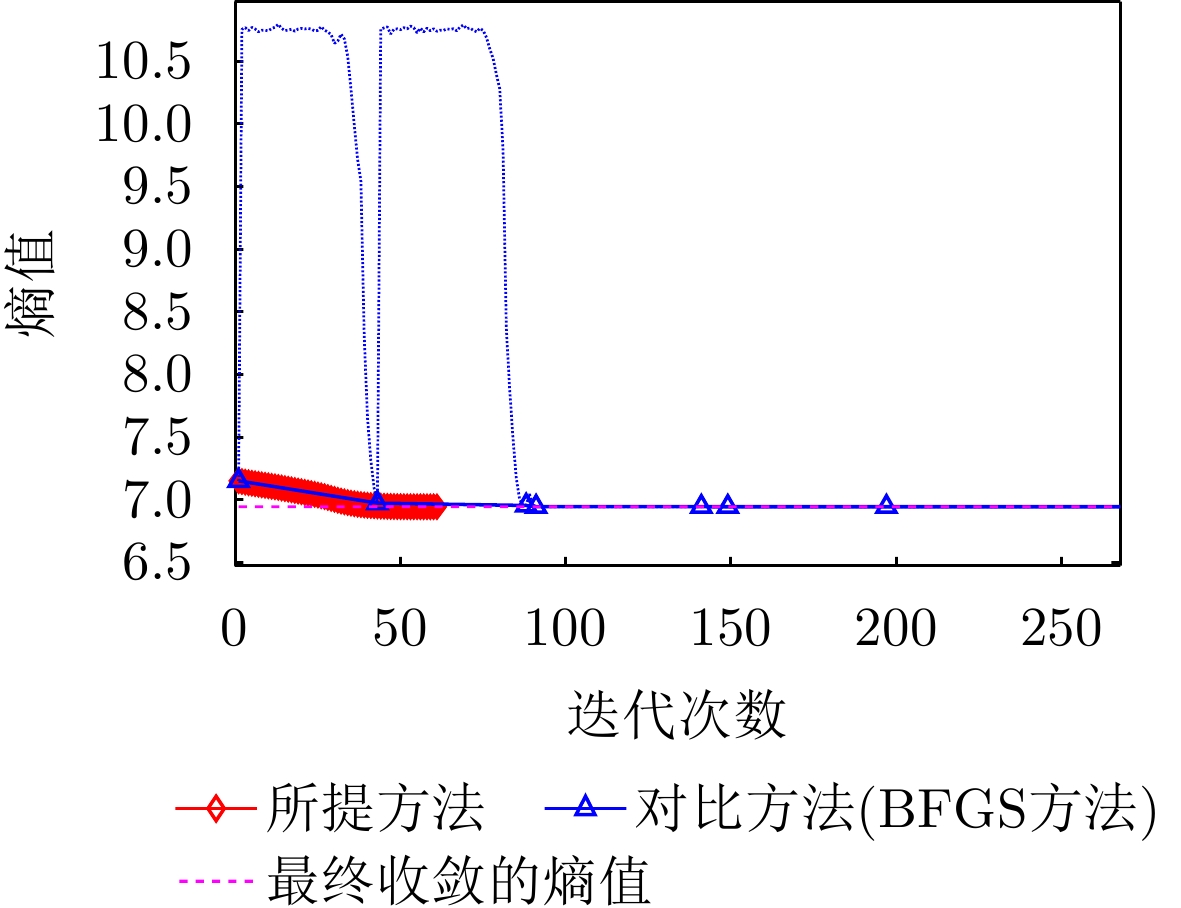
- Figure 19. Image entropy change curves of the proposed method and the contrast method (BFGS)
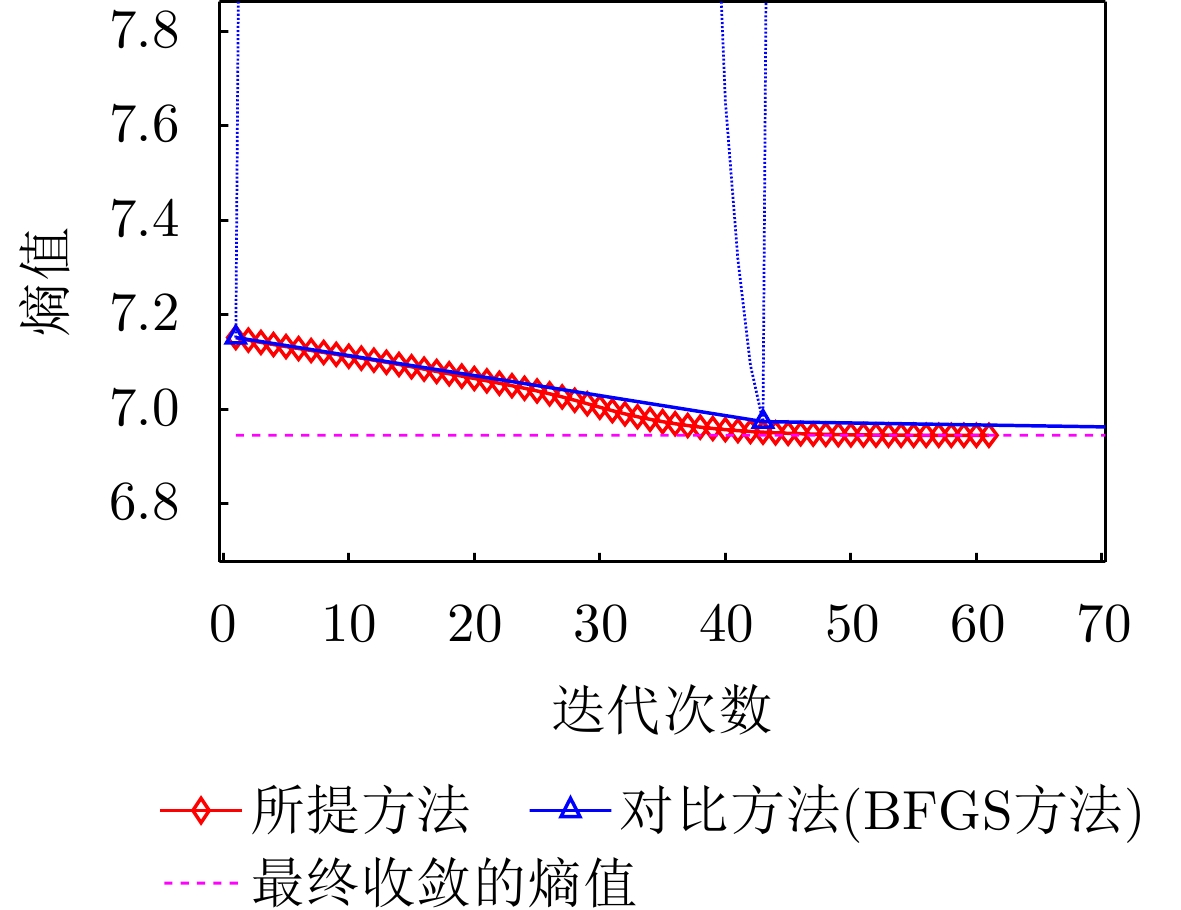
- Figure 20. Enlarged image of the entropy change curve of the proposed method
- Figure 21. Imaging results of two methods under different SNR
- Figure 22. CST software simulation satellite image (view 1)
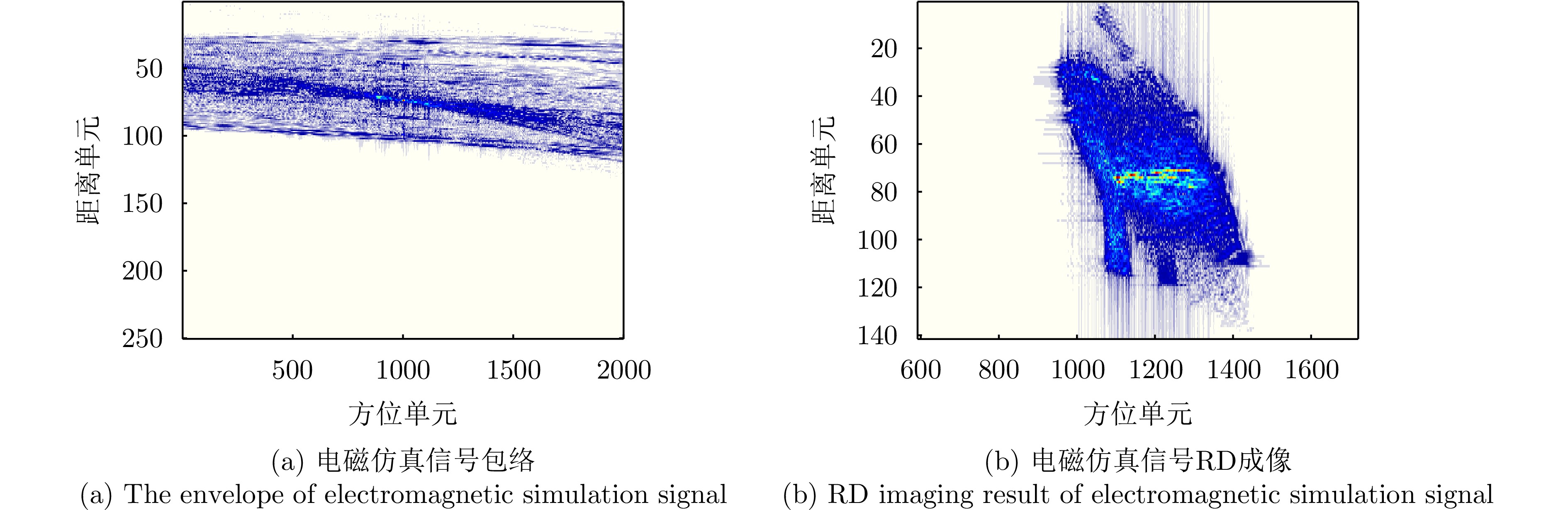
- Figure 23. Cross-polarized electromagnetic simulation signal’s envelope and RD imaging results
- Figure 24. Correction results of the proposed method under cross-polarization
- Figure 25. Imaging result of the contrast method (BFGS)
- Figure 26. Image entropy change curves of the proposed method and the contrast method (view 1)
- Figure 27. Enlarged image of the entropy change curve of the proposed method (view 1)
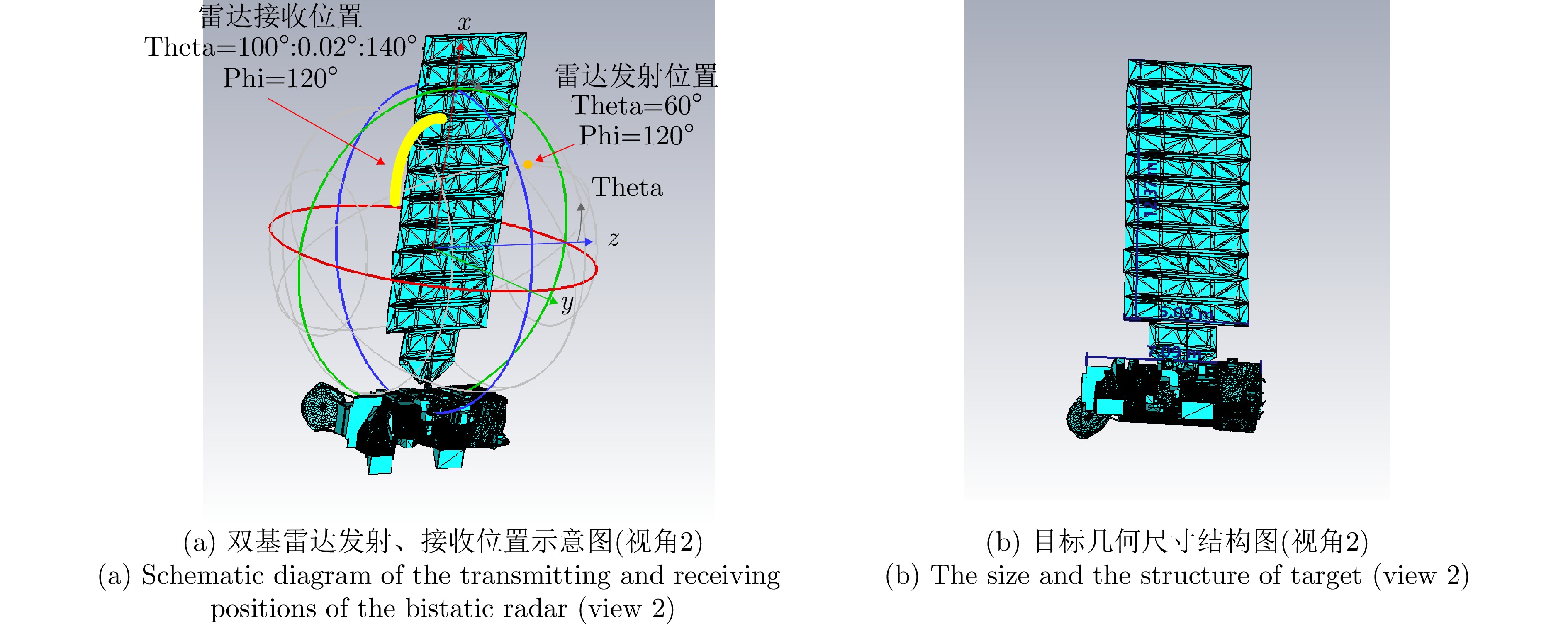
- Figure 28. CST software simulation satellite image (view 2)
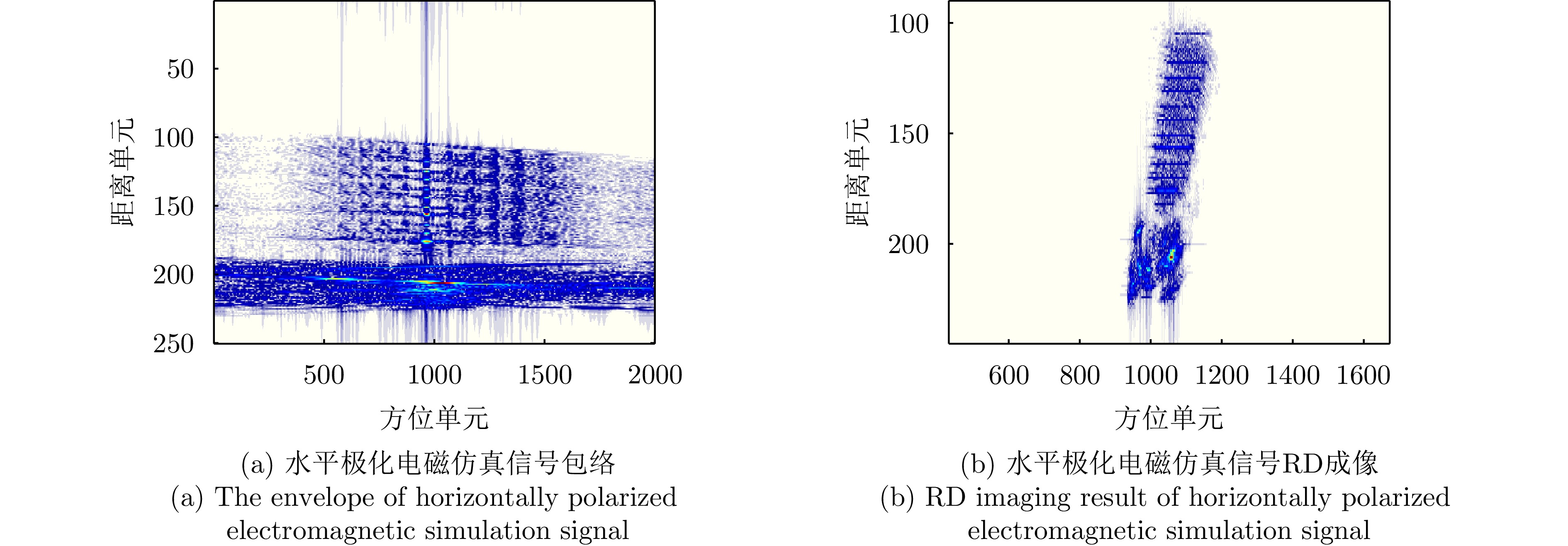
- Figure 29. Horizontally polarized and cross-polarized electromagnetic simulation signal’s envelope and RD imaging results
- Figure 30. Comparison of the results before and after two-dimensional space-variant correction for the proposed method
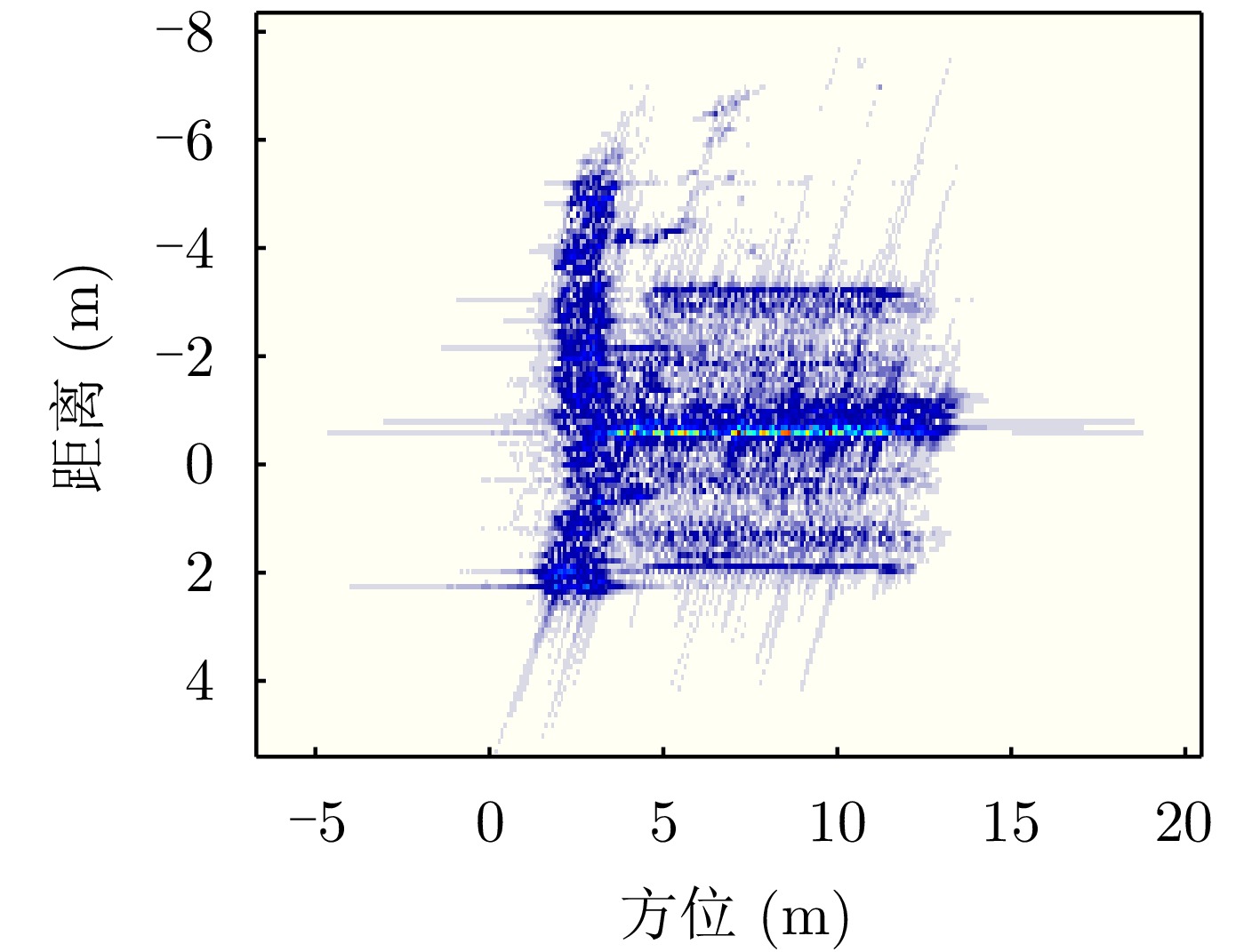
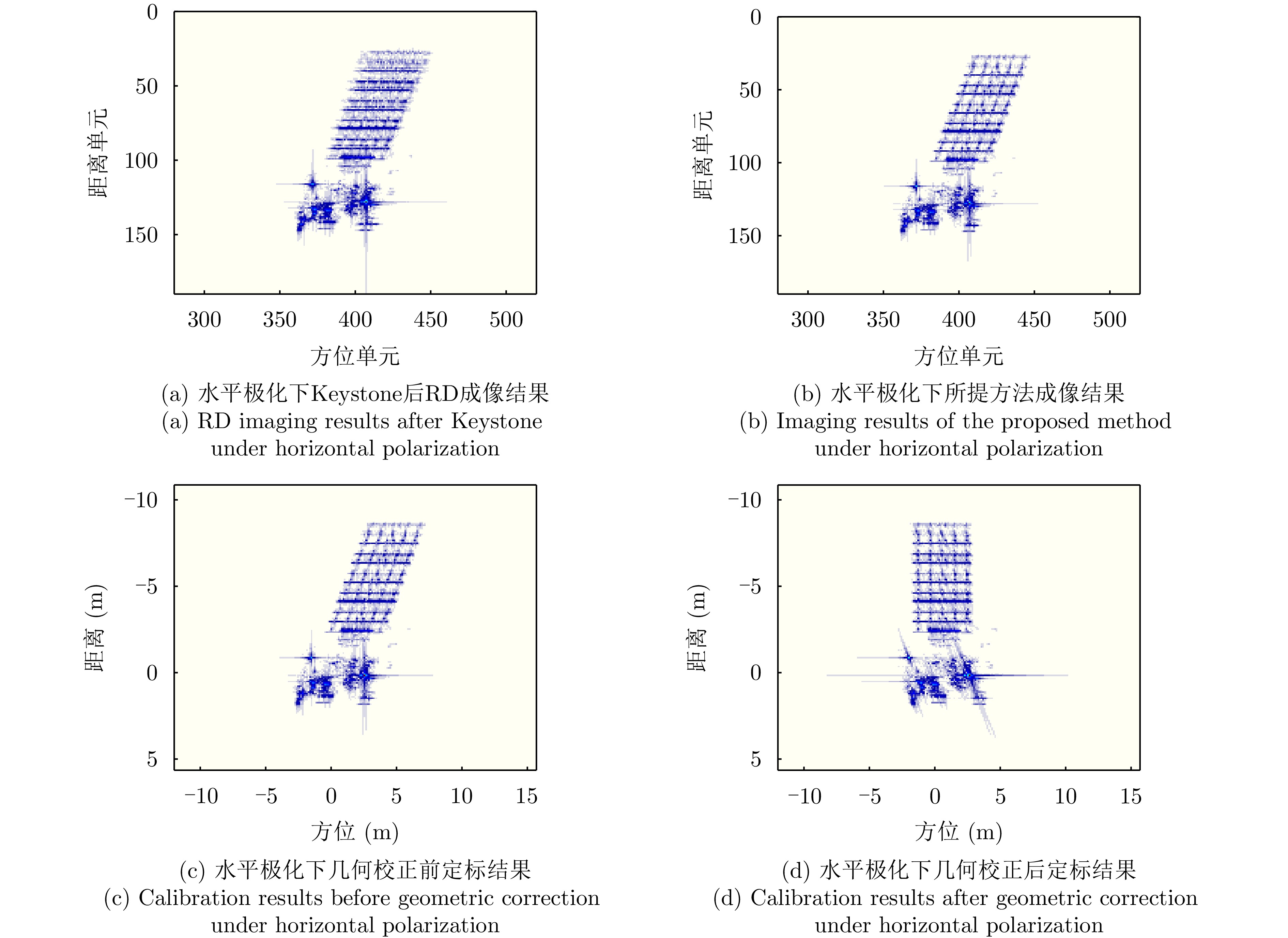
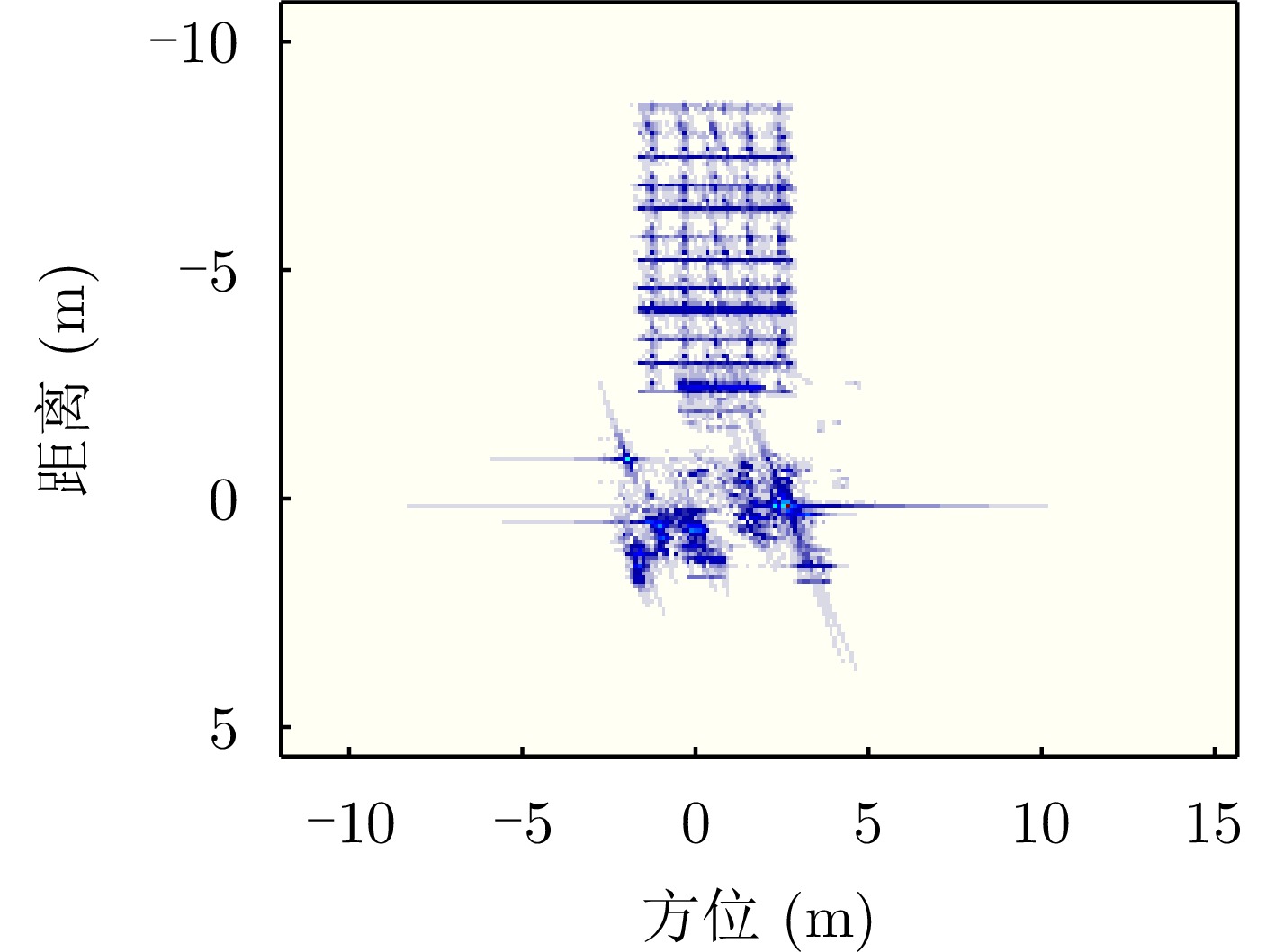
- Figure 31. Imaging results of the contrast method under horizontal polarization
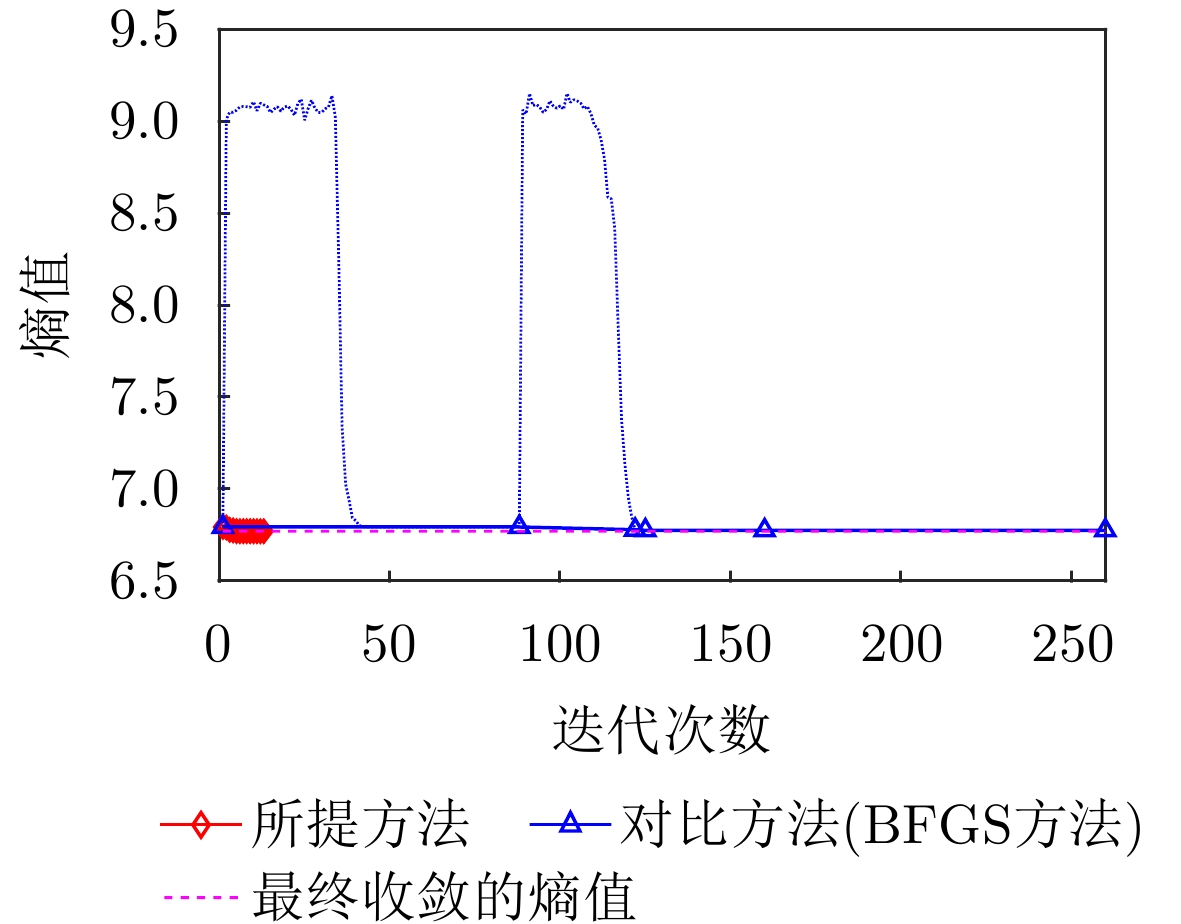
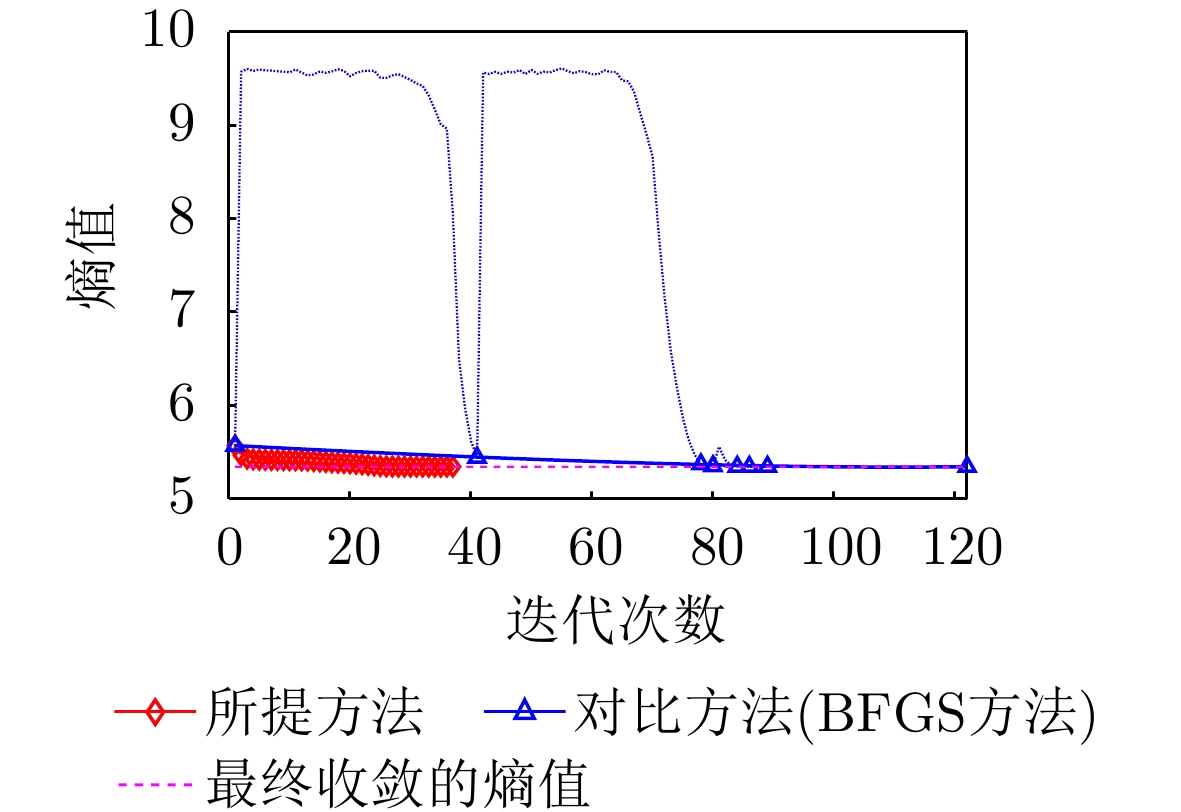
- Figure 32. Image entropy change curves of the proposed method and the contrast method (view 2)
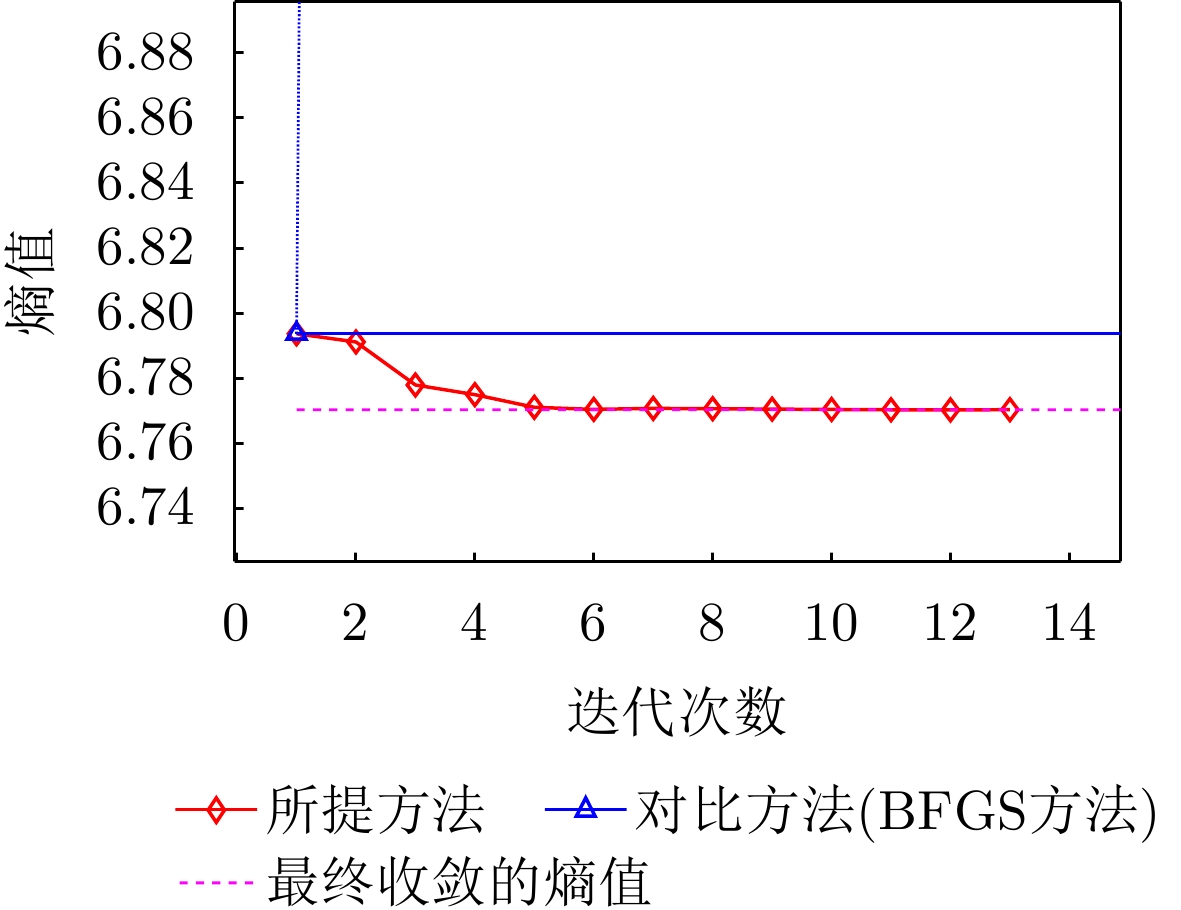
- Figure 33. Enlarged image of the entropy change curve of the proposed method (view 2)
- Figure 34. The picture of the experiment
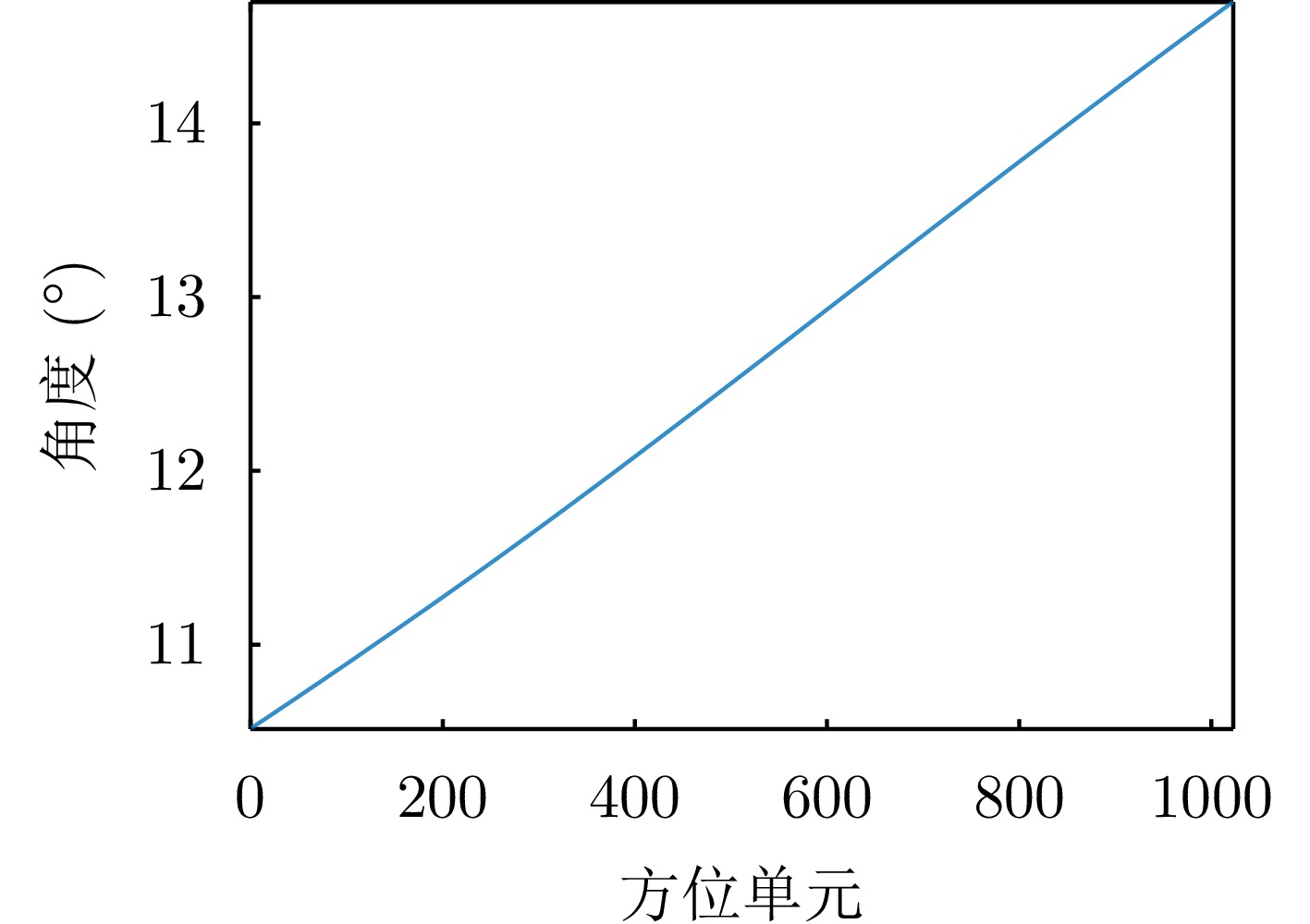
- Figure 35. The trend of the measured data of the bistatic angle
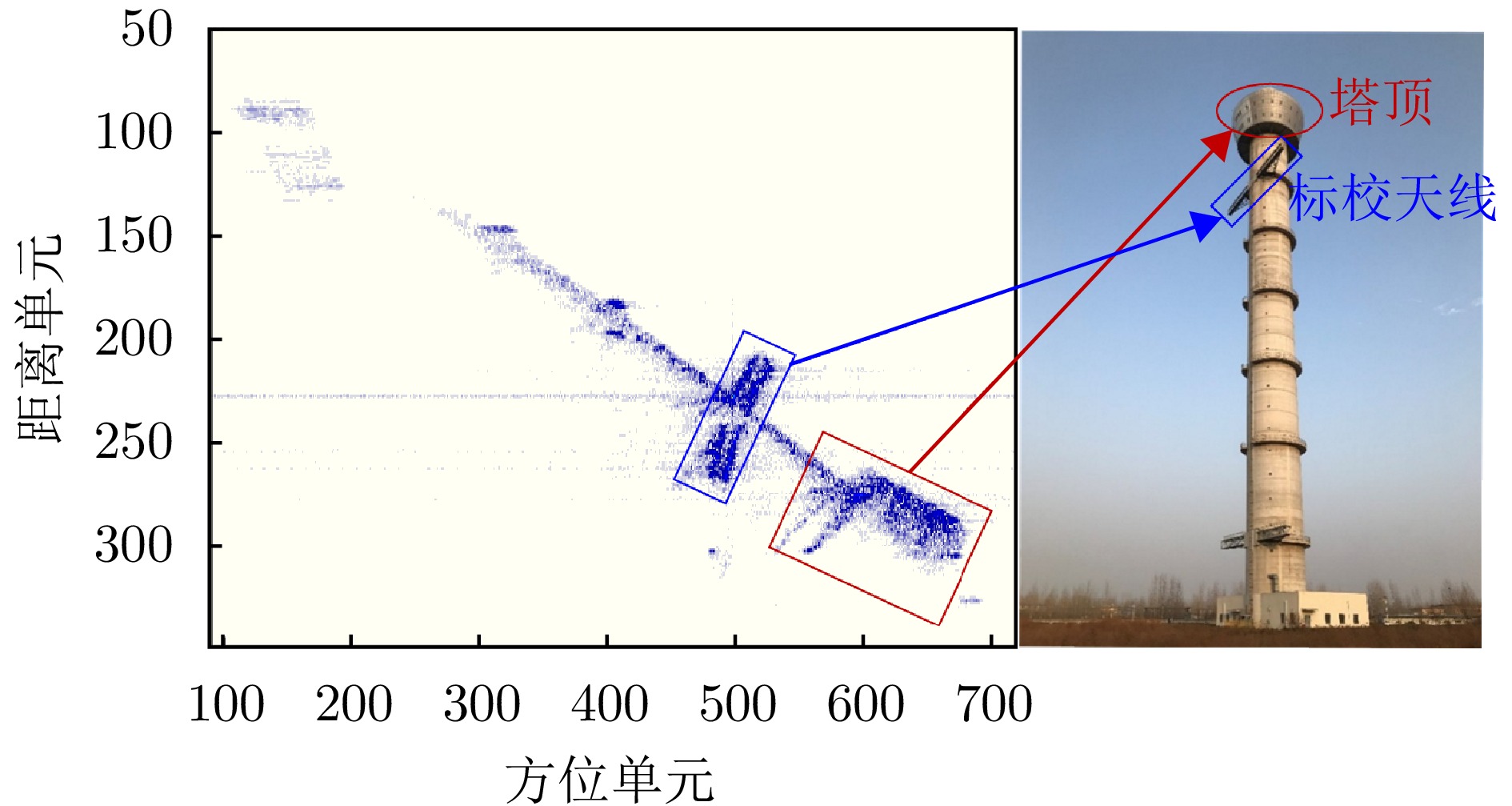
- Figure 36. Imaging result after Keystone transform and its corresponding part in the optical picture
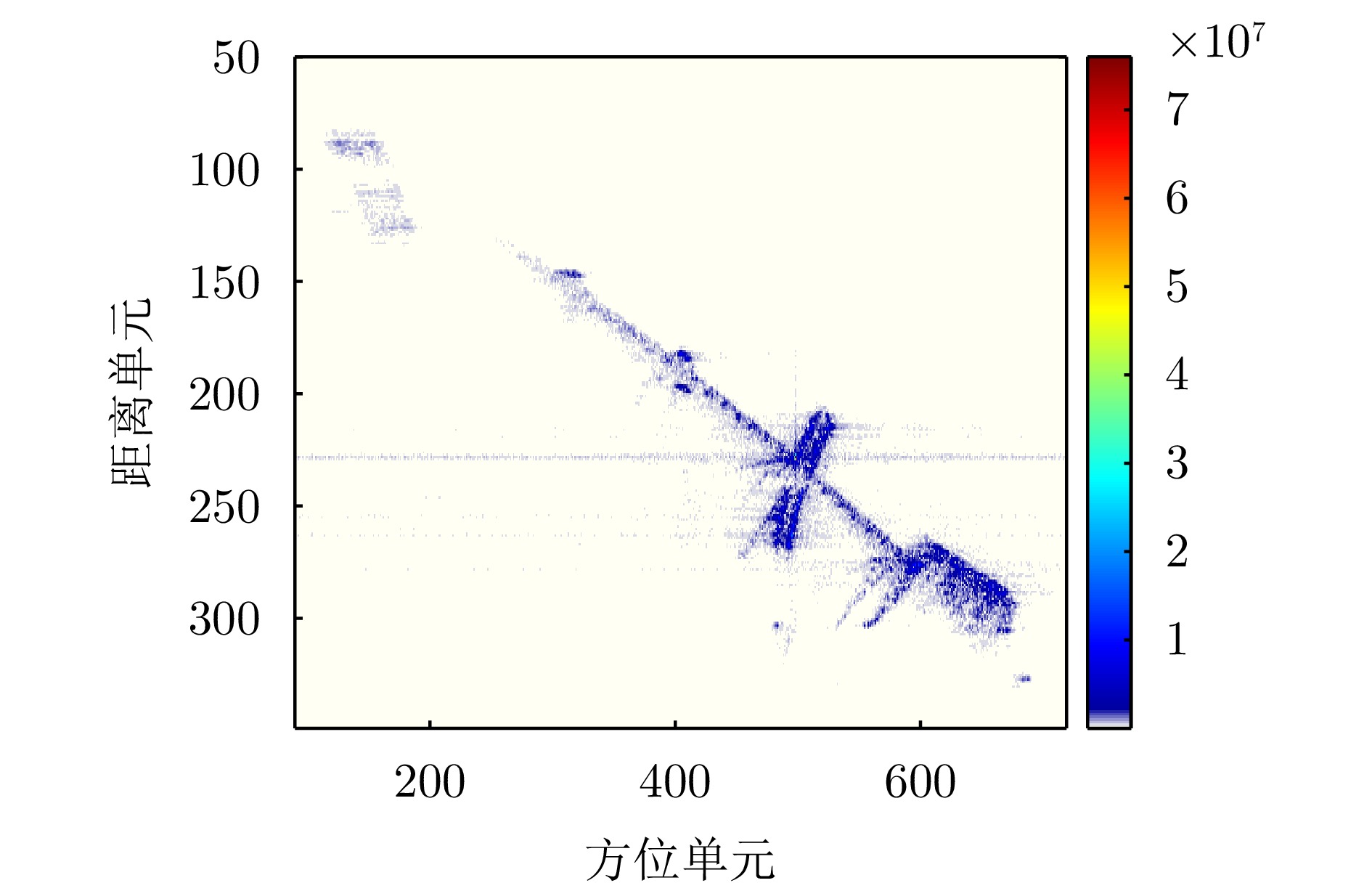
- Figure 37. Imaging results of measured data after initial parameter value compensation
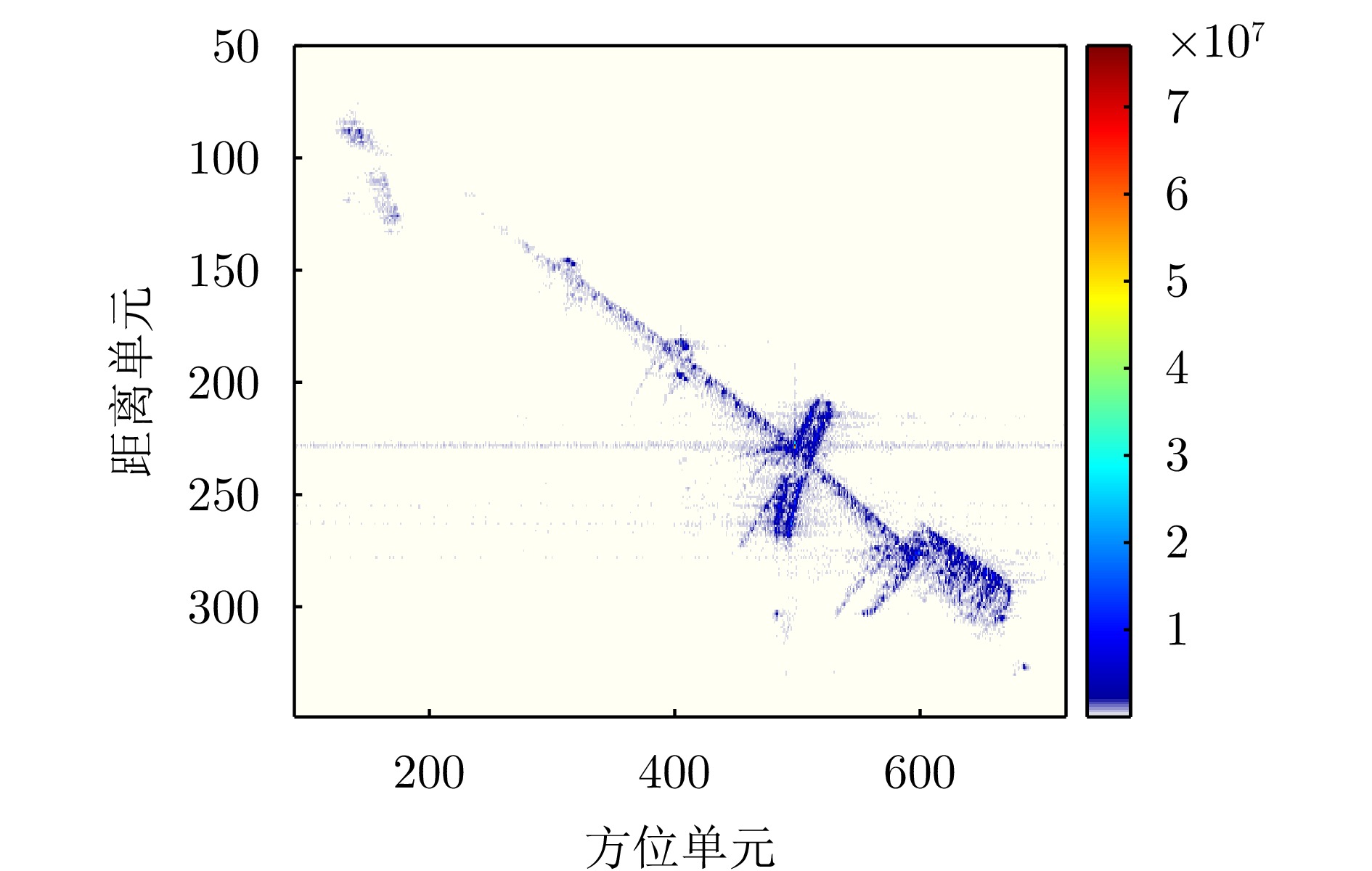
- Figure 38. RD imaging results of measured data after two-dimensional space-variation correction
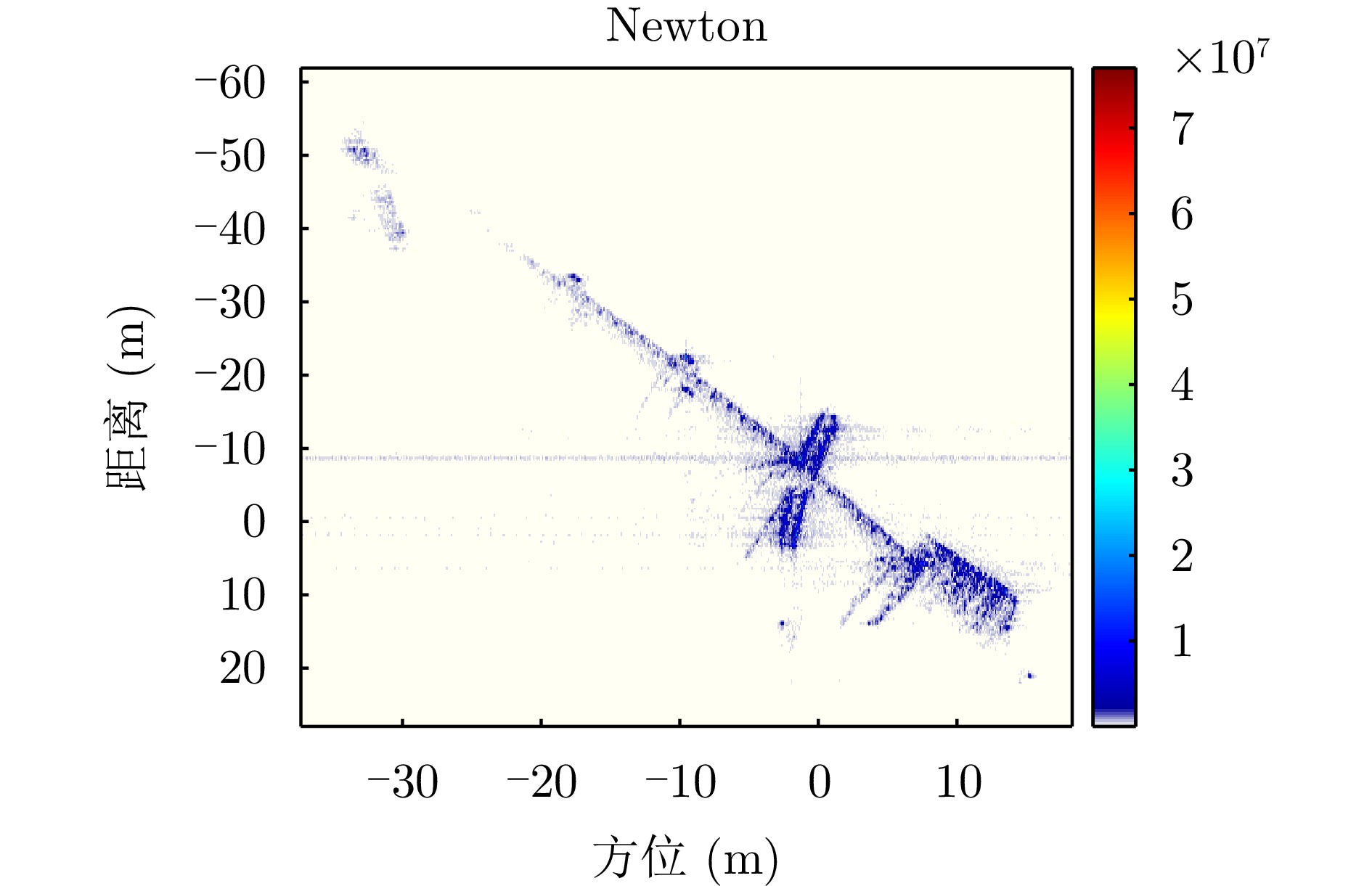
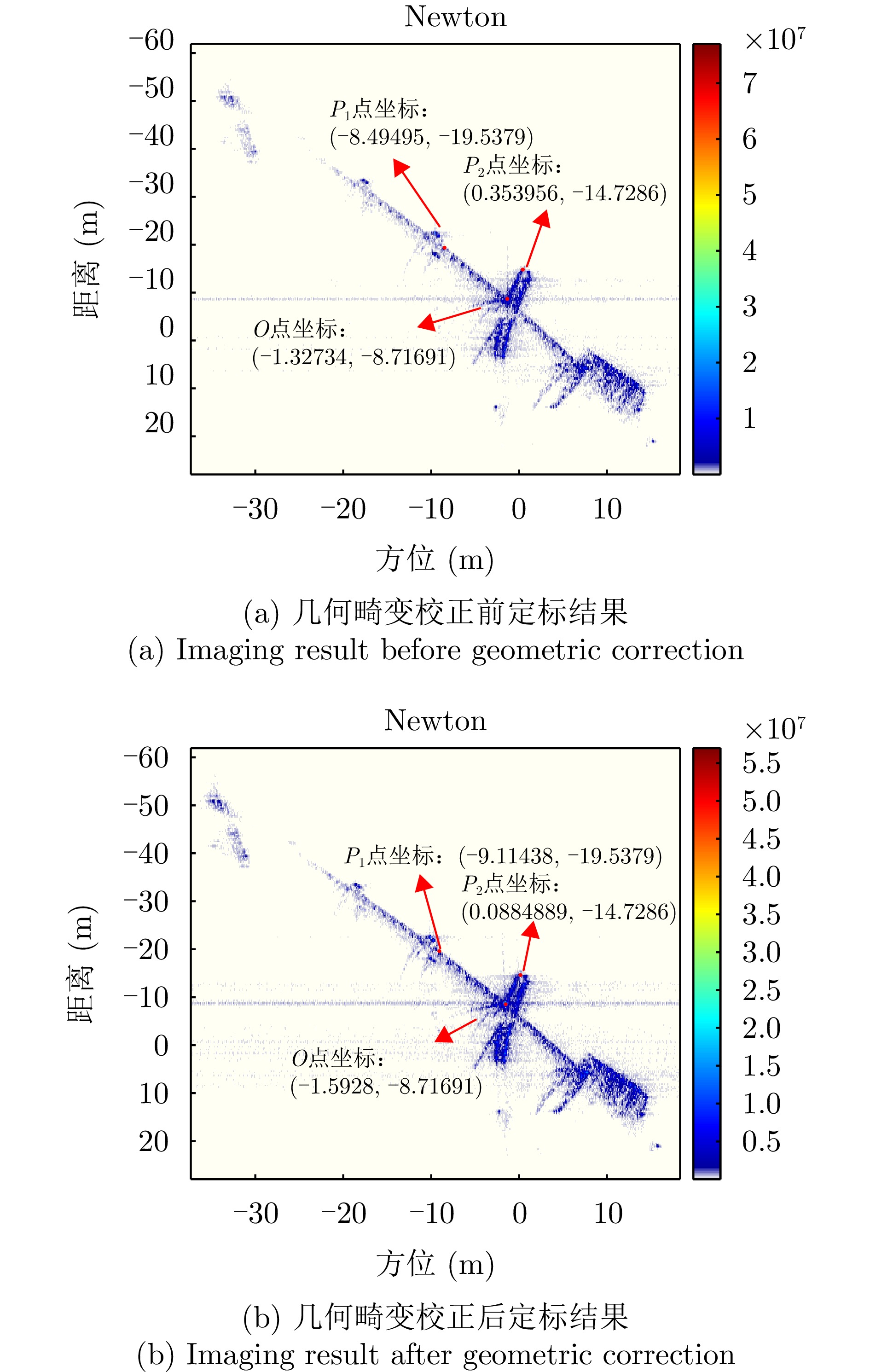
- Figure 39. Calibration results of measured data after two-dimensional space-variable correction
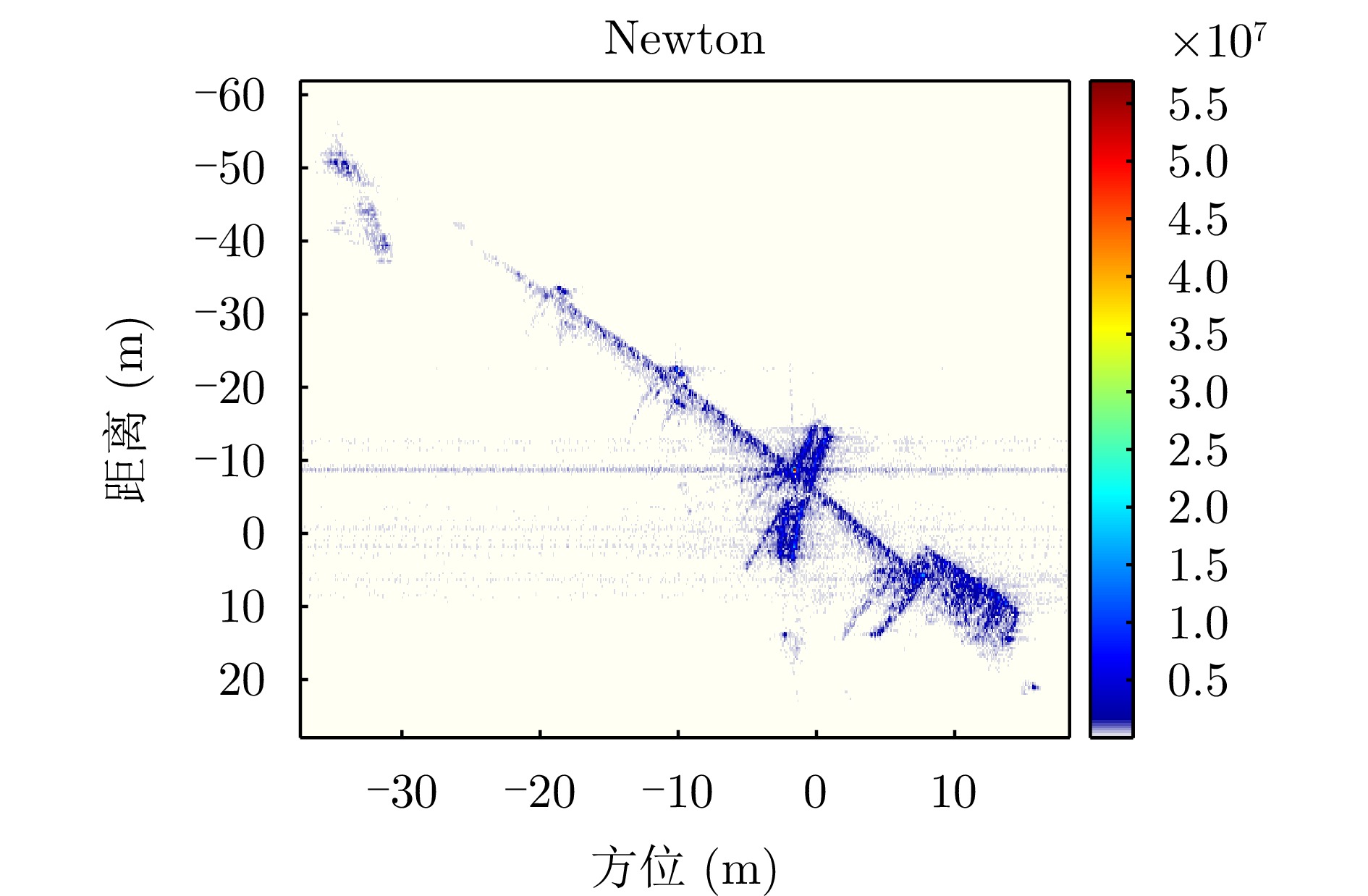
- Figure 40. Calibration results of measured data after geometric distortion correction
- Figure 41. The location map for the selection of marking points in the imaging results of the proposed method
- Figure 42. Calibration results of measured data after two-dimensional space-variable correction by contrast method
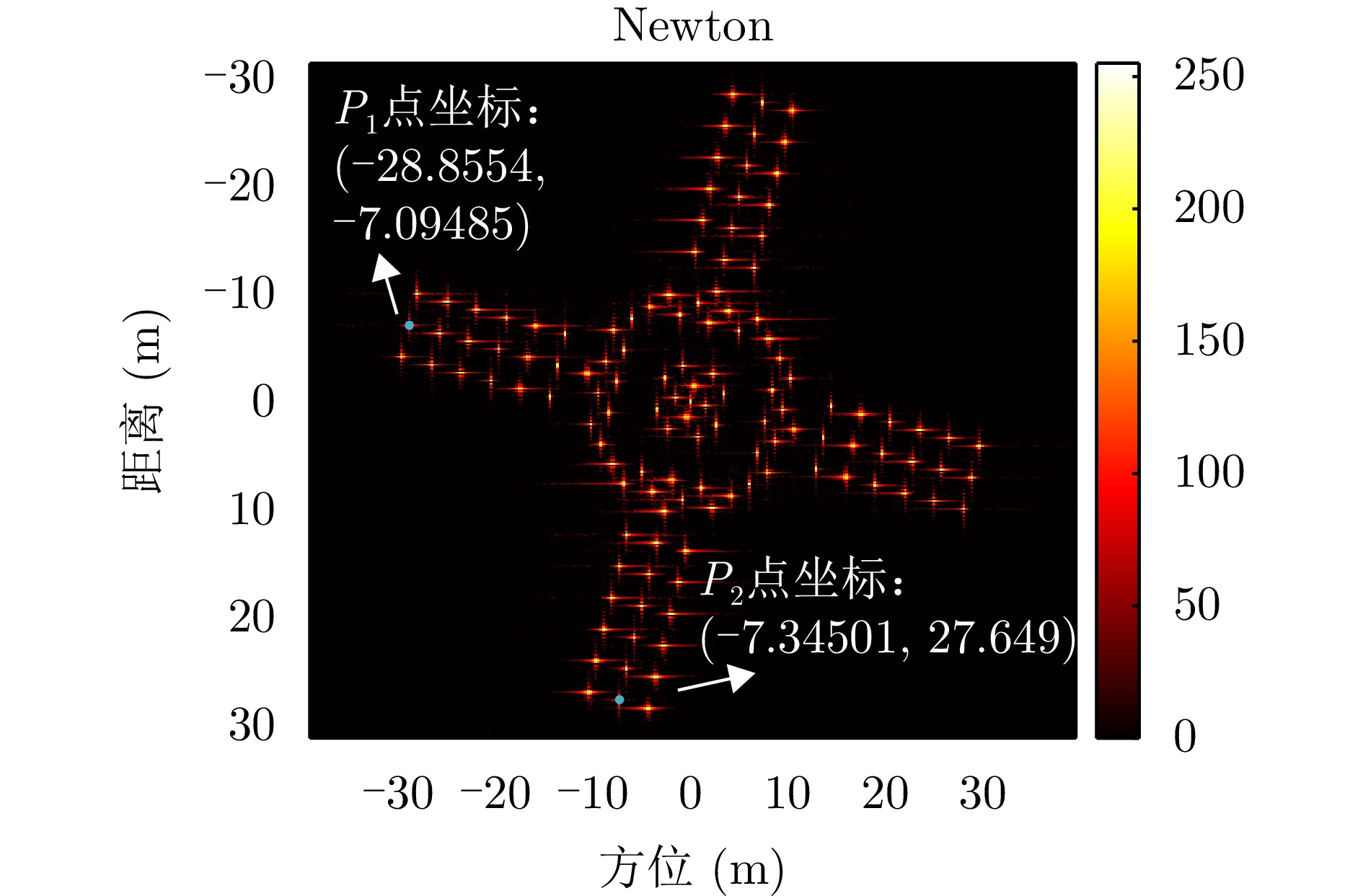
- Figure 43. Comparison method imaging results and marker point selection location map
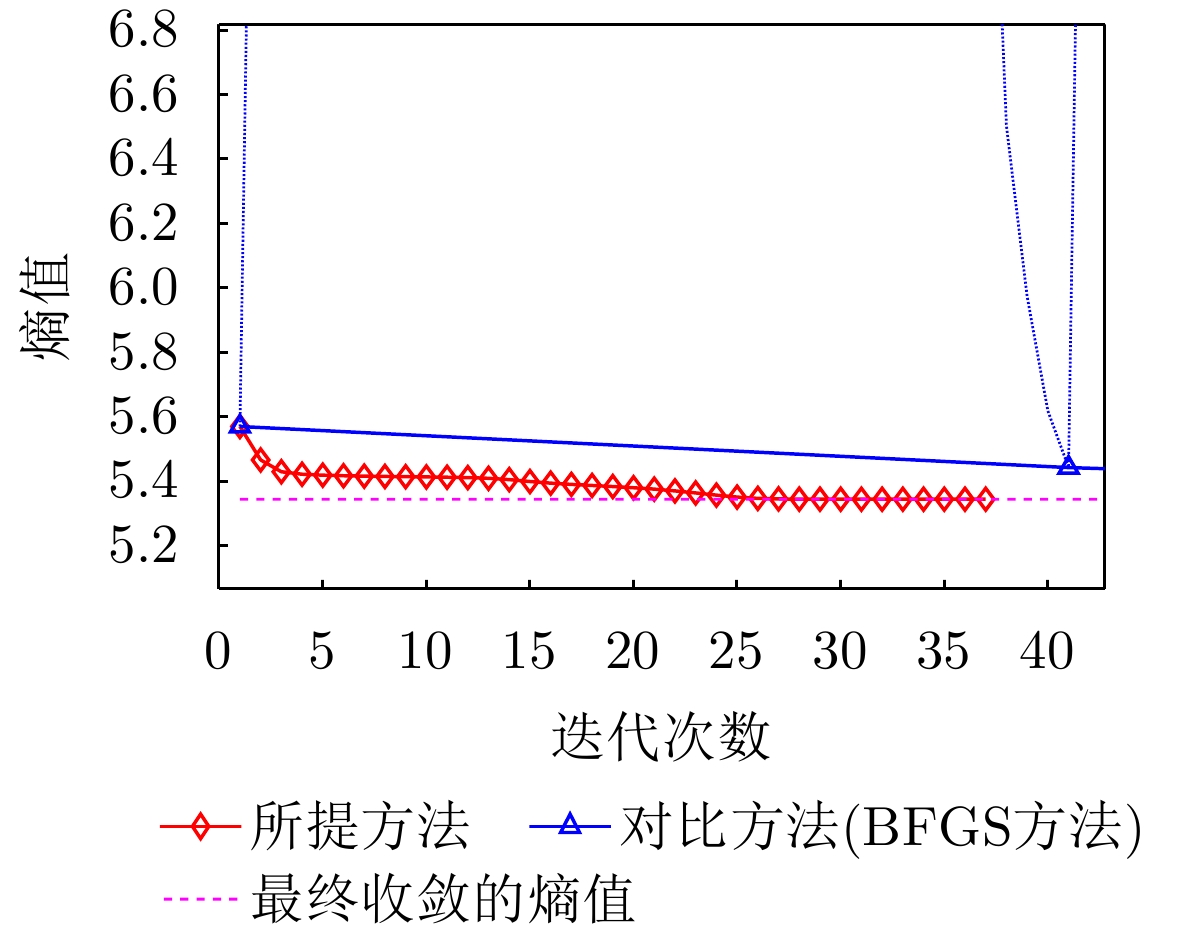
- Figure 44. Image entropy change curve of the proposed method and the comparison method for measured data
- Figure 45. Enlarged image of the entropy change curve of the proposed method for measured data


 Submit Manuscript
Submit Manuscript Peer Review
Peer Review Editor Work
Editor Work




 DownLoad:
DownLoad: