Turn off MathJax
Article Contents
Article Navigation >  Journal of Radars  > 2024  > Online First
WANG Xiaoge, LI Binbin, CHEN Hui, et al. Anti-ISRJ method based on intrapulse frequency-coded joint frequency modulation slope agile radar waveform[J]. Journal of Radars, in press. doi: 10.12000/JR24046
Citation: WANG Xiaoge, LI Binbin, CHEN Hui, et al. Anti-ISRJ method based on intrapulse frequency-coded joint frequency modulation slope agile radar waveform[J]. Journal of Radars, in press. doi: 10.12000/JR24046
shu

Anti-ISRJ Method Based on Intrapulse Frequency-coded Joint Frequency Modulation Slope Agile Radar Waveform

doi: 10.12000/JR24046
  • 1.

    Air Force Early Warning Academy, Wuhan 430019, China

  • 2.

    The People’s Liberation Army Unit 93209, Beijing 100094, China

Funds:  The National Natural Science Foundation of China (62001510, 62101593)
More Information
    Abstract
  • Interrupted Sampling Repeater Jamming (ISRJ) is a type of intrapulse coherent jamming that can form multiple realistic false targets that lead or lag behind the actual target, severely affecting radar detection. It is one of the hotspots of current research on electronic counter-countermeasures. To address this problem, an anti-ISRJ method based on an intrapulse frequency-coded joint Frequency Modulation (FM) slope agile waveform is proposed in this paper. In this method, the radar first transmits an intrapulse frequency-coded joint FM slope agile signal to improve the mutual coverability of subpulses by manipulating subpulse center frequency and FM slope agility. Next, the echo signal is divided into several slices according to the subpulse timing of the transmitted signal. Then, the Fuzzy C-Means (FCM) algorithm is used to classify the echo slices. Finally, the interference is suppressed via fractional-domain joint time domain filtering. Simulation results show that the FCM-based method can identify 100% of the interfered echo slices in a jammer synchronous sampling scenario when the Signal-to-Noise Ratio (SNR) is greater than −2.5 dB, and the Jamming-to-Signal Ratio (JSR) is greater than 5 dB. For high JSRs and low SNRs, the proposed method can effectively reduce the target energy loss and suppress the range sidelobes generated via residual interference. Moreover, the target detection probability after interference suppression exceeds 90% when JSR = 50 dB.

     

    • FullText(HTML)
  • loading
    • References(32)
  • [1]
    HANBALI S B S and KASTANTIN R. A review of self-protection deceptive jamming against chirp radars[J]. International Journal of Microwave and Wireless Technologies, 2017, 9(9): 1853–1861. doi: 10.1017/S1759078717000708.
    [2]
    SPARROW M J and CIKALO J. ECM techniques to counter pulse compression radar[P]. US, 7081846, 2006.
    [3]
    RIABUKHA V P, SEMENIAKA A V, KATIUSHYN Y A, et al. Pulse DRFM jamming formation and its mathematical simulation[C]. 2022 IEEE 2nd Ukrainian Microwave Week, Ukraine, 2022: 654–659. doi: 10.1109/UkrMW58013.2022.10037145.
    [4]
    WANG Xuesong, LIU Jiancheng, ZHANG Wenming, et al. Mathematic principles of interrupted-sampling repeater jamming (ISRJ)[J]. Science in China Series F: Information Sciences, 2007, 50(1): 113–123. doi: 10.1007/s11432-007-2017-y.
    [5]
    LAN Lan, MARINO A, AUBRY A, et al. GLRT-based adaptive target detection in FDA-MIMO radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(1): 597–613. doi: 10.1109/TAES.2020.3028485.
    [6]
    LAN Lan, XU Jingwei, LIAO Guisheng, et al. Suppression of mainbeam deceptive jammer with FDA-MIMO radar[J]. IEEE Transactions on Vehicular Technology, 2020, 69(10): 11584–11598. doi: 10.1109/TVT.2020.3014689.
    [7]
    全英汇, 方文, 沙明辉, 等. 频率捷变雷达波形对抗技术现状与展望[J]. 系统工程与电子技术, 2021, 43(11): 3126–3136. doi: 10.12305/j.issn.1001-506X.2021.11.11.

    QUAN Yinghui, FANG Wen, SHA Minghui, et al. Present situation and prospects of frequency agility radar waveform countermeasures[J]. Systems Engineering and Electronics, 2021, 43(11): 3126–3136. doi: 10.12305/j.issn.1001-506X.2021.11.11.
    [8]
    王晓戈, 陈辉, 倪萌钰, 等. 基于相位调制的雷达抗假目标干扰方法[J]. 系统工程与电子技术, 2021, 43(9): 2476–2483. doi: 10.12305/j.issn.1001-506X.2021.09.14.

    WANG Xiaoge, CHEN Hui, NI Mengyu, et al. Radar anti-false target jamming method based on phase modulation[J] Systems Engineering and Electronics, 2021, 43(9): 2476–2483. doi: 10.12305/j.issn.1001-506X.2021.09.14.
    [9]
    YAN Yifei, CHEN Hao, and SU Junhai. Overview on anti-jamming technology in main lobe of radar[C]. 2021 IEEE 4th International Conference on Automation, Electronics and Electrical Engineering, Shenyang, China, 2021: 67–71. doi: 10.1109/AUTEEE52864.2021.9668666.
    [10]
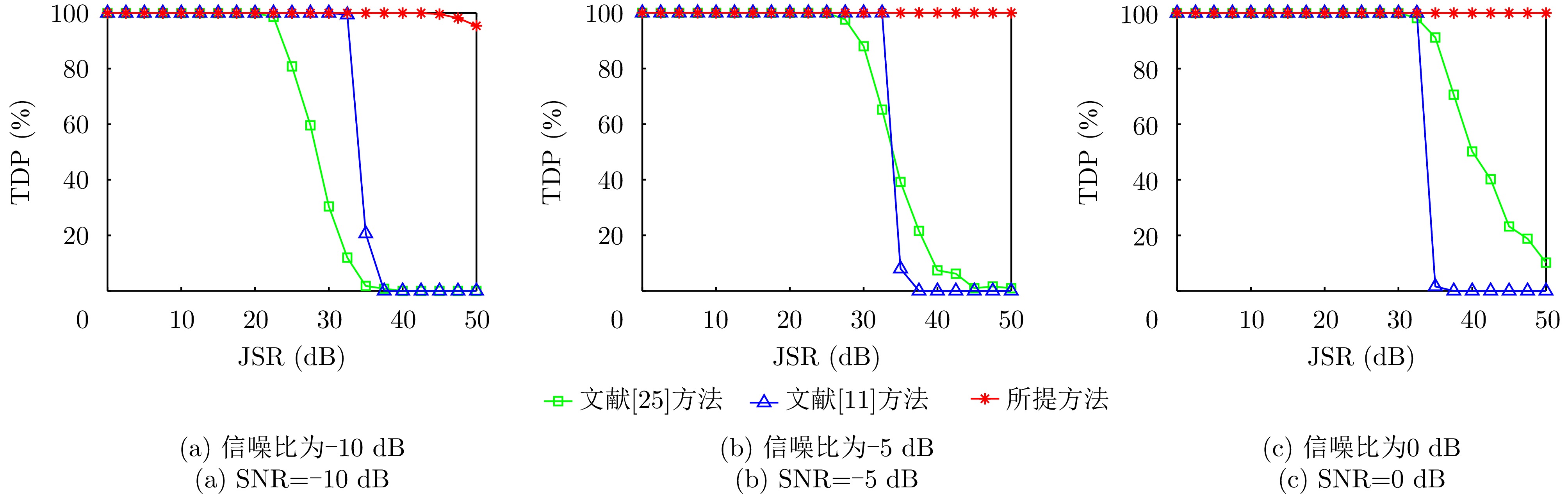
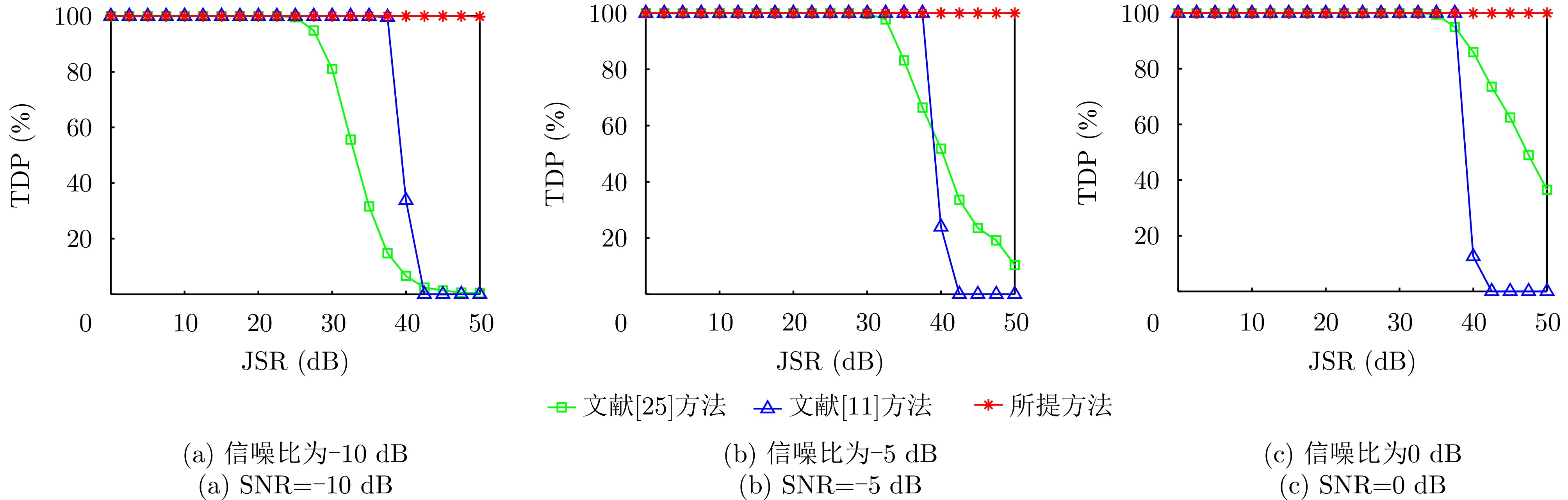
    张建中, 穆贺强, 文树梁, 等. 基于LFM分段脉冲压缩的抗间歇采样转发干扰方法[J]. 电子与信息学报, 2019, 41(7): 1712–1720. doi: 10.11999/JEIT180851.

    ZHANG Jianzhong, MU Heqiang, WEN Shuliang, et al. Anti-intermittent sampling repeater jamming method based on LFM segmented pulse compression[J]. Journal of Electronics & Information Technology, 2019, 41(7): 1712–1720. doi: 10.11999/JEIT180851.
    [11]
    万鹏程, 白渭雄, 付孝龙. 基于FrFT的LFM间歇采样转发干扰对抗方法[J]. 火力与指挥控制, 2018, 43(10): 35–39. doi: 10.3969/j.issn.1002-0640.2018.10.007.

    WAN Pengcheng, BAI Weixiong, and FU Xiaolong. Fractional fourier transform-based LFM radars for countering interrupted-sampling repeater jamming[J]. Fire Control & Command Control, 2018, 43(10): 35–39. doi: 10.3969/j.issn.1002-0640.2018.10.007.
    [12]
    CHEN Jian, WU Wenzhen, XU Shiyou, et al. Band pass filter design against interrupted-sampling repeater jamming based on time-frequency analysis[J]. IET Radar, Sonar & Navigation, 2019, 13(10): 1646–1654. doi: 10.1049/iet-rsn.2018.5658.
    [13]
    YUAN Hui, WANG Chunyang, LI Xin, et al. A method against interrupted-sampling repeater jamming based on energy function detection and band-pass filtering[J]. International Journal of Antennas and Propagation, 2017, 2017: 6759169. doi: 10.1155/2017/6759169.
    [14]
    周超, 刘泉华, 胡程. 间歇采样转发式干扰的时频域辨识与抑制[J]. 雷达学报, 2019, 8(1): 100–106. doi: 10.12000/JR18080.

    ZHOU Chao, LIU Quanhua, and HU Cheng. Time-frequency analysis techniques for recognition and suppression of interrupted sampling repeater jamming[J]. Journal of Radars, 2019, 8(1): 100–106. doi: 10.12000/JR18080.
    [15]
    盖季妤, 姜维, 张凯翔, 等. 基于差分特征的间歇采样转发干扰辨识与抑制方法[J]. 雷达学报, 2023, 12(1): 186–196. doi: 10.12000/JR22058.

    GAI Jiyu, JIANG Wei, ZHANG Kaixiang, et al. A method for interrupted-sampling repeater jamming identification and suppression based on differential features[J]. Journal of Radars, 2023, 12(1): 186–196. doi: 10.12000/JR22058.
    [16]
    ZHOU Chao, LIU Quanhua, and CHEN Xinliang. Parameter estimation and suppression for DRFM-based interrupted sampling repeater jammer[J]. IET Radar, Sonar & Navigation, 2018, 12(1): 56–63. doi: 10.1049/iet-rsn.2017.0114.
    [17]
    刘孟斐, 陈吉源, 潘小义, 等. 基于信息熵的分段脉压间歇采样干扰抑制[J]. 雷达科学与技术, 2023, 21(3): 264–272, 281. doi: 10.3969/j.issn.1672-2337.2023.03.004.

    LIU Mengfei, CHEN Jiyuan, PAN Xiaoyi, et al. Interrupted sampling jamming suppression based on piecewise pulse compression and shannon entropy[J]. Radar Science and Technology, 2023, 21(3): 264–272, 281. doi: 10.3969/j.issn.1672-2337.2023.03.004.
    [18]
    LU Lu and GAO Meiguo. An improved sliding matched filter method for interrupted sampling repeater jamming suppression based on jamming reconstruction[J]. IEEE Sensors Journal, 2022, 22(10): 9675–9684. doi: 10.1109/JSEN.2022.3159561.
    [19]
    张建中, 穆贺强, 文树梁, 等. 基于脉内步进LFM波形的抗间歇采样转发干扰方法[J]. 系统工程与电子技术, 2019, 41(5): 1013–1020. doi: 10.3969/j.issn.1001-506X.2019.05.12.

    ZHANG Jianzhong, MU Heqiang, WEN Shuliang, et al. Anti interrupted-sampling repeater jamming method based on stepped LFM waveform[J]. Systems Engineering and Electronics, 2019, 41(5): 1013–1020. doi: 10.3969/j.issn.1001-506X.2019.05.12.
    [20]
    ZHOU Kai, LI Dexin, SU Yi, et al. Joint design of transmit waveform and mismatch filter in the presence of interrupted sampling repeater jamming[J]. IEEE Signal Processing Letters, 2020, 27: 1610–1614. doi: 10.1109/LSP.2020.3021667.
    [21]
    周凯, 何峰, 粟毅. 一种快速抗间歇采样转发干扰波形和滤波器联合设计算法[J]. 雷达学报, 2022, 11(2): 264–277. doi: 10.12000/JR22015.

    ZHOU Kai, HE Feng, and SU Yi. Fast algorithm for joint waveform and filter design against interrupted sampling repeater jamming[J]. Journal of Radars, 2022, 11(2): 264–277. doi: 10.12000/JR22015.
    [22]
    WANG Fulai, LI Nanjun, PANG Chen, et al. Complementary sequences and receiving filters design for suppressing interrupted sampling repeater jamming[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4022305. doi: 10.1109/LGRS.2022.3156164.
    [23]
    董淑仙, 吴耀君, 方文, 等. 频率捷变雷达联合模糊C均值抗间歇采样干扰[J]. 雷达学报, 2022, 11(2): 289–300. doi: 10.12000/JR21205.

    DONG Shuxian, WU Yaojun, FANG Wen, et al. Anti-interrupted sampling repeater jamming method based on frequency-agile radar joint fuzzy C-means[J]. Journal of Radars, 2022, 11(2): 289–300. doi: 10.12000/JR21205.
    [24]
    刘智星, 杜思予, 吴耀君, 等. 脉间-脉内捷变频雷达抗间歇采样干扰方法[J]. 雷达学报, 2022, 11(2): 301–312. doi: 10.12000/JR22001.

    LIU Zhixing, DU Siyu, WU Yaojun, et al. Anti-interrupted sampling repeater jamming method for interpulse and intrapulse frequency-agile radar[J]. Journal of Radars, 2022, 11(2): 301–312. doi: 10.12000/JR22001.
    [25]
    杜思予, 刘智星, 吴耀君, 等. 频率捷变波形联合时频滤波器抗间歇采样转发干扰[J]. 系统工程与电子技术, 2023, 45(12): 3819–3827. doi: 10.12305/j.issn.1001-506X.2023.12.11.

    DU Siyu, LIU Zhixing, WU Yaojun, et al. Frequency agility waveform combined with time-frequency filter to suppress interrupted-sampling repeater jamming[J]. Systems Engineering and Electronics, 2023, 45(12): 3819–3827. doi: 10.12305/j.issn.1001-506X.2023.12.11.
    [26]
    牛闯, 林强, 段敏, 等. 脉内频率-时延捷变雷达抗间歇采样转发干扰方法[J]. 系统工程与电子技术, 2024, 46(5): 1583–1598. doi: 10.12305/j.issn.1001-506X.2024.05.13.

    NIU Chuang, LIN Qiang, DUAN Min, et al. Anti-interrupted sampling and repeater jamming method for intra-pulse frequency and time delay agile radar[J]. Systems Engineering and Electronics, 2024, 46(5): 1583–1598. doi: 10.12305/j.issn.1001-506X.2024.05.13.
    [27]
    张亮, 王国宏, 张翔宇, 等. 基于分数阶字典的间歇采样转发干扰自适应抑制算法[J]. 系统工程与电子技术, 2020, 42(7): 1439–1448. doi: 10.3969/j.issn.1001-506X.2020.07.02.

    ZHANG Liang, WANG Guohong, ZHANG Xiangyu, et al. Interrupted-sampling repeater jamming adaptive suppression algorithm based on fractional dictionary[J]. Systems Engineering and Electronics, 2020, 42(7): 1439–1448. doi: 10.3969/j.issn.1001-506X.2020.07.02.
    [28]
    BAHER S and HANBALI S. Countering self-protection smeared spectrum jamming against chirp radars[J]. IET Radar, Sonar & Navigation, 2021, 15(4): 382–389. doi: 10.1049/rsn2.12046.
    [29]
    BEZDEK J C, EHRLICH R, and FULL W. FCM: The fuzzy c-means clustering algorithm[J]. Computers & Geosciences, 1984, 10(2/3): 191–203. doi: 10.1016/0098-3004(84)90020-7.
    [30]
    WANG Cong, ZHOU Mengchu, PEDRYCZ W, et al. Comparative study on noise-estimation-based fuzzy C-means clustering for image segmentation[J]. IEEE Transactions on Cybernetics, 2024, 54(1): 241–253. doi: 10.1109/TCYB.2022.3217897.3.
    [31]
    ALMEIDA L B. The fractional Fourier transform and time-frequency representations[J]. IEEE Transactions on Signal Processing, 1994, 42(11): 3084–3091. doi: 10.1109/78.330368.
    [32]
    WANG Xiaoge, CHEN Hui, LIU Weijian, et al. Echo preprocessing-based smeared spectrum interference suppression[J]. Electronics, 2023, 12(17): 3690. doi: 10.3390/electronics12173690.
    • Relative Articles
    • Supplements(0)
    • Cited By
  • 加载中

Catalog

    通讯作者: 陈斌, bchen63@163.com
    • 1. 

      沈阳化工大学材料科学与工程学院 沈阳 110142

    1. 本站搜索
    2. 百度学术搜索
    3. 万方数据库搜索
    4. CNKI搜索
    Get Citation
    PDF
    XML
    Article views(69) PDF downloads(12) Cited by()
    Proportional views
    Related

    京ICP备20021838号-8   Supported by: Beijing Renhe Information Technology Co. Ltd     百度统计

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return