Submit Manuscript
Peer Review
Editor Work
| Citation: | WANG Ding, YIN Jiexin, GAO Lu, et al. A novel cooperative positioning method for over-the-horizon shortwave emitter based on two-dimensional direction-of-arrival and time-difference-of-arrival measurements[J]. Journal of Radars, 2024, 13(6): 1135–1156. doi: 10.12000/JR24136
|
A Novel Cooperative Positioning Method for Over-the-horizon Shortwave Emitter Based on Two-dimensional Direction-of-arrival and Time-difference-of-arrival Measurements
DOI: 10.12000/JR24136
More Information-
Abstract
To reduce the large over-the-horizon localization errors of long-range shortwave emitter, a novel cooperative positioning method is proposed. This method combines two-Dimensional (2D) Direction-Of-Arrival (DOA) and Time-Difference-Of-Arrival (TDOA) measurements under scenarios in which observation stations can simultaneously obtain the two types of parameters. Initially, based on the single-hop ionospheric virtual height model, the nonlinear measurement models of 2D DOA and TDOA are established for over-the-horizon shortwave localization. Subsequently, by combining the over-the-horizon localization geometric and algebraic model, the two types of nonlinear measurement equations are successively transformed into the corresponding pseudo-linear measurement equations. On this basis, a novel two-stage cooperative positioning method is proposed without iteration. In the first stage, the closed-form solution of the target position vector is obtained by solving the roots of a sixth-order polynomial. In the second stage, an equality-constrained optimization problem is established to refine the localization result obtained in the first stage, yielding a more accurate target position estimate using the Lagrange multiplier technique. In addition, the estimation performance of the proposed cooperative positioning method is theoretically analyzed based on the constrained error perturbation theory, and the asymptotic efficiency of the new estimator is proved. Meanwhile, the influence of the altitude information error of the emitter on the positioning accuracy is quantitatively analyzed by applying the theory of constrained error perturbation, and the maximum threshold value of this error, which ensures that the constrained solution remains better than the unconstrained one, is deduced. Simulation results show that the newly proposed method can achieve significant cooperative gain. -
-
References
[1] 王金龙, 陈瑾, 徐煜华. 短波通信技术研究进展与发展需求[J]. 陆军工程大学学报, 2022, 1(1): 1–7. doi: 10.12018/j.issn.2097-0730.20211218001.WANG Jinlong, CHEN Jin, and XU Yuhua. On research advances and development requirements of high frequency communication technologies[J]. Journal of Army Engineering University of PLA, 2022, 1(1): 1–7. doi: 10.12018/j.issn.2097-0730.20211218001.[2] PANG Feifei, DOĞANÇAY K, NGUYEN N H, et al. AOA pseudolinear target motion analysis in the presence of sensor location errors[J]. IEEE Transactions on Signal Processing, 2020, 68: 3385–3399. doi: 10.1109/TSP.2020.2998896.[3] YAN Qingli, CHEN Jianfeng, ZHANG Jie, et al. Robust AOA-based source localization using outlier sparsity regularization[J]. Digital Signal Processing, 2021, 112: 103006. doi: 10.1016/j.dsp.2021.103006.[4] SUN Yimao, HO K C, and WAN Qun. Eigenspace solution for AOA localization in modified polar representation[J]. IEEE Transactions on Signal Processing, 2020, 68: 2256–2271. doi: 10.1109/TSP.2020.2981773.[5] CHEN Xianjing, WANG Gang, and HO K C. Semidefinite relaxation method for unified near-field and far-field localization by AOA[J]. Signal Processing, 2021, 181: 107916. doi: 10.1016/j.sigpro.2020.107916.[6] ZOU Yanbin, WU Liehu, FAN Jingna, et al. A convergent iteration method for 3-D AOA localization[J]. IEEE Transactions on Vehicular Technology, 2023, 72(6): 8267–8271. doi: 10.1109/TVT.2023.3242054.[7] CHEN Yonghua, YU Hua, LI Jie, et al. Three-dimensional source localization based on 1-D AOA measurements: Low-complexity and effective estimator[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 9510615. 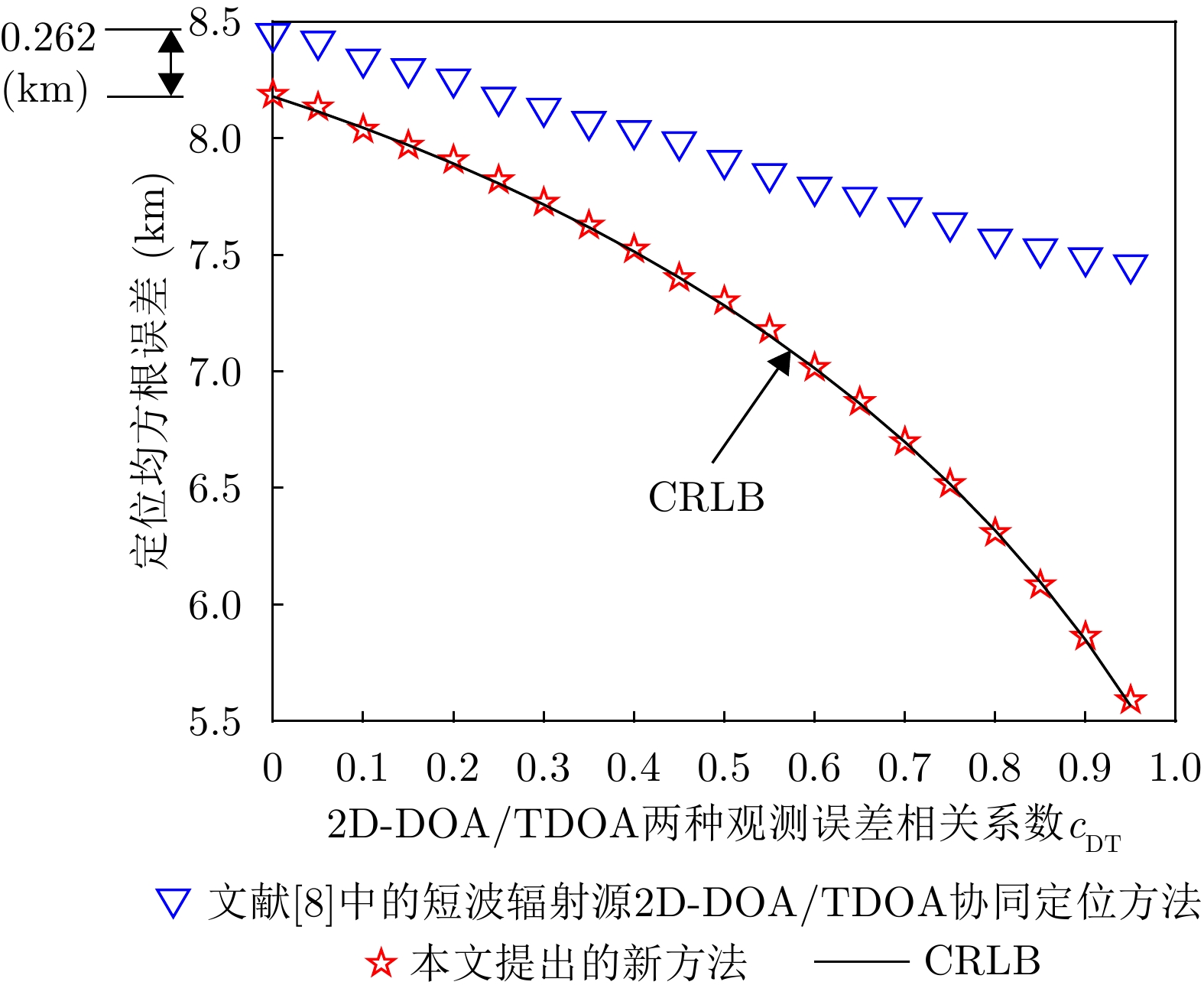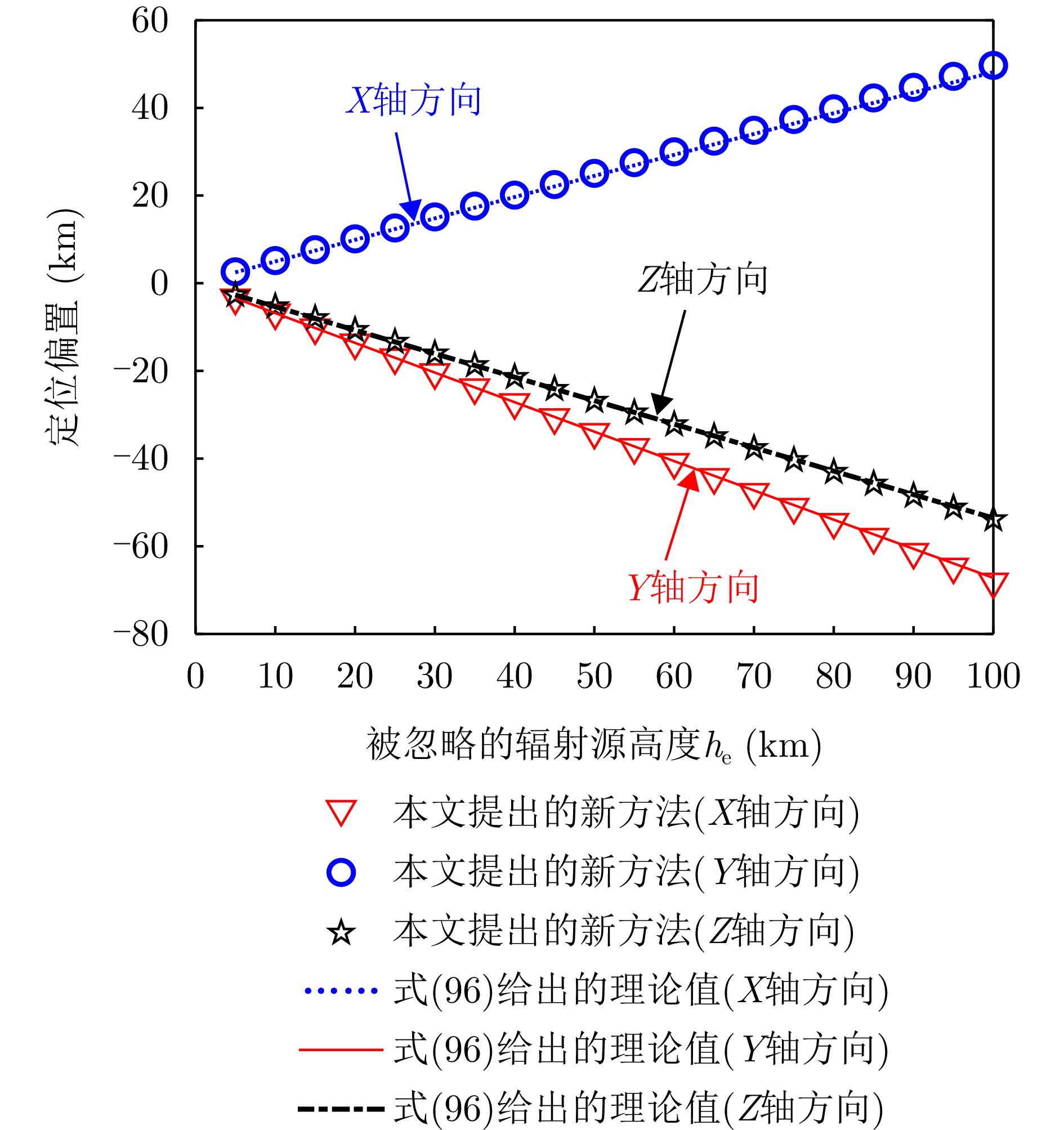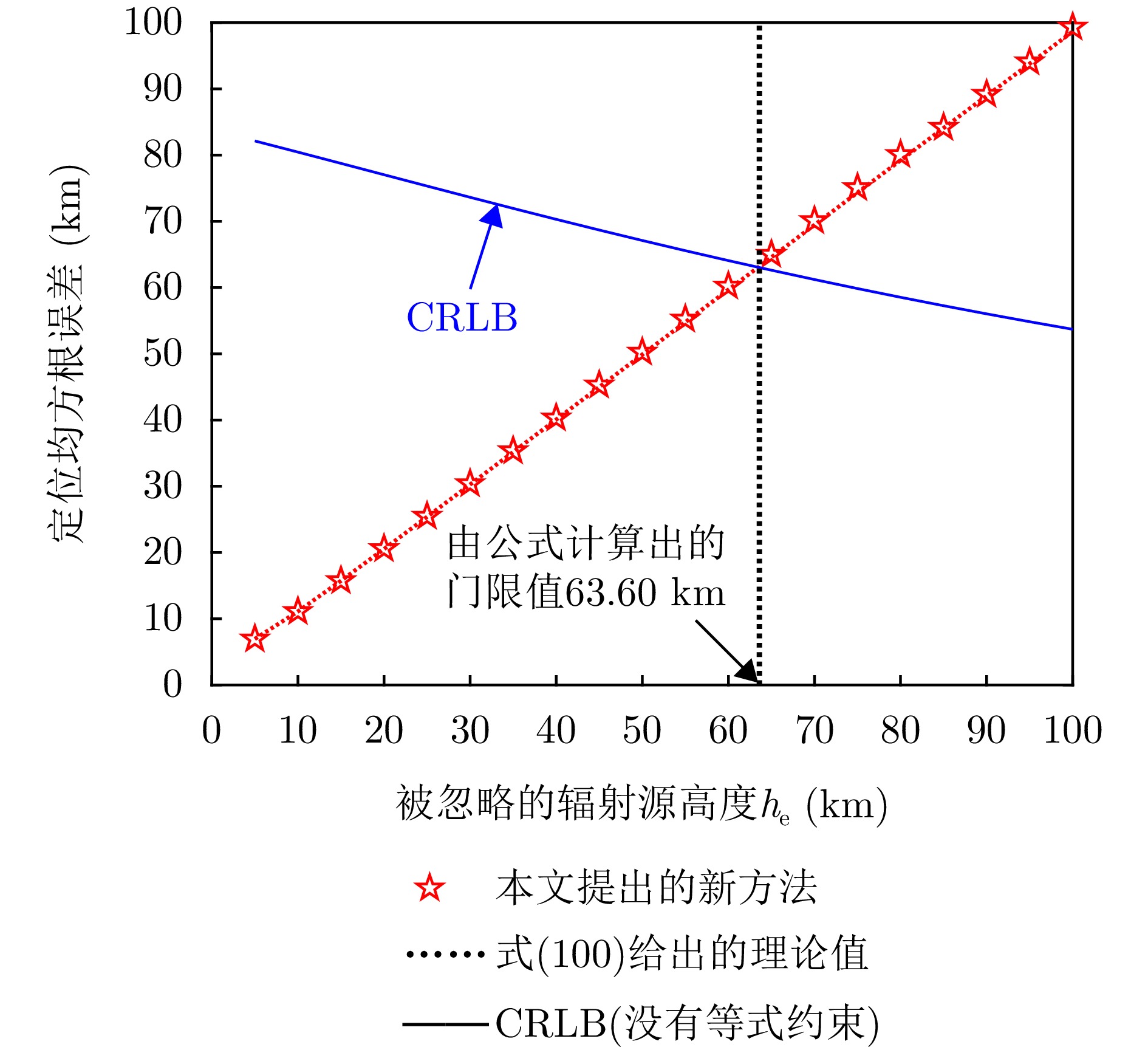doi: 10.1109/TIM.2023.3298680.[8] 王鼎, 尹洁昕, 朱中梁. 针对超视距短波辐射源的测角与测时差协同定位方法[J]. 中国科学: 信息科学, 2022, 52(11): 1942–1973. doi: 10.1360/SSI-2021-0331.WANG Ding, YIN Jiexin, and ZHU Zhongliang. Novel cooperative localization method of over-the-horizon shortwave emitters based on direction-of-arrival and time-difference-of-arrival measurements[J]. Scientia Sinica Informationis, 2022, 52(11): 1942–1973. doi: 10.1360/SSI-2021-0331.[9] JIANG Linqiang, TANG Tao, WU Zhidong, et al. An iterative method for short-wave source localization using direction of arrival measurements[C]. The 18th Chinese National Symposium on Radio Propogation, Qingdao, China, 2023: 595–600. doi: 10.26914/c.cnkihy.2023.050995.[10] 贺承杰. 天波超视距雷达海面目标定位方法研究[J]. 雷达科学与技术, 2020, 18(5): 568–572, 578. doi: 10.3969/j.issn.1672-2337.2020.05.017.HE Chengjie. Surface target location method of sky wave over-the-horizon radar[J]. Radar Science and Technology, 2020, 18(5): 568–572, 578. doi: 10.3969/j.issn.1672-2337.2020.05.017.[11] GUO Fucheng and HO K C. A quadratic constraint solution method for TDOA and FDOA localization[C]. 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 2011: 2588–2591. doi: 10.1109/ICASSP.2011.5947014.[12] LI Qian, CHEN Baixiao, and YANG Minglei. Improved two-step constrained total least-squares TDOA localization algorithm based on the alternating direction method of multipliers[J]. IEEE Sensors Journal, 2020, 20(22): 13666–13673. doi: 10.1109/JSEN.2020.3004235.[13] 王鼎, 尹洁昕, 高路, 等. 一种同步时钟偏差和传感器位置误差存在下的TDOA定位新方法[J]. 航空学报, 2022, 43(7): 325405. doi: 10.7527/S1000-6893.2021.25405.WANG Ding, YIN Jiexin, GAO Lu, et al. A novel method for TDOA localization in presence of synchronization clock bias and sensor position uncertainty[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(7): 325405. doi: 10.7527/S1000-6893.2021.25405.[14] JAIN A, PAGANI P, FLEURY R, et al. Accurate time difference of arrival estimation for HF radio broadcast signals[J]. Microwave and Optical Technology Letters, 2018, 60(6): 1406–1410. doi: 10.1002/mop.31178.[15] WANG Ting, HONG Xueli, LIU Wen, et al. Geolocation of unknown emitters using TDOA of path rays through the ionosphere by multiple coordinated distant receivers[C]. 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, Canada, 2018: 3509–3513. doi: 10.1109/ICASSP.2018.8462106.[16] HUANG Sen, PUN Y M, SO A M C, et al. A provably convergent projected gradient-type algorithm for TDOA-based geolocation under the quasi-parabolic ionosphere model[J]. IEEE Signal Processing Letters, 2020, 27: 1335–1339. doi: 10.1109/LSP.2020.3010676.[17] XIONG Wenxin, SCHINDELHAUER C, and SO H C. Globally optimized TDOA high-frequency source localization based on quasi-parabolic ionosphere modeling and collaborative gradient projection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(1): 580–590. doi: 10.1109/TAES.2022.3185971.[18] YANG Lijuan, GAO Huotao, LING Yun, et al. Localization method of wide-area distribution multistatic sky-wave over-the-horizon radar[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19(1): 3500305. doi: 10.1109/LGRS.2020.3018322.[19] 李琛, 周晨, 王君明, 等. 基于经验电离层模型的短波时差定位理论分析[J]. 系统工程与电子技术, 2023, 45(7): 1911–1919. doi: 10.12305/j.issn.1001-506X.2023.07.01.LI Chen, ZHOU Chen, WANG Junming, et al. Theoretical analysis of shortwave TDOA geolocation based on empirical ionospheric model[J]. Systems Engineering and Electronics, 2023, 45(7): 1911–1919. doi: 10.12305/j.issn.1001-506X.2023.07.01.[20] JAIN A, PAGANI P, FLEURY R, et al. Efficient time domain HF geolocation using multiple distributed receivers[C]. The 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 2017: 1852–1856. doi: 10.23919/EuCAP.2017.7928069.[21] JAIN A, PAGANI P, FLEURY R, et al. HF source geolocation using an operational TDoA receiver network: Experimental results[J]. IEEE Antennas and Wireless Propagation Letters, 2018, 17(9): 1643–1647. doi: 10.1109/LAWP.2018.2860459.[22] XU Chen, CAI Hongtao, GAO Shunzu, et al. A method for HF skywave source geolocation in unknown ionosphere environments and experimental results[J]. IEEE Antennas and Wireless Propagation Letters, 2023, 22(5): 1059–1063. doi: 10.1109/LAWP.2022.3232399.[23] ZHANG Tienan, MAO Xingpeng, ZHAO Chunlei, et al. A novel grid selection method for sky-wave time difference of arrival localisation[J]. IET Radar, Sonar & Navigation, 2019, 13(4): 538–549. doi: 10.1049/iet-rsn.2018.5308.[24] ZHANG Fengrui, SUN Yimao, and WAN Qun. Calibrating the error from sensor position uncertainty in TDOA-AOA localization[J]. Signal Processing, 2020, 166: 107213. doi: 10.1016/j.sigpro.2019.07.006.[25] KANG XU, WANG Dejiang, SHAO Yu, et al. An efficient hybrid multi-station TDOA and single-station AOA localization method[J]. IEEE Transactions on Wireless Communications, 2023, 22(8): 5657–5670. doi: 10.1109/TWC.2023.3235753.[26] XU Zhezhen, LI Hui, YANG Kunde, et al. A robust constrained total least squares algorithm for three-dimensional target localization with hybrid TDOA-AOA measurements[J]. Circuits, Systems, and Signal Processing, 2023, 42(6): 3412–3436. doi: 10.1007/s00034-022-02270-6.[27] CAO Yalu, LI Peng, LI Jinzhou, et al. A new iterative algorithm for geolocating a known altitude target using TDOA and FDOA measurements in the presence of satellite location uncertainty[J]. Chinese Journal of Aeronautics, 2015, 28(5): 1510–1518. doi: 10.1016/j.cja.2015.08.015.[28] PEI Yuhao, WU Guizhou, and GUO Fucheng. Geolocation a known-altitude moving source by TDOA and FDOA measurements[J]. Electronics Letters, 2022, 58(13): 514–516. doi: 10.1049/ell2.12508.[29] MORE J J. Generalizations of the trust region problem[J]. Optimization Methods and Software, 1993, 2(3/4): 189–209. doi: 10.1080/10556789308805542.[30] HO K C and CHAN Y T. Geolocation of a known altitude object from TDOA and FDOA measurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(3): 770–783. doi: 10.1109/7.599239. -
Proportional views
- Publishing Ethics
- Journal Insights
- Abstracting & Indexing
- Peer Review Policies
- Guide for Authors
- Conference
- ISSN 2095-283X (Print)ISSN 2097-339X (Online)
- CN 10-1030/TN
- CODEN LXEUAO
About Journal
- Sponsor: China Radio Detection and Ranging Industry Association (CRIA)
- Phone: 010-58887062
- Email：radars@aircas.ac.cn
- Publisher: Leida Xuebao Bianjibu (Editorial office of the Journal of Radars)
Contacts Us
京ICP备20021838号-8
Supported by: Beijing Renhe Information Technology Co. Ltd
Export File
Citation
Format
Content
DownLoad:
- Figure 1. Schematic diagram of 2D-DOA and TDOA geometric models of shortwave radiation source
- Figure 2. Scatter plot of positioning results and elliptical curve of positioning errors in the X-Y plane in the ECEF coordinate system
-
Figure 3. Correct root, the closest false root to the correct root and threshold value
$ - 1/{\kappa _{\max }}$ - Figure 4. Localization RMSE as a function of parameter δ1
- Figure 5. Localization RMSE as a function of parameter δ2
- Figure 6. Localization RMSE as a function of parameter δ3
- Figure 7. Localization RMSE as a function of correlation coefficient cDT
- Figure 8. Localization bias as a function of height he
- Figure 9. Localization RMSE as a function of height he