Submit Manuscript
Peer Review
Editor Work
| Citation: | MOU Xiaoqian, CHEN Xiaolong, GUAN Jian, et al. Clutter suppression and marine target detection for radar images based on INet[J]. Journal of Radars, 2020, 9(4): 640–653. doi: 10.12000/JR20090
|
Clutter Suppression and Marine Target Detection for Radar Images Based on INet
DOI: 10.12000/JR20090
More Information-
Abstract
A marine radar device is a major navigation tool for boaters and ships. The images produced by marine radars detect not only hard targets such as ships and coastlines, but also reflections from the sea surface, known as sea clutter. The strong sea clutter and the complex characteristics of marine targets result in transmission of weak echo signals of the images to the radar, which makes difficult for radars to distinguish and analyze. So, effective sea clutter suppression and robust, fast target detection mechanisms are needed for radar to detect marine targets efficiently. However, the existing marine target detection algorithms have limited performance for target detection under complex environments, and have poor adaptability to environment and target characteristics. In this paper, an Integrated Network (INet) for clutter suppression and target detection algorithm is proposed and designed to optimize the signals received from the targets. The layer normalization algorithm integrated with transfer function is used to extract key target features, and the spatial attention network is used to suppress the clutter and to enhance the target signals, and a local cross-scale residual network is built to ensure the weightlessness of the system and accuracy of the detection network. Based on the echo data collected by the navigation radar under various observation conditions, radar images with marine target dataset were constructed. INet was optimized through pre-training of the model and inter-frame accumulation of Plan Position Indicator (PPI) images to obtain the Optimized INet (O-INet). The measured data were verified, tested, and compared with data obtained through various algorithms such as YOLOv3, YOLOv4, two-parameter CFAR, and two-dimensional CA-CFAR. The results obtained prove that the proposed method has superior advantages over other methods in improving detection probability, reducing false alarm rate, and strong generalization ability under complex conditions. -
-
References
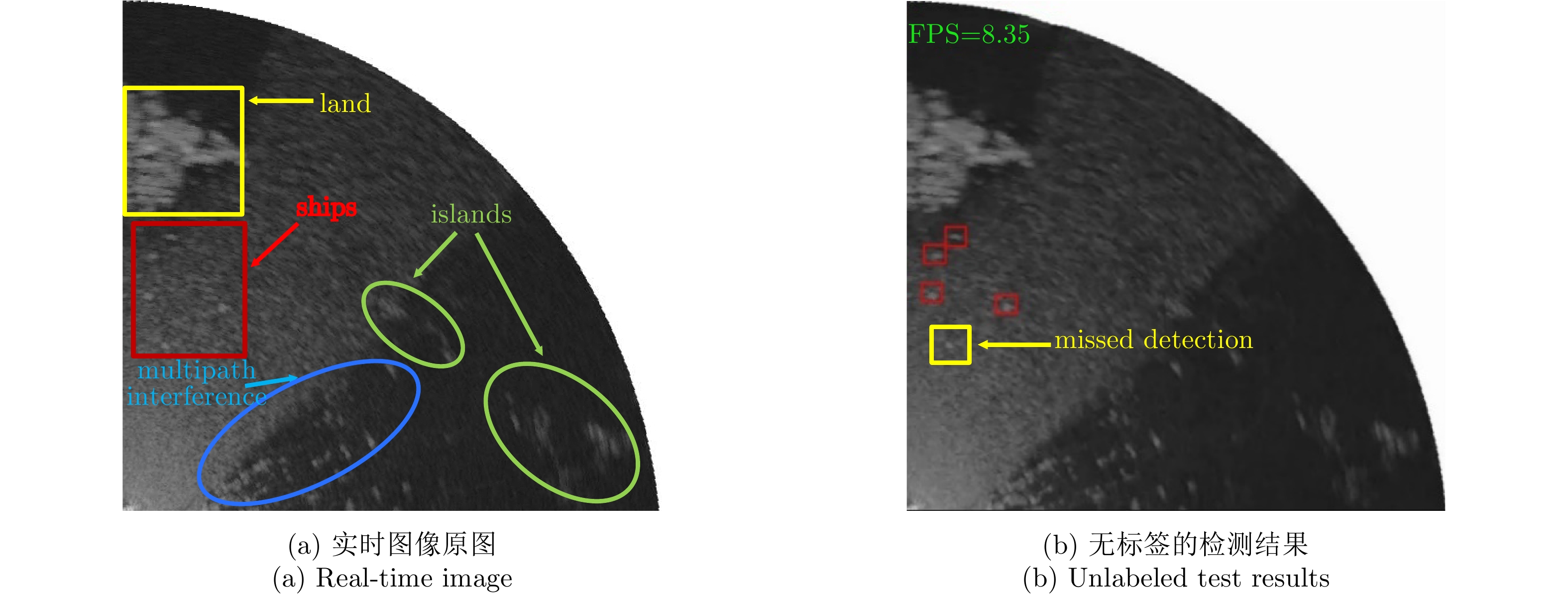
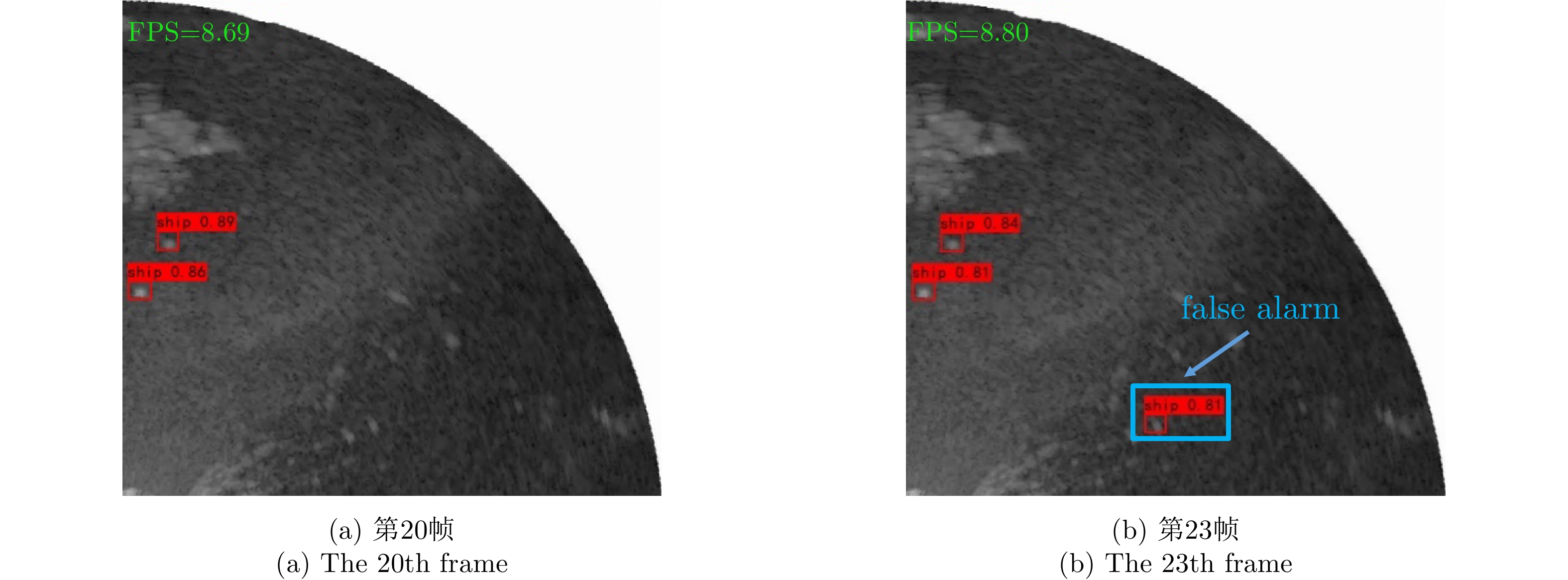
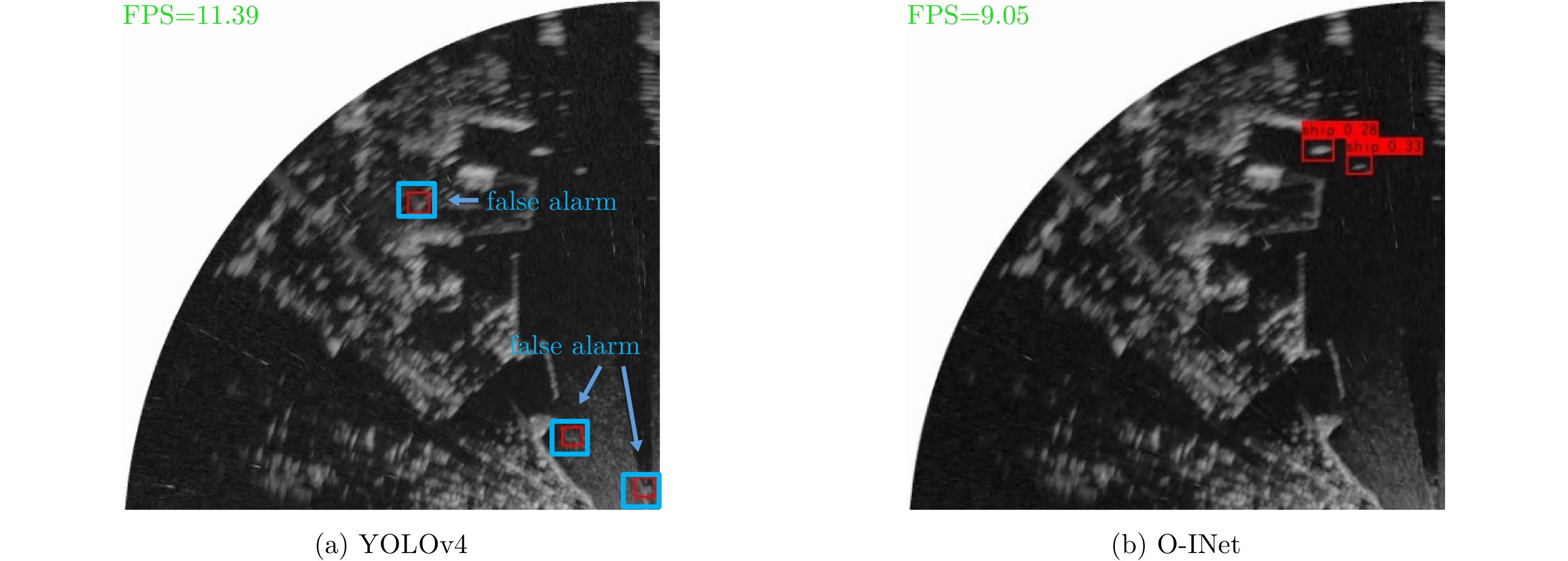
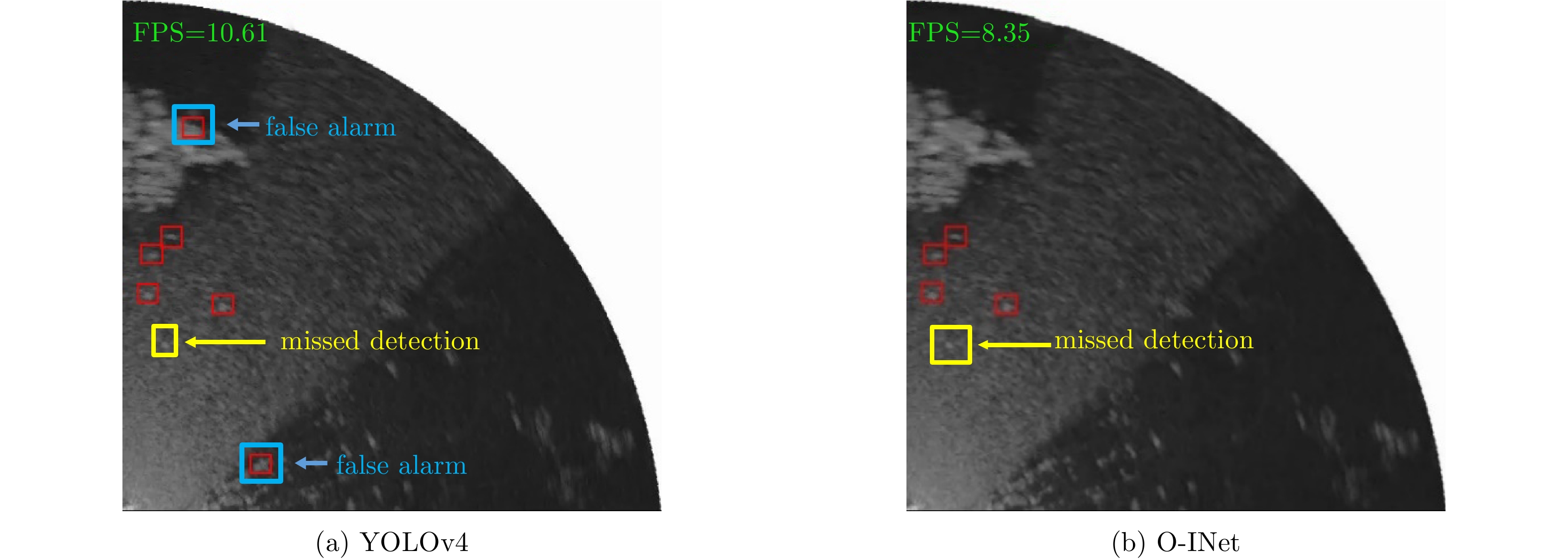
[1] 何友, 关键, 孟祥伟. 雷达目标检测与恒虚警处理[M]. 2版. 北京: 清华大学出版社, 2011: 1–15.HE You, GUAN Jian, and MENG Xiangwei. Radar Target Detection and CFAR Processing[M]. 2nd ed. Beijing: Tsinghua University Press, 2011: 1–15.[2] 黄勇, 陈小龙, 关键. 实测海尖峰特性分析及抑制方法[J]. 雷达学报, 2015, 4(3): 334–342. doi: 10.12000/JR14108HUANG Yong, CHEN Xiaolong, and GUAN Jian. Property analysis and suppression method of real measured sea spikes[J]. Journal of Radars, 2015, 4(3): 334–342. doi: 10.12000/JR14108[3] TRUNK G V and GEORGE S F. Detection of targets in non-Gaussian sea clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 1970, AES-6(5): 620–628. doi: 10.1109/TAES.1970.310062[4] 刘宁波, 董云龙, 王国庆, 等. X波段雷达对海探测试验与数据获取[J]. 雷达学报, 2019, 8(5): 656–667. doi: 10.12000/JR19089LIU Ningbo, DONG Yunlong, WANG Guoqing, et al. Sea-detecting X-band radar and data acquisition program[J]. Journal of Radars, 2019, 8(5): 656–667. doi: 10.12000/JR19089[5] YU Xiaohan, CHEN Xiaolong, HUANG Yong, et al. Fast detection method for low-observable maneuvering target via robust sparse fractional Fourier transform[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(6): 978–982. doi: 10.1109/LGRS.2019.2939264[6] 许述文, 石星宇, 水鹏朗. 复合高斯杂波下抑制失配信号的自适应检测器[J]. 雷达学报, 2019, 8(3): 326–334. doi: 10.12000/JR19030XU Shuwen, SHI Xingyu, and SHUI Penglang. An adaptive detector with mismatched signals rejection in compound Gaussian clutter[J]. Journal of Radars, 2019, 8(3): 326–334. doi: 10.12000/JR19030[7] LIU Yi, ZHANG Shufang, SUO Jidong, et al. Research on a new Comprehensive CFAR (Comp-CFAR) processing method[J]. IEEE Access, 2019, 7: 19401–19413. doi: 10.1109/ACCESS.2019.2897358[8] WANG H and CAI L. A localized adaptive MTD processor[J]. IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(3): 532–539. doi: 10.1109/7.81435[9] CHEN Xiaolong, GUAN Jian, WANG Guoqing, et al. Fast and refined processing of radar maneuvering target based on hierarchical detection via sparse fractional representation[J]. IEEE Access, 2019, 7: 149878–149889. doi: 10.1109/ACCESS.2019.2947169[10] CHEN Xiaolong, YU Xiaohan, HUANG Yong, et al. Adaptive clutter suppression and detection algorithm for radar maneuvering target with high-order motions via sparse fractional ambiguity function[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 1515–1526. doi: 10.1109/JSTARS.2020.2981046[11] 王俊, 郑彤, 雷鹏, 等. 深度学习在雷达中的研究综述[J]. 雷达学报, 2018, 7(4): 395–411. doi: 10.12000/JR18040WANG Jun, ZHENG Tong, LEI Peng, et al. Study on deep learning in radar[J]. Journal of Radars, 2018, 7(4): 395–411. doi: 10.12000/JR18040[12] 牟效乾, 陈小龙, 苏宁远, 等. 基于时频图深度学习的雷达动目标检测与分类[J]. 太赫兹科学与电子信息学报, 2019, 17(1): 105–111. doi: 10.11805/TKYDA201901.0105MOU Xiaoqian, CHEN Xiaolong, SU Ningyuan, et al. Radar detection and classification of moving target using deep convolutional neural networks on time-frequency graphs[J]. Journal of Terahertz Science and Electronic Information Technology, 2019, 17(1): 105–111. doi: 10.11805/TKYDA201901.0105[13] REN Shaoqing, HE Kaiming, GIRSHICK R, et al. Faster R-CNN: Towards real-time object detection with region proposal networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 39(6): 1137–1149. doi: 10.1109/TPAMI.2016.2577031[14] REDMON J and FARHADI A. YOLOv3: An incremental improvement[EB/OL]. https://arxiv.org/abs/1804.02767, 2018.[15] BOCHKOVSKIY A, WANG C Y, and LIAO H Y M. YOLOv4: Optimal speed and accuracy of object detection[EB/OL]. https://arxiv.org/abs/2004.10934,2020.[16] 杜兰, 王兆成, 王燕, 等. 复杂场景下单通道SAR目标检测及鉴别研究进展综述[J]. 雷达学报, 2020, 9(1): 34–54. doi: 10.12000/JR19104DU Lan, WANG Zhaocheng, WANG Yan, et al. Survey of research progress on target detection and discrimination of single-channel SAR images for complex scenes[J]. Journal of Radars, 2020, 9(1): 34–54. doi: 10.12000/JR19104[17] 苏宁远, 陈小龙, 陈宝欣, 等. 雷达海上目标双通道卷积神经网络特征融合智能检测方法[J]. 现代雷达, 2019, 41(10): 47–52, 57. doi: 10.16592/j.cnki.1004-7859.2019.10.009SU Ningyuan, CHEN Xiaolong, CHEN Baoxin, et al. Dual-channel convolutional neural networks feature fusion method for radar maritime target intelligent detection[J]. Modern Radar, 2019, 41(10): 47–52, 57. doi: 10.16592/j.cnki.1004-7859.2019.10.009[18] 苏宁远, 陈小龙, 关键, 等. 基于卷积神经网络的海上微动目标检测与分类方法[J]. 雷达学报, 2018, 7(5): 565–574. doi: 10.12000/JR18077SU Ningyuan, CHEN Xiaolong, GUAN Jian, et al. Detection and classification of maritime target with micro-motion based on CNNs[J]. Journal of Radars, 2018, 7(5): 565–574. doi: 10.12000/JR18077[19] CHEN Chen, HE Chuan, HU Changhua, et al. MSARN: A deep neural network based on an adaptive recalibration mechanism for multiscale and arbitrary-oriented SAR ship detection[J]. IEEE Access, 2019, 7: 159262–159283. doi: 10.1109/ACCESS.2019.2951030[20] 黄洁, 姜志国, 张浩鹏, 等. 基于卷积神经网络的遥感图像舰船目标检测[J]. 北京航空航天大学学报, 2017, 43(9): 1841–1848. doi: 10.13700/j.bh.1001-5965.2016.0755HUANG Jie, JIANG Zhiguo, ZHANG Haopeng, et al. Ship object detection in remote sensing images using convolutional neural networks[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(9): 1841–1848. doi: 10.13700/j.bh.1001-5965.2016.0755[21] WEI Xiukun, WEI Dehua, SUO Da, et al. Multi-target defect identification for railway track line based on image processing and improved YOLOv3 model[J]. IEEE Access, 2020, 8: 61973–61988. doi: 10.1109/ACCESS.2020.2984264[22] XIAO Dong, SHAN Feng, LI Ze, et al. A target detection model based on improved Tiny-Yolov3 under the environment of mining truck[J]. IEEE Access, 2019, 7: 123757–123764. doi: 10.1109/ACCESS.2019.2928603[23] ZHANG Huibing, QIN Longfei, LI Jun, et al. Real-time detection method for small traffic signs based on Yolov3[J]. IEEE Access, 2020, 8: 64145–64156. doi: 10.1109/ACCESS.2020.2984554[24] BA J L, KIROS J R, and HINTON G E. Layer normalization[EB/OL]. https://arxiv.org/abs/1607.06450, 2016.[25] WANG C Y, LIAO H Y M, YEH I H, et al. CSPNet: A new backbone that can enhance learning capability of CNN[EB/OL]. https://arxiv.org/abs/1911.11929,2019.[26] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, USA, 2016: 770–778. doi: 10.1109/CVPR.2016.90.[27] AI Jiaqiu, YANG Xuezhi, DONG Zhangyu, et al. A new two parameter CFAR ship detector in Log-Normal clutter[C]. 2017 IEEE Radar Conference (RadarConf), Seattle, USA, 2017: 195–199. doi: 10.1109/RADAR.2017.7944196.[28] YANG Jianyu, LU Chao, and LI Liangchao. Target detection in passive millimeter wave image based on two-dimensional cell-weighted average CFAR[C]. The IEEE 11th International Conference on Signal Processing, Beijing, China, 2012: 917–921. doi: 10.1109/ICoSP.2012.6491729. -
Proportional views
- Publishing Ethics
- Journal Insights
- Abstracting & Indexing
- Peer Review Policies
- Guide for Authors
- Conference
- ISSN 2095-283X (Print)ISSN 2097-339X (Online)
- CN 10-1030/TN
- CODEN LXEUAO
About Journal
- Sponsor: China Radio Detection and Ranging Industry Association (CRIA)
- Phone: 010-58887062
- Email：radars@aircas.ac.cn
- Publisher: Leida Xuebao Bianjibu (Editorial office of the Journal of Radars)
Contacts Us
京ICP备20021838号-8
Supported by: Beijing Renhe Information Technology Co. Ltd
Export File
Citation
Format
Content
DownLoad:
- Figure 1. The network structure of INet
- Figure 2. The network structure of ARN
- Figure 3. The network structure of CSPRM
- Figure 4. Flowchart of target detection algorithm based on INet
- Figure 5. Detection environment and radar PPI interface
- Figure 6. Feature maps of the clutter suppression network in Part Ⅰ
- Figure 7. Comparison before and after model optimization (Data_03#)
- Figure 8. Moving target detection under simple background of low sea state (Data_01#)
- Figure 9. Moving target detection under complex background of low sea state (Data_02#)
- Figure 10. Multi-target detection under high sea conditions (Data_03#)
- Figure 11. Multi-target detection under heavy snow (Data_04#)
- Figure 12. Comparison of multi-target detection results under rain weather (Data_05#)
- Figure 13. Comparison of moving targets under simple background of low sea state (Data_01#)
- Figure 14. Moving target detection under complex background of low sea state (Data_02#)
- Figure 15. Multi-target detection under high sea conditions (Data_03#)
- Figure 16. Multi-target detection under heavy snow (Data_04#)
- Figure 17. Comparison of multi-target detection results under rain weather (Data_05#)
- Figure 18. Multi-target detection results under high sea conditions (Data_03#)