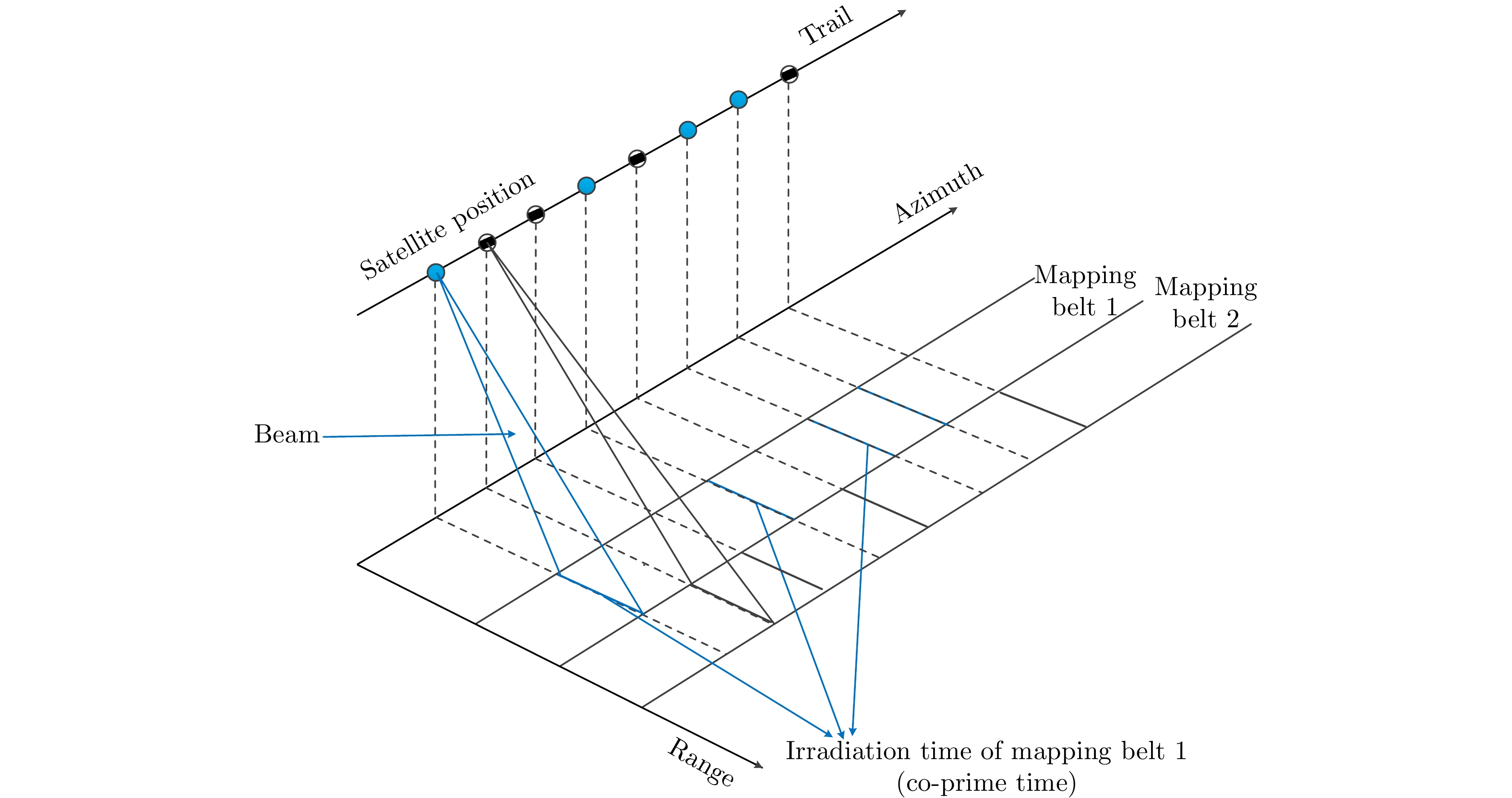
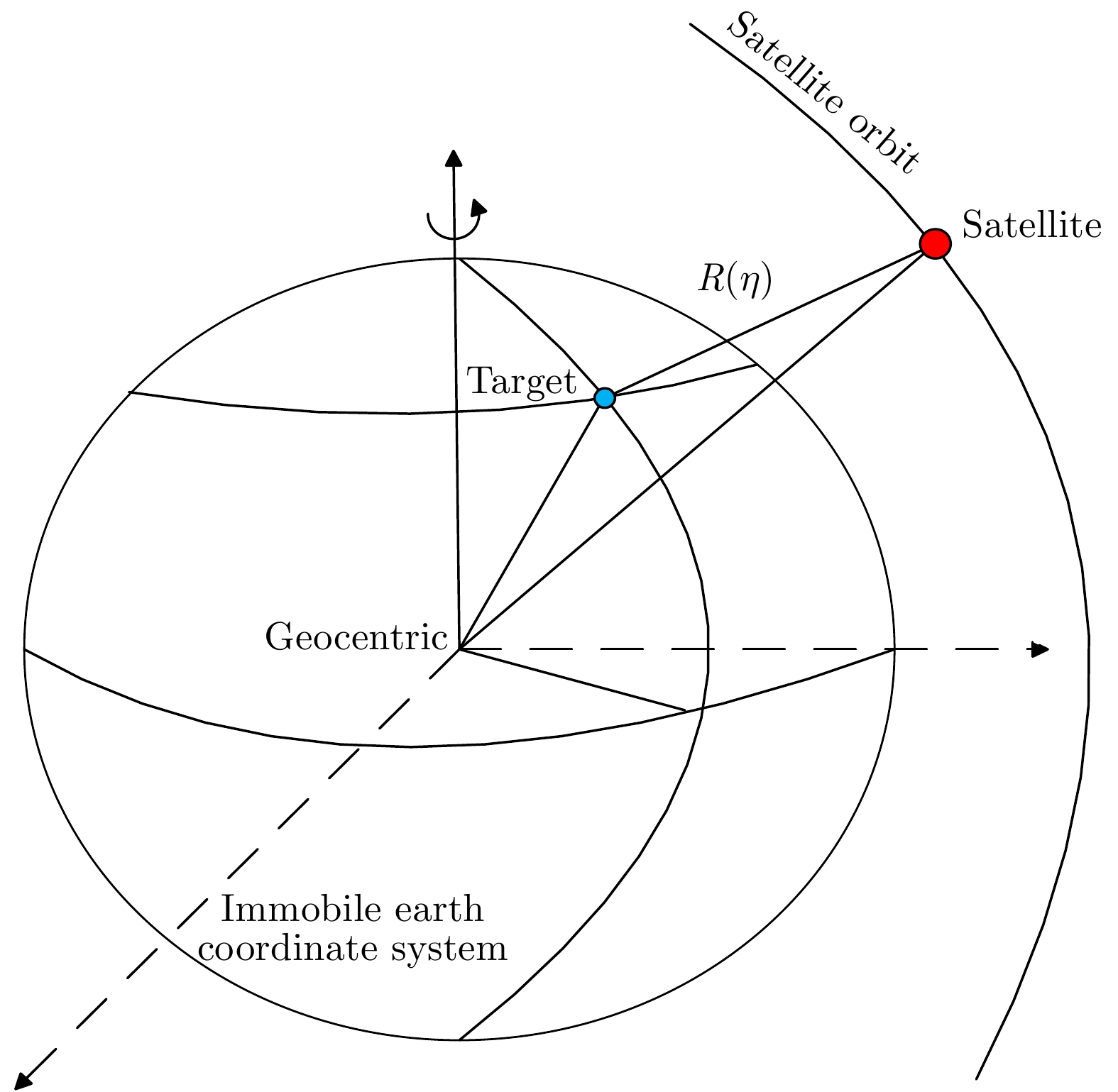
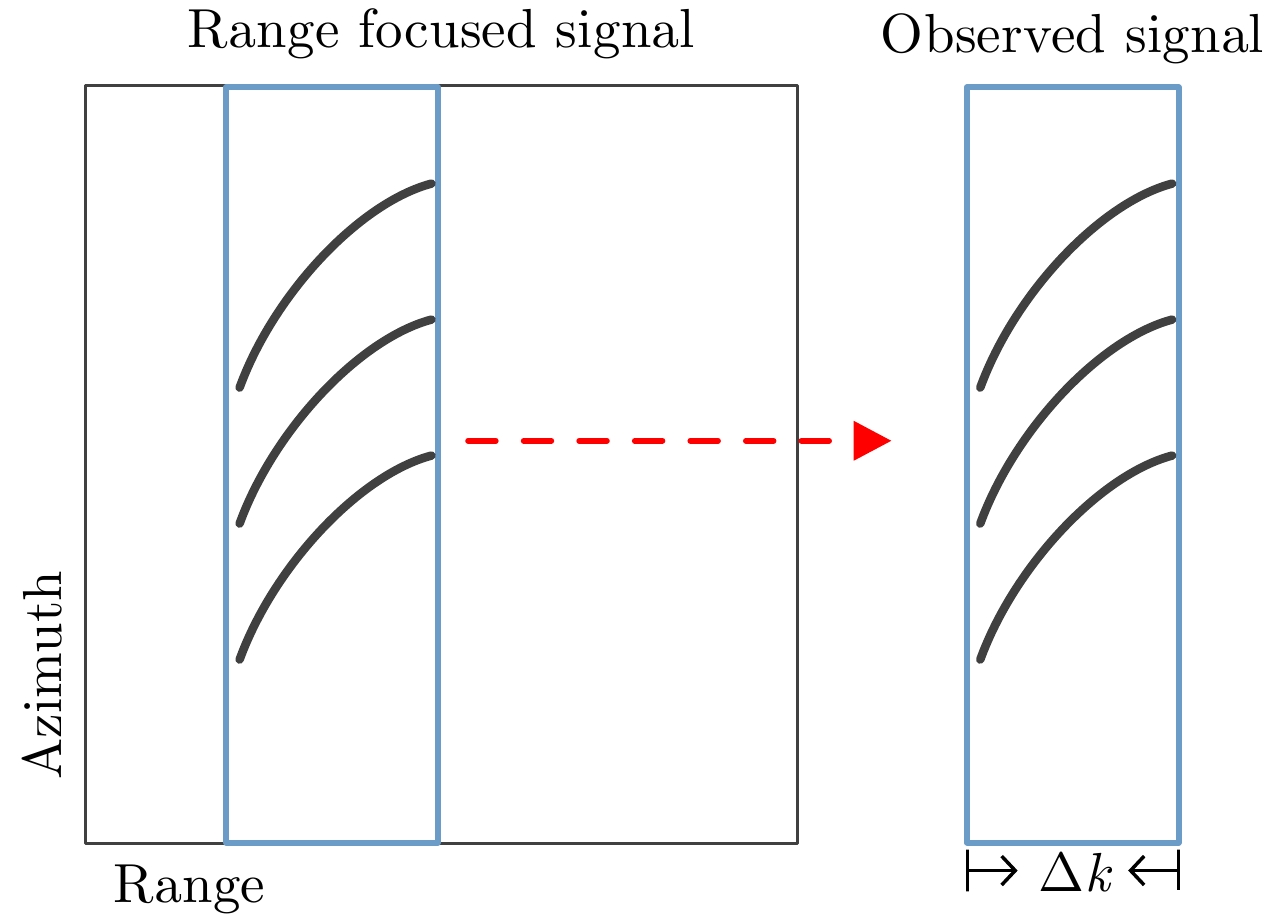
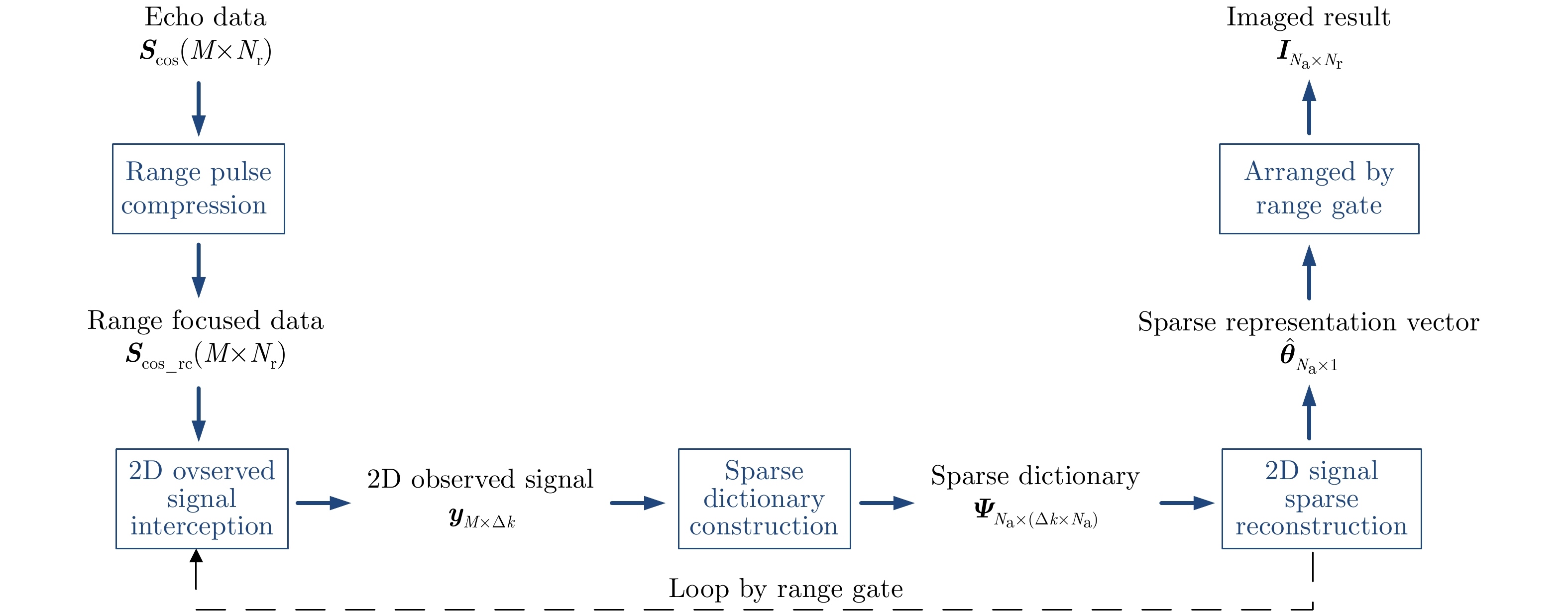
| [1] |
LI Chunsheng, YANG Wei, and WANG Pengbo. A review of spaceborne SAR algorithm for image formation[J]. Journal of Radars, 2013, 2(1): 111–122. doi: 10.3724/SP.J.1300.2013.20071 |
| [2] |
DENG Yunkai, ZHAO Fengjun, and WANG Yu. Brief analysis on the development and application of spaceborne SAR[J]. Journal of Radars, 2012, 1(1): 1–10. doi: 10.3724/SP.J.1300.2012.20015 |
| [3] |
赵耀, 邓云凯, 王宇, 等. 原始数据压缩对方位向多通道SAR系统影响研究[J]. 雷达学报, 2017, 6(4): 397–407. doi: 10.12000/JR17030ZHAO Yao, DENG Yunkai, WANG Yu, et al. Study of effect of raw data compression on azimuth multi-channel SAR system[J]. Journal of Radars, 2017, 6(4): 397–407. doi: 10.12000/JR17030 |
| [4] |
罗绣莲, 徐伟, 郭磊. 捷变PRF技术在斜视聚束SAR中的应用[J]. 雷达学报, 2015, 4(1): 70–77. doi: 10.12000/JR14149LUO Xiulian, XU Wei, and GUO Lei. The application of PRF variation to squint spotlight SAR[J]. Journal of Radars, 2015, 4(1): 70–77. doi: 10.12000/JR14149 |
| [5] |
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582 |
| [6] |
|
| [7] |
VAIDYANATHAN P P and PAL P. Sparse sensing with co-prime samplers and arrays[J]. IEEE Transactions on Signal Processing, 2011, 59(2): 573–586. doi: 10.1109/TSP.2010.2089682 |
| [8] |
VAIDYANATHAN P P and PAL P. Theory of sparse coprime sensing in multiple dimensions[J]. IEEE Transactions on Signal Processing, 2011, 59(8): 3592–3608. doi: 10.1109/tsp.2011.2135348 |
| [9] |
ZHANG Y D, AMIN M G, and HIMED B. Sparsity-based DOA estimation using co-prime arrays[C]. 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, Canada, 2013. doi: 10.1109/ICASSP.2013.6638403. |
| [10] |
TAN Zhao, ELDAR Y C, and NEHORAI A. Direction of arrival estimation using co-prime arrays: A super resolution viewpoint[J]. IEEE Transactions on Signal Processing, 2014, 62(21): 5565–5576. doi: 10.1109/TSP.2014.2354316 |
| [11] |
YU Lei, WEI Yinsheng, and LIU Wei. Adaptive beamforming based on nonuniform linear arrays with enhanced degrees of freedom[C]. TENCON 2015- 2015 IEEE Region 10 Conference, Macao, China, 2015. doi: 10.1109/TENCON.2015.7373099. |
| [12] |
QIN Si, ZHANG Y D, and AMIN M G. Generalized coprime array configurations for direction-of-arrival estimation[J]. IEEE Transactions on Signal Processing, 2015, 63(6): 1377–1390. doi: 10.1109/TSP.2015.2393838 |
| [13] |
SUN Fenggang, GAO Bin, CHEN Lizhen, et al. A low-complexity ESPRIT-based DOA estimation method for co-prime linear arrays[J]. Sensors, 2016, 16(9): 1367. doi: 10.3390/s16091367 |
| [14] |
王龙刚, 李廉林. 基于互质阵列雷达技术的近距离目标探测方法(英文)[J]. 雷达学报, 2016, 5(3): 244–253. doi: 10.12000/JR16022WANG Longgang and LI Lianlin. Short-range radar detection with ( M, N)-coprime array configurations[J]. Journal of Radars, 2016, 5(3): 244–253. doi: 10.12000/JR16022 |
| [15] |
SUN Fenggang, LAN Peng, and ZHANG Guowei. Reduced dimension based two-dimensional DOA estimation with full DOFs for generalized co-prime planar arrays[J]. Sensors, 2018, 18(6): 1725. doi: 10.3390/s18061725 |
| [16] |
RAZA A, LIU Wei, and SHEN Qing. Thinned coprime array for second-order difference co-array generation with reduced mutual coupling[J]. IEEE Transactions on Signal Processing, 2019, 67(8): 2052–2065. doi: 10.1109/TSP.2019.2901380 |
| [17] |
DI MARTINO G and IODICE A. Orthogonal coprime synthetic aperture radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(1): 432–440. doi: 10.1109/TGRS.2016.2608140 |
| [18] |
TAO Yu, ZHANG Gong, and LI Daren. Coprime sampling with deterministic digital filters in compressive sensing radar[C]. 2016 CIE International Conference on Radar, Guangzhou, China, 2016. doi: 10.1109/RADAR.2016.8059224. |
| [19] |
SHI Hongyin and JIA Baojing. SAR imaging method based on coprime sampling and nested sparse sampling[J]. Journal of Systems Engineering and Electronics, 2015, 26(6): 1222–1228. doi: 10.1109/JSEE.2015.00134 |
| [20] |
CAFFORIO C, PRATI C, and ROCCA F. SAR data focusing using seismic migration techniques[J]. IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(2): 194–207. doi: 10.1109/7.78293 |
| [21] |
MITTERMAYER J, MOREIRA A, and LOFFELD O. Spotlight SAR data processing using the frequency scaling algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2198–2214. doi: 10.1109/36.789617 |
| [22] |
SUN Xiaobing, YEO T S, and ZHANG Chengbo, et al. Time-varying step-transform algorithm for high squint SAR imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(6): 2668–2677. doi: 10.1109/36.803414 |
| [23] |
WANG Pengbo, LIU Wei, CHEN Jie, et al. A high-order imaging algorithm for high-resolution spaceborne SAR based on a modified equivalent squint range model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1225–1235. doi: 10.1109/TGRS.2014.2336241 |
| [24] |
DO T T, GAN Lu, NGUYEN N, et al. Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]. The 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, 2008. doi: 10.1109/ACSSC.2008.5074472. |




 Submit Manuscript
Submit Manuscript Peer Review
Peer Review Editor Work
Editor Work




 DownLoad:
DownLoad: