ResCalib: Joint LiDAR and Camera Calibration Based on Geometrically Supervised Deep Neural Networks

1.   引言

无源定位技术是一种自身不发射电磁信号，仅利用单个或多个接收站截获的信号，确定辐射源位置的技术，又称为被动定位技术。相对于有源的定位方式，该技术具有电磁隐蔽性好、可定位距离远等优势，在电子侦察、搜索救援、无人驾驶、智能物流等军用和民用领域具有重要应用价值，已经成为世界各国的研究热点^[1-26]。

根据估计辐射源位置的步骤，可以将无源定位技术分为两类，即传统两步法与一步法。传统两步法定位的基本思路^[1]为：第1步，通过接收机截获辐射源信号，对原始采样信号进行处理，使用空间谱等方法^[2-4]估计蕴含辐射源位置信息的定位参数；第2步，利用定位参数与辐射源位置之间的关系建立并求解方程，实现定位。第1步中估计的定位参数多种多样，例如由于信号到达干涉仪不同天线波程差导致的相位差^[5-7]，或者由于信号到达不同观测站传播路径的差异导致的时间差(Time Difference Of Arrival, TDOA)^[8-11]，或者由于目标和观测站之间相对速度差异导致的信号到达不同观测站的频差(Frequency Different Of Arrival, FDOA)^[12,13]，以及多普勒变化率(Doppler rate)^[14-17]、或者信号到达角方向(Direction Of Arrival, DOA)^[18-20]、接收信号强度(Received Signal Strength, RSS)^[21-25]等。实际上以上定位参数在空间中对应的是定位线或者定位面(曲面)^[26]，例如TDOA对应的是双曲线或双曲面、DOA对应的是直线或平面、FDOA对应的是等频差曲面等。传统两步定位法在第2步中利用这些定位线或定位面相交，通过穷尽搜索法^[27,28]、最小二乘法^[29]、伪线性法^[30]、泰勒展开和梯度结合法^[31]等方法，估计辐射源的位置。

另一种无源定位方法为一步定位法。相对于传统两步定位法，一步定位法不需要估计定位参数的过程，而是直接对原始采样信号进行处理，利用信号中蕴含的辐射源位置信息，构建仅与辐射源位置相关的目标函数(代价函数)，通过穷尽搜索等优化算法实现定位^[32-37]，由于其实现的是从信号到辐射源位置的直接估计，因此一般被称为直接定位法(Direct Position Determination, DPD)。DPD的基本思路最早可以追溯到Wax和Kailath^[38]在1985年提出的分散式处理方法，随后在2004年由以色列学者Weiss^[33]正式提出。

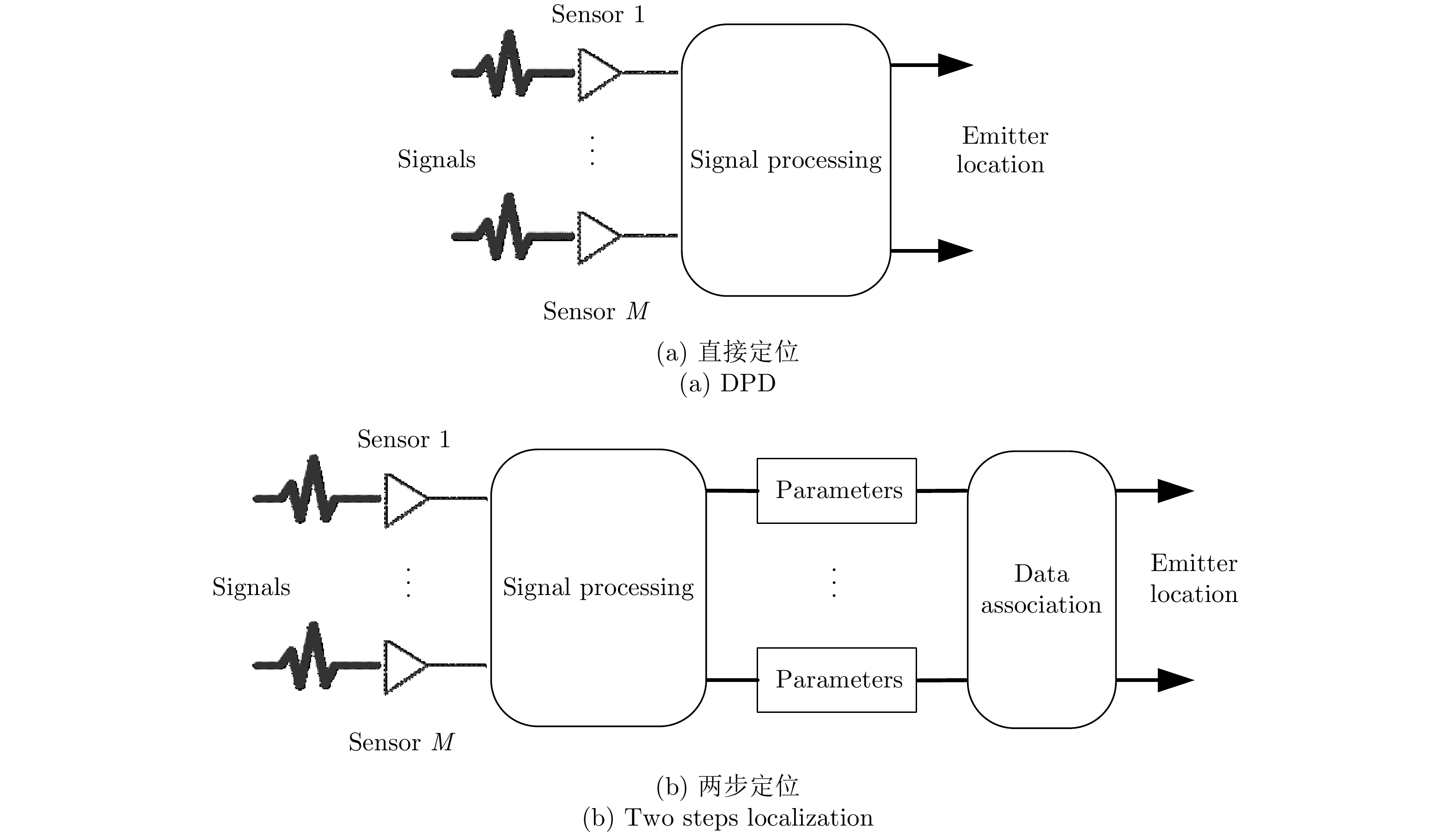
根据已有研究^[39-44]，可以总结以下直接定位方法相对于传统两步定位方法的优势和不足。由于DPD无需估计定位参数，因此避免了不同辐射源参数关联的过程，可以对同时同频等传统方法难以处理的信号进行定位^[39]。另外，DPD的代价函数仅与辐射源位置有关，充分利用了信号来自于同一个辐射源的先验信息^[33]，因此其在低信噪比下具有更高的定位精度。最后，也有相关研究表明^[40-42]，在模型误差干扰的情况下，DPD相较于两步法具有更好的鲁棒性。DPD获得以上优势的同时，也伴随着一定的代价。由于DPD处理的是原始采样信号，而不是像两步定位法那样处理的是定位参数，并且难以获得辐射源位置的解析解，因此其计算量相对较大^[45]。图1给出了传统两步法定位系统和直接定位系统的示意图。

图  1  直接定位系统与传统两步定位系统示意图

Figure  1.  Diagrammatic drawings of DPD and two steps localization systems

下载: 全尺寸图片 幻灯片

DPD自提出以来，受到了国内外诸多学者的研究，本文针对DPD目前研究的5个热点问题，总结国内外直接定位技术的研究成果，具体安排如下：第2节介绍基于不同信息类型的典型直接定位技术；第3节总结针对某些特殊信号的直接定位技术；第4节分析直接定位在高分辨率高精度方面的成果；第5节归纳直接定位在快速算法的研究；第6节描述了现有的直接定位模型误差校正技术，最后在第7节中给出直接定位技术的总结和展望。

2.   基于不同信息类型的典型直接定位技术

对于传统两步定位法，由于使用的是DOA, TDOA, FDOA等定位参数实现定位，因此这些参数也可以被称为观测量。虽然DPD并不需要估计这些参数，但是当对信号建模时，依然需要考虑辐射源位置信息蕴含在哪些变量中，为了与两步法进行区分，将DPD中蕴含辐射源位置信息的变量统一称为信息类型。DPD早期的研究主要集中于建立基于不同信息类型的信号模型，然后利用不同信号模型构建代价函数实现定位。最早的直接定位是基于到达角(Angle Of Arrival, AOA)和TDOA两个信息类型提出的^[33]。它利用多个固定阵列对单个窄带信号进行定位，除了通过阵列响应考虑辐射源的AOA之外，还使用傅里叶变换，提取信号中的TOA信息，最终构建了基于AOA和TDOA的信号模型，随后利用最小二乘法建立了仅与辐射源位置相关的代价函数，最终通过穷尽搜索法实现了辐射源位置的估计。其仿真结果表明，在低信噪比情况下，DPD定位精度要优于仅使用AOA的两步定位法、仅使用TDOA的两步定位法以及两者的组合。同样使用AOA和TDOA两种信息类型，对单个辐射源的直接定位也可以推广至对多个辐射源的直接定位^[46,47]。

当TDOA带来的辐射源位置信息无法使用时，仅使用DOA也可实现直接定位。例如仅使用单个运动阵列截获信号并对其定位时，不存在多观测站截获信号的TDOA，此时可以使用DOA构造直接定位代价函数进行定位^[34,35,48]。而当需要采用相参处理的方式联立多个阵列的响应向量时，为了避免TDOA造成观测模型无法相参处理，可以将TDOA视为观测信号的未知相位量，构建仅基于DOA的相参类型直接定位代价函数实现定位^[49]。

除此之外，当多普勒频移显著时，FDOA这一信息类型也可以实现辐射源的直接定位^[42-45]，利用空间分布的多个运动的单传感器截获静止辐射源的信号，在假设信号载频已知的情况下，可以建立了截获信号与辐射源位置之间的直接关系，使用最大似然(Maximum Likelihood, ML)准则构建代价函数并利用穷尽搜索的方法也实现了对辐射源的直接定位。除了仅使用FDOA这一信息类型的直接定位方法之外，多普勒效应相关的信息类型在直接定位中也常与其它信息类型相组合以提高定位的精度，例如文献[50-52]提出了一种基于TDOA和FDOA的直接定位方法，它们同样采用了多个运动的单传感器截获静止辐射源的信号，除了FDOA之外，还考虑了信号到达不同传感器的波程差导致的TDOA，从而直接建立了截获信号和辐射源位置之间的模型，通过穷尽搜索法实现直接定位。而文献[53]则使用多个运动的阵列截获静止辐射源信号，忽略TDOA，提出了一种仅基于到达角和FDOA的运动多站直接定位方法。如果观测站和辐射源之间相对静止，多普勒效应可以忽略，此时仅有TDOA这一信息类型蕴含着辐射源的位置信息，文献[45,54]就在这一定位场景下，提出了仅基于TDOA的多站直接定位方法。

从以上介绍中不难看出，直接定位利用的信息类型包括DOA, TDOA, FDOA、多普勒频移等，在实际应用中，直接定位会根据具体定位场景设定选取合适的信息类型。例如，如果使用空间分布的多个静止单传感器进行直接定位，仅需要考虑TDOA，如果使用空间分布的多个静止阵列进行直接定位，则需要考虑DOA和TDOA，如果观测站运动，则需要额外考虑FDOA等多普勒参数。选取恰当的信息类型并建立准确的信号模型是保证直接定位精确度的前提。

3.   特殊信号的直接定位技术

对于DPD来说，截获信号的模型是构建代价函数进而实现定位的关键。现有的信号直接定位技术研究大部分以窄带信号为目标^[33-56]，在本节中主要介绍特殊信号的直接定位相关研究。为了增加DPD对信号种类的适应性，拓展DPD的应用范围，许多学者对特殊信号的直接定位进行了研究。这些研究可以分为两类，一类是针对原本直接定位方法无法处理的信号开展的，它通过增加预处理、改进代价函数等手段，使得直接定位方法具备对这种信号进行处理的能力；另一类则是在直接定位过程中，充分利用特殊信号的性质作为先验信息，改进代价函数，从而提升直接定位的性能。

3.1   第1类特殊信号

直接定位处理的第1类特殊信号主要包括宽带信号、跳频信号以及相干信号等。文献[57]是最早考虑一般性宽带信号的直接定位的，它建立了运动多站截获宽带信号的模型，利用TDOA和FDOA两个信息类型构建了直接定位代价函数，将直接定位的应用拓展到了一般性宽带信号。文献[58]则将宽带信号划分成多个片段进行相参累加处理，进一步提高了直接定位对宽带信号的定位性能，这种相参累加的信号处理方式也将在下一节中进行介绍。此外，利用多个观测阵列截获的宽带信号，可以构建一种基于空间-时间观测向量的代价函数，这种处理方式将所有的截获信号蕴含在一个单独的空时协方差矩阵之中，有效增强了DPD的鲁棒性^[59,60]，并且提升了DPD的自由度^[61]。以上考虑的宽带信号其带宽相较于载频实际上还是很小的，因此其基带信号的多普勒变化是被忽略的。文献[62]则考虑更大带宽的信号，其带宽的大小与采样率相当，因此可以将截获信号建模成为随时间平移和缩放的函数，在此基础上构造了基于最大似然的代价函数，实现了对该类信号的直接定位。

直接定位技术相关研究中一般假设信号频率固定，但目前跳频通信信号等频率时变的信号也被广泛应用。基于跳频信号多个子带只在频带范围内占用部分带宽，频带范围内只有少数非0值的特征(即频域有限分布特性)，文献[63]用跳频信号的离散谱建立截获信号模型，分别基于最大似然和最大相关积累两种方法构建了直接定位代价函数，实现了对单个跳频信号辐射源的直接定位。在实际情况中，跳频信号和固定频率信号可能同时存在，但目前未见有相关研究，针对更为复杂电磁环境的直接定位技术研究依然存在相当大的空白。

另外相干(coherent)信号在阵列信号处理中受到了学者们的广泛研究^[64-69]，对于直接定位来说，如果依然使用多重信号分类(MUltiple SIgnal Classification, MUSIC) 的方法构建代价函数，直接定位性能将会严重衰减甚至失效。为此，文献[70]提出了基于解相干MUSIC的直接定位算法，通过接收信号协方差矩阵共轭重构，实现了相干信号的直接定位；文献[71]提出使用自适应迭代的方式避免协方差矩阵秩亏，也可以实现相干信号的直接定位。除此之外，空间平滑等在相干信号阵列测向中已经验证有效的方法^[72-74]，也可以推广到直接定位之中，相应方法的优势和不足在直接定位之中也待分析讨论。

3.2   第2类特殊信号

直接定位处理的第2类特殊信号主要包括正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)信号、非圆信号(noncircular signal)、恒模信号、周期平稳信号(cyclostationary signals)以及同步相参脉冲串(Synchronous Coherent Pulse Trains, SCPT)信号。OFDM是一种应用广泛的信号调制技术，它可以有效对抗色散信道、多径等问题。其通过发射器反快速傅里叶变换(Inverse Fast Fourier Transform, IFFT)产生OFDM信号，然后在接收端通过快速傅里叶变换(Fast Fourier Transform, FFT) 转换到频域。文献[75,76]针对OFDM信号提出了一种基于最大似然的直接定位方法，该方法既考虑了OFDM信号中未知的数据部分(data tones)，也考虑了已知的导频部分(pilot tones)，据此提出了对其位置估计的最大似然估计器(Maximum Likelihood Estimator, MLE)，其性能要优于忽略已知导频部分的一般性DPD。文献[77]则提出了基于谱的OFDM信号直接定位方法，减少了搜索的维数。非圆复信号也是一种备受关注的信号^[78-82]，它与圆复信号最大的区别就是非圆复信号的实部和虚部不是独立的。常见的非圆复信号有幅度(Amplitude Modulation, AM)调制信号、幅移键控(Amplitude Shift Keying, ASK)信号和二进制移相键控(Binary Phase Shift Key, BPSK)信号。文献[83,84]就是利用非圆复信号的上述性质对其进行直接定位，由于先验信息的引入，提升了直接定位的性能。恒模信号(相位调制信号)是一种应用广泛的通信信号，例如FM, FSK, PSK等，它们的显著特征是其复包络具有恒模特征。利用该特征，文献[85]改进了恒模信号直接定位代价函数，构建的基于最大似然的直接定位方法可以明显提高目标位置估计精度。周期平稳信号是一种期望和自相关函数为周期性的信号，利用这种周期性可以将信号自相关的离散傅里叶变换进行改写^[86]，从而构建周期性的直接定位方法。利用这一先验，该方法在白高斯环境下和窄带干涉环境下都表现出了优良的性能。

SCPT信号是相参脉冲雷达系统中常用的信号类型，它可以视为由一个稳定的主振荡器产生的连续波截取形成的具有相同初始相位的脉冲串信号。基于SCPT信号的这一特性，仅使用单个运动天线，基于多普勒和多普勒频移即可实现该信号的直接定位，具体方法在文献[87]中给出了介绍。除此之外，本文作者还依据该类信号的特点，提出了单站相参的直接定位技术^[88]，仿真表明虽然其定位精度没有改善，但是分辨率提升显著。

4.   高分辨率高精度的多目标直接定位技术

随着电磁环境日益复杂，实现多个辐射源高精度高分辨率的定位成为无源定位领域迫切的需求。同样，很多学者也致力于研究高分辨率高精度的直接定位。目前相关研究主要分为两类，一类是通过改进构建代价函数的方法提高直接定位的分辨率和定位精度，另外一类则是通过改进信号处理方式实现高分辨率高精度的直接定位。

4.1   改进代价函数

最早提出的直接定位方法在构建代价函数时，使用的是最小二乘或ML的准则^[33]。但是，为了实现对多个辐射源的定位，文献[46,47]提出了使用MUSIC算法构建代价函数的直接定位。但是，在使用MUSIC方法之前，首先需要对辐射源数量进行估计。为了避免这一问题，文献[89-93]提出使用最小方差无失真响应(Minimum Variance Distortionless Response, MVDR) 方法构建直接定位的代价函数。不同的是，文献[89]处理的是仅包含多普勒频移这一信息类型的观测信号模型，文献[90]处理的是包含DOA 和TDOA信息类型的观测信号模型，而文献[91,92]处理的是包含DOA和FDOA信息类型的观测信号模型，文献[93]则处理的是仅包含DOA信息类型的观测信号模型。不管MVDR是在哪种截获信号模型基础上建立的代价函数，其分辨率都要优于基于ML构建的代价函数，对相邻辐射源的定位精度也更高。但是其分辨率与基于MUSIC的代价函数相差无几，并且正如文献[94]所评价的那样，当存在多个辐射源时，基于MVDR的直接定位问题实际上是渐进有偏的^[95-97]，其定位精度难以达到理论的克拉美罗下限(Cramér-Rao Lower Bound, CRLB)。

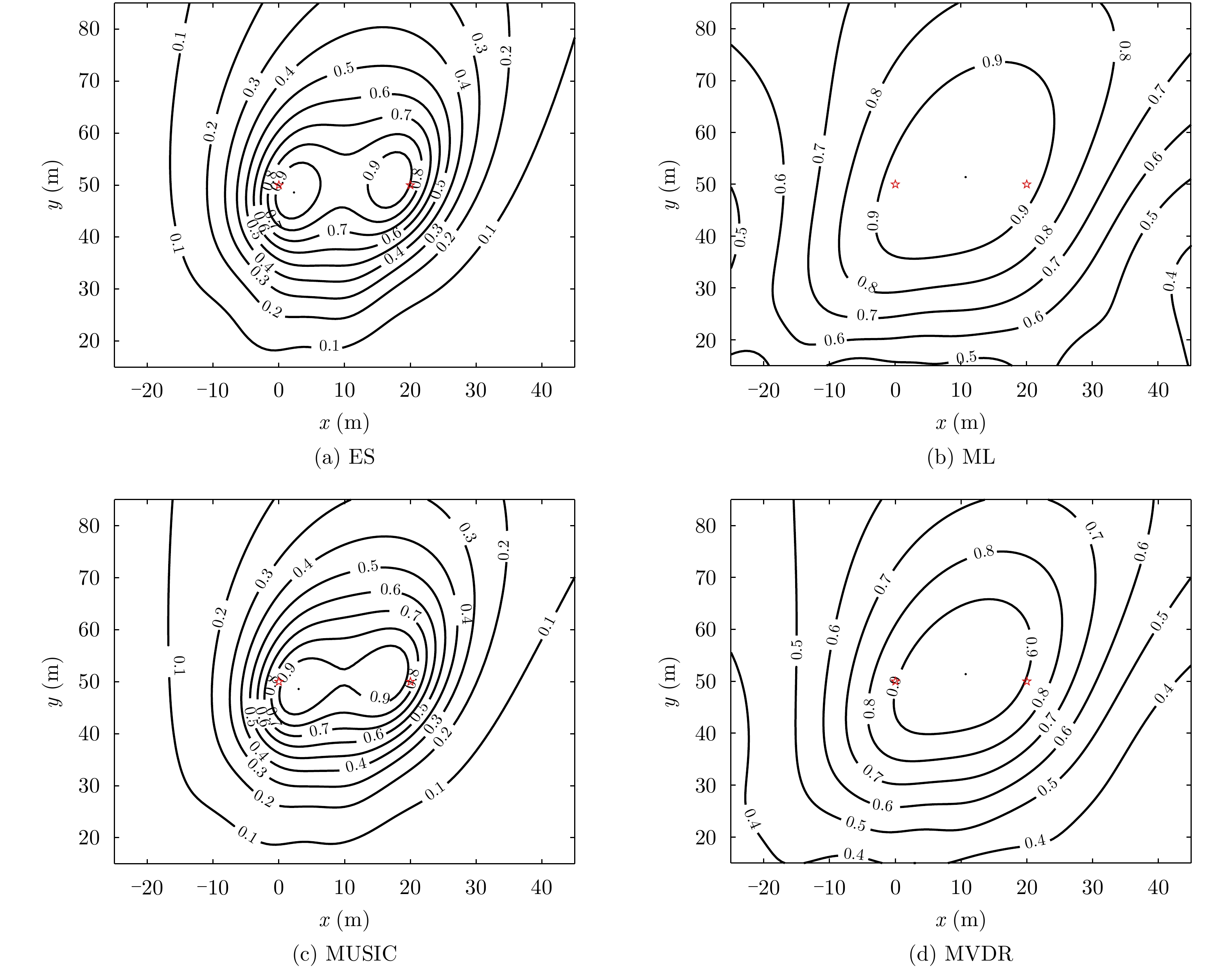
除了MUSIC和MVDR两种改进的直接定位代价函数，本文作者曾尝试使用基于特征空间(Eigen Space, ES)的方法构建代价函数^[48]。该类型的代价函数是对基于MUSIC代价函数的一种改进，可以表示为

其中，分母 ${f_{{\rm{MUSIC}}}}$ 是基于MUSIC的代价函数，而分子 ${f_{\rm{e}}}$ 是利用噪声子空间和信号子空间的正交特性建立的，它的特征是若当前搜索位置在辐射源真实位置处时，它是一个较大的值，而当前搜索位置不在辐射源真实位置处时，它的值几乎为0。这相当于是一种加权的MUSIC改进方法，该方法可以有效提升直接定位的分辨率。在某次蒙特卡洛仿真中，对空间中两个临近辐射源进行直接定位，各代价函数的归一化空间谱等高线图如图2所示。

图  2  ES, ML, MUSIC, MVDR代价函数单位等高线图(星为辐射源真实位置)

Figure  2.  The unitized contours of the cost functions based on ES, ML, MUSIC and MVDR (The stars stand for the real positions of the emitters)

下载: 全尺寸图片 幻灯片

4.2   相参处理

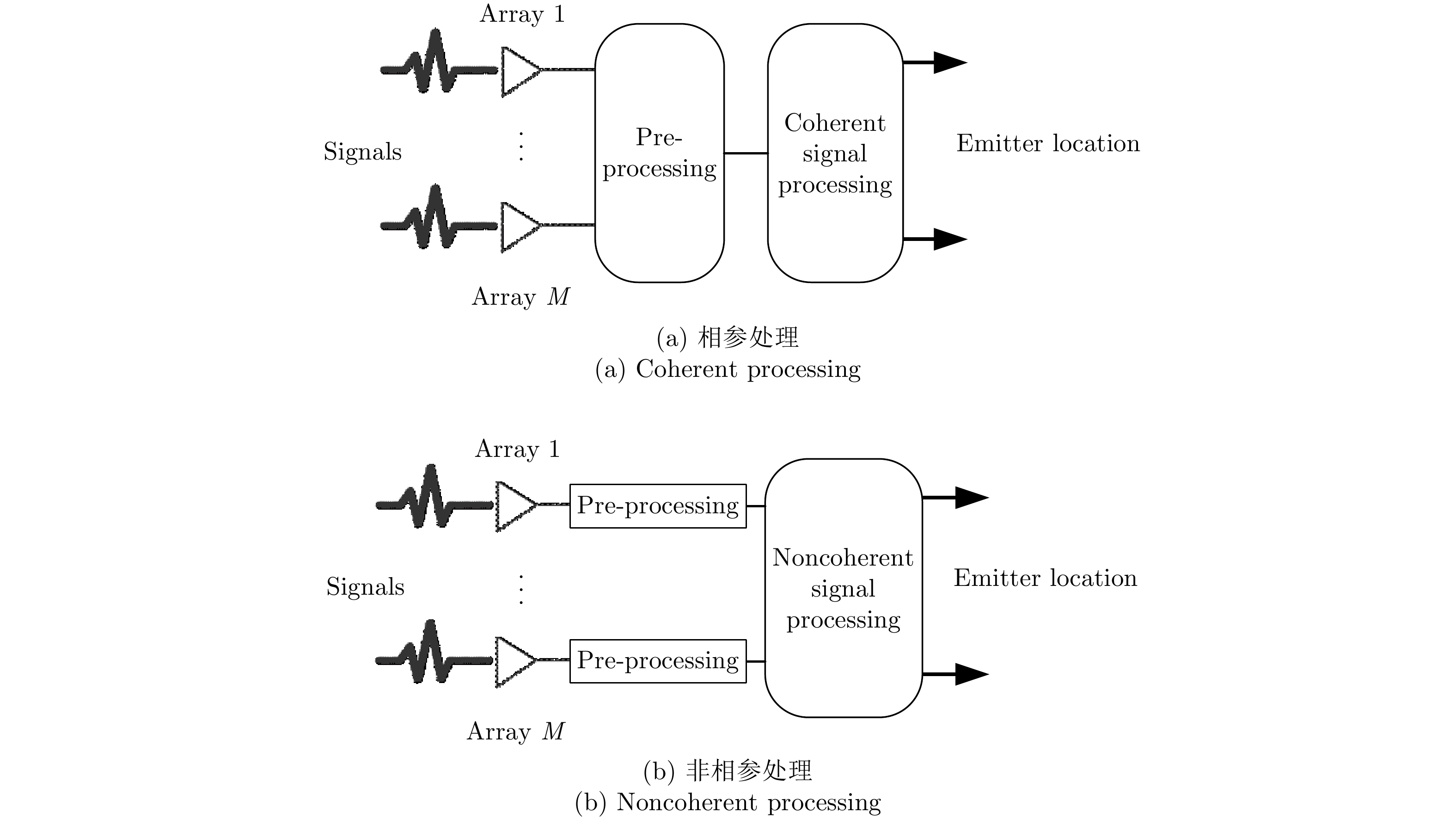
另外一类则是通过相参处理的方式对观测信号进行处理，构建相参类型的代价函数。目前直接定位相参的处理方式可以分为两种，一种是针对宽带信号提出的^[58]，它将一个完整的宽带信号采样划分成多个不重叠的短时间信号片段，等效形成多个窄带信号采样，分别对这些短时间信号片段进行处理，通过累加的方式构建代价函数，估计辐射源的位置。这种处理方式与非相参的直接定位法^[57]相比，虽然都利用的是TDOA和FDOA这两个信息类型，代价函数也都是基于ML的方法建立的，但是前者具有更高的定位精度。另外一种相参处理则是将多个阵列的阵列响应向量联立成为一个大的阵列响应向量^[49]，将空间中多个阵列分别进行信号处理的方式转变成空间中一个大的阵列集中进行信号处理的方式，可以等效视为阵列孔径的增加。这种相参处理和其它非相参处理的示意图如图3所示。通过这种处理，直接定位的定位精度和分辨率都大幅度提升，但是由于联合的阵列向量维数的提升，使得计算量也大大增加。除此之外，由于这种相参处理将多个阵列等效成一个阵列，因此其定位性能受阵列间时频不同步、阵列模型误差等因素影响较大。

图  3  相参直接定位信号处理和非相参直接定位信号处理示意图

Figure  3.  Diagrammatic drawings of coherent processing and noncoherent processing of DPD

下载: 全尺寸图片 幻灯片

4.3   改进阵列构型

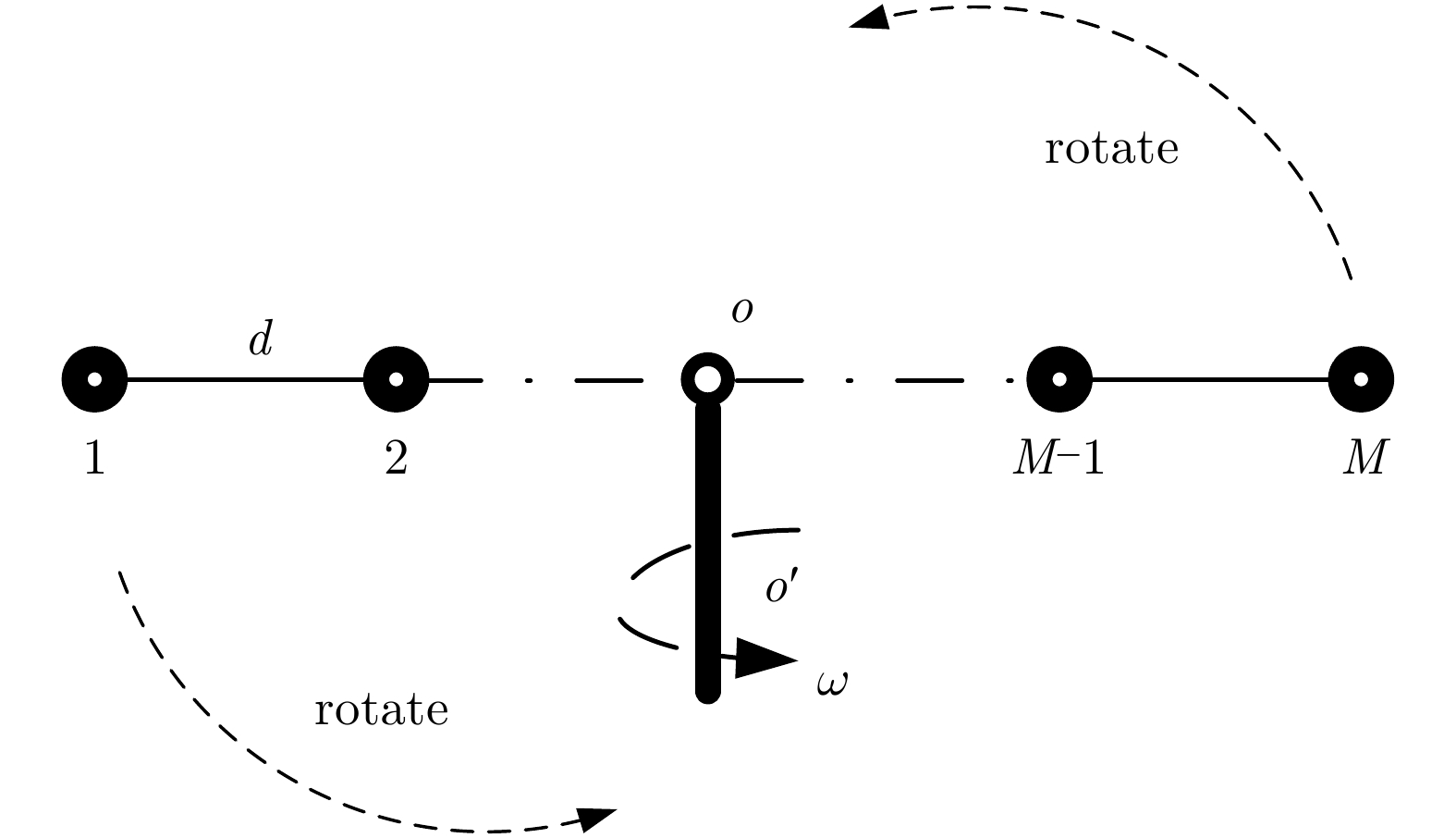
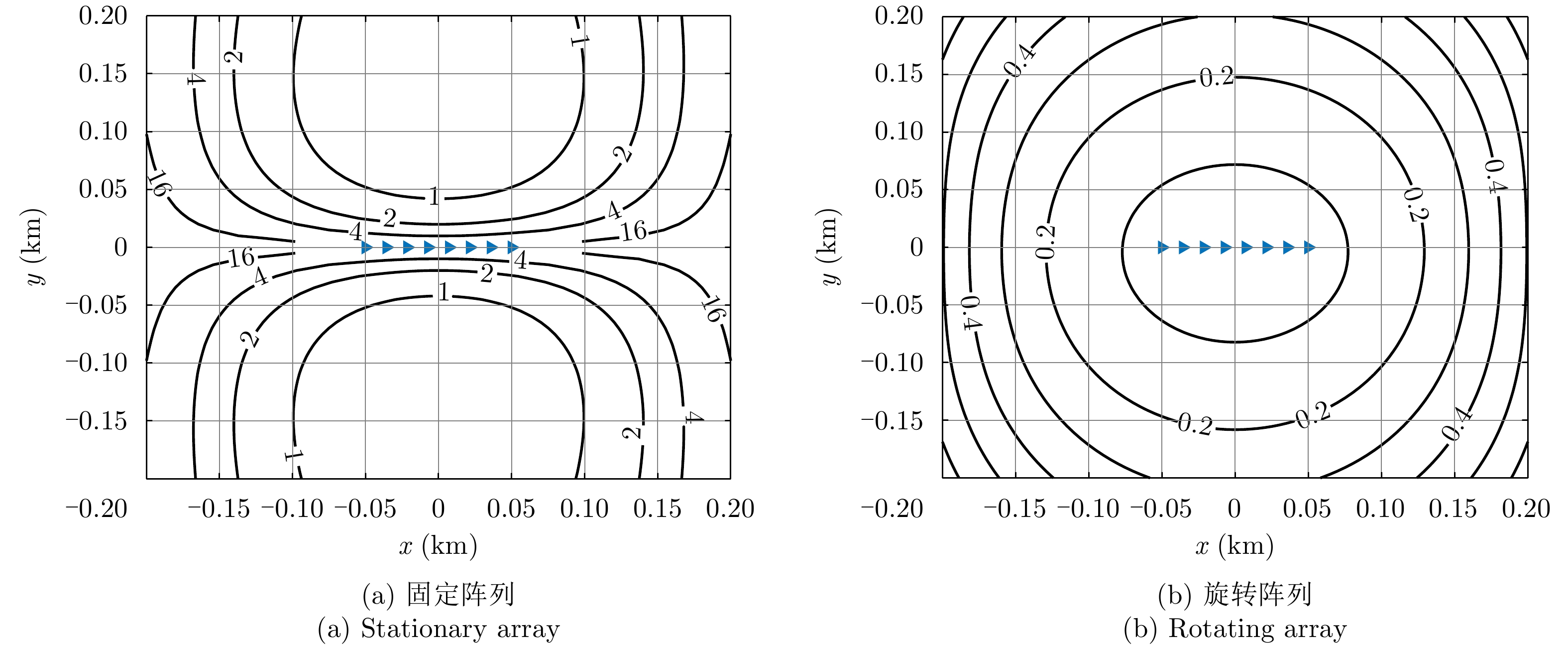
目前直接定位技术主要依托均匀线阵实现信号截获，并利用谱分解的方法实现多个辐射源的定位，因此其最多可定位的辐射源个数为 $M - 1$ 个，其中 $M$ 为均匀线阵的阵元数。这种较低自由度的直接定位技术难以满足当前多目标复杂电磁环境。为解决这一问题，稀疏阵列(Sparse Array, SA)中的互质阵列首先被应用于对非圆信号波形的直接定位之中^[98]，实现了直接定位自由度和定位精度的提升。该工作是基于非圆信号特征实现的阵列孔径和观测数据维度的增加，实质上其性能提升仅仅来自于互质阵列物理阵列孔径的增加和非圆信号的特性，并未充分利用互质阵列对应的差分共性阵列(difference co-array)的优势。同样是针对非圆信号，为了充分挖掘稀疏阵列特性对直接定位性能的提升，文献[99,100]分别将互质阵列和嵌套阵列引入到对非圆信号的直接定位之中，除了应用非圆信号的特征，该工作发挥了嵌套阵列和互质阵列在增加直接定位自由度方面的优势。

改进阵列构型除了在增加自由度方面的效果，对于提升定位的精度和分辨率又会带来增益。最近，本文作者提出了一种基于旋转线阵(Rotating Linear Array, RLA)的运动直接定位方法^[88]。通过转台等时变机构牵引阵列旋转，实现各阵元相对参考阵元的时变，其结构示意图如图4所示，其中 $\omega$ 为旋转角速度， $d$ 为阵元间隔。经过理论性能分析和计算机仿真验证可知，采用旋转均匀线阵截获信号，并构建相适应的直接定位代价函数，可以显著提升直接定位的定位精度和分辨率，并且可以消除固定均匀线阵的定位模糊区域，增加系统的可观测性。以CRLB计算的使用单个均匀线阵和旋转均匀线阵直接定位的几何精度因子(Geometrical Dilution Of Precision, GDOP)如图5所示。

图  4  旋转线阵结构示意图

Figure  4.  The diagrammatic drawing of rotating array

下载: 全尺寸图片 幻灯片

图  5  固定线阵和旋转线阵直接定位GDOP

Figure  5.  The GDOP of DPD using stationary array and rotating array

下载: 全尺寸图片 幻灯片

除了将稀疏阵列和旋转阵列应用于直接定位，多输入多输出(Multiple-Input Multiple-Output, MIMO)领域的部分学者也倡议将MIMO系统应用于直接定位。利用MIMO雷达的多个接收天线截获目标信号，文献[101]提出了一种基于最大似然的直接定位算法，该方法充分利用了MIMO雷达分辨率精度方面的优势，适用于有源和无源两种MIMO系统，在低信噪比下表现出比两步法更高的定位精度。文献[102]则提出了一种多径条件下基于MIMO的直接定位算法，实现了对信号已知辐射源的高精度定位。以上提到的定位方法都利用的是AOA和TDOA这两种信息量，而文献[103]则提出一种利用MIMO雷达仅基于多普勒频移实现直接定位的方法，该方法在多个运动站发送信号，经目标发射后被多个静止观测站接收的有源应用场景中有效。

除了以上介绍的3种方法之外，也有部分学者使用稀疏重构或者压缩感知的手段直接估计辐射源的位置^[104,105]。这种处理方式无需辐射源个数的先验信息，并提升采样数较少状态下的直接定位精度和分辨率。

5.   直接定位快速算法

给定直接定位的代价函数之后，就可以通过代价函数求解辐射源的位置。由于代价函数与辐射源位置之间高度非线性，难以给出位置估计的解析解。目前，已有的直接定位方法大部分都是通过穷尽搜索法进行求解的。但是由于其处理的是原始信号采样点，相比于两步定位法中的中间参数，数据量极大，因此带来的计算复杂度也很高。穷尽搜索法需要在可行解空间中进行网格划分，而划分的网格密度决定着计算量的大小，这就造成了计算复杂度与精度之间的矛盾。

目前交替投影(Alternating Projection, AP)技术^[106]、解耦算法(Decoupled Algorithm, DA)^[52]、期望最大算法(Expectation Maximization, EM)^[45]以及牛顿或泰勒级数迭代算法^[56,107]已经应用于快速求解直接定位的代价函数。AP算法在解决基于ML的直接定位问题中可以有效地将多维搜索转换为多个低维搜索，一定程度减少了计算复杂度^[108]。EM算法也可以用来解决基于ML的多站直接定位的计算复杂度问题，它将所有阵元的输出建立为不完备集(incomplete data)，而将所有阵元与辐射源位置之间的距离建立为未观测到的完备集(unobserved complete data)，使用EM算法，将辐射源位置和各个阵列的不同增益以及信号发射时间分离开，将多维的优化问题转换为多个低维优化的问题，对使用多站进行单目标的直接定位具有明显的效果。文献[52]则针对非圆信号(noncircular signals)提出了一种解耦的快速算法。利用非圆信号的特征，该方法可以将复数的特征值分解问题转换成实数的特征值分解，同时将2Q 维的优化问题转换成为Q 个2 维迭代优化问题，它本质上是一种利用非圆信号的特征改良的AP算法，仅对非圆信号有效，对于其它信号，其等效为AP算法。针对将矩阵最大特征值作为代价函数的直接定位方法，基于Hermitian矩阵特征值扰动定理可以使用Newton迭代对该类型代价函数进行迭代求解^[56]；此外，也可以类似地使用泰勒级数迭代法则实现一般性代价函数的迭代求解^[107]。它们都极大程度地降低了直接定位代价函数求解的计算复杂度。与其它类似的迭代方法一样，这两种方法对初始迭代点敏感，当初始点选取不当时，容易造成迭代发散。相关文献中提出使用两步法^[56,107]来确定初始点，但这种思路有可能在低信噪比下失效，难以体现DPD对低信噪比的适应能力。

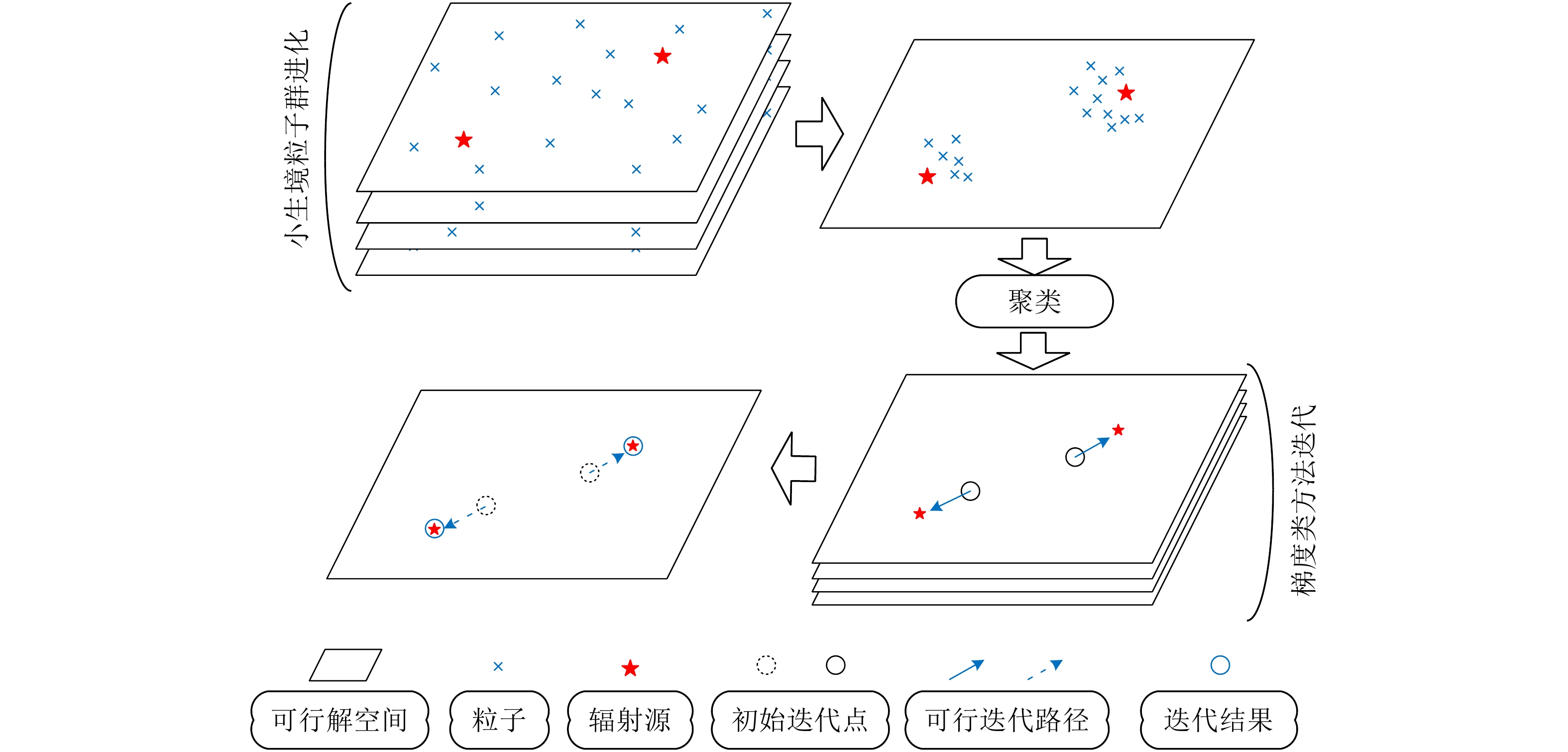
以上提到的方法都难以避免重复多次对代价函数进行低维搜索或者初始化困难的问题。为了进一步降低计算复杂度，部分学者尝试将智能优化算法应用到求解直接定位的代价函数之中^[48]。实际上，利用直接定位代价函数求解辐射源位置实际上是一个优化问题，而优化问题是一个广泛存在于科学研究中各个领域的问题。从优化问题求解极值解个数的角度出发，求解直接定位代价函数本质上属于多模态优化 (Multimodal Optimization, MO)^[109]。基于环邻域拓扑的无参数粒子群算法(Ring Neighborhood Topology based PSO, RNTPSO)^[110,111]在解决这一问题上表现出了较为理想的效果。因此，本文作者在文献[48]中提出了一种基于小生境粒子群优化法(RNTPSO中的一种)和梯度类法(Broyden-Fletcher-Goldfarb-Shanno, BFGS)的融合直接定位快速算法，大大降低了直接定位算法的计算复杂度。该快速算法的基本思路是，先利用基于小生境粒子群优化法在较少的粒子进化次数后，通过简单的聚类方法对进化结果进行聚类，给出辐射源位置的粗估计；然后利用梯度类方法对其进行迭代，直至收敛。所提算法一种可能的代价函数优化过程如图6所示。

图  6  基于小生境粒子群优化和BFGS的直接定位代价函数优化过程示意图

Figure  6.  The optimized process of DPD cost function based on RNTPSO and BFGS

下载: 全尺寸图片 幻灯片

6.   直接定位模型误差校正技术

与其它参数估计问题一样，直接定位对辐射源位置估计的高精度特性是以准确的模型为前提的。当模型存在误差，直接定位的性能将严重退化，因此分析误差模型下直接定位方法的性能以及研究消除模型误差干扰的方法对于将直接定位推广到实际应用中具有重要的意义，已经吸引了国内外学者大量的研究。

目前，已有的针对模型误差条件下的直接定位方面的研究可见于文献[39-42,112-115]。其中，文献[39,41]测试了在阵列位置误差、多径、耦合等误差项存在的情况下直接定位方法的性能。结果表明由于直接定位可以在处理过程中忽略较差的观测而使用高质量的观测进行定位，其定位性能在误差模型条件下依然保持着对两步定位法的优势。与这些研究类似，文献[114]仅考虑了由于区域反射体造成的多径现象对直接定位的影响，并获得了与前面文献中得到的类似结果。此外，文献[115]考虑了非视距(Non-Line-Of-Sight, NLOS)路径传播的多径对直接定位性能的影响，并推导了该情况下多径造成的定位误差协方差矩阵的解析表达式。所有以上所提文献都集中于验证各种各样误差影响下的直接定位的性能。然而，它们并没有提出能有效消除这些误差干扰的方法。

与其不同的是，文献[107,112]将这些误差造成的阵列模型的不确定性建模为高斯随机变量，然后使用自校正(self-calibration) 方法消除这些误差的干扰。它们的方法可以有效减少阵列模型误差并达到定位的CRLB。然而，该方法依赖于误差的先验信息，即误差的均值和协方差是已知的。在实际情况中，这些先验信息是难以获得的。针对确定性的传感器幅/相误差，文献[116]建立了其干扰下的截获信号模型，分别基于MUSIC和ML构建了自校正的直接定位方法。这种自校正的方法不需要任何先验信息，并且在自校正过程中传感器幅/相误差的估计是通过解析解的形式给出的，计算量不大，因此具有较好的实用性。但是由于自校正的精度依赖于外辐射源信号的信噪比，当信噪比较低时自校正性能衰减，这将导致直接定位在低信噪比下定位精度高的优势无法保障。

为了解决这一问题，在工程应用中习惯借助友方已知位置辐射源(标校站)对确定性误差进行校准。文献[117]考虑了多个传感器时钟不同步的问题，并使用几个锚源(例如已知位置的广播站等)对时钟不同步进行了校准。为了解决文献[116]中的问题，本文作者提出了基于标校源的直接定位方法对确定性传感器幅/相误差进行校正^[118]，考虑了标校源信号准确已知和信号未知两种情况，给出的校正定位算法可以达到相应的CRLB。

7.   总结与展望

7.1   信号直接定位技术总结

依据直接定位所针对的信息类型、截获信号所用的阵列类型、构建代价函数所使用的方法，可以将直接定位进行详细分类，其在计算复杂度、定位精度、分辨率、自由度各方面也表现出了不同的性能，本节首先对以上内容进行总结，从上述角度出发给出了直接定位技术的总结如表1所示。其中ExS表示穷尽搜索。

表  1  直接定位技术总结表

Table  1.  Conclusive table of DPD

信息类型	阵列	代价函数	优化方法	文献	精度	分辨率	自由度	计算复杂度
DOA/TDOA	ULA	ML	ExS	文献[33]	中	低	低	高
FDOA	ULA	MUSIC	ExS	文献[46,47]	中	中	低	中
TDOA/FDOA	ULA	ML	ExS	文献[50—52]	中	低	低	高
DOA/ FDOA	ULA	ML	ExS	文献[53]	中	低	低	高
DOA/TDOA	ULA	MVDR	ExS	文献[89—93]	中	中	低	中
DOA	ULA	ES	RNTPSO	文献[48]	中	高	低	低
DOA/TDOA	MIMO	ML	ExS	文献[101,102]	高	高	低	高
FDOA	MIMO	ML	ExS	文献[103]	高	高	低	高
TDOA/FDOA	ULA	ML(Coherent)	ExS	文献[58]	高	中	低	高
TDOA/DOA	ULA	MUSIC(Coherent)	ExS	文献[49]	高	高	高	高
Doppler Shift/Rate	Antenna	ML	ExS	文献[87]	中	–	–	高
DOA	SA	MUSIC	ExS	文献[98—100]	低	中	高	高
DOA	RLA	MUSIC	ExS	文献[88]	高	高	低	中
DOA	ULA	MUSIC	AP	文献[106]	中	中	低	低
DOA/TDOA	ULA	ML	EM	文献[45]	中	低	低	中
DOA/TDOA	ULA	ML	DA	文献[52]	中	低	低	中

下载: 导出CSV 

| 显示表格

以上介绍的都是在无源定位应用背景下的直接定位技术，但实际上还有很多学者探讨了有源条件下的直接定位技术^{[46,58,101,103,107,119-123]}。两者的区别主要体现为接收传感器截获信号的未知和准确已知^[46,103]。从信号处理的角度讲，信号已知情况下的模型更为简单，构建的代价函数也更为直观^[58]。已有文献证明即使在信号已知条件下，直接定位相对于传统两步定位法低信噪比适应性更强的优势依然保持^[119]，这一特征使得直接定位在MIMO等雷达系统中被广泛应用^{[101-103,120,122]}。此外，还有学者将长合成孔径的技术引入到直接定位之中^[124]，通过单个平台的移动模拟形成长的阵列孔径，并以合成孔径雷达的方式处理截获数据，实现了辐射源的定位。该技术本质上是一种运动单站直接定位技术，不同的是该技术涵盖了通过带通滤波器和傅里叶变换处理估计发射信号频率的过程，并以辐射源与观测站间的距离和方位代替辐射源位置的描述，通过合成孔径雷达的处理方式实现了信号频率和辐射源位置的联合估计，该技术在一定程度上拓展了直接定位算法的设计思路。

7.2   信号直接定位技术展望

虽然到目前为止，直接定位技术的相关研究已经取得了大量的成果，但受限于自由度难以满足当前复杂电磁环境、通信压力大(多站直接定位)以及计算复杂度高等实际问题，其难以在工程中应用。针对直接定位技术依然存在的上述挑战，相关学者也取得了一定的理论研究成果。例如，采用自适应的直接定位方式减少站间转发次数，降低多站直接定位的通信压力^[125,126]；采用互模糊函数补全的方法，降低代价函数的计算复杂度及观测站间数据传输量^[127]等。从信号直接定位技术发展的角度看，瞄准实际工程应用的直接定位技术已经成为目前研究的主要趋势。在提升直接定位自由度、分辨率，降低计算复杂度，消除实际情况下的典型误差等方面存在着巨大的研究价值。因此，以下3个方面的研究可能会成为后续直接定位研究的重要方向。

(1) 基于智能优化方法的直接定位快速算法。直接定位代价函数求解本质上是一个多模优化的问题。基于智能优化方法的直接定位快速算法研究可以进一步降低直接定位计算复杂度，突破现有硬件条件的限制，有望实现直接定位的实时处理。特别是对于利用单观测站的直接定位，实时处理还将避免原始采样信号的下传、消除硬件存储容量的限制，同时考虑靠单观测站直接定位无需时频同步、无需站间通信的优势，其在工程中具有很好的应用前景。目前已有学者开展了初步的探索，利用训练好的多层感知器神经网络和径向基函数神经网络实现了直接定位代价函数的快速求解，在保持定位精度性能的条件下降低了算法的复杂度^[128]。

(2) 模型误差条件下的智能化直接定位与误差校正技术。在实际应用中，多种类型的模型误差可能同时存在，并且往往也难以确定其数值到底是固定的、波动的还是随机分布的，这使得误差条件下的信号模型非常复杂。当模型误差难以准确建模，通过常规的标校源或自校正的方法难以对误差进行校正时，借助神经网络等数据驱动的智能化方法进行直接定位的思路体现出了较强的吸引力。针对扰动型的阵列模型误差，已有研究尝试使用基于多层感知器的神经网络实现偏差的校准，该方法在有效修正定位偏差方面取得了良好的效果^[129]。但是，在探索更完备的模型误差种类、选取更优智能化方法上依然需要开展大量的研究工作。

(3) 基于先进稀疏阵列的信号直接定位技术。为提高直接定位技术对复杂电磁环境多目标的适应能力，已有学者用非圆信号的特点以及稀疏阵列的特性初步探索了增加运动单站直接定位技术自由度的可能性^[98,100]。虽然基于稀疏阵列的直接定位技术已经提出，但是稀疏阵列的优势还未在直接定位中得到充分挖掘。并且，在使用稀疏阵列对信号进行高自由度直接定位的同时，还需考虑通过信号处理、阵列构型改造等手段保证高自由度下的定位精度和分辨率性能，这一研究是使直接定位技术走向工程应用的重要条件。