- Home
- Articles & Issues
-
Data
- Dataset of Radar Detecting Sea
- SAR Dataset
- SARGroundObjectsTypes
- SARMV3D
- AIRSAT Constellation SAR Land Cover Classification Dataset
- 3DRIED
- UWB-HA4D
- LLS-LFMCWR
- FAIR-CSAR
- MSAR
- SDD-SAR
- FUSAR
- SpaceborneSAR3Dimaging
- Sea-land Segmentation
- SAR Multi-domain Ship Detection Dataset
- SAR-Airport
- Hilly and mountainous farmland time-series SAR and ground quadrat dataset
- SAR images for interference detection and suppression
- HP-SAR Evaluation & Analytical Dataset
- GDHuiYan-ATRNet
- Multi-System Maritime Low Observable Target Dataset
- DatasetinthePaper
- DatasetintheCompetition
- Report
- Course
- About
- Publish
- Editorial Board
- Chinese
| Citation: | Xiang Zhe, Chen Baixiao. Range-angle Decoupled Transmit Beamforming with Frequency Diverse Array (in English)[J]. Journal of Radars, 2018, 7(2): 212-219. doi: 10.12000/JR16113 |
Range-angle Decoupled Transmit Beamforming with Frequency Diverse Array (in English)
DOI: 10.12000/JR16113 CSTR: 32380.14.JR16113
More Information-
Abstract
It has been shown that Frequency Diverse Arrays (FDA) exhibit a range-angle dependent beam steering feature by employing a uniform frequency increment across the array elements. However, this beam pattern generates maxima at multiple range values, possibly leading to loss of signal-to-interference-plus-noise ratio when the interferences are located at any of the maxima. Herein, we prove that the beam pattern of FDA is range-periodic and propose the basic criteria for the FDA configuration to decouple the range and angle. In an illuminated space, a single-maximum beam pattern can be obtained by configuring the frequency increment between the elements. Specific examples have been discussed herein, and the simulation results verify the proposed theory.
-
-
References
[1] Antonik P, Wicks M C, and Griffiths H D. Range dependent beamforming using element level waveform diversity[C]. International Waveform Diversity Design Conference, Las Vegas, NV, USA, Jan. 2006: 22–27.[2] Secmen M, Demir S, and Hizal A. Frequency diverse array antenna with periodic time modulated pattern in range and angle[C]. IEEE Radar Conference, Boston, MA, USA, Apr. 2007: 427–430.[3] Antonik P, Wicks M C, and Griffiths H D. Multi-mission, multi-mode waveform diversity[C]. IEEE Radar Conference, Verona, NY, USA, Apr. 2006: 580–582.[4] Zhuang L and Liu X Z. Precisely beam steering for frequency diverse arrays based on frequency offset selection[C]. International Radar Conference, Bordeaux, France, Oct. 2009: 1–4.[5] Chen Y G, Li Y T, and Wu Y H. Research on the linear frequency diverse array performance[C]. IEEE International Conference on Signal Processing, Beijing, China, Oct. 2010: 2324–2327.[6] Sammartino P F, Backer C J, Griffiths H D. Frequency diverse MIMO techniques for radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 201–222. DOI: 10.1109/TAES.2013.6404099[7] Xu J W, Liao G S, and Zhu S Q. Receive beamforming of frequency diverse array radar systems[C]. 31th URSI General Assembly and Scientific Symposium (URSIGASS), Beijing, China, Aug. 2014: 1–5.[8] Wang W Q. Range-angle dependent transmit beampattern synthesis for linear frequency diverse arrays[J]. IEEE Transactions on Antennas Propagation, 2014, 61(8): 4073–4081.[9] Khan W, Qureshi I M. Frequency diverse array radar with time dependent frequency offset[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13: 758–761. DOI: 10.1109/LAWP.2014.2315215[10] Wang W Q, So H C, Shao H. Nonuniform frequency diverse array for range-angle imaging of targets[J].IEEE Sensors Journal, 2014, 14(8): 2469–2476. DOI: 10.1109/JSEN.2014.2304720[11] Khan W, Qureshi I M, Saeed S. Frequency diverse array radarwith logarithmically increasing frequency offset[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14: 499–502. DOI: 10.1109/LAWP.2014.2368977[12] Xu Y H, Shi X W, Xu J W. Range-angle-dependent beamforming of pulsed frequency diverse array[J]. IEEE Transactions on Antennas Propagation, 2015, 63(7): 3262–2367. DOI: 10.1109/TAP.2015.2423698[13] Gao K, Wang W Q. Decoupled frequency diverse array range-angle-dependent beampattern synthesis using non-linearly increasing frequency offsets[J]. IET Microwaves,Antennas&Propagation, 2016, 10(8): 880–884.[14] Gao K, Wang W Q. Transmit beamspace design for multi-carrier frequency diverse array sensor[J]. IEEE Sensors Journal, 2016, 16(14): 5709–5714. DOI: 10.1109/JSEN.2016.2573379[15] Shao H, Dai J, Xiong J. Dot-shaped range-angle beampattern synthesis for frequency diverse array[J]. IEEE Antennas and Wireless Propagation(published online), 2016. DOI: 10.1109/LAWP.2016.2527818 [16] Schmidt R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas Propagation, 1986, 34(1): 276–280. -
Proportional views
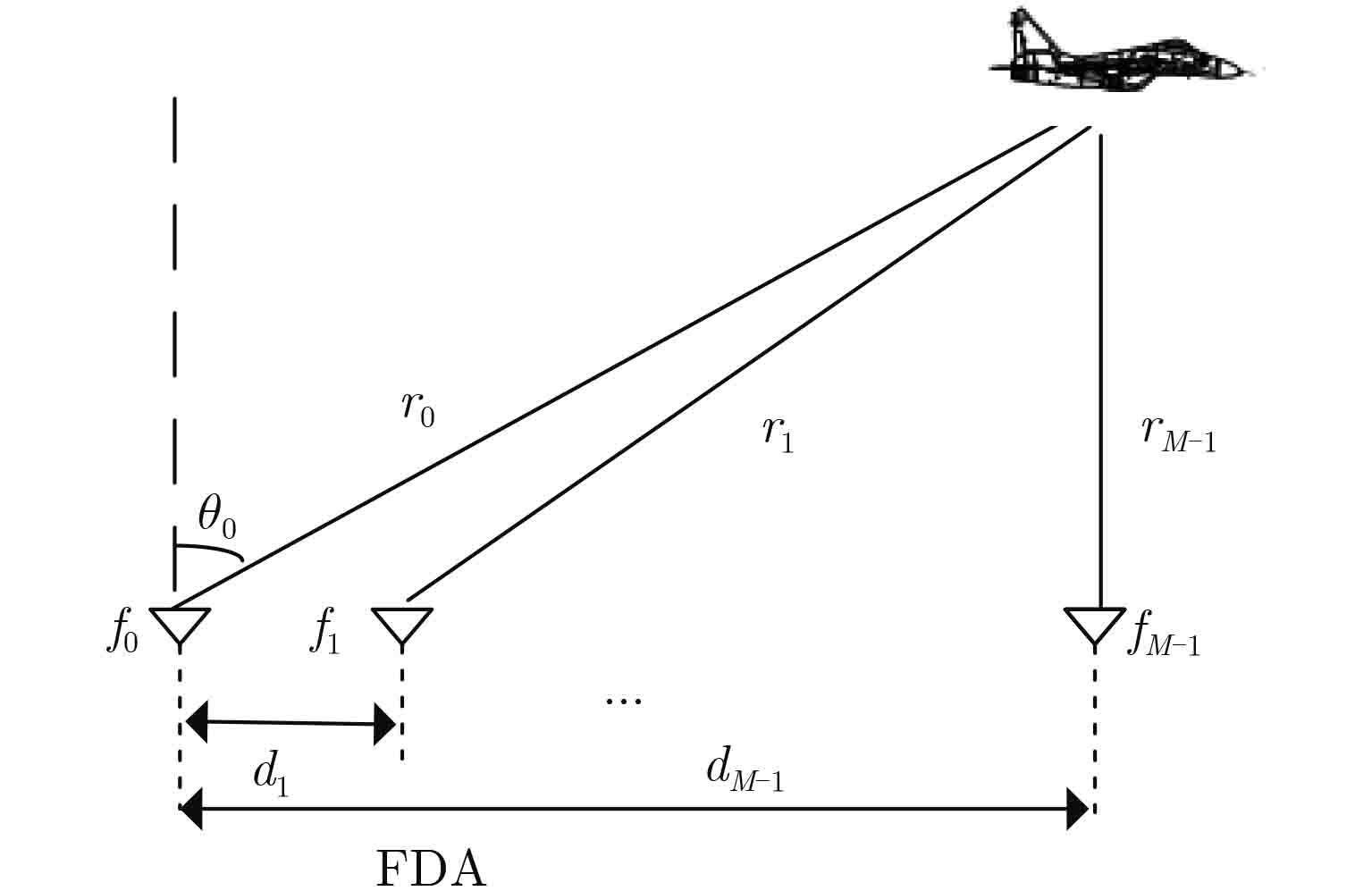
- Figure 1. FDA configuration
- Figure 2. The range-angle distribution diagram for different element
- Figure 4. Range and angle section views of beampattern
- Figure 5. Range versus angle normalized beampattern (target position at (400 km, 20°))
- Figure 3. Range versus angle normalized beampattern


 Submit Manuscript
Submit Manuscript Peer Review
Peer Review Editor Work
Editor Work




 DownLoad:
DownLoad:



