Volume 10 Issue 6
Dec.  2021
Turn off MathJax
Article Contents
Article Navigation >  Journal of Radars  > 2021  >  10(6): 795-810
ZHU Shengqi, YU Kun, XU Jingwei, et al. Research progress and prospect for the noval waveform diverse array radar[J]. Journal of Radars, 2021, 10(6): 795–810. doi: 10.12000/JR21188
Citation: ZHU Shengqi, YU Kun, XU Jingwei, et al. Research progress and prospect for the noval waveform diverse array radar[J]. Journal of Radars, 2021, 10(6): 795–810. doi: 10.12000/JR21188
shu

Research Progress and Prospect for the Noval Waveform Diverse Array Radar

DOI: 10.12000/JR21188

  • National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China

Funds:  The National Natural Science Foundation of China (61931016, 62071344, 62101402, 61911530246), The Excellent Youth Foundation of Shaanxi Scientific Committee (2019JC-16), The China Postdocatoral Science Foundation (2021TQ0261, 2021M702547)
More Information
  • Corresponding author: ZHU Shengqi, zhushengqi8@163.com
  • Received Date: 2021-11-24
  • Accepted Date: 2021-12-23
  • Rev Recd Date: 2021-12-23
    • Available Online: 2021-12-24
  • Publish Date: 2021-12-28
    Abstract
  • It is difficult for the traditional radar to suppress deceptive mainlobe interference and separate the range ambiguous clutter. The proposal of a waveform diverse array changes the way of obtaining information through utilizing degrees-of-freedom in the transmit dimension. Through flexible system design and signal processing methods, this array enhances the ability of information extraction and improves the anti-jamming and detection performance, compared with the traditional phased array and Multiple-Input Multiple-Output (MIMO) radar. This paper summarizes the research progress of waveform diverse array radars in China and overseas and provides the basic concepts of the array diversity system regarding frequency, time, and phase modulation. Furthermore, the research trend of waveform diverse array radars has been discussed. Based on the existing basic theory and key technology research, the advantages of a waveform diverse array in providing new information about targets and increasing the additional controllable degrees-of-freedom of the system are verified, thereby improving the multidimensional detection capability of the new radar system.

     

    • FullText(HTML)
  • loading
    • References(85)
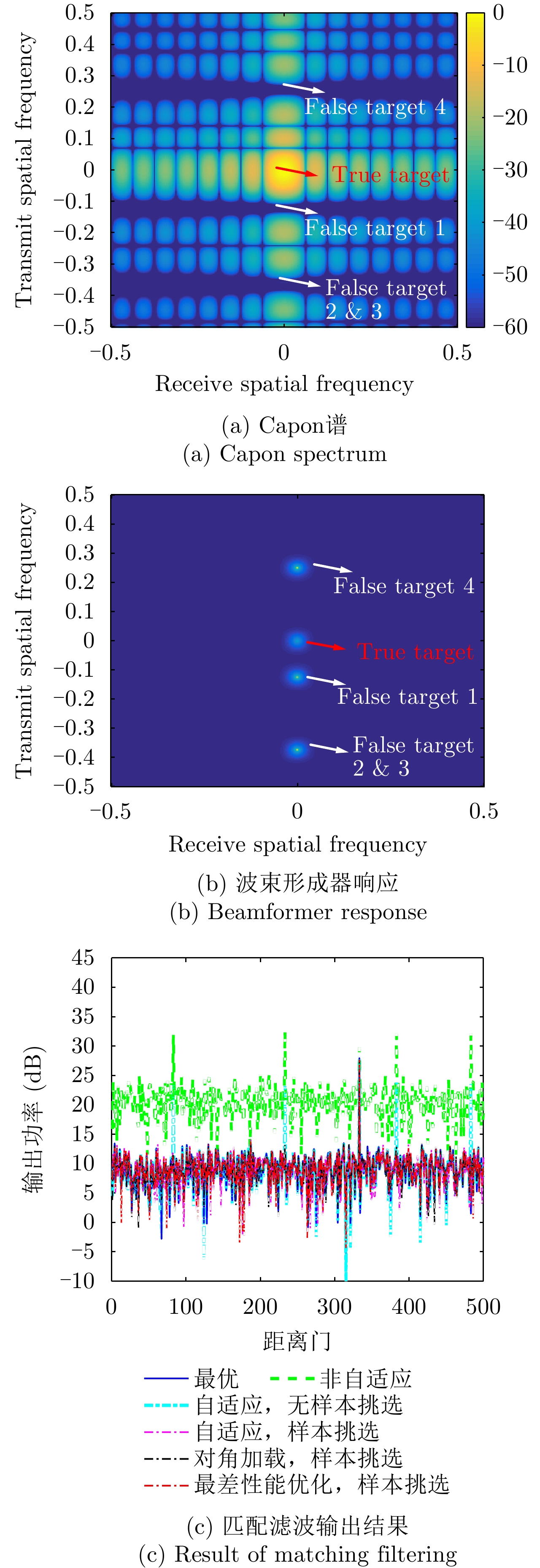
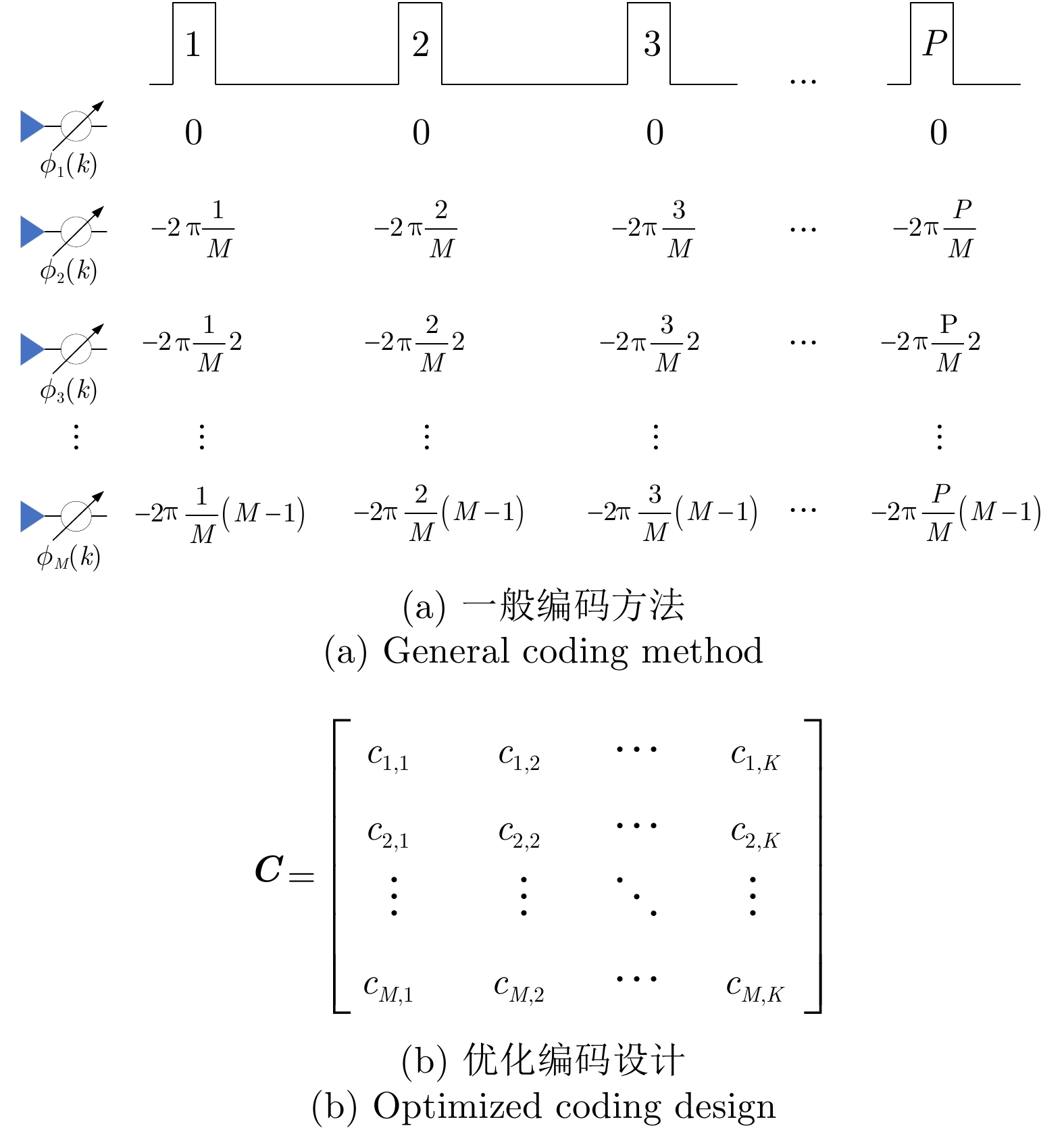
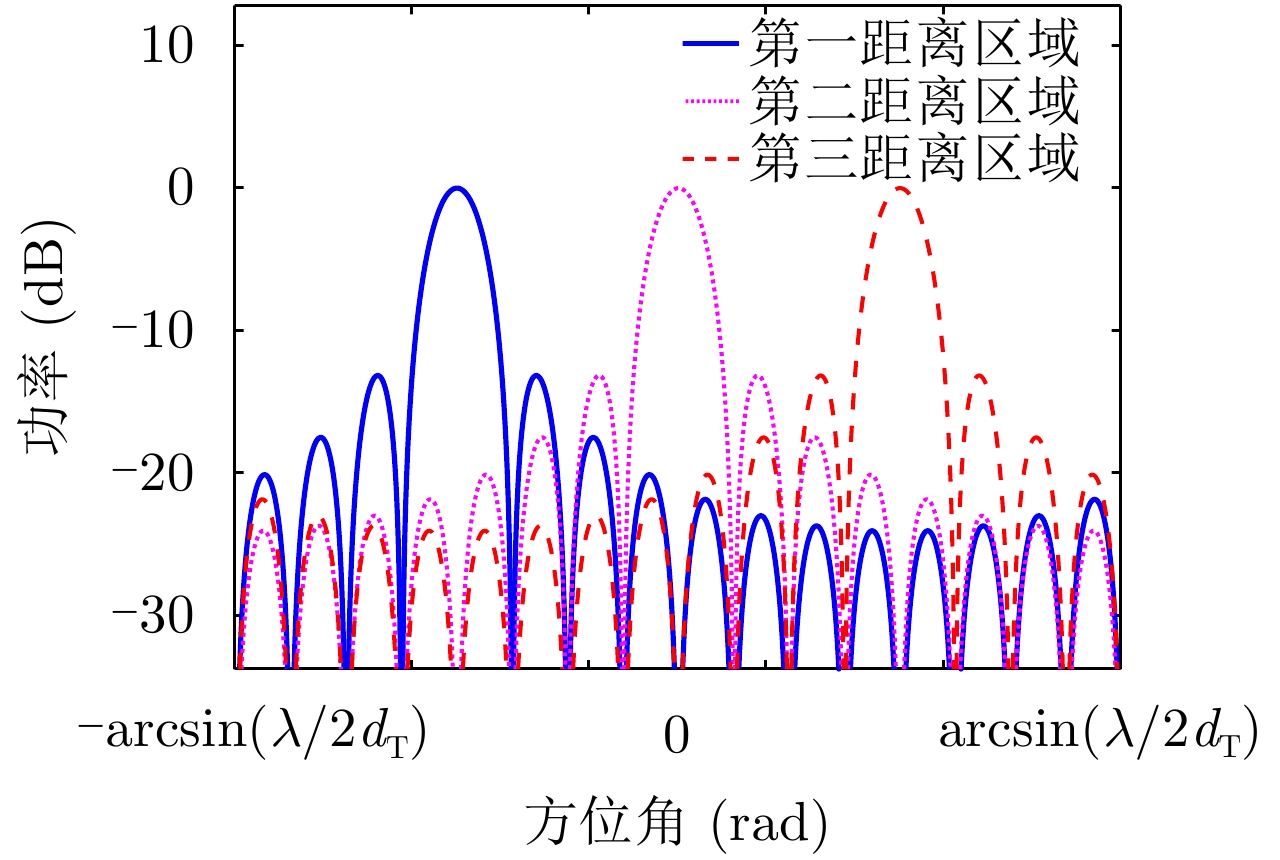
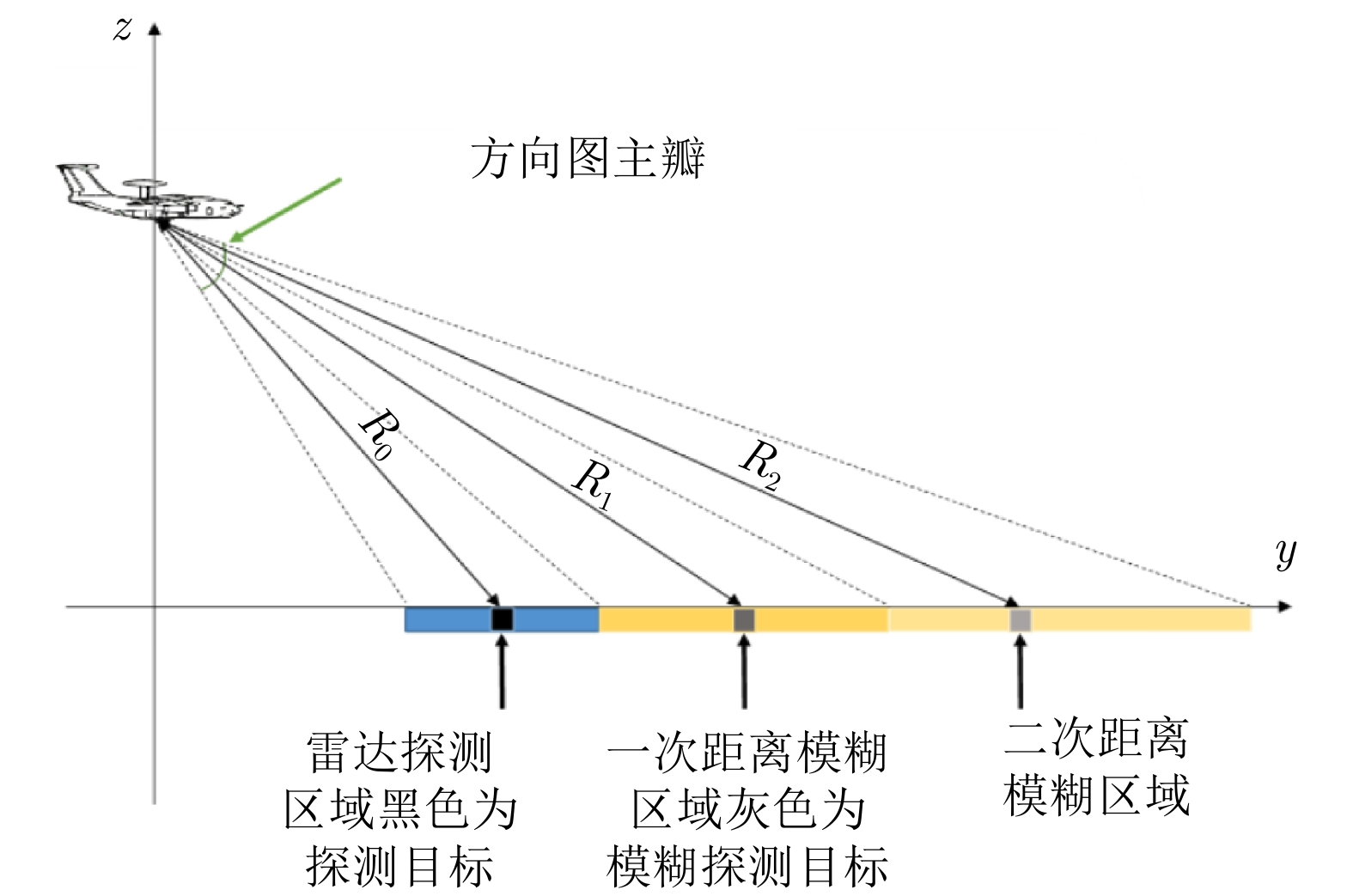
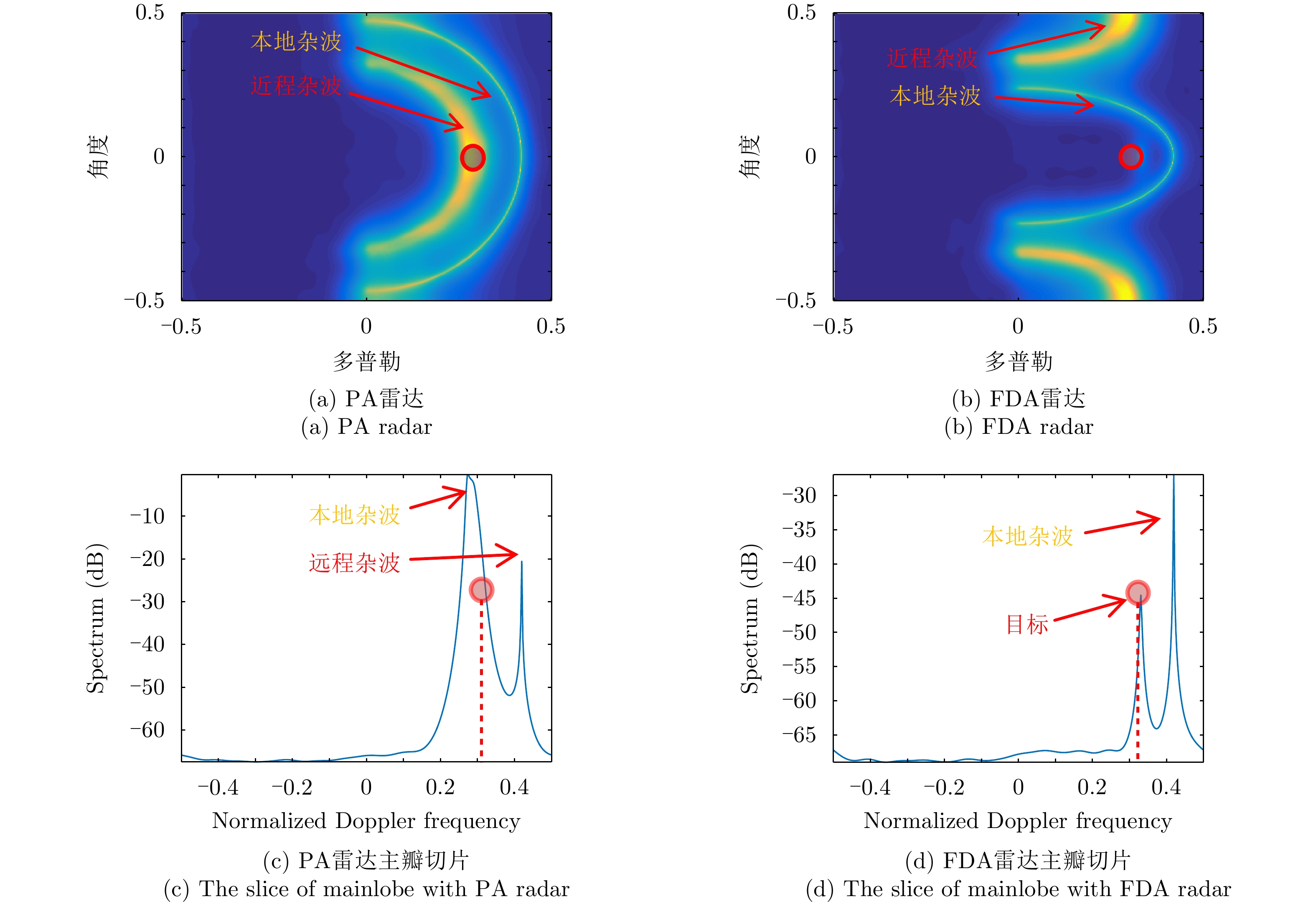
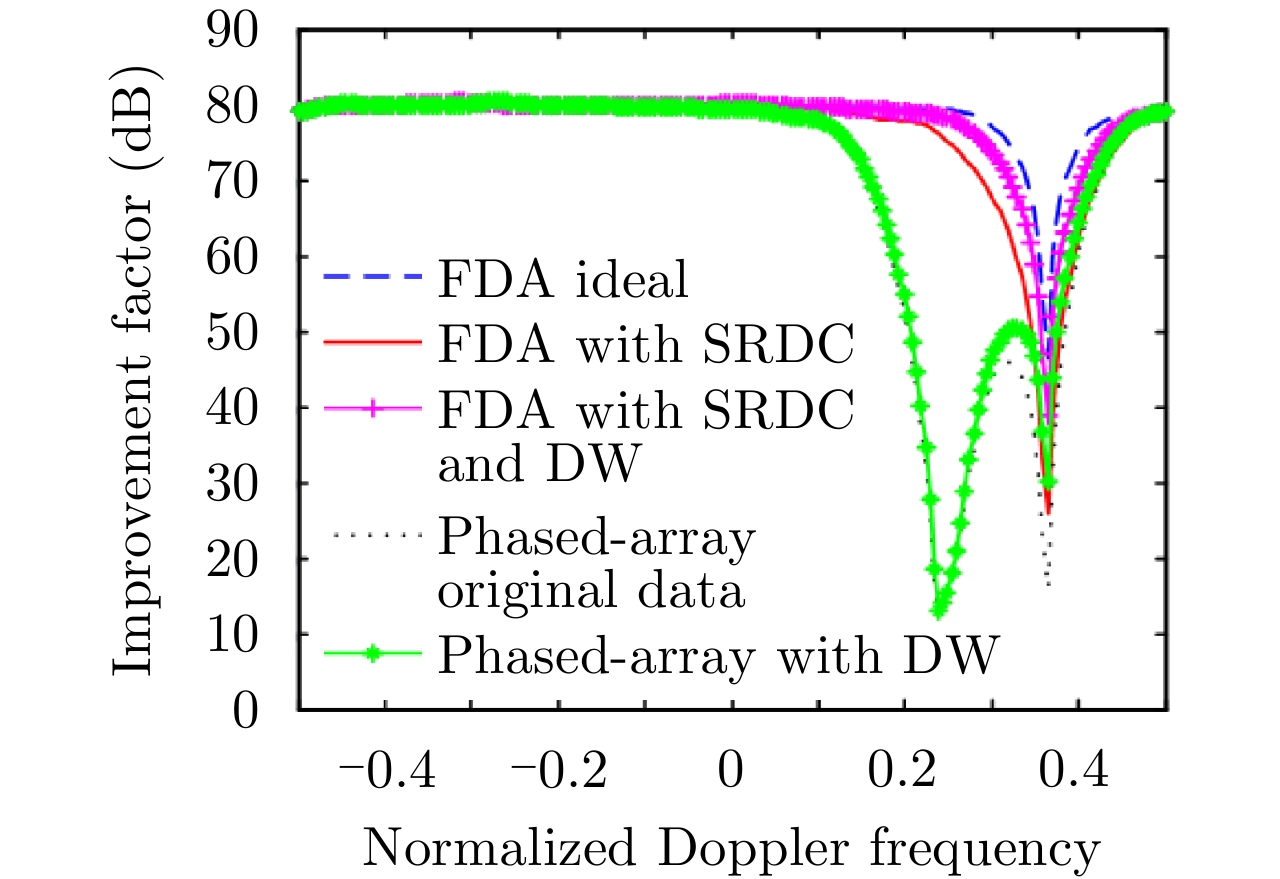
  • [1]
    WICKS M C. A brief history of waveform diversity[C]. 2009 IEEE Radar Conference, Pasadena, USA, 2009: 328–333. doi: 10.1109/RADAR.2009.4977142.
    [2]
    CAPRARO G T, BRADARIC I, and WICKS M C. Waveform diversity and electromagnetic compatibility[C]. 2007 IEEE International Symposium on Electromagnetic Compatibility, Honolulu, USA, 2007: 1–7. doi: 10.1109/ISEMC.2007.40.
    [3]
    GARNHAM J W and ROMAN J R. Why and what is waveform diversity, and how does it affect electromagnetics?[C]. 2007 IEEE International Symposium on Electromagnetic Compatibility, Honolulu, USA, 2007: 1–5. doi: 10.1109/ISEMC.2007.41.
    [4]
    GARNHAM J W and ROMAN J R. How will waveform diversity affect electromagnetic compatibility?[C]. 2007 International Waveform Diversity and Design Conference, Pisa, Italy, 2007: 98–101. doi: 10.1109/WDDC.2007.4339388.
    [5]
    NEHORAI A, GINI F, GRECO M S, et al. Introduction to the issue on adaptive waveform design for agile sensing and communication[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(1): 2–5. doi: 10.1109/jstsp.2007.897065
    [6]
    PAPANDREOU-SUPPAPPOLA A, NEHORAI A, and CALDERBANK R. Waveform-agile sensing and processing [From the Guest Editors][J]. IEEE Signal Processing Magazine, 2009, 26(1): 10–11. doi: 10.1109/msp.2008.930413
    [7]
    兰岚, 许京伟, 朱圣棋, 等. 波形分集阵列雷达抗干扰进展[J]. 系统工程与电子技术, 2021, 43(6): 1437–1451. doi: 10.12305/j.issn.1001-506X.2021.06.01

    LAN Lan, XU Jingwei, ZHU Shengqi, et al. Advances in anti-jamming using waveform diverse array radar[J]. Systems Engineering and Electronics, 2021, 43(6): 1437–1451. doi: 10.12305/j.issn.1001-506X.2021.06.01
    [8]
    ANTONIK P, WICKS M C, GRIFFITHS H D, et al. Multi-mission multi-mode waveform diversity[C]. 2006 IEEE Conference on Radar, Verona, USA, 2006: 580–582. doi: 10.1109/RADAR.2006.1631858.
    [9]
    许京伟, 朱圣棋, 廖桂生, 等. 频率分集阵雷达技术探讨[J]. 雷达学报, 2018, 7(2): 167–182. doi: 10.12000/JR18023

    XU Jingwei, ZHU Shengqi, LIAO Guisheng, et al. An overview of frequency diverse array radar technology[J]. Journal of Radars, 2018, 7(2): 167–182. doi: 10.12000/JR18023
    [10]
    WANG Wenqin. Overview of frequency diverse array in radar and navigation applications[J]. IET Radar, Sonar & Navigation, 2016, 10(6): 1001–1012. doi: 10.1049/iet-rsn.2015.0464
    [11]
    王文钦, 邵怀宗, 陈慧. 频控阵雷达: 概念、原理与应用[J]. 电子与信息学报, 2016, 38(4): 1000–1011. doi: 10.11999/JEIT151235

    WANG Wenqin, SHAO Huaizong, and CHEN Hui. Frequency diverse array radar: Concept, principle and application[J]. Journal of Electronics &Information Technology, 2016, 38(4): 1000–1011. doi: 10.11999/JEIT151235
    [12]
    王文钦, 陈慧, 郑植, 等. 频控阵雷达技术及其应用研究进展[J]. 雷达学报, 2018, 7(2): 153–166. doi: 10.12000/JR18029

    WANG Wenqin, CHEN Hui, ZHENG Zhi, et al. Advances on frequency diverse array radar and its applications[J]. Journal of Radars, 2018, 7(2): 153–166. doi: 10.12000/JR18029
    [13]
    SECMEN M, DEMIR S, HIZAL A, et al. Frequency diverse array antenna with periodic time modulated pattern in range and angle[C]. 2007 IEEE Radar Conference, Waltham, USA, 2007: 427–430. doi: 10.1109/RADAR.2007.374254.
    [14]
    XU Yanhong, SHI Xiaowei, XU Jingwei, et al. Beampattern analysis of planar frequency diverse array[J]. International Journal of RF and Microwave Computer-Aided Engineering, 2015, 25(5): 436–444. doi: 10.1002/mmce.20881
    [15]
    WANG Wenqin and SO H C. Transmit subaperturing for range and angle estimation in frequency diverse array radar[J]. IEEE Transactions on Signal Processing, 2014, 62(8): 2000–2011. doi: 10.1109/TSP.2014.2305638
    [16]
    KHAN W, QURESHI I M, and SAEED S. Frequency diverse array radar with logarithmically increasing frequency offset[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 14: 499–502. doi: 10.1109/LAWP.2014.2368977
    [17]
    SHAO Huaizong, DAI Jun, XIONG Jie, et al. Dot-shaped range-angle beampattern synthesis for frequency diverse array[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 1703–1706. doi: 10.1109/LAWP.2016.2527818
    [18]
    LIU Yimin, RUAN Hang, WANG Lei, et al. The random frequency diverse array: A new antenna structure for uncoupled direction-range indication in active sensing[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11(2): 295–308. doi: 10.1109/JSTSP.2016.2627183
    [19]
    BASIT A, QURESHI I M, KHAN W, et al. Beam pattern synthesis for an FDA radar with hamming window-based nonuniform frequency offset[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 2283–2286. doi: 10.1109/LAWP.2017.2714761
    [20]
    XIONG Jie, WANG Wenqin, SHAO Huaizong, et al. Frequency diverse array transmit beampattern optimization with genetic algorithm[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 16: 469–472. doi: 10.1109/LAWP.2016.2584078
    [21]
    LAN Lan, LIAO Guisheng, XU Jingwei, et al. Range-angle pencil-beamforming for non-uniformly distributed array radar[J]. Multidimensional Systems and Signal Processing, 2018, 29(3): 867–886. doi: 10.1007/s11045-017-0477-9
    [22]
    WANG Wenqin, DAI Miaomiao, and ZHENG Zhi. FDA Radar ambiguity function characteristics analysis and optimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(3): 1368–1380. doi: 10.1109/TAES.2017.2785598
    [23]
    XU Yanhong, SHI Xiaowei, XU Jingwei, et al. Range-angle-dependent beamforming of pulsed frequency diverse array[J]. IEEE Transactions on Antennas and Propagation, 2015, 63(7): 3262–3267. doi: 10.1109/TAP.2015.2423698
    [24]
    SHAO Huaizong, LI Xiong, WANG Wenqin, et al. Time-invariant transmit beampattern synthesis via weight design for FDA radar[C]. 2016 IEEE Radar Conference, Philadelphia, USA, 2016: 1–4. doi: 10.1109/RADAR.2016.7485212.
    [25]
    WANG Yuxi, LI Wei, HUANG Guoce, et al. Time-invariant range-angle-dependent beampattern synthesis for FDA radar targets tracking[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 2375–2379. doi: 10.1109/LAWP.2017.2718580
    [26]
    CHEN Baoxin, CHEN Xiaolong, HUANG Yong, et al. Transmit beampattern synthesis for the FDA radar[J]. IEEE Antennas and Wireless Propagation Letters, 2018, 17(1): 98–101. doi: 10.1109/LAWP.2017.2776957
    [27]
    XU Jingwei, LIAO Guisheng, ZHU Shengqi, et al. Joint range and angle estimation using MIMO radar with frequency diverse array[J]. IEEE Transactions on Signal Processing, 2015, 63(13): 3396–3410. doi: 10.1109/TSP.2015.2422680
    [28]
    XIONG Jie, WANG Wenqin, and GAO Kuandong. FDA-MIMO radar range-angle estimation: CRLB, MSE, and resolution analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 284–294. doi: 10.1109/TAES.2017.2756498
    [29]
    卢刚. 雷达有源假目标抑制方法研究[D]. [博士论文], 电子科技大学, 2008.

    LU Gang. Study of algorithms on suppression of radar active false targets[D]. [Ph. D. dissertation], University of Electronic Science and Technology of China, 2008.
    [30]
    XU Jingwei, LIAO Guisheng, ZHU Shengqi, et al. Deceptive jamming suppression with frequency diverse MIMO radar[J]. Signal Processing, 2015, 113: 9–17. doi: 10.1016/j.sigpro.2015.01.014
    [31]
    LAN Lan, LIAO Guisheng, XU Jingwei, et al. Suppression approach to main-beam deceptive jamming in FDA-MIMO radar using nonhomogeneous sample detection[J]. IEEE Access, 2018, 6(1): 34582–34597. doi: 10.1109/ACCESS.2018.2850816
    [32]
    LAN Lan, LIAO Guisheng, and XU Jingwei. A method to suppress the main-beam deceptive jamming in FDA-MIMO radar with random polyphase codes[C]. The 10th Sensor Array and Multichannel Signal Processing Workshop, Sheffield, UK, 2018: 509–513. doi: 10.1109/SAM.2018.8448892.
    [33]
    谭清莉, 张艺乐, 张伟, 等. FDA-MIMO雷达主瓣欺骗干扰对抗方法[J]. 雷达科学与技术, 2017, 15(6): 671–676. doi: 10.3969/j.issn.1672-2337.2017.06.017

    TAN Qingli, ZHANG Yile, ZHANG Wei, et al. A method of mainlobe deception jamming countermeasure in FDA-MIMO radar[J]. Radar Science and Technology, 2017, 15(6): 671–676. doi: 10.3969/j.issn.1672-2337.2017.06.017
    [34]
    张昭建, 谢军伟, 李欣, 等. 基于FDA-MIMO的距离欺骗干扰鉴别方法[J]. 北京航空航天大学学报, 2017, 43(4): 738–746. doi: 10.13700/j.bh.1001-5965.2016.0257

    ZHANG Zhaojian, XIE Junwei, LI Xin, et al. Discrimination method of range deception jamming based on FDA-MIMO[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(4): 738–746. doi: 10.13700/j.bh.1001-5965.2016.0257
    [35]
    张劲东, 李彧晟, 朱晓华. 基于波形分集的雷达抗欺骗干扰[J]. 数据采集与处理, 2010, 25(2): 138–142. doi: 10.3969/j.issn.1004-9037.2010.02.002

    ZHANG Jindong, LI Yusheng, and ZHU Xiaohua. Approach of radar against deception jamming based on waveform diversity[J]. Journal of Data Acquisition &Processing, 2010, 25(2): 138–142. doi: 10.3969/j.issn.1004-9037.2010.02.002
    [36]
    LI Zhihui, ZHANG Yongshun, GE Qichao, et al. A robust deceptive jamming suppression method based on covariance matrix reconstruction with frequency diverse array MIMO radar[C]. 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 2017: 1–5. doi: 10.1109/ICSPCC.2017.8242590.
    [37]
    WANG Yuzhuo and ZHU Shengqi. Range Ambiguous clutter suppression for FDA-MIMO forward looking airborne radar based on main lobe correction[J]. IEEE Transactions on Vehicular Technology, 2021, 70(3): 2032–2046. doi: 10.1109/TVT.2021.3057436
    [38]
    WANG Yuzhuo and ZHU Shengqi. Main-beam range deceptive jamming suppression with simulated annealing FDA-MIMO radar[J]. IEEE Sensors Journal, 2020, 20(16): 9056–9070. doi: 10.1109/JSEN.2020.2982194
    [39]
    XU Jingwei, ZHU Shengqi, and LIAO Guisheng. Range ambiguous clutter suppression for airborne FDA-STAP radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1620–1631. doi: 10.1109/JSTSP.2015.2465353
    [40]
    XU Jingwei, LIAO Guisheng, and SO H C. Space-time adaptive processing with vertical frequency diverse array for range-ambiguous clutter suppression[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(9): 5352–5364. doi: 10.1109/TGRS.2016.2561308
    [41]
    XU Jingwei, LIAO Guisheng, ZHANG Yuhong, et al. An adaptive range-angle-Doppler processing approach for FDA-MIMO radar using three-dimensional localization[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11(2): 309–320. doi: 10.1109/JSTSP.2016.2615269
    [42]
    WEN Cai, PENG Jinye, ZHOU Yan, et al. Enhanced three-dimensional joint domain localized STAP for airborne FDA-MIMO radar under dense false-target jamming scenario[J]. IEEE Sensors Journal, 2018, 8(10): 4154–4166. doi: 10.1109/JSEN.2018.2820905
    [43]
    WANG Wenqin, SO H C, and SHAO Huaizong. Nonuniform frequency diverse array for range-angle imaging of targets[J]. IEEE Sensors Journal, 2014, 14(8): 2469–2476. doi: 10.1109/JSEN.2014.2304720
    [44]
    王成浩, 廖桂生, 许京伟. FDA-SAR 高分辨宽测绘带成像距离解模糊方法[J]. 电子学报, 2017, 45(9): 2085–2091. doi: 10.3969/j.issn.0372-2112.2017.09.005

    WANG Chenghao, LIAO Guisheng, and XU Jingwei. Range ambiguity resolving method for high-resolution and wide-swath imaging with FDA-SAR[J]. Acta Electronica Sinica, 2017, 45(9): 2085–2091. doi: 10.3969/j.issn.0372-2112.2017.09.005
    [45]
    XU Luzhou, LI Jian, and STOICA P. Radar imaging via adaptive MIMO techniques[C]. The 14th European Signal Processing Conference, Florence, Italy, 2006.
    [46]
    LI Jian and STOICA P. MIMO radar with colocated antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5): 106–114. doi: 10.1109/MSP.2007.904812
    [47]
    TABRIKIAN J. Bounds for target localization by MIMO radars[C]. The Fourth IEEE Workshop on Sensor Array and Multichannel Processing, 2006, Waltham, USA, 2006: 278–281. doi: 10.1109/SAM.2006.1706137.
    [48]
    HUA Guang and ABEYSEKERA S S. MIMO radar transmit beampattern design with ripple and transition band control[J]. IEEE Transactions on Signal Processing, 2013, 61(11): 2963–2974. doi: 10.1109/TSP.2013.2252173
    [49]
    BABUR G, AUBRY P, and CHEVALIER F L. Space-time radar waveforms: Circulating codes[J]. Journal of Electrical and Computer Engineering, 2013, 2013: 809691. doi: 10.1155/2013/809691
    [50]
    CHEVALIER F L. Space-time transmission and coding for airborne radars[J]. Radar Science and Technology, 2008, 6(6): 411–421.
    [51]
    MELVIN W L and SCHEER J A. Principles of Modern Radar: Advanced Techniques[M]. Edison: SciTech, 2013.
    [52]
    BABUR G, AUBRY P, and CHEVALIER F L. Space-time codes for active antenna systems: Comparative performance analysis[C]. The IET International Radar Conference 2013, Xi’an, China, 2013: 1–6. doi: 10.1049/cp.2013.0240.
    [53]
    FAUCON T, PINAUD G, and CHEVALIER F L. Mismatched filtering for circulating space-time codes[C]. The IET International Radar Conference 2015, Hangzhou, China, 2015. doi: 10.1049/cp.2015.1185.
    [54]
    BABUR G, AUBRY P, and CHEVALIER F L. Simple transmit diversity technique for phased array radar[J]. IET Radar, Sonar & Navigation, 2016, 10(6): 1046–1056. doi: 10.1049/iet-rsn.2015.0311
    [55]
    ROUSSEL K, BABUR G, and CHEVALIER F L. Optimization of low sidelobes radar waveforms: Circulating codes[C]. 2014 International Radar Conference, Lille, France, 2014: 1–6. doi: 10.1109/RADAR.2014.7060290.
    [56]
    BABUR G, AUBRY P J, and CHEVALIER F L. Antenna coupling effects for space-time radar waveforms: Analysis and calibration[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(5): 2572–2586. doi: 10.1109/TAP.2014.2309111
    [57]
    BABUR G, MANOKHIN G O, GELTSER A A, et al. Low-cost digital beamforming on receive in phased array radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1355–1364. doi: 10.1109/TAES.2017.2671078
    [58]
    BABUR G, MANOKHIN G O, MONASTYREV E A, et al. Simple calibration technique for phased array radar systems[J]. Progress in Electromagnetics Research M, 2017, 55: 109–119. doi: 10.2528/PIERM16101203
    [59]
    LI Shengyuan, LIU Nan, ZHANG Linrang, et al. Transmit beampattern synthesis for MIMO radar using extended circulating code[J]. IET Radar, Sonar & Navigation, 2018, 12(6): 610–616. doi: 10.1049/iet-rsn.2017.0386
    [60]
    WANG Huake, LIAO Guisheng, ZHANG Yuhong, et al. Transmit beampattern synthesis for chirp space-time coding array by time delay design[J]. Digital Signal Processing, 2021, 110: 102901. doi: 10.1016/j.dsp.2020.102901
    [61]
    WANG Huake, LIAO Guisheng, XU Jingwei, et al. Direction-of-Arrival estimation for circulating space-time coding arrays: From beamspace MUSIC to spatial smoothing in the transform domain[J]. Sensors, 2018, 18(11): 3689. doi: 10.3390/s18113689
    [62]
    LI Shengyuan, ZHANG Linrang, LIU Nan, et al. Transmit diversity technique based on joint slow-time coding with circulating code[J]. IET Radar, Sonar & Navigation, 2017, 11(8): 1243–1250. doi: 10.1049/iet-rsn.2016.0595
    [63]
    王华柯, 廖桂生, 许京伟, 等. 空时编码阵波束域超分辨角度估计方法[J]. 系统工程与电子技术, 2019, 41(7): 1433–1440. doi: 10.3969/j.issn.1001-506X.2019.07.01

    WANG Huake, LIAO Guisheng, XU Jingwei, et al. Beam-space MUSIC spectral estimation method based on the Space-time coding array[J]. Systems Engineering and Electronics, 2019, 41(7): 1433–1440. doi: 10.3969/j.issn.1001-506X.2019.07.01
    [64]
    NUNN C J and COXSON G E. Best-known autocorrelation peak sidelobe levels for binary codes of length 71 to 105[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(1): 392–395. doi: 10.1109/TAES.2008.4517015
    [65]
    NUNN C J and COXSON G E. Polyphase pulse compression codes with optimal peak and integrated sidelobes[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(2): 775–781. doi: 10.1109/TAES.2009.5089560
    [66]
    BORDONI F, YOUNIS M, and KRIEGER G. Ambiguity suppression by azimuth phase coding in multichannel SAR systems[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(2): 617–629. doi: 10.1109/TGRS.2011.2161672
    [67]
    WANG Hanbing, ZHANG Yuhong, XU Jingwei, et al. Range ambiguity suppression in a synthetic aperture radar using pulse phase coding and two-pulse cancellation[J]. International Journal of Remote Sensing, 2018, 39(20): 6525–6539. doi: 10.1080/01431161.2018.1460509
    [68]
    DALL J and KUSK A. Azimuth phase coding for range ambiguity suppression in SAR[C]. 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, USA, 2004: 1734–1737. doi: 10.1109/IGARSS.2004.1370667.
    [69]
    KRIEGER G, GEBERT N, and MOREIRA A. Multidimensional waveform encoding: A new digital beamforming technique for synthetic aperture radar remote sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 31–46. doi: 10.1109/TGRS.2007.905974
    [70]
    LOMBARDO P, PASTINA D, and TURIN F. Ground moving target detection based on MIMO SAR systems[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(11): 5081–5095. doi: 10.1109/JSTARS.2015.2461594
    [71]
    KIM J H, YOUNIS M, MOREIRA A, et al. Spaceborne MIMO synthetic aperture radar for multimodal operation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5): 2453–2466. doi: 10.1109/TGRS.2014.2360148
    [72]
    DENG Hai and HIMED B. Interference mitigation processing for spectrum-sharing between radar and wireless communications systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(3): 1911–1919. doi: 10.1109/TAES.2013.6558027
    [73]
    弗朗索瓦·勒舍瓦利耶. 机载雷达的空时发射与编码[J]. 雷达科学与技术, 2008, 6(6): 411–421. doi: 10.3969/j.issn.1672-2337.2008.06.003

    CHEVALIER F L. Space-time transmission and coding for airborne radars[J]. Radar Science and Technology, 2008, 6(6): 411–421. doi: 10.3969/j.issn.1672-2337.2008.06.003
    [74]
    JAJAMOVICH G H, LOPS M, and WANG Xiaodong. Space-time coding for MIMO radar detection and ranging[J]. IEEE Transactions on Signal Processing, 2010, 58(12): 6195–6206. doi: 10.1109/TSP.2010.2072923
    [75]
    WANG Huake, QUAN Yinghui, LIAO Guisheng, et al. Space-time coding technique for coherent frequency diverse array[J]. IEEE Transactions on Signal Processing, 2021, 69: 5994–6008. doi: 10.1109/TSP.2021.3114998
    [76]
    CALVARY P and JANER D. Spatio-temporal coding for radar array processing[C]. The 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, Seattle, USA, 1998: 2509–2512. doi: 10.1109/ICASSP.1998.681661.
    [77]
    SONG Xiufeng, ZHOU Shengli, and WILLETT P. Reducing the waveform cross correlation of MIMO radar with space-time coding[J]. IEEE Transactions on Signal Processing, 2010, 58(8): 4213–4224. doi: 10.1109/TSP.2010.2048207
    [78]
    XU Jingwei, ZHANG Yuhong, LIAO Guisheng, et al. Resolving range ambiguity via multiple-input multiple-output radar with element-pulse coding[J]. IEEE Transactions on Signal Processing, 2020, 68: 2770–2783. doi: 10.1109/TSP.2020.2988371
    [79]
    XU Jingwei and SO H C. Study on coding scheme with EPC-MIMO radar in clutter-free scenario[C]. 2020 IEEE 11th Sensor Array and Multichannel Signal Processing Workshop (SAM), Hangzhou, China, 2020. doi: 10.1109/SAM48682.2020.9104270.
    [80]
    LAN Lan, LIAO Guisheng, XU Jingwei, et al. Mainlobe deceptive jammer suppression using element-pulse coding with MIMO radar[J]. Signal Processing, 2021, 182: 107955. doi: 10.1016/j.sigpro.2020.107955
    [81]
    WANG Hanbing, ZHANG Yuhong, XU Jingwei, et al. Study on coding scheme for space-pulse-phase-coding-based high-resolution and wide-swath SAR imaging[J]. International Journal of Remote Sensing, 2020, 41(18): 7202–7216. doi: 10.1080/01431161.2020.1754498
    [82]
    WANG Hanbing, ZHANG Yuhong, XU Jingwei, et al. A novel range ambiguity resolving approach for high-resolution and wide-swath SAR imaging utilizing space-pulse phase coding[J]. Signal Processing, 2020, 168: 107323. doi: 10.1016/j.sigpro.2019.107323
    [83]
    许京伟, 兰岚, 朱圣棋, 等. 相干频率分集阵雷达匹配滤波器设计[J]. 系统工程与电子技术, 2018, 40(8): 1720–1728. doi: 10.3969/j.issn.1001-506X.2018.08.08

    XU Jingwei, LAN Lan, ZHU Shengqi, et al. Design of matched filter for coherent FDA radar[J]. Systems Engineering and Electronics, 2018, 40(8): 1720–1728. doi: 10.3969/j.issn.1001-506X.2018.08.08
    [84]
    LAN Lan, LIAO Guisheng, XU Jingwei, et al. Transceive beamforming with accurate nulling in FDA-MIMO radar for imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(6): 4145–4159. doi: 10.1109/TGRS.2019.2961324
    [85]
    WANG Chenghao, XU Jingwei, LIAO Guisheng, et al. A range ambiguity resolution approach for high-resolution and wide-swath SAR imaging using frequency diverse array[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11(2): 336–346. doi: 10.1109/JSTSP.2016.2605064
    • Relative Articles
    • Supplements(0)
    • Cited By
  • 加载中

Catalog

    通讯作者: 陈斌, bchen63@163.com
    • 1. 

      沈阳化工大学材料科学与工程学院 沈阳 110142

    1. 本站搜索
    2. 百度学术搜索
    3. 万方数据库搜索
    4. CNKI搜索
    Get Citation
    PDF
    XML
    Article views(3544) PDF downloads(461) Cited by()
    Proportional views
    Related

    京ICP备20021838号-8   Supported by: Beijing Renhe Information Technology Co. Ltd     百度统计

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return