Submit Manuscript
Peer Review
Editor Work
| Citation: | WANG Zengfu, YANG Guangyu, and JIN Shuling. A non-myopic and fast resource scheduling algorithm for multi-target tracking of space-based radar considering optimal integrated performance[J]. Journal of Radars, 2024, 13(1): 253–269. doi: 10.12000/JR23162
|
A Non-myopic and Fast Resource Scheduling Algorithm for Multi-target Tracking of Space-based Radar Considering Optimal Integrated Performance
doi: 10.12000/JR23162
More Information-
Abstract
Appropriate and effective resource scheduling is the key to achieving the best performance for a space-based radar. Considering the resource scheduling problem of multi-target tracking in a space-based radar system, we establish a cost function that considers target threat, tracking accuracy, and Low Probability of Interception (LPI). Considering target uncertainty and constraints of the space-based platform and long-term expected cost, we establish a resource scheduling model based on the Partially Observable Markov Decision Process (POMDP) with multiple constraints. To transform and decompose the resource scheduling problem of multi-target tracking with multiple constraints into multiple unconstrained sub-problems, we use the Lagrangian relaxation method. To deal with the curse of dimensionality caused by the continuous state space, continuous action space and continuous observation space, we use the online POMDP algorithm based on the Monte Carlo Tree Search (MCTS) and partially observable Monte Carlo planning with observation widening algorithm. Finally, a non-myopic and fast resource scheduling algorithm with comprehensive performance indices for multi-target tracking in a space-based radar system is proposed. Simulation results show that the proposed algorithm, when compared with the existing scheduling algorithms, allocates resources more appropriately and shows better performance. -
-
References
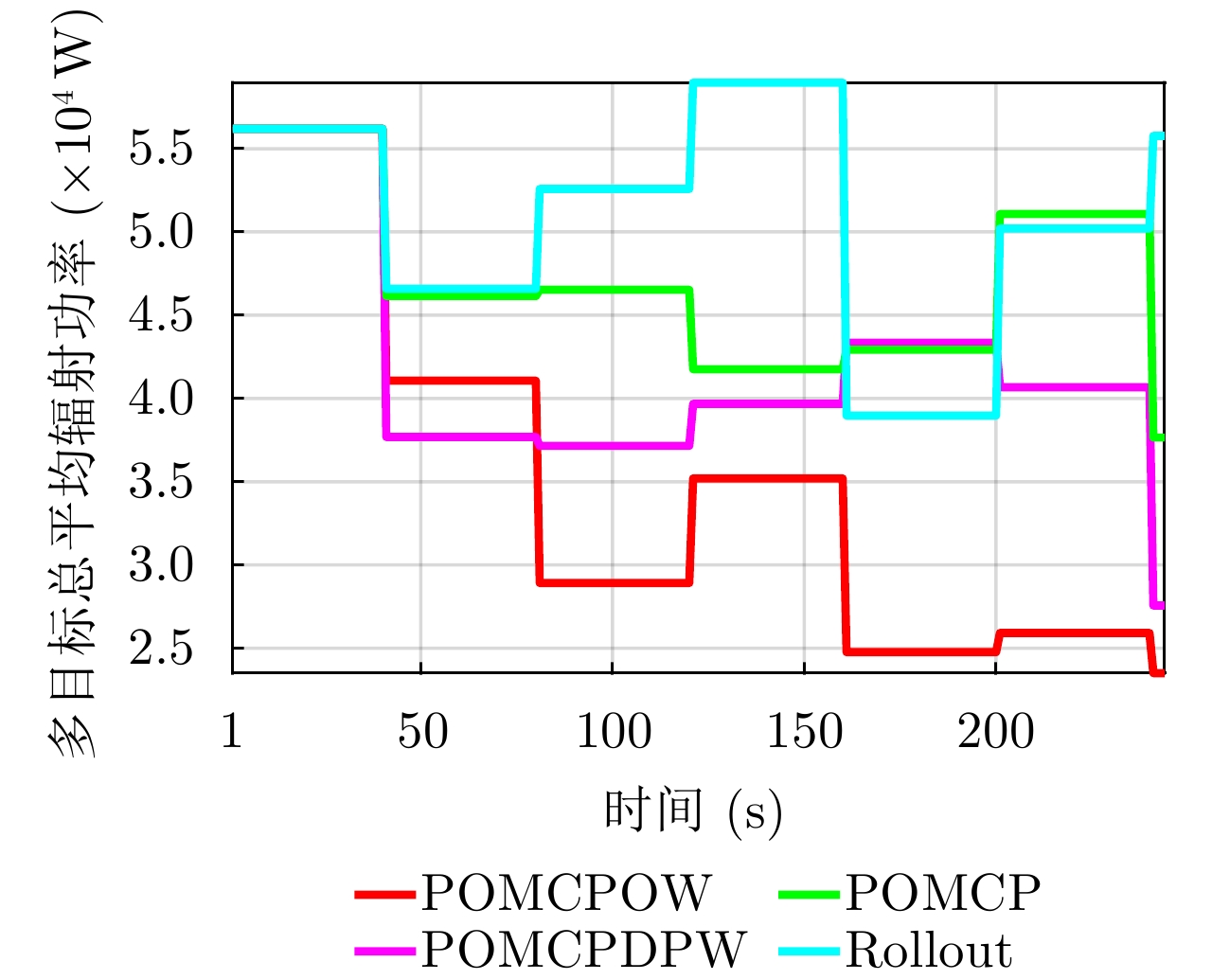
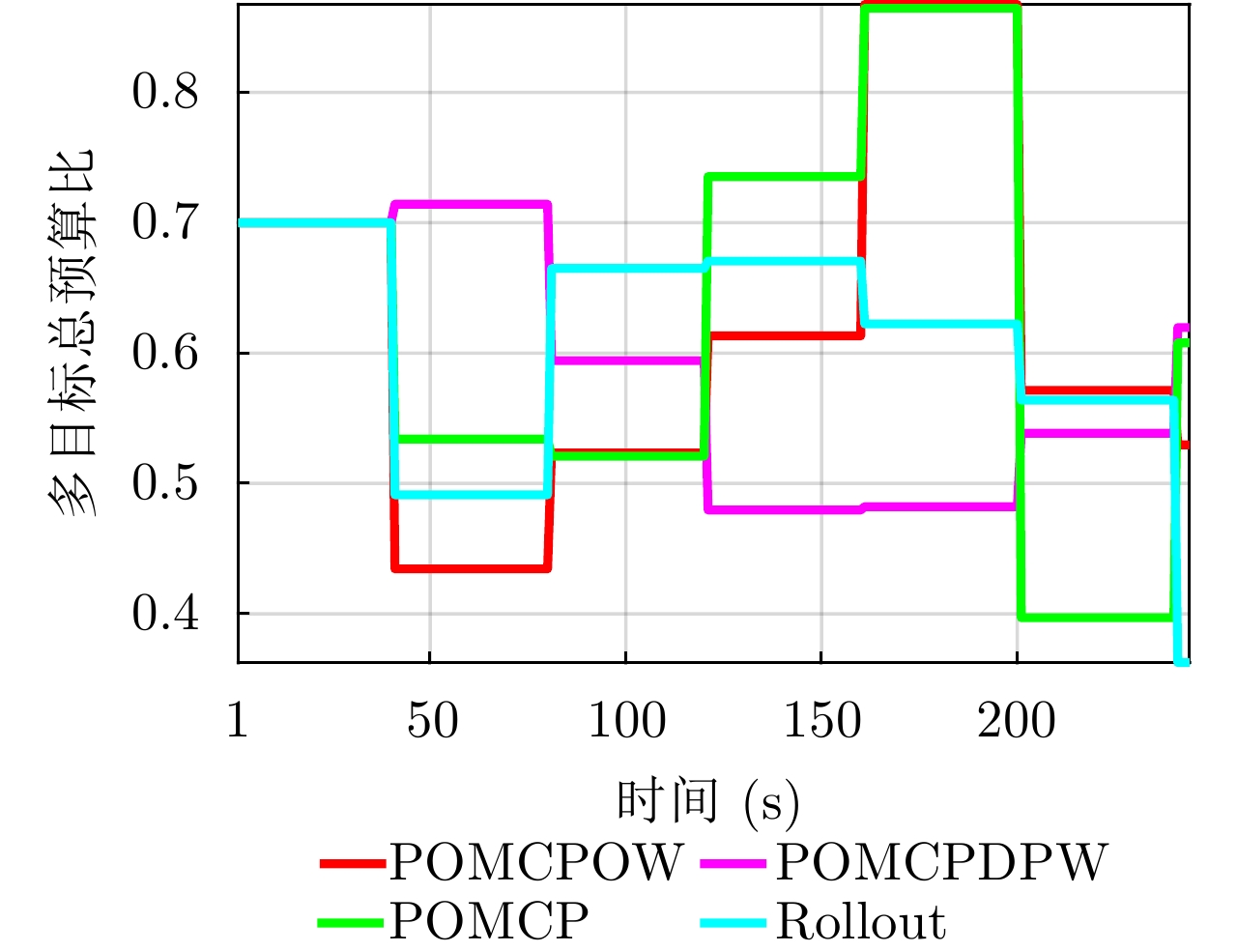
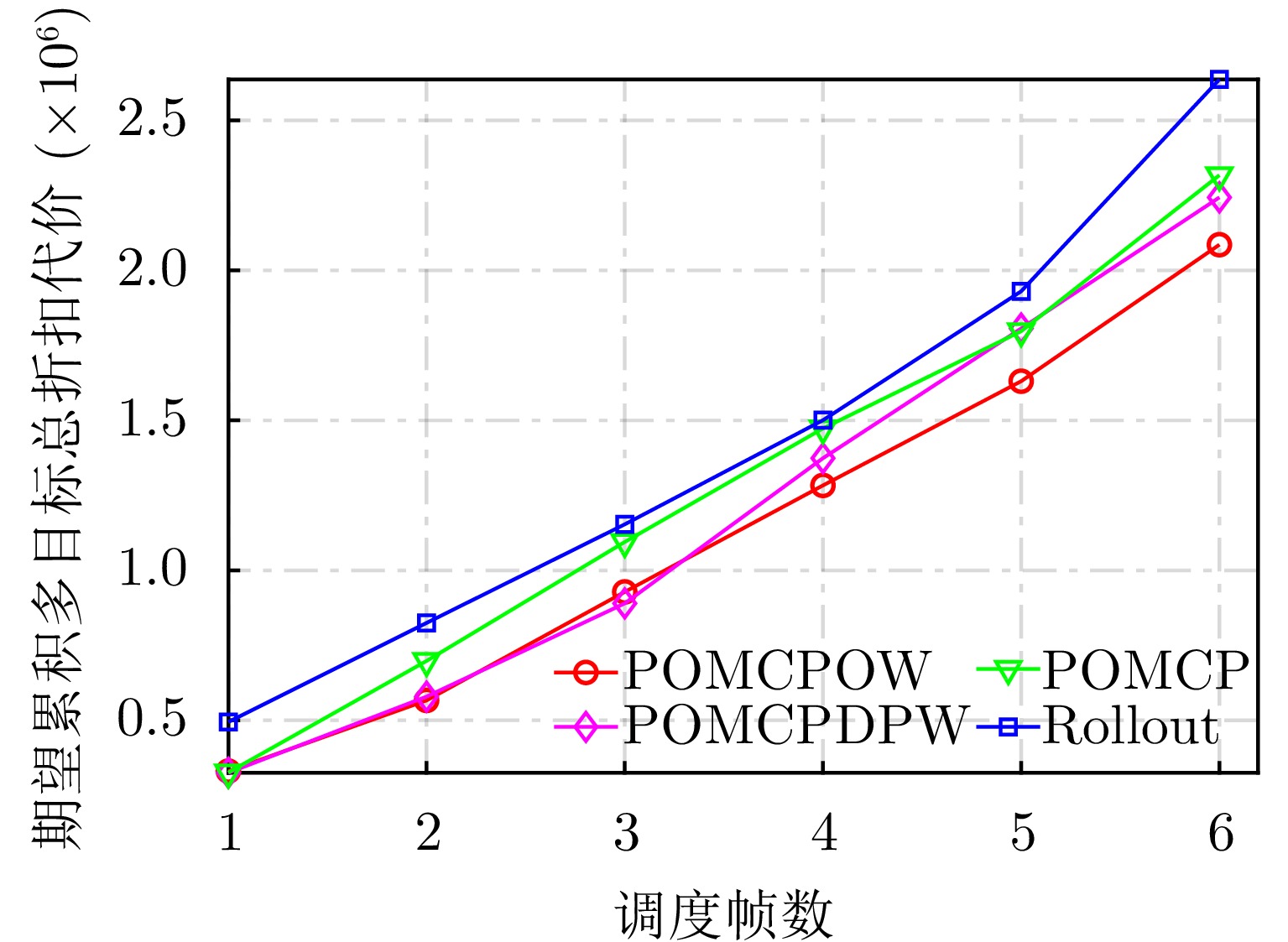
[1] XIE Mingchi, YI Wei, KIRUBARAJAN T, et al. Joint node selection and power allocation strategy for multitarget tracking in decentralized radar networks[J]. IEEE Transactions on Signal Processing, 2018, 66(3): 729–743. doi: 10.1109/TSP.2017.2777394[2] DAI Jinhui, YAN Junkun, WANG Penghui, et al. Optimal resource allocation for multiple target tracking in phased array radar network[C]. 2019 International Conference on Control, Automation and Information Sciences (ICCAIS), Chengdu, China, 2019: 1–4.[3] SUN Jun, LU Xiujuan, YUAN Ye, et al. Resource allocation for multi-target tracking in multi-static radar systems with imperfect detection performance[C]. 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 2020: 1–6.[4] ZHANG Haowei, LIU Weijian, ZONG Binfeng, et al. An efficient power allocation strategy for maneuvering target tracking in cognitive MIMO radar[J]. IEEE Transactions on Signal Processing, 2021, 69: 1591–1602. doi: 10.1109/TSP.2020.3047227[5] LU Xiujuan, YI Wei, and KONG Lingjiang. Joint online route planning and resource optimization for multitarget tracking in airborne radar systems[J]. IEEE Systems Journal, 2022, 16(3): 4198–4209. doi: 10.1109/JSYST.2021.3116020[6] SHI Chenguang, ZHOU Jianjiang, and WANG Fei. Adaptive resource management algorithm for target tracking in radar network based on low probability of intercept[J]. Multidimensional Systems and Signal Processing, 2018, 29(4): 1203–1226. doi: 10.1007/s11045-017-0494-8[7] SHI Chenguang, WANG Yijie, SALOUS S, et al. Joint transmit resource management and waveform selection strategy for target tracking in distributed phased array radar network[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(4): 2762–2778. doi: 10.1109/TAES.2021.3138869[8] CHHETRI A S, MORRELL D, and PAPANDREOU-SUPPAPPOLA A. Energy efficient target tracking in a sensor network using non-myopic sensor scheduling[C]. 2005 7th International Conference on Information Fusion, Philadelphia, USA, 2005: 558–565.[9] HERO A O and COCHRAN D. Sensor management: Past, present, and future[J]. IEEE Sensors Journal, 2011, 11(12): 3064–3075. doi: 10.1109/JSEN.2011.2167964[10] FERRI G, MUNAFÒ A, GOLDHAHN R, et al. A non-myopic, receding horizon control strategy for an AUV to track an underwater target in a bistatic sonar scenario[C]. 53rd IEEE Conference on Decision and Control, Los Angeles, USA, 2014: 5352–5358.[11] JI Shihao, PARR R, and CARIN L. Nonmyopic multiaspect sensing with partially observable Markov decision processes[J]. IEEE Transactions on Signal Processing, 2007, 55(6): 2720–2730. doi: 10.1109/TSP.2007.893747[12] KRISHNAMURTHY V and DJONIN D V. Optimal threshold policies for multivariate POMDPs in radar resource management[J]. IEEE Transactions on Signal Processing, 2009, 57(10): 3954–3969. doi: 10.1109/TSP.2009.2022915[13] JIANG Xiaofeng, ZHOU Feng, JIAN Yang, et al. An optimal POMDP-based anti-jamming policy for cognitive radar[C]. 2017 13th IEEE Conference on Automation Science and Engineering (CASE), Xi’an, China, 2017: 938–943.[14] SHAN Ganlin, XU Gongguo, and QIAO Chenglin. A non-myopic scheduling method of radar sensors for maneuvering target tracking and radiation control[J]. Defence Technology, 2020, 16(1): 242–250. doi: 10.1016/j.dt.2019.10.001[15] SCHÖPE M I, DRIESSEN H, and YAROVOY A. A constrained POMDP formulation and algorithmic solution for radar resource management in multi-target tracking[J]. ISIF Journal of Advances in Information Fusion, 2021, 16(1): 31–47.[16] HAWKINS J T. A Langrangian decomposition approach to weakly coupled dynamic optimization problems and its applications[D]. [Ph.D. dissertation], Massachusetts Institute of Technology, 2003.[17] CASTANON D A. Approximate dynamic programming for sensor management[C]. The 36th IEEE Conference on Decision and Control, San Diego, USA, 1997: 1202–1207.[18] LI Yuan, ZHU Huayong, and SHEN Lincheng. The Lagrangian relaxation based resources allocation methods for air-to-ground operations under uncertainty circumstances[C]. 2009 Chinese Control and Decision Conference, Guilin, China, 2009: 5609–5614.[19] KURNIAWATI H, HSU D, and LEE W S. SARSOP: Efficient Point-based POMDP Planning by Approximating Optimally Reachable Belief Spaces[M]. BROCK O, TRINKLE J, and RAMOS F. Robotics: Science and Systems. Cambridge: MIT Press, 2009: 1–8.[20] PINEAU J, GORDON G, and THRUN S. Point-based value iteration: An anytime algorithm for POMDPs[C]. The 18th International Joint Conference on Artificial Intelligence, Acapulco, Mexico, 2003: 1025–1030.[21] SPAAN M T J and VLASSIS N. Perseus: Randomized point-based value iteration for POMDPs[J]. Journal of Artificial Intelligence Research, 2005, 24: 195–220. doi: 10.1613/jair.1659[22] SMITH T and SIMMONS R. Heuristic search value iteration for POMDPs[C]. The 20th Conference on Uncertainty in Artificial Intelligence, Banff, Canada, 2004: 520–527.[23] ROSS S, PINEAU J, PAQUET S, et al. Online planning algorithms for POMDPs[J]. Journal of Artificial Intelligence Research, 2008, 32: 663–704. doi: 10.1613/jair.2567[24] SILVER D and VENESS J. Monte-Carlo planning in large POMDPs[C]. The 23rd International Conference on Neural Information Processing Systems, Vancouver, British, 2010: 2164–2172.[25] YE Nan, SOMANI A, HSU D, et al. DESPOT: Online POMDP planning with regularization[J]. Journal of Artificial Intelligence Research, 2017, 58: 231–266. doi: 10.1613/jair.5328[26] KURNIAWATI H and YADAV V. An online POMDP Solver for Uncertainty Planning in Dynamic Environment[M]. INABA M and CORKE P. Robotics Research: The 16th International Symposium ISRR. Cham, Switzerland: Springer, 2016: 611–629.[27] SUNBERG Z and KOCHENDERFER M. Online algorithms for POMDPs with continuous state, action, and observation spaces[C]. The Thirty-Third International Conference on Automated Planning and Scheduling, Delft, The Netherlands, 2018: 259–263.[28] KERSHAW D J and EVANS R J. Optimal waveform selection for tracking systems[J]. IEEE Transactions on Information Theory, 1994, 40(5): 1536–1550. doi: 10.1109/18.333866[29] SIRA S P, PAPANDREOU-SUPPAPPOLA A, and MORRELL D. Dynamic configuration of time-varying waveforms for agile sensing and tracking in clutter[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3207–3217. doi: 10.1109/TSP.2007.894418[30] LI Xi, CHENG Ting, SU Yang, et al. Joint time-space resource allocation and waveform selection for the collocated MIMO radar in multiple targets tracking[J]. Signal Processing, 2020, 176: 107650. doi: 10.1016/j.sigpro.2020.107650[31] KOCH W. Adaptive parameter control for phased-array tracking[C]. SPIE 3809, Signal and Data Processing of Small Targets 1999, Denver, USA, 1999: 444–455.[32] KATSILIERIS F, DRIESSEN H, and YAROVOY A. Threat-based sensor management for target tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(4): 2772–2785. doi: 10.1109/TAES.2015.140052[33] HU Yumei, WANG Xuezhi, LAN Hua, et al. An iterative nonlinear filter using variational Bayesian optimization[J]. Sensors, 2018, 18(12): 4222. doi: 10.3390/s18124222[34] 何子述, 程子扬, 李军, 等. 集中式MIMO雷达研究综述[J]. 雷达学报, 2022, 11(5): 805–829. doi: 10.12000/JR22128HE Zishu, CHENG Ziyang, LI Jun, et al. A survey of collocated MIMO radar[J]. Journal of Radars, 2022, 11(5): 805–829. doi: 10.12000/JR22128[35] LIM M H, TOMLIN C J, and SUNBERG Z N. Sparse tree search optimality guarantees in POMDPs with continuous observation spaces[C]. Twenty-Ninth International Joint Conference on Artificial Intelligence, Yokohama, Japan, 2020: 1–16.[36] JI Shihao, PARR R, LI Hui, et al. Point-based policy iteration[C]. The Twenty-Second National Conference on Artificial Intelligence, Vancouver, British, 2007: 1243–1249.[37] SCHÖPE M I, DRIESSEN H, and YAROVOY A. Multi-task sensor resource balancing using Lagrangian relaxation and policy rollout[C]. 2020 IEEE 23rd International Conference on Information Fusion (FUSION), Rustenburg, South Africa, 2020: 1–8. -
Proportional views
- Publishing Ethics
- Journal Insights
- Abstracting & Indexing
- Peer Review Policies
- Guide for Authors
- ISSN 2095-283X (Print)ISSN 2097-339X (Online)
- CN 10-1030/TN
- CODEN LXEUAO
About Journal
- Sponsor: China Radio Detection and Ranging Industry Association (CRIA)
- Phone: 010-58887062
- Email：radars@aircas.ac.cn
- Publisher: Leida Xuebao Bianjibu (Editorial office of the Journal of Radars)
Contacts Us
京ICP备20021838号-8
Supported by: Beijing Renhe Information Technology Co. Ltd
Export File
Citation
Format
Content
DownLoad:
- Figure 1. Schematic diagram of the proposed LR-POMCPOW for resource scheduling of space-based radar multi-target tracking
- Figure 2. The process of the MCTS algorithm
- Figure 3. STK-based demonstration for impact of distinct target threat levels on radar resource allocation
- Figure 4. Target threat level results
-
Figure 5. Budget ratio (
$\tau/T $ - Figure 6. STK-based demonstration for impact of distinct relative distances on radar resource allocation
- Figure 7. The slant range of targets
-
Figure 8. Budget ratio (
$\tau / T $ - Figure 9. STK-based demonstration for multi-target tracking
- Figure 10. Target tracking trajectory
-
Figure 11. Budget ratio (
$ \tau / T$ - Figure 12. The average radiation power allocated to each target
- Figure 13. RMSE on position of target1
- Figure 14. RMSE on speed of target1
- Figure 15. Comparison of total average radiation power
-
Figure 16. Comparison of the total budget ratio (
$ \tau / T $ - Figure 17. Comparison of the expected cumulative multi-target discount cost