Submit Manuscript
Peer Review
Editor Work
| Citation: | YU Longlong, FENG Dong, WANG Jian, et al. Estimation of the minimum number of acquisitions for coprime tomographic synthetic aperture radar[J]. Journal of Radars, 2022, 11(4): 618–636. doi: 10.12000/JR22047
|
Estimation of the Minimum Number of Acquisitions for Coprime Tomographic Synthetic Aperture Radar
DOI: 10.12000/JR22047
More Information-
Abstract
In the practical application of Tomographic Synthetic Aperture Radar (TomoSAR), the number of acquisitions is usually restricted due to their expensive cost. A coprime TomoSAR technique was proposed to reduce the required number of acquisitions by sparsely distributing acquisitions and elongating baseline aperture. To guarantee a reliable tomogram, this study aims to determine the minimum number of acquisitions for the coprime TomoSAR when adopting a subspace method for performing the tomographic reconstruction. However, the performance of the subspace method depends on multiple parameters. In light of this, the selection of acquisition times has to comprehensively weigh the effects of all these parameters on the reconstruction performance. To this end, a prerequisite for reliable reconstruction is established by quantifying the relationship between the sample eigenvalues and all related parameters. Compared with conventional estimation approaches for the minimum number of acquisitions, the proposed approach has twofold advantages of containing all related parameters and of having a closed-form expression. Finally, the simulation experiments verify that the number of acquisitions estimated by our approach is close to the minimum and can guarantee reconstruction reliability. -
-
References
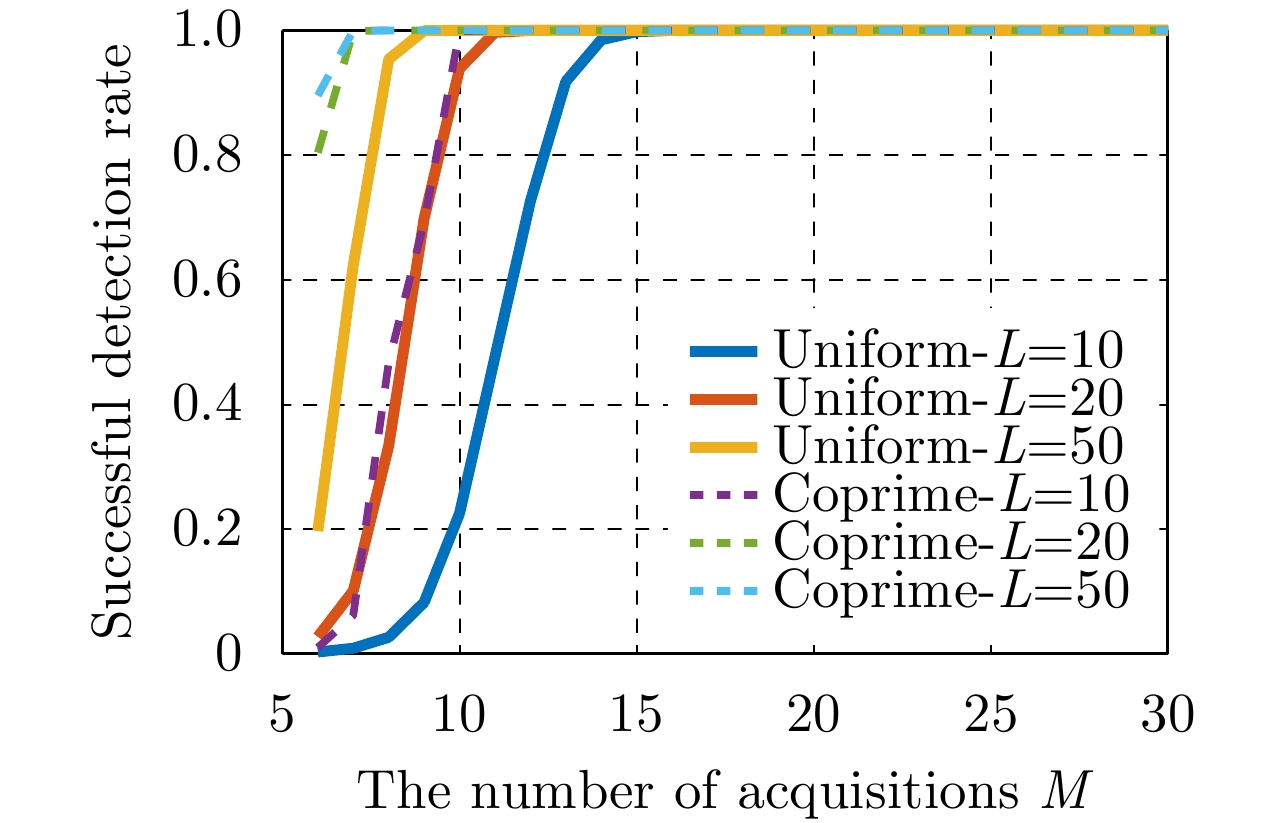
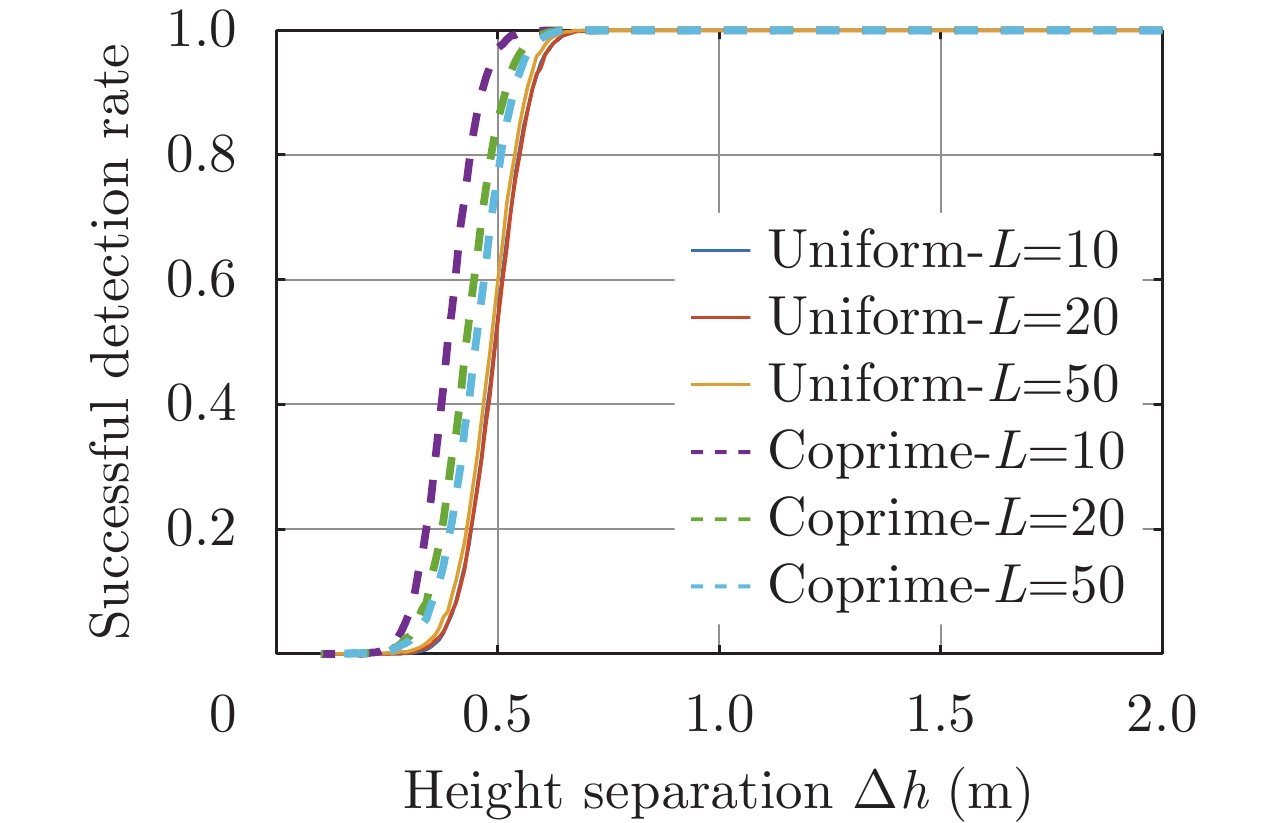
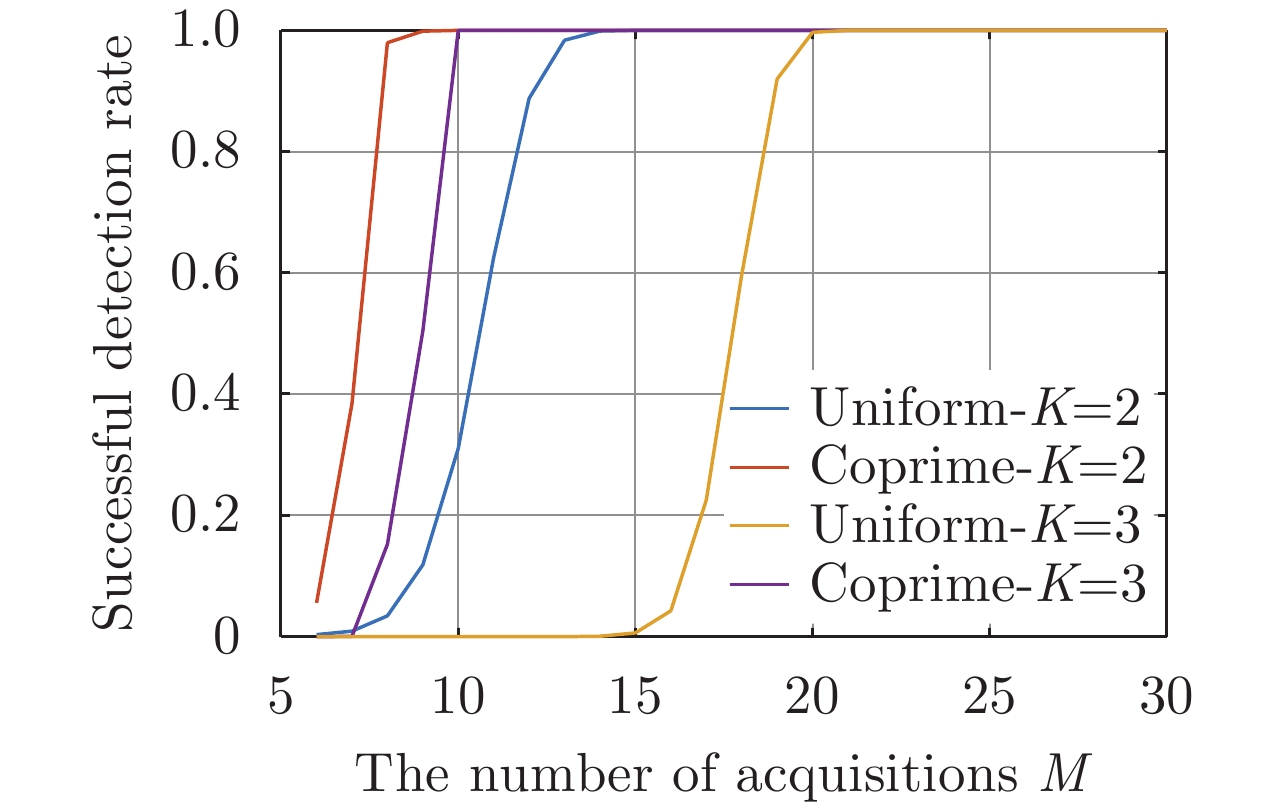
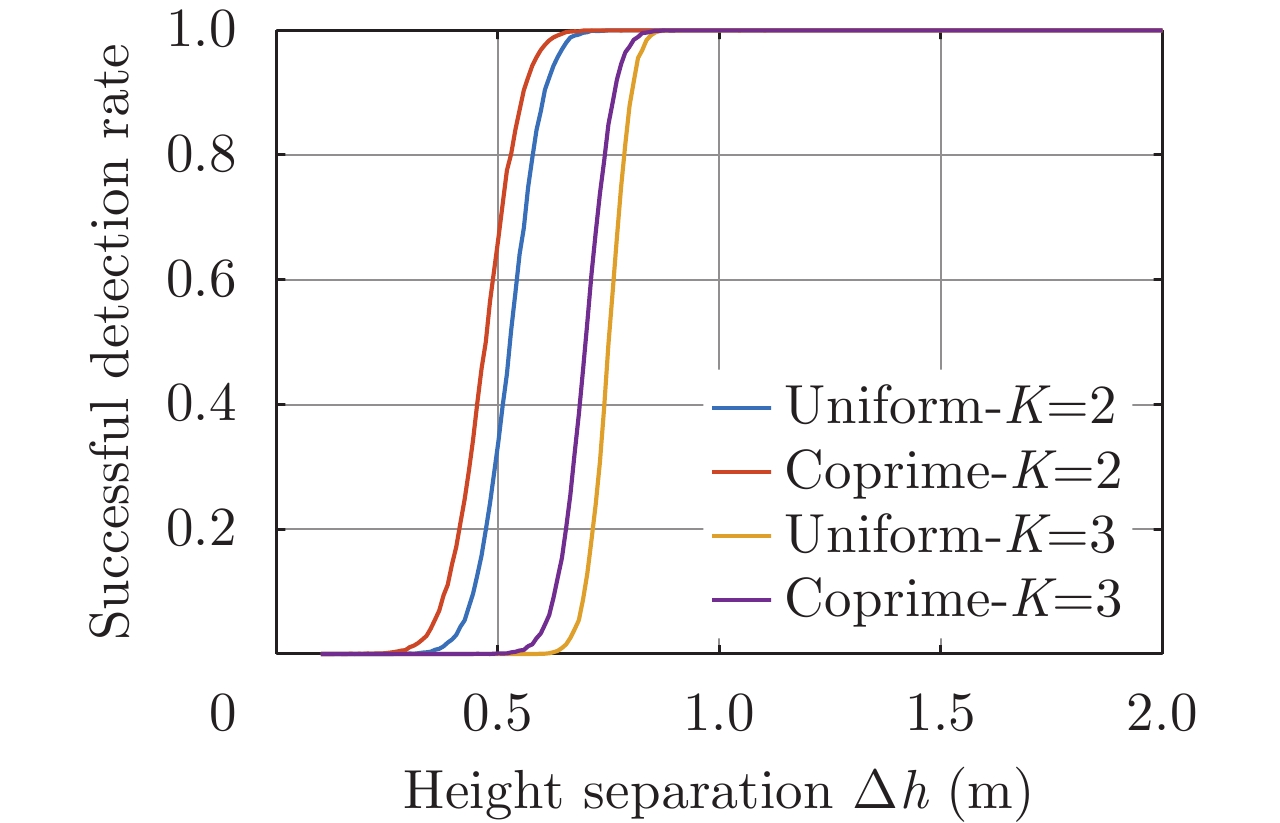
[1] RAMBOUR C, BUDILLON A, JOHNSY A C, et al. From interferometric to tomographic SAR: A review of synthetic aperture radar tomography-processing techniques for scatterer unmixing in urban areas[J]. IEEE Geoscience and Remote Sensing Magazine, 2020, 8(2): 6–29. doi: 10.1109/MGRS.2019.2957215[2] REIGBER A and MOREIRA A. First demonstration of airborne SAR tomography using multibaseline L-band data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2142–2152. doi: 10.1109/36.868873[3] YU Longlong, HUANG Xiaotao, FENG Dong, et al. Coprime synthetic aperture radar tomography[C]. 2021 2nd China International SAR Symposium (CISS), Shanghai, China, 2021: 1–6.[4] YU Longlong, FENG Dong, WANG Jian, et al. An efficient reconstruction approach based on atomic norm minimization for coprime tomographic SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4503705. doi: 10.1109/LGRS.2022.3143662[5] VAIDYANATHAN P P and PAL P. Sparse sensing with Co-prime samplers and arrays[J]. IEEE Transactions on Signal Processing, 2011, 59(2): 573–586. doi: 10.1109/TSP.2010.2089682[6] LOMBARDINI F and PARDINI M. 3-D SAR tomography: The multibaseline sector interpolation approach[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(4): 630–634. doi: 10.1109/LGRS.2008.2001283[7] NANNINI M, REIGBER A, and SCHEIBER R. A study on irregular baseline constellations in SAR tomography[C]. 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 2010: 1–4.[8] WEI Lianhuan, FENG Qiuyue, LIU Shanjun, et al. Minimum redundancy array—A baseline optimization strategy for urban SAR tomography[J]. Remote Sensing, 2020, 12(18): 3100. doi: 10.3390/rs12183100[9] NANNINI M, SCHEIBER R, and MOREIRA A. Estimation of the minimum number of tracks for SAR tomography[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(2): 531–543. doi: 10.1109/TGRS.2008.2007846[10] ZHU Xiaoxiang and BAMLER R. Super-resolution power and robustness of compressive sensing for spectral estimation with application to spaceborne tomographic SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 247–258. doi: 10.1109/TGRS.2011.2160183[11] ZHU Xiaoxiang, GE Nan, and SHAHZAD M. Joint sparsity in SAR tomography for urban mapping[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1498–1509. doi: 10.1109/JSTSP.2015.2469646[12] NADLER B. Finite sample approximation results for principal component analysis: A matrix perturbation approach[J]. The Annals of Statistics, 2008, 36(6): 2791–2817. doi: 10.1214/08-aos618[13] NADAKUDITI R R and EDELMAN A. Sample eigenvalue based detection of high-dimensional signals in white noise using relatively few samples[J]. IEEE Transactions on Signal Processing, 2008, 56(7): 2625–2638. doi: 10.1109/TSP.2008.917356[14] FORNARO G, VERDE S, REALE D, et al. CAESAR: An approach based on covariance matrix decomposition to improve multibaseline-multitemporal interferometric SAR processing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(4): 2050–2065. doi: 10.1109/TGRS.2014.2352853[15] NAVNEET S, KIM J W, and LU Zhong. A new InSAR persistent scatterer selection technique using top eigenvalue of coherence matrix[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(4): 1969–1978. doi: 10.1109/TGRS.2017.2771386[16] PAUCIULLO A, REALE D, FRANZÉ W, et al. Multi-look in GLRT-based detection of single and double persistent scatterers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(9): 5125–5137. doi: 10.1109/TGRS.2018.2809538[17] D’HONDT O, LÓPEZ-MARTÍNEZ C, GUILLASO S, et al. Nonlocal filtering applied to 3-D reconstruction of tomographic SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(1): 272–285. doi: 10.1109/TGRS.2017.2746420[18] ZHU Xiaoxiang and BAMLER R. Superresolving SAR tomography for multidimensional imaging of urban areas: Compressive sensing-based TomoSAR inversion[J]. IEEE Signal Processing Magazine, 2014, 31(4): 51–58. doi: 10.1109/MSP.2014.2312098[19] JOHNSON B A, ABRAMOVICH Y I, and MESTRE X. MUSIC, G-MUSIC, and maximum-likelihood performance breakdown[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3944–3958. doi: 10.1109/TSP.2008.921729[20] SHAGHAGHI M and VOROBYOV S A. Subspace leakage analysis and improved DOA estimation with small sample size[J]. IEEE Transactions on Signal Processing, 2015, 63(12): 3251–3265. doi: 10.1109/TSP.2015.2422675[21] FRIEDLANDER B. The root-MUSIC algorithm for direction finding with interpolated arrays[J]. Signal Processing, 1993, 30(1): 15–29. doi: 10.1016/0165-1684(93)90048-F[22] RUBSAMEN M and GERSHMAN A B. Direction-of-arrival estimation for nonuniform sensor arrays: From manifold separation to fourier domain MUSIC methods[J]. IEEE Transactions on Signal Processing, 2009, 57(2): 588–599. doi: 10.1109/TSP.2008.2008560[23] STOICA P and NEHORAI A. MUSIC, maximum likelihood, and Cramer-Rao bound[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(5): 720–741. doi: 10.1109/29.17564 -
Proportional views
- Publishing Ethics
- Journal Insights
- Abstracting & Indexing
- Peer Review Policies
- Guide for Authors
- Conference
- ISSN 2095-283X (Print)ISSN 2097-339X (Online)
- CN 10-1030/TN
- CODEN LXEUAO
About Journal
- Sponsor: China Radio Detection and Ranging Industry Association (CRIA)
- Phone: 010-58887062
- Email：radars@aircas.ac.cn
- Publisher: Leida Xuebao Bianjibu (Editorial office of the Journal of Radars)
Contacts Us
京ICP备20021838号-8
Supported by: Beijing Renhe Information Technology Co. Ltd
Export File
Citation
Format
Content
DownLoad:
- Figure 1. The acquisition geometry of the coprime TomoSAR
- Figure 2. The flow chart for the propose approach to estimate the minimum number of acquisitions
- Figure 3. Successful detection rate varies with the number of acquisitions (K=2; SNR1=0 dB, SNR2=10 dB; Δh=1 m)
- Figure 4. The RMSE of the height estimation varies with the number of acquisitions (K=2; SNR1=0 dB, SNR2=10 dB; Δh=1 m)
- Figure 5. Successful detection rate varies with the height separation (K=2; SNR1=0 dB, SNR2=10 dB; ρh=1 m)
- Figure 6. The RMSE of the height estimation varies with the height separation (K=2; SNR1=0 dB, SNR2=10 dB; ρh=1 m)
- Figure 7. Successful detection rate varies with the number of acquisitions (Δh=1 m; L=20; all the SNRs=0 dB)
- Figure 8. The RMSE of the height estimation varies with the number of acquisitions (Δh=1 m; L=20; all the SNRs=0 dB)
- Figure 9. Successful detection rate varies with the height separation (L=20; all the SNRs=0 dB; ρh=1 m)
- Figure 10. The RMSE of the height estimation varies with the height separation (L=20; all the SNRs=0 dB; ρh=1 m)
- Figure 11. The constraint relationship between the minimum number of acquisitions and the SNR (K=2; Δh=1 m; L=10)
- Figure 12. |<a1, a2>|/M varies with the number of acquisitions (d=7.5 m; K=2; Δh=1 m)
- Figure 13. The phase transition of the RMSE as a function of the number of acquisitions and the SNR (K=2; Δh=1 m; L=10)
- Figure 14. The reconstruction results from the uniform TomoSAR and the coprime TomoSAR which are designed by Ref. [9] vary with the SNR [the uniform TomoSAR (M=16; d=7.5 m; B=112 m); the coprime TomoSAR (M1=9, M2=8; d=1.8 m; B=112 m)]
- Figure 15. Successful detection rate calculated from the deviated tracks and the nominal tracks (K=2; all the SNRs=0 dB; L=20; ρh=1 m)
- Figure 16. RMSE of the height estimation calculated from the deviated tracks and the nominal tracks (the simulation parmeters are seted as the same as in Fig. 15)