② 微波成像技术重点实验室 北京 100190
③ 中国科学院大学 北京 100049
②Science and Technology on Microwave Imaging Laboratory, Beijing 100190, China
③University of Chinese Academy of Sciences, Beijing 100049, China
圆迹SAR是为了满足精细观测需求提出并发展的一种全方位高分辨3维成像模式,近些年得到国内外广泛关注[1, 2, 4]。常规条带或聚束SAR在直线路径上观测目标区域,限制了空间频率范围的扩展,进而成像分辨率受到局限,而圆迹SAR利用圆周路径突破直线路径观测对空间频率范围的限制[3],从而获得高分辨影像。圆迹SAR还能克服常规SAR成像几何下由地形起伏引起的迭掩、透视缩短和阴影等现象[4],有效提取目标几何特征,在军事侦察、地形测绘和地物分类等应用上具有重要意义。国内外很多研究机构已经开展圆迹SAR机载实验并展示了圆迹成像的应用潜力[6],其中中科院电子所开展了国内首次P波段全极化圆迹SAR机载实验,获得了全方位高分辨图像[4],成功地应用到3维成像等应用中。
作为SAR图像解译的重点研究课题之一[7, 8],SAR图像统计建模从统计角度描述图像数据,能有效指导相干斑滤波、边缘检测、目标识别、地物分类等算法研究[9]。Goodman[10]基于中心极限定理提出散射矢量实虚部均服从零均值高斯分布,建立了相干斑统计模型。Ward[11]于1981年提出SAR图像乘积模型,被广泛应用于后续统计模型的建立。
对于圆迹SAR成像中的统计模型研究国内外尚比较空白,因此本文依据圆迹SAR子孔径序列影像的3种合成方法:相干累加、非相干累加和取子孔径最大强度值[12]法,建立每种方法成像后的统计模型,并分析不同方法对图像相干斑的影响和应用范围,对后续相干斑滤波、地物分类有重要指导意义。
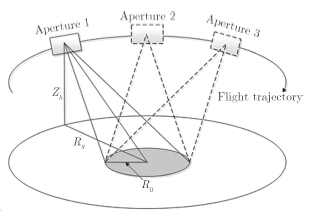
2 圆迹SAR成像统计模型 2.1 圆迹SAR成像图 1为圆迹SAR成像几何示意图,雷达平台在距地面高度为Zh的平面上以半径Rg沿圆周轨迹匀速运动,波束始终照射在半径为${R_0}$的目标区域,通过多角度观测获取方位向的序列影像。圆迹SAR方位向波束角为360°,沿着方位向被分解为多个子孔径图像,每个子孔径角度为$\theta $,则孔径数$ N = {{2π} \mathord{\left/{\vphantom {{2π} \theta }} \right. } \theta }$。
|
图 1 圆迹SAR成像几何示意图 Fig.1 The diagram of CSAR imaging mode |
对于N个子孔径影像,每幅图像被投影到统一的地理坐标平面上,且样本相隔一致。每个孔径获得的散射矢量为${{S}_i} = {x_i} + {\rm{j}}{y_i}$,那么全孔径相干累加(Coherent Adding,CA)合成方法即对散射矢量进行叠加,表示为:
| ${S} = \sum\limits_{i = 1}^N {{{S}_i} = \sum\limits_{i = 1}^N {({x_i} + {\rm{j}}{y_i})} } $ | (1) |
相干累加法合成的图像强度为:
| ${I_{{\rm{CA}}}} = {\left( {\sum\limits_{i = 1}^N {{x_i}} } \right) \! \! {^2}} + {\left( {\sum\limits_{i = 1}^N {{y_i}} } \right) \! \! {^2}}$ | (2) |
这种方法简单直接,并忽略目标非各向同性散射问题,弱化散射差异性。还有一种常用的处理方法是对强度采用提取子孔径最大强度值的方法[12],可以被表示为:
| $\begin{aligned} {I_{{\rm{max}}}} & = \max \left\{ {{I_1},\cdots ,{I_N}} \right\}\\ & = \max \left\{ {\left( {x_1^2 + y_1^2} \right),\cdots ,\left( {x_N^2 + y_N^2} \right)} \right\} \end{aligned}$ | (3) |
另一种忽略目标非各向异性散射问题的处理方法是非相干累加法(Incoherent Adding,IA),对子孔径图像强度进行累加,可以表示为:
| ${I_{{\rm{IA}}}} = \sum\limits_{i = 1}^N {{I_i}} = \sum\limits_{i = 1}^N {x_i^2 + y_i^2} $ | (4) |
SAR图像中的相干斑是由大量散射单元反射波的相干叠加引起的,相干斑使相邻像素间的信号强度发生变化,视觉上表现为颗粒状的噪声。它增加了图像解译分析的难度[13],降低了图像分割和特征分类的性能,研究SAR图像相干斑统计特性有助于设计有效的相干斑滤波、地物参数估计、土地利用、地物覆盖分类等算法,能更好地提取所需的信息。
根据建模过程,SAR图像相干斑统计模型可分为两类:参量模型和非参量模型。参量模型是根据图像区域可能服从的几种概率分布通过实际数据估计统计参数,通过检验比较不同分布的匹配程度建立最优模型,而非参量模型是基于图像区域的数据驱动方式获取最优的概率分布模型。尽管非参量模型灵活性更大,对实际数据拟合的精度较高,但其建模过程计算耗时大,需要样本数据较大,较难满足实际应用的需求[14]。参量模型建模较为简单,耗时短,因此得到了更为广泛和深入的研究。
雷达散射回波是由一个分辨单元内大量散射单元所反射的电磁波合成的结果。根据中心极限定理,散射矢量的实部x和虚部y相互独立,各自服从均值为0、方差为${{{\sigma ^2}} \mathord{\left/ {\vphantom {{{\sigma ^2}} 2}} \right. } 2}$的高斯分布。则SAR图像强度服从负指数分布:
| ${P_I}\left( {I;\sigma ,L} \right) = \frac{1}{{{\sigma ^2}}}\exp \left( { - \frac{I}{{{\sigma ^2}}}} \right),\,\,I \ge 0 $ | (5) |
降斑的一个常用方法是对若干独立的反射率测量值进行平均,即多视处理[15]。对于L视SAR强度图像而言,强度I概率密度函数为阶参数为L的伽马分布:
| \[{P_I}\left( {I;\sigma ,L} \right) = \frac{1}{{\Gamma \left( L \right)}}\left( {\frac{L}{{{\sigma ^2}}}} \right){{\rm{ }}^L}{I^{L - 1}}{{\rm{e}}^{ - LI/{\sigma ^{\rm{2}}}}}\] | (6) |
| ${M_L}\left( I \right) = {\sigma ^2},\quad {\rm{Va}}{{\rm{r}}_L}\left( I \right) = {{{\sigma ^4}} \mathord{\left/ {\vphantom {{{\sigma ^4}} L}} \right. } L}$ | (7) |
定义归一化SAR图像强度为:
| $T = \frac{I}{{E\left( I \right)}} = \frac{I}{{{\sigma ^2}}}$ | (8) |
则通过累积分布函数可证明归一化强度服从如下分布:
| ${P_T}\left( {T \ ;L} \right) = \frac{{{{\left( L \right)}^L}}}{{\Gamma \left( L \right)}}{T^{L - 1}}{{\rm{e}}^{ - LT}}$ | (9) |
负指数分布和伽马分布都属于瑞利相干斑模型,可以较好地描述均匀区域的SAR图像,但不适用于描述非均匀区域图像。对于非均匀区域,乘积模型认为图像观测强度为后向散射截面积和相干斑的乘积。在相干斑和RCS分布分别服从伽马分布条件下,非均匀区域归一化强度图像服从K分布:
| ${P_T}\left( {T \ ;L} \right) \! = \! \frac{{2{{\left( {L\nu } \right)}^{{{\left( {L + \nu } \right)} \mathord{\left/ {\vphantom {{\left( {L + \nu } \right)} 2}} \right. } 2}}}}}{{\Gamma \left( L \right)\Gamma \left( \nu \right)}}{T^{{\large \frac{1}{2}}\left( {\nu + L - 2} \right)}}{K_{v - L}}\left[{2\sqrt {\nu LT} } \right]$ | (10) |
在SAR图像相干斑统计建模中,为了准确衡量SAR图像的相干斑噪声水平,引入等效视数(Equivalent Number of Looks,ENL)的概念[16],等效视数越高则相干斑噪声水平越低,强度等效视数定义为:
| ${\hat L_e} = \frac{{{{\left\langle I \right\rangle}^2}}}{{\left\langle {{I^2}} \right\rangle - {{\left\langle I \right\rangle }^2}}} = \frac{{{{\left\langle T \,\right\rangle }^2}}}{{\left\langle {{T \; ^2}} \right\rangle - {{\left\langle T \,\right\rangle }^2}}}$ | (11) |
为了从统计角度对3种合成法建模,假设圆迹SAR子孔径图像在各观测角度间独立且各向同性。对于圆迹SAR图像相干累加合成法而言,合成的回波矢量是每个子孔径散射回波矢量相加,单个子孔径散射矢量的实部x和虚部y均服从均值为0、方差为${{{\sigma ^2}} \mathord{\left/ {\vphantom {{{\sigma ^2}} 2}} \right. } 2}$的高斯分布,且由于独立高斯分布的和依旧服从高斯分布,则相干累加后散射矢量实部虚部服从均值为0、方差为${{N{\sigma ^2}} \mathord{\left/{\vphantom {{N{\sigma ^2}} 2}} \right. } 2}$的高斯分布。因此对于均匀区域相干累加后图像强度依旧服从于单视SAR图像中的负指数分布,故相干累加法对图像降斑并没有明显作用。
非相干累加法中,圆迹SAR合成图像强度为各子孔径强度之和。为了计算N个独立随机变量之和的分布,可以利用随机变量的动差生成函数(MGF):
| $M\left( t \right) = {M_X}\left( t \right) = E\left[{{{\rm{e}}^{tX}}} \right] = \int_{ - \infty }^\infty {{\rm{e}}^{tx}}f\left( x \right){\rm{d}}x$ | (12) |
若$t = {\rm{ - j}}w$,则动差生成函数为傅里叶变换后函数形式,根据傅里叶变换理论,动差生成函数和概率密度函数是唯一对应的。
若${T_{s}} = {T_1} + {T_2} + \cdots + {T_N}$,且${T_1},{T_2},\cdots ,{T_N}$独立,则
| $\begin{aligned} {M_{T_{\large s}}}\left( t \right) & = E\left[{{\rm{e}}^{tT}} \right] = E\left[{{\rm{e}}^{t{T_1}}} \cdots {{\rm{e}}^{t{T_N}}} \right] \\ & = E\left[{{t^{{T_1}}}} \right] \cdots E\left[{{t^{{T_N}}}} \right] = {M_{{T_1}}}\left( t \right) \cdots {M_{{T_N}}}\left( t \right) \end{aligned}$ | (13) |
当圆迹SAR中子孔径图像均匀区域强度服从伽马分布时,尽管每个子孔径并非严格各向同性,为了从理论角度分析最大相干斑抑制程度,我们认为每个孔径同一块区域是独立同分布的。对于独立同分布的$N$个伽马随机变量而言,单个变量动差生成函数为:
| $\begin{aligned} {M_{{T_{\large i}}}}\left( t \right) & = E\left( {{\rm{e}}^{t{T_i}}} \right) \\ & = \frac{{{L^L}}}{{\Gamma \left( L \right)}}\int_0^\infty {{\rm{e}}^{t{t_i}}}t_i^{L - 1}{{\rm{e}}^{ - L{t_i}}}{\rm{d}}{t_i} = {\left( {\frac{L}{{L - t}}} \right) \! \! {^L}} \end{aligned}$ | (14) |
则非相干累加后${T_s}$动差生成函数为:
| $\begin{aligned} {M_{{T_s}}}\left( t \right) & = \prod\limits_{i = 1}^N {{M_{{T_i}}}\left( t \right)}\\ & = \prod\limits_{i = 1}^N {{{\left( {\frac{L}{{L - t}}} \right)}^L}} = {\left( {\frac{L}{{L - t}}} \right)^{NL}} \end{aligned}$ | (15) |
对${M_{{T_s}}}\left( t \right)$作逆傅里叶变换,则非相干累加后SAR图像服从阶数为NL的伽马分布:
| ${P_{{T_s}}}\left( {{t_s}} \right) = \frac{{{{\left( L \right)}^{NL}}}}{{\Gamma \left( {NL} \right)}}{T_s}^{\left( {NL - 1} \right)}{{\rm{e}}^{ - L{t_s}}}$ | (16) |
在取子孔径最大值法中,合成图像强度是N个子孔径强度的最大值。若${T_m} = \max \left\{ {{T_1},\cdots ,{T_N}} \right\}$且$ {{T_i}} ~ \Gamma {\rm{(}}L,1/L{\rm{)}}$ ,基于单个伽马随机变量的累积分布函数,则${T_m}$的累积分布函数为:
| $\begin{aligned} {F_{{T_m}}}\left( {{t_m}} \right) & = P\left( {\max \left\{ {{T_1},{T_2},\cdots ,{T_N}} \right\} \le {t_m}} \right) \\ & = P\left( {{T_1} \le {t_m},{T_2} \le {t_m},\cdots ,{T_N} \le {t_m}} \right)\\ {\rm{ }} \\ & = P\left( {{T_1} \le {t_m}} \right)P\left( {{T_2} \le {t_m}} \right) \cdots P\left( {{T_N} \le {t_m}} \right) \\ & = \prod\limits_{i = 1}^N {\frac{{\gamma \left( {L,L{t_m}} \right)}}{{\Gamma \left( L \right)}}} \end{aligned}$ | (17) |
K-S检验是基于样本数据的经验分布函数与拟合分布模型的累积分布函数之差的非参统计检验[17, 18],二者偏差越近,则样本数据越接近于拟合分布。对于样本数据的累积分布函数F(x)和拟合分布的累积分布函数F(x),K-S距离D作为一种检验统计量,定义D为两者的最大偏差:
| $D = \mathop {\max }\limits_x \left| {{F_0}\left( x \right) - F\left( x \right)} \right|$ | (18) |
从几何角度看K-S距离表征了两个分布之间的距离,是表示观测数据与假设分布模型之间的匹配程度的一个观测指标。
3 实验结果与分析图 2为2011年P波段机载圆迹SAR在四川绵阳地区获取的HH极化通道图像,本文对其中一块可以近似为均匀区域的农田数据进行仿真分析。实验中,圆迹SAR共有N=10个子孔径,每个孔径观测角为36°,每幅图像被投影到统一的地理坐标平面上,且样本相隔一致。

|
图 2 圆迹SAR图像仿真区域 Fig.2 Experimental CSAR image |
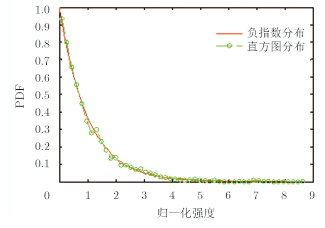
首先,对相干累加法合成法的统计特性进行分析,为了减小动态范围,对子孔径图像进行归一化处理,合成图像的直方图分布曲线和拟合的负指数分布的曲线如图 3所示。直方图分布是指用实际数据的直方图与样本大小比值来模拟样本的概率密度曲线,表征实际数据概率分布。相干合成法中理论分布与样本数据的K-S距离为0.0306,证明实际数据的分布较好地服从理论分布。由于存在图像像素间的相关性,估计出的ENL为0.9472,稍小于理论值1。
|
图 3 相干累加合成法图像强度概率分布 Fig.3 The distribution of coherent sum of the intensity |
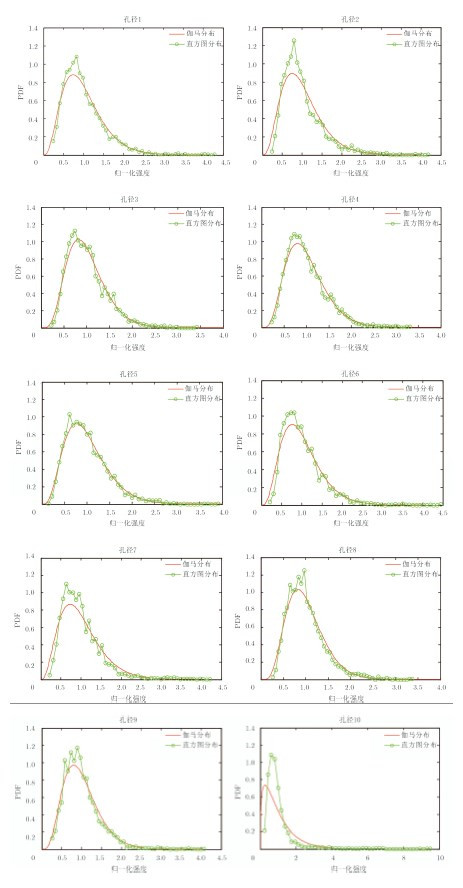
分析非相干累加法和取子孔径最大值法中,为了模拟多视图像,对子孔径图像进行3×3均值滤波。图 4给出了10个子孔径的直方图分布和拟合伽马分布,其中阶参数通过矩估计法得到,每个孔径与理论分布的K-S距离和估计出的ENL参数如表 1所示。从图 4中,我们可以看出除了最后一个孔径,子孔径图像强度能较好地服从伽马分布,每个孔径分布统计参数较为接近,而孔径10的较大的K-S距离与差异较大的ENL参数表明在圆迹SAR成像中,即便是均匀区域也存在某些子孔径较大的散射各向异性情况。
| 表 1 子孔径样本与拟合分布K-S距离和估计ENL Tab. 1 The K-S Distance and ENL of each aperture |
|
图 4 10个子孔径强度直方图分布与拟合分布 Fig.4 Histogram of 10 aperture’s intensity image and estimated PDFs |
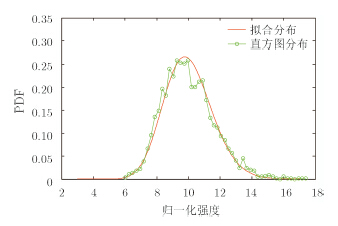
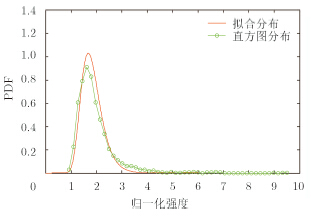
尽管子孔径图像强度分布并不严格满足推导中所假设的独立同分布条件,而非各向同性与地物类型,成像角度等关系较为复杂,为了初步从理论角度分析合成图像后的统计分布和相干斑抑制情况,我们忽略非各向同性将统计参数进行平均,并根据式(16)-式(17)得到非相干累加法和取子孔径最大值法的样本直方图分布和理论分布分别如图 5和图 6所示,表 2则给出两种合成方法的统计参数,K-S距离与估计ENL。从图中可看出,即便在非各向同性的情况下,理论分布依然较好地拟合实际数据,这对后续的应用有一定指导意义。
|
图 5 非相干累加合成图像概率分布 Fig.5 Histogram and estimated PDF of the incoherently-added imaging mode |
|
图 6 取子孔径最大值合成图像概率分布 Fig.6 Histogram and estimated PDF of the maximum-intensity imaging mode |
| 表 2 非相干累加法与取子孔径最大值法统计参数 Tab. 2 The K-S Distance and ENL of different methods |
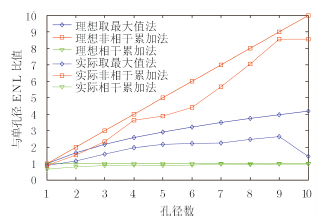
在对样本数据进行分布拟合后,依据完全满足各向同性的假设得到理想ENL随孔径数量变化图与实际圆迹SAR成像ENL随孔径变化图,如图 7所示。可以看出,实际折线图与最理想条件下折线图表现出一致的趋势,由于ENL大小可以衡量相干斑噪声水平,因此非相干累加方法对相干斑抑制效果是最好的,且随着孔径数增多,总体上降斑效果越明显。取子孔径最大值法也具有一定的降斑作用,但趋势随孔径数增多而变缓。相干累加法对相干斑抑制几乎没有作用。
|
图 7 孔径数对ENL影响 Fig.7 The impact of aperture numbers on ENL value |
值得注意的是,实际数据中第10个孔径由于强烈的非各向同性反而降低了合成图像的相干斑抑制效果,这说明散射各向异性的存在会使合成图像的噪声变大,滤波处理也会变得复杂。
尽管非相干累加法具有最好的相干斑抑制效果,但在实际应用中,若区域目标具有较强的非各向同性,如角反射器、建筑物等人造目标,为了完整保持目标的散射特性,此时取子孔径最大值法是较为合理的。因此实际中,要根据需求采用不同的图像合成方法。
4 结论本文基于常规SAR相干斑统计模型对圆迹SAR成像中3种图像合成方法的相干斑统计分布进行推导,并通过实际均匀区域数据进行验证,同时分析并比较每种方法对相干斑抑制的作用。分析结果表明非相干累加法能最有效地降低相干斑,但在实际应用中要考虑到较强散射各向异性的目标时,此时取子孔径最大值法是在降斑与完整保持散射特性的折衷方法。
| [1] | Soumekh M. Reconnaissance with slant plane circular SAR imaging[J]. IEEE Transactions on Image Processing, 1996, 5(8): 1252-1265.( 1) 1) |
| [2] | 洪文. 圆迹SAR成像技术研究进展[J]. 雷达学报, 2012, 1(2): 124-135. Hong Wen. Progress in Circular SAR imaging technique[J]. Journal of Radars, 2012, 1(2): 124-135.(  1) 1) |
| [3] | 张祥坤. 高分辨率圆迹合成孔径雷达成像机理及方法研究[D]. [博士论文], 北京: 中国科学院研究生院, 2007: 65-70. Zhang Xiang-kun. High-resolution Circular Synthetic Aperture Radar[D]. [Ph.D. dissertation], Beijing: University of Chinese Academy of Sciences, 2007: 65-70.(  1) 1) |
| [4] | Lin Y, Hong W, Tan W X, et al.. Airborne Circular SAR imaging: results at P-band[C]. Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 2012: 5594-5597.( 3) 3) |
| [5] | Pinheiro M. Processing, radiometric correction, autofocus and polarimetric classification of Circular SAR data[D]. [Ph.D. dissertation], the Department of Graduate Studies of the Aeronautics Institute of Technology, 2010: 38-50.( 1) 1) |
| [6] | Guo Z Y, Lin Y, Tan W X, et al.. Circular SAR motion compensation using trilateration and phase correction[C]. Proceedings of the IET International Radar Conference, Xi’an, 2013: 1-5.( 1) 1) |
| [7] | Lee J S and Pottier E. Polarimetric Radar Imaging: From Basics to Applications[M]. Boca Raton FL: CRC Press, 2009: 101-111.( 1) 1) |
| [8] | Li H C, H W, Wu Y R, et al.. An efficient and flexible statistical model based on generalized Gamma distribution for amplitude SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(6): 2711-2722.( 1) 1) |
| [9] | Gao G, Shi G T, Kuang G Y, et al.. Statistical Modeling of SAR Images: Models and Applications[M]. Beijing: National Defense Industry Press, 2013: 1-5.( 1) 1) |
| [10] | Goodman J W. Statistical Properties of Laser Speckle Patterns[M]. Berlin: Springer-Verlag, 1975: 9-75.( 1) 1) |
| [11] | Ward K D. Compound representation of high resolution sea clutter[J]. Electronics Letters, 1981, 17(16): 561-563.( 1) 1) |
| [12] | Chan T K, Kuga Y, and Ishimaru A. Experimental studies on Circular SAR imaging in clutter using angular correlation function technique[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2192-2197.( 2) 2) |
| [13] | Oliver C and Quegan S. Understanding Synthetic Aperture Radar Images[M]. SciTech Publishing, 2004: 59-66.( 1) 1) |
| [14] | 高贵. SAR图像统计建模研究综述[J]. 信号处理, 2009(8): 1270-1278. Gao Gui. Review on the statistical modeling of SAR images[J]. Signal Processing, 2009(8): 1270-1278.(  1) 1) |
| [15] | Foucher S, Boucher J M, and Bénie G B. Maximum likelihood estimation of the number of looks in SAR images[C]. 13th International Conference on Microwaves, Radar and Wireless Communications, Wroclaw, Poland, 2000, 2: 657-660.( 1) 1) |
| [16] | Anfinsen S N, Doulgeris A P, and Eltoft T. Estimation of the equivalent number of looks in polarimetric synthetic aperture radar imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(11): 3795-3809.( 1) 1) |
| [17] | Stephens M A. EDF statistics for goodness of fit and some comparisons[J]. Journal of the American Statistical Association, 1974, 69(347): 730-737.( 1) 1) |
| [18] | Press W H, Teukolsky S A, Vetterling W T, et al.. Numerical Recipes in C[M]. Cambridge: Cambridge University Press, 1996: 623-626.( 1) 1) |
 2015, Vol. 4
2015, Vol. 4
