针对传统的先检测后跟踪(Detect-Before-Track, DBT)方法在对低信杂(噪)比(一般小于10 dB)目标检测造成的目标信息损失问题[1,2],检测前跟踪(Track-Before-Detect, TBD)技术是一种良好的应对策略。TBD是一种雷达多帧信号积累技术,介于信号处理和数据处理之间,不严格设定检测与跟踪之间的界限,直接使用原始量测信号,在检测前引入跟踪滤波思想,建立跟踪模型对目标实施跟踪维持,挖掘目标运动信息来辅助检测[3–5]。由于充分利用了原始数据信息,TBD技术对实际雷达系统的性能有一定程度的提升[6–8]。
有限集统计学(FInite Set STatistics, FISST)方法将多目标状态集合和量测集合建模元素数目可变的随机有限集(Random Finite Set, RFS),利用最优贝叶斯滤波避免数据关联的不确定,实现检测不确定和杂波干扰背景下的多目标估计。但由于多目标状态空间和量测空间是无限维的,最优多目标贝叶斯滤波器在实际中难以应用,Mahler[9]计算RFS中多目标后验概率密度的1阶矩,提出概率假设密度(Probability Hypothesis Density, PHD)滤波有效降低最优多目标贝叶斯滤波的运算量。目前,两种PHD的收敛形式应用较为广泛,分别是高斯混合PHD(Gaussian Mixture-PHD, GM-PHD)[10]和序贯蒙特卡洛PHD(Sequential Monte Carlo-PHD, SMC-PHD)[11,12],后者也称为粒子滤波PHD(Particle Filter, PF-PHD)。PF-PHD-TBD算法以非归一化粒子权重之和进行目标数目估计,不需要目标数目的先验信息,并且新生粒子的采样数量在算法执行前便已确定,不存在概率转移矩阵的设置问题,不存在多目标关联和配对问题,相比于GM-PHD-TBD更适合处理雷达信号中的非线性非高斯问题[13,14]。
但目前将PHD理论运用在TBD领域尚存在诸多不足之处[15],在多目标检测与跟踪问题中,目标状态的维数是随着目标数目线性增长的,在联合采样中会造成维数灾难,而且在非线性非高斯条件下,难以直接得到高维集合积分的解析解,因此本文采用粒子滤波的实现方法。为实现多目标检测前跟踪,粒子数目必须足够大,才能解决高维度的联合采样问题[16],但过多粒子又会使得计算负担加重。为解决上述问题,本文选择引入两层粒子的概念,将平行分割理论(Parallel Partition, PP)与辅助粒子滤波(Auxiliary Particle Filter, APF)结合,在PHD滤波的序贯蒙特卡洛实现方法基础上进行改进,提出一种基于平行分割理论的辅助粒子滤波概率假设密度检测前跟踪算法(APP-PF-PHD-TBD)。本算法利用平行分割理论,避免联合采样时的维数灾难;利用APF的辅助变量对第2层粒子标记,对当前目标进行状态预测时,结合与当前目标相邻近目标的状态似然,得到目标的预测似然函数;最后利用两层粒子的更新迭代,可以实现在粒子数较少或是目标较多的情况下对密集多目标状态的准确估计。仿真结果和海杂波数据实验表明,APP-PF-PHD-TBD算法相较PF-PHD-TBD具有更好的目标数目和状态估计效果,在目标密集情况下优势更为明显。
2 目标系统状态模型和量测模型 2.1 系统状态模型考虑多个目标在平面进行2维运动,假设在k时刻目标总数为
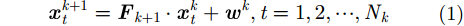
|
其中,
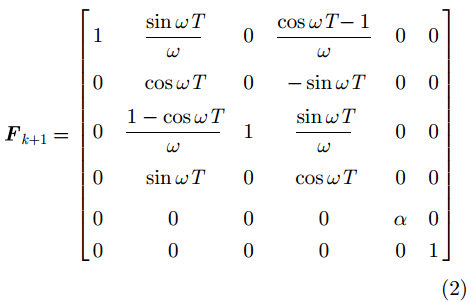
|
针对匀速(Constant Velocity, CV)状态模型,
雷达传感器TBD量测模型需要对回波信号进行距离-多普勒-方位的3维量测[13,18],k 时刻1次扫描的量测信息
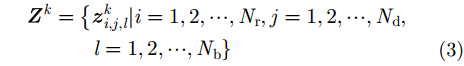
|
其中,
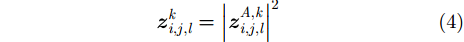
|
其中,
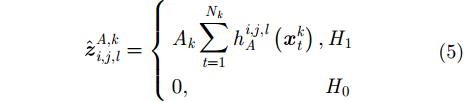
|
其中,
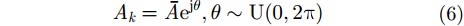
|
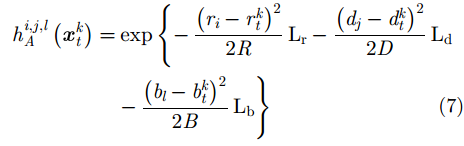
|

|
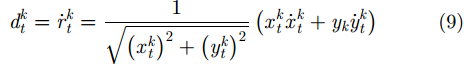
|

|
其中,
需注意的是,PHD滤波器对于多目标贝叶斯滤波器的近似需要满足[19]1个分辨单元最多只能存储1个目标的幅度信息,由此得到的雷达量测似然比函数为
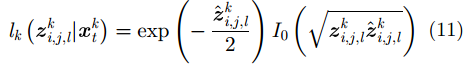
|
其中,
针对非线性滤波问题,PHD的解析解难以得到,PHD-TBD两种实现方式中粒子实现方式PF-PHD-TBD应用更为广泛。在多目标检测前跟踪问题中,目标状态的维数随着目标数量线性增长[16],但为达到理想跟踪效果,粒子必须足够多才足以解决高维度的联合采样问题,但粒子数目增大会带来不可避免的计算负担。为解决计算量与估计精度之间的矛盾,本文将粒子平行分割理论应用于PF-PHD-TBD以减弱粒子滤波中维数灾难所带来的影响。
3.1 粒子平行分割理论后验独立假设[21](posterior independence assumption)假定目标的后验概率相互独立,可以在滤波迭代的下一步先验估计中减弱维数灾难的影响。独立分割[22](Independent Partition, IP)以及平行分割[23]的实例都有效证明了该观点。但不同的是,PP方法在采样过程中结合周围目标进行估计,因此在目标移动紧密的情况下性能优于IP方法。
假设已知获得目标总数的先验知识,并且已知目标运动相互独立。分割单个粒子
根据后验独立假设,后验概率密度可以重写为[24]
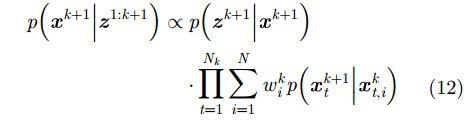
|
为在采样步骤中考虑周围目标的影响,得到对目标
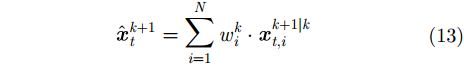
|
其中,
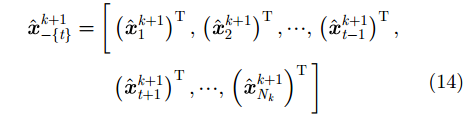
|
根据目标t的预测状态
辅助粒子滤波旨在借助辅助变量,可以更加准确地考虑量测,模拟出最优重要性采样的采样过程[25]。但在目标数增加时,由于APF的采样过程是在整个状态空间联合采样以至于会受到维数灾难的影响,从而导致性能降低[26]。而APP-PF将粒子平行分割和辅助粒子滤波相结合,通过平行分割理论,可以减弱维数灾难对滤波性能的影响。
定义预测目标似然
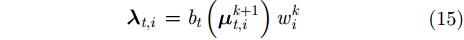
|
其中,
对于APP-PF而言,其重要性密度函数进行目标采样时相互独立,借助辅助变量
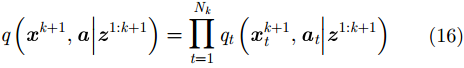
|
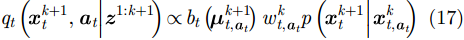
|
其中,
利用针对于单个目标的辅助变量
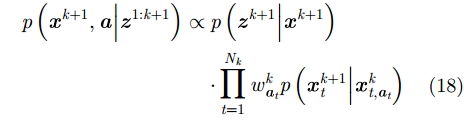
|
由于
APP-PF-PHD-TBD算法与现有PF-PHD-TBD的不同之处在于预测和更新过程,其具体实现为:
(1) 初始化。用一定数量的粒子根据目标的初始建议密度进行采样,
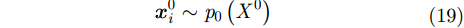
|
(2) PHD预测。假设在
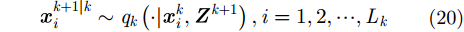
|
假设
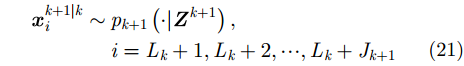
|
并根据式(22)计算存活粒子的权重
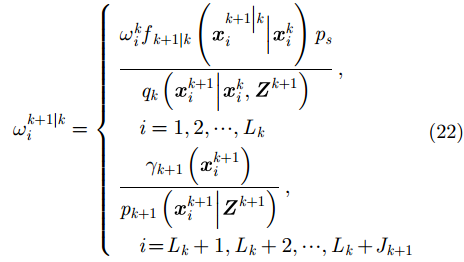
|
在预测过程中生成粒子对应的子粒子,当k+1=1时根据目标数目的先验知识确定每个粒子对应的子粒子数目;当k+1>1时则根据上一时刻的估计目标数目确定。子粒子的空间分布依照粒子的分布进行采样,即
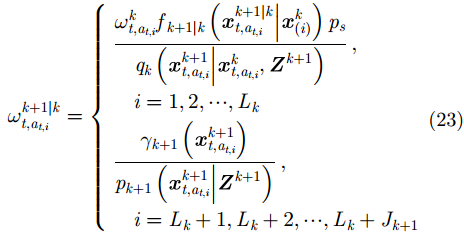
|
使用辅助变量定义的粒子一步预测概率
(3) PHD更新。对于
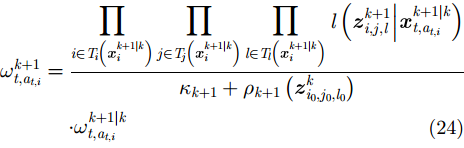
|
其中,
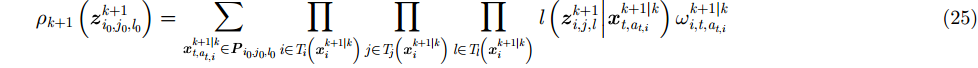
|
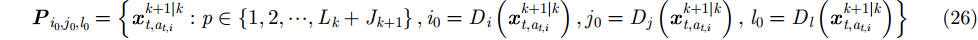
|
在此更新之外还需要对第1层粒子
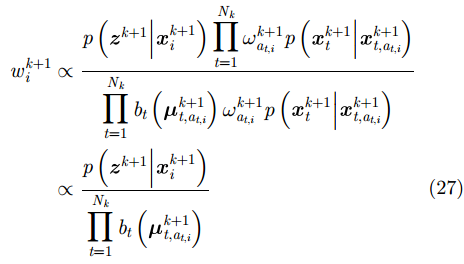
|
另外对k+1时刻高似然比子粒子进行选择,令子粒子在k+1时刻根据似然比对目标的索引t相互交叉替换,之后继续将k+1时刻的子粒子组合成为k+1时刻的粒子。此时的粒子是经由子粒子权重进行交叉选择,合并得到的结果。
(4) 重采样与状态提取。为避免粒子权重退化,首先进行粒子重采样删除小权重,复制大权重。PHD在测量区域内的积分即为该区域内期望的目标数目
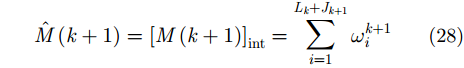
|
PHD函数中,目标状态的估计值即为峰值点所在位置,就是粒子通过聚类得到聚类中心的位置。
4 仿真分析 4.1 仿真条件说明本节将给出杂波背景下多目标TBD的应用仿真实例,仿真设置40个雷达传感器扫描周期,产生40帧仿真数据,一共100次蒙特卡洛实验取统计均值。扫描间隔
仿真中参数设置为:目标存活概率
因为量测模型经过由笛卡尔坐标系到距离-多普勒-方位的转换,就实现方式而言高斯混合形式不及粒子滤波形式的滤波性能,因此本文仿真主要讨论粒子滤波实现,仿真过程利用PF-PHD-TBD, APP-PF-PHD-TBD方法在相同的仿真场景9 dB, 8 dB, 6 dB的信杂(噪)比环境下依次试验。仿真实验算法性能评估指标采用最优子模式分配(Optional SubPattern Assignment, OSPA)[27]距离作为目标状态估计精度的评价标准,选取OSPA参数截断距离
实验1 多目标仿真场景(CV模型,无目标交叉)检测性能对比。
仿真首先在较为一般的场景下进行,假设目标之间航迹没有交叉,且目标的运动模型符合匀速模型,多目标的初始位置设置如表1所示,一共经过100次蒙特卡洛仿真,得到两种算法的性能对比。
| 表 1 实验1中目标运动状态 Tab.1 The state of the targets in Exp.1 |
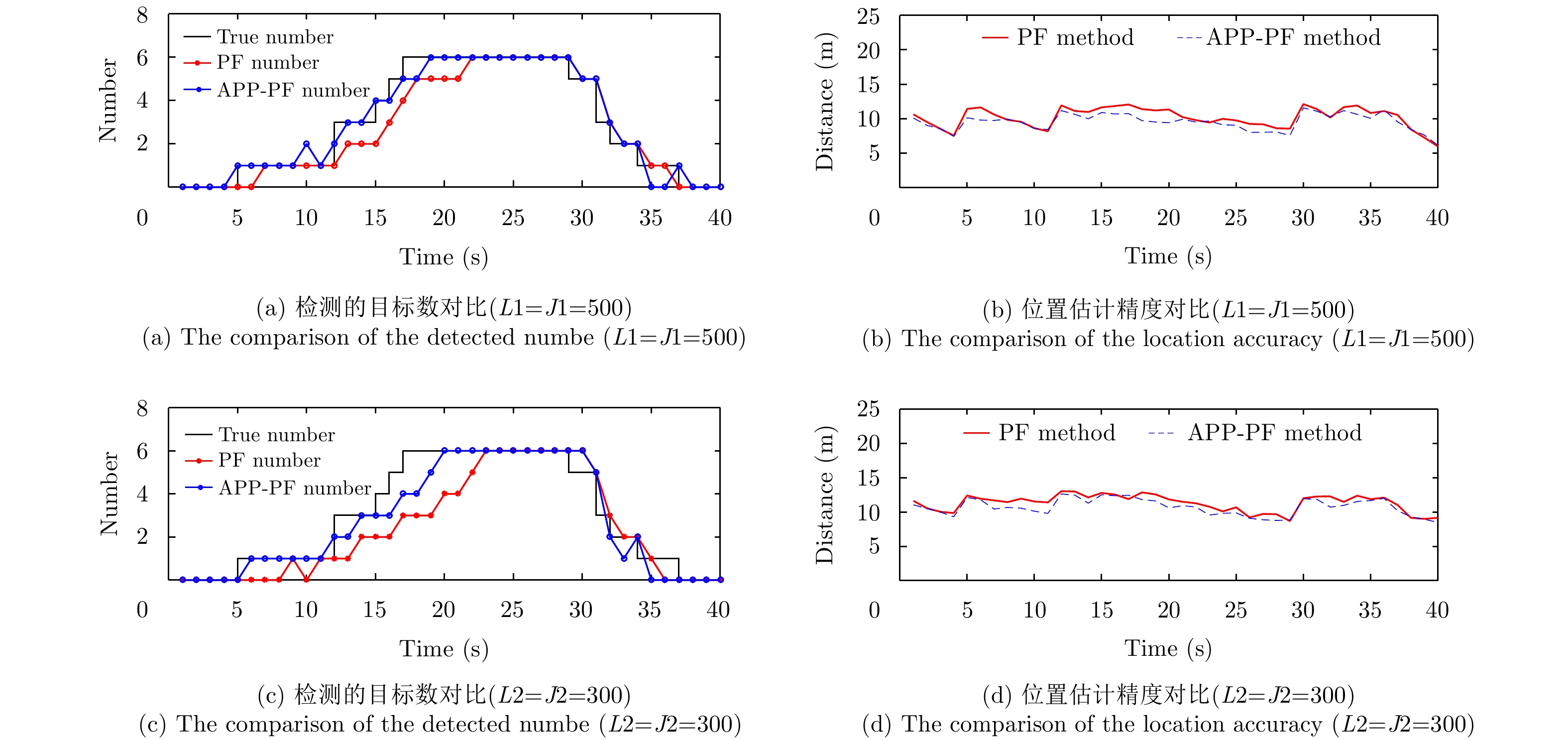
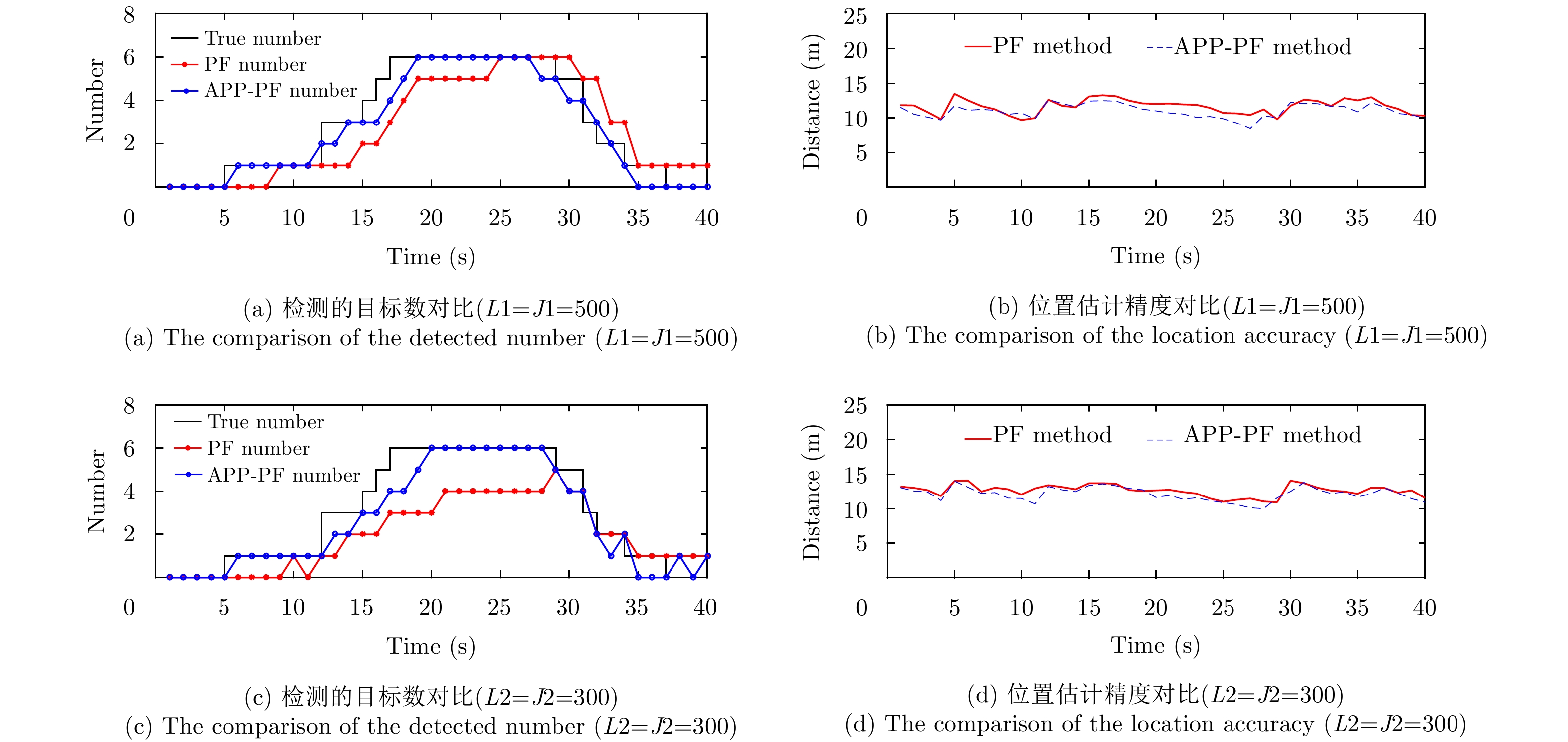
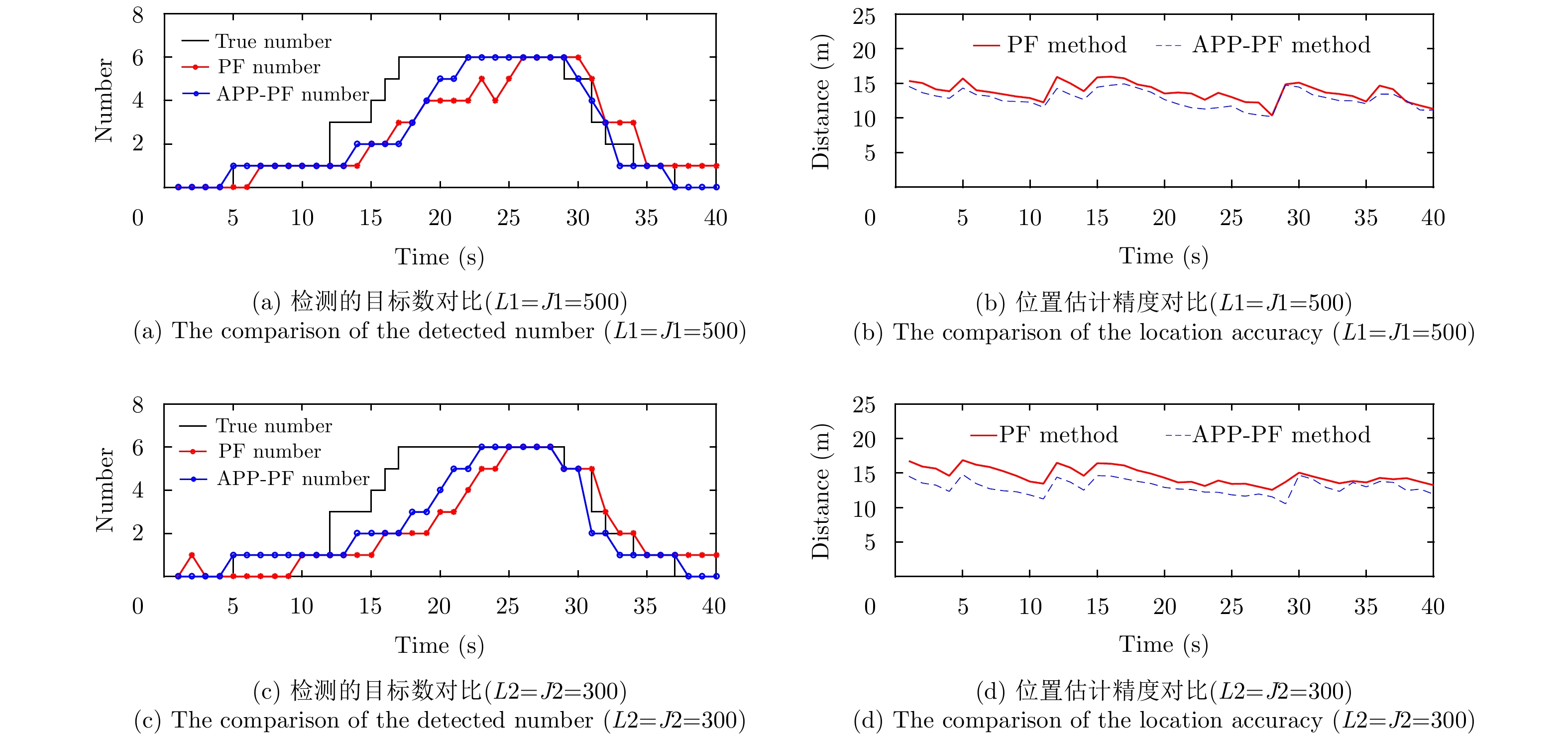
在图1至图3中子图(a), (b)和子图(c), (d)分别代表L1=J1=500和L2=J2=300的情况。由图1—图3可见 ,在相同的仿真条件下,APP-PF-PHD-TBD算法与PF-PHD-TBD算法相比有着近似的目标数目估计性能,且性能都较为良好,作为误差评判的OSPA距离也较为接近。需注意的是,在单个目标分配的粒子数减少时,APP-PF-PHD-TBD算法无论是在估计目标数目还是目标估计位置精度,性能相比于PF-PHD-TBD更好。
|
图 1 实验1 9 dB时两种方法的目标数目检测性能对比 Fig.1 Exp.1 the performance of the two method in 9 dB |
|
图 2 实验1 8 dB时两种方法的目标数目检测性能对比 Fig.2 Exp.1 the performance of the two method in 8 dB |
|
图 3 实验1 6 dB时两种方法的目标数目检测性能对比 Fig.3 Exp.1 the performance of the two method in 6 dB |
实验2 多目标仿真场景(CT模型,存在目标航迹交叉)检测性能对比。
仿真假设邻近多目标之间航迹相互交叉,且目标的运动模型符合协同转弯模型,实验中多目标的运动状态如表2所示,同样经过100次蒙特卡洛仿真得到两种算法的性能对比。
| 表 2 实验2中目标运动状态 Tab.2 The state of the targets in Exp.2 |
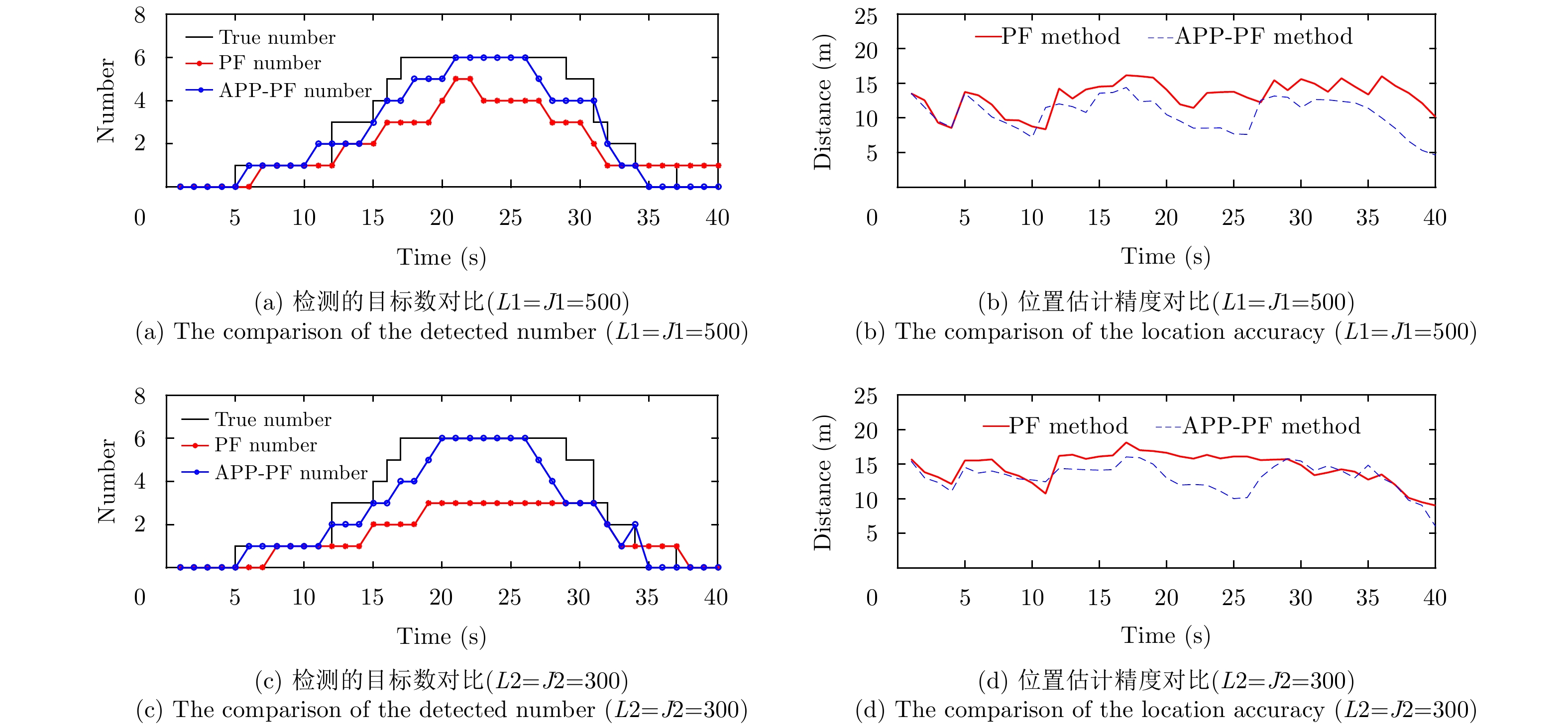
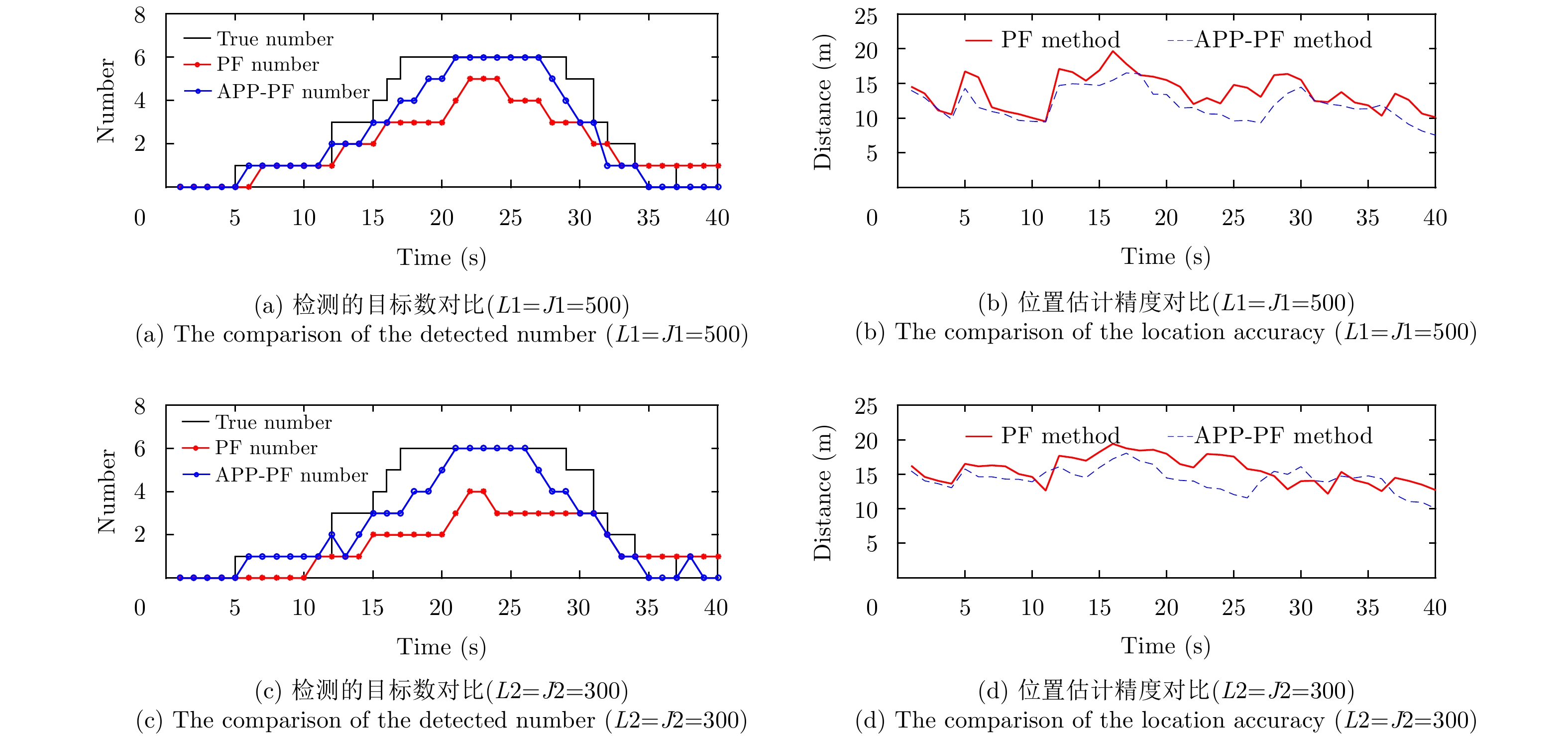
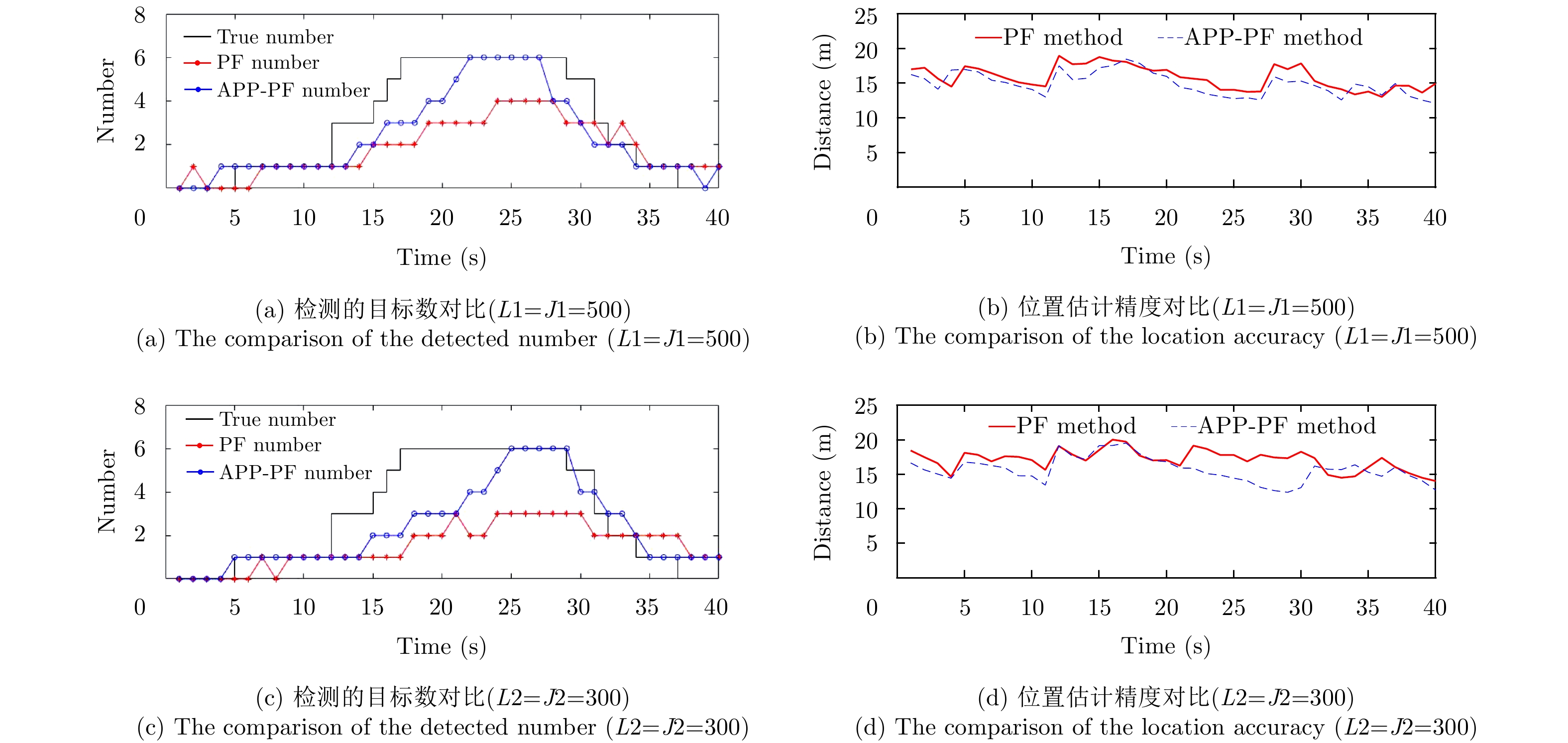
在图4—图6中子图(a), (b)和子图(c), (d)依然分别代表L1=J1=500和L2=J2=300的情况。由图4–图6得,目标密集时APP-PF-PHD-TBD算法明显拥有比PF-PHD-TBD算法更加优越的目标数目估计性能。信杂(噪)比较低以及粒子数目较少,算法性能都会下降,但APP-PF-PHD-TBD依然优于传统PHD-TBD。PF-PHD-TBD没有考虑邻近目标的重要性密度,因此其估计性能随着目标交叉而急剧下降,另外PF-PHD-TBD在多目标状态空间的联合采样会受到维数灾难的影响,相较之下APP-PF-PHD-TBD因为后验独立采样不会受到维数灾难的影响,同时考虑了相互邻近的目标状态,不会受到邻近目标的影响。
|
图 4 实验2 9 dB时两种方法的目标数目检测性能对比 Fig.4 Exp.2 the performance of the two method in 9 dB |
|
图 5 实验2 8 dB时两种方法的目标数目检测性能对比 Fig.5 Exp.2 the performance of the two method in 8 dB |
|
图 6 实验2 6 dB时两种方法的目标数目检测性能对比 Fig.6 Exp.2 the performance of the two method in 6 dB |
在图4–图6的子图(b)和子图(d)中,新生目标在既定时刻出现,在对应时刻,算法对目标数目估计有延迟,需要多帧跟踪估计才能检测到新生目标。随着多帧累积处理,目标数估计趋于稳定。由于传统PF-PHD-TBD此时目标数目已经估计不准,造成OSPA距离明显较高且接近截断距离
实验3 实际海杂波背景检测性能对比
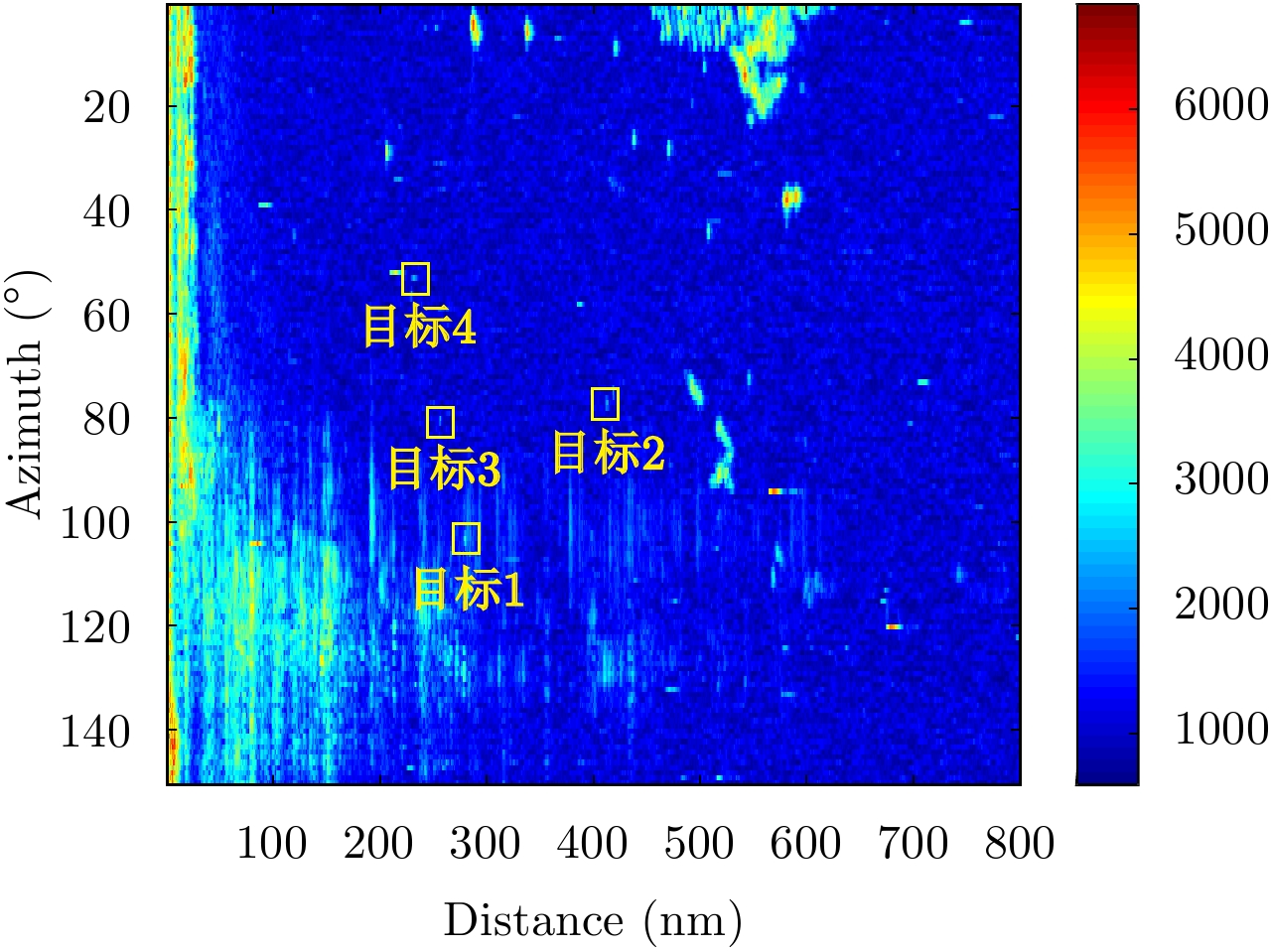
本部分实验选取实际导航雷达采集的实际海杂波背景数据,进行多目标运动场景下的检测性能对比。雷达实际采样率为60 MHz,每圈扫描包含的脉冲数为3000。导航雷达设置每5秒扫描1圈,扫描1圈得到1帧数据,一共40帧数据。我们截取雷达扫描信息的1/4数据作为海杂波实验数据,在雷达海杂波背景数据下添加目标运动信息,运动服从CV模型,目标信息如表3所示,设置信杂(噪)比为9 dB,在第20帧得到的数据为图7所示。
| 表 3 实验3中目标运动状态 Tab.3 The state of the targets in Exp.3 |
|
图 7 加入目标后雷达第20帧扫描的数据信息 Fig.7 The data of the 20th scan after adding the targets |
在TBD检测之前先设置第1级门限
|
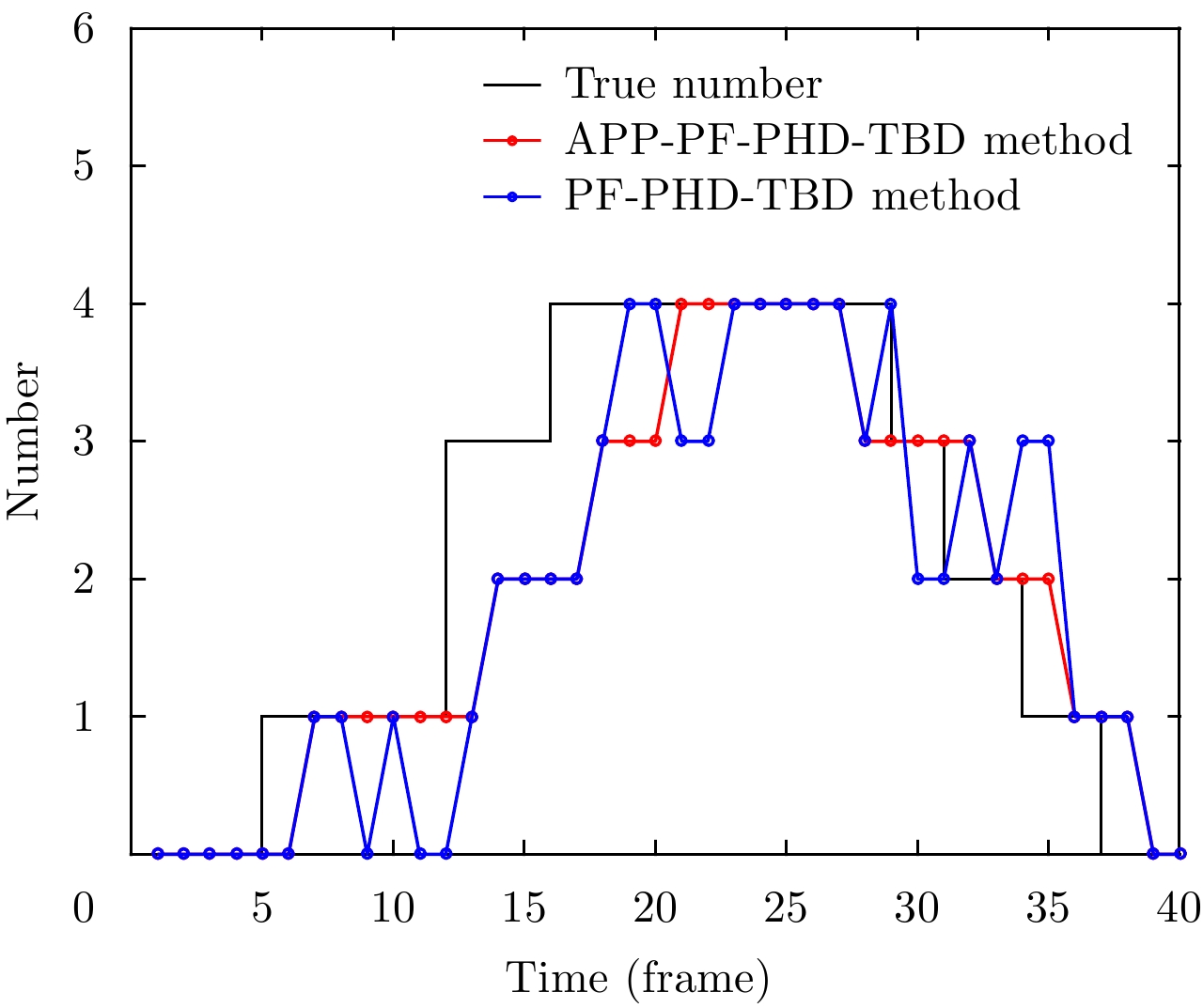
图 8 实验3两种方法目标检测数目对比 Fig.8 The comparison of the detected targets number in Exp.3 |
|
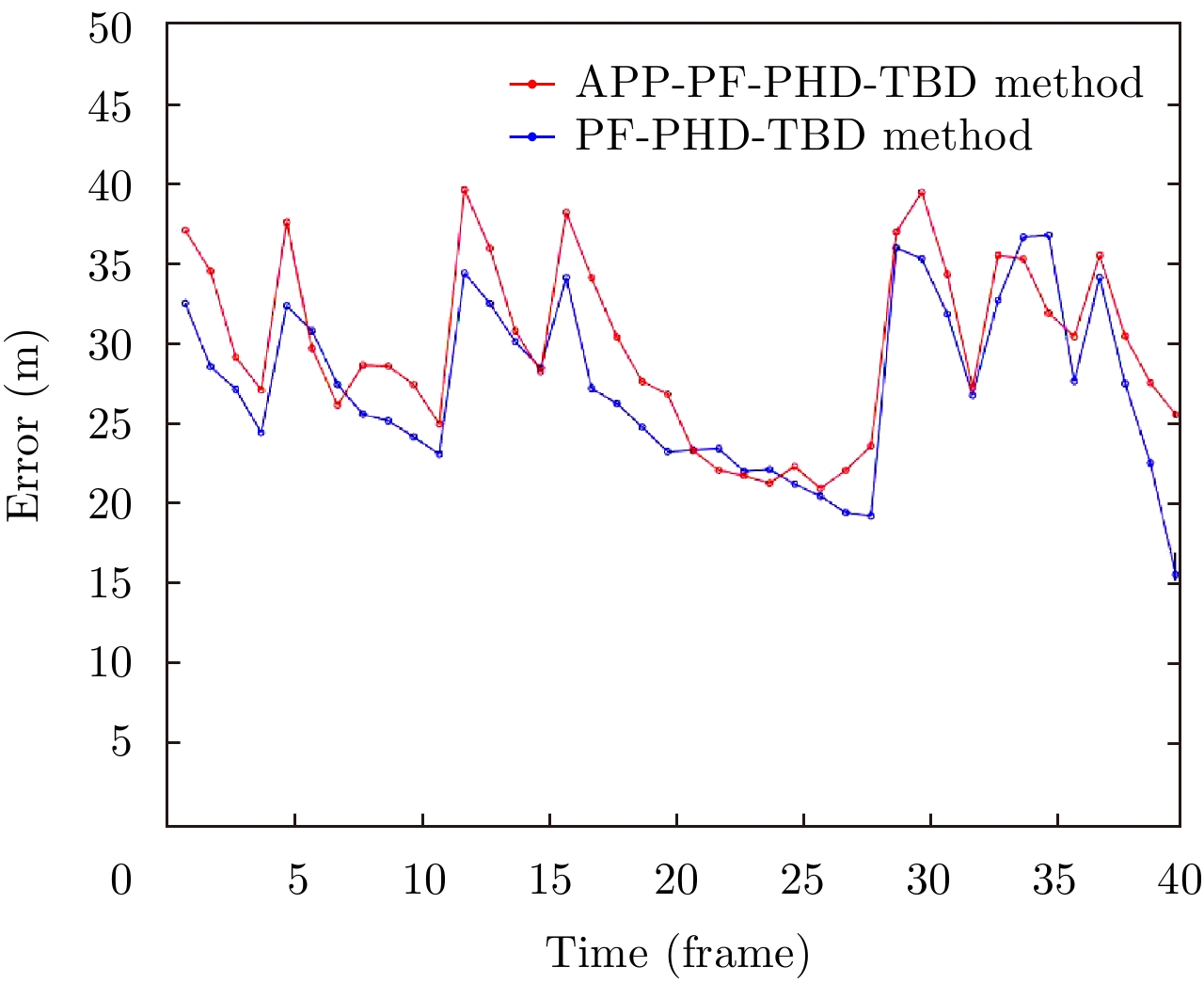
图 9 实验3两种方法位置估计精度对比 Fig.9 The comparison of the location accuracy in Exp. 3 |
海杂波背景数据量较大,因此在本实验中每个存活目标和新生目标的粒子个数均为1000。结果中可以看出信杂(噪)比为9 dB时,在实际海杂波背景的数据下,APP-PF-PHD-TBD和PF-PHD-TBD两种方法对目标都能实现较为准确的估计,但在目标数目变化时的估计都出现了延迟,相较之下APP-PF方法的目标数目检测性能更为平稳,未出现目标数目波动的情况,而且在图9中APP-PF方法的位置误差相对较小。
综上所述,理论分析PHD-TBD的算法复杂度为
| 表 4 实验1算法蒙特卡洛实验平均运行时间(s) Tab.4 The mean running time of per Monte Carlo experiment in Exp. 1 (s) |
| 表 5 实验2算法蒙特卡洛实验平均运行时间(s) Tab.5 The mean running time of per Monte Carlo experiment in Exp. 2 (s) |
| 表 6 实验3算法蒙特卡洛实验平均运行时间(s) Tab.6 The mean running time of per Monte Carlo experiment in Exp. 3 (s) |
经上述综合对比,发现由于APP-PF方法在算法过程中进行了两层粒子的运算过程,在上述3项实验中,运算效率略低于PF-PHD-TBD,这一点在实验1中表现明显;但在实验2中,由于PF-PHD-TBD方法在目标航迹交叉存在时无法精确检测目标个数,造成估计不准的问题,运算时间与实验1中相比还要短,其实是算法缺陷造成的,反观APP-PF-PHD-TBD方法在实验2多目标邻近,航迹相互交叉的情况下,虽然以运算效率为代价,但对目标的估计结果更具有优势;实验3采用海杂波背景数据的仿真,数据量较大,因此在时间上两种方法都有延长。APP-PF方法虽然在效率上较为欠缺,但是算法的稳定性和鲁棒性更强,因此在算法时间允许的情况下,APP-PF-PHD-TBD表现更加优异。
5 结束语本文基于序贯蒙特卡洛概率假设密度滤波,结合粒子分割算法,应用于检测前跟踪过程,主要针对在粒子数目较少时,密集多目标在杂波背景下的目标检测问题,给出算法的系统模型以及测量模型,引入平行分割思想,生成第2层粒子,并阐述算法的具体实施过程。仿真以及海杂波背景实验表明,APP-PF-PHD-TBD算法在目标密集区域的检测效果优于PF-PHD-TBD;在相同信杂(噪)比条件但粒子数目较少的情况下,既能避免维数灾难的影响也能保持较好的目标估计优势。但缺点是不可避免地增加了运算负担,效率较传统算法低;同时,平行分割算法目前假设目标总数先验知识已知,解决目标总数先验未知情况也将是下一步的研究重点。
| [1] |
陈小龙, 关键, 黄勇, 等. 雷达低可观测动目标精细化处理及应用[J].
科技导报, 2017, 35(20): 19-27. Chen Xiao-long, Guan Jian, Huang Yong, et al. Radar refined processing and its applications for low-observable moving target[J]. Science & Technology Review, 2017, 35(20): 19-27. DOI:10.3981/j.issn.1000-7857.2017.20.002 (  0) 0)
|
| [2] |
陈小龙, 关键, 何友, 等. 高分辨稀疏表示及其在雷达动目标检测中的应用[J].
雷达学报, 2017, 6(3): 239-251. Chen Xiao-long, Guan Jian, He You, et al. High-resolution sparse representation and its applications in radar moving target detection[J]. Journal of Radars, 2017, 6(3): 239-251. DOI:10.12000/JR16110 (  0) 0)
|
| [3] |
Zwaga J H, Driessen H, and Meijer W D. Track-before-detect for surveillance radar: A recursive filter-based approach[C]. Proceedings of SPIE 4728, Signal and Data Processing of Small Targets 2002, Orlando, USA, 2002: 103–115. DOI: 10.1117/12.478496.
( 0) 0)
|
| [4] |
杨亚波, 夏永红, 匡华星, 等. 雷达微弱目标检测前跟踪技术研究综述[J].
雷达与对抗, 2015, 35(2): 22-28. Yang Ya-bo, Xia Yong-hong, Kuang Hua-xing, et al. An overview on track-before-detect technique for radar weak targets[J]. Radar & ECM, 2015, 35(2): 22-28. (  0) 0)
|
| [5] |
战立晓, 汤子跃, 朱振波. 雷达微弱目标检测前跟踪算法综述[J].
现代雷达, 2013, 35(4): 45-52, 57. Zhan Li-xiao, Tang Zi-yue, and Zhu Zhen-bo. An overview on track-before-detect algorithms for radar weak targets[J]. Modern Radar, 2013, 35(4): 45-52, 57. DOI:10.3969/j.issn.1004-7859.2013.04.010 (  0) 0)
|
| [6] |
Boers Y and Driessen J N. Multitarget particle filter track before detect application[J].
IEE Proceedings-Radar, Sonar and Navigation, 2004, 151(6): 351-357. DOI:10.1049/ip-rsn:20040841 ( 0) 0)
|
| [7] |
吴孙勇, 薛秋条, 朱圣棋, 等. 杂波环境下基于粒子滤波的微弱扩展目标检测前跟踪算法[J].
雷达学报, 2017, 6(3): 252-258. Wu Sun-yong, Xue Qiu-tiao, Zhu Sheng-qi, et al. Track-before-detect algorithm for weak extended target based on particle filter under clutter environment[J]. Journal of Radars, 2017, 6(3): 252-258. DOI:10.12000/JR16128 (  0) 0)
|
| [8] |
李洋漾, 李雯, 易伟, 等. 基于DP-TBD的分布式异步迭代滤波融合算法研究[J].
雷达学报, 2018, 7(2): 254-262. Li Yang-yang, Li Wen, Yi Wei, et al. A distributed asynchronous recursive filtering fusion algorithm via DP-TBD[J]. Journal of Radars, 2018, 7(2): 254-262. DOI:10.12000/JR17057 (  0) 0)
|
| [9] |
Mahler R P S M. Multitarget bayes filtering via first-order multitarget moments[J].
IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178. DOI:10.1109/TAES.2003.1261119 ( 0) 0)
|
| [10] |
Vo B N and Ma W K. The Gaussian mixture probability hypothesis density filter[J].
IEEE Transactions on Signal Processing, 2006, 54(11): 4091-4104. DOI:10.1109/TSP.2006.881190 ( 0) 0)
|
| [11] |
Vo B N and Ma W K. A closed-form solution for the probability hypothesis density filter[C]. Proceedings of the 2005 7th International Conference on Information Fusion, Philadelphia, USA, 2005: 856–863. DOI: 10.1109/ICIF.2005.1591948.
( 0) 0)
|
| [12] |
吴伟, 尹成友. 一种用于多目标跟踪的增强型SMC-PHD滤波算法[J].
雷达学报, 2012, 1(4): 406-413. Wu Wei and Yin Cheng-you. An improved SMC-PHD filter for multiple targets tracking[J]. Journal of Radars, 2012, 1(4): 406-413. DOI:10.3724/SP.J.1300.2012.20094 (  0) 0)
|
| [13] |
Punithakumar K, Kirubarajan T, and Sinha A. A sequential monte carlo probability hypothesis density algorithm for multitarget track-before-detect[C]. Proceedings of SPIE 5913, Signal and Data Processing of Small Targets 2005, San Diego, USA, 2005: 1–8. DOI: 10.1117/12.618438.
( 0) 0)
|
| [14] |
Vo B N, Vo B T, Pham N T, et al. Reply to " Comments on ‘Joint detection and estimation of multiple objects from image observations’”[J].
IEEE Transactions on Signal Processing, 2012, 60(3): 1540-1541. DOI:10.1109/TSP.2011.2173686 ( 0) 0)
|
| [15] |
占荣辉, 刘盛启, 欧建平, 等. 基于序贯蒙特卡罗概率假设密度滤波的多目标检测前跟踪改进算法[J].
电子与信息学报, 2014, 36(11): 2593-2599. Zhan Rong-hui, Liu Sheng-qi, Ou Jian-ping, et al. Improved multitarget track before detect algorithm using the sequential Monte Carlo probability hypothesis density filter[J]. Journal of Electronics & Information Technology, 2014, 36(11): 2593-2599. DOI:10.3724/SP.J.1146.2013.02029 (  0) 0)
|
| [16] |
Daum Fred and Huang J. Curse of dimensionality and particle filters[C]. Proceedings of 2003 IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 2003: 1979–1993. DOI: 10.1109/AERO.2003.1235126.
( 0) 0)
|
| [17] |
Deng X, Pi Y, Morelande M, et al. Track-before-detect procedures for low pulse repetition frequency surveillance radars[J].
IET Radar, Sonar & Navigation, 2011, 5(1): 65-73. DOI:10.1049/iet-rsn.2009.0245 ( 0) 0)
|
| [18] |
林再平, 周一宇, 安玮. 改进的概率假设密度滤波多目标检测前跟踪算法[J].
红外与毫米波学报, 2012, 31(5): 475-480. Lin Zai-ping, Zhou Yi-yu, and An Wei. Improved multitarget track-before-detect using probability hypothesis density filter[J]. Journal of Infrared and Millimeter Waves, 2012, 31(5): 475-480. DOI:10.3724/SP.J.1010.2012.00475 (  0) 0)
|
| [19] |
童慧思, 张颢, 孟华平, 等. PHD滤波器在多目标检测前跟踪中的应用[J].
电子学报, 2011, 39(9): 2046-2051. Tong Hui-si, Zhang Hao, Meng Hua-dong, et al. Probability hypothesis density filter multitarget track-before-detect application[J]. Acta Electronica Sinica, 2011, 39(9): 2046-2051. (  0) 0)
|
| [20] |
Geelen B D B. Accurate solution for the modified bessel function of the first kind[J].
Advances in Engineering Software, 1995, 23(2): 105-109. DOI:10.1016/0965-9978(95)00069-9 ( 0) 0)
|
| [21] |
Yi W, Morelande M R, Kong L J, et al. A computationally efficient particle filter for multitarget tracking using an independence approximation[J].
IEEE Transactions on Signal Processing, 2013, 61(4): 843-856. DOI:10.1109/TSP.2012.2229999 ( 0) 0)
|
| [22] |
Kreucher C, Kastella K, and Hero III A O. Multitarget tracking using the joint multitarget probability density[J].
IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1396-1414. DOI:10.1109/TAES.2005.1561892 ( 0) 0)
|
| [23] |
García-Fernández Á F, Grajal J, and Morelande M R. Two-layer particle filter for multiple target detection and tracking[J].
IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(3): 1569-1588. DOI:10.1109/TAES.2013.6558005 ( 0) 0)
|
| [24] |
Úbeda-Medina, García-Fernández Á F, and Grajal J. Adaptive auxiliary particle filter for track-before-detect with multiple targets[J].
IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(5): 2317-2330. DOI:10.1109/TAES.2017.2691958 ( 0) 0)
|
| [25] |
Pitt M K and Shephard N. Filtering via simulation: Auxiliary particle filters[J].
Journal of the American Statistical Association, 1999, 94(446): 590-599. DOI:10.1080/01621459.1999.10474153 ( 0) 0)
|
| [26] |
García Fernández Á F. Detection and tracking of multiple targets using wireless sensor networks[D]. [Ph. D. dissertation], Universidad Politécnica de Madrid, 2011: 61–78.
( 0) 0)
|
| [27] |
Schuhmacher D, Vo B T, and Vo B N. A consistent metric for performance evaluation of multi-object filters[J].
IEEE Transactions on Signal Processing, 2008, 56(8): 3447-3457. DOI:10.1109/tsp.2008.920469 ( 0) 0)
|




