(中国科学院大学 北京 100049)
(University of Chinese Academy of Sciences, Beijing 100049, China)
相干变化检测(Coherent Change Detection, CCD)是一种可以检测场景中发生的微小变化的技术,它利用相位信息形成的相干性观测度量可以探测出亚波长量级的变化,并以相干性变化差异的形式将其表现出来[1]。这是利用相干信息相对于非相干信息用于变化检测的优势之处。通过CCD处理形成的相干变化差异图具体表现为:场景中发生变化的区域呈现低相干特性(相干系数趋于0),未发生变化的区域呈现高相干特性(相干系数趋于1)。然而,场景中并非所有呈现低相干特性的区域均为我们所关注的变化区域(称为目标变化区域),也可能是低相干干扰造成的虚警。这些低相干干扰区域包括回波散射强度弱形成的低信噪比区域,极易受风吹雨淋造成体散射失相干的植被区域等。形成这些低相干干扰的根本原因是:CCD方法采用相位信息进行的相干性度量过于敏感,许多不是我们关注的区域也因发生足以用CCD方法检测出的相位变化而被SAR传感器敏锐地探测出来。因此,如何从低相干区域中排除引起虚警的干扰,是改善CCD性能的关键技术,最直观的解决方法为对低相干区域分类。传统的CCD方法只能区分高、低相干区域,不具备进一步区分能力。因此需要增加新的观测量实现进一步的分类。
目前,国内外的学者针对这一问题开展了许多研究工作。文献[2,3]从时间维度扩展,分别建立以时间为参量的模型对场景中的变化区域分类,提取出仅在特定时间发生变化的低相干区域;文献[4]考虑全极化情况,利用极化相干矩阵建立检验统计量,对不同极化散射类型的变化场景分类,提取出属于表面散射的冰雪消融变化;文献[5]通过估计场景中的噪声功率建立统计量,将真实变化区域与低信噪比区域区分,去除场景中低信噪比引起的低相干虚警干扰;还有的文献利用图像中目标的散射特征,分别采用聚类,半监督甚至深度学习的方式进行场景分类,实现变化检测[6–8]。以上各方法或是侧重于观测方式的选取,或是关注于场景本身的散射属性,没有将二者有机地结合起来考虑,因而在适用范围上有一定的局限性。CCD方法如同使用一把具有精细刻度的尺子,能够丈量微小的变化,传统CCD方法之所以产生低相干虚警干扰,是因为这把尺子的尺度虽精细但单一,能够同时观测到目标变化与虚警干扰但无法对其进一步区分。将CCD方法在频率维度上扩展,采用不同频率电磁波对场景观测,利用场景中目标对多波段雷达信号的散射差异形成多尺度观测,使得对目标变化区域与虚警干扰区域形成不同的观测结果,从而将其有效区分。目前进行多波段CCD研究的文献较少。文献[9,10]采用极化变化检测的方法处理C, L两个波段的农作物场景SAR图像,文中所采用的方法将两个波段的数据结合起来,可检测出的变化区域为两个单独波段变化检测结果的并集。文献[11]使用X, C, S, L不同波段的SAR数据对北极地区分别进行CCD与非相干变化检测(NCCD)处理,通过对比实验结果得出结论:(1)CCD比NCCD能检测出更微小的变化;(2)NCCD处理结果与所使用的波段关系不大;(3)CCD中,观测电磁波波长越短(频率越高),变化区域去相干程度越高。该文献只是对实验结果做初步定性分析,并指出:需要进一步对检测出的变化进行分类才具有应用意义。
在多波段观测模式下,不同波段的电磁波对场景探测,获得的目标散射特性存在较大差异,这与电磁波在不同频率下的穿透性能,可探测目标最小截面积,观测目标变化去相干程度等特性有关。不同类型的目标发生不同尺度的变化在各个波段探测下形成不同的相干变化检测结果。我们依此对各种变化分类,并从中提取我们感兴趣的目标变化区域。基于上述原理,本文充分分析不同波段电磁波的目标探测特性及其对不同尺度变化的去相干程度,据此提出一种多波段CCD方法。该方法首先获取场景在不同波段下的相干变化差异图像,然后根据目标在不同波段下的相干变化差异表征用改进的期望最大化(Expectation-Maximization, EM)算法进行分类,根据先验知识确定目标变化区域所属的类别,最后用Dempster-Shafer(DS)证据理论实现多波段相干变化差异图融合,提取目标变化区域。由于自然界中绝大多数场景对不同波段电磁波照射下呈现明显不同的散射差异[12],故采用本文提出的多波段CCD方法可适用于军事、农业、灾害监测等更广阔领域的场景中。通过实验数据处理结果表明,本文方法可以有效减小除目标变化区域外低相干干扰区域造成的影响。
本文的结构安排如下:第2节介绍不同波段电磁波探测目标特性的差异,第3节为多波段CCD算法原理与处理流程,第4节为实验数据验证,第5节对本文内容作总结。
2 目标的多波段相干性表征场景中目标受电磁波照射,产生的响应为场景中各个目标散射中心响应之和,即目标反映在SAR图像上的复投影结果。我们参考文献[13,14]建立的参数模型,获取的SAR图像
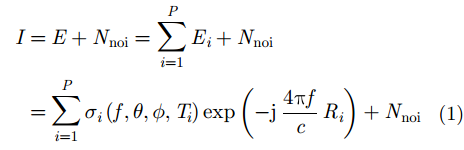
|
其中,
关于场景中的不同结构目标在不同频率电磁波探测下对相干系数的影响,已有一些文献从不同角度直接或间接地通过理论分析与实验验证得出结论[15–19],可总结如下:
(1) 高波段雷达可通过CCD方法检测小尺寸或表面粗糙程度较弱的目标造成的微小尺度变化,同时对大尺寸或表面粗糙程度强的目标造成的变化更具有良好检测性能;
(2) 低波段雷达通过CCD方法可检测大尺寸或表面粗糙程度较强的目标造成的较大尺度变化,对于小尺寸或表面粗糙程度弱目标的幅值响应弱,使得图像信噪比低,导致相干性差,易引起虚警;
(3) 中间波段雷达对目标的检测效果介于高、低波段之间,使得在目标尺寸结构或表面粗糙程度处于一定范围内的情况下,对于一定尺度目标变化的检测结果具有区分度;
(4) 低波段雷达独有穿透特性,可以检测深层或植被冠层以下目标发生的较大尺度变化。
根据上述结论可知,在场景中存在尺寸和表面粗糙度有较大差异的目标,且发生不同尺度变化的时候,得到的CCD结果会有许多值,可据此把场景中的目标分成许多类;每种目标在不同波段电磁波探测下得到不同大小的CCD结果,分别分属于每个波段的不同分类。我们利用这种分类及不同波段结果中分类的差异性设计多波段CCD方法,具体在第3节中阐述。
3 多波段CCD方法根据上一节分析的目标在多波段探测下的相干性表征特性,本文提出一种多波段CCD方法。该方法能够充分利用不同波段电磁波探测目标及目标变化造成的散射差异进行相干变化检测,通过对多波段相干变化差异图分类,结合目标在不同波段探测下的散射特性构成的先验知识提取目标变化区域,排除CCD结果中的虚警。多波段CCD方法的主要步骤如下:
步骤1 对场景多波段SAR图像进行基于SIFT特征的图像配准与辐射校正,使之满足CCD处理需求[20]。
步骤2 分别计算配准后各个波段变化前后SAR图像的相干变化统计量(一般为相干系数),形成各波段的相干变化差异图。
步骤3 对每个波段分别处理:以该波段的相干变化差异图为数据,建立基于相干变化检验统计量概率密度函数(probability density function, pdf)的有限混合模型(Finite Mixture Modem, FMM),用改进的EM算法自适应求解FMM中分模型数量
步骤4 在各个波段中,根据场景待检测区域中感兴趣地物的少量监督样本在该波段相干变化差异图的直方统计结果确定目标变化区域与非变化区域所属分类,然后根据响应度结果采用DS证据理论进行多波段相干变化差异图像融合,获取最终的多波段CCD结果。
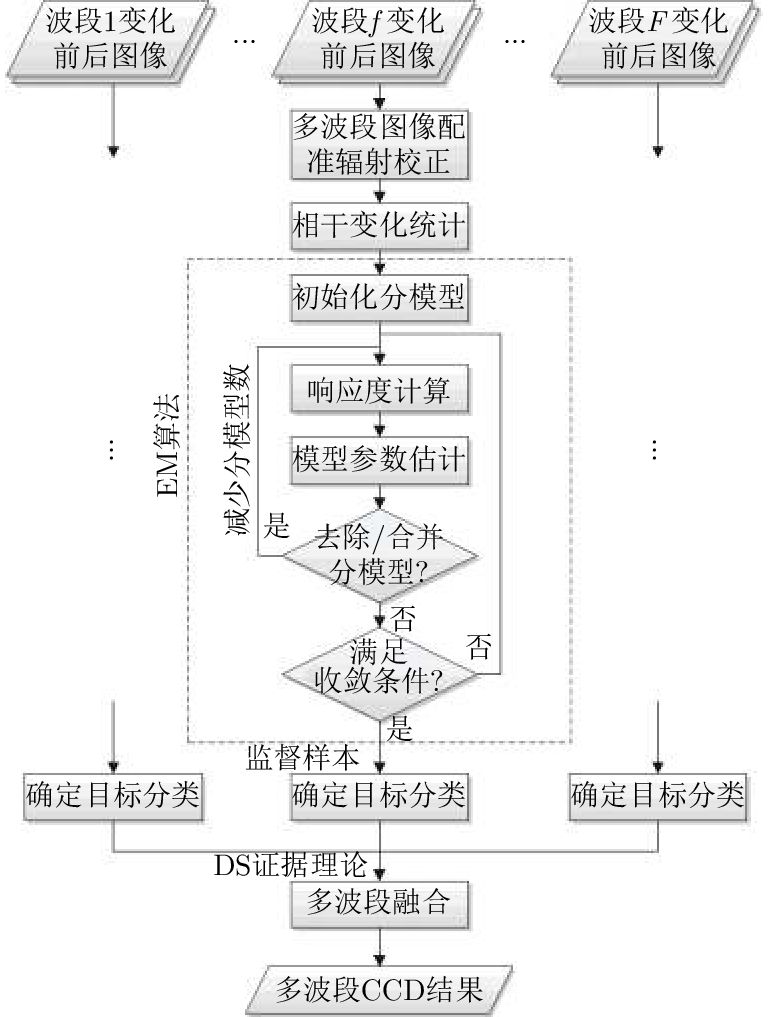
基于上述处理步骤形成的多波段CCD方法流程图如图1所示。
|
图 1 多波段CCD方法流程图 Fig.1 Workflow of proposed multi-band CCD method |
上述处理过程中,步骤1和步骤2已有较多文献进行相关方法研究,可以分别参考文献[21]与文献[1]中的算法进行处理。下面针对能够体现多波段CCD方法特点的步骤3和步骤4进行详细讨论。
3.1 变化检测场景分类根据第2节的理论,受雷达频率,目标尺寸,表面粗糙程度,变化尺度等因素影响,使用不同波段探测场景中的目标获取的CCD检测结果中存在相干程度的差异。因此,需要根据每个波段获取的相干变化差异图对检测场景的变化情况依相干度大小进行分类,为下一步根据分类结果实现多波段融合提供可靠的数据。
在每个波段数据中,我们需要借助步骤2采用相干变化检验统计量的pdf进行场景分类。这里我们不妨采用传统的相干系数检验统计量,其pdf表示为[22]:
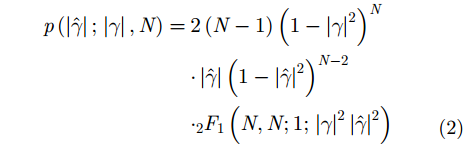
|
式(2)中,
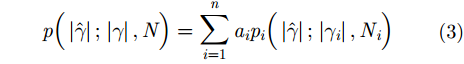
|
其中,
EM算法是一种极大似然估计算法,它先构建初始分类,通过迭代的方式用最大似然准则调整样本的类别归属,其中E步计算场景中每个像元对当前模型参数中的每个分模型的响应度,M步根据E步计算的响应度估计每个分模型新的模型参数。这样循环迭代,直至模型参数满足收敛条件,实现混合分布模型中各个分模型的参数估计。将传统EM算法用于本文应用中存在以下两个问题:一是分模型个数
针对第1个问题,本文采用自适应估计方法。首先,建立一个足够多分模型个数的混合分布模型。然后在迭代过程中,如果某一个分模型的加权系数
针对第2个问题,本文在M步中采用中心矩估计量估计分模型参数。对于式(2)所示的分布,其各阶原点矩表达式[22]为:
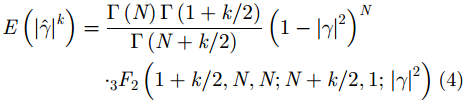
|
对于统计数据,我们用样本加权平均方法计算每个分模型的样本
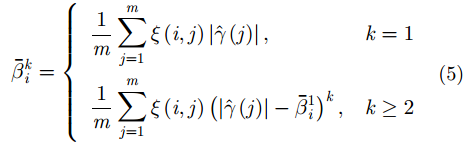
|
其中,
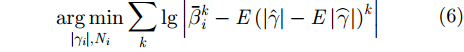
|
在实际处理中,我们建立关于参数
我们将3.1节获取的变化检测中第
多波段图像融合方法主要有基于DS证据理论[24]和基于模糊集理论[25]的融合方法,它们都具有不确定信息的处理能力。针对本文对多波段差异图像融合的具体应用,我们采用没有对分类状态响应度函数作近似的DS证据理论融合方法。
在进行多波段融合之前,我们先根据DS证据理论框架构建变化状态空间,并需要根据一定的先验知识确定各个波段中每个分类隶属的变化状态。根据3.1节描述,每个分类所属变化状态与该波段探测下目标的信噪比以及变化程度有关,在这些参数难以预估的情况下,选择少量监督样本可以辅助确定分类所属的变化类型[3]。监督样本的选择有两个准则:一是选择的样本区域在场景中为具有一定代表性的地物,二是所选择区域具有明确的变化状态(变化/不变化),且这两种状态均有与之相符的样本。根据监督样本所属的变化状态及其相干变化差异图的直方图统计结果确定变化类集合
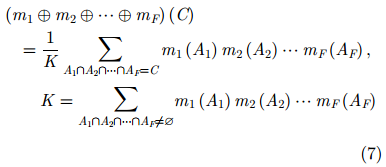
|
其中,
需要说明的是,所有波段电磁波对水面等几乎完全镜面反射区域的散射强度都比较弱,一般均低于噪声水平,因此在各个波段的相干变化差异图中均呈现低相干特性。对这类区域的变化检测超出了本文多波段CCD方法的检测范围,因此我们假定该区域没有发生变化,将其看作虚警干扰从SAR幅度图像上做掩模处理将其滤除,即:在所有波段变化前后SAR图像上,幅度均低于某一阈值(噪声水平)的像元,所在区域认为未发生变化,在最终的多波段CCD结果中将该位置数据置为1。
4 实验数据验证采用ESAR机载SAR数据对本文方法进行实验验证。该数据变化前后采集时间间隔为1个月(2007年2月-2007年3月),地点为瑞典Eggby小镇郊外的一片场景。对该场景分别用L波段与P波段HH极化雷达进行变化前后数据采集,所得SAR图像及对照光学图像如图2所示。在变化前后的两次数据采集时间间隔内,场景中发生土壤翻修,草地修剪,冰雪消融等类型的目标变化,主要发生在场景中草地,裸地的部分区域以及湖面区域,在图2(e)的光学图像中将部分变化区域予以简要标注。经过图像配准后对每个波段SAR图像进行CCD处理,得到的相干变化差异图如图3所示。比较图3中两幅图可发现,场景中左侧大面积植被区域在L波段差异图中呈现低相干特性,在P波段差异图中为高相干特性,这是因为相比于L波段,P波段电磁波具有良好的穿透特性,没有受到植被冠层受风吹雨淋发生的变化去相干影响;场景中局部裸地、草地区域(红色圆圈部分)在L波段中呈现高相干特性,而在P波段中呈现低相干特性,这是因为该处场景表面粗糙度较弱,导致波长较长的P波段对该处的目标散射强度较弱,造成低信噪比,从而受到噪声去相干的影响。这两部分区域均不是我们感兴趣的目标变化区域,在各自波段的检测结果中形成虚警干扰。

|
图 2 待检测场景各波段变化前后SAR图像与光学参考图像 Fig.2 SAR images of each band of scene before and after change to be detected and optical reference image |

|
图 3 待检测场景相干变化差异图 Fig.3 CCD images of scene to be detected |
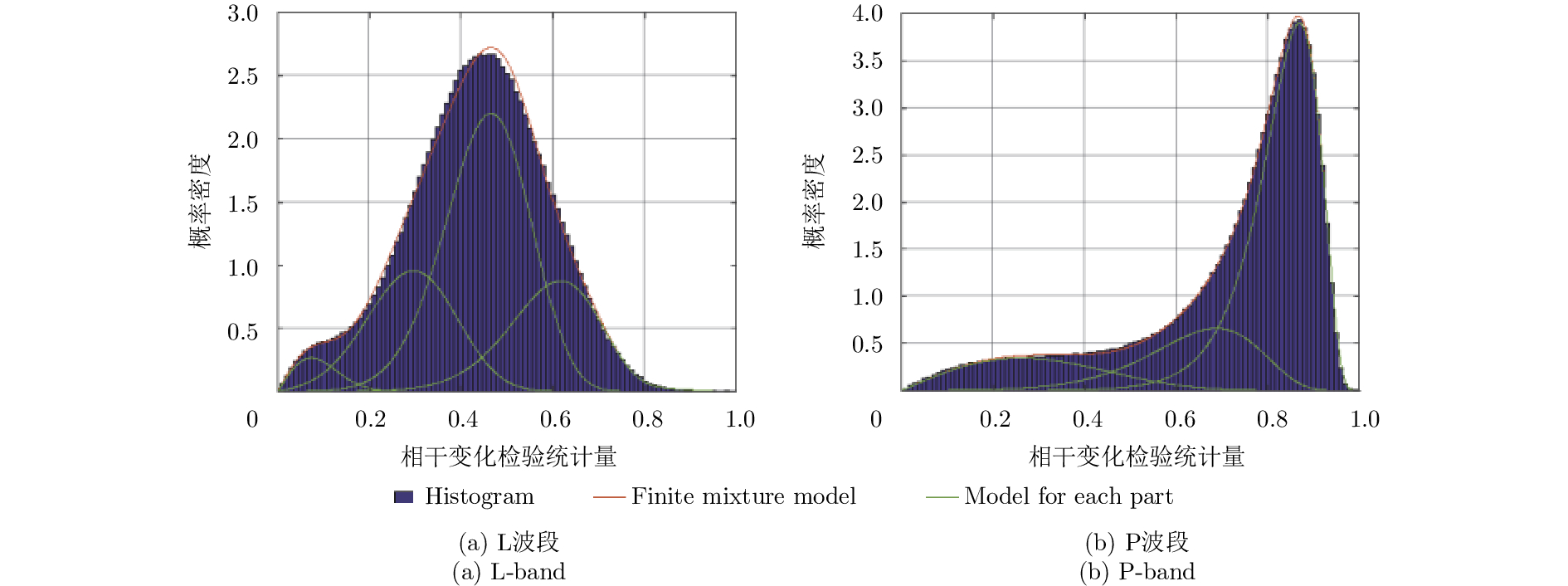
基于图3所示两个波段的相干变化差异图,我们用3.1节提出的FMM及EM算法对场景分类。结合SAR图像与差异图信息,我们初始制定分模型数目均为5, M步迭代中取式(6)参数
|
图 4 相干变化差异图的统计直方图及其拟合分布模型对比结果 Fig.4 Comparison results between histogram of CCD image and fitting distribution model |
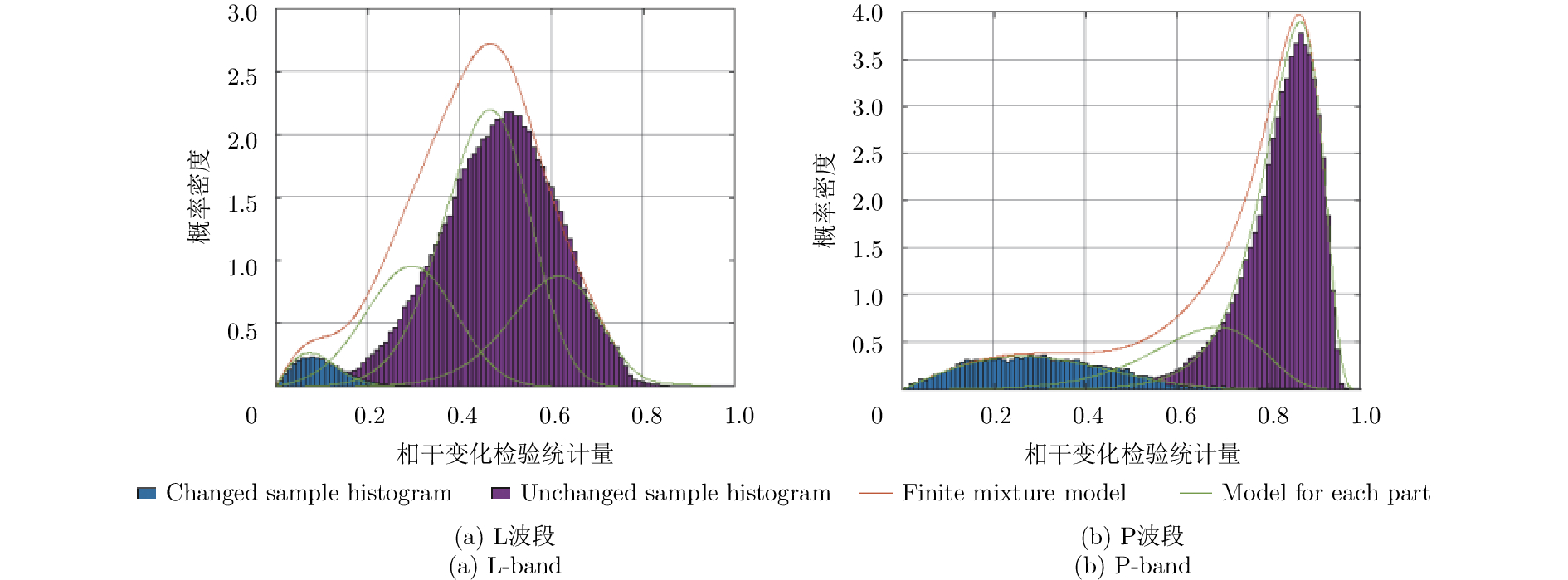
在图3的两幅相干变化差异图中,我们分别选取黄色和绿色方框区域作为变化区域与非变化区域的样本监督数据,并将各自波段的直方图与各自的拟合分布模型比较,结果如图5所示。为方便比较,图5中将样本监督数据直方图乘以相应的倍数,使其与拟合分布分模型的概率密度大小相当。通过比较我们得知,L波段数据中,变化类与非变化类分别对应第1分模型与第3、第4分模型;P波段数据中,变化类与非变化类分别对应第1分模型与第3分模型。根据3.2节处理方法可得,两个波段的第2分模型分别对应各自的不确定类。然后计算像元在各个分类中的响应度(即计算概率分配函数),代入式(7)计算,求得多波段融合相干变化差异图结果
|
图 5 样本监督数据直方图与拟合分布模型比较结果(为方便比较,将样本监督数据直方图乘以相应的倍数,使其与拟合分布分模型的概率密度大小相当) Fig.5 Comparison results between histogram of supervised sample data and fitting distribution model(For the reason of comparing conveniently, the histogram of supervised sample data times a corresponding multiple, so that it can be equal to the probability density of some fitting model part) |

|
图 6 多波段CCD实验结果 Fig.6 Multi-band CCD result of experiment area |
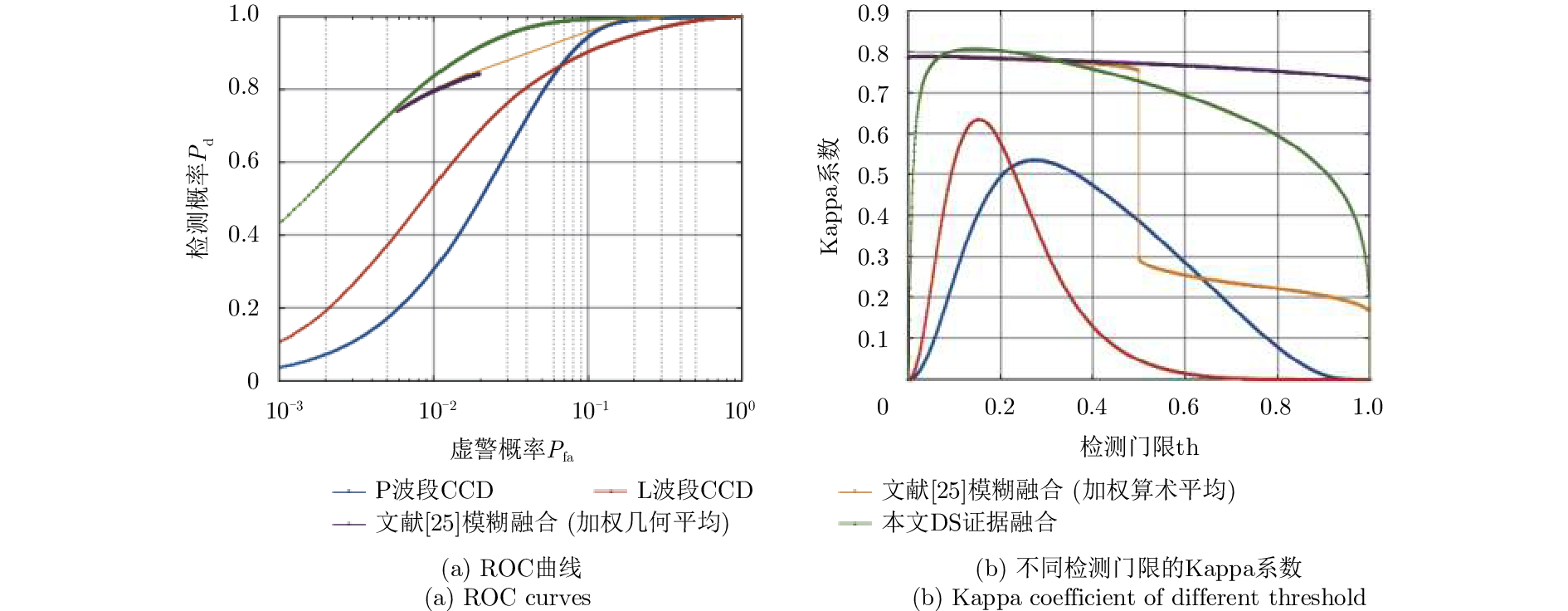
为了进一步说明本文使用的多波段CCD方法的性能,采用受试者工作特征(Receiver Operating Characteristic, ROC)曲线与最优Kappa系数两个指标进行分析。ROC曲线越靠近左上角,最优Kappa系数值越大,说明方法性能越好。图7(a),图7(b)分别展示了实验采用的两个单波段CCD与多波段CCD方法的ROC曲线和选取不同检测门限的Kappa系数。从图中可以看出,本文使用的DS证据融合多波段CCD方法的ROC曲线更接近左上方,最优Kappa系数值为0.81,大于两个单波段CCD方法(L波段:0.63,P波段:0.54)和两种模糊融合方法(均为0.79)。因此,以上分析验证了本文提出的多波段CCD方法对去除单波段CCD方法中低相干干扰,降低虚警率方面的正确性与有效性。
|
图 7 单波段CCD与多波段CCD方法指标分析 Fig.7 Index analysis between mono-band CCD and multi-band CCD methods |
本文根据场景中目标及其发生的变化在多波段电磁波观测情况下表征出的相干性差异,提出一种多波段CCD方法。该方法先将待检测场景根据各波段的相干变化差异图用改进EM算法进行各自的自适应分类处理,然后依据少量监督样本分别在各个波段中确定分类的变化状态,最后使用DS证据理论方法处理,获取多波段融合CCD结果,去除了每个波段各自产生的低相干干扰,达到降低虚警率的目的。由于用于多波段CCD处理的重轨SAR数据较少,本文中仅用一组双波段数据验证该方法的有效性与正确性。接下来的研究应以更多波段对不同场景探测的重轨SAR数据为基础,进一步分析波段种类、波段数目、场景地物类型等因素对多波段CCD方法实现效果的影响。
致谢 本文作者感谢欧空局提供ESAR机载L波段与P波段重轨SAR数据。
| [1] |
Preiss M and Stacy N J S. Coherent change detection: Theoretical description and experimental results[R]. DSTO-TR-1851, 2006
( 0) 0)
|
| [2] |
Jung J, Kim D J, Lavalle M, et al. Coherent change detection using InSAR temporal decorrelation model: A case study for volcanic ash detection[J].
IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(10): 5765-5775. DOI:10.1109/TGRS.2016.2572166 ( 0) 0)
|
| [3] |
Barber J and Kogon S. Probabilistic three-pass SAR coherent change detection[C]. Proceedings of 2012 Conference Record of the Forty Sixth Asilomar Conference on Signals, Systems and Computers (ASILOMAR), Pacific Grove, California, USA, 2012: 1723–1726. DOI: 10.1109/ACSSC.2012.6489327
( 0) 0)
|
| [4] |
Muhuri A, Ratha D, and Bhattacharya A. Seasonal snow cover change detection over the Indian Himalayas using polarimetric SAR images[J].
IEEE Geoscience and Remote Sensing Letters, 2017, 14(12): 2340-2344. DOI:10.1109/LGRS.2017.2764123 ( 0) 0)
|
| [5] |
Wahl D E, Yocky D A, Jakowatz C V, et al. A new maximum-likelihood change estimator for two-pass SAR coherent change detection[J].
IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(4): 2460-2469. DOI:10.1109/TGRS.2015.2502219 ( 0) 0)
|
| [6] |
冷英, 李宁. 一种改进的变化检测方法及其在洪水监测中的应用[J].
雷达学报, 2017, 6(2): 204-212. Leng Ying and Li Ning. Improved change detection method for flood monitoring[J]. Journal of radars, 2017, 6(2): 204-212. DOI:10.12000/JR16139 (  0) 0)
|
| [7] |
An L, Li M, Zhang P, et al. Discriminative random fields based on maximum entropy principle for semisupervised SAR image change detection[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(8): 3395-3404. DOI:10.1109/JSTARS.2015.2483320 ( 0) 0)
|
| [8] |
徐真, 王宇, 李宁, 等. 一种基于CNN的SAR图像变化检测方法[J].
雷达学报, 2017, 6(5): 483-491. Xu Zhen, Wang Robert, Li Ning et al. A novel approach to change detection in SAR images with CNN classification[J]. Journal of radars, 2017, 6(5): 483-491. DOI:10.12000/JR17075 (  0) 0)
|
| [9] |
Nielsen A A, Conradsen K, and Skriver H. Change detection in full and dual polarization, single-and multifrequency SAR data[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(8): 4041-4048. DOI:10.1109/JSTARS.2015.2416434 ( 0) 0)
|
| [10] |
Nielsen A A, Conradsen K, and Skriver H. Corrections to " change detection in full and dual polarization, single-and multi-frequency SAR data”[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(11): 5143-5144. DOI:10.1109/JSTARS.2017.2761038 ( 0) 0)
|
| [11] |
Reigber A, Jäger M, and Krogager E. Polarimetric SAR change detection in multiple frequency bands for environmental monitoring in Arctic regions[C]. IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 2016: 5702–5705. DOI: 10.1109/IGARSS.2016.7730489
( 0) 0)
|
| [12] |
Li Y L, Liang X D, Zhou L J, et al.. Introduction to IECAS-SAR — A multi-frequency polarimetric airborne SAR[C]. IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, Quebec, Canada, 2014: 1085–1088. DOI: 10.1109/IGARSS.2014.6946617
( 0) 0)
|
| [13] |
Jackson J A and Moses R L. Feature extraction algorithm for 3D scene modeling and visualization using monostatic SAR[C]. Proceedings of SPIE 6237 Algorithms for Synthetic Aperture Radar Imagery XIII, Orlando, 2006, 6237: 623708. DOI: 10.1117/12.666558
( 0) 0)
|
| [14] |
文贡坚, 朱国强, 殷红成, 等. 基于三维电磁散射参数化模型的SAR目标识别方法[J].
雷达学报, 2017, 6(2): 115-135. Wen Gongjian, Zhu Guoqiang, Yin Hongcheng, et al. SAR ATR based on 3D parametric electromagnetic scattering model[J]. Journal of radars, 2017, 6(2): 115-135. DOI:10.12000/JR17034 (  0) 0)
|
| [15] |
袁孝康. 星载合成孔径雷达导论[M]. 北京: 国防工业出版社, 2003: 234–235
Yuan Xiao-kang. Introduce to the Spaceborne Sythetic Aperture Radar[M]. Beijing: National Defense Industry Press, 2003: 234–235 (  0) 0)
|
| [16] |
陈述彭, 童庆禧, 郭华东. 遥感信息机理研究[M]. 北京: 科学出版社, 1998: 274–288
Chen Shu-peng, Tong Qing-xi, and Guo Hua-dong. Mechanism of Remote Sensing Information[M]. Beijing: Science Press, 1998: 274–288 (  0) 0)
|
| [17] |
周智敏, 黄晓涛. VHF/UHF超宽带合成孔径雷达穿透性能分析[J].
系统工程与电子技术, 2003, 25(11): 1336-1340. Zhou Zhi-min and Huang Xiao-tao. Penetration performance analysis of VHF/UHF ultra-wideband synthetic aperture radar[J]. Systems Engineering and Electronics, 2003, 25(11): 1336-1340. DOI:10.3321/j.issn:1001-506X.2003.11.007 (  0) 0)
|
| [18] |
Yin Q, Li Y, Huang P P, et al. Analysis of InSAR coherence loss caused by soil moisture variation[J].
Journal of Radars, 2015, 4(6): 689-697. DOI:10.12000/JR15075 ( 0) 0)
|
| [19] |
黄培康, 殷红成, 许小剑. 雷达目标特性[M]. 北京: 电子工业出版社, 2005: 9–62
Huang Pei-kang, Yin Hong-cheng, and Xu Xiao-jian. Radar Target Characteristics[M]. Beijing: Publishing House of Electronics Industry, 2005: 9–62 (  0) 0)
|
| [20] |
冀广宇, 董勇伟, 李焱磊, 等. 一种基于概率图模型的多时相SAR相干变化检测方法[J].
电子与信息学报, 2017, 39(12): 2912-2920. Ji Guang-yu, Dong Yong-wei, Li Yan-lei, et al. A multi-temporal SAR coherent change detection method based on probabilistic graphical models[J]. Journal of Electronics & Information Technology, 2017, 39(12): 2912-2920. DOI:10.11999/JEIT170208 (  0) 0)
|
| [21] |
尤红建, 付琨. 合成孔径雷达图像精准处理[M]. 北京: 科学出版社, 2011: 125–139
You Hong-jian and Fu Kun. Precise Processing of Synthetic Aperture Radar Images[M]. Beijing: Science Press, 2011: 125–139 (  0) 0)
|
| [22] |
Touzi R, Lopes A, Bruniquel J, et al. Coherence estimation for SAR imagery[J].
IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(1): 135-149. DOI:10.1109/36.739146 ( 0) 0)
|
| [23] |
Anfinsen S N and Eltoft T. Application of the matrix-variate mellin transform to analysis of polarimetric radar images[J].
IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2281-2295. DOI:10.1109/TGRS.2010.2103945 ( 0) 0)
|
| [24] |
杨祥立, 徐德伟, 黄平平, 等. 融合相干/非相干信息的高分辨率SAR图像变化检测[J].
雷达学报, 2015, 4(5): 582-590. Yang Xiang-li, Xu De-wei, Huang Ping-ping, et al. Change detection of high resolution SAR images by the fusion of coherent/incoherent information[J]. Journal of Radars, 2015, 4(5): 582-590. DOI:10.12000/JR15073 (  0) 0)
|
| [25] |
王桂婷, 王幼亮, 焦李成. 基于快速EM算法和模糊融合的多波段遥感影像变化检测[J].
红外与毫米波学报, 2010, 29(5): 383-388. Wang Gui-ting, Wang You-liang, and Jiao Li-cheng. Change detection method of multiband remote sensing images based on fast expectation-maximization algorithm and fuzzy fusion[J]. Journal of Infrared and Millimeter Waves, 2010, 29(5): 383-388. (  0) 0)
|




