② (中国科学院大学 北京 100049)
② (University of Chinese Academy of Sciences, Beijing 100049, China)
合成孔径雷达干涉(Interferometry Synthetic Aperture Radar, InSAR)技术,是广泛应用在地理测量中的一种雷达遥感技术。利用同一场景的两幅合成孔径雷达(Synthetic Aperture Radar, SAR)复数据,提取相位信息来获取地面的高程信息[1,2]。可以应用于地形测绘、形变监测、海洋应用、以及地球动力学应用[3–5]。
传统的单波段InSAR系统只需两幅SAR图像形成一幅干涉图,即可实现高程反演,其处理流程[1]主要包括复图像配准、干涉相位去平地、干涉相位滤波、相位解缠、数字高程模型(Digital Elevation Model, DEM)重建等步骤。虽然单波段InSAR系统数据获取相对容易,处理流程相对简单[3],但是单波段相位解缠必须满足Iton假设[6],无法实现地形起伏比较大的高程反演。90年代以后多通道InSAR技术快速发展,多通道InSAR技术主要包括多频率干涉和多基线干涉两种。1994年,Xu Wei等人[7]提出了中国剩余定理(Chinese Reminder Theorem, CRT)、投影法和线性组合法3种多通道联合相位解缠算法。2000年,Pascazio 和Schirinzi[8]提出将大带宽的SAR数据进行分割来获取多频率干涉数据,并且使用最大似然估计(Maximum Likelihood, ML)来实现多频率联合相位解缠。2003年,Hoge等人[9]提出了一种基于频域奇异值分解(Singular Value Decomposition, SVD)的配准方法,可以很高效的实现图像亚像素级配准。2004年,Ferraiuolo等人[10]提出了一种高斯能量项的最大后验估计(Maximum A Posterior, MAP)的算法来多通道联合高程重建,该方法使用马尔科夫随机场来建模地形高程的先验分布,并通过仿真的多频率干涉验证了算法的有效性。2009年,Ferraioli等人[11]提出了一种基于图割法的变分能量项最大后验估计(Maximum Posteriori Estimation of Total Variational Energy Term, TV-MAP)的多通道联合高程重建方法。Ferraiuolo和 Meglio等人[12]深入分析最大似然估计和最大后验估计等两种多通道联合相位解缠算法,证明了最大后验估计法鲁棒性优于最大似然估计。2011年,于翰雯等人[13]提出了一种基于聚类分析的多通道联合相位解缠绕算法,该方法将具有相同模糊矢量的像素点聚成一类,随后逐类进行联合解缠。Deledalle等人[14]提出了一种非局部参数估计(Nonlocal Interferogram Estimation, NL-InSAR)的方法,可以实现对干涉相位、相干系数、幅度图的精确估计。2013年,袁志辉[15]提出了一种基于闭合形式鲁棒性中国剩余定理(CRT)的多通道联合高程重建算法。2016年,曾涛[16]等人提出了结合最大似然估计相位梯度和枝切法的多频率联合相位解缠算法。2017年,斯奇等人[17]提出了一种基于最大后验框架的聚类分析多基线干涉SAR高度重建算法。
双频InSAR技术利用不同频段的两幅干涉图进行联合高程反演,可以有效地提取地形复杂区域的高程信息。为实现高精度、强鲁棒性的高程反演,双频干涉数据处理需要解决不同频段之间的非相干配准、干涉相位降噪、联合相位解缠等一系列问题。针对这些问题,结合现有图像配准、相位滤波、多通道InSAR技术等研究进展[18,19],本文提出了一种有效的双频干涉SAR地表高程重建方法。该方法对常规处理流程中的关键步骤进行了改进,首先采用NL-InSAR技术对幅度图、相干系数、干涉相位通过迭代进行精确估计,利用各个波段的幅度信息来实现不同波段的干涉相位的配准。然后采用聚类分析技术对联合解缠相位标记有效点和噪点,并利用有效点对联合解缠相位进行均值滤波。通过这些改进,提高了高程重建效果与高程反演精度。目前该方法已经应用在实际机载双频InSAR系统中,取得了较好的结果。
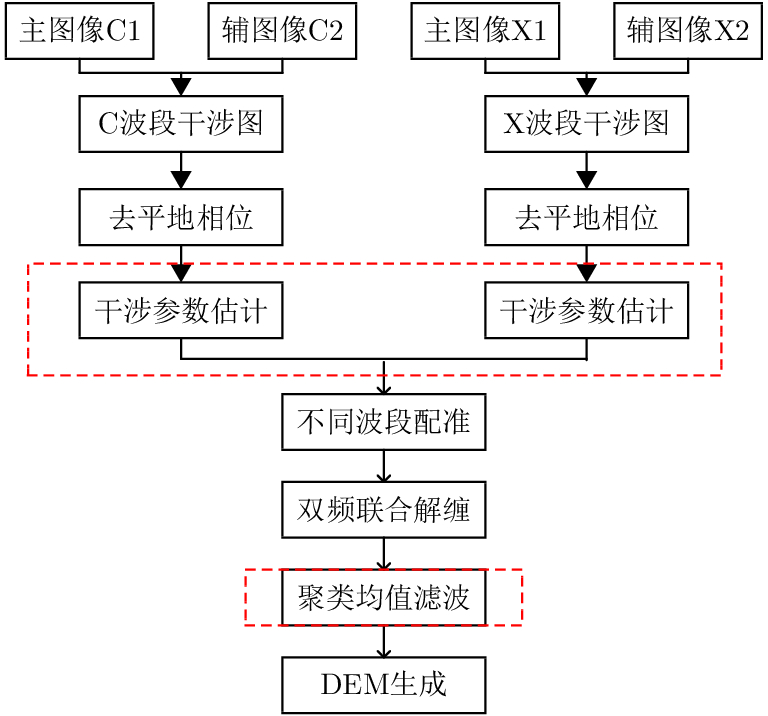
2 高程重建算法本文针对常规的双频干涉处理流程中的关键步骤进行了改进,改进后的流程图如图1所示,主要包括频段内图像配准、去平地相位、干涉参数精确估计、频段间干涉相位配准、双频联合相位解缠、解缠相位噪点剔除等步骤。下面通过比较分析,将给出各个步骤的处理方法,并在机载实测双频干涉处理中验证其有效性。
|
图 1 改进的双频干涉处理流程图 Fig.1 Improved processes of dual-frequency interferometry |
图像配准是通过调整主、辅SAR复图像,使得两幅图像上相同的点对应地面场景上的同一点。配准的步骤如下[20,21]:
步骤1 主辅图像选取若干控制点,采用相关法计算控制点处粗偏移量,精度为1个像素。
计算控制点处的偏移量可以采用空域相关函数法的计算基于窗口的配准方法,分别在主图像
步骤2 利用相关法求得图像粗偏移量,并修正辅图像控制点的位置,为得到亚像素级的精配准,可以通过空域相干系数法[21]、傅里叶变换法[21]、频域SVD法[9]求得控制点处的精确偏移量;
步骤3 在求得控制点处精确偏移量后,可以利用二项式进行拟合:
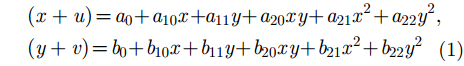
|
其中,
下面采用某机载双频干涉系统飞行的数据为例来分析图像配准技术。
空域相关法、傅里叶变换法、频域SVD分解法这3种方法都具有较高的配准精度,本文分别采用了这3种方法对上述图像进行了配准,配准结果如图2所示。由于频域SVD分解法运算效率最高,因此机载双频干涉高重建过程中采用频域SVD法配准。

|
图 2 3种配准方法配准后干涉条纹 Fig.2 Three interferometric phase images after registration |
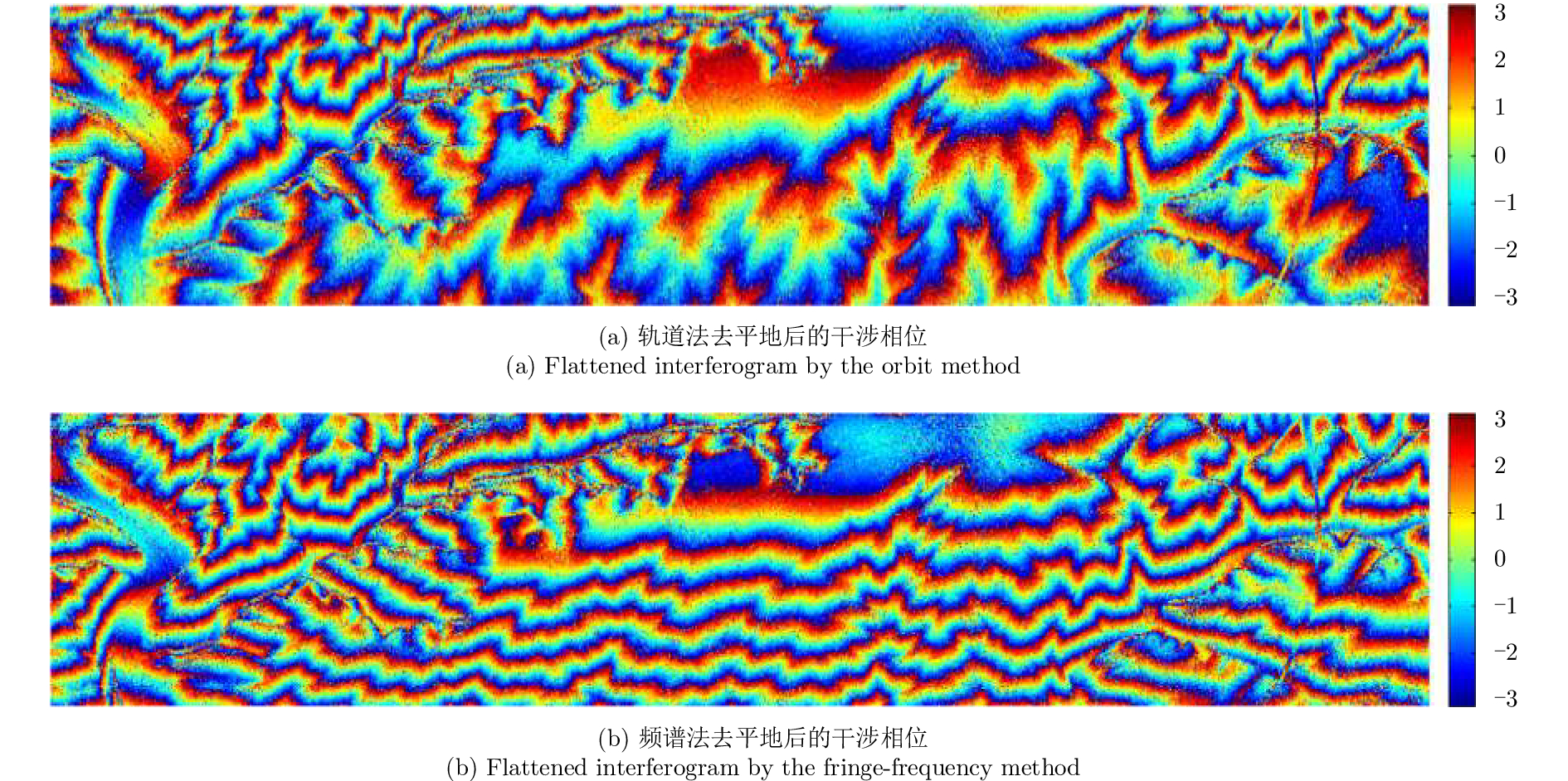
配准后的干涉相位由于平地相位的存在,使干涉相位缠绕量较大,干涉条纹过密,会影响后续的相位解缠。因此在相位解缠之前,需要去除平地相位,以便降低联合相位解缠的难度。去平地方法主要有频谱法和轨道法两种,频谱法是将干涉复图像变换到频域,找出频谱中最大值对应的频率并搬移到零频。轨道法是根据轨道参数计算平地相位。两种方法的处理结果如图3所示。由于在实测数据处理中频谱法并不能有效地去除平地相位,因此,本文采用轨道法去平地。
|
图 3 两种去平地方法去平地之后的干涉图 Fig.3 The two flattened interferograms removed flat-Earth phase |
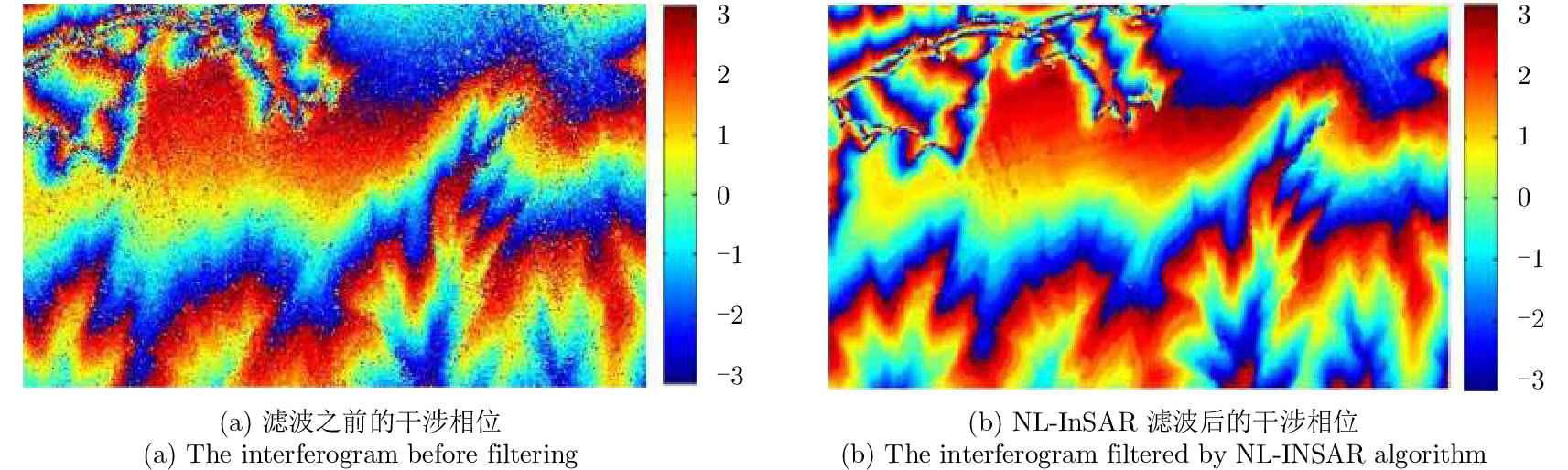
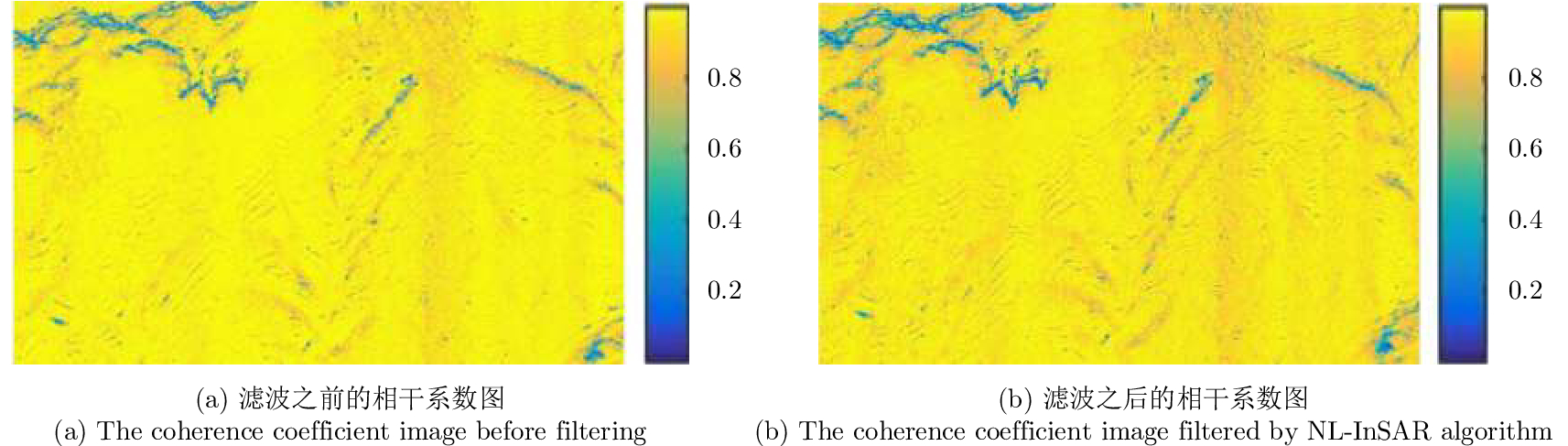
为了提高不同频段配准和联合解缠的精度,采用NL-InSAR技术分别对各个频段的干涉相位、相干系数、幅度进行精确估计[14],再进行不同波段配准,可以有效提高不同频段之间干涉相位的配准精度,并且实现了对干涉相位去噪的同时较好地保持了干涉相位的纹理信息。图4给出了NL-InSAR滤波前后的干涉相位对比情况。从图中可以看出,NL-InSAR在去除干涉相位存在的斑点噪声。NL-InSAR滤波前的幅度图和滤波后的幅度图如图5所示,对比表明NL-InSAR在保持SAR图像边缘细节信息的前提下能较好地去除SAR图像的斑点噪声。NL-InSAR估计前的相干系数如图6所示,可以看出,NL-InSAR估计后的相干系数的可靠性更强,可以有效辅助后续双频联合解缠。
|
图 4 NL-InSAR滤波前后的干涉相位对比 Fig.4 Contrast between interferogram before filtering and filtered interferogram |

|
图 5 NL-InSAR滤波前后的SAR图像对比 Fig.5 Contrast between SAR image before filtering and filtered SAR image |
|
图 6 NL-InSAR滤波前后的相干系数 Fig.6 Contrast between coherence coefficient image before filtering and filtered coherence coefficient image |
交叉频段干涉相位配准精度往往较低,本文采用的方法为首先进行同频段图像配准、滤波、去平地,通过利用各自主图像的幅度信息拟合出多项式系数,进而来实现频段间干涉相位的配准。
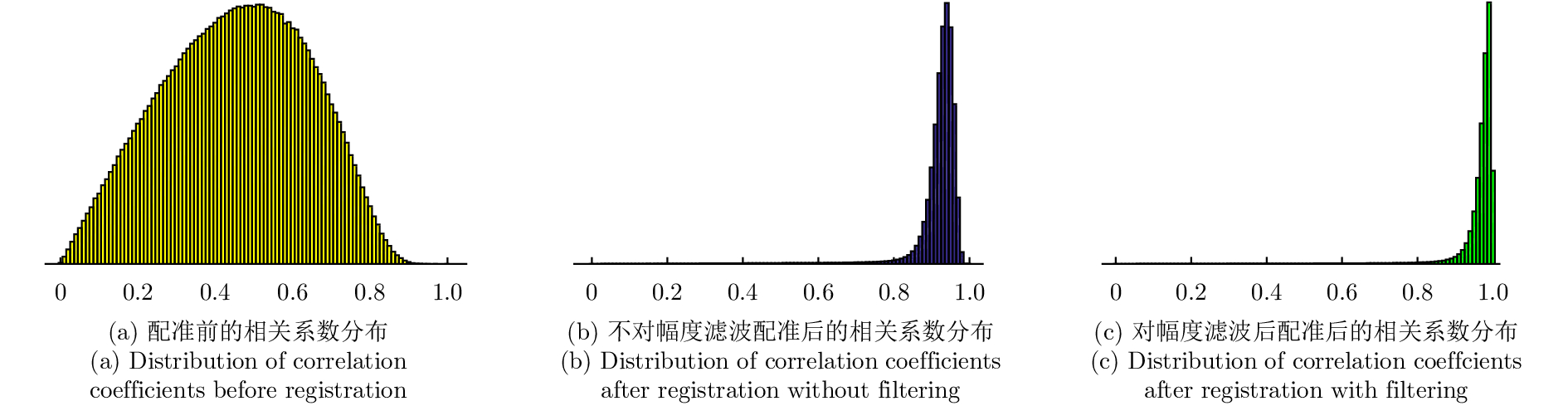
由于不同频段的主图像幅度存在较多的斑点噪声,造成不同频段的主图像幅度图的相似性较差。由图5可知,NL-InSAR可以有效地对SAR图像的幅度图进行去噪。图7(a)为不进行NL-InSAR幅度滤波的C波段主图像幅度图,图7(b)为不进行NL-InSAR滤波的X波段主图像幅度。可以看出不进行NL-InSAR滤波的不同波段主图像幅度图较多的斑点噪声,造成不同波段的主图像幅度图之间相似性较差。图8(a)为采用NL-InSAR对幅度滤波后的C波段主图像幅度,图8(b)为采用NL-InSAR对幅度滤波后的X波段主图像。NL-InSAR可以很好地去除SAR图像幅度图的斑点噪声,同时较好地保持了图像的边缘细节信息,提高了不同波段主图像幅度图之间的相似性。因此本文采用经过NL-InSAR滤波后的两个频段的主图像幅度拟合出式(1)的多项式系数,从而实现对两个频段的干涉相位图之间的配准。针对实测数据不同频段配准前后的不同波段之间相关系数图如图9所示。图9(a)所示的配准前X波段和C波段的相关系数较低,均值为0.46,图9(b)所示的不采用NL-InSAR对幅度进行滤波的配准后的相关系数相对较高,均值为0.90。图9(c)所示为采用NL-InSAR对幅度进行滤波的配准好的相关系数最高,均值为0.94,验证了本文提出的不同波段干涉相位配准方法的有效性。

|
图 7 NL-InSAR滤波前的不同波段幅度图对比 Fig.7 Comparison of different band amplitude graphs before NL-InSAR filtering |

|
图 8 NL-InSAR滤波后的不同波段幅度图对比 Fig.8 Comparison of different band amplitude graphs after NL-InSAR filtering |
|
图 9 NL-InSAR滤波前后的不同波段配准后的相关系数分布直方图对比 Fig.9 Comparison of the distribution histogram of correlation coefficients of different bands before and after NL-InSAR filtering |
目前,多频段联合相位解缠算法大致有基于统计信号处理和非统计信号处理两类,本文仿真对比了非统计信号处理类的鲁棒性中国剩余定理(CRT)[15],统计信号处理类的最大似然估计(ML)[8]和变分最大后验估计(TV-MAP)[11]。在实测数据处理中,双频联合相位解缠算法对算法鲁棒性要求较高,本文选用鲁棒性较强的变分最大后验估计作为双频联合解缠的处理方案。最大后验估计相位解缠就利用观测相位
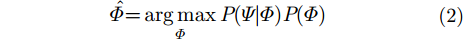
|
假设所有像素点之间是相互独立的,那么:
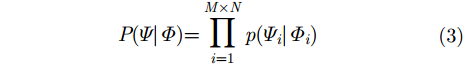
|
其中,
对于
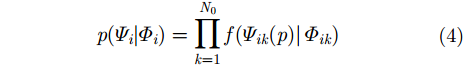
|
其中单个波段的观测相位的似然函数为:
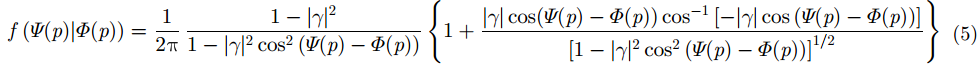
|
我们可以使用马尔科夫随机场来描述图像的局部特性,根据MarKov-Gibbs等价性可以用Gibbsian分布来描述马尔科夫先验分布[8]:
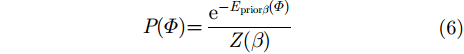
|
变分能量项最大后验估计使用的是一种在图像领域常用的整体变分(TV)模型,其能量函数定义为:
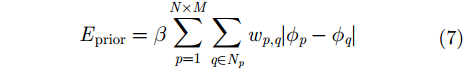
|
式(7)中,
把式(7)代入式(6)结合式(2)–式(5)并取对数且添加负号,可以得到变分能量项最大后验估计的在TV模型下的相位估计公式为:
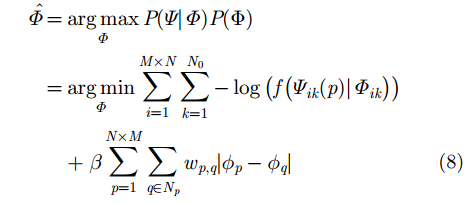
|
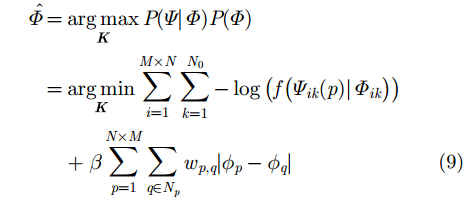
|
上述优化模型可以通过图割理论求解[11],通过求解上述优化模型可以求解得到各个波段干涉相位的缠绕量和联合解缠绕相位。
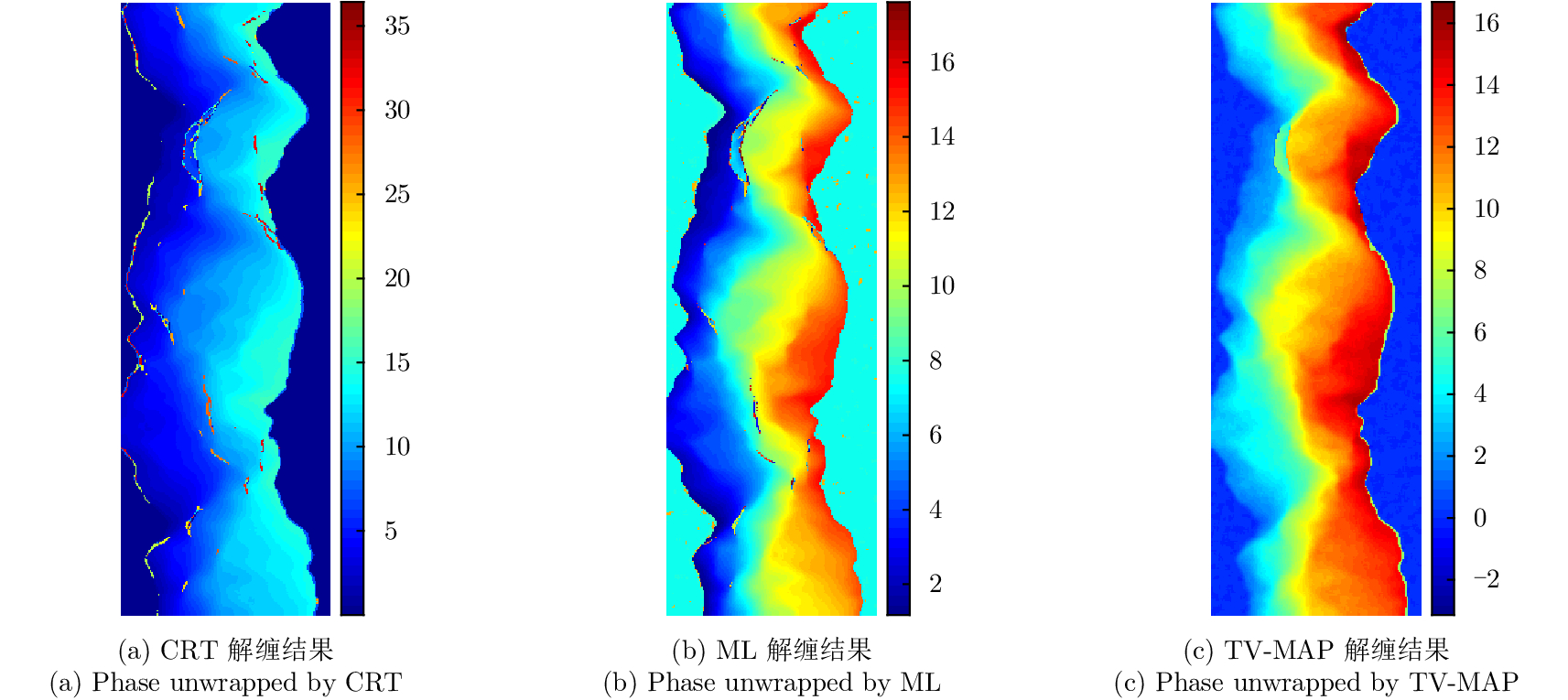
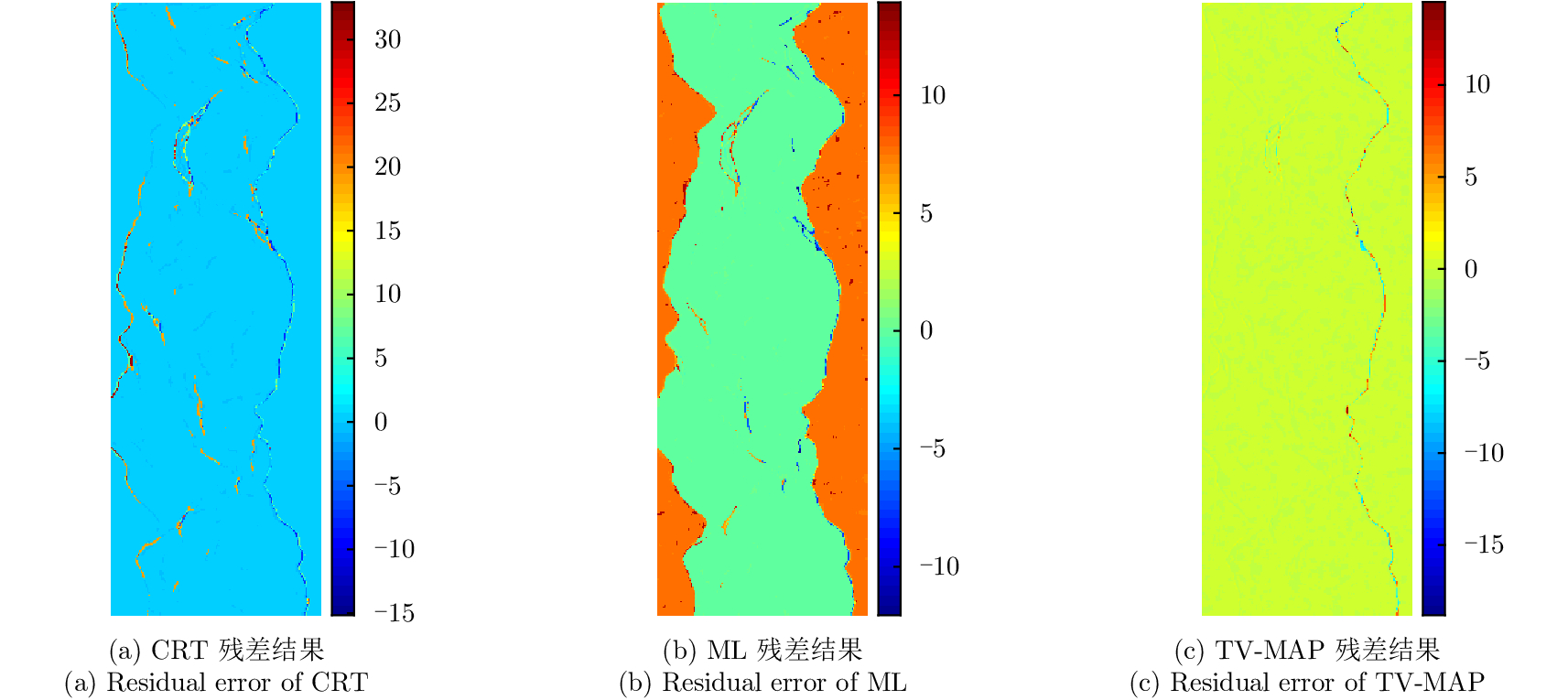
对添加相同噪声的仿真数据,采用上述3种方法分别进行联合解缠结果如图10所示,用来仿真干涉相位的原始相位相减的残差图如图11所示。通过上述仿真分析,进一步验证了变分能量项最大后验估计用于双频联合解缠的鲁棒性。
|
图 10 对相同的仿真数据3种联合解缠算法的结果对比 Fig.10 The unwrapped phase images unwrapped by diffenent algorithms |
|
图 11 3种联合解缠算法解缠结果和原始相位的残差结果对比 Fig.11 The residual error images of different algorithms |
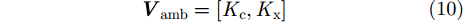
|
其中,
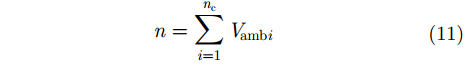
|
其中,
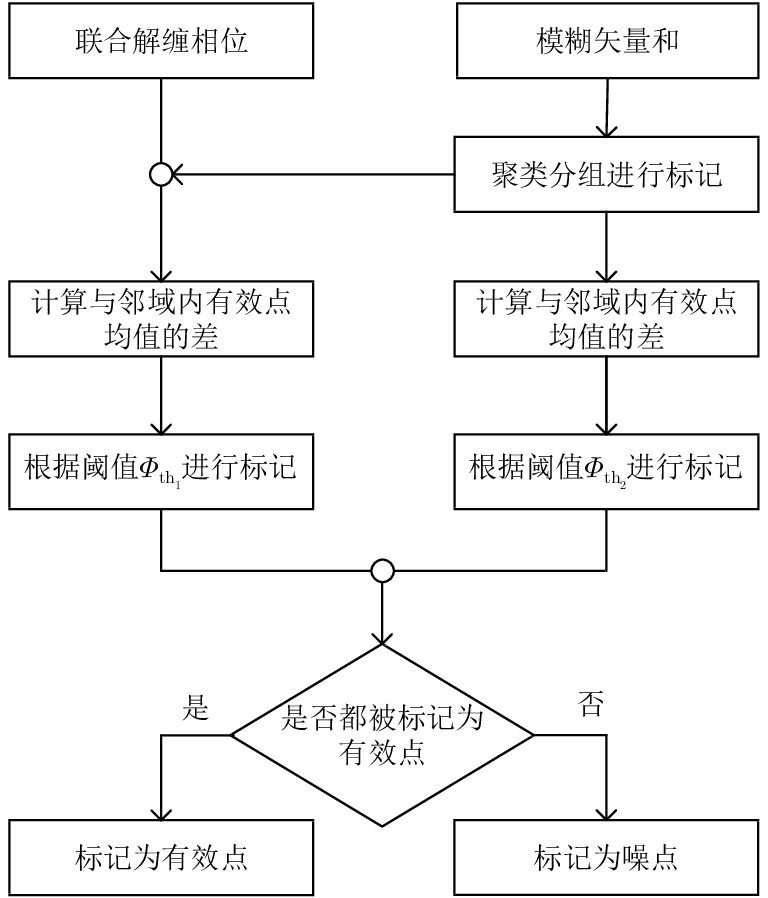
|
图 12 有效点和噪点标记流程图 Fig.12 Flow chart of effective point and noise marking |
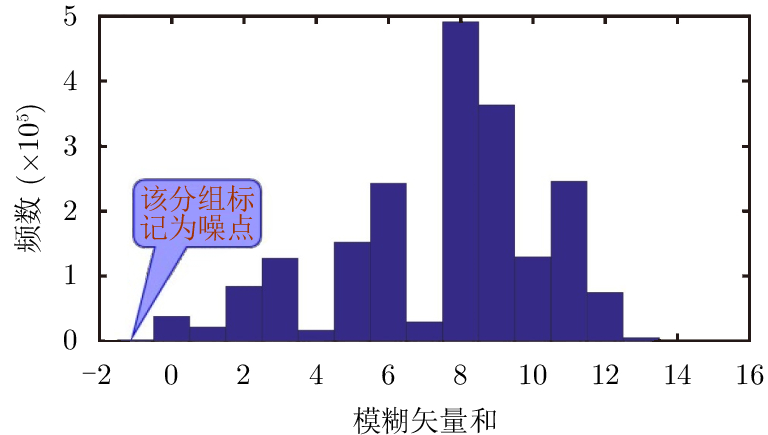
|
图 13 模糊矢量和的分布直方图 Fig.13 Histogram distribution of ambiguity vector summation |
如图12所示,将两种标记结果相与,得到用于加权均值滤波的标记结果,对联合解缠结果进行如下加权均值滤波:
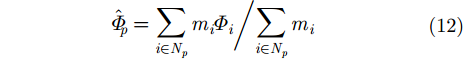
|
其中,
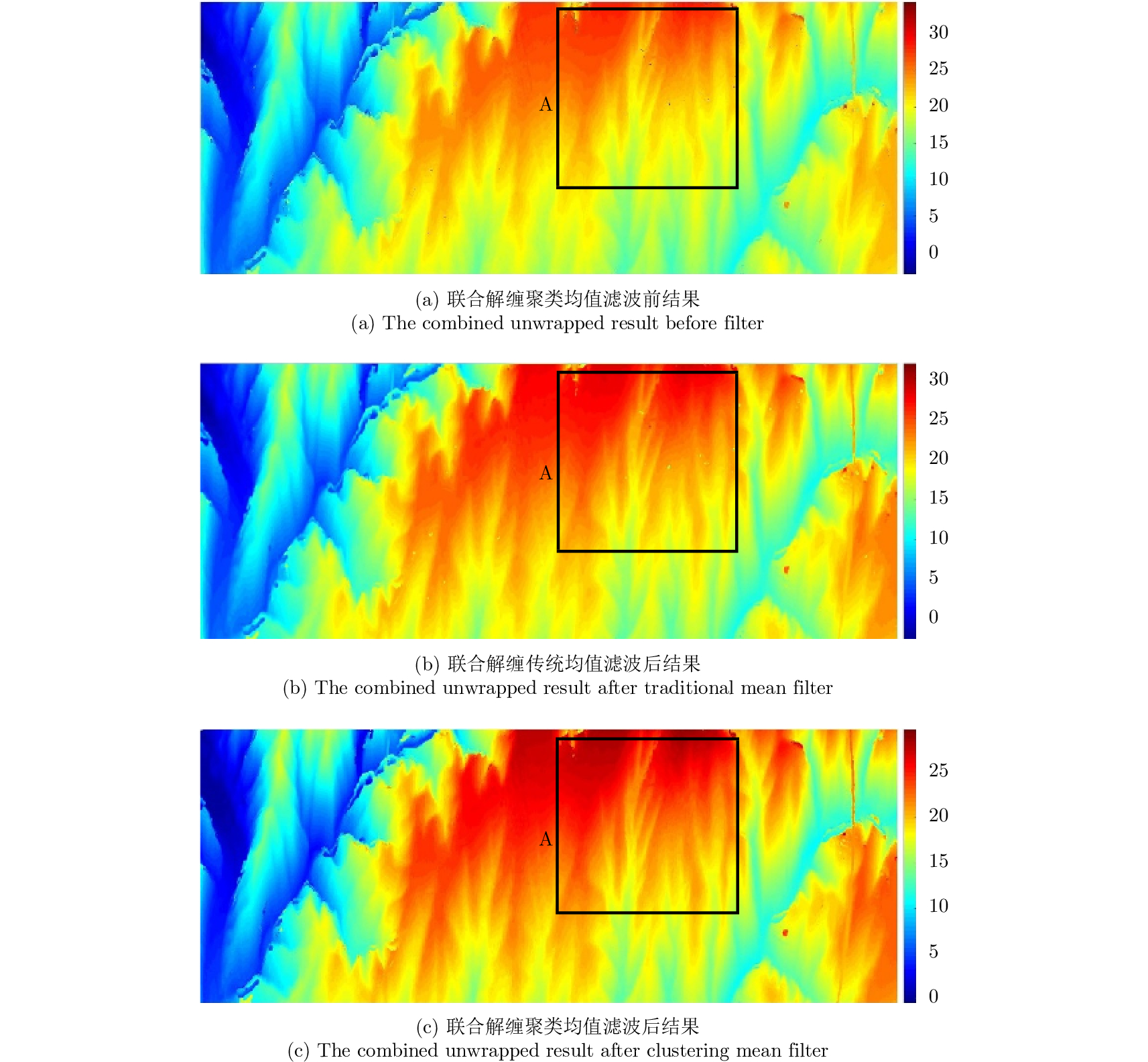
|
图 14 聚类均值滤波和传统均值滤波结果对比 Fig.14 Contrast between clustering Mean filter resultand traditional mean filter result |
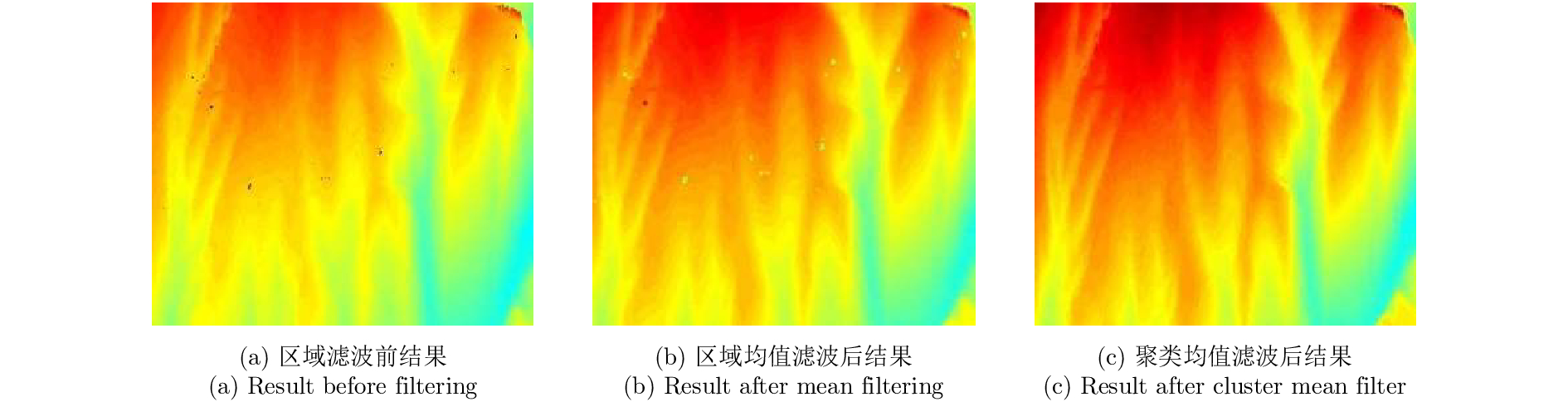
|
图 15 A区域聚类均值滤波和传统均值滤波结果对比 Fig.15 Contrast between clustering mean filter result and traditional mean filter result in area A |
下面采用实际飞行数据对本文方法进行验证,同时对比了单波段和双波段的高程重建效果。实测数据是由中国科学院电子学研究所航天微波遥感系统部提供的某场景双波段(C波段中心频率5.4 GHz和X波段中心频率9.6 GHz)的机载双频干涉数据。
实测数据包括同一场景的C波段和X波段主、辅SAR图像复数据,处理数据的场景如图16所示,为陕西澄城地区的某山区,其中地形起伏比较大区域为图中右上角的高架,不同波段配准之后的C波段干涉图和X波段干涉图分别如图17所示。

|
图 16 处理数据的场景 Fig.16 The scene of processing data |

|
图 17 不同波段配准之后的干涉图 Fig.17 Interferograms after registration of different bands |
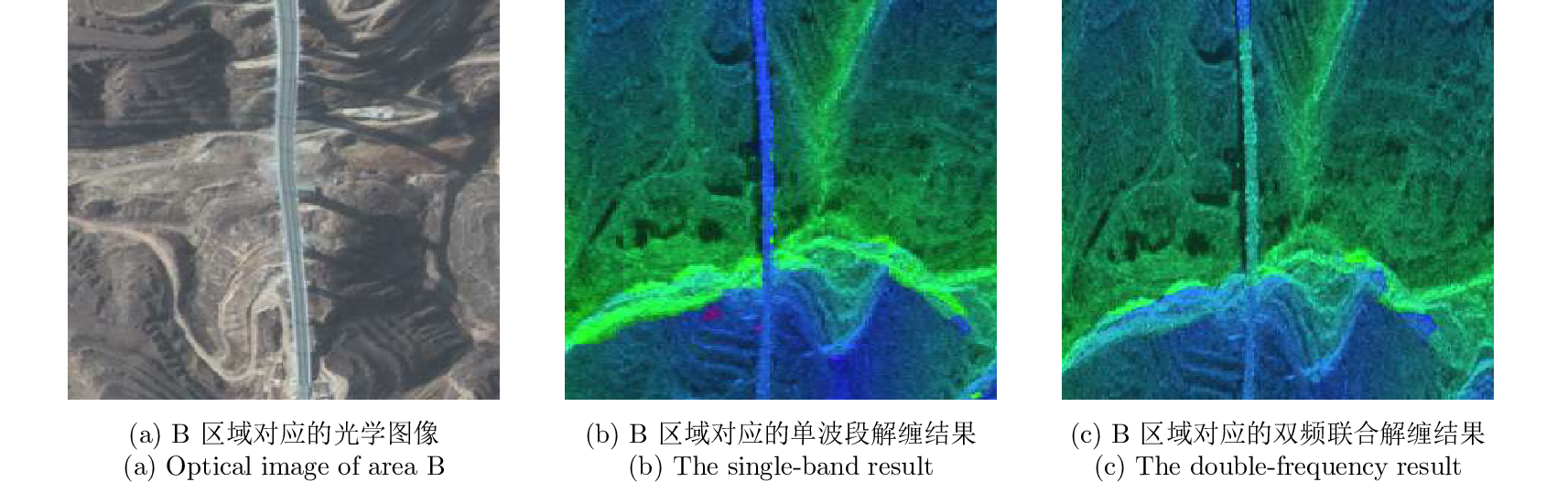
单波段使用最小代价流(MCF)解缠,处理结果如图18所示。使用最大似然估计方法双频联合解缠结果如图19所示,由于波段数较少,最大似然估计鲁棒性较差,完全无法实现正确的相位解缠。按照本文方法,双频联合解缠结果如图20所示。对图中B区域红框内地形起伏比较大的高架区域解缠结果放大对比如图21所示,从图中可以看出在地形起伏较大的区域,单波段也无法实现正确解缠,而使用本文提出的双频联合解缠算法可以正确解缠。
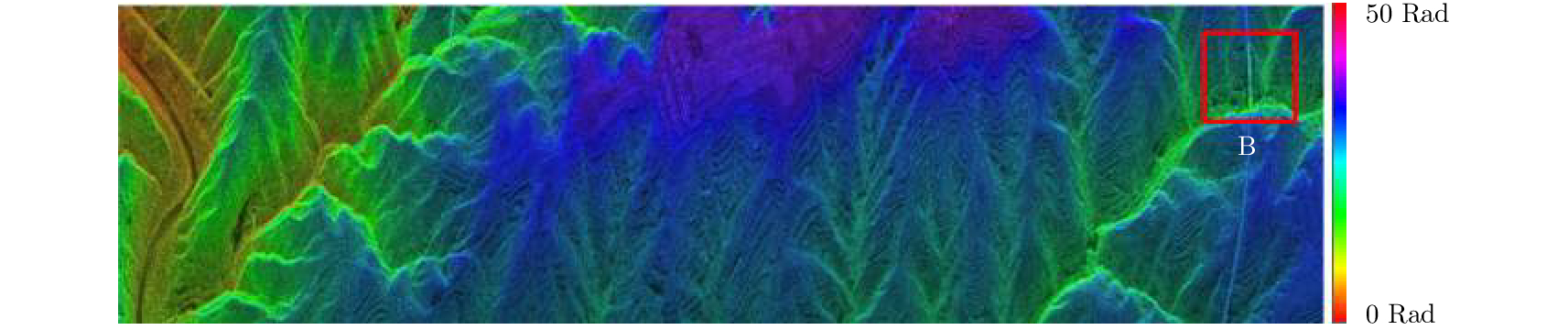
|
图 18 单通道使用最小代价流解缠(MCF)结果 Fig.18 The single-channel phase unwrapped by MCF algorithm |

|
图 19 ML联合解缠结果 Fig.19 The dual-frequency phase unwrapped by ML algorithm |

|
图 20 聚类均值滤波后的TV-MAP联合解缠结果 Fig.20 The dual-frequency phase unwrapped by TV-MAP and cluster mean filter |
|
图 21 地形起伏比较大高架区域单波段和双频联合解缠结果对比 Fig.21 Contrast between single-band unwrapped phase and dual-frequency combined uwrapped phase |
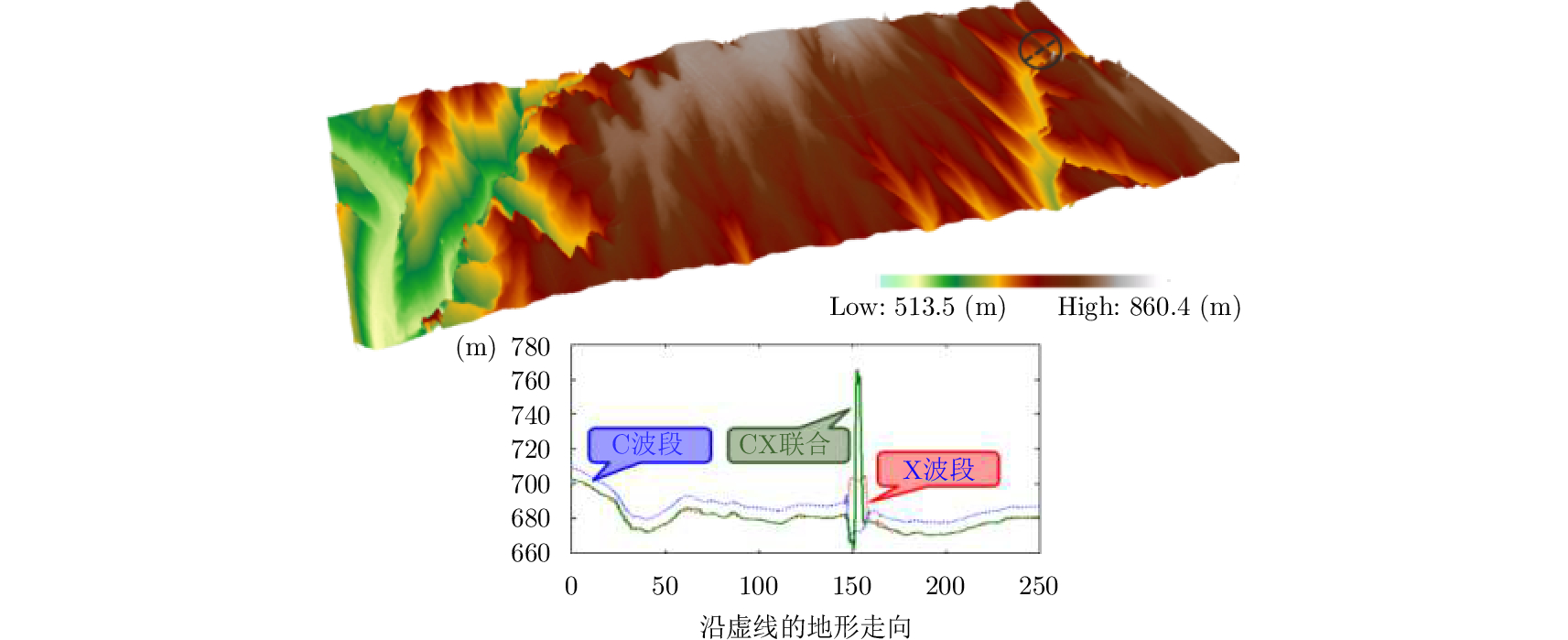
根据轨道参数反演的DEM如图22所示,图中下半部分为上半部分中沿虚线的地形走势,通过对比可知,无论是X波段还是C波段,都无法正确反演高架桥高程,只有联合X波段和C波段,才能正确反演。这也更加明确地说明了,在地形起伏比较大的区域,只有双频联合才可以有效地反演高程信息。
|
图 22 双频联合根据轨道参数反演的DEM Fig.22 The airborne double-frequency rebuilding DEM |
由于本文所用的实测数据场景中没有准确的地面控制点,本文采用的方法是将谷歌光学地图作为主图像和SAR图像的幅度图进行配准,得到配准的多项式系数,利用拟合的多项式系数实现对DEM进行配准。在光学图像上选取5个控制点对DEM进行精度分析。单波段反演高程的均方根误差(Root Mean Square Error, RMSE)为4.5826 m,且存在部分地区高程反演失败,而双频联合反演的RMSE为1.3476 m,可以看出本文提出双频联合高程重建方法精度优于单波段高程重建。
4 结束语本文提出了一种有效的双频干涉处理方法,分析并给出了算法中各个步骤的处理方案。针对双频联合处理中的双频联合配准、双频解缠绕等关键技术难题,给出了有效的解决方案,提高了双频联合反演DEM的精度和鲁棒性。采用常规单波段方法和本文方法对机载实际飞行数据处理,处理结果表明,单波段使用MCF进行相位解缠,无法实现大起伏地形区域的高程重建;而采用本文提出的处理流程能够准确地反演大起伏地形区域的高程,验证了本文所提出的双频干涉处理方法的有效性。
| [1] |
Rogers A E E and Ingalls R P. Venus: Mapping the surface reflectivity by radar interferometry[J].
Science, 1969, 165(3895): 797-799. ( 0) 0)
|
| [2] |
Van Zyl J J. The Shuttle Radar Topography Mission (SRTM): A breakthrough in remote sensing of topography[J].
Acta Astronautica, 2001, 48(5/12): 559-565. ( 0) 0)
|
| [3] |
Griffiths H. Interferometric synthetic aperture radar[J].
Electronics & Communication Engineering Journal, 1995, 7(6): 247-265. ( 0) 0)
|
| [4] |
王岩飞, 刘畅, 詹学丽, 等. 无人机载合成孔径雷达系统技术与应用[J].
雷达学报, 2016, 5(4): 333-349. Wang Yanfei, Liu Chang, Zhan Xueli, et al. Technology and applications of UAV synthetic aperture radar system[J]. Journal of Radars, 2016, 5(4): 333-349. DOI:10.12000/JR16089 (  0) 0)
|
| [5] |
侯丽英, 林赟, 洪文. 干涉圆迹SAR的目标三维重建方法研究[J].
雷达学报, 2016, 5(5): 538-547. Hou Liying, Lin Yun, and Hong Wen. Three-dimensional reconstruction method study based on interferometric circular SAR[J]. Journal of Radars, 2016, 5(5): 538-547. DOI:10.12000/JR16009 (  0) 0)
|
| [6] |
Ghiglia D C and Pritt M D. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software[M]. New York: Wiley, 1998
( 0) 0)
|
| [7] |
Xu W, Chang E C, Kwoh L K, et al.. Phase-unwrapping of SAR interferogram with multi-frequency or multi-baseline[C]. Proceedings of 1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 1994, 2: 730–732
( 0) 0)
|
| [8] |
Pascazio V and Schirinzi G. Estimation of terrain elevation by multifrequency interferometric wide band SAR data[J].
IEEE Signal Processing Letters, 2001, 8(1): 7-9. DOI:10.1109/97.889635 ( 0) 0)
|
| [9] |
Hoge W S. A subspace identification extension to the phase correlation method[MRI application][J].
IEEE Transactions on Medical Imaging, 2003, 22(2): 277-280. DOI:10.1109/TMI.2002.808359 ( 0) 0)
|
| [10] |
Ferraiuolo G, Pascazio V, and Schirinzi G. Maximum a posteriori estimation of height profiles in InSAR imaging[J].
IEEE Geoscience and Remote Sensing Letters, 2004, 1(2): 66-70. DOI:10.1109/LGRS.2003.822882 ( 0) 0)
|
| [11] |
Ferraioli G, Shabou A, Tupin F, et al. Multichannel phase unwrapping with graph cuts[J].
IEEE Geoscience and Remote Sensing Letters, 2009, 6(3): 562-566. DOI:10.1109/LGRS.2009.2021165 ( 0) 0)
|
| [12] |
Ferraiuolo G, Meglio F, Pascazio V, et al. DEM reconstruction accuracy in multichannel SAR interferometry[J].
IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(1): 191-201. DOI:10.1109/TGRS.2008.2002644 ( 0) 0)
|
| [13] |
Yu H W, Li Z F, and Bao Z. A cluster-analysis-based efficient multibaseline phase-unwrapping algorithm[J].
IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 478-487. DOI:10.1109/TGRS.2010.2055569 ( 0) 0)
|
| [14] |
Deledalle C A, Denis L, and Tupin F. NL-InSAR: Nonlocal interferogram estimation[J].
IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(4): 1441-1452. DOI:10.1109/TGRS.2010.2076376 ( 0) 0)
|
| [15] |
Yuan Z H, Deng Y K, Li F, et al. Multichannel InSAR DEM reconstruction through improved closed-form robust Chinese remainder theorem[J].
IEEE Geoscience and Remote Sensing Letters, 2013, 10(6): 1314-1318. DOI:10.1109/LGRS.2013.2238886 ( 0) 0)
|
| [16] |
Zeng T, Liu T D, Ding Z G, et al. Phase unwrapping method based on multi-frequency InSAR in highly sloped terrain[J].
Electronics Letters, 2016, 52(12): 1058-1059. DOI:10.1049/el.2015.3795 ( 0) 0)
|
| [17] |
斯奇, 王宇, 邓云凯, 等. 一种基于最大后验框架的聚类分析多基线干涉SAR高度重建算法[J].
雷达学报, 2017, 6(6): 640-652. Si Qi, Wang Yu, Deng Yunkai, et al. A novel cluster-analysis algorithm based on MAP framework for multi-baseline InSAR height reconstruction[J]. Journal of Radars, 2017, 6(6): 640-652. DOI:10.12000/JR17043 (  0) 0)
|
| [18] |
李杭, 梁兴东, 张福博, 等. 基于高斯混合聚类的阵列干涉SAR三维成像[J].
雷达学报, 2017, 6(6): 630-639. Li Hang, Liang Xingdong, Zhang Fubo, et al. 3D imaging for array InSAR based on Gaussian mixture model clustering[J]. Journal of Radars, 2017, 6(6): 630-639. DOI:10.12000/JR17020 (  0) 0)
|
| [19] |
赵耀, 邓云凯, 王宇, 等. 原始数据压缩对方位向多通道SAR系统影响研究[J].
雷达学报, 2017, 6(4): 397-407. Zhao Yao, Deng Yunkai, Wang Yu, et al. Study of effect of raw data compression on azimuth multi-channel SAR system[J]. Journal of Radars, 2017, 6(4): 397-407. DOI:10.12000/JR17030 (  0) 0)
|
| [20] |
尤红建, 胡岩峰. SAR和光学图像精配准技术的研究[J].
雷达学报, 2014, 3(1): 78-84. You Hong-jian and Hu Yan-feng. Investigation on fine registration for SAR and optical image[J]. Journal of Radars, 2014, 3(1): 78-84. DOI:10.3724/SP.J.1300.2014.13154 (  0) 0)
|
| [21] |
刘钰菲. InSAR图像配准算法研究[D]. [硕士论文], 西安电子科技大学, 2011
Liu Yu-fei. Research on image registration for InSAR system[D]. [Master dissertation], Xidian University, 2011 (  0) 0)
|
| [22] |
袁志辉. 多通道干涉SAR关键技术研究[D]. [博士论文], 中国科学院大学, 2013
Yuan Zhi-hui. Study on the key techniques of multichannel interferometric synthetic aperture radar[D]. [Ph.D. dissertation], The University of Chinese Academy of Sciences, 2013 (  0) 0)
|




