② (96630部队 北京 102206)
② (Unit 96630, Beijing 102206, China)
认知雷达是一种智能化雷达,可以根据对环境和目标信息的认知自适应地调整发射波形,是未来雷达的发展趋势之一[1,2]。认知雷达的发射波形不仅与其所面向的任务有关,而且也受某些约束条件的限制。现阶段,在进行面向检测的波形设计时,大部分方法仅考虑了发射能量的约束,而未对所设计信号的包络加以制约。在工程实际中,为了能够使雷达发射机发挥其最大效能通常要求雷达发射波形具有较低的峰均比(Peak-to-Average power Ratio, PAR)或者恒定包络[3,4]。然而,恒模约束又过于苛刻,往往与雷达的检测或估计性能不能兼顾,与恒模约束相比,PAR是一种更加泛化的约束,恒模波形只是PAR=1时的一种特殊波形,低PAR约束下的波形将具有更高的自由度[5–7]。
在信号相关杂波背景下进行检测波形设计时,通常选择最大化信干噪比(Signal-to-Interference- plus-Noise Ratio, SINR)作为优化准则[8,9]。然而,基于该准则进行发射波形和接收机滤波器联合设计时,现有大部分方法主要将匹配滤波器(Matched Filter, MF)作为最佳接收机,而在相关杂波背景下,采用失配滤波器(MisMatched Filter, MMF)可以获得更优的性能。文献[10]对杂波背景下发射波形和MMF的联合设计问题进行了研究,该方法可以保证SINR逐渐递增并收敛于一个定值。但其只对发射能量进行了约束,所求波形的包络不受限制。为了增加恒模或者低PAR约束,文献[11–13]采用凸优化方法,通过半正定松弛(Semi-Definite Relaxation, SDR)技术,对恒模和低PAR波形的优化问题进行了研究。然而,上述文献中均未考虑信号相关杂波对波形设计的影响。文献[14]弥补了这方面的不足,在信号相关杂波背景下,将恒模波形的求解引入到认知雷达中,通过SDR
综上,本文将波形的约束条件松弛为低PAR,同时考虑信号相关杂波的影响,并且兼顾算法的运算速率,提出了一种面向扩展目标检测的低PAR发射波形和接收机MMF的联合设计方法。该方法可同时兼顾波形的检测性能和放大器效能,在给定的PAR范围内可使波形的输出SINR达到最大。此外,本文采用秩1近似法结合最近邻方法[15],取代高斯随机化方法,进一步降低了算法运算量(详见第4节分析)。仿真结果验证了所提方法理论分析的正确性和算法的有效性。
2 信号模型本文考虑相关杂波背景下针对扩展目标检测的低PAR波形设计。目标的散射特性用目标冲激响应(Target Impulse Response, TIR)表示,相关杂波用杂波冲激响应(Clutter Impulse Response, CIR)表示。为方便起见,本文对单输入单输出(Single Input Single Output, SISO)雷达进行研究,主要在时域对离散的时间信号进行分析,信号模型如图1所示。
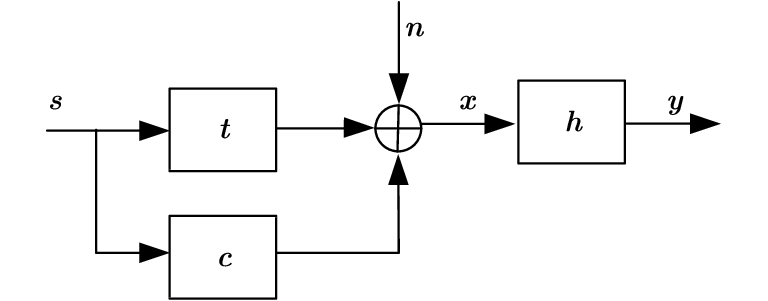
|
图 1 相关杂波下的信号模型 Fig.1 Signal model |
图1中,
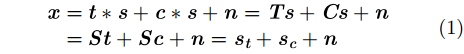
|
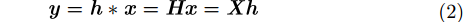
|
其中,“*”代表卷积运算。
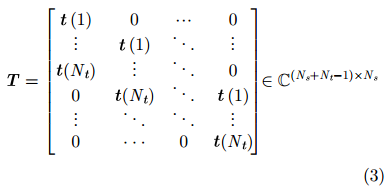
|
根据式(1)和式(2),并令噪声和杂波的和为:

|
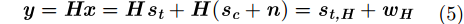
|
因此,接收MMF输出信号的SINR可表示为:
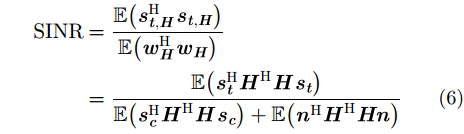
|
其中,
本小节主要采用循环迭代的思想对发射波形
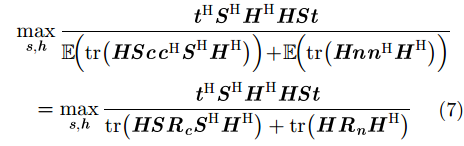
|
其中,
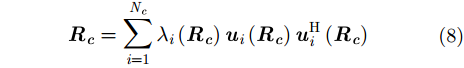
|
其中,
假定
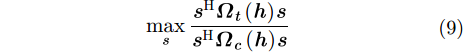
|
其中,
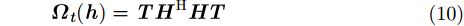
|
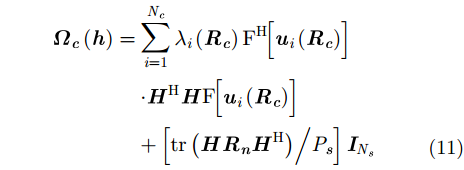
|
其中,F代表的是由向量到Toeplitz矩阵的映射,
同理,假定
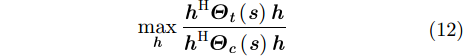
|
其中,

|
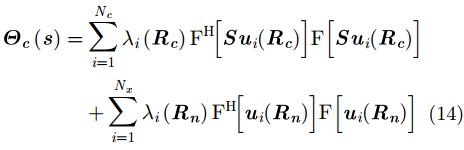
|
当
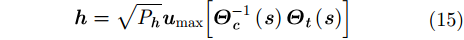
|
其中,
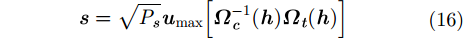
|
然而,考虑到实际的工程需求,当约束条件变为恒模或者低PAR时,问题就变得复杂起来。
3.2 低PAR波形设计实际雷达系统中,发射波形的总能量是有限的,不失一般性,设发射波形的最大能量不超过
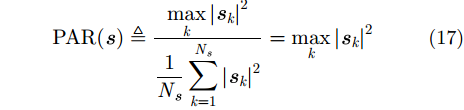
|
其中,
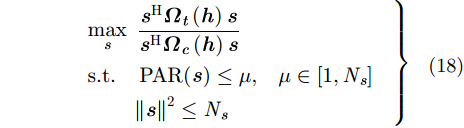
|
式中,当
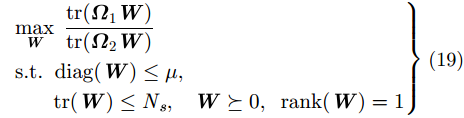
|
其中,diag(·)代表矩阵的对角线元素,rank(·)代表矩阵的秩,
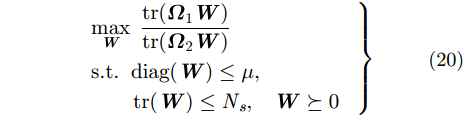
|
接下来,需要对目标函数进行等量代换,使其转化为凸函数。由于
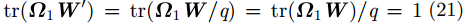
|
由于仿射空间并不对除法运算封闭,所以需要对变量q进行处理,令
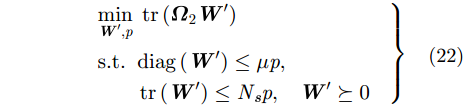
|
式中,由于
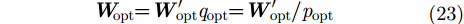
|
如果
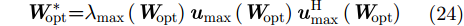
|
式中,
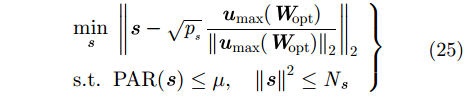
|
此时,式(25)是一个凸问题,该凸问题有成熟的求解方法,实际使用中有相应的CVX工具箱[22]。但直接使用这些成熟的算法时,其复杂度较高。由于式(25)的目标函数和约束条件的形式与文献[15]中的最近邻算法相同,采用该算法可以对问题进行快速求解,每一步迭代的运算复杂度为
综上,基于凸优化的认知雷达低PAR波形设计算法可总结如下:
步骤1 令
步骤2 令
步骤3 通过求解式(22)得到
步骤4 如果
步骤5 如果
本文算法通过对
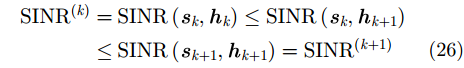
|
式中,第1个不等式成立的原因是由于
本文主要与文献[14]算法的运算复杂度进行对比。文献[14]采用SDR
假设发射波形和接收滤波器的长度
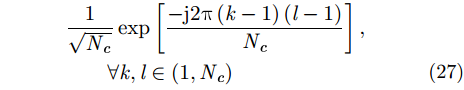
|
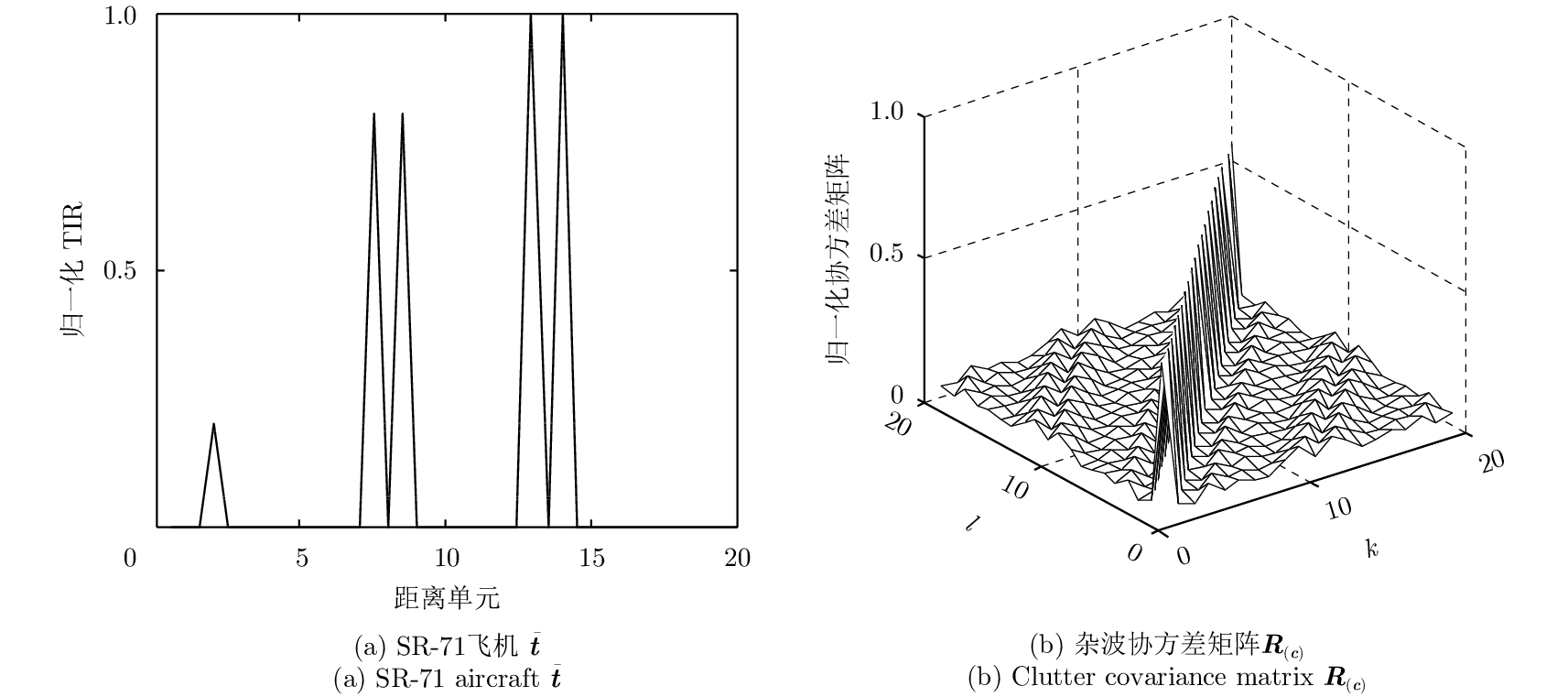
归一化的TIR和CIR协方差矩阵如图2所示。为便于分析,令噪声为高斯白噪声,其协方差矩阵为
|
图 2 确定TIR和随机CIR Fig.2 Determinate TIR and random CIR |
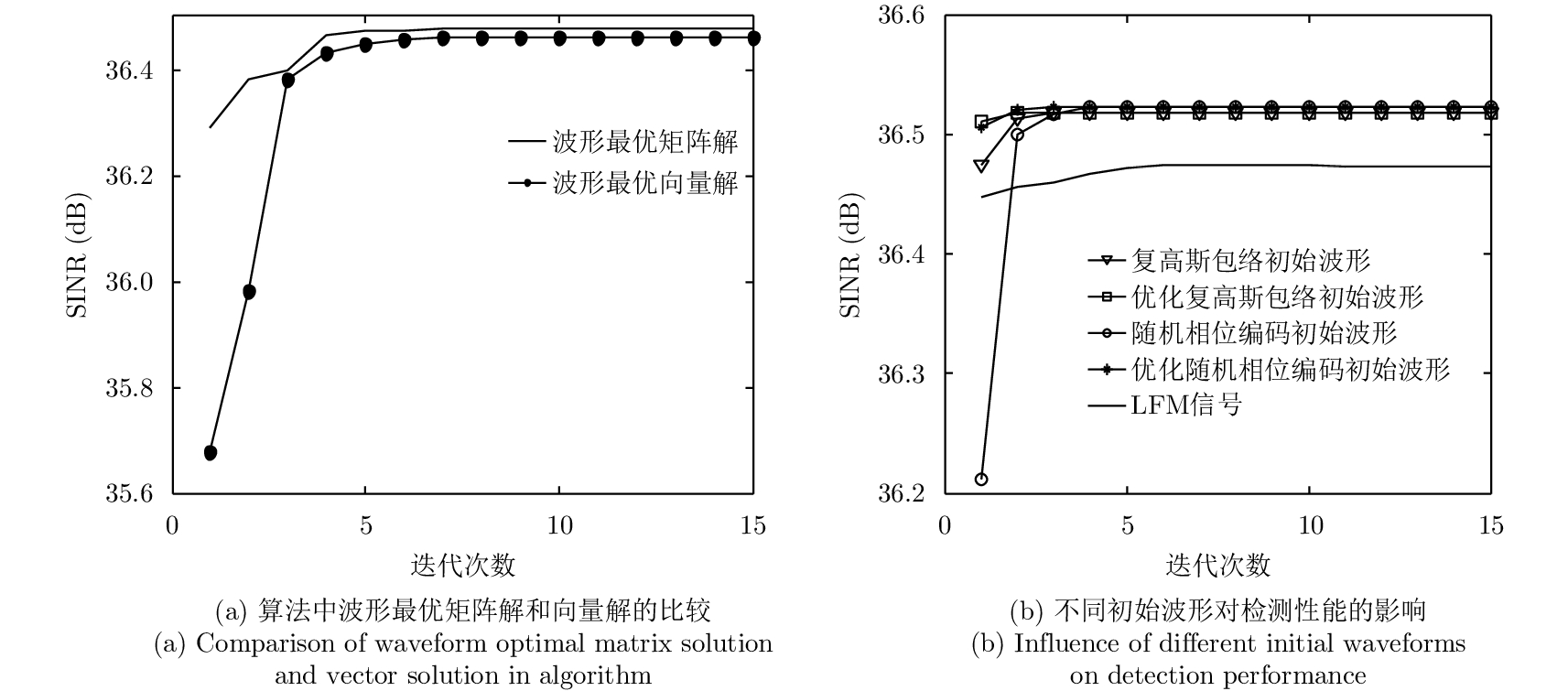
令PAR=1,初始波形为随机的相位编码波形,比较算法中波形最优矩阵解和波形最优向量解的检测性能,如图3(a)所示。可以看出,随着迭代次数的增加,二者均递增收敛,且后者的检测性能要略差于前者,这是因为从矩阵解转化为向量解时,还需要再进行一次PAR的约束,缩小了可行解的求解区域。图3(b)验证了不同初始波形对算法的影响。其中,优化复高斯包络初始波形和优化随机相位编码波形是通过文献[10]中的算法1,将其进行一步优化而得到的初始波形。可以看出,优化初始波形的收敛速度和初始SINR都要更优;此外,线性调频(Linear Frequency Modulation, LFM)信号的性能较差。这表明算法对初始值是敏感的,为了提高收敛速率可选择性能较好的波形作为初始发射波形。
|
图 3 随迭代次数的算法性能分析 Fig.3 Algorithm performance analysis with iterations |
图4将本文算法与现有算法进行了对比。设门限
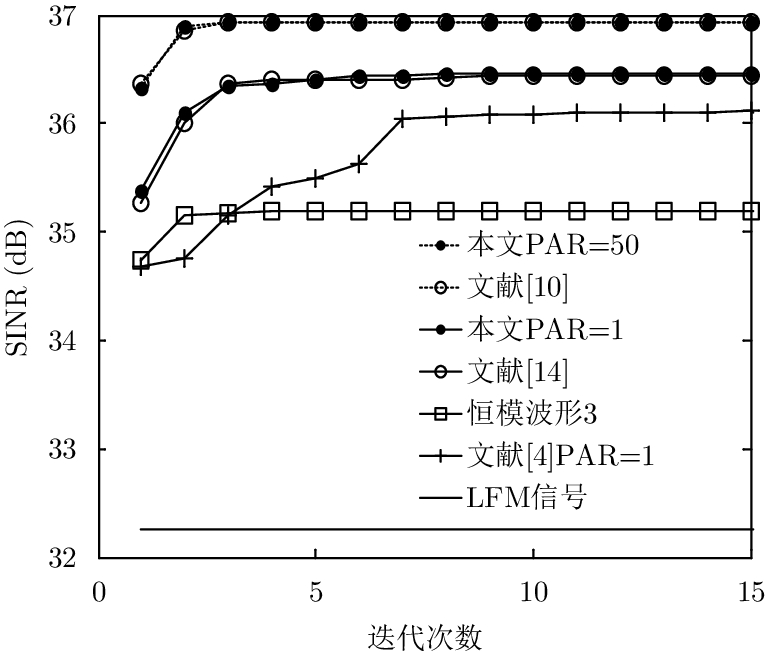
|
图 4 不同算法信干噪比随着迭代次数变化的曲线 Fig.4 Comparison of the SINR for different algorithms with iterations |
图5在不同杂噪比(Clutter-to-Noise Ration, CNR)下对各种算法进行比较。图5(b)是图5(a)的放大。由于在PAR=1时,本文方法与文献[14]性能较为接近,故在该仿真中不与文献[14]作比较。可以看出,随着CNR的增大,本文方法产生的恒模波形检测性能优于文献[4]和恒模波形3,验证了本文算法的有效性。
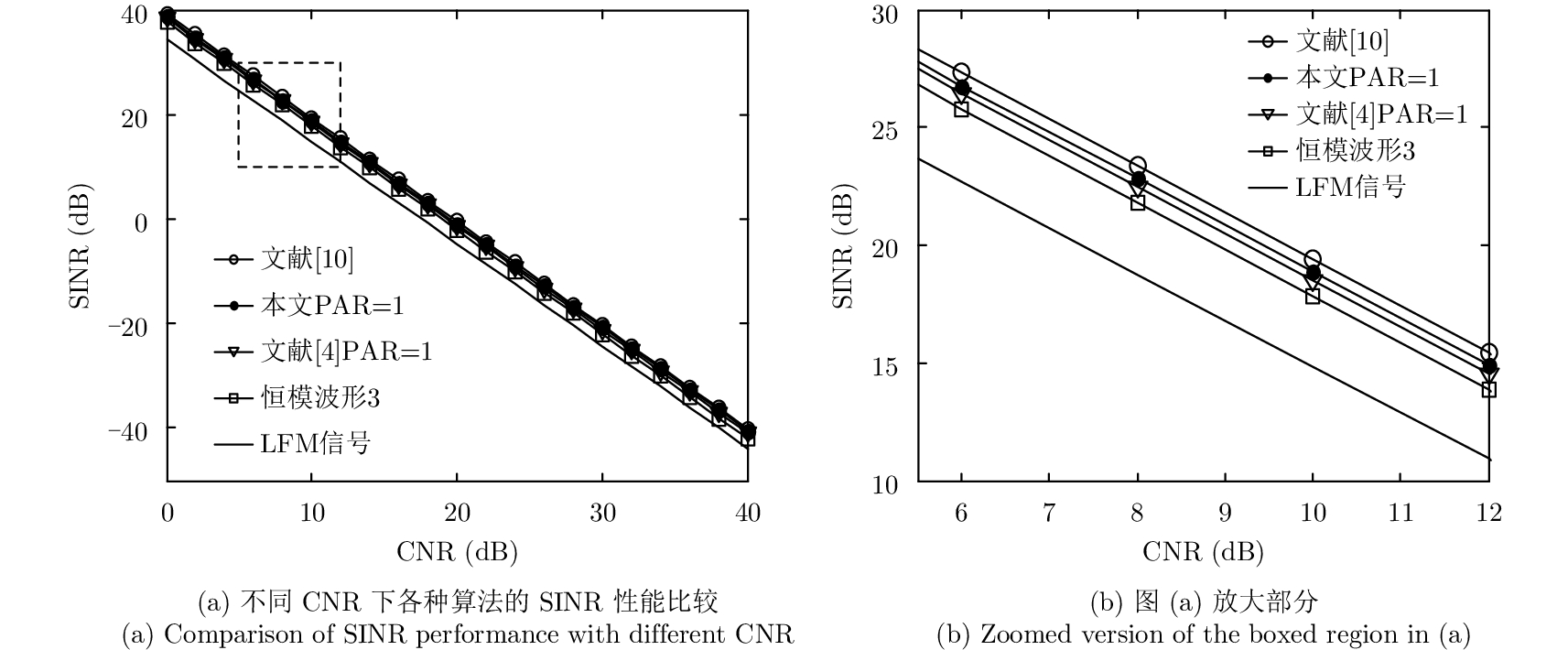
|
图 5 不同算法信干噪比随着CNR变化的曲线 Fig.5 Comparison of the SINR for different algorithms with different CNR |
图6对不同PAR(1.0, 1.3, 1.6, 2.0, 2.6, 3.0)下优化波形的输出SINR进行了比较,图中每条实线对应着不同的PAR,随着箭头的指向PAR的值由1.0增大到3.0。可以看出,随着PAR的增大,式(18)的可行解区域也变大,因此输出SINR不仅收敛速度更快,而且最终收敛值也会相应变大。当PAR>2时,得到的SINR最终收敛于同一值,接近能量约束下SINR的上限。图7为不同PAR波形实部和虚部的表示,
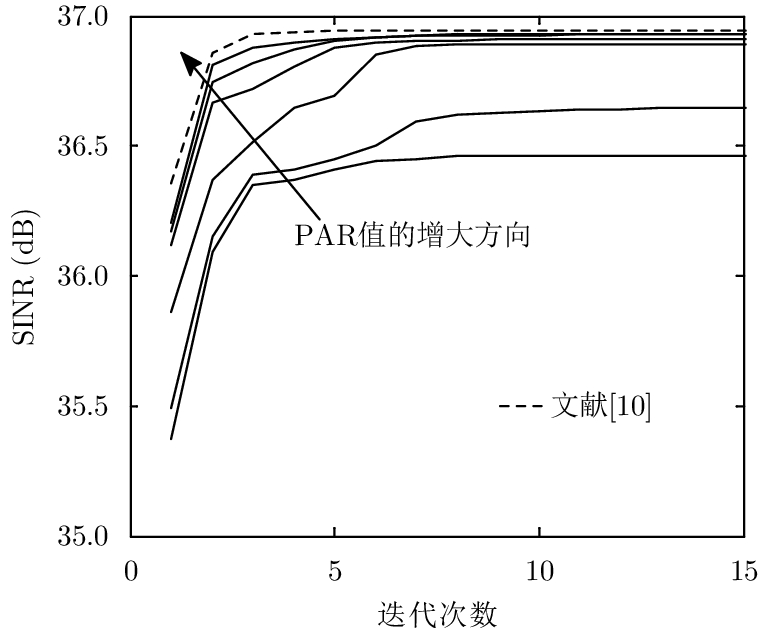
|
图 6 本文算法不同PAR下的信干噪比性能对比 Fig.6 Comparison of the SINR vs different PAR |
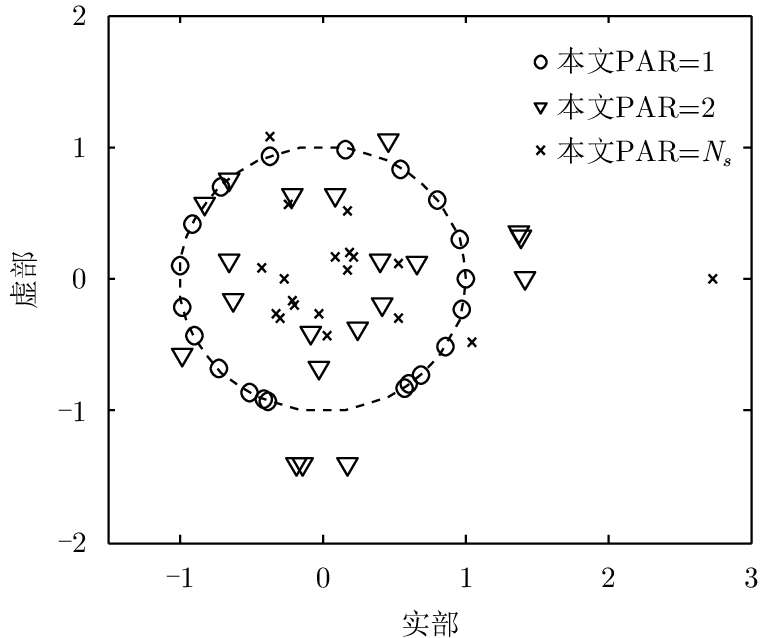
|
图 7 不同PAR波形的实部和虚部 Fig.7 Real and imaginary parts of different PAR |
针对传统雷达波形设计方法中发射机发射功率不被充分利用的问题,以PAR为约束条件,从时域出发,在信号相关杂波背景下,提出了一种低PAR发射波形和接收机联合设计方法。相比现有方法,本文方法可以实现任意PAR下的联合设计。理论分析和仿真实验表明,通过将非凸问题转化为凸问题,可以有效提高相关杂波背景下距离扩展目标的检测性能;随着PAR的增大,波形性能逐渐接近能量约束下的曲线;相比于高斯随机法,通过将秩1近似法和最近邻算法相结合,可以在波形性能保持相当的情况下使算法复杂度进一步降低。值得注意的是,本文分析了确定TIR和随机CIR假设下的优化问题,对其他形式的TIR和CIR的组合,算法同样适用。
| [1] |
Haykin S. Cognitive radar: A way of the future[J].
IEEE Signal Processing Magazine, 2006, 23(1): 30-40. DOI:10.1109/MSP.2006.1593335 ( 0) 0)
|
| [2] |
Guerci J R. Cognitive Radar: The Knowledge-Aided Fully Adaptive Approach[M]. Norwood, MA: Artech House, Inc., 2010: 13–30
( 0) 0)
|
| [3] |
Wang Z J, Babu P, and Palomar D P. Design of PAR-constrained sequences for MIMO channel estimation via majorization-minimization[J].
IEEE Transactions on Signal Processing, 2016, 64(23): 6132-6144. DOI:10.1109/TSP.2016.2607181 ( 0) 0)
|
| [4] |
Stoica P, He H, and Li J. Optimization of the receive filter and transmit sequence for active sensing[J].
IEEE Transactions on Signal Processing, 2012, 60(4): 1730-1740. DOI:10.1109/TSP.2011.2179652 ( 0) 0)
|
| [5] |
唐波, 张玉, 李科, 等. 杂波中MIMO雷达恒模波形及接收机联合优化算法研究[J].
电子学报, 2014, 42(9): 1705-1711. Tang Bo, Zhang Yu, Li Ke, et al. Joint constant-envelope waveform and receiver design for MIMO radar in the presence of clutter[J]. Acta Electronica Sinica, 2014, 42(9): 1705-1711. DOI:10.3969/j.issn.0372-2112.2014.09.007 (  0) 0)
|
| [6] |
郝天铎, 周青松, 孙从易, 等. 非准确先验知识下认知雷达低峰均比稳健波形设计[J].
电子与信息学报, 2018, 40(3): 532-540. Hao Tian-duo, Zhou Qing-song, Sun Cong-yi, et al. Low-PAR robust waveform design for cognitive radar with imprecise prior knowledge[J]. Journal of Electronics & Information Technology, 2018, 40(3): 532-540. DOI:10.11999/JEIT170560 (  0) 0)
|
| [7] |
Sen S. Characterizations of PAPR-constrained radar waveforms for optimal target detection[J].
IEEE Sensors Journal, 2014, 14(5): 1647-1653. DOI:10.1109/JSEN.2014.2299283 ( 0) 0)
|
| [8] |
Bell M R. Information theory and radar waveform design[J].
IEEE Transactions on Information Theory, 1993, 39(5): 1578-1597. DOI:10.1109/18.259642 ( 0) 0)
|
| [9] |
Tang B and Tang J. Robust waveform design of wideband cognitive radar for extended target detection[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Shanghai, China, 2016: 3096–3100. DOI: 10.1109/ICASSP.2016.7472247
( 0) 0)
|
| [10] |
Chen C Y and Vaidyanathan P P. MIMO radar waveform optimization with prior information of the extended target and clutter[J].
IEEE Transactions on Signal Processing, 2009, 57(9): 3533-3544. DOI:10.1109/TSP.2009.2021632 ( 0) 0)
|
| [11] |
Chen X X, Deng X B, and Hao Z M. Waveform design for extended target detection under a peak to average power ratio constraint[C]. Proceedings of 2016 CIE International Conference on Radar, Guangzhou, China, 2016: 1–4. DOI: 10.1109/RADAR.2016.8059566
( 0) 0)
|
| [12] |
Tang Y H, Zhang Y D, Amin M G, et al. Wideband multiple-input multiple-output radar waveform design with low peak-to-average ratio constraint[J].
IET Radar, Sonar & Navigation, 2016, 10(2): 325-332. DOI:10.1049/iet-rsn.2015.0189 ( 0) 0)
|
| [13] |
Gorji A A and Adve R S. Waveform optimization for random-phase radar signals with PAPR constraints[C]. IEEE International Radar Conference, Lille, France, 2014: 1–5. DOI: 10.1109/RADAR.2014.7060340
( 0) 0)
|
| [14] |
Yue W Z, Zhang Y, Liu Y M, et al. Radar constant-modulus waveform design with prior information of the extended target and clutter[J].
Sensors, 2016, 16(6): 889 DOI:10.3390/s16060889 ( 0) 0)
|
| [15] |
唐波. 宽带认知雷达低峰均比波形快速设计算法[J].
航空学报, 2016, 37(2): 688-694. Tang B. Efficient design algorithm of low PAR waveform for wideband cognitive radar[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 688-694. DOI:10.7527/S1000-6893.2015.0125 (  0) 0)
|
| [16] |
Romero R A, Bae J, and Goodman N A. Theory and application of SNR and mutual information matched illumination waveforms[J].
IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 912-927. DOI:10.1109/TAES.2011.5751234 ( 0) 0)
|
| [17] |
Chen P, Qi C H, Wu L N, et al. Estimation of extended targets based on compressed sensing in cognitive radar system[J].
IEEE Transactions on Vehicular Technology, 2017, 66(2): 941-951. DOI:10.1109/TVT.2016.2565518 ( 0) 0)
|
| [18] |
邹鲲, 廖桂生, 李军. 复合高斯杂波中知识辅助检测器的先验信息感知方法[J].
中国科学: 信息科学, 2014, 44(8): 993-1003. Zou Kun, Liao Gui-sheng, and Li Jun. Prior information cognitive method for knowledge aided detector in compound Gaussian clutter[J]. Scientia Sinica Informationis, 2014, 44(8): 993-1003. DOI:10.1360/N112013-00116 (  0) 0)
|
| [19] |
张贤达. 矩阵分析与应用[M]. 第2版, 北京: 清华大学出版社, 2013: 447–450
Zhang Xian-da. Matrix Analysis and Application[M]. Second Edition, Beijing: Tsinghua University Press, 2013: 447–450 (  0) 0)
|
| [20] |
Luo Z Q, Ma W K, So A M C, et al. Semidefinite relaxation of quadratic optimization problems[J].
IEEE Signal Processing Magazine, 2010, 27(3): 20-34. DOI:10.1109/MSP.2010.936019 ( 0) 0)
|
| [21] |
Yue W Z, Zhang Y, and Xie J W. Radar constant-modulus waveform design for multiple extended targets[J].
IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2017, E100-A(3): 888-892. DOI:10.1587/transfun.E100.A.888 ( 0) 0)
|
| [22] |
Grant M and Boyd S. CVX: Matlab software for disciplined convex programming (Web page and software) 2008[EB/OL]. http://cvxr.com/cvx/
( 0) 0)
|
| [23] |
Leshem A, Naparstek O, and Nehorai A. Information theoretic adaptive radar waveform design for multiple extended targets[J].
IEEE Journal of Selected Topics in Signal Processing, 2007, 1(1): 42-55. DOI:10.1109/JSTSP.2007.897047 ( 0) 0)
|
| [24] |
Yang Y and Blum R S. MIMO radar waveform design based on mutual information and minimum mean-square error estimation[J].
IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(1): 330-343. DOI:10.1109/TAES.2007.357137 ( 0) 0)
|




