合成孔径雷达(Synthetic Aperture Radar, SAR)作为一种具有全天时、全天候、高分辨力、大区域观测及信息量丰富的雷达成像技术,已成为当今遥感对地观测的重要手段。因具备3维成像能力,线阵SAR (Linear Array Synthetic Aperture Radar, LASAR)是近几年来被广泛关注的一种新体制SAR 3维成像技术[1–4]。本质上,LASAR主要利用线阵天线运动合成一个大的虚拟2维阵列实现观测目标的2维分辨,再利用距离脉冲压缩技术实现观测目标的3维成像。相对于其它常规SAR 3维成像体制(如圆周SAR、层析SAR等),LASAR具备成像模式多样、应用灵活等优势,克服了常规SAR 3维成像体制无法下视、前视成像的缺陷,在城市地形测绘、飞行器导航及盲降、目标精定位与识别、战场情报获取等民用和军用领域具有重要的研究价值和应用前景。
目前,LASAR 3维成像处理主要采用基于匹配滤波理论的成像算法[1,2],如距离多普勒算法和后向投影算法。受载荷平台(如飞机、无人机、卫星等)空间及线阵天线长度限制,传统匹配滤波成像算法在LASAR线阵方向的分辨能力通常比其它维向的分辨力低,一定程度约束了LASAR高分辨成像应用。然而,由于地面、空中等观测目标在3维空间通常具有强稀疏性,故可利用目标稀疏先验信息提升LASAR 3维成像精度。近几年,基于压缩感知(Compressed Sensing, CS)理论的稀疏成像已经成为LASAR高分辨成像的研究热点之一,并提出了多种基于CS稀疏重构的LASAR 3维高分辨稀疏成像方法[5–8]。但是,CS稀疏重构对成像模型的精确性要求非常高,如在X波段雷达时位置精度通常需要达到毫米级,现有压缩感知LASAR 3维稀疏成像算法通常以成像模型精确已知为前提,并没有考虑实际平台运动误差的影响。当LASAR存在运动误差、阵列抖动时,则会导致成像模型存在偏差,CS稀疏重构出现散焦、畸变、虚假目标等成像质量恶化现象,甚至不能成像。另外,与传统SAR系统单个或少量天线工作不同,LASAR需要成百上千天线阵元同时工作,故仅利用雷达系统中单个位置的导航测量系统(如IMU (Inertial Measurement Unit)系统、GPS (Global Positioning System)或北斗系统)数据难以实现LASAR多个天线阵元运动误差的精确补偿。为了提高压缩感知LASAR 3维成像质量,在利用导航测量数据进行运动误差补偿后,还需结合回波数据和自聚焦成像技术实现多天线阵元的残余运动误差补偿。
至今,针对传统SAR成像中的运动误差补偿,相关学者已经提出了多种基于不同准则的自聚焦成像算法,如最大似然估计(Maximum Likelihood Estimation, MLE)自聚焦、最小熵估计(Minimum Entropy Estimation, MEE)自聚焦、最大锐度(Maximum Sharpness Estimation, MSE)自聚焦等方法。相位梯度自聚焦(Phase Gradient Autofocus, PGA)算法作为一种在SAR实际成像中广泛应用的典型MLE自聚焦成像算法,已被成功用于压缩感知SAR稀疏成像中的残余相位误差补偿[9]。但是,当回波数据欠采样时,传统自聚焦算法不一定适用于压缩感知SAR稀疏自聚焦成像[10]。针对压缩感知SAR 稀疏自聚焦问题,近几年相关学者也已经提出一些解决方法。文献[11]提出了一种基于稀疏驱动的联合SAR稀疏成像及相位误差校正方法,采用迭代估计方法求解非二次正则化问题实现SAR稀疏自聚焦成像。文献[12]提出一种针对稀疏微波成像的自聚焦方法,采用贪婪算法实现相位误差的高精度估计。文献[13]提出了一种基于子孔径参数稀疏表示的机载SAR自聚焦成像算法,实测数据结果表明该方法相对于传统PGA算法具有更好的自聚焦性能。文献[14]针对运动误差造成的网格偏离现象,提出了一种基于稀疏重构的聚束式SAR自聚焦成像算法,采用正交匹配追踪及最速下降法实现稀疏自聚焦成像。另外,还有一些文献提出基于其它准则或估计模型的SAR 稀疏自聚焦算法[15–17]。然而,与传统SAR运动误差形式不同,由于受线阵稀疏分布及平台颤动、线阵抖动等联合运动误差影响,LASAR成像模型中相位误差具有多维度、高阶项分布等更复杂的形式,现有 SAR稀疏自聚焦算法不一定适用于LASAR自聚焦成像。对此,本文作者也提出了基于稀疏贝叶斯学习的LASAR自聚焦成像算法,在欠采样数据条件下可有效估计相位误差[18,19],但是该方法需已知目标及相位的先验分布特性并且要求较高的回波信噪比条件。
为了补偿欠采样条件下LASAR多维度高阶相位误差,本文提出了一种基于半正定规划(Semi-Definite Programming, SDP)的压缩感知LASAR自聚焦成像算法,即半正定规划自聚焦(Semi-Definite Programming Sparse Autofocus, SDPSA)算法,简称为SDPSA算法。该方法利用LASAR压缩感知成像原理、图像最大锐度及最小均方误差准则,构造了欠采样条件下稀疏目标相位误差估计模型,并通过松弛半正定规划及迭代逼近方法实现压缩感知LASAR的高精度稀疏自聚焦成像。为了进一步提高SDPSA算法自聚焦运算效率,利用主散射目标区域提取,仅采用主散射区域进行相位误差估计。仿真数据和实测数据验证了本文SDPSA算法的有效性,相对于PGA自聚焦算法,SDPSA算法在欠采样数据时具有更好的成像质量。本文的主要结构如下:第2节简单介绍了压缩感知LASAR成像模型和稀疏成像原理,阐述了其阵列多相位中心的相位误差影响;第3节建立LASAR相位误差估计的半正定规划模型,提出了基于半正定规划的压缩感知LASAR稀疏自聚焦成像方法,并介绍了该方法的基本步骤;第4节利用LASAR仿真及实测数据,分析SDPSA稀疏自聚焦成像算法性能,验证了算法的有效性;第5节给出了本文算法的主要结论。
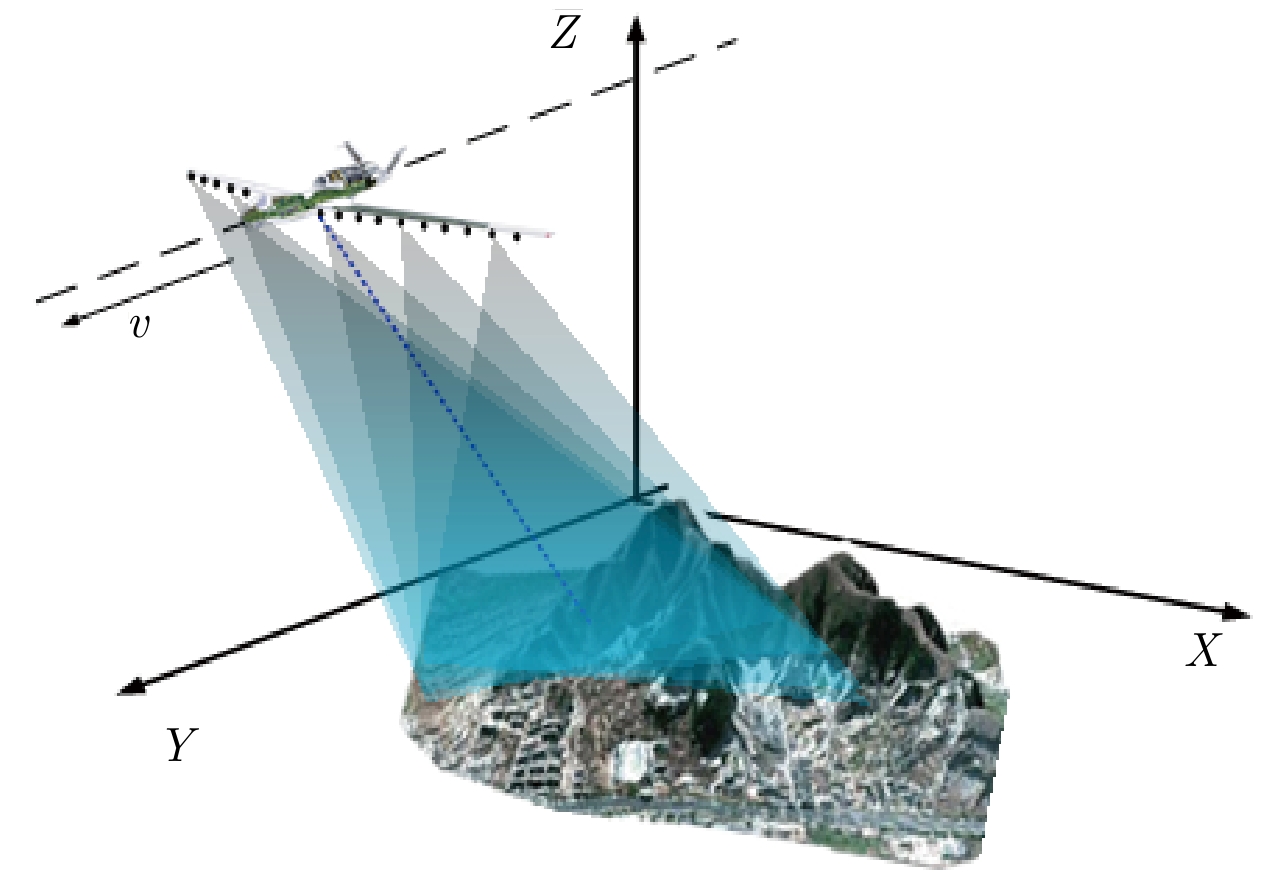
2 压缩感知LASAR成像原理 2.1 回波线性测量模型LASAR 3维成像的典型几何模型如图1所示,其中X, Y和Z轴分别表示切航迹、沿航迹和高度向,线阵天线平行于X轴放置。假设LASAR系统工作于正下视成像模式,
|
图 1 LASAR正下视3维成像的几何模型 Fig.1 The geographic model of down-looking LASAR imaging |
假设LASAR系统发射线性调频信号,其原始回波经过距离压缩后,散射单元
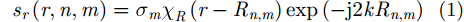
|
其中,
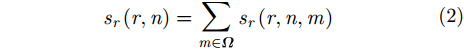
|
此时,回波信号
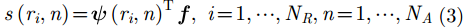
|
其中,
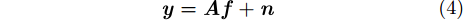
|
其中,
CS理论指出当信号可稀疏表示时,可利用远低于Nyquist采样率进行采样,将原始信号重构问题转化为线性约束最优化求解问题,实现稀疏信号的精确重构[20]。若LASAR观测场景散射系数
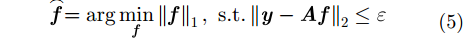
|
其中,
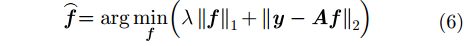
|
其中,
由于受平台颤动、线阵抖动等联合运动误差影响,LASAR 2维APC存在位置误差,会导致 LASAR成像模型存在多维度、高阶项分布的复杂相位误差。令
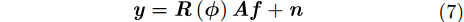
|
其中,
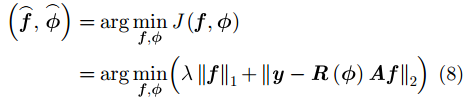
|
若线阵天线阵元稀疏分布或回波信号欠采样,LASAR自聚焦稀疏本质上是一个病态求逆问题,直接求解
为了实现欠采样数据条件下LASAR稀疏自聚焦,联合压缩感知LASAR成像原理、图像最大锐度及最小均方误差重构准则,本文提出一种基于半正定规划的LASAR稀疏自聚焦成像算法。该方法采用迭代估计方法,给定估计初值及参数后,主要由稀疏目标重构、相位误差估计两个独立过程循环实现,其具体理论推导及实现过程如下。
(1) 稀疏目标重构。在算法第
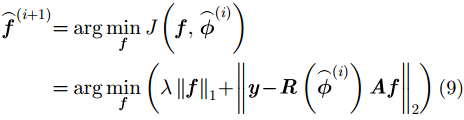
|
该过程为标准CS稀疏重构,可采用现有稀疏重构方法求解
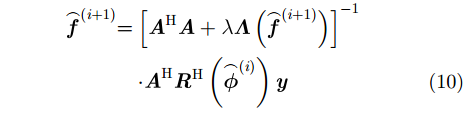
|
其中,
(2) 相位误差估计。利用式(9)得到的
对于最大锐度准则,采用传统匹配滤波重构结果进行判定,因
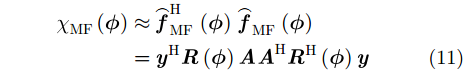
|
对于最小MSE准则,根据式(9),回波数据的重构MSE表示为:
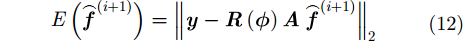
|
相位误差估计的代价函数
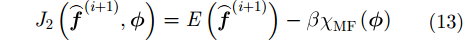
|
其中,
因此,第
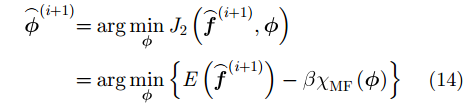
|
若令相位误差向量
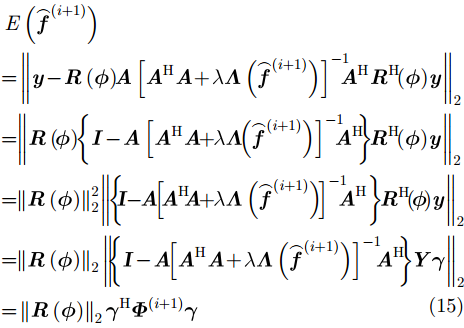
|
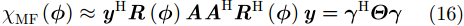
|
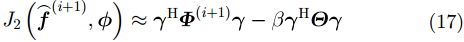
|
其中,矩阵
由于
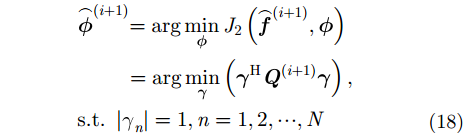
|
显然,式(18)最优化问题可采用恒定常数二次规划(Constant Modulus Quadratic Programming, CMQP)方法求解。相位误差向量
近年来,半正定规划(SDP)方法成为求解CMQP等式最优化问题的热门方法。对于CMQP最优化问题求解,SDP过程的典型表达式为:
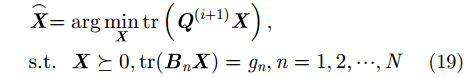
|
其中,
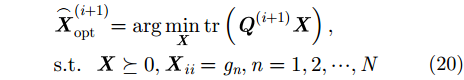
|
为了求解式(20)中的SDP问题,可利用现有的凸优化算法估计求解,如共轭梯度方法、内点法等。另外,目前许多学者也开发了各种SDP求解软件工具箱,如CVX工具箱[23]、SDPT3工具箱[24]等,可用于式(20) SDP问题的快速求解。获得矩阵
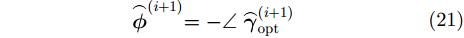
|
获取相位误差估计
为了提高相位误差
针对LASAR稀疏自聚焦成像,根据半正定规划自聚焦成像原理,本文SDPSA算法的主要步骤如表1所示,其主要步骤是迭代估计过程。
| 表 1 SDPSA算法 Tab.1 SDPSA algorithm |
一般情况下,SDPSA算法经过20次迭代左右可实现收敛。另外,SDPSA算法估计得到的相位误差可能会存在线性偏移项,该误差仅导致SDPSA自聚焦成像结果与原始图像存在固定偏移,此时可利用定标技术或其它线性相位误差估计方法进行补偿校正,本文不再详述。
4 实验结果 4.1 仿真数据为了验证SDPSA稀疏自聚焦成像方法的性能,本节先利用LASAR仿真数据进行成像验证,并对比基于传统PGA相位误差估计补偿的后向投影(Back Projection, BP)算法及迭代最小二乘(IRLS)稀疏成像算法结果进行分析,分别简称为BP-PGA算法和IRLS-PGA算法。其中,IRLS-PGA算法是将BP-PGA算法得到的相位误差对回波数据进行补偿后,再利用IRLS算法进行稀疏成像。为了简便,该仿真实验中只对LASAR单个等距离单元切面进行成像,实际中对全部等距离单元切面进行成像后进行合并即可得LASAR观测场景3维成像。
仿真中假设LASAR系统采用正下视工作模式,主要仿真参数如下:雷达中心频率
首先,在回波数据中加入沿航向缓变、切航迹陡变的相位误差,其中沿航迹相位误差在

|
图 2 沿航迹二次项及切航迹随机分布相位误差下仿真点目标成像结果(上:全部回波数据;中:50%回波数据;下:25%回波数据) Fig.2 The results of the point targets in the case of the along-track quadratic phase errors and cross-track random phase errors(Top: all samples; Middle: 50% samples; Bottom: 25% samples) |
其次,在回波数据沿航向和切航迹向均加入随机相位误差,其在

|
图 3 沿航迹及切航迹随机分布相位误差下仿真点目标成像结果(上:全部回波数据;中:50%回波数据;下:25%回波数据) Fig.3 The results of the point targets in the case of the along-track random phase errors and cross-track random phase errors(Top: all samples; Middle: 50% samples; Bottom: 25% samples) |
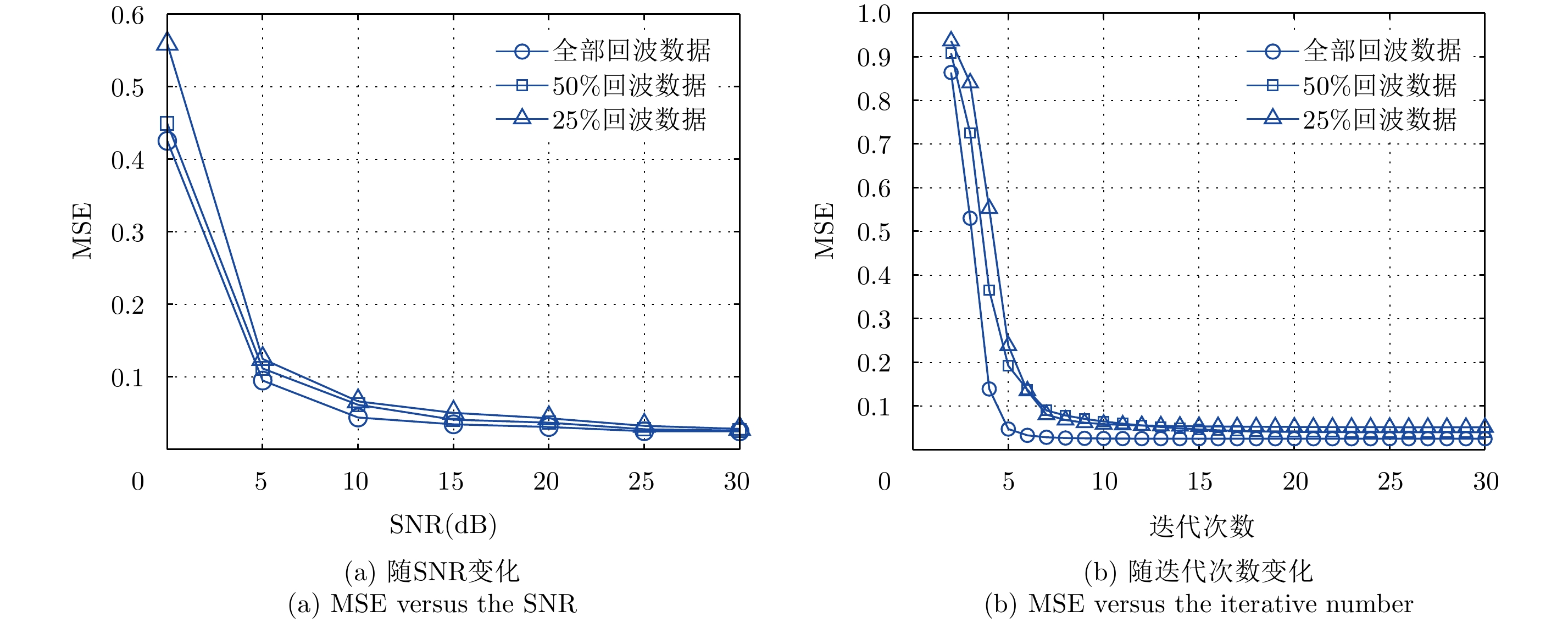
最后,为了分析SDPSA算法在不同SNR及迭代次数情况下自聚焦性能,将图2中SNR变为0至30 dB,图4(a)给出了全部、50%和25%回波数据量时SDPSA算法成像结果与原始仿真场景的MSE。可知,SDPSA算法的MSE随着SNR增大而变小,并且在SNR为0 dB至5 dB时MSE大于0.1,但SNR大于10 dB后MSE均小于0.1且变化很小。因此,当脉压后回波数据SNR大于10 dB时,SDPSA算法可良好实现稀疏自聚焦成像。对于LASAR原始回波数据,通常其脉冲压缩后回波数据SNR可优于10 dB,满足SDPSA算法稀疏自聚焦成像要求。图4(b)给出了回波数据SNR为20 dB,全部、50%和25%回波数据量时SDPSA算法MSE随迭代次数变化曲线,可知全部数据成像时5次迭代后基本收敛,而在50%和25%回波数据时10次迭代后基本收敛,此时算法MSE均小于0.1。
|
图 4 SDPSA算法MSE变化曲线 Fig.4 The MSE curve of SDPSA |
为了进一步验证本文SDPSA算法的有效性,利用本课题组地基等效LASAR实验系统获取的实测数据进行稀疏自聚焦成像分析。地基等效LASAR实验系统实物图如图5(a)所示,系统主要参数如下:雷达中心频率

|
图 5 地基等效LASAR成像实验 Fig.5 The ground-based LASAR experiment |
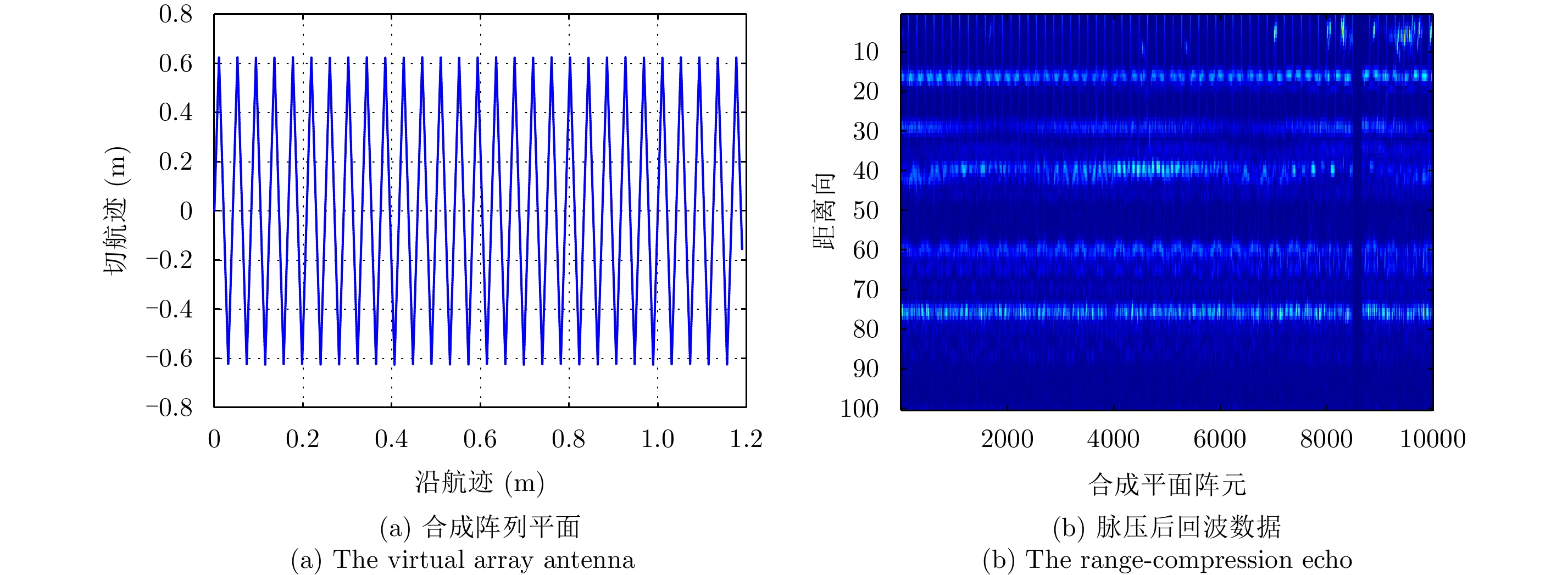
图6(a)给出了实验系统天线扫描的2维轨迹,可等效为一个虚拟的2维天线阵列,此虚拟阵列大小为1.25 m×1.25 m,阵列的阵元个数为10416,此时观测区域成像不会出现栅瓣。图6(b)为图6(a)对应的脉压后回波数据,其中球1回波对应于第18个距离单元数据、球2和球3对应于第29个距离单元数据,路灯对应于第76个距离单元数据。为了分析测量阵元样本数对压缩感知LASAR稀疏自聚焦成像的影响,本节图6(b)选择
|
图 6 地基LASAR合成阵列平面及回波数据 Fig.6 The virtual array antenna and the echo of the ground-based LSAR |
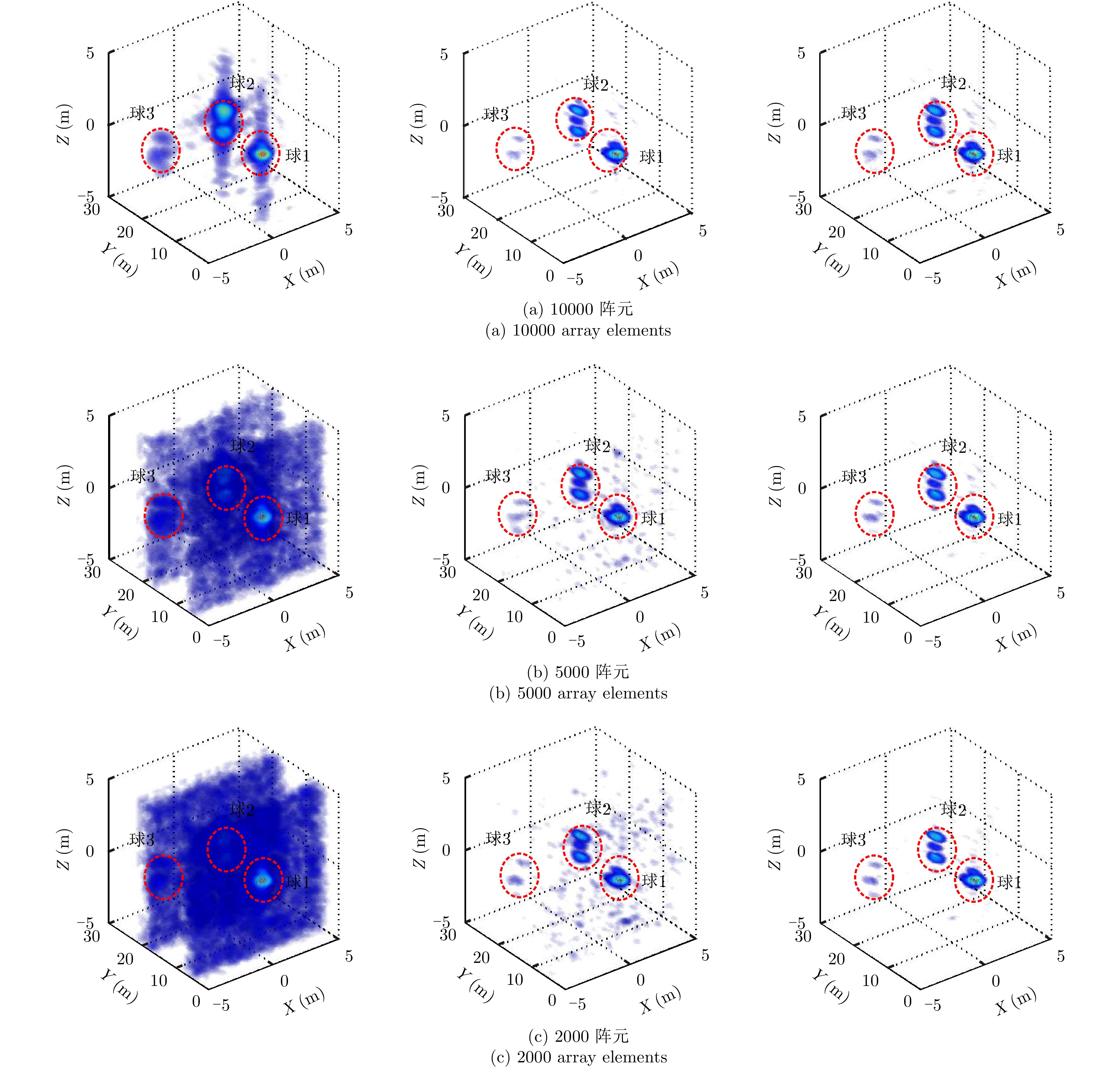
图7给出了10000, 5000和2000阵元回波数据条件下采用BP-PGA, IRLS-PGA及本文SDPSA算法获得的实验球目标自聚焦成像结果,其中图像已归一化且显示门限为最大值–25 dB。从图7成像结果看出,在10000个阵元回波数据时3种算法对3个参考球目标均能良好自聚焦成像,且IRLS-PGA算法和本文SDPSA算法结果相似,说明PGA算法和本文算法在10000个阵元回波数据时自聚焦性能相当。但是,在5000和2000阵元回波数据成像时,BP-PGA算法出现严重旁瓣干扰,3个参考球目标在X-Z平面存在很高的旁瓣串扰;IRLS-PGA算法在球体目标周围出现虚假目标,且2000阵元样本时结果更加恶化,说明PGA自聚焦算法在数据欠采样时相位误差估计精度下降,并且随着样本数减少自聚焦性能变差。然而,SDPSA算法在5000和2000稀疏阵元样本时,成像结果与10000阵元基本一致,较IRLS-PGA算法结果大大抑制了虚假目标,说明SDPSA算法的相位误差估计性能优于PGA算法,在稀疏欠采样数据时仍可良好实现LASAR相位误差估计和校正。
|
图 7 球目标实测数据稀疏自聚焦成像结果(左:BP-PGA算法;中:IRLS-PGA算法;右:SDPSA算法) Fig.7 The sparse autofocusing results of the experimental balls data (Left: BP-PGA; Middle: IRLS-PGA; Right: SDPSA) |
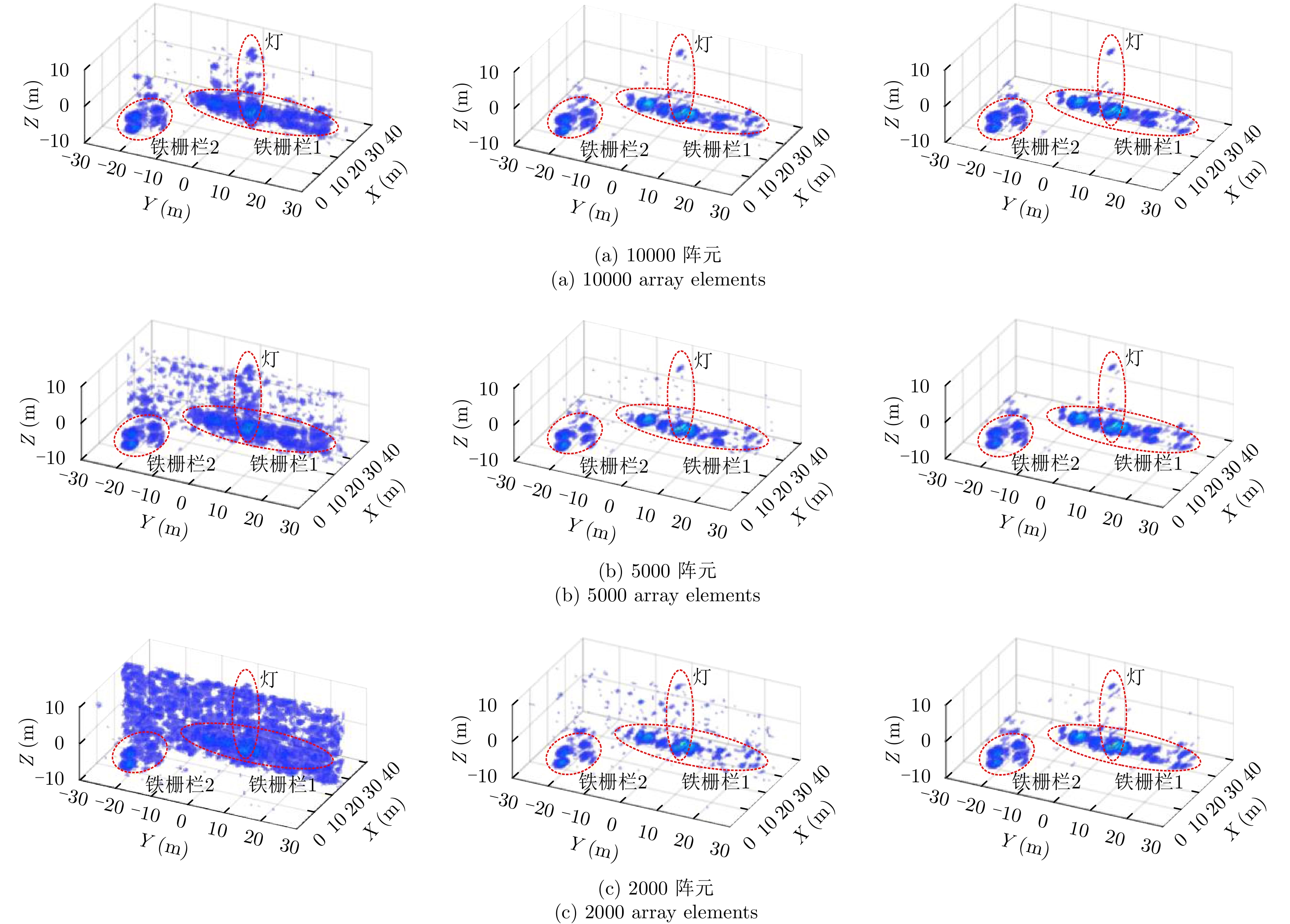
图8给出了10000, 5000和2000阵元回波数据条件下采用BP-PGA, IRLS-PGA及本文SDPSA算法获得的路灯铁栅栏目标自聚焦成像结果,其中图像已归一化且显示门限为最大值–20 dB。从图8成像结果看出,相对传统BP-PGA和IRLS-PGA算法,SDPSA算法在10000, 5000和2000阵元样本时对路灯和铁栅栏目标成像均有明显提升,同样验证了SDPSA算法稀疏自聚焦性能优于传统PGA算法,在稀疏阵元采样数据时可实现LASAR相位误差估计和校正。综上,地基LASAR实测数据实验结果验证了本文SDPSA算法的有效性。
|
图 8 路灯目标实测数据稀疏自聚焦成像结果(左:BP-PGA算法;中:IRLS-PGA算法;右:SDPSA算法) Fig.8 The sparse autofocusing results of the experimental light data(Left: BP-PGA; Middle: IRLS-PGA; Right: SDPSA) |
本文提出了一种基于半正定规划的压缩感知LASAR自聚焦3维成像算法。该SDPSA方法结合LASAR压缩感知成像原理及最小均方误差准则,利用松弛半正定规划方法及迭代最优方法估计相位误差,实现压缩感知LASAR的高精度自聚焦成像,并且为了进一步提高自聚焦算法运算效率,通过主散射目标区域进行相位误差估计。仿真数据和实测数据验证了本文SDPSA算法的有效性,实验结果说明相对于传统PGA自聚焦算法,SDPSA算法在稀疏采样数据条件下具备更好的稀疏自聚焦成像结果,可为LASAR 3维成像技术实际应用提供技术途径。在未来工作中,可开展算法优化研究,进一步提升SDPSA算法的运算效率。
| [1] |
Du L, Wang Y P, Hong W, et al. A three-dimensional range migration algorithm for downward-looking 3D-SAR with single-transmitting and multiple-receiving linear array antennas[J].
EURASIP Journal on Advances in Signal Processing, 2010, 2010: 957916 DOI:10.1155/2010/957916 ( 0) 0)
|
| [2] |
Liao K F, Zhang X L, and Shi J. Plane-wave synthesis and RCS extraction via 3-D linear array SAR[J].
IEEE Antennas and Wireless Propagation Letters, 2015, 14: 994-997. DOI:10.1109/LAWP.2015.2389264 ( 0) 0)
|
| [3] |
Han K Y, Wang Y P, Tan W X, et al. Efficient pseudopolar format algorithm for down-looking linear-array SAR 3-D imaging[J].
IEEE Geoscience and Remote Sensing Letters, 2015, 12(3): 572-576. DOI:10.1109/LGRS.2014.2351792 ( 0) 0)
|
| [4] |
Zhang S Q, Zhu Y T, and Kuang G Y. Imaging of downward-looking linear array three-dimensional SAR based on FFT-MUSIC[J].
IEEE Geoscience and Remote Sensing Letters, 2015, 12(4): 885-889. DOI:10.1109/LGRS.2014.2365611 ( 0) 0)
|
| [5] |
Wei S J, Zhang X L, and Shi J. Linear array SAR imaging via compressed sensing[J].
Progress In Electromagnetics Research, 2011, 117: 299-319. DOI:10.2528/PIER11033105 ( 0) 0)
|
| [6] |
Zhang S Q, Zhu Y T, Dong G G, et al. Truncated SVD-based compressive sensing for downward-looking three-dimensional SAR imaging with uniform/nonuniform linear array[J].
IEEE Geoscience and Remote Sensing Letters, 2015, 12(9): 1853-1857. DOI:10.1109/LGRS.2015.2431254 ( 0) 0)
|
| [7] |
Zhang S Q, Dong G G, Kuang G Y, et al. Superresolution downward-looking linear array three-dimensional SAR imaging based on two-dimensional compressive sensing[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(6): 2184-2196. DOI:10.1109/JSTARS.2016.2549548 ( 0) 0)
|
| [8] |
Peng X M, Tan W X, Hong W, et al. Airborne DLSLA 3-D SAR image reconstruction by combination of polar formatting and L1 regularization[J].
IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(1): 213-226. DOI:10.1109/TGRS.2015.2453202 ( 0) 0)
|
| [9] |
Tian J H, Sun J P, Han X, et al.. Motion compensation for compressive sensing SAR imaging with autofocus[C]. Proceedings of the 6th IEEE Conference on Industrial Electronics and Applications (ICIEA), Beijing, China, 2011: 1564–1567. DOI: 10.1109/ICIEA.2011.5975839.
( 0) 0)
|
| [10] |
Cetin M, Stojanovic I, Onhon O, et al. Sparsity-driven synthetic aperture radar imaging: Reconstruction, autofocusing, moving targets, and compressed sensing[J].
IEEE Signal Processing Magazine, 2014, 31(4): 27-40. DOI:10.1109/MSP.2014.2312834 ( 0) 0)
|
| [11] |
Onhon N Ö and Cetin M. A sparsity-driven approach for joint SAR imaging and phase error correction[J].
IEEE Transactions on Image Processing, 2012, 21(4): 2075-2088. DOI:10.1109/TIP.2011.2179056 ( 0) 0)
|
| [12] |
Zhe Z, Yao Z, Jiang C L, et al.. Autofocus of sparse microwave imaging radar based on phase recovery[C]. Proceedings of 2013 IEEE International Conference on Signal Processing, Communication and Computing (ICSPCC), Kunming, China, 2013: 1–5. DOI: 10.1109/ICSPCC.2013.6663989.
( 0) 0)
|
| [13] |
Chen Y C, Li G, Zhang Q, et al. Motion compensation for airborne SAR via parametric sparse representation[J].
IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(1): 551-562. DOI:10.1109/TGRS.2016.2611522 ( 0) 0)
|
| [14] |
Camlica S, Gurbuz A C, Arikan O, et al. Autofocused spotlight SAR image reconstruction of off-grid sparse scenes[J].
IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(4): 1880-1892. DOI:10.1109/TAES.2017.2675138 ( 0) 0)
|
| [15] |
Uḡur S and Arıkan O. SAR image reconstruction and autofocus by compressed sensing[J].
Digital Signal Processing, 2012, 22(6): 923-932. DOI:10.1016/j.dsp.2012.07.011 ( 0) 0)
|
| [16] |
Kelly S, Yaghoobi M, and Davies M. Sparsity-based autofocus for undersampled synthetic aperture radar[J].
IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 972-986. DOI:10.1109/TAES.2014.120502 ( 0) 0)
|
| [17] |
Uḡur S, Arıkan O, and Gürbüz A C. Off-grid sparse SAR image reconstruction by EMMP algorithm[C]. Proceedings of 2013 IEEE Radar Conference (RADAR), Ottawa, ON, Canada, 2013: 1–4. DOI: 10.1109/RADAR.2013.6586034.
( 0) 0)
|
| [18] |
Wei S J and Zhang X L. Sparse autofocus recovery for under-sampled linear array SAR 3-D imaging[J].
Progress In Electromagnetics Research, 2013, 140: 43-62. DOI:10.2528/PIER13020614 ( 0) 0)
|
| [19] |
Wei S J, Zhang X L, and Shi J. Sparse autofocus via Bayesian learning iterative maximum and applied for LASAR 3-D imaging[C]. Proceedings of 2014 IEEE Radar Conference, Cincinnati, OH, USA, 2014: 666–669. DOI: 10.1109/RADAR.2014.6875674.
( 0) 0)
|
| [20] |
Donoho D L. Compressed sensing[J].
IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 ( 0) 0)
|
| [21] |
Figueiredo M A T, Nowak R D, and Wright S J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems[J].
IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 586-597. DOI:10.1109/JSTSP.2007.910281 ( 0) 0)
|
| [22] |
Ji S H, Xue Y, and Carin L. Bayesian compressive sensing[J].
IEEE Transactions on Signal Processing, 2008, 56(6): 2346-2356. DOI:10.1109/TSP.2007.914345 ( 0) 0)
|
| [23] |
Grant M and Boyd S. CVX: Matlab software for disciplined convex programming, version 1.21[R]. CVX Research, Inc., 2010. Available from: URL: http://cvxr.com/cvx.
( 0) 0)
|
| [24] |
Toh K C, Todd M J, and Tütüncü R H. SDPT3—A Matlab software package for semidefinite programming, version 1.3[J].
Optimization Methods and Software, 1999, 11(1/4): 545-581. DOI:10.1080/10556789908805762 ( 0) 0)
|
| [25] |
Liu K H, Wiesel A, and Munson D C. Synthetic aperture radar autofocus via semidefinite relaxation[J].
IEEE Transactions on Image Processing, 2013, 22(6): 2317-2326. DOI:10.1109/TIP.2013.2249084 ( 0) 0)
|




