近年来关于太赫兹的研究日趋增加,相对于微波频段雷达,太赫兹雷达以其更高的空间分辨率和角分辨率具有更大的优势受到了越来越多的重视[1,2]。太赫兹辐射的光子能量低,对穿透物不会造成损伤,并且可以穿过大多数介电物质,实现无损检测。太赫兹波具有穿透性,能够实现对隐蔽物体的有效检测,可应用于安检相关的领域。太赫兹频段相比于微波频段频率更高,更容易发射大带宽信号,具有更高的分辨率,具有海量的频谱资源,可用于超宽带超高速无线通信。太赫兹波段目标表面的细微结构、粗糙度等细节会显著影响其后向散射特性,实现更小尺寸目标的探测、更精确目标的运动与物理参数反演[3]。太赫兹(terahertz, THz)波段位于微波与红外波之间,其频率范围为0.1~10 THz (1 THz=1012 Hz),对应的波长为30 μm~3 mm。太赫兹频段目标散射特性是太赫兹雷达探测和成像应用的物理基础[4,5],同时也是太赫兹雷达系统进行链路设计、特征提取以及成像算法的重要依据。国内首都师范大学太赫兹实验室研制了太赫兹数字全息成像系统,对太赫兹电磁波的振幅、相位、频率及偏振等全部光学信息的3维空间分布进行精确测量[6]。针对太赫兹波段目标的散射特性,美国麻省LOWELL大学毫米波实验室利用1.56 THz源在紧缩场中对粗糙表面圆柱体的目标散射特性进行了研究[4]。天津大学太赫兹研究中心搭建了以0.2 THz返波管振荡器源、热释电探测器、小型自动旋转光学平台等组成的太赫兹波目标散射特性实验测试系统,并对粗糙铜面的散射特性等进行了研究[7,8]。对于介质[9]和涂覆目标的太赫兹散射,北京航空航天大学江月松等人考虑粗糙度修正表面的散射系数研究了基于经验公式的涂覆目标的太赫兹散射特性[10]。
本文区别于以往采用经验公式[10]以粗糙度修正散射系数的研究方法,把随机粗糙面的建模理念应用到太赫兹波段表面粗糙目标的建模中。首先模拟生成了分形粗糙面近似代替实际复杂的粗糙面,对生成的分形粗糙面进行坐标变换导入计算机辅助设计(Computer Aided Design, CAD)建模软件建立具有粗糙表面的目标模型;然后对表面粗糙目标按照入射波的频率以满足物理光学近似的要求进行剖分。根据菲涅尔反射系数求得表面电流进而计算涂覆粗糙目标的雷达散射截面(Radar Cross Section, RCS)。并针对不同频率以及不同涂覆厚度的表面粗糙涂覆目标,分别进行了仿真分析。
2 表面粗糙目标模型 2.1 分形粗糙面自1982年Mandelbrot首次提出“分形”的概念[11],指的是组成部分与整体以某种方式相形似,分形理论就在很多领域中得到应用。“分形”不同于通常意义上的长度、面积、体积等几何概念,分形内部的任何一个相对独立的部分,在一定程度上都应该是整体的再现和缩影,分形几何体内部存在无穷层次、具有见微知著、由点及面的自相似结构,即具有自相似性。由于粗糙面一般具有非线性的几何结构,因此采用非线性的方法模拟粗糙面更能反映其物理本质。自然界的许多物体,如地、海表面、植被和森林等都在一定尺度范围内存在统计意义上的自相似性,由此很多学者将分形理论应用于电磁散射领域中,用于粗糙面的模拟[12,13]。
1维带限Weierstrass-Mandelbrot分形函数的表达式为:
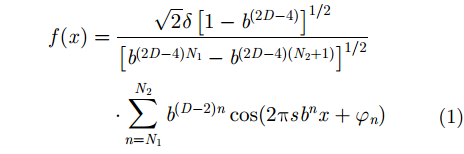
|
其中,
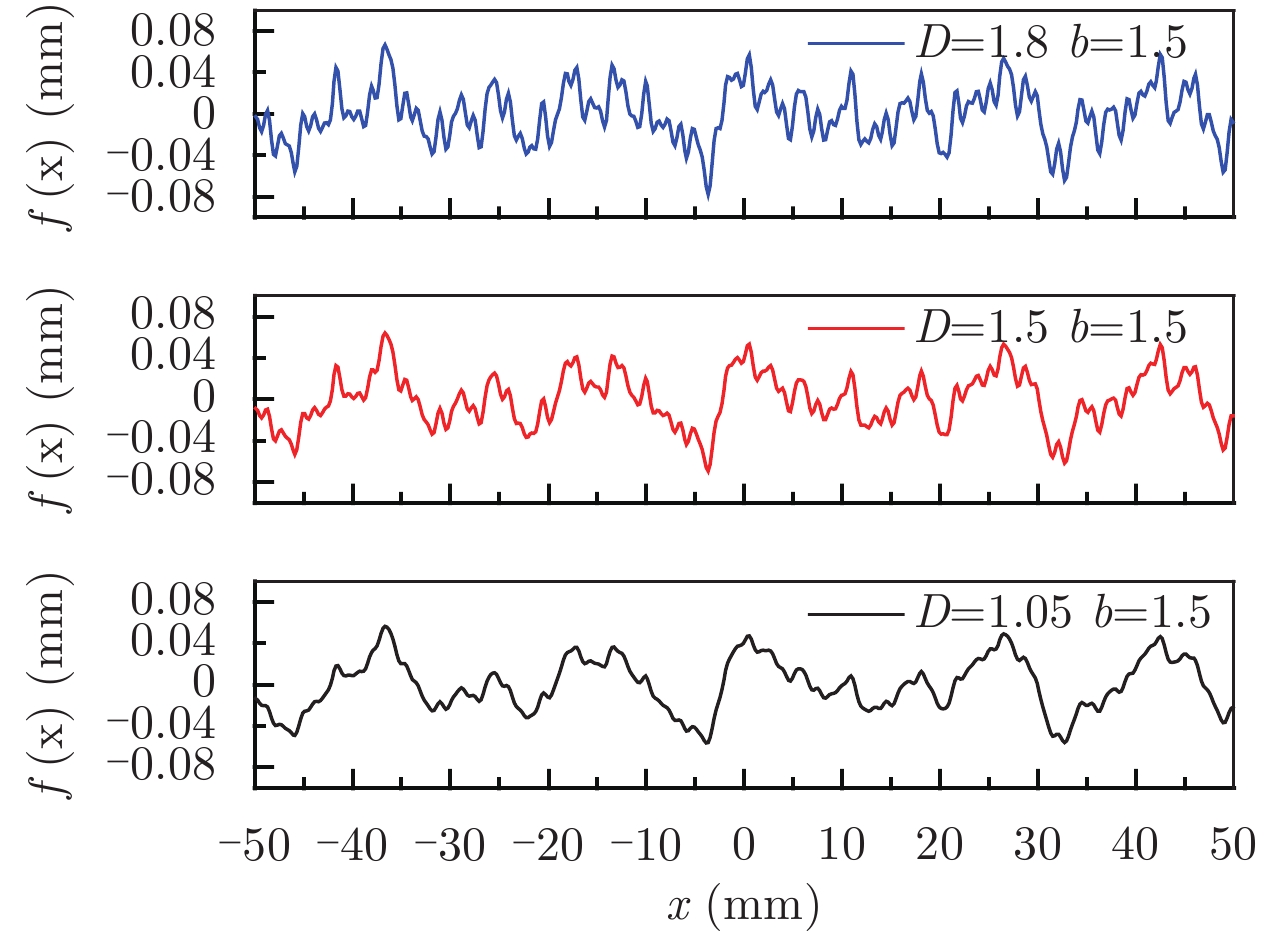
|
图 1 1维分形粗糙面 Fig.1 One dimensional fractal rough surface |
目标表面粗糙度引起的表面起伏一般在其对应的光滑表面的法线方向[14]。因此,对于轴对称旋转目标而言,其表面的粗糙度可近似考虑为对应母线的起伏。将生成的1维分形粗糙面叠加到光滑目标模型对应的母线进行坐标变换,建立具有分形粗糙表面的目标模型。
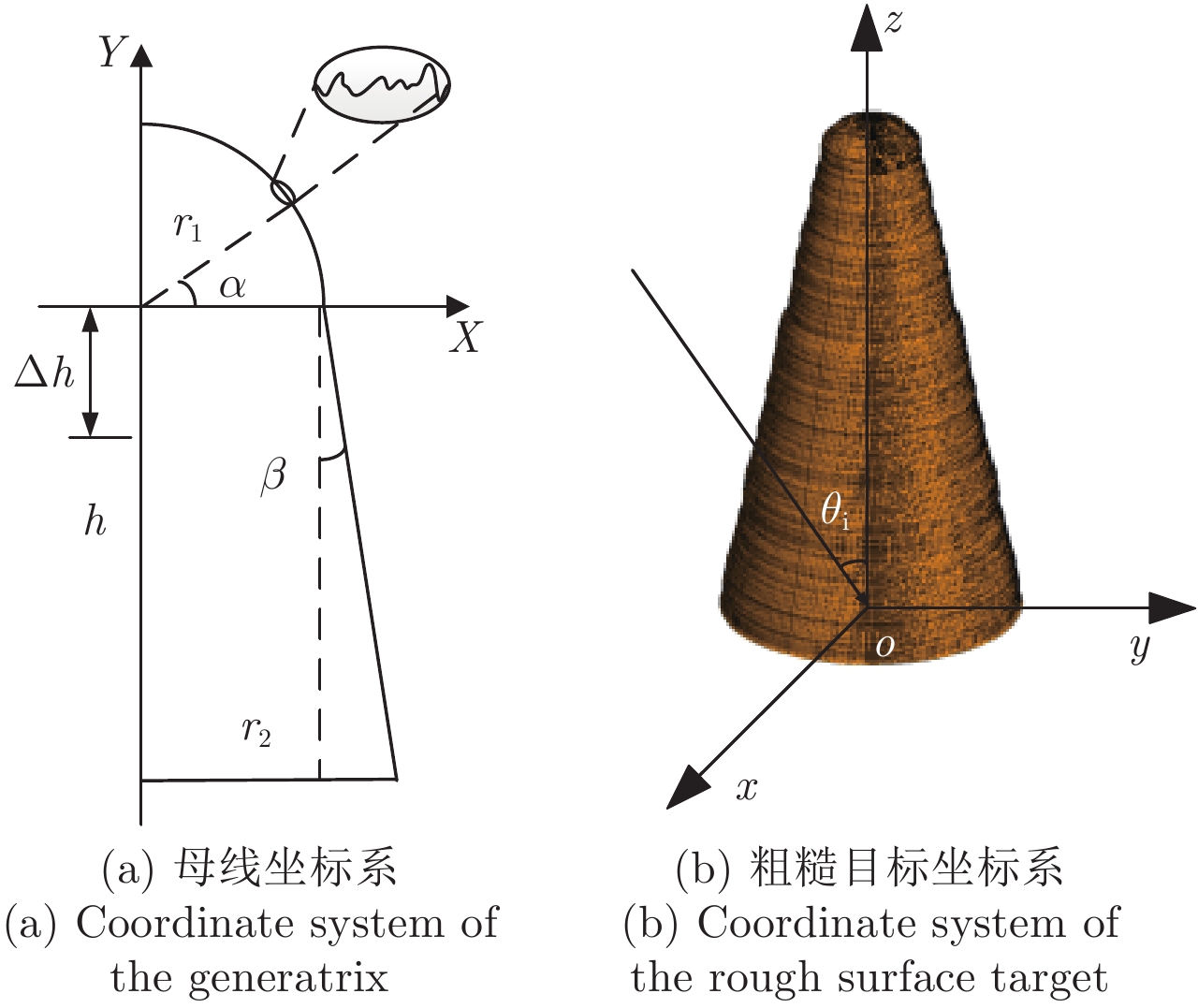
|
图 2 表面分形粗糙钝锥模型 Fig.2 The roughness surface targets model |
对于如图2(a)所示的顶部为半球的粗糙钝锥模型,其母线可以表示为:
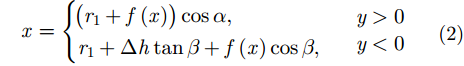
|
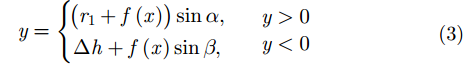
|
其中,r1为顶部半球半径,r2为底面半径,h为下部锥台高度,
由Stratton-Chu积分公式,目标远区散射场利用物理光学可表示为[15]:
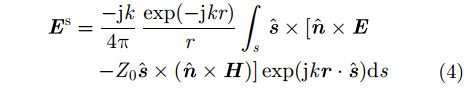
|
其中,k和Z0分别为自由空间的波数和本征阻抗,
|
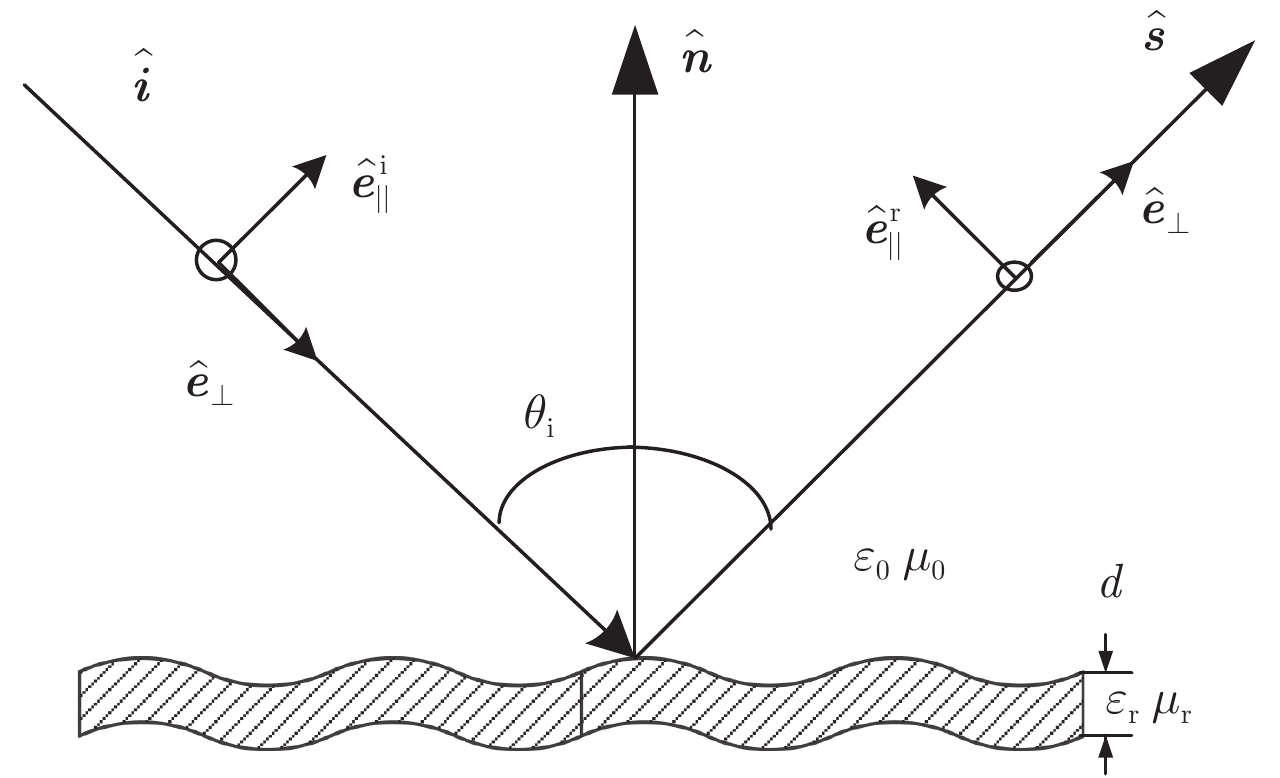
图 3 表面涂覆目标示意图 Fig.3 Local coordinate systems for PO calculation with coating dielectric |
涂覆介质表面的散射示意图如图3所示。其中
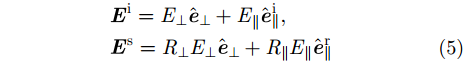
|
其中,
涂覆目标雷达散射截面的计算公式为:
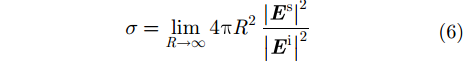
|
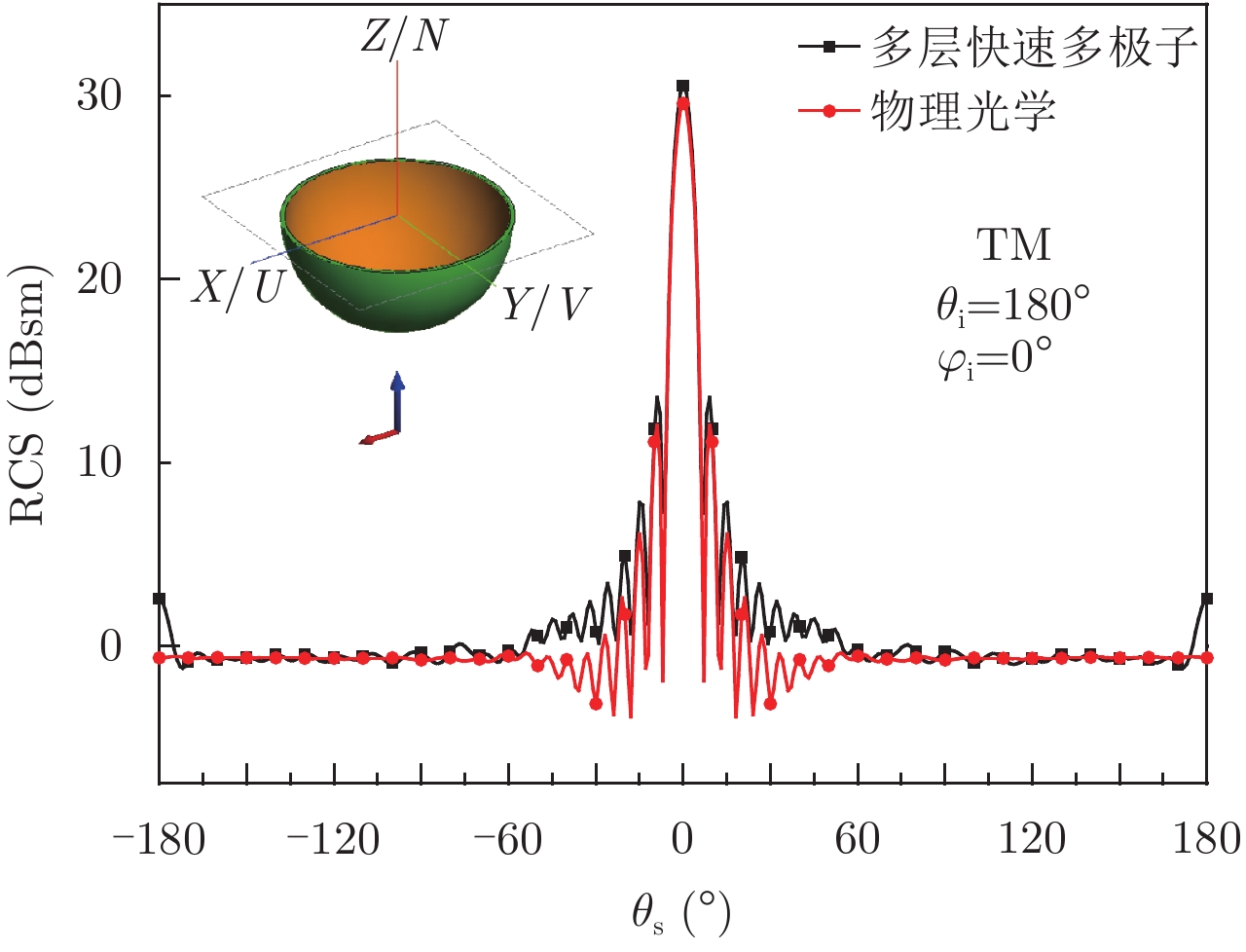
为了验证算法的正确性,先通过下面的模型算例加以说明。图4给出了3 GHz平面波TM极化入射下涂覆半球的双站雷达散射截面,其中半球的半径为0.5 m,涂覆厚度为d=2 cm,涂层介质相对介电常数为
|
图 4 涂覆半球模型双站RCS Fig.4 Bistatic RCS of the verification models |
|
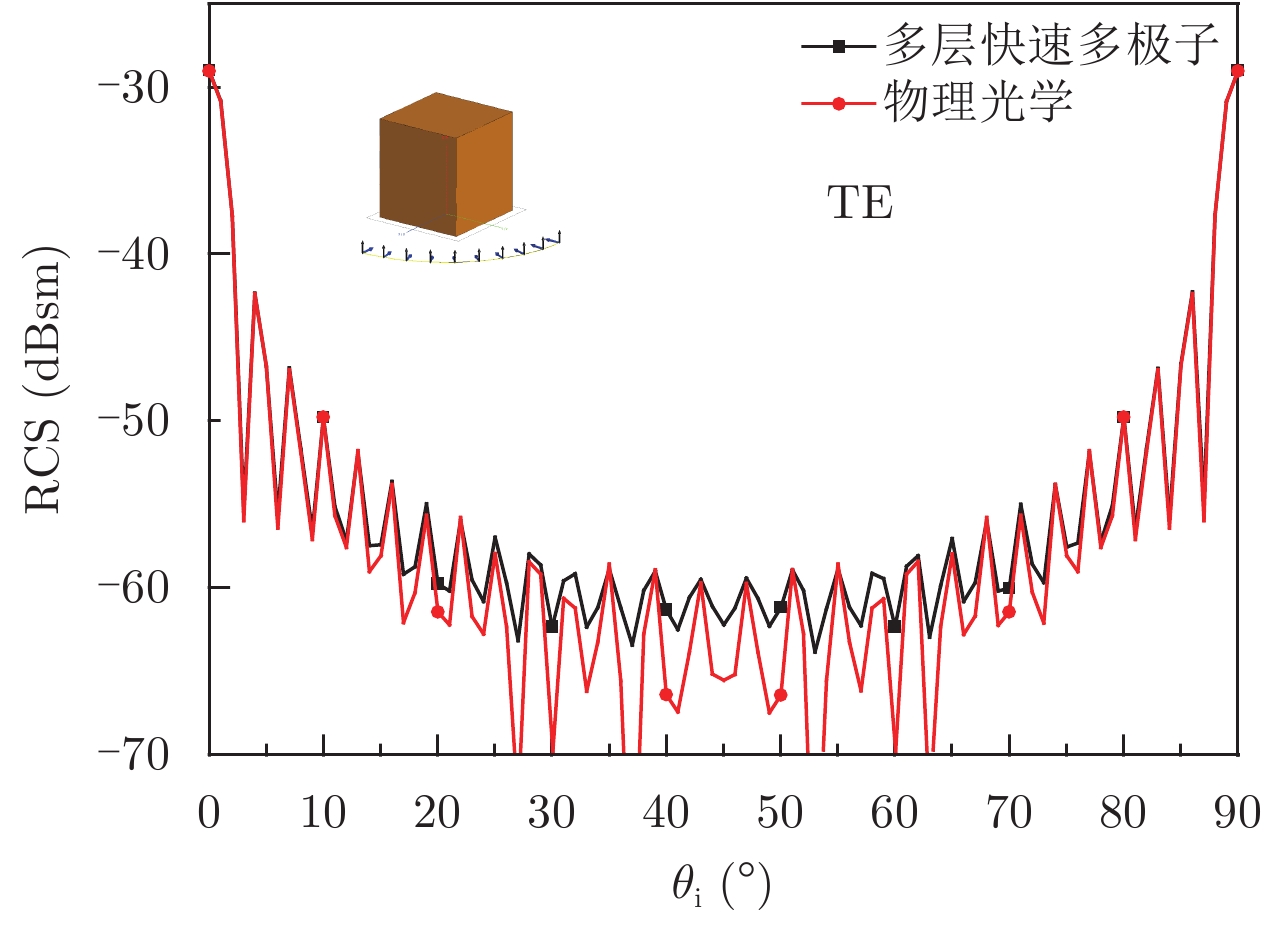
图 5 导体立方体模型单站RCS Fig.5 Mono-static RCS of the PEC cube model |
图5给出了频率为3 THz的平面波入射下导体立方体的单站雷达散射截面,结果与文献[3]中采用多层快速多极子方法结果一致,可以看出物理光学方法用于计算THz频段目标散射的有效性。
3.2 数值结果对于图2(b)所示的具有分形粗糙表面的钝锥模型,其顶部半球半径r1=1 mm,底面半径r2=3 mm,锥台高度h=12 mm,分形粗糙面的分维数D=1.5,b=1.5,均方根高度

|
图 6 钝锥模型单站RCS Fig.6 Mono-static RCS of the coated blunt cone model with different incident frequency |
从图6中结果可以看出,对于模型尺寸相同的光滑钝锥与表面粗糙钝锥的单站雷达散射截面曲线走势基本一致,随着入射角的增大,RCS增大,垂直于锥面照射时达到最大峰值。图6(a)入射频率为30 GHz的情况下光滑钝锥与分形粗糙钝锥的RCS除了小角度基本上重合,可以看出在微波频段目标表面的微粗糙度对RCS的影响很小,可以忽略。图6(b)、图6(c)表明太赫兹波段下光滑钝锥和分形粗糙钝锥目标雷达散射截面出现差异,表面的分形粗糙度引起目标RCS曲线震荡起伏,且频率越高起伏越明显,曲线波动越大。因此在太赫兹波段,目标表面的粗糙度对其散射特性的影响需要考虑。
|
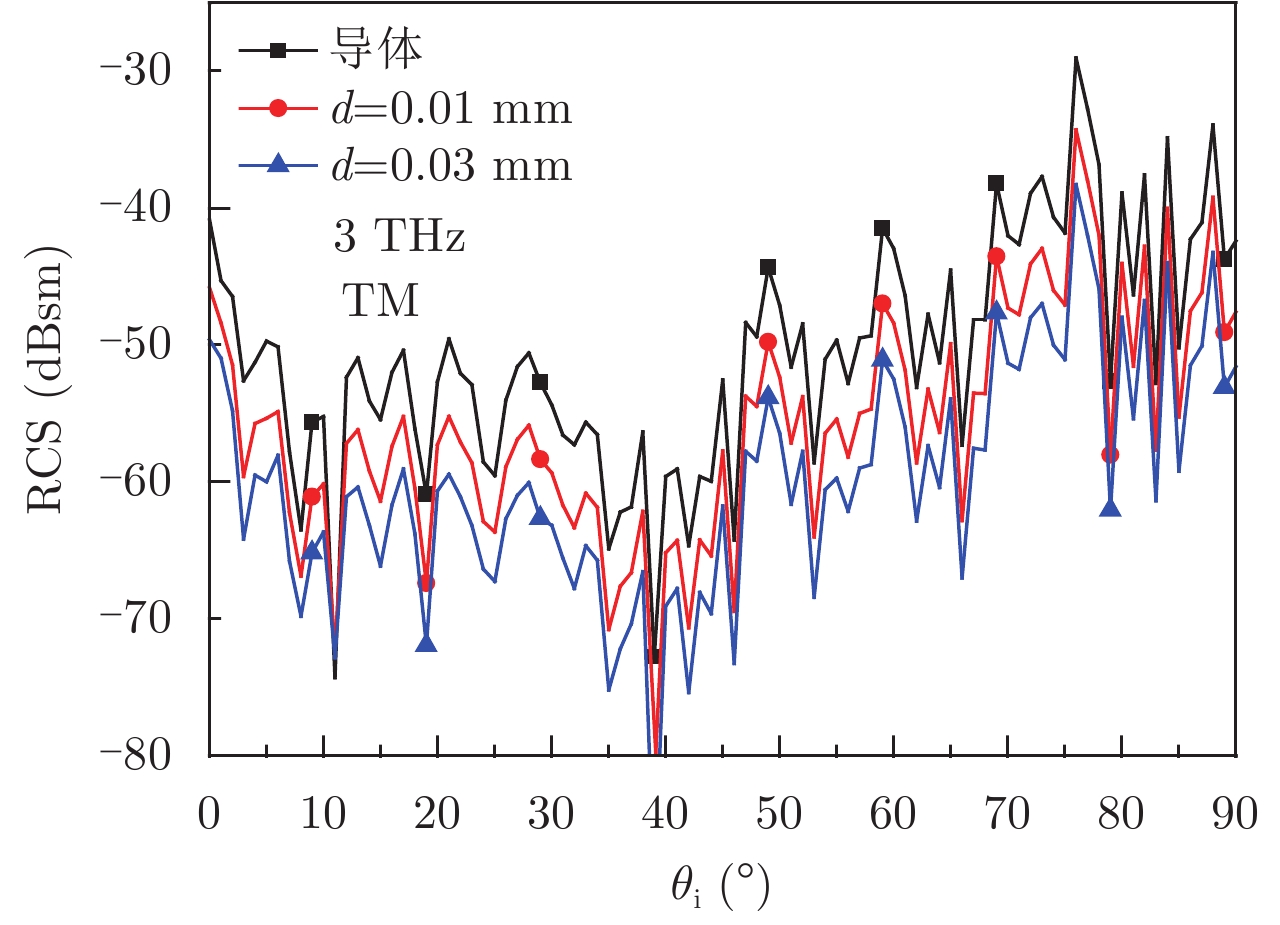
图 7 不同涂覆厚度的钝锥单站RCS Fig.7 Mono-static RCS of the blunt cone models coated with different thicknesses |
图7给出了入射波频率为3 THz的不同涂层厚度的粗糙表面目标的后向RCS。可以看出相对于表面为导体的情况,涂覆介质以后,钝锥目标的雷达散射截面几乎在所有角度都有明显减小,并且随着涂层厚度的增大,雷达散射截面持续减小。涂覆介质层对雷达散射截面的缩减有明显的作用,在一定范围内随着涂层厚度的增大,涂覆介质对电磁波的吸收增加表面粗糙钝锥的后向RCS减小。
|
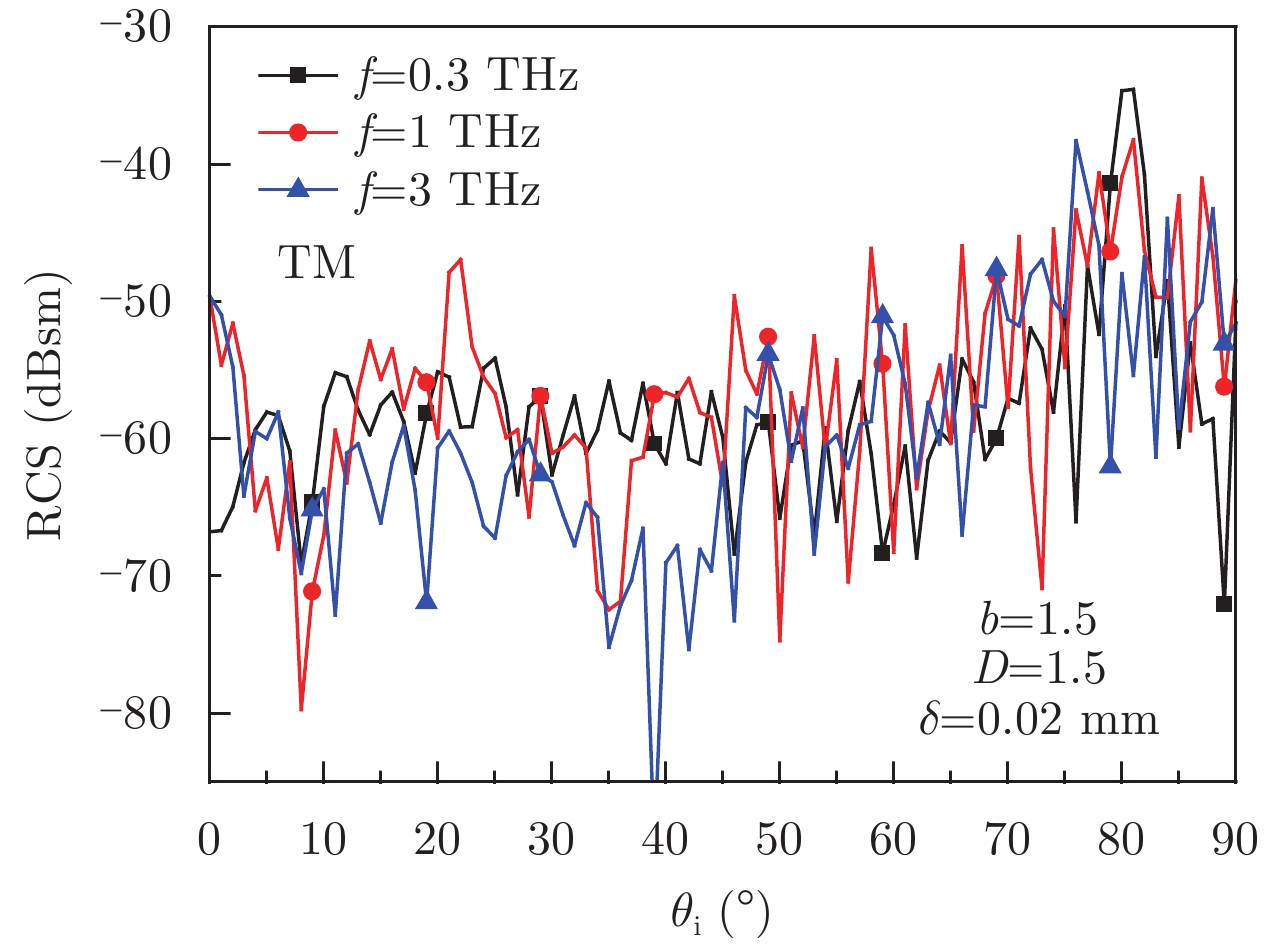
图 8 不同入射频率钝锥模型单站RCS Fig.8 Mono-static RCS of the coating blunt cone models with different incident frequency |
图8给出了不同入射频率下钝锥单站RCS。随着频率的升高,表面粗糙钝锥的后向RCS多数角度下降,且频率越高RCS值下降得越多。随着频率的增大,入射波的波长变小,目标表面的粗糙度与入射波长的比值增大,粗糙度引起的漫散射效应增大,目标RCS受到表面粗糙度的影响,曲线峰值变得不明显。
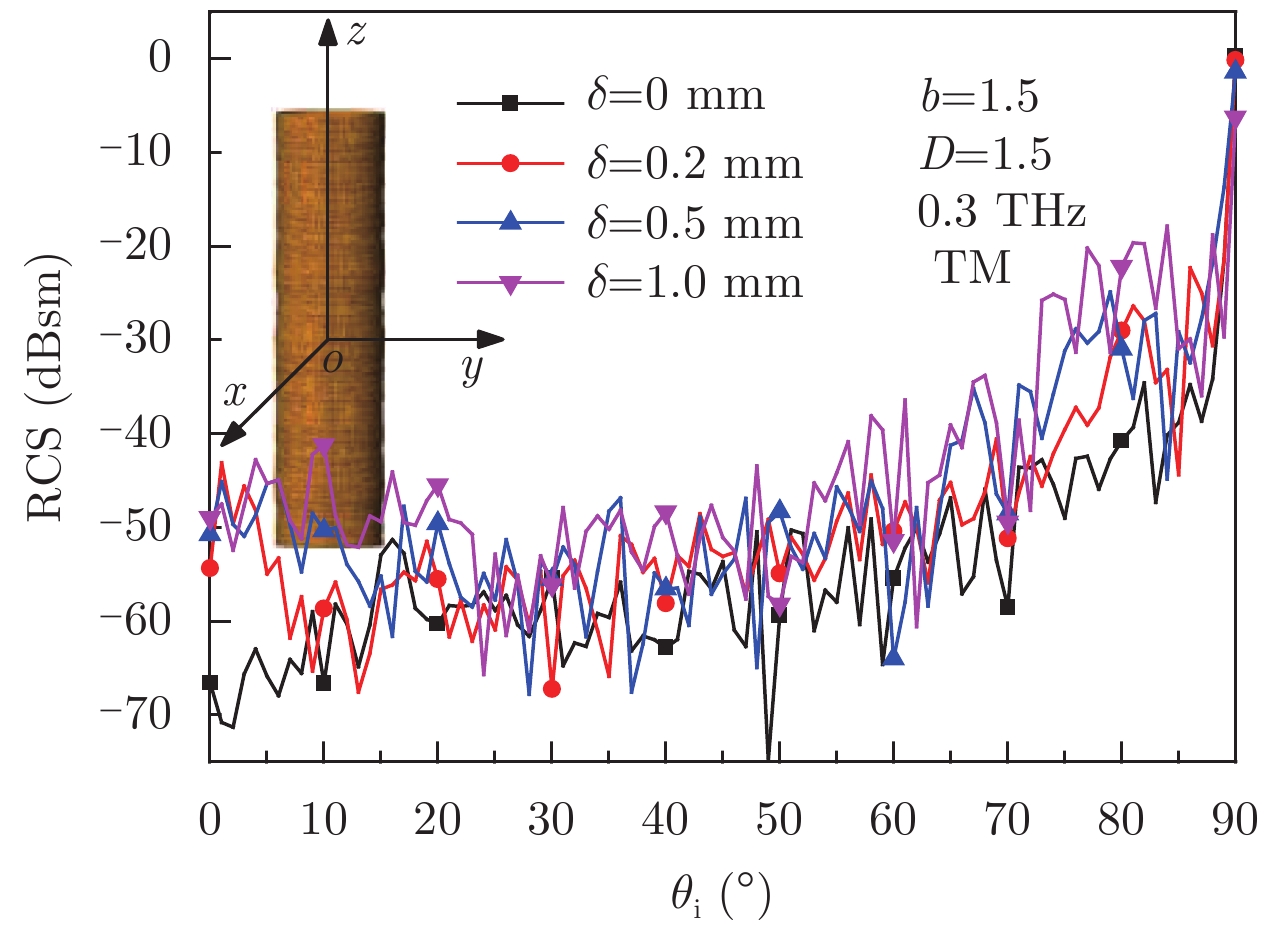
图9给出了不同表面粗糙度的圆柱模型单站雷达散射截面,其半径为r=16.25 mm,高度为h=102 mm,入射波频率为0.3 THz。
|
图 9 不同粗糙度圆柱模型单站RCS
Fig.9 Mono-static RCS of the cylinder models with different
|
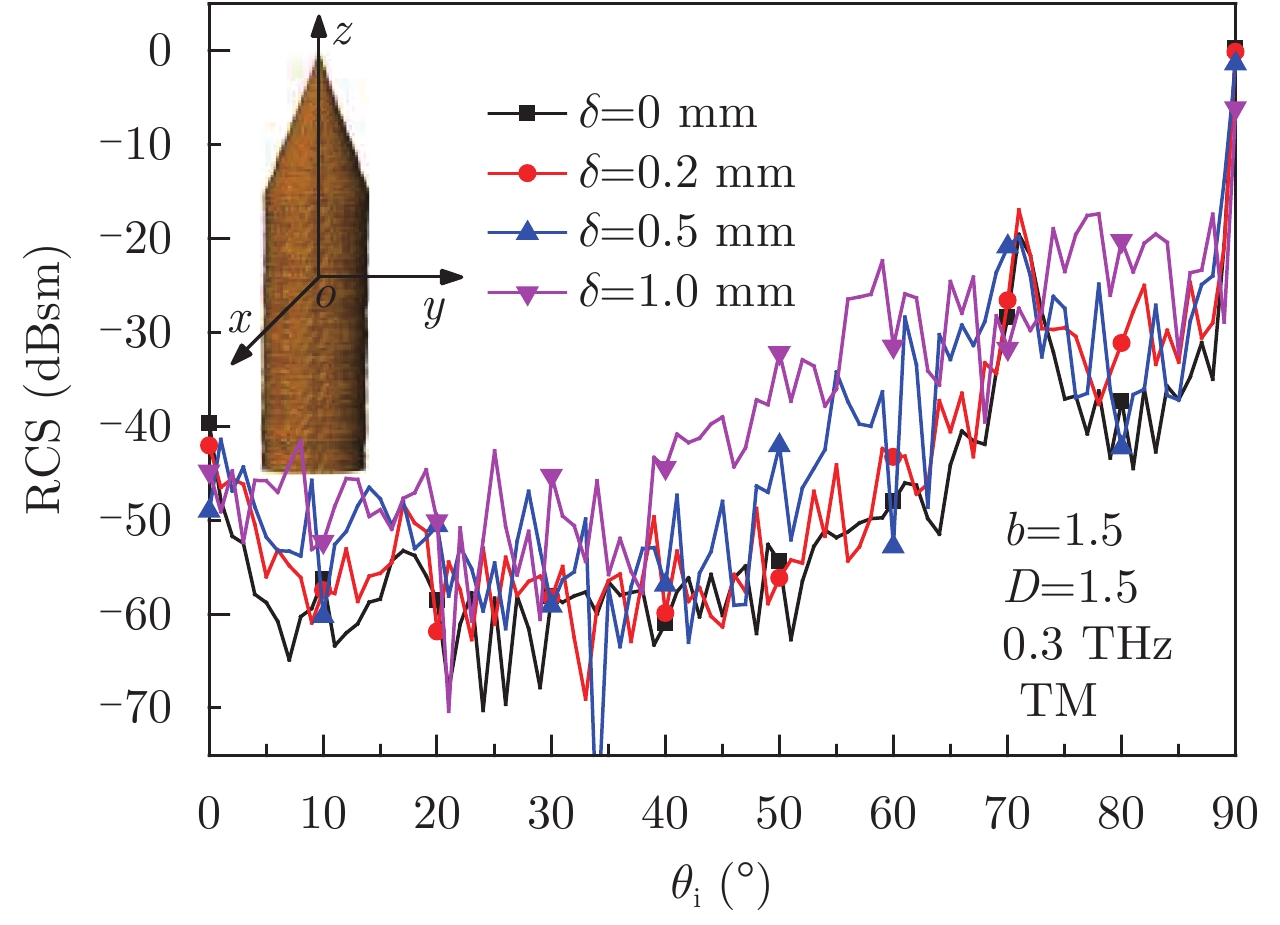
图10给出了不同表面粗糙度的锥柱模型单站雷达散射截面,半径r=16.25 mm,顶部圆锥高度h1=48.5 mm,底部圆柱部分高度h2=102 mm,入射波频率为0.3 THz。从图9和图10给出的结果可以看出,随着均方根高度的增加,目标表面的粗糙度变大,相对于0.3 THz的入射波其波长仅有1 mm,目标更加粗糙,粗糙度对目标的散射结果影响增大。当粗糙度较小时,RCS曲线可以看作是在光滑模型散射结果叠加小起伏震荡;粗糙度增大以后由表面粗糙度引起的RCS起伏甚至在某些角度可以改变光滑模型的散射曲线。
|
图 10 不同粗糙度锥柱模型单站RCS
Fig.10 Mono-static RCS of the cone-cylinder models with different
|
本文参考分形粗糙面模拟随机环境的方法来建立具有分形粗糙表面目标,采用基于基尔霍夫近似的物理光学方法研究了涂覆目标的太赫兹散射特性。分析了不同的入射波频率以及不同涂层厚度的分形粗糙表面模型在太赫兹波段的散射特性。相对于微波频段波长远大于目标表面微米量级的粗糙度,粗糙度的影响可以不考虑,而在太赫兹波段,波长与粗糙度处于等量级,必须考虑到粗糙度对于目标散射结果的影响。目标表面有涂覆介质材料时,目标的雷达散射截面小于导体情况下的结果,且在一定的范围内涂覆层越厚,目标雷达散射截面吸收越明显。
| [1] |
Episkopou E, Papantonis S, Otter W J, et al.. Defining material parameters in commercial EM solvers for arbitrary metal-based THz structures[J].
IEEE Transactions on Terahertz Science and Technology, 2012, 2(5): 513-524. DOI:10.1109/TTHZ.2012.2208456 ( 0) 0)
|
| [2] |
Kirley M P and Booske J H. Terahertz conductivity of copper surfaces[J].
IEEE Transactions on Terahertz Science and Technology, 2015, 5(6): 1012-1020. DOI:10.1109/TTHZ.2015.2468074 ( 0) 0)
|
| [3] |
Li Z, Cui T J, Zhong X J, et al.. Electromagnetic scattering characteristics of PEC targets in the terahertz regime[J].
IEEE Antennas and Propagation Magazine, 2009, 51(1): 39-50. DOI:10.1109/MAP.2009.4939018 ( 0) 0)
|
| [4] |
Danylov A A, Goyette T M, Waldman J, et al.. Terahertz inverse synthetic aperture radar (ISAR) imaging with a quantum cascade laser transmitter[J].
Optics Express, 2010, 18(15): 16264-16272. DOI:10.1364/OE.18.016264 ( 0) 0)
|
| [5] |
Younus A, Desbarats P, Bosio S, et al.. Terahertz dielectric characterisation of photopolymer resin used for fabrication of 3D THz imaging phantoms[J].
Electronics Letters, 2009, 45(13): 702-703. DOI:10.1049/el.2009.0688 ( 0) 0)
|
| [6] |
张存林, 牧凯军. 太赫兹波谱与成像[J].
激光与光电子学进展, 2010, 47(2): 023001 Zhang Cun-lin and Mu Kai-jun. Terahertz spectroscopy and imaging[J]. Laser & Optoelectronics Progress, 2010, 47(2): 023001 (  0) 0)
|
| [7] |
杨洋, 姚建铨, 张镜水, 等. 粗糙铜表面对低频太赫兹波的散射实验[J].
红外与毫米波学报, 2013, 32(1): 36-39, 79. Yang Yang, Yao Jian-quan, Zhang Jing-shui, et al.. Terahertz scattering on rough copper surface[J]. Journal of Infrared and Millimeter Waves, 2013, 32(1): 36-39, 79. DOI:10.3724/SP.J.1010.2013.00036 (  0) 0)
|
| [8] |
杨洋, 景磊. 金属介电常数对雷达目标散射截面的影响[J].
激光与红外, 2013, 43(2): 155-158. Yang Yang and Jing Lei. Impact of the metal permittivity on radar target scattering cross section[J]. Laser & Infrared, 2013, 43(2): 155-158. DOI:10.3969/j.issn.1001-5078.2013.02.008 (  0) 0)
|
| [9] |
程志华, 谢拥军, 马晓东, 等. 介质目标的太赫兹波近场散射特性计算[J].
电子与信息学报, 2015, 37(4): 1002-1007. Cheng Zhi-hua, Xie Yong-jun, Ma Xiao-dong, et al.. Near-field electromagnetic scattering characteristics of dielectric targets in the terahertz regime[J]. Journal of Electronics & Information Technology, 2015, 37(4): 1002-1007. DOI:10.11999/JEIT140807 (  0) 0)
|
| [10] |
江月松, 聂梦瑶, 张崇辉, 等. 粗糙表面涂覆目标的太赫兹波散射特性研究[J].
物理学报, 2015, 64(2): 94-100. Jiang Yue-song, Nie Meng-yao, Zhang Chong-hui, et al.. Terahertz scattering property for the coated object of rough surface[J]. Acta Physica Sinica, 2015, 64(2): 94-100. DOI:10.7498/aps.64.024101 (  0) 0)
|
| [11] |
Mandelbrot B B. The Fractal Geometry of Nature[M]. New York: Macmillan, 1983.
( 0) 0)
|
| [12] |
Michopoulos J G, Young M and Iliopoulos A. A multiphysics theory for the static contact of deformable conductors with fractal rough surfaces[J].
IEEE Transactions on Plasma Science, 2015, 43(5): 1597-1610. DOI:10.1109/TPS.2015.2416980 ( 0) 0)
|
| [13] |
Iodice A, Natale A and Riccio D. Kirchhoff scattering from fractal and classical rough surfaces: Physical interpretation[J].
IEEE Transactions on Antennas and Propagation, 2013, 61(4): 2156-2163. DOI:10.1109/TAP.2012.2236531 ( 0) 0)
|
| [14] |
李昌泽, 童创明, 王童, 等. 不稳定表面粗糙目标的太赫兹波段散射特性分析[J].
强激光与粒子束, 2016, 28(4): 043101 Li Chang-ze, Tong Chuang-ming, Wang Tong, et al.. Analysis of teraherta wave scattering characteristics of unstable rough surface target[J]. High Power Laser and Particle Beams, 2016, 28(4): 043101 DOI:10.11972/j.issn.1001-9014.2016.02.020 (  0) 0)
|
| [15] |
Yin H C, Huang P K, Liu X G, et al.. PO solution for scattering by the complex object coated with anisotropic materials[J].
Journal of Systems Engineering and Electronics, 2003, 14(2): 1-7. ( 0) 0)
|
| [16] |
Li X, Xie Y and Yang R. High-frequency method for scattering from coated targets with electrically large size in half space[J].
IET Microwaves, Antennas & Propagation, 2009, 3(2): 181-186. ( 0) 0)
|




