② (信息感知技术协同创新中心 西安 710077)
② (Collaborative Innovation Center of Information Sensing and Understanding, Xi’an 710077, China)
目标或目标结构部件除过主体平动之外的旋转、振动等微小运动称为微动[1]。微动反映了目标的精细运动信息与结构信息,因此微动特征通常被认为是区分不同目标独一无二的特征。通过从目标回波中提取精细的微动特征,可为目标的分类识别提供可靠依据[2]。近年来,基于目标微动特征提取的空间、空中、地面目标、海面舰船等的分辨与识别技术得到了广泛的研究[3,4]。旋转、振动、进动等微动引起回波的周期性附加多普勒调制,针对这一周期性特征,基于联合时频分布(Joint Time-Frequency Distribution, JTFD)的微动特征提取技术得到了广泛的应用[5–8]。此类方法首先计算目标回波的时频分布,并通过其周期性参数来获得目标的微动特征。由于回波频率时变,因此JTFD的窗长设定应远小于微动周期,同时为了获得精确的微动频率,窗长又需尽可能地涵盖足够多的采样点,可见微动特征提取精度易受窗长影响;此外,JTFD方法对噪声较为敏感,在低信噪比条件下算法鲁棒性难以保证。归一化幅度差函数法与自相关法不受窗长影响,以其简单易行、运算速度快得到了广泛的应用[9,10]。然而,这类方法存在多周期混淆的现象,且微动频率提取精度受到采样频率的制约,不适用于精度要求较高的场合。此外,由于常见周期性运动引起的回波附加多普勒调制,多表现为正弦调频或相位项为多个正弦信号叠加的形式,因此,基于微动回波为正弦调频形式的特征提取技术近年来也得到了发展。Hough变换是微多普勒特征提取较为有效的方法之一,它通过谱图域提取曲线参数信息,再通过换算至正弦域得到目标的微多普勒特征[11,12]。
以上方法主要针对孤立目标回波进行微动特征提取,然而在实际场景中常常面临由多个目标组成的群目标,此时以上方法将不再适用。对于群目标回波,正弦调频傅里叶变换通过将回波分解在正交三角函数基上计算出回波的微动频谱[13],从而能够完成两个微动目标的回波频率提取,然而对于3个或3个以上的目标其频谱将出现干扰项,难以获得准确的微动频率[14]。近年来,由于Bessel函数良好的正交性及其与信号频率成分的线性关系,使得以Bessel函数为基函数的傅里叶-贝塞尔变换(Fourier-Bessel Transform, FBT)在信号分离中得到了良好的应用[15,16]。然而,由于与Bessel函数基对应的信号频率成分不可细分,因此FBT很少应用于特征提取中。为克服这一问题,k分辨参数被引入Bessel函数基中,使得一定时间积累下的信号频率分辨率得到了提升[17]。
针对以上问题,本文在传统FBT及文献[17]的基础上,综合考虑调制指数、信号幅度等参数对分解结果的影响,提出了一种正弦调频Fourier-Bessel变换(Sinusoidal Frequency Modulation Fourier-Bessel Transform, SFMFBT),分析了SFMFBT的相关性质,并将其引入群目标微动特征提取与回波分离重构中,具体工作内容如下:(1)将k分辨参数引入Bessel函数基,基于该函数基提出SFMFBT变换对,并对相关性质进行了推导;(2)将SFMFBT引入微动特征提取中,分析了误差的产生原因,并讨论了离散信号处理中的相关问题。与现有部分算法相比,基于SFMFBT的微动频率提取方法不需时域加窗,因此能够获得更高的积累增益与提取精度;此外,该方法同样适用于时频域交叠的微动群目标回波。
2 正弦调频Fourier-Bessel变换 2.1 变换定义SFMFBT将信号的相位历程分解至各项
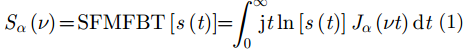
|
其中,

|
对于有限时域信号,

|
其中,k为SFMFB核函数分辨率,Cm为第m项SFMFB系数,
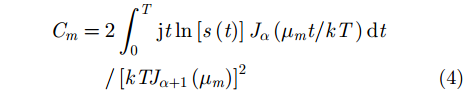
|
下面以正弦调频信号

|
其中,
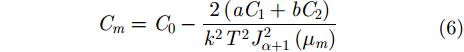
|
其中,C0为虚数,C1, C2分别为:
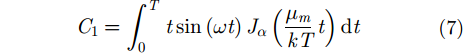
|

|
考虑Bessel函数的不定积分性质[18]
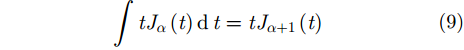
|
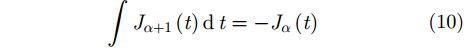
|
及以下积分[19]
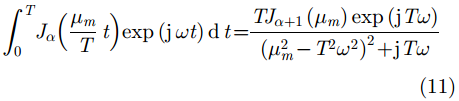
|
将k分辨参数引入式(11),并与式(9)、式(10)代入式(6),可得C1和C2分别为:

|
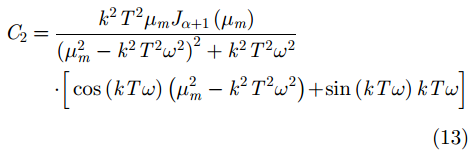
|
联立式(6)、式(12)和式(13)可得第m项SFMFB级数为

|
其中,C0为虚数项,
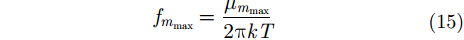
|
其中,
由Bessel函数根的性质[20],当
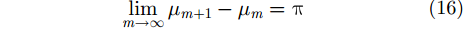
|
因此,相邻两项SFMFB级数对应的频率分辨率为:

|
令信号实际频率f与提取频率
设空间存在某自旋群目标,雷达与群目标质心
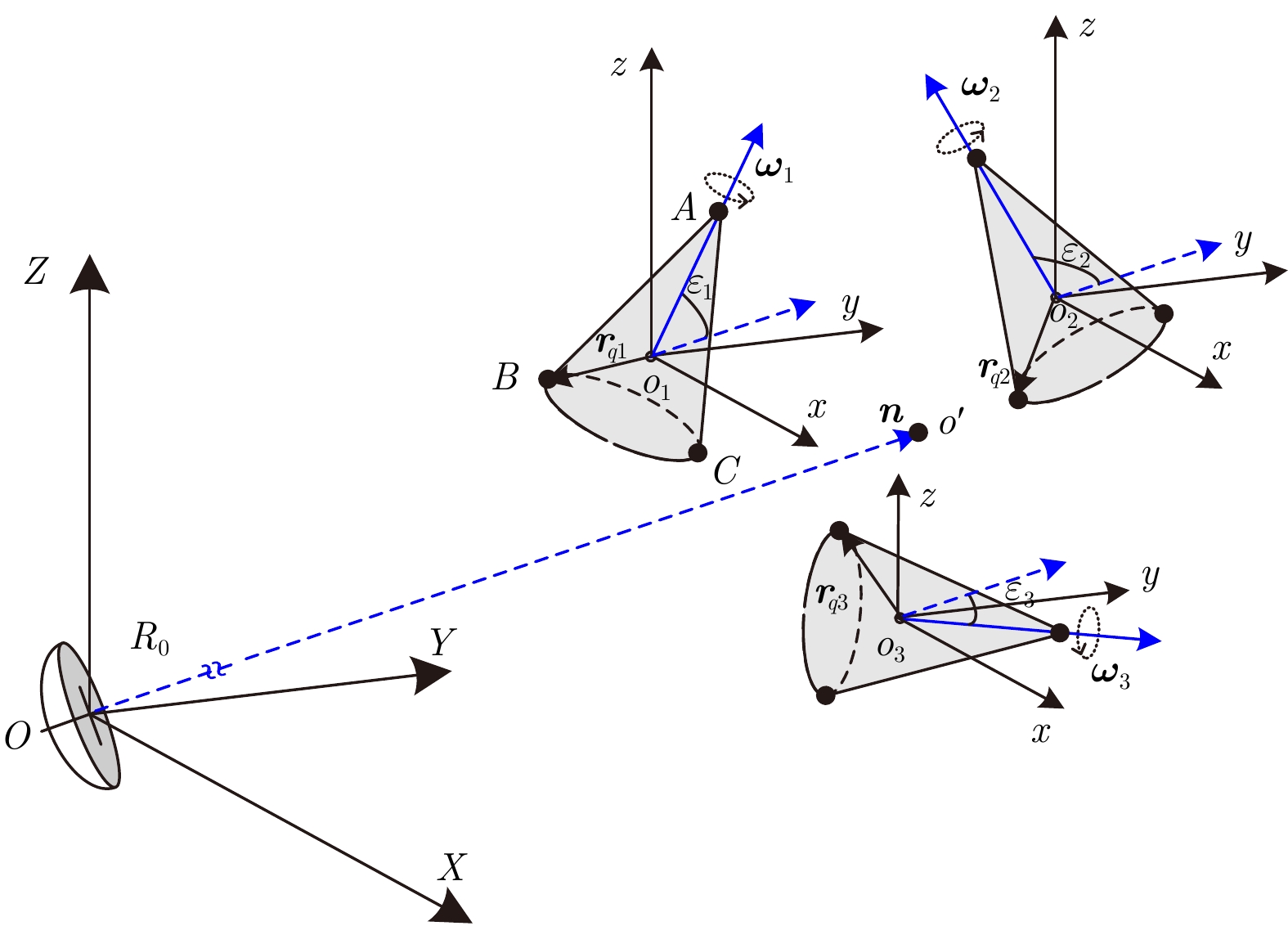
|
图 1 雷达与群目标几何关系 Fig.1 The geometry model of the radar and the group target |
雷达发射载频为fc的单频连续波,则在t时刻散射点qp的回波为:
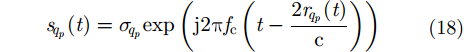
|
其中,
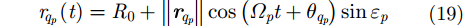
|
其中,
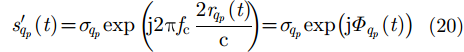
|
其中,

|
由式(21)可知,自旋目标的回波频率为正弦形式,自旋群目标回波为多分量正弦调频信号的叠加。
3.2 微动频率提取算法在实际应用中,雷达回波经数字采样后为离散形式,已知离散回波的相位测量范围为

|
则有

|
由式(15)可知,在对信号进行SFMFBT的计算过程中,微动频率可根据信号的SFMFB系数实部绝对值的最大项得到。接下来将对SFMFBT算法的频率误差进行分析,并在此基础上给出一种误差减小的方法进行微动频率修正。
如我们所知,若对信号进行傅里叶变换(Fourier Transform, FT),其FT频谱谱线与信号实际频率的差值不超过相邻谱线频率差值(即频率分辨率)的二分之一,即最大误差与FT基函数的频率分辨率相同,当且仅当信号实际频率落在相邻两函数基等分处时取得最大误差。然而,这一情况仅适用于单频率成分投影在单项级数或单根谱线上。与FT频谱不同,在SFMFB级数中单频率成分投影在若干项SFMFB系数上,即第m项SFMFB系数对应的理论频率fm在第m项系数上的投影值虽为最大,但其在与第m项邻近的若干项系数上的投影不为零。对信号
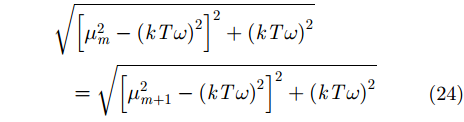
|
由基本不等式性质,则信号
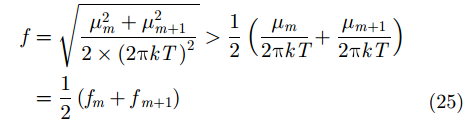
|
其中,
|
下面给出一种将最大绝对误差减小至
在对群目标回波进行微动频率提取与回波分离重构的过程中,以能量大小作为判别SFMFB系数中是否含有目标回波的依据。由于SFMFB系数与信号频率成分一一对应,则信号能量与SFMFB系数的平方成正比。令
综上所述,利用SFMFBT算法进行微动群目标频率提取及信号分离重构的步骤如下:
Step 1 初始化:目标个数i=0,幅值最大项系数对应项数
Step 2 计算最大有效项数
Step 3 计算
Step 4 离散化
Step 5 计算
Step 6 令
设空间存在3个自旋锥形目标,每个目标各含有1个锥顶散射点和2个锥底边缘散射点,其中锥顶散射点位于自旋轴上对回波不存在微多普勒调制。目标1以3.0 Hz进行自旋,自旋轴与LOS方向夹角为
|
图 2 回波信号SFMFBT结果 Fig.2 SFMFBT of returned signals |
从图2可以看出,信号经SFMFBT后表现为SFMFB级数,在不同k分辨率下SFMFB级数均分别在3处取得峰值。按照级数峰值项数计算得到3个目标的初始频率、修正频率和绝对误差如表1所示。在k=10条件下,目标回波及采用ISFMFBT得到的各目标分离重构回波的时频分析如图3所示。
| 表 1 微动频率提取结果 Tab.1 The m-D frequency extraction result |
|
图 3 目标回波及各目标重构回波时频分析 Fig.3 Time-frequency analysis of the echo signal and the individual reconstructed signals |
从图3可以看出,从原始目标回波的时频图像难以直接读取群目标的有效频率信息,而各子目标重构信号的时频分布则较好地反映了3个目标各自的频率信息。
4.2 性能分析 4.2.1 算法鲁棒性分析本节在不同信噪比(Signal-to-Noise Ratio, SNR)条件下对算法的鲁棒性进行验证,并与联合时频分布结合扩展Hough变换(TF-Hough)的微动参数提取方法[11]进行对比分析。TF-Hough方法在对回波进行时频分析的基础上,通过时频分析结果与扩展Hough空间的映射关系,完成对正弦曲线进行检测及参数提取。以4.1节旋转目标1回波信号为例,分别在SNR=–30 dB至SNR=20 dB的高斯白噪声条件下进行300次Monte Carol实验,频率提取正确概率pe随SNR及k分辨率的变化曲线如图4所示。
|
图 4 频率提取正确概率pe随SNR及k分辨率变化曲线 Fig.4 The curve of m-D frequency extraction probability pe in different SNR and k-resolution conditions |
从图4可以看出,取k=1且当SNR>0 dB时,所提算法的频率提取正确概率可达90%以上。即使当信号序列足够长时,频率提取精确程度与k分辨率成正比,但随着k的增大,级数的划分也越为精细,算法也越易受噪声干扰。可见,虽然k分辨率越小频率提取精度越低,但算法在高斯白噪声下鲁棒性越强。对于TF-Hough方法,由于时频分析结果对噪声较为敏感且精度易受窗长影响,当SNR>15 dB时,正弦检测及频率提取的正确概率可达90%。由此可见,基于SFMFBT的方法作为一种参数化微动频率提取方法,与TF-Hough方法相比具有更高的检测精度,在低SNR条件下算法的鲁棒性更强。
下面对阈值

|
取w=2k,以4.1节信号模型为例:①在接收信号全部为高斯白噪声(不包含目标回波),有
在实际应用中,对于信号
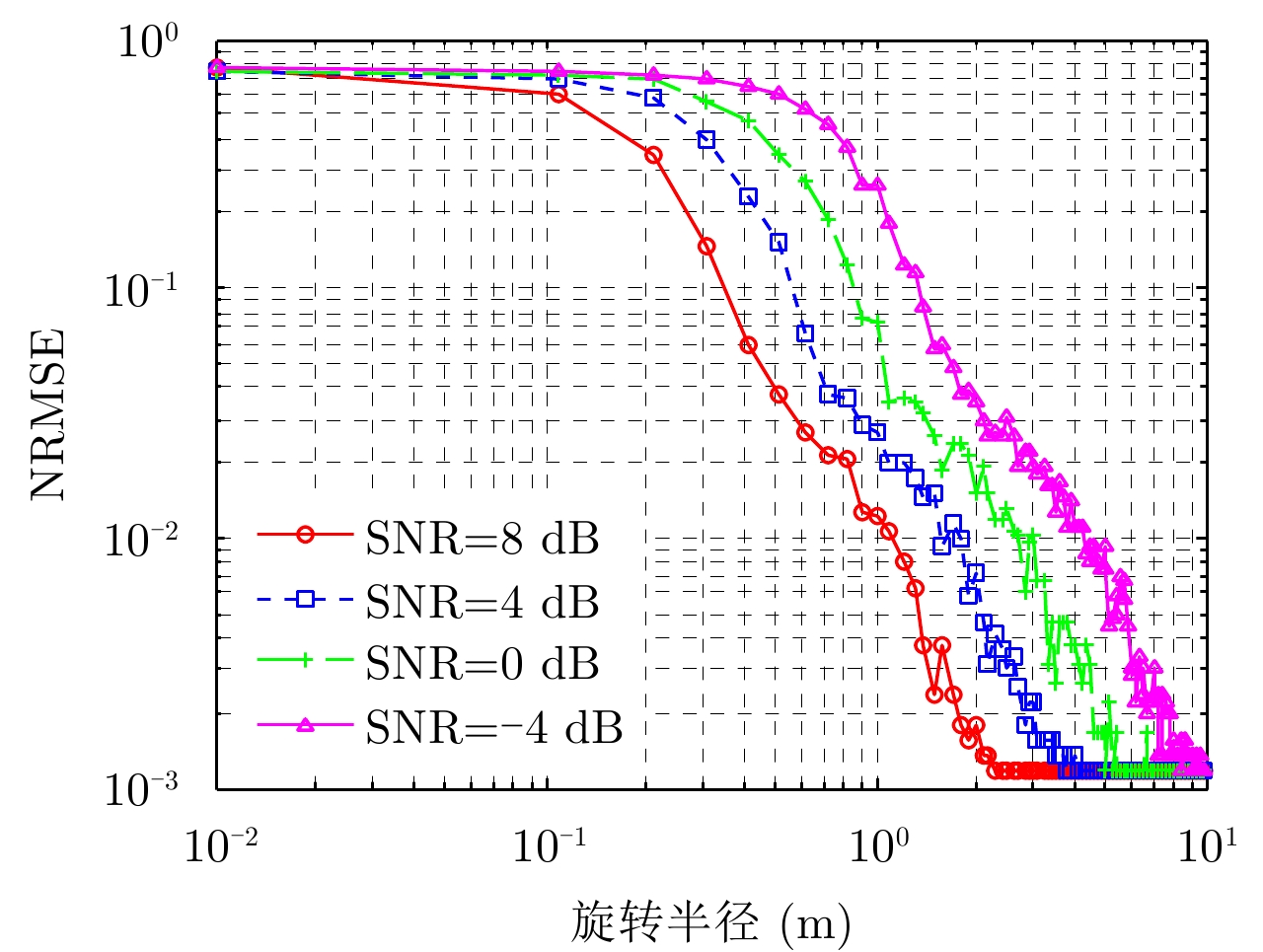
同样以自旋目标为例,讨论目标旋转半径对微动频率提取精度的影响。以归一化均方误差(Normalized Root-Mean-Square Error, NRMSE)进行算法提取频率
|
图 5 提取旋转频率NRMSE随旋转半径及SNR变化曲线 Fig.5 NRMSE curves with different rotation radius and SNR |
从图5可以看出,在相同旋转半径下,SNR越大提取频率与实际频率越为接近,对应的NRMSE越小;在相同SNR条件下,旋转半径越大则最大SFMFB级数幅值越为显著,提取频率与实际频率的NRMSE越小,这与式(14)结论一致。
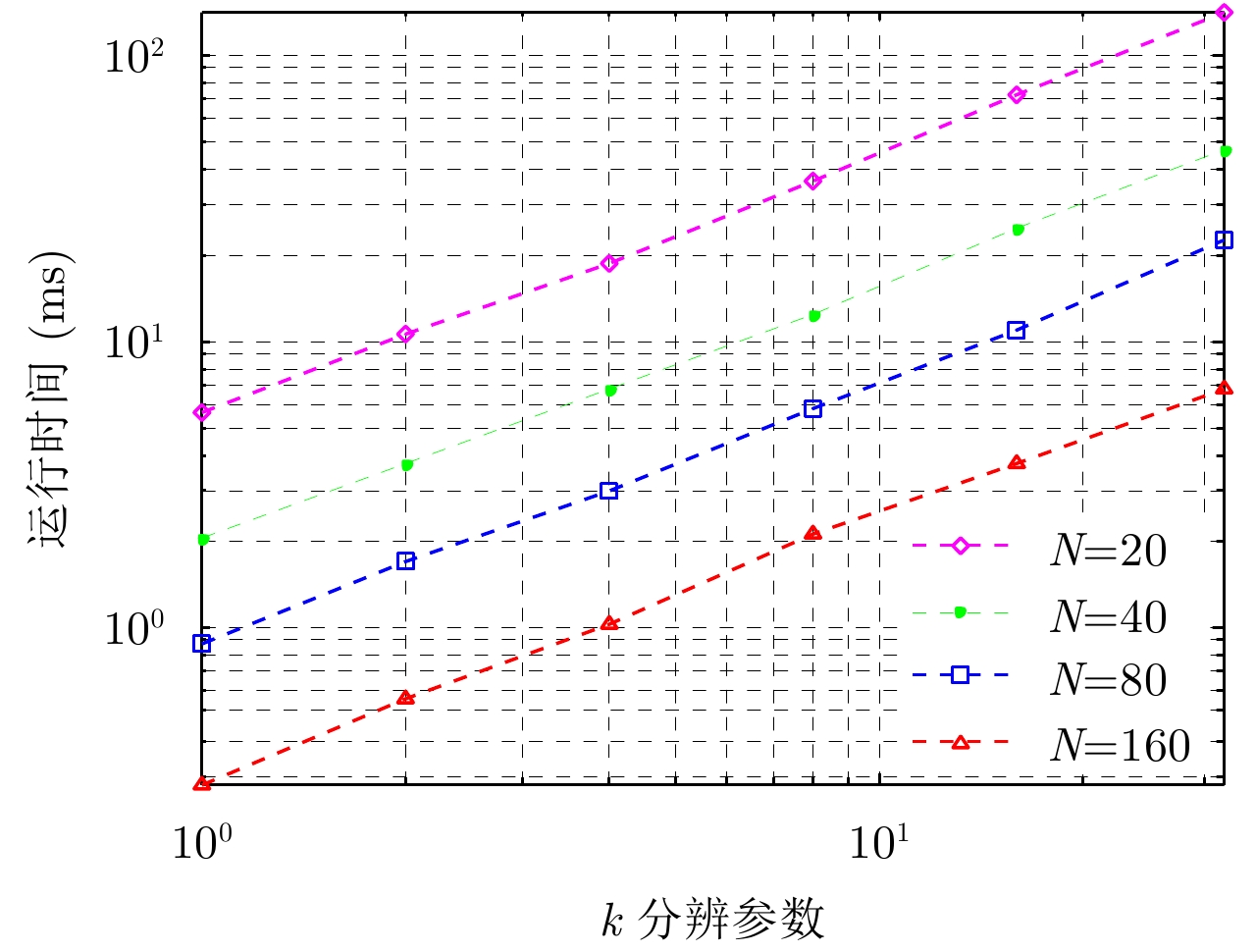
4.2.3 运算量分析对所提算法进行运算量分析。由式(24)可知,信号的SFMFB级数最大有效项数M与k分辨和信号序列长N的乘积成正比,则计算序列长为N的信号的k分辨SFMFB级数,其算法复杂度为
|
图 6 算法运行时间 Fig.6 Computation time of the SFMFB series |
由图6可知,SFMFB级数的运算量受到信号序列长和k分辨参数的共同影响。对于某一信号,算法采用的函数基的k分辨值越大,运算量越大;相应地,对于相同k分辨函数基,信号序列越长则运算量越大。这一结论与算法复杂度为
本文提出了一种正弦调频Fourier-Bessel变换,对变换的相关性质进行了推导,并将SFMFBT引入群目标微动频率提取中,并对离散信号处理中的相关问题进行了讨论。基于SFMFBT的微动频率提取方法利用全部信号序列长,相比于加窗算法其具有更高积累增益与提取精度,此外,该方法同样适用于群目标的微动频率提取与信号分离重构。下一步可将该方法与其他微动特征提取算法进行结合以提取更多的微动特征。
附录由式(24)所述,当第m项与第m+1项SFMFB系数的实部绝对值相等,即
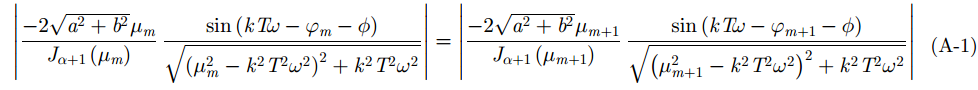
|
其中
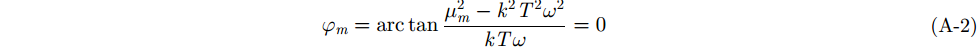
|
于是有
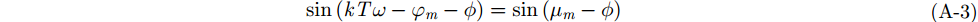
|
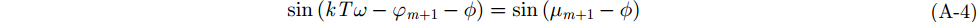
|
令

|
即为式(24)所述。
| [1] |
Chen V C. Doppler signatures of radar backscattering from objects with micro-motions[J].
IET Signal Processing, 2008, 2(3): 291-300. DOI:10.1049/iet-spr:20070137 ( 0) 0)
|
| [2] |
Tahmoush D. Review of micro-Doppler signatures[J].
IET Radar, Sonar & Navigation, 2015, 9(9): 1140-1146. ( 0) 0)
|
| [3] |
陈小龙, 关键, 何友. 微多普勒理论在海面目标检测中的应用及展望[J].
雷达学报, 2013, 2(1): 123-134. Chen Xiao-long, Guan Jian, and He You. Applications and prospect of micro-motion theory in the detection of sea surface target[J]. Journal of Radars, 2013, 2(1): 123-134. DOI:10.3724/SP.J.1300.2013.20102 (  0) 0)
|
| [4] |
赵双, 鲁卫红, 冯存前, 等. 基于窄带雷达网的弹道目标三维进动特征提取[J].
雷达学报, 2017, 6(1): 98-105. Zhao Shuang, Lu Weihong, Feng Cunqian, et al. Three-dimensional precession feature extraction of ballistic targets based on narrowband radar network[J]. Journal of Radars, 2017, 6(1): 98-105. DOI:10.12000/JR15129 (  0) 0)
|
| [5] |
韩勋, 杜兰, 刘宏伟, 等. 基于时频分布的空间锥体目标微动形式分类[J].
系统工程与电子技术, 2013, 35(4): 684-691. Han Xun, Du Lan, Liu Hong-wei, et al. Classification of micro-motion form of space cone-shaped objects based on time-frequency distribution[J]. Systems Engineering and Electronics, 2013, 35(4): 684-691. (  0) 0)
|
| [6] |
Shui Peng-lang, Bao Zheng, and Su Hong-tao. Nonparametric detection of FM signals using time-frequency ridge energy[J].
IEEE Transactions on Signal Processing, 2008, 56(5): 1749-1760. DOI:10.1109/TSP.2007.909322 ( 0) 0)
|
| [7] |
陈小龙, 刘宁波, 王国庆, 等. 基于高斯短时分数阶Fourier变换的海面微动目标检测方法[J].
电子学报, 2014, 42(5): 971-977. Chen Xiao-long, Liu Ning-bo, Wang Guo-qing, et al. Gaussian short-time fractional Fourier transform based detection algorithm of target with micro-motion at sea[J]. Acta Electronica Sinica, 2014, 42(5): 971-977. (  0) 0)
|
| [8] |
Chen Xiaolong, Guan Jian, Bao Zhonghua, et al. Detection and extraction of target with micromotion in spiky sea clutter via short-time fractional Fourier transform[J].
IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(2): 1002-1018. DOI:10.1109/TGRS.2013.2246574 ( 0) 0)
|
| [9] |
Li K, Liu Y, Huo K, et al. Estimation of micro-motion parameters based on cyclostationary analysis[J].
IET Signal Processing, 2010, 4(3): 218-223. DOI:10.1049/iet-spr.2009.0044 ( 0) 0)
|
| [10] |
Orović I, Stankovic S, and Thayaparan T. Time-frequency-based instantaneous frequency estimation of sparse signals from incomplete set of samples[J].
IET Signal Processing, 2014, 8(3): 239-245. DOI:10.1049/iet-spr.2013.0354 ( 0) 0)
|
| [11] |
Luo Ying, Zhou Liang, Lin Yong-zhao, et al.. Micro-Doppler extraction of frequency-stepped chirp signal based on the Hough transform[C]. Proceedings of the 8th International Symposium on Antennas, Propagation and EM Theory, Kunming, China, 2008: 408–411.
( 0) 0)
|
| [12] |
Zhang Qun, Yeo T S, Tan H S, et al. Imaging of a moving target with rotating parts based on the Hough transform[J].
IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 291-299. DOI:10.1109/TGRS.2007.907105 ( 0) 0)
|
| [13] |
Peng Bo, Wei Xizhang, Deng Bin, et al. A sinusoidal frequency modulation Fourier transform for radar-based vehicle vibration estimation[J].
IEEE Transactions on Instrumentation and Measurement, 2014, 63(9): 2188-2199. DOI:10.1109/TIM.2014.2308031 ( 0) 0)
|
| [14] |
杨陈, 池龙, 张群, 等. 正弦调频傅里叶变换的自旋微动群目标分辨[J].
空军工程大学学报(自然科学版), 2016, 17(3): 51-56. Yang Chen, Chi Long, Zhang Qun, et al. Resolution of group targets with spinning micro motion based on sinusoidal frequency modulation Fourier transform[J]. Journal of Air Force Engineering University (Natural Science Edition), 2016, 17(3): 51-56. DOI:10.3969/j.issn.1009-3516.2016.03.010 (  0) 0)
|
| [15] |
Suresh P, Thayaparan T, and Venkataramaniah K. Fourier-Bessel transform and time-frequency-based approach for detecting manoeuvring air target in sea-clutter[J].
IET Radar, Sonar & Navigation, 2015, 9(5): 481-491. ( 0) 0)
|
| [16] |
Suresh P, Thayaparan T, Obulesu T, et al. Extracting micro-Doppler radar signatures from rotating targets using Fourier-Bessel transform and time-frequency analysis[J].
IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3204-3210. DOI:10.1109/TGRS.2013.2271706 ( 0) 0)
|
| [17] |
张群, 何其芳, 罗迎. 基于贝塞尔函数基信号分解的微动群目标特征提取方法[J].
电子与信息学报, 2016, 38(12): 3056-3062. Zhang Qun, He Qifang, and Luo Ying. Micro-Doppler feature extraction of group targets using signal decomposition based on Bessel function basis[J]. Journal of Electronics & Information Technology, 2016, 38(12): 3056-3062. DOI:10.11999/JEIT161036 (  0) 0)
|
| [18] |
Spiegel M R, Lipschutz S L, and Liu J. Mathematical Handbook of Formulas and Tables[M]. Third Edition, New York: Academic Press Co., 2009.
( 0) 0)
|
| [19] |
McLachlan N W. Bessel Functions for Engineers[M]. Oxford, England: Clarendon Press, 1955.
( 0) 0)
|
| [20] |
Mathematical Handbook[M]. Athens, Abbrev. State: ESPI Publishing, 2007.
( 0) 0)
|




