双基星载合成孔径雷达(Synthetic Aperture Radar, SAR)利用信号收发平台的分置,能够同时获取不同视角的观测数据,在测绘、干涉测量、地面目标识别、自然灾害监测等领域[1,2]具有重要的应用价值。以Tandem-L为代表的新一代双基星载SAR系统应用多通道、数字波束形成(Digital Beam Forming, DBF)等技术,实现方位向高分辨率和距离向宽测绘带SAR(High Resolution Wide Swath SAR, HRWS-SAR)成像,系统的成像能力得到显著改善[3,4]。
HRWS-SAR系统在方位向采用多通道采样降低系统的脉冲重复频率(Pulse Recurrence Frequency, PRF),在不降低方位分辨率的前提下实现系统的宽测绘带成像。HRWS-SAR系统进行成像处理时,若方位向信号为均匀采样可直接采用传统SAR成像处理方法,而受载星平台轨迹约束及应用场景的限制,方位向的非均匀采样更为普遍[5],因而对方位向信号进行重构以获得其均匀采样信号或多普勒谱是HRWS-SAR系统成像处理的一项关键技术。单基星载HRWS-SAR系统的方位向信号重构得到了广泛而深入的研究[6–17]。重排算法[6]和插值算法[7]是两种典型的时域重构算法。重排算法依据接收信号的方位向位置将各通道信号重新排列,只能在特定的PRF得到方位向信号的均匀采样。插值算法则依据文献[7]所提出的周期性非均匀采样信号重构公式通过时域插值得到方位向信号的均匀采样,该算法运算复杂度高且精度依赖于插值核的长度。Krieger等依据广义采样定理提出矩阵求逆算法[8,9],该算法通过线性方程求解从混叠的多通道信号中重构出无模糊的多普勒谱。该算法不需要协方差矩阵等先验信息且易于实现,但在重叠采样时该算法无法进行信号重构,接近重叠采样时重构性能也较差。文献[10–13]则采用不同的方法对矩阵求逆算法进行改进,实现重叠采样附近的高性能信号重构。文献[14,15]基于统一的信号模型,选取不同代价函数进行优化,提出了多种自适应波束形成(DBF)算法:正交投影算法、信号最大化算法、最大化信号模糊噪声比算法、最小均方误差算法等。与矩阵求逆算法相比,DBF类算法运算复杂度较高,并假定各通道的噪声为高斯白噪声且相互独立。文献[16]则对方位向信号重构算法的性能进行了仿真对比分析。文献[17]采用NUFFT直接重构方位向非均匀采样信号的多普勒频谱。
上述方位向信号重构方法理论上均能推广到双基星载HRWS-SAR系统。考虑到矩阵求逆算法易于实现且研究较为广泛,本文研究该算法在双基HRWS-SAR系统中的实现。本文首先将方位照射时间内时变的发射接收距离比近似为一个常数,推导了双基星载HRWS-SAR系统与某个单基系统在方位向多信道间传递函数上的等效性,从而构建了双基星载HRWS-SAR系统的方位向信号模型。而后,提出了适用于一般双基构型星载HRWS-SAR系统方位向信号重构的矩阵求逆算法,并给出了信噪比缩放因子及方位模糊比这两个重构性能指标的计算公式。最后,通过对几种典型双基构型的星载HRWS-SAR系统进行方位向信号重构仿真,验证了矩阵求逆算法在一般双基构型星载HRWS-SAR系统中的适用性。
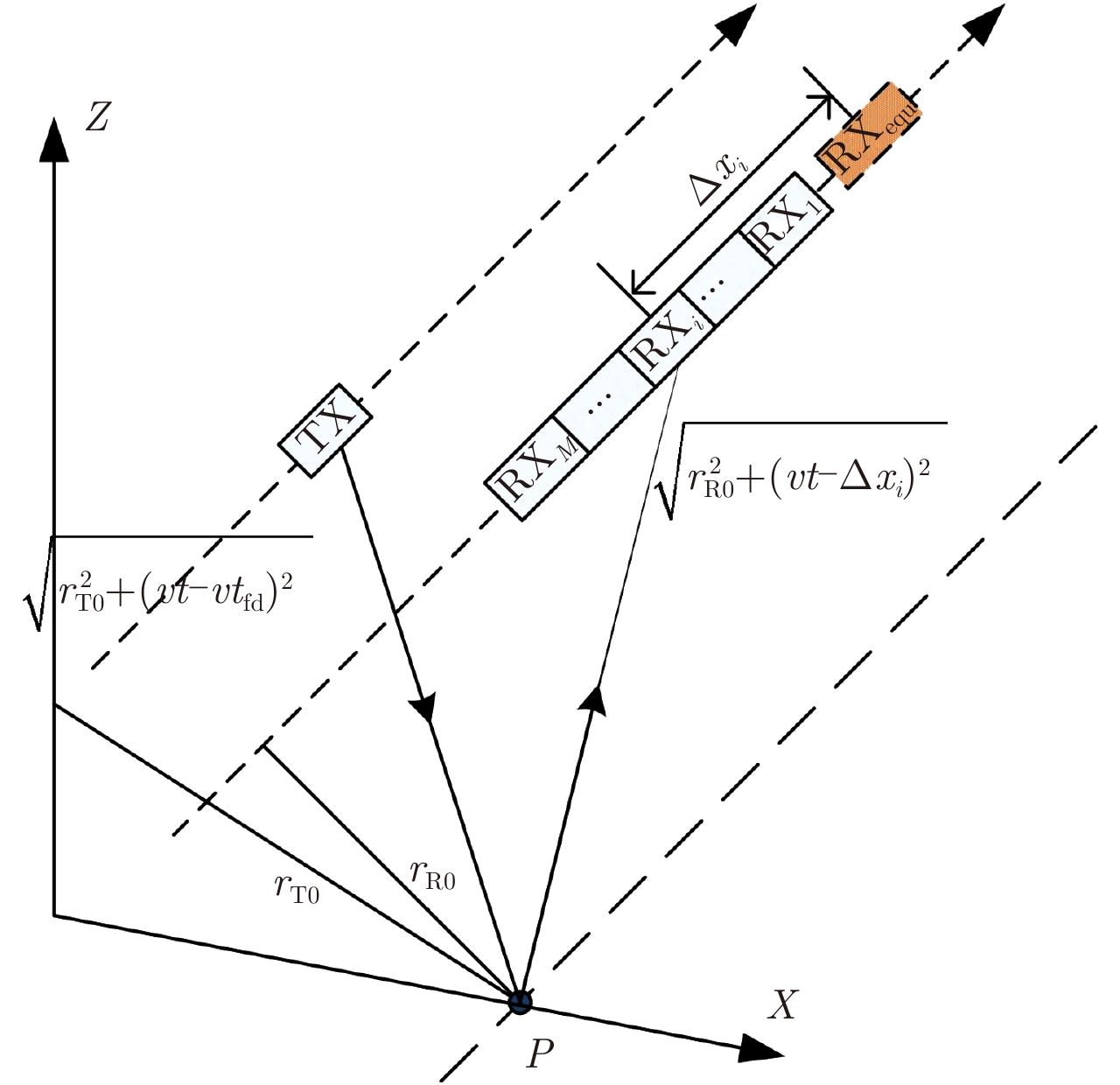
2 双基星载HRWS-SAR系统的方位向信号 模型为保持双基星载HRWS-SAR系统对地面的持续观测,收发平台应置于同一轨道(顺飞模式)或高度相同的平行轨道(平飞模式)。图1给出了一般构型双基星载HRWS-SAR系统的信号收发几何。发射天线和接收天线的最短距离分别为rT0, rR0,接收天线共有M个通道,RXequ为方位向信号重构后的等效接收通道,通道i到等效接收通道RXequ的方位向距离为
|
图 1 双基星载HRWS-SAR系统的双基构型 Fig.1 Bistatic configuration of bistatic spaceborne HRWS-SAR |
不失一般性,假定点目标P在t=0时刻位于接收天线的零多普勒面,容易得到t时刻点P在接收通道i的收发距离和
|
$\begin{aligned}R\left( t \right) =& \sqrt {r_{{\rm{T}}0}^2 + {{\left( {vt - v{t_{{\rm{fd}}}}} \right)}^2}} \\& + \sqrt {r_{{\rm{R}}0}^2 + {{\left( {vt - \Delta {x_i}} \right)}^2}} \end{aligned}$
|
(1) |
忽略天线方向图的影响,接收通道i的冲激响应函数可表示为:
|
$\begin{aligned}{h_i}\left( t \right) = & \exp \left( { - {\rm j}\frac{{2{{π}} }}{\lambda }R\left( t \right)} \right) \\ = & \exp \Biggr( { - {\rm j}\frac{{2{{π}} }}{\lambda }\biggr( {\sqrt {r_{{\rm{T}}0}^2 + {{\left( {vt - v{t_{{\rm{fd}}}}} \right)}^2}}}} \\ & { {\left.+ {\sqrt {r_{{\rm{R}}0}^2 + {{\left( {vt - \Delta {x_i}} \right)}^2}} } \right)} \Biggr)}\end{aligned}$
|
(2) |
单基星载HRWS-SAR系统可视为rT0=rR0=r0, tfd=0,发射天线为等效接收通道的特殊情况。由式(2)可得此时接收通道i的冲激响应为:
|
$\begin{aligned}{\tilde h_i}\left( t \right) = & \exp \Biggr( { - {\rm j}\frac{{2{{π}} }}{\lambda }\biggr( {\sqrt {r_0^2 + {{\left( {vt} \right)}^2}}}} \\& + {{\sqrt {r_0^2 + {{\left( {vt - \Delta {x_i}} \right)}^2}} } \biggr)} \Biggr)\end{aligned}$
|
(3) |
令此时单基单通道SAR的冲激响应函数为
|
${\tilde h_{{\rm{mono}}}}\left( t \right) = \exp \left( { - {\rm j}\frac{{4{{π}} }}{\lambda }\sqrt {r_0^2 + {{\left( {vt} \right)}^2}} } \right)$
|
(4) |
文献[9]对
|
$\left\{ \begin{aligned}&{{\tilde h}_{{\rm{mono}}}}\left( t \right) \approx \exp \left( { - {\rm j}\frac{{4{{π}} }}{\lambda }{r_0}} \right) \cdot \exp \left( { - {\rm j}\frac{{2{{π}} {v^2}{t^2}}}{{\lambda {r_0}}}} \right)\\&{{\tilde h}_i}\left( t \right) \approx \exp \left( { - {\rm j}\frac{{4{{π}} }}{\lambda }{r_0}} \right) \cdot \exp \left( { - {\rm j}\frac{{{{π}} \Delta x_i^2}}{{2\lambda {r_0}}}} \right) \\& \quad\quad\quad\ \cdot \exp \left( { - {\rm j}\frac{{2{{π}} {v^2}{{\left( {t - \displaystyle\frac{{\Delta {x_i}}}{{2v}}} \right)}^2}}}{{\lambda {r_0}}}} \right)\end{aligned} \right.\quad$
|
(5) |
因而
|
${\tilde h_i}\left( t \right) \!=\! \exp \left( { \!- {\rm j}\!\frac{{{{π}} \Delta x_i^2}}{{2\lambda {r_0}}}} \right) \!\cdot\! \delta \left( {t \!-\! \frac{{\Delta {x_i}}}{{2v}}} \right)\! *\! {\tilde h_{{\rm{mono}}}}\left( t \right)$
|
(6) |
将式(6)进行Fourier变换,可得单基单通道SAR与接收通道i的系统函数关系:
|
$\begin{aligned}{\tilde H_i}\left( f \right) = & \exp \left( { - {\rm j}\frac{{{{π}} \Delta x_i^2}}{{2\lambda {r_0}}}} \right) \cdot \exp \left( { - {\rm j}2{{π}} \frac{{\Delta {x_i}}}{{2v}}f} \right) \\&\cdot {\tilde H_{{\rm{mono}}}}\left( f \right)\end{aligned}$
|
(7) |
单基单通道SAR到接收通道i的传递函数
|
${\tilde G_i}\left( f \right) = \exp \left( { - {\rm j}\frac{{{{π}} \Delta x_i^2}}{{2\lambda {r_0}}}} \right) \cdot \exp \left( { - {\rm j}2{{π}} \frac{{\Delta {x_i}}}{{2v}}f} \right)$
|
(8) |
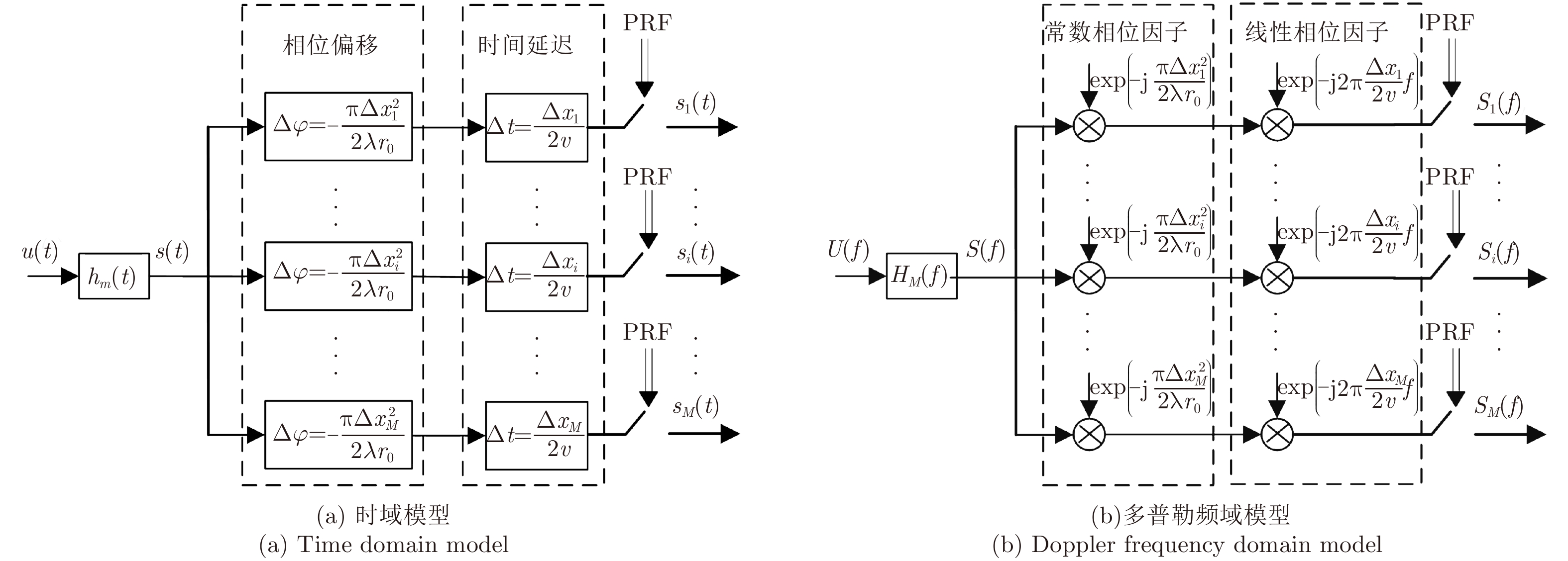
基于上述分析,单基星载HRWS-SAR系统的方位向信号生成模型可由图2进行描述。方位向各通道信号在时域为单基单通道SAR信号经对应的相位偏移和时间延迟的结果,而在多普勒域为单基单通道SAR信号与对应的常数相位因子和线性相位因子相乘后的结果。PRF小于多普勒带宽时,方位向各通道信号为时域上的欠采样,将导致多普勒域的频谱混叠。
|
图 2 单基星载HRWS-SAR系统的方位向信号生成模型 Fig.2 Azimuth signal generating model in monostatic spaceborne HRWS-SAR |
一般双基构型的星载HRWS-SAR系统中rT0≠rR0, tfd≠0,不能通过对hmono及hi的泰勒级数展开进行2阶相位近似处理得到与式(6)、式(7)相似的表达式。本节将对式(2)进一步处理,推导一般双基构型星载HRWS-SAR系统中
引入点目标P的收发距离比函数
|
$\begin{aligned}{h_i}\left( t \right) = & \exp \Biggr( { - {\rm j}\frac{{2{{π}} }}{\lambda }\biggr( {C\left( t \right)\sqrt {r_{{\rm{R}}0}^2 + {{\left( {vt} \right)}^2}}}} \\& + {{\sqrt {r_{{\rm{R}}0}^2 + {{\left( {vt - \Delta {x_i}} \right)}^2}} } \biggr)} \Biggr)\end{aligned}$
|
(9) |
等效接收通道RXequ的冲激响应函数为:
|
${{h}_{\text{mono}}}\left( t \right)=\exp (-\text{j}\frac{2\pi }{\lambda }\left( \left( C\left( t \right)+1 \right)\sqrt{r_{\text{R}0}^{2}+{{\left( vt \right)}^{2}}} \right))$
|
(10) |
对式(9)、式(10)的泰勒级数展开进行2阶相位近似处理,可得:
|
$\left\{ \begin{aligned}&{h_i}\left( t \right) \approx \exp \left( { - {\rm j}\frac{{2{{π}} }}{\lambda }\left( {C\left( t \right) + 1} \right){r_{{\rm{R}}0}}} \right) \\& \quad\quad\quad\ \cdot \exp \left( { - {\rm j}\frac{{{π}} }{{\lambda {r_{{\rm{R}}0}}}} \cdot \frac{{C\left( t \right)\Delta x_i^2}}{{C\left( t \right) + 1}}} \right) \\& \quad\quad\quad\ \cdot \exp \Biggr( { - {\rm j}\frac{{{π}} }{{\lambda {r_{{\rm{R}}0}}}} \cdot \Big( {C^{} \left( t \right) + 1} \Big) }\\& \quad\quad\quad\ {\cdot {v^2}{{\left( {t - \frac{{\Delta {x_i}}}{{\left( {C\left( t \right) + 1} \right)v}}} \right)}^2}} \Biggr)\\& {h_{{\rm{mono}}}}\left( t \right) \approx \exp \left( { - {\rm j}\frac{{2{{π}} }}{\lambda }\left( {C\left( t \right) + 1} \right){r_{{\rm{R}}0}}} \right) \\& \quad\quad\quad\quad\ \cdot \exp \left( { - {\rm j}\frac{{{π}} }{{\lambda {r_{{\rm{R}}0}}}} \cdot \left( {C\left( t \right) + 1} \right) \cdot {v^2}{t^2}} \right)\end{aligned} \right.$
|
(11) |
在目标照射时间Ta内,
|
$\begin{aligned}{h_i}\left( t \right) = & \exp \left( { - {\rm j}\frac{{{π}} }{{\lambda {r_{{\rm{R}}0}}}} \cdot \frac{{{C_0}\Delta x_i^2}}{{{C_0} + 1}}} \right) \\& \ \cdot \delta \left( {t - \frac{{\Delta {x_i}}}{{\left( {{C_0} + 1} \right)v}}} \right) * {h_{{\rm{mono}}}}\left( t \right)\end{aligned}$
|
(12) |
式(12)进行Fourier变换,可得等效接收通道RXequ与接收通道i的系统函数关系:
|
$\begin{aligned}{H_i}\left( f \right) = & \exp \left( { - {\rm j}\frac{{{π}} }{{\lambda {r_{{\rm{R}}0}}}} \cdot \frac{{{C_0}\Delta x_i^2}}{{{C_0} + 1}}} \right) \\& \cdot \exp \left( { - {\rm j}2{{π}} \frac{{\Delta {x_i}}}{{\left( {{C_0} + 1} \right)v}}f} \right) \cdot {H_{{\rm{mono}}}}\left( f \right)\end{aligned}$
|
(13) |
等效接收通道RXequ到接收通道i的传递函数为:
|
$\begin{aligned}{G_i}\left( f \right) = & \exp \left( { - {\rm j}\frac{{{π}} }{{\lambda {r_{{\rm{R}}0}}}} \cdot \frac{{{C_0}\Delta x_i^2}}{{{C_0} + 1}}} \right) \\& \cdot \exp \left( { - {\rm j}2{{π}} \frac{{\Delta {x_i}}}{{\left( {{C_0} + 1} \right)v}}f} \right)\end{aligned}$
|
(14) |
考察式(8)、式(14),传递函数
|
${G_i}\left( {f,\Delta {x_i}} \right) = {\tilde G_i}\left( {f,\frac{2}{{\left( {{C_0} + 1} \right)}}\Delta {x_i}} \right)$
|
(15) |
式(15)表明双基星载HRWS-SAR系统的方位向信号的生成模型可等效为一单基系统模型,只需将图2中的
式(12)、式(13)、式(14)是在
文献[8]给出了单基HRWS-SAR系统方位向信号重构的矩阵求逆算法,由于双基HRWS-SAR系统在方位向信号模型上与单基系统的等效性,矩阵求逆算法在双基系统同样适用。
3.1 双基HRWS-SAR系统的矩阵求逆算法矩阵求逆算法的理论依据是广义采样定理。在双基HRWS-SAR系统中,通过发射到接收通道i的传递函数,能够得到单基单通道SAR的信号
矩阵求逆算法主要包括3个步骤:
首先,构造系统的传递函数矩阵
|
${{G}}\left( f \right) = \left( {\begin{array}{*{20}{c}}{{G_1}\left( f \right)} & {{G_1}\left( {f + {\rm{PRF}}} \right)} & ·\!·\!· & {{G_1}\left( {f + \left( {M - 1} \right) \cdot {\rm{PRF}}} \right)}\\{{G_2}\left( f \right)} & {{G_2}\left( {f + {\rm{PRF}}} \right)} & ·\!·\!· & {{G_2}\left( {f + \left( {M - 1} \right) \cdot {\rm{PRF}}} \right)}\\ \vdots & \vdots & \ddots & \vdots \\{{G_M}\left( f \right)} & {{G_M}\left( {f + {\rm{PRF}}} \right)} & ·\!·\!· & {{G_M}\left( {f + \left( {M - 1} \right) \cdot {\rm{PRF}}} \right)}\end{array}} \right)$
|
(16) |
|
${\tilde{{S}}}\left( f \right) = {\Big( {{S_1}\left( f \right),{S_2}\left( f \right), \cdots ,{S_M}\left( f \right)} \Big)^{\rm{T}}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\,\, $
|
(17) |
然后,对
|
${{P}}\left( f \right) = \\
\left( {\begin{array}{*{20}{c}}{{P_1}\left( f \right)} & {{P_2}\left( f \right)} & ·\!·\!· & {{P_M}\left( f \right)}\\{{P_1}\left( {f + {\rm{PRF}}} \right)} & {{P_2}\left( {f + {\rm{PRF}}} \right)} & ·\!·\!· & {{P_M}\left( {f + {\rm{PRF}}} \right)}\\ \vdots & \vdots & \ddots & \vdots \\{{P_1}\left( {f + \left( {M - 1} \right) \cdot {\rm{PRF}}} \right)} & {{P_2}\left( {f + \left( {M - 1} \right) \cdot {\rm{PRF}}} \right)} & ·\!·\!· & {{P_M}\left( {f + \left( {M - 1} \right) \cdot {\rm{PRF}}} \right)}\end{array}} \right)$
|
(18) |
最后,利用公式
星载HRWS-SAR系统的单通道信号带宽为PRF,采用矩阵求逆算法重构后的方位向信号带宽为
文献[8]定义信噪比缩放因子表征方位向重构对信噪比的影响,其定义式及计算公式为:
|
${\varPhi _{{\rm{bf}}}} \!=\! \frac{{{\rm{SN}}{{\rm{R}}_{{\rm{in}}}}/{\rm{SN}}{{\rm{R}}_{{\rm{out}}}}}}{{\left( {{\rm{SN}}{{\rm{R}}_{{\rm{in}}}}/{\rm{SN}}{{\rm{R}}_{{\rm{out}}}}} \right)\left| {_{{\rm{PR}}{{\rm{F}}_{{\rm{uni}}}}}} \right.}} \!=\! \frac{{\displaystyle\sum\limits_{j = 1}^M {{\mathop{\rm E}\nolimits} \left( {{{\left| {{P_j}\left( f \right)} \right|}^2}} \right)} }}{N}$
|
(19) |
其中,SNRin, SNRout为方位向信号重构前后的信噪比,PRFuni表示方位向均匀采样时的PRF,
|
${\varPhi _{{\rm{bf}}}} = \frac{{\displaystyle\sum\limits_{j = 1}^M {{\lambda _j}\left( f \right)} }}{N}$
|
(20) |
其中,
文献[8]详细推导了单基HRWS-SAR系统的方位模糊比(AASR)计算公式,与之类似可推导出双基HRWS-SAR系统的AASR计算公式,可概括为如下4个计算式:
|
$\begin{aligned}\\{e_k}\left( f \right) = & {A_k}\left( f \right)\sum\limits_m^{} {\sum\limits_{j = 1}^M {{G_j}\left( {f + k \cdot {\rm{PRF}}} \right)} } \\\text{} & \ \cdot {P_j}\left( {f + m \cdot {\rm{PRF}}} \right)\end{aligned}$
|
(21) |
|
$\begin{aligned} {e_\Sigma }\left( f \right) = & \sum\limits_{k = - \infty ,k \ne 0}^\infty {{e_k}\left( f \right)} \\= & \sum\limits_{k = - \infty ,k \ne 0}^\infty {\Biggr( {{A_k}\left( f \right)\sum\limits_m^{} {\sum\limits_{j = 1}^M {{G_j}\left( {f + k \cdot {\rm{PRF}}} \right)} } }} \\ \text{ } & {\cdot {P_j}\big( {f + m \cdot {\rm{PRF}}}\big)}\Biggr) \end{aligned}\quad\quad$
|
(22) |
|
${p_{\rm{s}}} = {\rm{E}}\left( {{{\Big| {A\left( f \right) \cdot {\rm{rect}}\left( {f/{{I}}} \right)} \Big|}^2}} \right)\quad\quad\quad\quad\quad\quad\quad \$
|
(23) |
|
${\rm{AASR}} = \frac{{{\rm{E}}\left( {{{\left| {{e_\Sigma }\left( f \right)} \right|}^2}} \right)}}{{{p_{\rm{s}}}}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\$
|
(24) |
本节对几种典型的双基构型星载HRWS-SAR系统进行方位向信号重构进行仿真,验证矩阵求逆算法的正确性,并分析算法的重构性能。表1列出了系统的方位向系统参数,对于单基系统容易计算出多普勒带宽Bfd=5.61 kHz,照射时间Ta=1.05 s。
| 表 1 双基星载HRWS-SAR系统的方位向系统参数 Tab.1 Azimuth parameters in bistatic spaceborne HRWS-SAR |
| 表 2 双基星载HRWS-SAR系统的7种双基构型 Tab.2 Seven configurations for bistatic spaceborne HRWS-SAR |
表2列出了7种典型的双基构型。表2中采用发射天线和接收天线的零多普勒时间差tfd与轨道距离L对双基构型进行表征:tfd=0时系统工作在平飞模式,L=0时系统工作在顺飞模式,L<0时发射天线位于测绘带近端,反之L>0时接收天线位于测绘带近端,构型Ⅰ中tfd=0且L=0退化为单基系统。
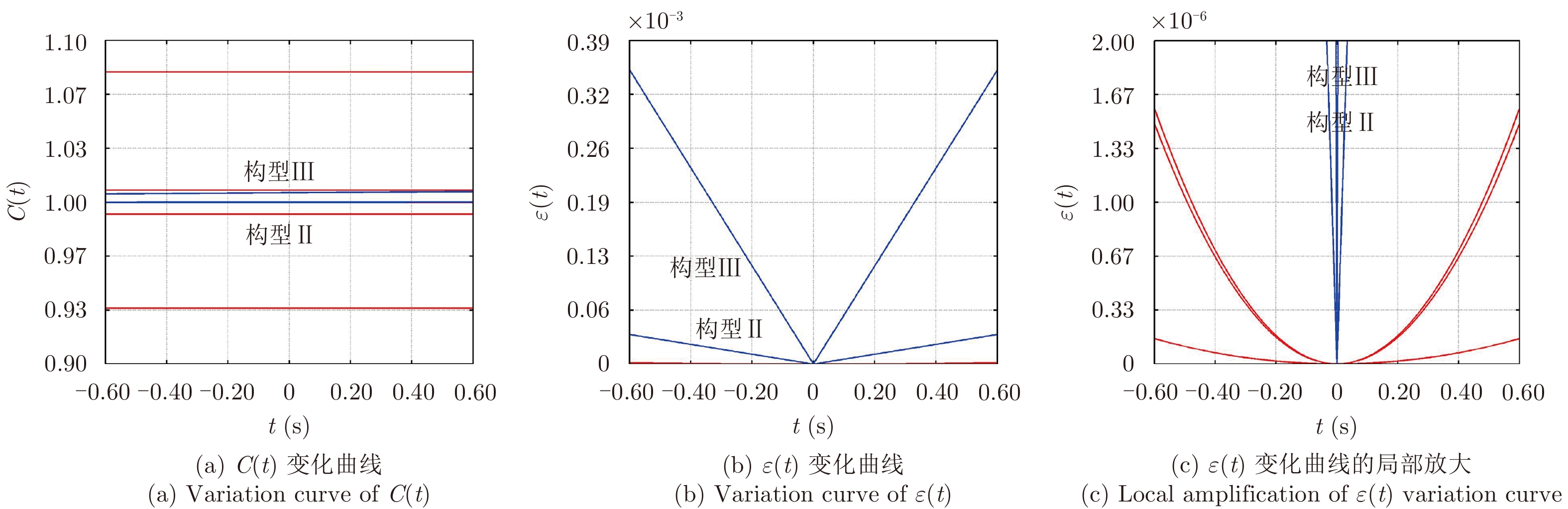
4.1 C0对C(t)的近似性能将
|
图 3 照射时间Ta范围内的
|
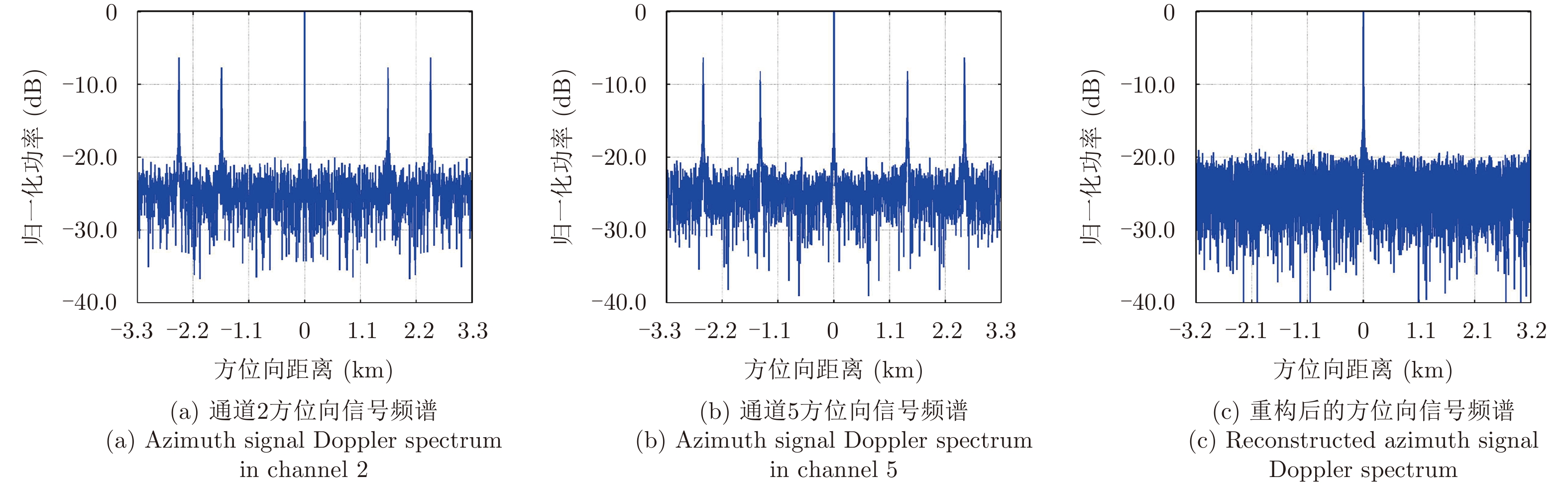
各接收通道的信噪比设置为20 dB,取PRF=2.0 kHz,对图1所示的点目标P方位向信号重构过程进行仿真,其结果如图4和图5所示。
|
图 4 构型Ⅰ方位向信号重构前后的成像结果 Fig.4 Unreconstructed and reconstructed azimuth signal Doppler spectrum for bistatic configuration Ⅰ |
|
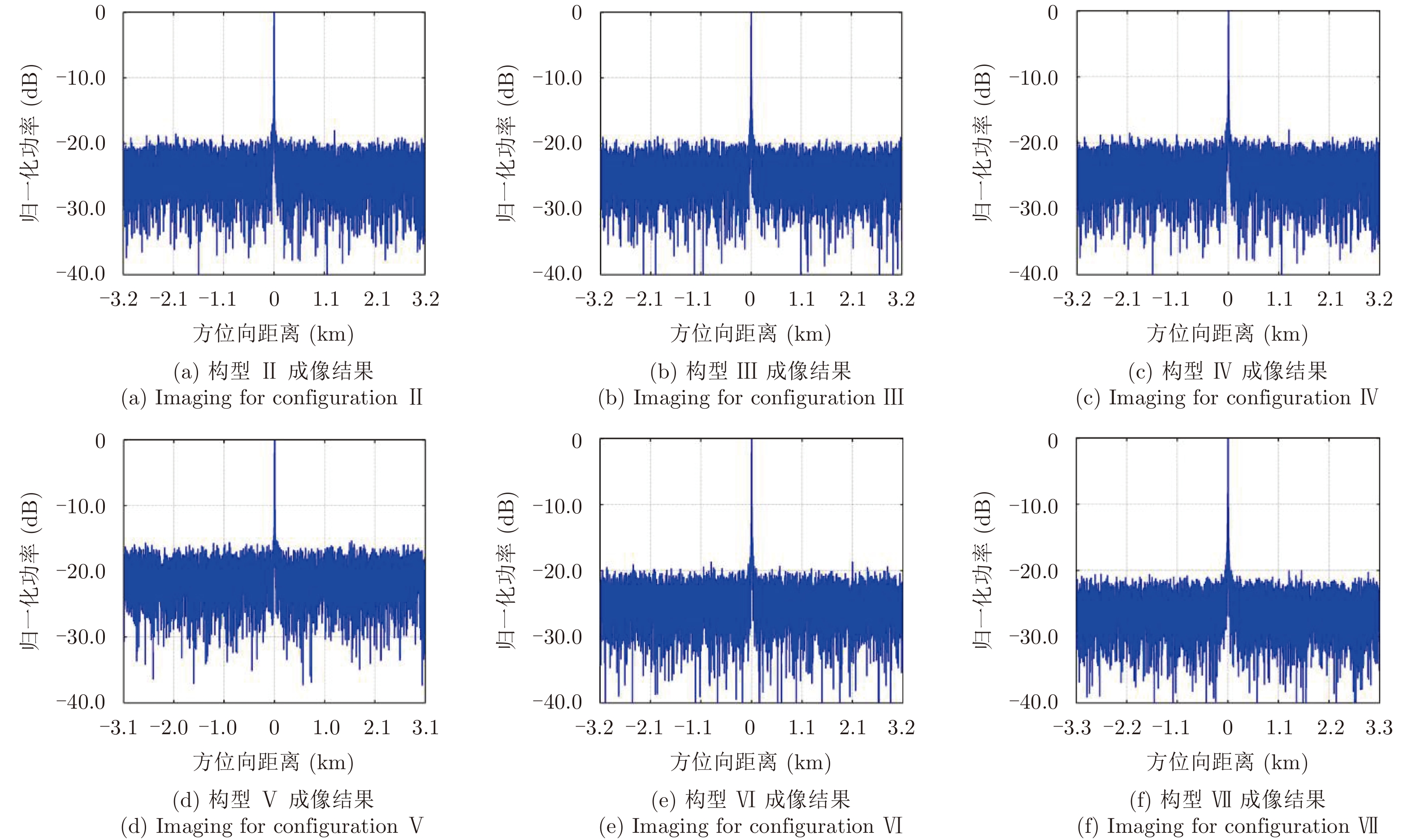
图 5 方位向信号重构后的成像结果 Fig.5 Imaging for reconstructed azimuth signal Doppler spectrum |
图4(a)、图4(b)中,由于PRF小于多普勒带宽Bfd,单个接收通道的多普勒频谱有严重的混叠现象,图4(c)则表明采用矩阵求逆算法进行方位向信号重构消除了多普勒频谱中的混叠现象。图4(c)及图5给出了各双基构型下的方位向信号重构后的成像结果,验证了矩阵求逆算法对一般双基构型的适用性,同时也表明重构性能受双基构型的影响,尤其是构型Ⅴ、Ⅶ与其他构型性能差异较为明显。
4.3 方位向信号重构性能将PRF设置在区间1.4 kHz≤PRF≤2.8 kHz,采用表1的系统参数和表2的双基构型,利用式(20)、式(24)可以得到方位向信号的重构性能曲线,如图6所示。为了便于图6的分析,首先计算各双基构型下的C0及典型PRF值,计算结果为表3,其中PRFuni为均匀采样时的PRF值,PRFrep1及PRFrep2为PRF范围内出现重叠采样的两个PRF值。构型Ⅰ的PRFuni, PRFrep1和PRFrep2在图6中予以标注。
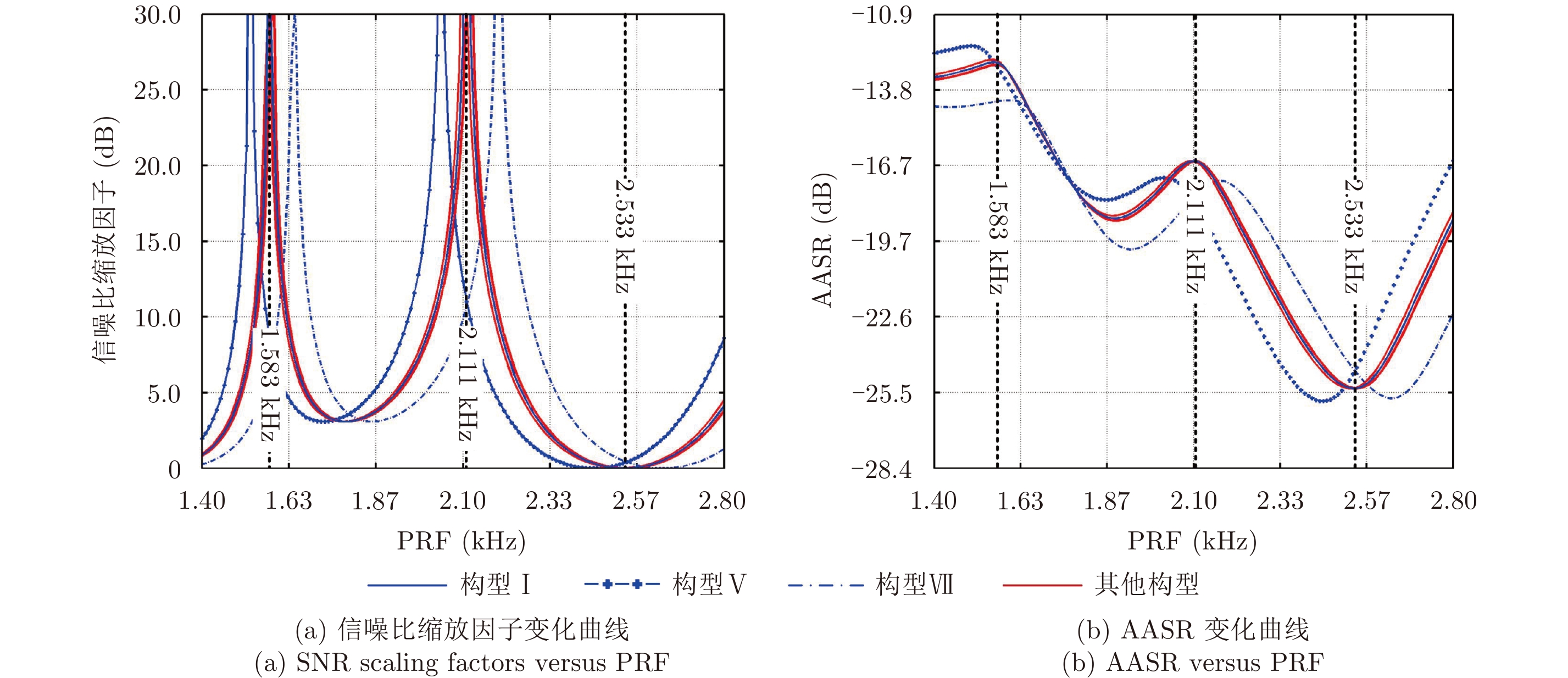
|
图 6 方位向信号重构性能曲线 Fig.6 Azimuth signal reconstruction performance curve |
| 表 3 C0及典型PRF值 Tab.3 C0 and typical PRF |
(1) 均匀采样时PRF=PRFuni,方位向信号的重构性能达到局部最优;重叠采样时PRF=PRFrep,信噪比缩放因子趋向于无穷大,矩阵求逆算法将不能实现信号重构;PRF位于PRFrep附近时,矩阵求逆算法的性能急剧下降。从矩阵理论的观点分析,PRF=PRFrep时,传递函数
(2) C0值的差异直接导致同一PRF时方位向信号重构性能差异。与其他构型相比构型Ⅴ、Ⅶ的C0值差异较大因而构性能差异也大,与图5的结论相一致。根本原因在于与双基HRWS-SAR系统等效的单基系统,通道间的方位向距离为
本文通过分析单基与双基星载HRWS-SAR系统的方位向信号模型,给出了适用于一般双基构型星载HRWS-SAR系统方位向信号重构的矩阵求逆算法,并使用信噪比缩放因子及方位模糊比两个指标分析了该算法的重构性能。本文的分析方法对其他方位向信号重构算法推广到双基星载HRWS-SAR系统具有借鉴意义。双基星载HRWS-SAR系统方位向信号重构的工程应用中,需改进矩阵求逆算法以改善重叠采样附近的重构性能。
| [1] |
Zink M, Bachmann M, Brautigam B, et al.. TanDEM-X: The new global DEM takes shape[J].
IEEE Geoscience and Remote Sensing Magazine, 2014, 2(2): 8-23. DOI:10.1109/MGRS.2014.2318895 ( 0) 0)
|
| [2] |
Bueso-Bello J L, Prats-Iraola P, Martone M, et al.. Performance evaluation of the TanDEM-X quad polarization acquisitions in the science phase[C]. Proceedings of EUSAR 2016: 11th European Conference on Synthetic Aperture Radar, Hamburg, 2016: 627–632.
( 0) 0)
|
| [3] |
Moreira A, Krieger G, Hajnsek I, et al.. Tandem-L: A highly innovative bistatic SAR mission for global observation of dynamic processes on the earth’s surface[J].
IEEE Geoscience and Remote Sensing Magazine, 2015, 3(2): 8-23. DOI:10.1109/MGRS.2015.2437353 ( 0) 0)
|
| [4] |
Huber S, Villano M, Younis M, et al.. Tandem-L: Design concepts for a next-generation spaceborne SAR system[C]. Proceedings of EUSAR 2016: 11th European Conference on Synthetic Aperture Radar, Hamburg, 2016: 1–5.
( 0) 0)
|
| [5] |
范强, 吕晓德, 张平, 等. 星载SAR DPCMAB技术的方位向非均匀采样研究[J].
电子与信息学报, 2006, 28(1): 31-35. Fan Qiang, Lü Xiao-de, Zhang Ping, et al.. Study of nonuniform azimuth sampling of DPCMAB technique in spaceborne SAR[J]. Journal of Electronics & Information Technology, 2006, 28(1): 31-35. (  0) 0)
|
| [6] |
Currie A and Brown M A. Wide-swath SAR[J].
IEE Proceedings F-Radar and Signal Processing, 1992, 139(2): 122-135. DOI:10.1049/ip-f-2.1992.0016 ( 0) 0)
|
| [7] |
Yen J. On nonuniform sampling of bandwidth-limited signals[J].
IRE Transactions on Circuit Theory, 1956, 3(4): 251-257. DOI:10.1109/TCT.1956.1086325 ( 0) 0)
|
| [8] |
Gebert N, Krieger G and Moreira A. Digital beamforming on receive: Techniques and optimization strategies for high-resolution wide-swath SAR imaging[J].
IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(2): 564-592. DOI:10.1109/TAES.2009.5089542 ( 0) 0)
|
| [9] |
Krieger G, Gebert N and Moreira A. Unambiguous SAR signal reconstruction from nonuniform displaced phase center sampling[J].
IEEE Geoscience and Remote Sensing Letters, 2004, 1(4): 260-264. DOI:10.1109/LGRS.2004.832700 ( 0) 0)
|
| [10] |
Cheng Pu, Wan Jian-wei, Xin Qin, et al.. An improved azimuth reconstruction method for multichannel SAR using vandermonde matrix[J].
IEEE Geoscience and Remote Sensing Letters, 2017, 14(1): 67-71. DOI:10.1109/LGRS.2016.2626309 ( 0) 0)
|
| [11] |
Liu Bao-chang and He Yi-jun. Improved DBF algorithm for multichannel high-resolution wide-swath SAR[J].
IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 1209-1225. DOI:10.1109/TGRS.2015.2476496 ( 0) 0)
|
| [12] |
Liu Na, Wang R, Deng Yun-kai, et al.. Modified multichannel reconstruction method of SAR with highly nonuniform spatial sampling[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(2): 617-627. DOI:10.1109/JSTARS.2016.2630048 ( 0) 0)
|
| [13] |
Wang Ming-jian, Yu Wei-dong, Wang R, et al.. Improved azimuth multichannel SAR imaging for configurations with redundant measurements[J].
IEEE Geoscience and Remote Sensing Letters, 2015, 12(8): 1610-1614. DOI:10.1109/LGRS.2015.2415511 ( 0) 0)
|
| [14] |
Cerutti-Maori D, Sikaneta I, Klare J, et al.. MIMO SAR processing for multichannel high-resolution wide-swath radars[J].
IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(8): 5034-5055. DOI:10.1109/TGRS.2013.2286520 ( 0) 0)
|
| [15] |
Sikaneta I, Gierull C H and Cerutti-Maori D. Optimum signal processing for multichannel SAR: With application to high-resolution wide-swath imaging[J].
IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(10): 6095-6109. DOI:10.1109/TGRS.2013.2294940 ( 0) 0)
|
| [16] |
Sikaneta I, Cerutti-Maori D, Klare J, et al.. Comparison of multi-channel high-resolution wide-swath SAR processing methods[C]. Proceedings of 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS) 2014, Quebec, 2014: 3834–3837. DOI: 10.1109/IGARSS.2014.6947320.
( 0) 0)
|
| [17] |
Zhao Shuo, Wang R, Deng Yun-kai, et al.. Modifications on multichannel reconstruction algorithm for SAR processing based on periodic nonuniform sampling theory and nonuniform fast Fourier transform[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(11): 4998-5006. DOI:10.1109/JSTARS.2015.2421303 ( 0) 0)
|




