Investigation on Processing Scheme for MIMO SAR with STSO Chirp Waveforms
1 引言
合成孔径雷达(Synthetic Aperture Radar, SAR)是一种主动式微波遥感系统,具有全天时、全天候的对地观测能力,在测绘、地面目标识别、自然灾害监测、军事侦察等领域具有重要的应用价值[1]。但是由于传统单通道合成孔径雷达不能同时获取方位向高分辨率和距离向宽测绘带的SAR图像[2],其有限的成像能力越来越不能满足人们对SAR图像质量的要求。随着多通道技术的发展和数字波束形成技术(Digital BeamForming, DBF)的应用,配备多个接收天线的SAR系统能够同时改善SAR图像的空间分辨率和测绘带宽度[3–5]。为了进一步提升成像性能,多发多收(Multiple-Input Multiple-Output, MIMO)体制的SAR系统成为未来新体制SAR发展方向上的研究热点[6–9]。MIMO SAR发射多个正交波形照射地面场景,利用所有天线接收回波并分离发射波形,能够获得最大化的空间自由度,从而具有潜力实现很多先进的成像模式[10,11],例如全极化高分宽幅成像模式、多模式混合成像等,因此MIMO SAR是未来遥感应用中能够满足用户矛盾需求的理想解决方案。
当前MIMO SAR系统所面临的主要挑战包括以下两个方面,合适的正交发射波形的设计以及相应的回波信号分离方法。根据Krieger在文献[12]中的分析,对分布目标场景成像时,不完全正交的发射波形之间的互相关积分能量将会分散开,导致SAR图像出现模糊效应。而对于完全正交波形,因为所占据的频谱相互分离,波形之间相干性很差,不利于实现MIMO SAR的应用价值。因此,设计占据相同频谱范围并能够有效分离的发射波形是实现MIMO SAR系统的基本要求。近年来,国内外学者提出和发展了许多有潜力的研究成果。由Kim提出的正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)波形[13,14]利用相互正交的子载频,能够确保波形之间的零互相关,但是如何减轻多普勒偏移的影响是一个需要仔细研究的课题。Alamouti波形[7,15,16]利用发射信号组合成的编码矩阵能够有效分离回波并获得高信噪比数据,但是如何保持稳定的通道响应是研究难点。除此之外,Krieger提出了一类新的短偏移正交(Short-Term Shift-Orthogonal, STSO)波形[12],不仅能够满足MIMO SAR波形设计的要求,而且避免了OFDM波形和Alamouti波形的缺陷。尽管利用数字波束形成技术分离STSO波形的概念已经提出,但是在MIMO SAR系统中实现这类波形的具体处理方案并未得到研究。
根据对发射波形信号模型的分析,该文提出采用多波束DBF技术来实现STSO波形的回波分离。考虑星载MIMO SAR的成像几何模型,提出实现STSO波形成像的具体处理方案,主要包括以下3个重要步骤:利用俯仰向的DBF技术分离不同波形的回波;在方位向对分离信号进行多通道数据重构;采用传统成像算法对重构数据进行成像。针对DBF处理步骤,该文给出了确保STSO波形有效分离的天线宽度限制条件,并详细阐述DBF加权系数的计算方法。针对方位向数据处理步骤,该文给出了MIMO SAR多通道数据重构矩阵。仿真实验证明该处理方案能够有效抑制STSO波形之间的相互干扰,并实现这类波形在MIMO SAR系统中的应用。
2 MIMO SAR系统模型和信号模型
2.1 MIMO SAR成像几何模型和天线结构
图1描述了两波形情况下的MIMO SAR成像几何模型和天线结构。接收天线在俯仰向具有Ne个子孔径,在方位向具有Na个子孔径。两个发射天线Tx 1(红色)和Tx 2(蓝色)分别发射波形1和波形2,所有接收天线接收地面场景回波,该系统在1个脉冲重复间隔(PRI)内能获得2Na–1个方位向等效相位中心。因此,MIMO SAR系统的脉冲重复频率相比传统单通道SAR系统的脉冲重复频率可降低
$1/\left( {2{N_{\rm{a}}} - 1} \right)$
![]()
![]() 倍,这也远低于单发多收SAR系统对脉冲重复频率的要求。受益于额外的等效相位中心数目,MIMO SAR能够实现很多有价值的应用,如提升高分宽幅成像性能、增强地面移动目标探测能力、提升全极化模式的成像性能等。
倍,这也远低于单发多收SAR系统对脉冲重复频率的要求。受益于额外的等效相位中心数目,MIMO SAR能够实现很多有价值的应用,如提升高分宽幅成像性能、增强地面移动目标探测能力、提升全极化模式的成像性能等。
2.2 短偏移正交波形的信号模型
短偏移正交波形是由相互循环时移的线性调频信号组成,两波形的信号模型表达式如下:
$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! {s_1}(t) = {\rm rect}\left( {\frac{t}{{{T_{\rm{p}}}}}} \right){\rm{exp}}({\rm j}{{π}} {k_{\rm{r}}}{t^2})$
![]()
![]()
|
(1) |
$\begin{aligned}{s_2}(t) = &{\rm rect}\left( {\frac{{t + {T_{\rm{p}}}/4}}{{{T_{\rm{p}}}/2}}} \right){\rm{exp}}({\rm j}{{π}} {k_{\rm{r}}}{(t + {T_{\rm{p}}}/2)^2})\\& + {\rm rect}\left( {\frac{{t - {T_{\rm{p}}}/4}}{{{T_{\rm{p}}}/2}}} \right){\rm{exp}}({\rm j}{{π}} {k_{\rm{r}}}{(t - {T_{\rm{p}}}/2)^2})\end{aligned}$
![]()
![]()
|
(2) |
其中,Tp为脉冲时宽,kr为调频率,rect(t)表示范围在[–0.5, 0.5]的归一化矩形窗。根据图2的STSO波形信号模型示意图、式(1)和式(2)可知,这类波形不仅占据相同时域范围,而且占据相同的频谱范围,因此有利于在MIMO SAR系统设计过程中减轻脉冲重复频率、发射功率等因素的限制。由于两波形的瞬时频率偏移很大,它们之间满足短偏移正交性质,其表达式如下:
$\int {{\mathop{\rm rect}\nolimits} \left( {\frac{{\Delta t}}{{{T_{\rm{p}}}/2}}} \right)} s_1^ * (t){s_{\rm{2}}}(t \!+\! \Delta t){\rm d}t \!=\! 0,\ \ \forall \Delta t \in {\mathbb{R}}$
![]()
![]()
|
(3) |
这意味着两波形之间存在一个相互正交的时间间隔
${{{T_{\rm{p}}}} \mathord{\left/ {\vphantom {{{T_{\rm{p}}}} 2}} \right.} 2}$
![]()
![]() ,在这个间隔内,两者之间的互相关积分为零。对式(1)和式(2)进行脉冲压缩处理可得:
,在这个间隔内,两者之间的互相关积分为零。对式(1)和式(2)进行脉冲压缩处理可得:
$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! {p_1}(t) = \sqrt {\left| {{k_{\rm{r}}}} \right|} {T_{\rm{p}}}{\rm{sinc(}}{k_{\rm{r}}}{T_{\rm{p}}}t{\rm{)}}$
![]()
![]()
|
(4) |
$\begin{aligned}{p_2}(t) = &\frac{{\sqrt {\left| {{k_{\rm{r}}}} \right|} {T_{\rm{p}}}}}{2}{\rm{sinc}}\left( {\frac{{{k_{\rm{r}}}{T_{\rm{p}}}}}{2}\left( {t + \frac{{{T_{\rm{p}}}}}{2}} \right)} \right) \\ &\cdot{\rm{exp}}\left( {\frac{{{\rm j}{{π}} {k_{\rm{r}}}{T_{\rm{p}}}t}}{2}} \right){\rm{ + }}\frac{{\sqrt {\left| {{k_{\rm{r}}}} \right|} {T_{\rm{p}}}}}{2}\\ &\cdot {\rm{sinc}}\left( {\frac{{{k_{\rm{r}}}{T_{\rm{p}}}}}{2}\left( {t - \frac{{{T_{\rm{p}}}}}{2}} \right)} \right){\rm{exp}}\left( {\frac{{ - {\rm j}{{π}} {k_{\rm{r}}}{T_{\rm{p}}}t}}{2}} \right)\end{aligned}$
![]()
![]()
|
(5) |
根据以上两式可知波形1和波形2的脉压结果峰值相距
${{{T_{\rm{p}}}} \mathord{\left/ {\vphantom {{{T_{\rm{p}}}} 2}} \right.} 2}$
![]()
![]() ,这意味着对于地面场景中双程回波时延相差
${{{T_{\rm{p}}}} \mathord{\left/ {\vphantom {{{T_{\rm{p}}}} 2}} \right.} 2}$
,这意味着对于地面场景中双程回波时延相差
${{{T_{\rm{p}}}} \mathord{\left/ {\vphantom {{{T_{\rm{p}}}} 2}} \right.} 2}$
![]()
![]() 的两个点目标,它们的回波脉压结果将相互重叠,导致SAR图像出现严重模糊。但是如果地面场景的回波时间范围小于半个脉宽,不同波形对应的接收回波距离向脉压结果将相互分离。如图2(d)所示,在这种情况下,波形1的脉压峰值将只处于灰色区域范围内,而波形2的脉压峰值将处于灰色区域之外。如图3所示,在实际情况下,星载SAR照射的地面场景远大于半个脉宽对应的地距范围,因此可以利用多波束DBF技术在俯仰向同时产生多个窄波束,将整个场景的回波在角度域进行分割,确保提取的回波角度范围受限于
${{{T_{\rm{p}}}} \mathord{\left/ {\vphantom {{{T_{\rm{p}}}} 2}} \right.} 2}$
的两个点目标,它们的回波脉压结果将相互重叠,导致SAR图像出现严重模糊。但是如果地面场景的回波时间范围小于半个脉宽,不同波形对应的接收回波距离向脉压结果将相互分离。如图2(d)所示,在这种情况下,波形1的脉压峰值将只处于灰色区域范围内,而波形2的脉压峰值将处于灰色区域之外。如图3所示,在实际情况下,星载SAR照射的地面场景远大于半个脉宽对应的地距范围,因此可以利用多波束DBF技术在俯仰向同时产生多个窄波束,将整个场景的回波在角度域进行分割,确保提取的回波角度范围受限于
${{{T_{\rm{p}}}} \mathord{\left/ {\vphantom {{{T_{\rm{p}}}} 2}} \right.} 2}$
![]()
![]() 对应的角度范围。所提取的回波角度范围可通过以下公式进行计算:
对应的角度范围。所提取的回波角度范围可通过以下公式进行计算:
$\theta (\tau ) = {\rm{acos}}\left( {\frac{{4{{({R_{\rm{E}}} + {H_{{\rm{orbit}}}})}^2} - 4R_{\rm{E}}^2 + {{({\rm c}\tau )}^2}}}{{4{\rm c}\tau ({R_{\rm{E}}} + {H_{{\rm{orbit}}}})}}} \right)$
![]()
![]()
|
(6) |
其中,
$\theta $
![]()
![]() 为星下点偏移角,
$\tau $
为星下点偏移角,
$\tau $
![]()
![]() 为目标回波时间,RE为地球半径,Horbit为轨道高度,c为光速。
为目标回波时间,RE为地球半径,Horbit为轨道高度,c为光速。
3 俯仰向DBF处理方法
3.1 接收天线宽度的限制条件
根据上节的分析可知,对于STSO波形,成像场景中任意点目标的干扰来源于与其相隔半个脉宽时间的回波信号,因此由DBF形成的接收窄波束的旁瓣将影响所提取的子测绘带的回波信号。如图4所示,由于旁瓣的存在,目标4的回波信号将受到目标1和7的回波信号的干扰。为了确保可靠的信号分离,接收天线宽度Hr需要满足以下限制条件:
${H_{\rm{r}}} \ge \frac{{8\lambda {R_{{\rm{far}}}}\tan ({\eta _{{\rm{far}}}})}}{{{\rm c}{T_{\rm{p}}}}}$
![]()
![]()
|
(7) |
其中,
$\lambda $
![]()
![]() 为波长,Rfar为最远斜距,
${\eta _{{\rm{far}}}}$
为波长,Rfar为最远斜距,
${\eta _{{\rm{far}}}}$
![]()
![]() 为最大入射角。式(7)的基本想法是确保所提取子测绘带回波信号的干扰信号位于接收波束的零点波束宽度范围外,其中零点波束宽度范围对应由半个脉宽时间间隔计算得到的角度范围。为了避免接收波束的栅瓣处于发射天线方向图的半功率波束宽度范围内,俯仰向接收天线子孔径宽度hr需要满足以下限制条件:
为最大入射角。式(7)的基本想法是确保所提取子测绘带回波信号的干扰信号位于接收波束的零点波束宽度范围外,其中零点波束宽度范围对应由半个脉宽时间间隔计算得到的角度范围。为了避免接收波束的栅瓣处于发射天线方向图的半功率波束宽度范围内,俯仰向接收天线子孔径宽度hr需要满足以下限制条件:
${h_{\rm{r}}} \le \frac{\lambda }{{2\sin ({{\bar \theta }_{{\rm{max}}}})}}$
![]()
![]()
|
(8) |
其中,
${\bar \theta _{{\rm{max}}}}$
![]()
![]() 为接收天线可调向的最大法线偏移角。根据式(7)和式(8)可计算得到俯仰向接收天线子孔径的数目
${N_{\rm{e}}} = {\rm{ceil}}\left( {{{{H_{\rm{r}}}} \mathord{\left/ {\vphantom {{{H_{\rm{r}}}} {{h_{\rm{r}}}}}} \right.} {{h_{\rm{r}}}}}} \right)$
为接收天线可调向的最大法线偏移角。根据式(7)和式(8)可计算得到俯仰向接收天线子孔径的数目
${N_{\rm{e}}} = {\rm{ceil}}\left( {{{{H_{\rm{r}}}} \mathord{\left/ {\vphantom {{{H_{\rm{r}}}} {{h_{\rm{r}}}}}} \right.} {{h_{\rm{r}}}}}} \right)$
![]()
![]() ,其中
${\rm{ceil}}( \cdot )$
,其中
${\rm{ceil}}( \cdot )$
![]()
![]() 表示向上取整。
表示向上取整。
3.2 DBF加权系数的计算
理想情况下,如果DBF形成的俯仰向接收波束方向图具有矩形窗的幅度分布,那么所提取的子测绘带的回波信号将不存在干扰。但是实际雷达系统无法实现如同矩形窗的窄波束,因此需要使用最优阵列处理的算法来进行逼近处理[17]。考虑具有Dolph-Chebychev幅度分布的波束方向图能够在指定峰值旁瓣比的条件下得到最小的零点波束宽度,采用这种加权方法符合利用多波束DBF提取STSO回波信号的要求。为了便于讨论,本文将首先推导计算天线法线方向的接收波束方向图的DBF加权系数。假设天线法线方向对应的场景中心目标的回波时间为tc,所需提取的子测绘带对应的回波时间范围为
$\left( {{t_{\rm{c}}} - {{{T_{\rm{p}}}} \mathord{\left/ {\vphantom {{{T_{\rm{p}}}} 4}} \right.} 4},\;{t_{\rm{c}}} + {{{T_{\rm{p}}}} \mathord{\left/ {\vphantom {{{T_{\rm{p}}}} 4}} \right.} 4}} \right)$
![]()
![]() ,利用式(6)可计算得到相应的法线偏移角范围
$ {\bar \theta _{{\rm{NN}}}}$
,利用式(6)可计算得到相应的法线偏移角范围
$ {\bar \theta _{{\rm{NN}}}}$
![]()
![]() ,这相当于DBF接收波束的零点波束宽度。假设天线俯仰向子孔径的数目Ne为奇数,加权系数w0的计算公式如下:
,这相当于DBF接收波束的零点波束宽度。假设天线俯仰向子孔径的数目Ne为奇数,加权系数w0的计算公式如下:
${{w}_0} = {\left[ {{{V}^{\rm{H}}}(\psi )} \right]^{ - 1}}{{I}_{{{{N}}_{\rm{e}}} \times 1}}$
![]()
![]()
|
(9) |
$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! {V}(\psi ) = \left[ {\begin{array}{*{20}{c}}{\bar{ {v}}(0)} ·\!·\!· {\bar{ {v}}({\psi _m})} ·\!·\!· {\bar{ {v}}({\psi _{{N_{\rm{e}}} - {\rm{1}}}})}\end{array}} \right]$
![]()
![]()
|
(10) |
$\begin{aligned}{\bar{ {v}}({\psi _m})} = \!\!& \left[\exp \left( - {\rm j}\left(\frac{{{N_{\rm{e}}} - 1}}{2}\right){\psi _m}\right){\rm{ }} ·\!·\!· {\rm{ }}\right.\\& \exp \left({\rm j} \left(n - \frac{{{N_{\rm{e}}} + 1}}{2}\right){\psi _m}\right){\rm{ }} ·\!· · \\& {\left. \exp \left({\rm j}\left(\frac{{{N_{\rm{e}}} - 1}}{2}\right){\psi _m}\right) \right]^{\rm{T}}}\!\!\!{\rm{, }} \ n = 1,{\rm{ }} ·\!· · ,{\rm{ }}{N_{\rm{e}}}\end{aligned}$
![]()
![]()
|
(11) |
$\begin{aligned}{\psi _m} = 2{\rm{acos}}\left( {\frac{{\cos \left( {\displaystyle \frac{{{{π}} {h_{\rm{r}}}\sin ({{\bar \theta }_{{\rm{NN}}}}/2)}}{\lambda }} \right){\rm cos}\left( {\displaystyle \frac{{(2m - 1){{π}} }}{{({N_{\rm{e}}} - 1)2}}} \right)}}{{\cos \left( {\displaystyle \frac{{{π}} }{{2({N_{\rm{e}}} - 1)}}} \right)}}} \right),\ \ m = 1,{\rm{ }} ·\!· · ,{\rm{ }}{N_{\rm{e}}} - 1\end{aligned}$
![]()
![]()
|
(12) |
${{I}_{{{{N}}_{\rm{e}}} \times 1}} = {\left[ {\begin{array}{*{20}{c}}1 & 0 & ·\!·\!· & 0\end{array}} \right]^{\rm{T}}}$
![]()
![]()
|
(13) |
其中,
${\left[ \cdot \right]^{\rm{H}}}$
![]()
![]() 为复共轭转置操作符,
${\left[ \cdot \right]^{\rm{T}}}$
为复共轭转置操作符,
${\left[ \cdot \right]^{\rm{T}}}$
![]()
![]() 为转置操作符。
为转置操作符。
如图5(a)所示,由Dolph-Chebychev加权系数(仿真参数参考表1)计算得到的波束方向图的主瓣对应于半个脉宽的角度范围。考虑主瓣半功率波束宽度范围外的幅度分布下降很快,为了确保可靠的模糊抑制,只提取3 dB角度范围
${\bar \theta _{{\rm{HP}}}}$
![]()
![]() 内的回波信号,对应于图5(a)中的金色区域。根据2.2节的分析,金色区域范围内的回波信号会受到来自相对时移
$ \pm {{{T_{\rm{p}}}} \mathord{\left/ {\vphantom {{{T_{\rm{p}}}} 2}} \right.} 2}$
内的回波信号,对应于图5(a)中的金色区域。根据2.2节的分析,金色区域范围内的回波信号会受到来自相对时移
$ \pm {{{T_{\rm{p}}}} \mathord{\left/ {\vphantom {{{T_{\rm{p}}}} 2}} \right.} 2}$
![]()
![]() 回波信号的干扰,即图5(a)中的灰色区域。对比金色区域和灰色区域的幅度分布可知,干扰信号受到的幅度加权远小于提取信号的幅度加权,因此可以确保STSO波形之间的相互干扰得到有效抑制。如图5(b)所示,为了减轻所提取回波信号的幅度波动,将相邻
$ \pm {\rm{ }}{{{{\bar \theta }_{{\rm{HP}}}}} \mathord{\left/ {\vphantom {{{{\bar \theta }_{{\rm{HP}}}}} 2}} \right.} 2}$
回波信号的干扰,即图5(a)中的灰色区域。对比金色区域和灰色区域的幅度分布可知,干扰信号受到的幅度加权远小于提取信号的幅度加权,因此可以确保STSO波形之间的相互干扰得到有效抑制。如图5(b)所示,为了减轻所提取回波信号的幅度波动,将相邻
$ \pm {\rm{ }}{{{{\bar \theta }_{{\rm{HP}}}}} \mathord{\left/ {\vphantom {{{{\bar \theta }_{{\rm{HP}}}}} 2}} \right.} 2}$
![]()
![]() 的3个波束方向图进行叠加。考虑中间波束方向图的加权系数为w0,左右两侧相邻波束方向图的加权系数的计算公式分别为
$\displaystyle {{w}_{{\rm{left}}}} = {{w}_0} \odot {\left({v}\left( - {\rm{ }}{{{{\bar \theta }_{{\rm{HP}}}}} \mathord{\left/ {\vphantom {{{{\bar \theta }_{{\rm{HP}}}}} 2}} \right.} 2}\right)\right)^ * }$
的3个波束方向图进行叠加。考虑中间波束方向图的加权系数为w0,左右两侧相邻波束方向图的加权系数的计算公式分别为
$\displaystyle {{w}_{{\rm{left}}}} = {{w}_0} \odot {\left({v}\left( - {\rm{ }}{{{{\bar \theta }_{{\rm{HP}}}}} \mathord{\left/ {\vphantom {{{{\bar \theta }_{{\rm{HP}}}}} 2}} \right.} 2}\right)\right)^ * }$
![]()
![]() 和
$\displaystyle {{w}_{{\rm{right}}}} = {{w}_0} \odot $
和
$\displaystyle {{w}_{{\rm{right}}}} = {{w}_0} \odot $
![]()
![]() $ {\left({v}\left( {\rm{ }}{{{{\bar \theta }_{{\rm{HP}}}}} \mathord{\left/ {\vphantom {{{{\bar \theta }_{{\rm{HP}}}}} 2}} \right.} 2}\right)\right)^ * }$
$ {\left({v}\left( {\rm{ }}{{{{\bar \theta }_{{\rm{HP}}}}} \mathord{\left/ {\vphantom {{{{\bar \theta }_{{\rm{HP}}}}} 2}} \right.} 2}\right)\right)^ * }$
![]()
![]() ,
$ \odot $
,
$ \odot $
![]()
![]() 为Hadamard积,
${( \cdot )^*}$
为Hadamard积,
${( \cdot )^*}$
![]()
![]() 表示复共轭操作符,
${v}( \cdot )$
表示复共轭操作符,
${v}( \cdot )$
![]()
![]() 为导向矢量,其表达式为:
为导向矢量,其表达式为:
$\begin{align}
& v(\bar{\theta })=\left[ \exp \left( -\frac{\text{j}2\pi {{h}_{\text{r}}}\sin \bar{\theta }}{\lambda }\left( \frac{{{N}_{\text{e}}}-1}{2} \right) \right) \right. \\
& \cdots \ \exp \left( \frac{\text{j}2\pi {{h}_{\text{r}}}\sin \bar{\theta }}{\lambda }\left( n-\frac{{{N}_{\text{e}}}+1}{2} \right) \right) \\
& \cdots \ \exp {{\left( \frac{\text{j}2\pi {{h}_{\text{r}}}\sin \bar{\theta }}{\lambda }\left( \frac{{{N}_{\text{e}}}-1}{2} \right) \right)}^{\text{T}}}, \\
& n=1,\text{ }\cdots ,{{N}_{\text{e}}} \\
\end{align}$
![]()
![]()
|
(14) |
其中,
$\bar \theta $
![]()
![]() 为法线偏移角。由于接收天线法线方向波束方向图的加权系数可根据式(9)计算得到,成像场景中需要提取的其他子测绘带对应的波束方向图加权系数的计算公式可表示为
${w} = {{w}_0} \odot$
为法线偏移角。由于接收天线法线方向波束方向图的加权系数可根据式(9)计算得到,成像场景中需要提取的其他子测绘带对应的波束方向图加权系数的计算公式可表示为
${w} = {{w}_0} \odot$
![]()
![]() ${({v}(\bar \theta ))^ * }$
${({v}(\bar \theta ))^ * }$
![]()
![]() 。
。
4 主要处理流程
图6为基于STSO波形的MIMO SAR系统的主要处理流程,包含3个重要步骤:利用俯仰向的DBF技术分离两个波形的回波;在方位向对分离信号进行多通道数据重构;利用传统成像算法对重构数据进行成像。本节将详细推导俯仰向的STSO波形分离方法和方位向的多通道数据重构方法。
4.1 短偏移正交波形分离处理
如图3所示,MIMO SAR的接收天线在俯仰向由Ne个子孔径组成,第n个俯仰向子孔径接收到的回波信号可以表示为:
$\begin{aligned}{r_n}(t) = & \int_{{x_{{\rm{near}}}}}^{{x_{{\rm{far}}}}} {{A_{{\rm{2way}}}}} (\theta (x))\sigma (x){s_1}(t - {T_{{\rm{2way}}}}(x))\\ &\cdot {\rm{exp}}( - {\rm j}2{{π}} {f_{\rm{c}}}{T_{{\rm{2way}}}}(x))\\ &\cdot {\rm{exp}}\left( {\frac{{{\rm j}2{{π}} {f_{\rm{c}}}{h_n}\sin (\theta (x) - {\theta _{\rm{c}}})}}{\rm c}} \right){\rm{d}}x\\ & + \int_{{x_{{\rm{near}}}}}^{{x_{{\rm{far}}}}} {{A_{{\rm{2way}}}}} (\theta (x))\sigma (x){s_2}(t - {T_{{\rm{2way}}}}(x))\\ &\cdot {\rm{exp}}( - {\rm j}2{{π}} {f_{\rm{c}}}{T_{{\rm{2way}}}}(x))\\ &\cdot {\rm{exp}}\left( {\frac{{{\rm j}2{{π}} {f_{\rm{c}}}{h_n}\sin (\theta (x) - {\theta _{\rm{c}}})}}{\rm c}} \right){\rm{d}}x\end{aligned}$
![]()
![]()
|
(15) |
其中,
${A_{{\rm{2way}}}}(\theta (x))$
![]()
![]() 为俯仰向的双程天线方向图,
$\theta (x)$
为俯仰向的双程天线方向图,
$\theta (x)$
![]()
![]() 为星下点偏移角,x为地距,
$\sigma (x)$
为星下点偏移角,x为地距,
$\sigma (x)$
![]()
![]() 为地面场景的后向散射系数,
${T_{{\rm{2way}}}}(x)$
为地面场景的后向散射系数,
${T_{{\rm{2way}}}}(x)$
![]()
![]() 为目标回波双程时延,fc为载频,
${\theta _{\rm{c}}}$
为目标回波双程时延,fc为载频,
${\theta _{\rm{c}}}$
![]()
![]() 为场景中心的星下点偏移角。
${{h}_{n}}=\left( n-\left( {{N}_{\text{e}}}+1 \right)/2 \right){{h}_{\text{r}}}$
为场景中心的星下点偏移角。
${{h}_{n}}=\left( n-\left( {{N}_{\text{e}}}+1 \right)/2 \right){{h}_{\text{r}}}$
![]()
![]() ,表示俯仰向第n个子孔径相对俯仰向中间子孔径的距离。考虑所有俯仰向子孔径的接收回波可得:
,表示俯仰向第n个子孔径相对俯仰向中间子孔径的距离。考虑所有俯仰向子孔径的接收回波可得:
${r} = {\left[ {\begin{array}{*{20}{c}}{{r_1}(t)} & {{r_2}(t)} & ·\!·\!· & {{r_{{N_{\rm{e}}}}}(t)}\end{array}} \right]^{\rm{T}}}$
![]()
![]()
|
(16) |
根据前两节的分析,为了确保STSO波形的脉压结果相互分离,需要利用多波束DBF技术提取小于
${{{T_{\rm{p}}}} \mathord{\left/ {\vphantom {{{T_{\rm{p}}}} 2}} \right.} 2}$
![]()
![]() 对应角度范围的子测绘带回波。为了便于论述,该节将首先推导提取图4所示的子测绘带回波。假设该子测绘带中心的法线偏移角为
${\bar \theta _{{\rm{mid}}}}$
对应角度范围的子测绘带回波。为了便于论述,该节将首先推导提取图4所示的子测绘带回波。假设该子测绘带中心的法线偏移角为
${\bar \theta _{{\rm{mid}}}}$
![]()
![]() ,整个场景回波信号经过DBF处理得到:
,整个场景回波信号经过DBF处理得到:
${r_{{\rm{mid}}}}(t) = {{w}^{\rm{H}}}{r} = {({{w}_0} \odot {({v}({\bar \theta _{{\rm{mid}}}}))^ * })^{\rm{H}}}{r}$
![]()
![]()
|
(17) |
该子测绘带左右两侧的相邻子测绘带回波可表示为:
$\!{r_{{\rm{left}}}}(t) \!=\! {\left(\!{{w}_0} \!\odot\! {\left({v}\left({\bar \theta _{{\rm{mid}}}}\right)\right)^ * } \!\odot\! {\left(\!{v}\left( - \frac{{{{\bar \theta }_{{\rm{HP}}}}}}{2}\right)\right)^ * }\right)^{\rm{H}}}\!{r}$
![]()
![]()
|
(18) |
${r_{{\rm{right}}}}(t) \!=\!\! {\left(\!{{w}_0} \odot {\left({v}\left({\bar \theta _{{\rm{mid}}}}\right)\right)^ * }\! \odot\! {\left({v}\left(\frac{{{{\bar \theta }_{{\rm{HP}}}}}}{2}\right)\right)^ * }\right)^{\rm{H}}}\!{r}$
![]()
![]()
|
(19) |
为了减轻STSO波形之间的相互干扰,仅提取DBF接收波束3 dB角度范围内的回波信号,从这3个子测绘带回波中所提取的波形1可表示为:
$\begin{aligned}\!\!\!{\bar r_{{\rm{mid}}\_1}}(t) =& {{\cal F}^{ - 1}}\left\{ {{\cal F}\left\{ {{r_{{\rm{mid}}}}(t)} \right\}{S_{{\rm{MF}}}}(f)} \right\}\\ &\cdot {\rm{rect}}\left( {\frac{{t - {t_{{\rm{mid}}}}}}{{{T_{{\rm{mid}}}}}}} \right)\end{aligned}$
![]()
![]()
|
(20) |
$\begin{aligned}\!\!\!\!\!\!{\bar r_{{\rm{left}}\_1}}(t) = & {{\cal F}^{ - 1}}\left\{ {{\cal F}\left\{ {{r_{{\rm{left}}}}(t)} \right\}{S_{{\rm{MF}}}}(f)} \right\}\\ &\cdot {\rm{rect}}\left( {\frac{{t - {t_{{\rm{left}}}}}}{{{T_{{\rm{left}}}}}}} \right)\end{aligned}$
![]()
![]()
|
(21) |
$\begin{aligned}{\bar r_{{\rm{right\_1}}}}(t) = &{{\cal F}^{ - 1}}\left\{ {{\cal F}\left\{ {{r_{{\rm{right}}}}(t)} \right\}{S_{{\rm{MF}}}}(f)} \right\}\\ &\cdot {\rm{rect}}\left( {\frac{{t - {t_{{\rm{right}}}}}}{{{T_{{\rm{right}}}}}}} \right)\end{aligned}$
![]()
![]()
|
(22) |
其中,
${\cal F}\left\{ \cdot \right\}$
![]()
![]() 和
${{\cal F}^{ - 1}}\left\{ \cdot \right\}$
和
${{\cal F}^{ - 1}}\left\{ \cdot \right\}$
![]()
![]() 分别表示傅里叶变换和傅里叶逆变换,SMF表示波形1匹配滤波器的频域形式。tmid, tleft和tright分别表示这3个相邻子测绘带中心的双程时延。Tmid, Tleft和Tright分别表示这3个子测绘带需要提取的回波时间间隔。从这3个子测绘带回波中所提取的波形2可表示为:.
分别表示傅里叶变换和傅里叶逆变换,SMF表示波形1匹配滤波器的频域形式。tmid, tleft和tright分别表示这3个相邻子测绘带中心的双程时延。Tmid, Tleft和Tright分别表示这3个子测绘带需要提取的回波时间间隔。从这3个子测绘带回波中所提取的波形2可表示为:.
$\begin{aligned}{{\bar r}_{{\rm{mid\_2}}}}(t) =& {{\cal F}^{ - 1}}\left\{ {{\cal F}\left\{ {{r_{{\rm{mid}}}}(t)} \right\}{S_{{\rm{MF}}}}(f)} \right.\\&\left. \cdot ( {\rm{exp}}( - {\rm j}{π} f{T_{\rm{p}}}) + {\rm{exp}}({\rm j}{π} f{T_{\rm{p}}}))\right\}\\& \cdot{\rm{rect}}\left(\frac{{t - {t_{{\rm{mid}}}}}}{{{T_{{\rm{mid}}}}}}\right)\end{aligned}$
![]()
![]()
|
(23) |
$\begin{aligned}{{\bar r}_{{\rm{left\_}}2}}(t) =& {{\cal F}^{ - 1}}\left\{ {{\cal F}\left\{ {{r_{{\rm{left}}}}(t)} \right\}{S_{{\rm{MF}}}}(f)} \right.\\&\left. \cdot( {\rm{exp}}( - {\rm j}{π} f{T_{\rm{p}}}) + {\rm{exp}}({\rm j}{π} f{T_{\rm{p}}})) \right\}\\& \cdot{\rm{rect}}\left(\frac{{t - {t_{{\rm{left}}}}}}{{{T_{{\rm{left}}}}}}\right)\end{aligned}$
![]()
![]()
|
(24) |
$\begin{aligned}{{\bar r}_{{\rm{right}}\_2}}(t) =& {{\cal F}^{ - 1}}\left\{ {{\cal F}\left\{ {{r_{{\rm{right}}}}(t)} \right\}{S_{{\rm{MF}}}}(f)} \right.\\& \left.\cdot ( {\rm{exp}}( - {\rm j}{π} f{T_{\rm{p}}}) + {\rm{exp}}({\rm j}{π} f{T_{\rm{p}}}))\right\}\\& \cdot{\rm{rect}}\left(\frac{{t - {t_{{\rm{right}}}}}}{{{T_{{\rm{right}}}}}}\right)\end{aligned}$
![]()
![]()
|
(25) |
由3.2节可知,为了降低中间子测绘带提取信号的幅度波动,将相邻3个子测绘带提取回波的脉压结果进行叠加处理,可得到中间子测绘带的波形1, 2的脉压结果:
$\begin{aligned}{\overline{\overline r} _{{\rm{mid\_1}}}}(t) =& \left( {{{\bar r}_{{\rm{mid\_1}}}}(t) + {{\bar r}_{{\rm{left\_1}}}}(t) + {{\bar r}_{{\rm{right\_1}}}}(t)} \right)\\&\cdot {\rm{rect}}\left( {\frac{{t - {t_{{\rm{mid}}}}}}{{{T_{{\rm{mid}}}}}}} \right)\end{aligned}$
![]()
![]()
|
(26) |
$\begin{aligned}{\overline{\overline r}_{{\rm{mid\_2}}}}(t) =& \left( {{{\bar r}_{{\rm{mid\_2}}}}(t) + {{\bar r}_{{\rm{left\_2}}}}(t) + {{\bar r}_{{\rm{right\_2}}}}(t)} \right)\\&\cdot {\rm{rect}}\left( {\frac{{t - {t_{{\rm{mid}}}}}}{{{T_{{\rm{mid}}}}}}} \right)\end{aligned}$
![]()
![]()
|
(27) |
重复以上步骤,对整个成像场景回波进行STSO波形分离处理,最终可得到两种波形的脉压结果。为了便于应用传统成像算法进行成像处理,将两种波形的距离向脉压结果转换为未脉压的原始回波信号。STSO波形分离处理的系统框图如图7所示。
4.2 方位向多通道数据重构处理
根据MIMO SAR的脉冲重复周期和天线结构,方位向多通道数据需要被重构处理以恢复回波信号的多普勒频谱[18]。为了便于论述,本节将推导点目标的情况。如图1所示,方位向第na个子孔径接收到波形1的回波信号为:
$\begin{aligned}{{\bar h}_{{\rm{Tx}}1,{n_{\rm a}}}}(t) = & \exp \left( { - {\rm j}\frac{{2{π} }}{\lambda }\left( {\sqrt {V_{\rm{a}}^2{t^2} + {R_{{\rm{Tx}}}}\!\!\!\!\!^{{2}}} } \right.} \right.\\ &\left. {\left. { + \sqrt {{{({V_{\rm{a}}}t + \Delta {X_{{n_{\rm{a}}}}})}^2} + {R_{{\rm{Tx}}}}\!\!\!\!\!^{{2}}} } \right)} \right)\end{aligned}$
![]()
![]()
|
(28) |
其中,Va为平台速度。
$\Delta {X_{{n_{\rm{a}}}}} = ({n_{\rm{a}}} - 1) \cdot {l_{\rm a}}$
![]()
![]() ,表示方位向第na个子孔径与发射天线Tx 1之间的距离,la为方位向接收子孔径的长度。将上式进行泰勒级数展开得到:
,表示方位向第na个子孔径与发射天线Tx 1之间的距离,la为方位向接收子孔径的长度。将上式进行泰勒级数展开得到:
$ \begin{aligned} {{\bar h}_{{\rm{Tx}}1,{n_{\rm a}}}}(t) \approx &\! \ {\rm{exp}} \left(\frac{{ - {\rm j}{π} \Delta X_{{n_{\rm{a}}}}^2}}{{2\lambda {R_{{\rm{Tx}}}}}}\right) {\rm{exp}}\left( - \frac{{{\rm j}4{π} {R_{{\rm{Tx}}}}}}{\lambda }\right)\\& \cdot {\rm{exp}}\left( - \frac{{{\rm j}2{π} V_{\rm{a}}^2{{\left(t + \displaystyle\frac{{\Delta {X_{{n_{\rm{a}}}}}}}{{2{V_{\rm{a}}}}}\right)}^2}}}{{\lambda {R_{{\rm{Tx}}}}}}\right)\\ \approx &\exp\! \left(\!\frac{{ - {\rm j}{π} \Delta X_{{n_{\rm{a}}}}^2}}{{2\lambda {R_{{\rm{Tx}}}}}}\!\right)\!{{\bar h}_{{\rm{conv}}}}\left(t \!+\! \frac{{\Delta {X_{{n_{\rm{a}}}}}}}{{2{V_{\rm{a}}}}}\right)\quad\quad\end{aligned}$
![]()
![]()
|
(29) |
${\bar h_{{\rm{conv}}}}(t) = {\rm{exp}}\left( { - \frac{{{\rm j}4{{π}} {R_{{\rm{Tx}}}}}}{\lambda }} \right) {\rm{exp}}\left( { - \frac{{{\rm j}2{{π}} V_{\rm{a}}^2{t^2}}}{{\lambda {R_{{\rm{Tx}}}}}}} \right)$
![]()
![]()
|
(30) |
其中,
${\bar h_{{\rm{conv}}}}(t)$
![]()
![]() 表示传统单通道SAR的点目标响应。方位向第na个子孔径接收到波形2回波信号为:
表示传统单通道SAR的点目标响应。方位向第na个子孔径接收到波形2回波信号为:
$\begin{aligned}{{\bar h}_{{\rm{Tx2}},{n_{\rm a}}}}(t) = &\exp \left( { - {\rm j}\frac{{2{{π}} }}{\lambda }\left( {\sqrt {{{({V_{\rm{a}}}t + ({N_a} - 1){l_a})}^2} + {R_{{\rm{Tx}}}}\!\!\!\!\!^{{2}}} + \sqrt {{{({V_{\rm{a}}}t + \Delta {X_{{n_{\rm{a}}}}})}^2} + {R_{{\rm{Tx}}}}\!\!\!\!\!^{{2}}} } \right)} \right)\\ \approx &\exp \left( {\frac{{ - {\rm j}{{π}} {{(({N_{\rm a}} - {n_{\rm{a}}}){l_{\rm a}})}^2}}}{{2\lambda {R_{{\rm{Tx}}}}}}} \right) \cdot {{\bar h}_{{\rm{conv}}}}\left( {t + \frac{{(\Delta {X_{{n_{\rm{a}}}}} + ({N_{\rm a}} - 1){l_{\rm a}})}}{{2{V_{\rm{a}}}}}} \right)\end{aligned}$
![]()
![]()
|
(31) |
对比式(29)和式(31)可知,
${\bar h_{{\rm{Tx}}1,{N_{\rm a}}}} (t) = {\bar h_{{\rm{Tx2}},1}}(t)$
![]()
![]() ,这意味着在1个脉冲重复间隔内波形1和2的等效相位中心在中间相互重叠,如图1所示。因此,MIMO SAR系统在1个脉冲重复间隔内可得到2Na–1个方位向等效相位中心。考虑脉冲重复频率PRFsys满足不等式
$(2{N_{\rm{a}}} - 1){\rm{PR}}{{\rm{F}}_{{\rm{sys}}}} \ge {B_{\rm{a}}}$
,这意味着在1个脉冲重复间隔内波形1和2的等效相位中心在中间相互重叠,如图1所示。因此,MIMO SAR系统在1个脉冲重复间隔内可得到2Na–1个方位向等效相位中心。考虑脉冲重复频率PRFsys满足不等式
$(2{N_{\rm{a}}} - 1){\rm{PR}}{{\rm{F}}_{{\rm{sys}}}} \ge {B_{\rm{a}}}$
![]()
![]() 的情况,其中Ba表示多普勒带宽,该系统的传递函数矩阵
$\bar{ {H}}({f_{\rm {az}}})$
的情况,其中Ba表示多普勒带宽,该系统的传递函数矩阵
$\bar{ {H}}({f_{\rm {az}}})$
![]()
![]() 可表示为:
可表示为:
$\bar{ {H}}({f_{{\rm az}}}) = \left[ {\begin{array}{*{20}{c}}{{{\bar H}_1}({f_{{\rm az}}})} & ·\!·\!· & {{{\bar H}_{2{N_{\rm a}} - 1}}({f_{{\rm az}}})}\\ \vdots & \ddots & \vdots \\{{{\bar H}_1}({f_{{\rm az}}} + (2{N_{\rm a}} - 2){\rm{PR}}{{\rm{F}}_{{\rm{sys}}}})} & ·\!·\!· & {{{\bar H}_{2{N_{\rm a}} - 1}}({f_{{\rm az}}} + (2{N_{\rm a}} - 2){\rm{PR}}{{\rm{F}}_{{\rm{sys}}}})}\end{array}} \right]$
![]()
![]()
|
(32) |
$\!\!\!\!\!\!\!\!\!\!\!\!\!\! {\bar H_{{n_{{\rm{eq}}}}}}({f_{{\rm az}}}) = \left\{ \begin{array}{l}\exp \left( {\frac{{ - {\rm j}{{π}} {{(({n_{{\rm{eq}}}} - 1){l_{\rm a}})}^2}}}{{2\lambda {R_{{\rm{Tx}}}}}}} \right)\exp \left( {\frac{{{\rm j}2{{π}} {f_{{\rm az}}}(({n_{{\rm{eq}}}} - 1){l_{\rm a}})}}{{2{V_{\rm{a}}}}}} \right),\\ \quad\quad\quad {n_{{\rm{eq}}}} = 1, ·\!·\!· ,{N_{\rm{a}}}\\\exp \left( {\frac{{ - {\rm j}{{π}} {{((2{N_{\rm a}} - {n_{{\rm{eq}}}} - 1){l_{\rm a}})}^2}}}{{2\lambda {R_{{\rm{Tx}}}}}}} \right)\exp \left( {\frac{{{\rm j}2{{π}} {f_{{\rm az}}}(({n_{{\rm{eq}}}} - 1){l_{\rm a}})}}{{2{V_{\rm{a}}}}}} \right),\\\quad\quad\quad {n_{{\rm{eq}}}} = {N_{\rm{a}}} + 1, ·\!·\!· ,2{N_{\rm{a}}} - 1\end{array} \right.$
![]()
![]()
|
(33) |
假设系统传递函数矩阵
$\bar{ {H}}({f_{{\rm az}}})$
![]()
![]() 可求逆,由于通常情况下方位向原始数据是非均匀采样的,MIMO SAR回波信号的多普勒频谱需要使用重构矩阵
$\bar{ {P}}({f_{{\rm az}}}) = \bar{ {H}}{({f_{{\rm az}}})^{ - 1}}$
可求逆,由于通常情况下方位向原始数据是非均匀采样的,MIMO SAR回波信号的多普勒频谱需要使用重构矩阵
$\bar{ {P}}({f_{{\rm az}}}) = \bar{ {H}}{({f_{{\rm az}}})^{ - 1}}$
![]()
![]() 进行恢复,最终得到的重构数据可应用传统SAR成像算法进行处理。
进行恢复,最终得到的重构数据可应用传统SAR成像算法进行处理。
5 仿真实验
本节将通过一个X波段星载MIMO SAR系统来验证本文提出的处理方案。表1为系统参数,图8为系统所选波位。根据图1所示的天线结构示意图可知,接收天线在方位向由3个子孔径组成,因此该系统在一个脉冲重复间隔内可获取5个等效相位中心。为了确保回波信号在方位向过采样,系统脉冲重复频率需要满足不等式
$5{\rm{PR}}{{\rm{F}}_{{\rm{sys}}}} \ge {B_{\rm{a}}}$
![]()
![]() 。根据表1计算可得,方位向等效采样频率为4450 Hz,大于多普勒带宽3806 Hz,满足上述不等式。为了确保可靠的波形分离,接收天线宽度被设计为3.2 m,大于式(7)给出天线宽度下限3.05 m;而天线俯仰向子孔径的宽度被设计为0.0821 m,小于式(8)给出的俯仰向子孔径宽度上限0.11 m。如图9所示,根据天线参数计算得到的整个成像场景的距离模糊信号比(Range-Ambiguity-to-Signal Ratio, RASR)小于–33 dB,这确保了STSO波形之间的相互干扰能够得到充分抑制,保证MIMO SAR的图像质量。
。根据表1计算可得,方位向等效采样频率为4450 Hz,大于多普勒带宽3806 Hz,满足上述不等式。为了确保可靠的波形分离,接收天线宽度被设计为3.2 m,大于式(7)给出天线宽度下限3.05 m;而天线俯仰向子孔径的宽度被设计为0.0821 m,小于式(8)给出的俯仰向子孔径宽度上限0.11 m。如图9所示,根据天线参数计算得到的整个成像场景的距离模糊信号比(Range-Ambiguity-to-Signal Ratio, RASR)小于–33 dB,这确保了STSO波形之间的相互干扰能够得到充分抑制,保证MIMO SAR的图像质量。
表 1(Tab. 1
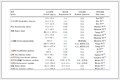
表 1 MIMO SAR系统参数
Tab. 1 MIMO SAR system parameters
| 参数 |
数值 |
| 轨道高度(km) |
500 |
| 卫星速度(m/s) |
7612 |
| 载频(GHz) |
9.65 |
| 视角范围(°) |
22.3–38.3 |
| 测绘带宽(km) |
200 |
| 信号带宽(MHz) |
75 |
| 脉冲宽度(μs) |
160 |
| 天线宽度(m) |
3.2 |
| 俯仰向子孔径数目 |
39 |
| 天线长度(m) |
12 |
| 方位向子孔径数目 |
3 |
| 多普勒带宽(Hz) |
3806 |
| 脉冲重复频率(Hz) |
890 |
|
表 1 MIMO SAR系统参数
Tab.1 MIMO SAR system parameters |
5.1 点目标仿真实验
本节将给出9点目标的仿真实验,图10为这些点目标的成像场景示意图。假设这些点目标的回波幅度都被归一化处理,在回波信号仿真中只考虑存在高斯白噪声。由图4和图10可见,成像场景中存在3个子测绘带,每个子测绘带包含3个点目标。根据这些点目标的斜距可计算得到,目标1, 4和7之间的双程时延差为
${{{T_{\rm{p}}}} \mathord{\left/ {\vphantom {{{T_{\rm{p}}}} 2}} \right.} 2}$
![]()
![]() ,目标2, 5和8之间的双程时延差为
${{{T_{\rm{p}}}} \mathord{\left/ {\vphantom {{{T_{\rm{p}}}} 2}} \right.} 2}$
,目标2, 5和8之间的双程时延差为
${{{T_{\rm{p}}}} \mathord{\left/ {\vphantom {{{T_{\rm{p}}}} 2}} \right.} 2}$
![]()
![]() ,目标3, 6和9之间的双程时延差为
${{{T_{\rm{p}}}} \mathord{\left/ {\vphantom {{{T_{\rm{p}}}} 2}} \right.} 2}$
,目标3, 6和9之间的双程时延差为
${{{T_{\rm{p}}}} \mathord{\left/ {\vphantom {{{T_{\rm{p}}}} 2}} \right.} 2}$
![]()
![]() 。根据第2节分析可知,STSO波形的相互干扰将存在于原始回波数据中。图11(a)为回波信号的实部,图11(b)为回波信号经过匹配滤波处理得到的距离向脉压结果。从图中可见9点目标回波的脉压结果相互重叠,并出现明显的虚假目标。使用多波束DBF提取中间子测绘带的回波,并对STSO波形进行分离处理,得到点目标4, 5, 6的两个波形距离向脉压结果。如图11(c)所示,点目标4, 5, 6的波形1脉压结果幅度存在明显起伏。经过相邻波束方向图的加权和叠加处理,这3个点目标的波形1脉压结果幅度起伏得到减轻,如图11(d)所示。图11(e)和图11(f)分别为波形1和波形2的9点目标距离向压缩结果,可以看出STSO波形的相互干扰被有效抑制,9点目标能被清楚辨别。对9点目标进行方位向多通道数据重构,用传统成像算法对重构数据进行成像处理,得到2维成像结果,如图12(a)所示。图12(b)、图12(c)和图12(d)分别是点目标2, 5和8的插值等高线图,表2为这3个点目标的图像质量参数,可以看出STSO波形的干扰能量被有效抑制,点目标聚焦良好,证明所提出的处理方案具有较好的成像性能。
。根据第2节分析可知,STSO波形的相互干扰将存在于原始回波数据中。图11(a)为回波信号的实部,图11(b)为回波信号经过匹配滤波处理得到的距离向脉压结果。从图中可见9点目标回波的脉压结果相互重叠,并出现明显的虚假目标。使用多波束DBF提取中间子测绘带的回波,并对STSO波形进行分离处理,得到点目标4, 5, 6的两个波形距离向脉压结果。如图11(c)所示,点目标4, 5, 6的波形1脉压结果幅度存在明显起伏。经过相邻波束方向图的加权和叠加处理,这3个点目标的波形1脉压结果幅度起伏得到减轻,如图11(d)所示。图11(e)和图11(f)分别为波形1和波形2的9点目标距离向压缩结果,可以看出STSO波形的相互干扰被有效抑制,9点目标能被清楚辨别。对9点目标进行方位向多通道数据重构,用传统成像算法对重构数据进行成像处理,得到2维成像结果,如图12(a)所示。图12(b)、图12(c)和图12(d)分别是点目标2, 5和8的插值等高线图,表2为这3个点目标的图像质量参数,可以看出STSO波形的干扰能量被有效抑制,点目标聚焦良好,证明所提出的处理方案具有较好的成像性能。
表 2(Tab. 2

表 2 点目标成像质量参数
Tab. 2 The imaging parameters of point targets
| 参数 |
目标2 |
目标5 |
目标8 |
| 距离向 |
PSLR (dB) |
–13.27 |
–13.26 |
–13.28 |
| ISLR (dB) |
–10.68 |
–10.67 |
–10.68 |
| 分辨率(m) |
1.81 |
1.79 |
1.80 |
| 方位向 |
PSLR (dB) |
–13.24 |
–13.25 |
–13.25 |
| ISLR (dB) |
–10.68 |
–10.66 |
–10.67 |
| 分辨率(m) |
1.79 |
1.80 |
1.81 |
|
表 2 点目标成像质量参数
Tab.2 The imaging parameters of point targets |
5.2 分布目标仿真实验
为了进一步验证所提出的处理方案,本节给出了分布目标的仿真试验结果。图13(a)为原始的SAR幅度图像。图13(b)为未经过处理的混合回波成像结果,可以看出STSO波形之间的干扰能量严重影响SAR图像的解译。使用本文提出的处理方案对分布目标混合回波进行处理后,得到的成像结果如图13(c)所示。对比图13(b)和图13(c)可见,针对基于STSO波形的MIMO SAR系统,该处理方案能够有效抑制波形之间的相互干扰,并且具有良好的成像性能。
6 结束语
本文提出了一种基于短偏移正交波形的MIMO SAR处理方案,该方案包含3个重要步骤:利用俯仰向的DBF技术分离两个波形的回波;在方位向对分离信号进行多通道数据重构;采用传统成像算法对重构数据进行成像。为了确保波形之间的干扰能够被有效抑制,本文分析了STSO波形信号模型,并给出了接收天线宽度的限制条件和DBF加权系数的计算方法。根据MIMO SAR的成像几何模型和天线结构,本文构建了方位向多通道数据重构矩阵。基于X波段的MIMO SAR系统对点目标和分布目标进行仿真实验,仿真结果表明本文所提处理方案能够有效对STSO波形进行分离和成像处理。在实际工程应用中,本文提出的处理方案还存在以下需要进一步研究的问题:(1)在系统设计中,为了确保发射波形的有效分离,需要增加接收天线的宽度和俯仰向子孔径的数目,这对平面天线的设计和星上数据处理能力提出了更高的要求,因此下一步将研究基于抛物面天线的MIMO SAR系统来降低系统实现复杂度;(2)由于地形起伏会加剧回波信号中STSO波形之间的干扰,下一步将研究结合数字高程图的DBF处理方案。