1 引言

干涉合成孔径雷达(Interferometric Synthetic Aperture Radar, InSAR)可以利用两幅SAR图像的复数据提取出相位信息以获取地表的高程信息，是对传统SAR成像技术的重要拓展^[1–3]。传统单基线InSAR技术利用相位解缠的方法求得干涉相位后，根据轨道参数及成像几何关系计算出相应的地形高程，即数字高程模型(Digital Elevation Model, DEM)。但是该方法建立在伊藤假设的基础上^[4]，即假定任意相邻两点的干涉相位差的绝对值小于 ${π} $ ，其本质是要求被测绘地区具有空间连续性，但在复杂场景区域(高山、城市等)，该假设通常不成立，此时相位解缠算法很难获得令人满意的结果^[5]。为解决这一问题，学者们提出了多基线干涉SAR技术，该技术可以有效地解决复杂地形的相位缠绕问题，从而提升高度重建精度^[6–9]。

目前，有很多利用多基线干涉SAR数据进行高度重建的技术得到了发展。理论上，当基线长度满足互质条件时，中国余数定理(Chinese Reminder Theorem, CRT)可被用于相位解缠^[10]，但是该算法噪声鲁棒性较差，实际应用中效果不佳。为解决这一问题，袁志辉等人提出了一种闭式解的鲁棒性CRT算法^[11]，得到了更高精度的DEM。通过研究多基线数据特有的聚类特性，于翰雯等人提出了一种基于聚类分析(Cluster-Analysis, CA)的多基线干涉SAR相位解缠算法^[12]，该算法运算速度较快但易受噪声干扰。为了提升CA算法的噪声鲁棒性，保铮等人提出了一种基于密度聚类的噪声鲁棒性相位解缠算法(Cluster-Analysis based Noise-Robust Phase-Unwrapping algorithm, CANOPUS)^[13]。近年来，通过求取概率极值完成高度重建的算法被广泛地研究，这些算法主要分为两种：较早的一种是基于最大似然(Maximum Likelihood, ML)估计的算法^[14]，这类算法可以在较短时间内重建出高度，但是其性能较依赖于干涉图的数目、工作频率、基线值和相干系数^[15]；另一类是基于最大后验(Maximum A Posterior, MAP)估计的算法^[16]，这类算法利用马尔可夫随机场统计分布模型来描述目标高度的先验分布，通过估计每个像素对应的超参数实现目标高度的估计。相比ML估计法，MAP估计法能够较精确地估计出高度，但是会产生运算复杂度变高、内存增加的问题^[17]。随后，又出现了一些MAP估计的改进算法^[18,19]。虽然基于MAP估计的方法比基于ML估计的方法精度高，但由于该方法需要重复迭代估计每个像素对应的超参数和高度值，因而存在运行时间长的缺陷，基于ML估计的方法则不存在这一缺点。

针对ML估计法精度不高、MAP估计法速度较慢的问题，本文提出了一种基于最大后验框架的聚类分析(Cluster-Analysis Based on Maximum A Posterior, CABMAP)高度重建算法。该算法首先利用ML估计法得到粗略的DEM后开始迭代，利用聚类分析判断噪声像素和非噪声像素后进行超参数估计，接着通过计算后验概率更新目标像素点的高度并以此为基础进行下一次迭代，重复上述步骤，直到满足阈值条件后终止算法得到最终重建结果。和ML估计法相比，CABMAP算法考虑了目标像素的先验分布，具有MAP估计法精度高的优势，并通过聚类分析区分了噪声像素和非噪声像素，比MAP估计法进一步地提升了重建精度；和MAP估计法相比，CABMAP算法以ML估计法得到的粗略DEM为基础，减少了MAP估计法重复迭代估计的次数，因此具有ML估计法运行速度快的优势。本文第2节简要介绍了基于ML估计的高度重建算法和基于MAP估计的高度重建算法，第3节详述CABMAP及其改进措施，第4节将分别给出仿真和实测实验的结果和分析，最后一节给出结论。

2 理论背景

本文提出的高度重建算法结合了ML估计法和MAP估计法的优点，因此在详细描述本文提出的算法之前，先简要介绍ML估计法和MAP估计法。

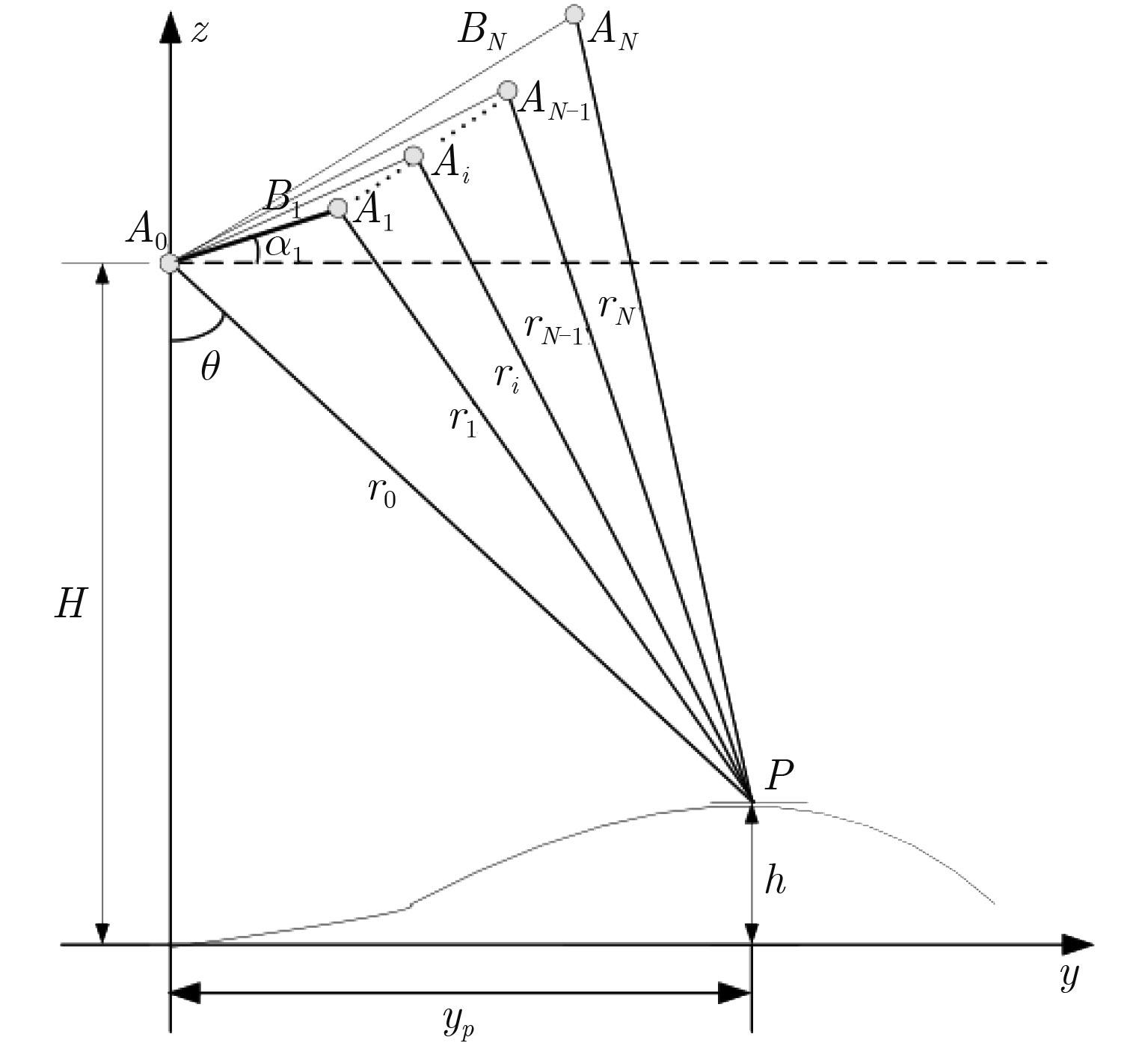
2.1 基于ML估计的多基线干涉SAR高度重建算法

多基线干涉SAR系统的几何示意图如图1所示，图中， ${A_0},{A_1}, ·\!·\!· ,{A_N}$ 为垂直于航迹方向的天线相位中心， $\theta $ 为主天线的侧视角， ${r_0},{r_1}, ·\!·\!· ,{r_N}$ 分别为地面某点P到 ${A_0},{A_1}, ·\!·\!· ,{A_N}$ 的斜距， ${y_p}$ 是地距，h为P点的高度值， ${A_1}, ·\!·\!· ,{A_N}$ 与 ${A_0}$ 分别形成稳定的干涉基线 ${B_1}, ·\!·\!· ,{B_N}$ ，对应的水平基线角分别为 ${\alpha _1},{\alpha _2}, ·\!·\!· ,{\alpha _N}$ 。

在多基线干涉SAR系统中，令 ${\varphi _l}(p)$ 为干涉图中像素p第l条基线对应的缠绕相位 $( - {π} \le {\phi _l}(p) \le {π} )$ , ${\phi _l}(p)$ 为像素p第l条基线对应的真实相位，那么缠绕相位和真实相位满足：

${\phi _l}(p) = 2{π} {K_l} + {\varphi _l}(p),\ \ \{ {K_l}|{K_l} \in N\} $

(1)

在基于ML估计的高度重建算法中，高程重建问题被转化成了一个寻找使似然函数最大化的高程值h(p)的问题，该似然函数可写成：

$\hat h(p) = \mathop {\arg \max }\limits_{{h}} F\left( {\varPhi \left( p \right)|h\left( p \right)} \right)$

(2)

其中， $\hat h(p)$ 是像素p的估计高度， $F\left( {\varPhi \left( p \right)|h\left( p \right)} \right)$ 为观测相位 $\varPhi \left( p \right)$ 关于真实高度 $h\left( p \right)$ 的概率密度。对多基线干涉SAR系统， $F\left( {\varPhi \left( p \right)|h\left( p \right)} \right)$ 可以近似看成K个独立的缠绕干涉相位观测值的乘积^[14]：

$F\left( {\varPhi \left( p \right)|h\left( p \right)} \right) = \prod\limits_{k = 1}^K {f({\phi _k}(p)|h(p))} $

(3)

对于K=1的特殊情况，式(3)可以写成^[14]：

$\begin{aligned}f(\phi (p)|h(p)) = & \frac{1}{{2{π} }}\frac{{1 - |\gamma {|^2}}}{{1 - |\gamma {|^2}{{\cos }^2}\left(\phi (p) - \displaystyle\frac{{4{π} {B_ \bot }}}{{\lambda {R_0}\sin \theta }}h(p)\right)}}\\& \cdot \left\{ {1 + \frac{{|\gamma |\cos \left(\phi (p) - \displaystyle\frac{{4{π} {B_ \bot }}}{{\lambda {R_0}\sin \theta }}h(p)\right){{\cos }^{ - 1}}\left[ - |\gamma |\cos \left(\phi (p) - \displaystyle\frac{{4{π} {B_ \bot }}}{{\lambda {R_0}\sin \theta }}h(p)\right)\right]}}{{{{\left[1 - |\gamma {|^2}{{\cos }^2}\left(\phi (p) - \displaystyle\frac{{4{π} {B_ \bot }}}{{\lambda {R_0}\sin \theta }}h(p)\right)\right]}^{1/2}}}}} \right\}\end{aligned}$

(4)

需注意，基于ML估计的重建算法速度较快，但是抗噪性能较差，且易受工作频率、基线数目和相干系数的影响^[20]。

2.2 基于MAP估计的多基线干涉SAR高度重建算法

基于MAP估计的高度重建算法认为目标高度是一个随机变量，并可用一个先验分布模型进行建模。通过引入关于地形高度的先验分布模型，寻找使后验概率最大化的高度 $h(p)$ ，从而达到高度重建的目的。假设目标区域的高度为一幅图像，所有像素的高度组成随机矢量H，而该随机矢量的一个具体实现形式为 ${h} = {[h(1),h(2),·\!·\!·,h(N \times M)]^{\rm T}}$ ，即其中的一个样本。如果对随机矢量H采用某种先验统计模型进行建模，且使某种样本h出现的概率达到最大，就可以使用最大后验估计的方法进行高程重建。马尔可夫随机场模型可以描述该矢量集合的分布，这种模型考虑了每个像素高度关于它的一组邻近像素高度的条件分布，可以有效地描述图像的局部特征，任何类型的马尔可夫随机场均可以用吉布斯分布的形式来表示^[17]：

$g({h};{σ} ) = \frac{1}{{Z({σ} )}}\exp \{ - \varepsilon ({h};{σ} )\} $

(5)

其中， $Z({σ} ) = \displaystyle\int {\exp \{ - \varepsilon ({h};{σ} )\} {\rm d}{h}} $ 是一个归一化因子，称为划分函数， $\varepsilon ( \cdot )$ 描述了相邻像素间的关系，称为能量函数， ${σ} $ 是未知参数的集合，称为超参数矢量。选取高斯马尔可夫随机场模型描述高程图像的特征^[16,21]：

$\varepsilon ({h};{σ} ) = \sum\limits_{p = 1}^{N \times M} {\sum\limits_{j \in {C_p}} {\frac{{{{(h(p) - h(j))}^2}}}{{2\sigma _{pj}^2}}} } $

(6)

其中， ${C_p}$ 为像素p对应的邻域系统^[17]，一般采用其周围的8个像素即可，而 ${\sigma _{pj}}$ 是超参数矢量 ${σ} $ 中的元素，描述了高度图像的局部空间变化特征。根据贝叶斯定律，多基线干涉SAR的后验概率密度函数可以写成^[21]：

$\begin{aligned} f({h}|{Φ} ) = & F({Φ} |{h}) \cdot g({h};{σ} )\\ = & \biggr\{ \prod\limits_{p = 1}^{N \times M} {\prod\limits_{k = 1}^K {f({\phi _k}(p)|h(p))\biggr\} \frac{1}{{Z({σ} )}}} } \\ & \cdot \exp \{ - \varepsilon ({h};{σ} )\} \end{aligned}$

(7)

其中， $F({Φ} |{h})$ 是最大似然项。可将高程重建问题转换成后验概率估计问题：

$\begin{array}{l}{\hat {h}} \!\! & = \mathop {\arg \max }\limits_{{h} \in {H}} f({h}|{Φ} ) = \mathop {\arg \max }\limits_{{h} \in {H}} [\ln f({{h}}|{Φ} )]\\& \!\!\!\! = \mathop {\arg \max }\limits_{{h} \in {H}} \left\{ {\sum\limits_{p = 1}^{N \times M} {\sum\limits_{k = 1}^K {\ln f({\phi _k}(p)|h(p))} } } \right.\\ & \!\!\!\!\!\!\!\!\!\!\!\!\! \left. { - \sum\limits_{p = 1}^{N \times M} {\sum\limits_{j \in {C_p}} {\frac{{{{(h(p) - h(j))}^2}}}{{2\sigma _{pj}^2}}} } } \right\}\end{array}$

(8)

有多种方法可以求解式(8)，如模拟退火算法^[17]，也可随机抽样后使用条件迭代模(Iterative Conditional Modes, ICM)算法进行求解^[16]。相比基于ML估计的方法，基于MAP估计的方法重建精度更高^[20]，但该方法需要重复迭代估计每个像素对应的超参数和高程值，因此算法速度较慢。

3 CABMAP算法及改进措施 3.1 CABMAP算法

基于ML估计的方法运行速度较快但精度较低，而基于MAP估计的方法精度较高、运行速度较慢。结合两种方法的优点，本文提出了CABMAP算法，该算法将ML估计法得到的粗略的地形高度作为初始高度，这样可以减少MAP估计法中重复迭代估计每个像素对应的高程值和超参数的次数，节约了算法的运行时间。将ML估计法得到的结果作为初始高度进行迭代，每次迭代中，利用聚类分析方法判断出噪声像素后利用MAP框架计算后验概率，取最大后验概率对应的高程值为该次迭代的结果，并以该结果为基础进行下一次迭代，直到迭代次数满足设定的阈值后结束算法，得到最终的高度重建结果。

基于MAP估计的方法利用了目标像素的邻域内所有的像素辅助重建^[16]，但是当其邻域中存在被噪声严重污染的像素时，目标像素的重建会受到严重干扰。为解决该问题，CABMAP算法采用了聚类的思想，对目标像素的邻域进行聚类处理，判断并剔除目标像素邻域内的噪声像素，有效地防止了噪声像素对结果的干扰，提高了重建精度。算法的具体步骤如下：

步骤1  设置算法的结束条件，当迭代次数达到N时结束；设置邻域内能聚成一类的高程差阈值为 $\Delta h$ ，邻域中能聚为一类的像素点个数阈值为 ${\rm{Hpt}}{{\rm{s}}_{{\rm{th}}}}$ 。将第i次迭代中的重建高度记为 ${{h}^{(i)}}$ ，超参数记为 ${{σ} ^{(i)}}$ 。首先利用ML估计出粗略的地形高度 ${{h}^{(0)}}$ 。

步骤2  对目标像素p，判断是否为噪声像素，若与其邻域 ${C_p}$ 中某个像素q的高程差不超过 $\Delta h$ ，则p, q判为一类。考查邻域中同类像素点的个数，如果不小于 ${\rm{Hpt}}{{\rm{s}}_{{\rm{th}}}}$ ，则像素p不是噪声像素，反之为噪声像素。下式中， ${\varOmega _{{\rm{noise}}}}$ 表示噪声像素的集合：

$\left\{ \begin{array}{l}\sum\limits_{q \in {C_p}} {f({h_p} - {h_q}} ) < {\rm{Hpt}}{{\rm{s}}_{{\rm{th}}}}, \ {\rm{ }}p \in {\varOmega _{{\rm{noise}}}}\\\sum\limits_{q \in {C_p}} {f({h_p} - {h_q}} ) \ge {\rm{Hpt}}{{\rm{s}}_{{\rm{th}}}}, \ {\rm{ }}p \notin {\varOmega _{{\rm{noise}}}}\end{array} \right.$

(9)

$f( \cdot )$ 为：

$f(x) = \left\{ \begin{array}{l}\!\!1, \ {\rm{ }}x \le \Delta h\\ \!\!0, \ {\rm{ }}x > \Delta h\end{array} \right.$

(10)

其中， ${\varOmega _{{\rm{noise}}}}$ 表示噪声像素的集合， $f({h_p} - {h_q}) = 1$ 表示像素p和像素q对应的高度差不超过 $\Delta h$ ，此时像素p和像素q判为一类， $f({h_p} - {h_q}) = 0$ 表示像素p和像素q对应的高度差超过 $\Delta h$ ，此时像素p和像素q不属于同一类。 $\sum\limits_{q \in {C_p}} {f({h_p} - {h_q}} )$ 表示目标像素p邻域内和p属于同一类的像素点个数，比较该值和 ${\rm{Hpt}}{{\rm{s}}_{{\rm{th}}}}$ ，若小于 ${\rm{Hpt}}{{\rm{s}}_{{\rm{th}}}}$ ，目标像素p则被判为噪声像素，否则为非噪声像素。

步骤3  对第i次迭代，如果像素p不是噪声像素，超参数 $\sigma {(p)^{(i)}}$ 可通过下式来估计：

$\sigma {(p)^{(i)}} = \frac{{\displaystyle\sum\limits_{j \in {C_p}} {{{\left(h{{(p)}^{(i)}} - h{{(j)}^{(i)}}\right)}^2}} }}{{|{{\tilde C}_p}|}}$

(11)

反之，如果像素p是噪声，超参数 $\hat \sigma {(p)^{(i)}}$ 可表示为：

$\sigma {(p)^{(i)}} = \frac{{\displaystyle\sum\limits_{j \in {C_p}} {{{\left(h{{(p)}^{(i)}} - h{{(j)}^{(i)}}\right)}^2}} }}{{|{C_p}|}}$

(12)

其中， $|{\tilde C_p}|$ 是非噪声目标像素邻域内同类像素的个数， $|{C_p}|$ 是噪声像素邻域内像素的个数。基于MAP的估计法中，估计超参数时没有区分噪声像素和非噪声像素，即在目标像素邻域内统一采用式(12)进行估计，这种做法会使被噪声严重污染的像素干扰目标像素的重建。CABMAP算法首先利用步骤2区分了噪声像素和非噪声像素，针对非噪声的目标像素，利用其邻域内的同类像素进行超参数估计，这样避免了噪声像素的干扰，而对噪声像素，则保留传统MAP估计法的处理方式，即采用式(12)进行超参数估计。

步骤4  估计出第i次迭代的高程。如果像素p是噪声像素，使用下式进行估计：

$h{(p)^{(i + 1)}} = \mathop {\arg \max }\limits_{{h} \in {H}} \left\{ {\ln F \left({Φ} (p)|h{{(p)}^{(i + 1)}}\right) - {{\sum\limits_{j \in {C_p}} {\left[ {\frac{{\left(h{{(p)}^{(i + 1)}} - h{{(j)}^{(i + 1)}}\right)}}{{\sqrt 2 \left(\displaystyle\frac{{\sigma {{(p)}^{(i + 1)}} + \sigma {{(j)}^{(i + 1)}}}}{2}\right)}}} \right]} }^2}} \right\}$

(13)

如果像素p不是噪声像素，则采用：

$h{(p)^{(i + 1)}} = \mathop {\arg \max }\limits_{{h} \in {H}} \left\{ {\ln {F_{MCh}}\left({Φ} (p)|h{{(p)}^{(i + 1)}}\right) - {{\sum\limits_{j \in {{\tilde C}_p}} {\left[ {\frac{{(h{{(p)}^{(i + 1)}} - h{{(j)}^{(i + 1)}}}}{{\sqrt 2 \left(\displaystyle\frac{{\sigma {{(p)}^{(i + 1)}} + \sigma {{(j)}^{(i + 1)}}}}{2}\right)}}} \right]} }^2}} \right\}$

(14)

对噪声像素，式(13)中邻域系统是 ${C_p}$ ，由目标像素的邻域像素构成；对非噪声像素，式(14)中邻域系统是 ${\tilde C_p}$ ，由 ${C_p}$ 中和目标像素同类的像素组成。在此步中，利用了噪声像素和非噪声像素的超参数，并根据噪声像素和非噪声像素不同的邻域特征进行高度重建，分别求式(13)、式(14)的极值从而得到此次迭代的高度重建结果。

步骤5  迭代次数加1，判断是否达到迭代阈值，如果达到结束算法，否则返回步骤2继续执行。

为了考查CABMAP算法的运行效率，需要量化分析该算法的时间复杂度。考虑在ML估计法中，令 ${{H}} = \{ {h_1},{h_2}, ·\!·\!· ,{h_L}\} $ 表示像素对应的候选高度值，干涉图大小为 ${\rm{row}} \times {\rm{col}}$ ，则ML估计法的时间复杂度为 $O(L \times {\rm{row}} \times {\rm{col}})$ , CABMAP算法ML估计法的结果上，进行聚类处理后计算后验概率，相比ML估计法，CABMAP算法增加了聚类步骤，令聚类迭代次数为N，则算法时间复杂度为 $O(L \times {\rm{row}} \times {\rm{col}} + N \times L \times {\rm{row}} \times {\rm{col}})$ ，当N取较小时，CABMAP算法运行时间和ML估计法近似。

3.2 改进措施

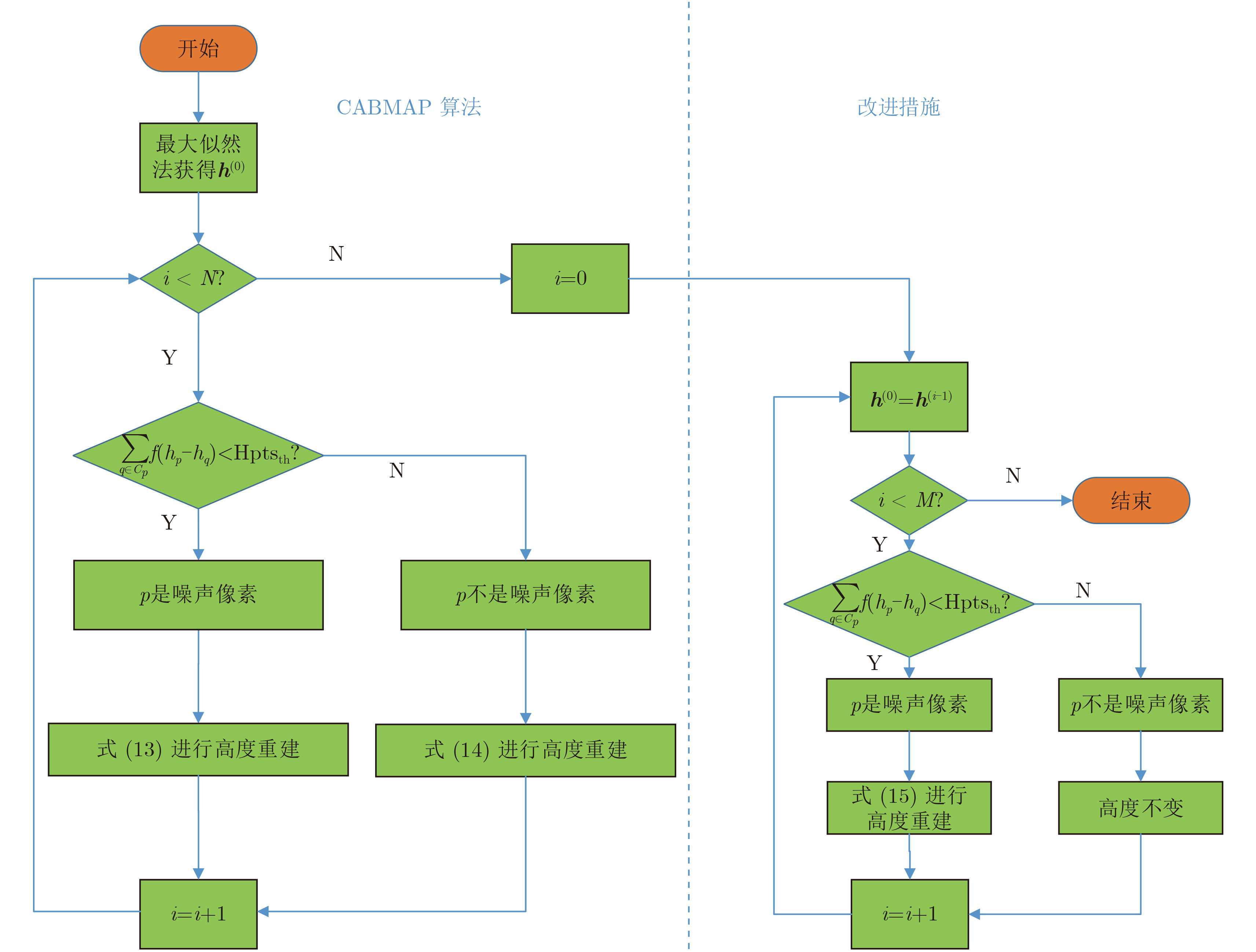
在CABMAP算法中，噪声像素的邻域中每个像素都对其重建有贡献，这种措施利用了噪声像素邻域中所有的像素进行均衡地重建，但却隐含着下列问题：当噪声像素的缠绕相位被严重污染时，后验概率中最大似然项的准确性会大大降低，此时即使利用了噪声像素的邻域特征作为先验项进行弥补，也无法准确地重建高度。为了解决该问题，本文在CABMAP算法的基础上加入了一种改进措施。图2是改进的CABMAP算法的流程图，其中虚线左边是CABMAP算法的流程，虚线右边是改进措施的流程。

具体的改进措施如下：

步骤1  设置算法的终止条件，当迭代次数达到M时结束。将CABMAP算法得到的高度作为初始的高度 ${{h}^{(0)}}$ 。

步骤2  对第i次迭代，判断像素p是否为噪声像素，具体判断方法仍如式(9)。若p是噪声像素，则采用均值滤波的方式对其进行高度重建，若p不是噪声像素，则保持高度不变。

${h_p}^{\!\!(i)} = \left\{ \begin{array}{l}\!\!\frac{1}{{|{{\tilde C}_p}|}}\sum\limits_{j \in {{\tilde C}_p}} {h_j^{(i - 1)}} , \ {\rm{ }}p \in {\varOmega _{{\rm{noise}}}}\\h_p^{(i - 1)}, \quad\quad\quad \ \, {\rm{ }}p \notin {\varOmega _{{\rm{noise}}}}\end{array} \right.$

(15)

其中， ${\tilde C_p}$ 表示邻域中能够聚成一类的像素， ${\varOmega _{{\rm{noise}}}}$ 为噪声像素的集合。 $h_p^{(i)}$ 为像素p第i次迭代的高度。

步骤3  迭代次数加1，判断是否达到阈值，如果达到则结束，否则转到步骤2继续执行。

4 实验结果与分析

本部分采用了仿真数据和实测数据进行实验，从算法运行时间、精度两个方面将本文提出的算法与其它几种算法进行对比，验证了该算法的可行性。另外，本文所有算法的实现均采用Matlab编程，并在内存为4 GB, CPU主频为3.2 GHz的主机上运行。

4.1 仿真实验

本文采用了一组接近真实地形的仿真数据进行实验，该仿真数据是根据美国Isolation Peak国家公园的真实数字高程得到的。仿真参数如表1所示，3条基线对应的高度模糊数分别为21.4 m, 32.1 m和53.5 m。图3(a)，图3(b)，图3(c)分别为仿真得到的3条不同基线对应的缠绕干涉相位图。图3(d)为Isolation Peak国家公园的真实DEM(458×157像素)。图3(d)右侧有一条垂直高度差达到137 m的悬崖，对应的干涉相位差分别为12.8 ${π} $ , 8.5 ${π} $ 和5.1 ${π} $ ，不满足相位连续性假设，不能使用传统的单基线相位解缠的方法对整个区域进行高程重建。

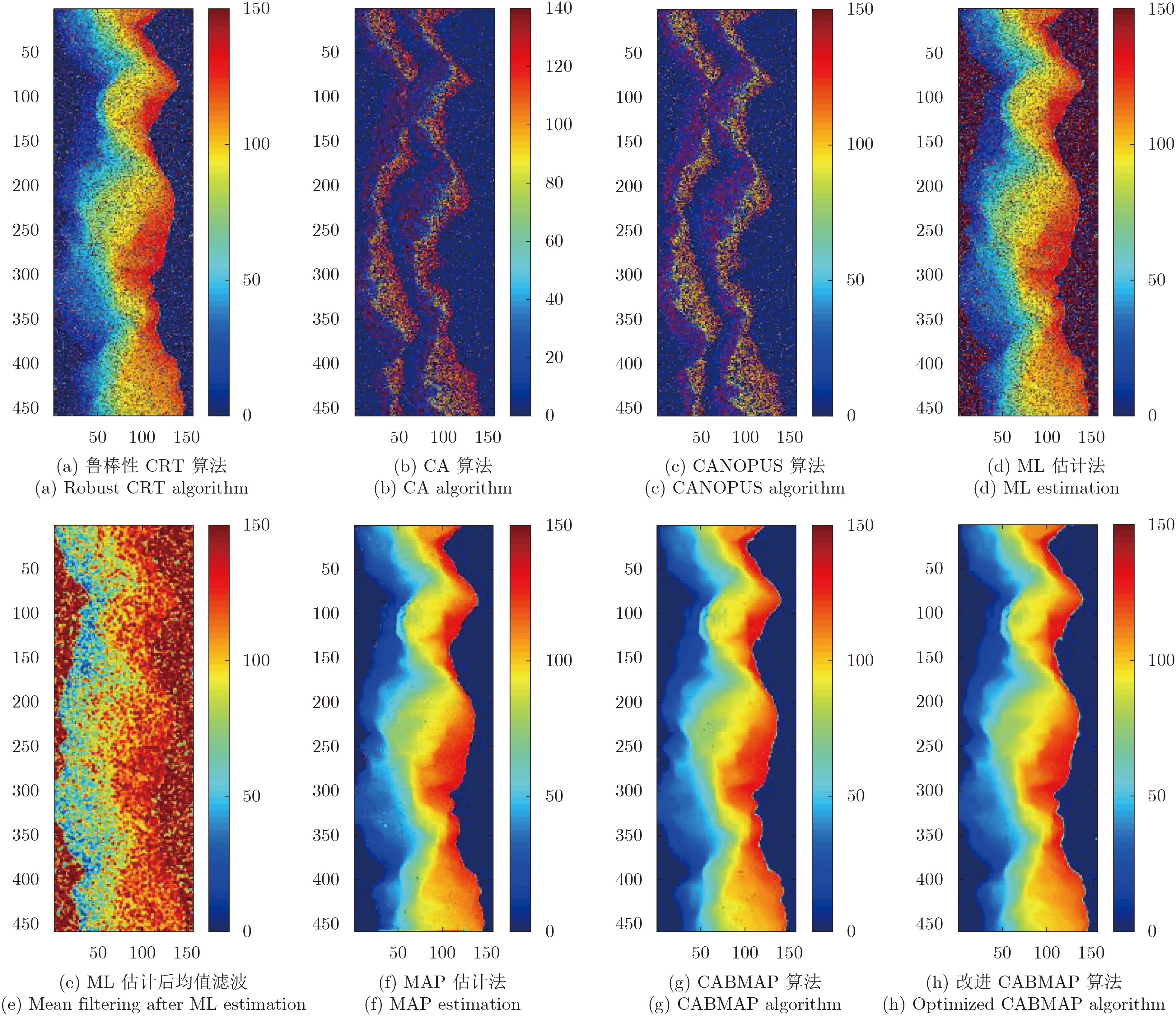
图4(a)–图4(h)分别是鲁棒性CRT, CA, CANOPUS, ML, ML估计后均值滤波、MAP估计、CABMAP及改进措施的高度重建结果。下面分别从精度和运行时间两个方面对上述算法的性能进行分析。采用归一化的均方误差来衡量精度，定义为： $\bar \varepsilon = \parallel {\hat {h}} - {h} {\parallel^2}/\parallel{h}{\parallel^2}$ ，其中h为各个像素的真实高度所组成的矩阵， ${\hat {h}}$ 为对应的估计值， ${\left\| \cdot \right\|^{\rm{2}}}$ 表示取范数的平方。在30 dB的信噪比水平下，这8种方法的归一化均方误差分别为1.2295, 0.9139, 0.8986, 3.8801, 2.0460, 0.0117, 0.0041, 0.0028，可以发现，采用本文方法得到的精度效果最好。其次，从运行时间来看，CA算法的速度最快，只要0.868110 s, MAP估计法则最慢，需要229.851504 s, CABMAP算法运行时间是22.921332 s，由于减少了重复估计每个像素的超参数次数，CABMAP算法运行速度快于MAP估计法，各算法的运行时间和精度具体见表2。从以上两个方面的对比分析，本文的算法在较短的时间内大大提高了重建精度，适用于多基线数据的处理。

为了探究噪声对重建精度的影响，分别对仿真数据加入不同程度的噪声后进行实验。仍然采用归一化均方误差作为精度指标。从表3中，在信噪比相同时，改进的CABMAP算法精度最高，其次是CABMAP算法。随着信噪比的增加，各算法的精度均会增加，对比各类算法的增速，CABMAP算法及改进措施的精度增速较快。综合以上两个方面，本文的算法可以在不同噪声水平的数据上均表现出良好的性能。

本文提出的CABMAP算法需要设置迭代次数N、高程差 $\Delta h$ 和阈值点数 ${\rm{Hpt}}{{\rm{s}}_{{\rm{th}}}}$ 3个参数，这些参数将会影响算法的高度重建结果，为了探究各参数对重建精度的影响，下面给出不同参数组合下的重建结果。

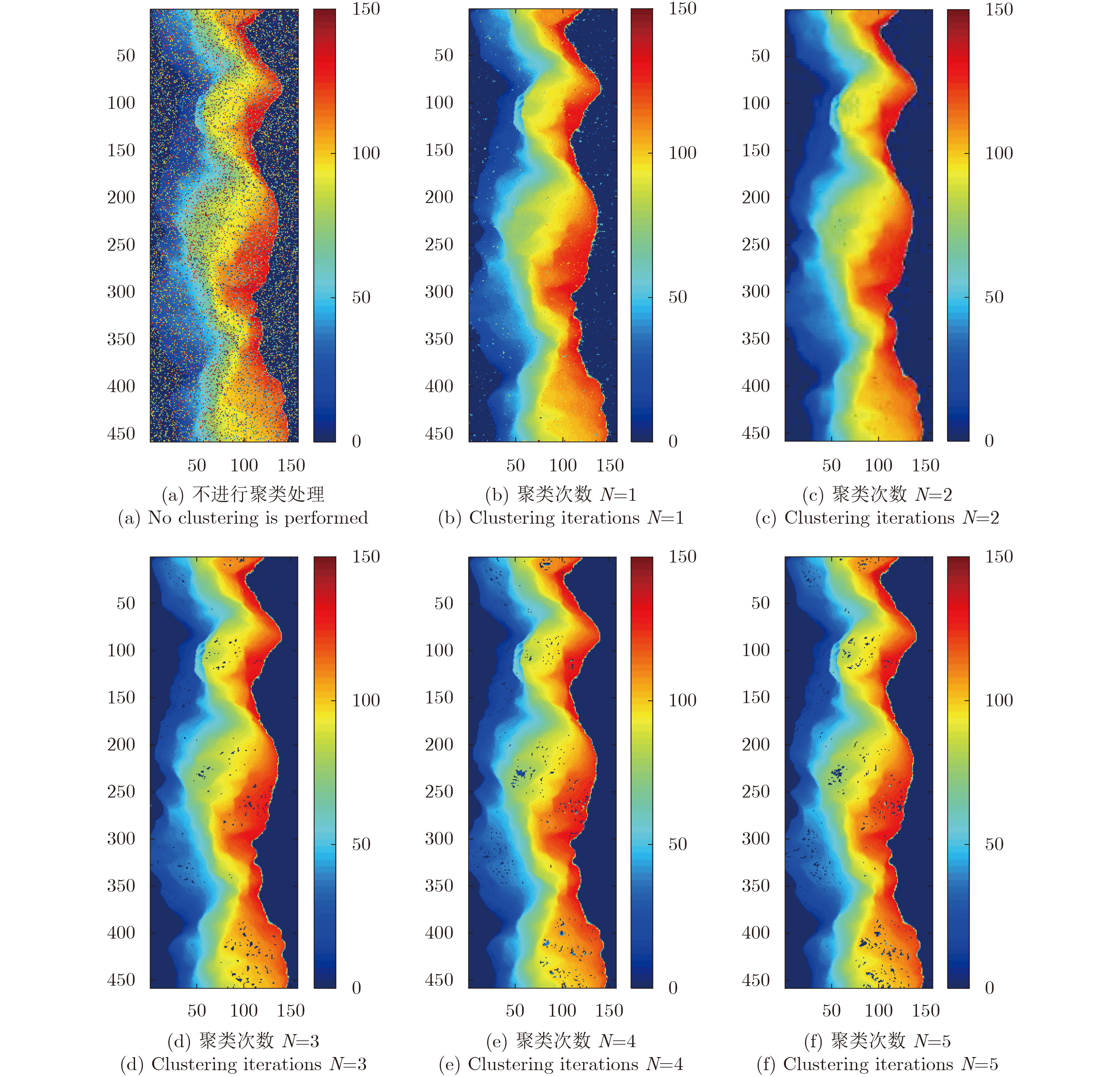
首先研究聚类迭代次数N对精度的影响，采用八邻域结构的邻域系统，分别固定阈值点数 ${\rm{Hpt}}{{\rm{s}}_{{\rm{th}}}} =$ 6和高程差 $\Delta h = 20\;{\rm{m}}$ ，变化迭代次数N，图5(a)–图5(f)分别是不经过聚类处理及聚类迭代次数分别是1～5时的重建结果。在不同的聚类迭代次数下，CABMAP的精度如表4所示。由表2, ML估计法的精度为3.8801, MAP估计法的精度为0.0117，由表4，如果不进行聚类处理，直接以ML估计法得到的结果为基础，采用MAP框架重建得到的精度为0.2378，即其精度虽然比ML估计法高，但低于MAP估计法。而通过聚类步骤判断出邻域内的噪声像素后再采用MAP框架进行重建，实验结果表明精度得到了显著提升。同时，随着迭代次数的增加，精度呈现先增后降的趋势，当N=2时可以取得最好的重建结果。

为了考查阈值点数 ${\rm{Hpt}}{{\rm{s}}_{{\rm{th}}}}$ 对重建精度的影响，固定迭代次数N=2和高程差 $\Delta h = 20\;{\rm{m}}$ 。从表5中，归一化均方误差会随着阈值点数 ${\rm{Hpt}}{{\rm{s}}_{{\rm{th}}}}$ 的增加呈现先降后增的趋势，当 ${\rm{Hpt}}{{\rm{s}}_{{\rm{th}}}} = 6$ 时可以取得最好的重建结果。

固定迭代次数N=2和阈值点数 ${\rm{Hpt}}{{\rm{s}}_{{\rm{th}}}} = 6$ ，考查高程差 $\Delta h$ 对重建精度的影响。从表6中，随着高程差 $\Delta h$ 的变化，归一化均方误差呈现先减小后增大的趋势，当高程差 $\Delta h = 20\;{\rm{m}}$ 时，可以取得最好的重建结果。

通过不同参数情况下精度的量化分析，聚类迭代次数N对重建结果的影响较明显，当N偏大时，时间消耗变大且精度下降，当N偏小时会导致重建结果未收敛，从而精度下降，从实验结果来看，选择较小的迭代次数可以取得良好的重建结果，一般将迭代次数设为2～4。阈值点数 ${\rm{Hpt}}{{\rm{s}}_{{\rm{th}}}}$ 和高程差 $\Delta h$ 同样也会影响重建精度，当 ${\rm{Hpt}}{{\rm{s}}_{{\rm{th}}}}$ 设置偏大时，目标像素被判为噪声像素的概率变大，存在将非噪声像素错判成噪声像素的问题，当 ${\rm{Hpt}}{{\rm{s}}_{{\rm{th}}}}$ 设置偏小时，存在将噪声像素错判成非噪声像素的问题；当 $\Delta h$ 设置偏大，则目标像素邻域内所有的像素被判为聚成一类，无法剔除邻域内的噪声像素，如果 $\Delta h$ 设置偏小，则邻域内的像素都被判断为噪声像素，也会使重建精度下降；实际中不同的噪声水平和数据特征均会影响 ${\rm{Hpt}}{{\rm{s}}_{{\rm{th}}}}$ 和 $\Delta h$ 的设置，为了得到较好的重建结果，需要给不同的参数设定步长，考查不同的参数组合从而得到较好的重建结果。

4.2 实测实验

实测实验采用的数据是西班牙巴塞罗那地区某建筑物场景的真实干涉SAR图像。该数据集有两幅干涉相位图，由TerraSAR-X卫星以重复轨道的方式获得。两条基线对应的高度模糊数分别为36.64 m, 64.12 m。在形成干涉条纹前，对SAR图像做了多视处理，距离向5视，方位向4视。参数如表7。

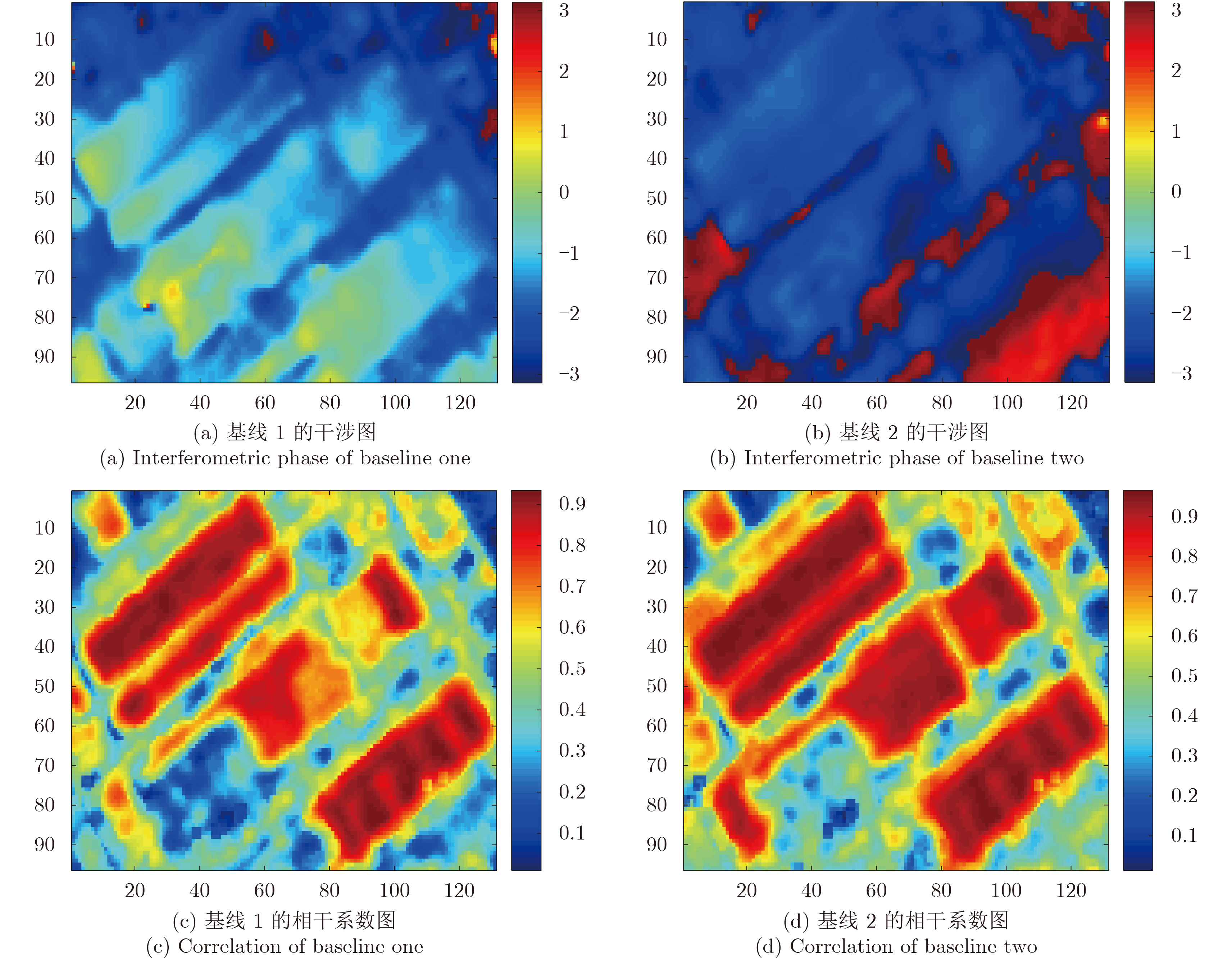
图6(a)、图6(b)分别是基线1和基线2的干涉相位图，由于已经去除平地效应，所以看不见明显的干涉条纹，图6(c)、图6(d)分别是基线1和基线2的相干系数图，可见大部分区域的相干性比较良好，因此适合做干涉处理。

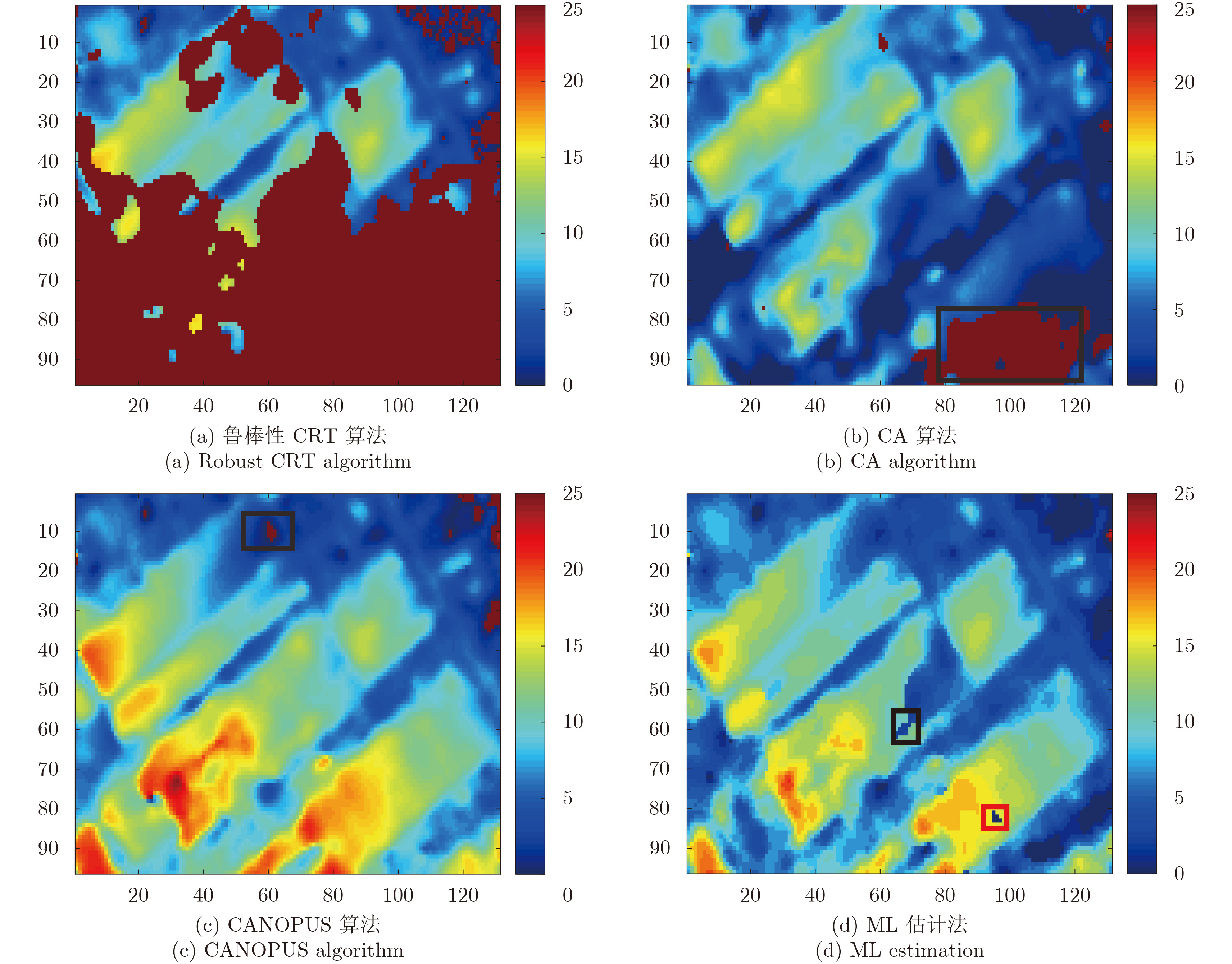
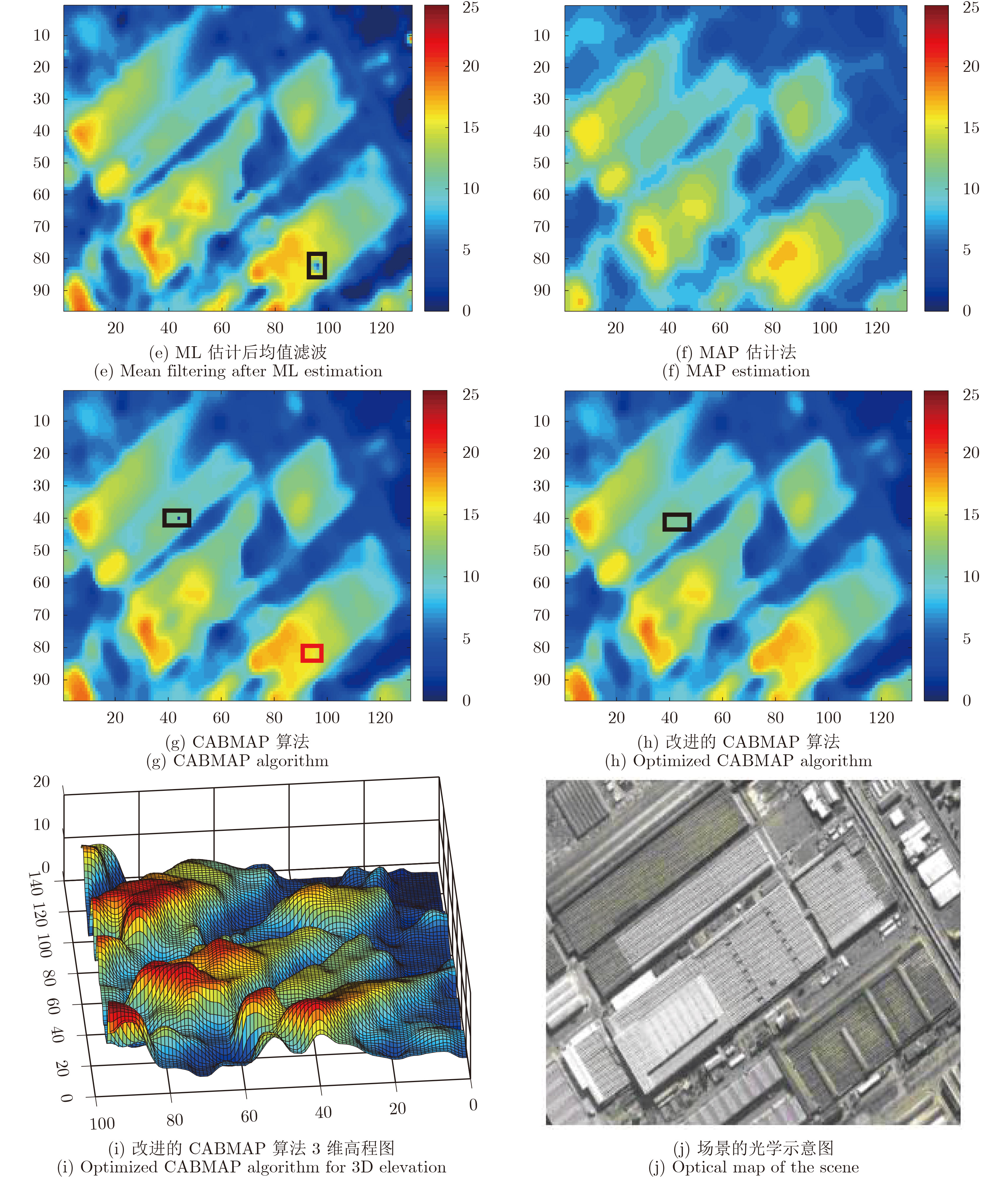
图7(a)–图7(h)分别是鲁棒的CRT, CA, CANOPUS, ML, ML估计后均值滤波、MAP, CABMAP及改进措施的高度重建结果，图7(i)是改进的CABMAP重建结果的3维图，图7(j)是场景的光学图。首先从运行时间方面来分析，CABMAP和MAP估计法的运行时间分别是5.175075 s, 11.617357 s，相比MAP估计法，CABMAP具有较快的处理效率，具体见表8。从精度方面来分析，对比场景的光学图，鲁棒性CRT的结果中场景下部区域没被正确地重建出；CA在较短的运行时间内正确地估计出部分场景的高程信息，但仍有一些区域估计地不准确，如图7(b)中的黑框区域。CANOPUS在CA的基础上，考虑了像素的位置信息，图7(c)中除了较小的黑框区域没被正确地建，整体上比CA的精度更高。ML估计法能在较短的运行时间内估计出精度不错的结果，但在图7(d)中，黑红两块区域产生了较明显的高度突变，对比光学图，这两块区域的估计失真。在ML估计法的结果上加入均值滤波措施后，会将部分孤立的噪声像素过滤掉，但当噪声像素连接成片后，也无法过滤掉这些噪声像素，如图7(e)中的黑框区域。在MAP估计法的结果中，没有出现较明显的高程突变，但建筑物的边缘被模糊化，损失了细节信息。CABMAP的精度较高，对比图7(d)和图7(g)中的红框区域，CABMAP有效地减少了ML估计法中的高程突变点，但仍有部分无法消除，如图7(g)中的黑框区域。改进的CABMAP进一步消除了高程突变点，图7(i)是改进的CABMAP的高程3维图，可以看出该算法在实测数据上也表现出较好的精度。综合来看，本文提出的算法在实测数据处理时表现出较高的处理效率和精度，因此具有良好的实用价值。由于数据有限，该实测数据的不模糊高度大于场景高度差，但能部分验证本文算法，后期条件允许，将进一步验证分析本文算法。

5 结论

本文提出了CABMAP算法，并利用了一种改进措施进行优化。采用了美国Isolation Peak国家公园的仿真数据和TerraSAR-X的巴塞罗那实测数据进行了实验验证。验证结果表明CABMAP算法重建精度高、运行时间短，并且能有效重建被噪声污染区域的高程信息。但同时，该算法只利用了SAR图像的干涉相位和相干系数等信息进行场景的高度重建。未来的工作可以考虑在改进的CABMAP基础上，利用SAR图像的幅度信息提升高度重建精度。