② (北京电子工程总体研究所 北京 100076)
② (Beijing Institute of Electronic Enginnering, Beijing 100076, China)
线性调频信号(Linear Frequency Modulated, LFM)具有良好的距离和速度分辨率,即使回波具有较大的多普勒频移,匹配滤波器仍能起到脉冲压缩的作用,信号处理系统便于实现,因而成为应用最广的雷达信号形式之一[1]。但距离-多普勒耦合效应的存在也使它容易受到攻击,转发移频干扰是对抗线性调频信号最为有效的手段。通过数字射频存贮器(Digital Radio Frequency Memory, DRFM)的存贮及频率调制,可以产生位置灵活的假目标,导前假目标干扰就是其中最为重要的干扰方式之一。所谓导前假目标干扰,是指通过巧妙利用雷达信号或数据处理的缺点,使得虚假目标位置前移,使得雷达“看到”位于真实目标前方的虚假目标,从而诱使其做出错误判断[2,3]。在物理上,真正的导前假目标(或称前置假目标)是不可实现的,因为采样、转发干扰带来的时间延迟无法避免,这必然导致干扰信号总是滞后于目标回波。在实现时,干扰机通过估计自身的物理延迟时间,采用精确的频率调制,利用距离-多普勒耦合效应,可以实现有源假目标相对真实目标的导前。当前,移频导前假目标干扰已经成为雷达对抗领域十分关注的一种新型干扰方式,在导弹突防等领域中具有十分重要的军事应用价值[4]。
移频导前假目标产生的原理并不复杂,但其鉴别却十分困难,根本原因在于其时频特性与目标回波十分相似。现有的抗干扰方法主要有两类,一类是脉间抗干扰,通过脉间的调频斜率的变化来实现抗干扰[5],这种方法需要多个脉冲,采用多种不同斜率的调频信号,当干扰方采用脉间频率调制变化时,该方法失效;另一类是脉内抗干扰,通过调频斜率的扰动,降低干扰信号获取的脉压增益,但这种方法增加了信号处理系统的复杂性[6]。但对于同一个发射信号脉冲,和实体目标回波相比,干扰信号不可避免地存在着转发延迟,因此其到接收机前端的时间必然要晚于实际的目标回波,更重要的是,经过匹配滤波处理后估计获得的到达时间必然和其实际到达时间是不一致的。利用这一特点,本文提出了一种对移频转发形成的导前假目标鉴别方法,该方法利用干扰机不可避免的转发延迟,可以实现移频产生的导前假目标有效鉴别。
2 移频导前假目标的生成原理LFM信号波形匹配滤波器具有群延迟特性,用它来理解移频导前假目标产生最为简便[7],文献[4]也对导前假目标的产生有详细论述。下面简单叙述。本文以线性调频信号为例,雷达发射线性调频信号,其中心频率为f0,脉宽为Tp,调频斜率为
|
$s\left( t \right) = {\rm {rect}} \left( {\frac{t}{{{T_{\rm{p}}}}}} \right) \cdot \exp \left[ {2{\rm j}{{π}} \left( {{f_0}t + \frac{\gamma }{2}{t^2}} \right)} \right]$
|
(1) |
当时宽带宽积
|
$S(f) \!=\! \frac{1}{{\sqrt B }}{\rm{exp}}\left( {{f_0} \!-\!\! {\rm{j}}{{π}} \frac{{{f^2}}}{\gamma } \!+\! {\rm{j}}\frac{{{π}} }{4}} \right),\; - \frac{B}{2} \!<\! f \!<\! \frac{B}{2}$
|
(2) |
根据文献[4]可知,LFM信号波形匹配滤波器的群延迟为:
|
${\tau _{\rm{M}}}(f) = {t_0} - \frac{f}{\gamma },\; - \frac{B}{2} < f < \frac{B}{2}$
|
(3) |
而LFM信号的群延迟为:
|
${\tau _{\rm{T}}}(f) = \frac{f}{\gamma },\; - \frac{B}{2} < f < \frac{B}{2}$
|
(4) |
从式(3)、式(4)可看出,LFM信号匹配滤波器群延迟是频率的函数,且随频率的增加而减小。LFM波形匹配滤波器群延迟正好和信号群延迟相反,因此LFM信号通过匹配滤波器后相位特性得到补偿而使输出信号相位均匀,保证信号出现峰值。若改变输入信号群延迟特性,而滤波器不变,则可使峰值点前移或滞后,因此可利用该性质,实现对LFM雷达的导前假目标干扰。在整个脉宽范围内,若干扰机在接收的LFM信号基础上再调制一个固定的正频率,则经匹配滤波器后形成导前假目标干扰。如果在整个脉宽范围内,干扰机调制的频率是时变的,则经匹配滤波器形成覆盖干扰。根据干扰机调制频率,并由式(3)可确定形成的假目标相对目标位置的导前量。若干扰机调制频率为fJ>0,导前的距离为:
|
$\Delta R = \frac{{{\rm c} \cdot {f_{\rm{J}}}}}{{2\gamma }}$
|
(5) |
式中c为光速,fJ为干扰机调制频率,可以是固定的,或时变的。通常干扰机要接收到信号后才能转发,本身还需要一定的反应时间,不妨设其总的延迟时间为
|
${f_{\rm{J}}} \ge \gamma {\tau _0}$
|
(6) |
在宽带雷达照射下,目标表现为分布式的多散射中心。进一步推导,当fJ<B时,干扰信号在移频后经匹配滤波器的输出为:
|
$y(t)=K\sqrt{BT}\left( 1-\frac{{{f}_{\text{J}}}}{B} \right)\cdot \frac{\sin \left[ \pi i\left( t-{{t}_{0}}+\frac{{{f}_{\text{J}}}}{\gamma } \right)\left( B-{{f}_{\text{J}}} \right) \right]}{\pi \left( t-{{t}_{0}}+\frac{{{f}_{\text{J}}}}{\gamma } \right)\left( B-{{f}_{\text{J}}} \right)}{{\text{e}}^{\text{j}\pi {{f}_{\text{J}}}(t-{{t}_{0}})}}$
|
(7) |
其中,K为常数。当fJ=0时上式即为匹配目标回波的输出,且在t=t0时刻输出达到最大。当fJ≠0时为失配干扰的输出,且在
|
${y_{{\rm{J}}\max }} = \left(1 - \frac{{{f_{\rm{J}}}}}{B}\right){y_{{\rm{T}}\max }}$
|
(8) |
上式和式(6)、式(7)一起约束了导前假目标形成时的前移距离、增益损失等条件。
3 移频导前假目标的特性分析从上一节可以看出,移频导前假目标的形成原理并不复杂,但对于雷达来说,对它的检测和鉴别却甚为困难,原因在于所产生的假目标具有和真实目标十分类似的时频特性。下面进行具体的分析。考虑自卫干扰的情形,设目标与雷达的距离为RT,干扰机延时为
|
$\begin{aligned}{S_{\rm{T}}}\left( t \right) = &{\sigma _{\rm{T}}} \cdot {\rm{rect}}\left( {\frac{{t - 2{R_{\rm{T}}}/{\rm c}}}{{{T_{\rm{P}}}}}} \right)\\ & \cdot \exp \!\left[ {2{\rm j}{π} \left(\! {{f_0}\left(\! {t \!-\! \frac{{2{R_{\rm{T}}}}}{\rm c}} \right) \!+\! \frac{\gamma }{2}{{\left(t \!-\! \frac{{2{R_{\rm{T}}}}}{\rm c}\right)}^2}} \!\right)} \!\right]\end{aligned}$
|
(9) |
|
$\begin{aligned}{S_{\rm{J}}}\left( t \right) = &{\sigma _{\rm{J}}} \cdot {\rm{rect}}\left( {\frac{{t - 2{R_{\rm{T}}}/{\rm c} - {\tau _0}}}{{{T_{\rm{P}}}}}} \right)\\& \cdot \exp \left[ {2{\rm j}{π} \left( {\left( {{f_0} + {f_{\rm{J}}}} \right)\left( {t - \frac{{2{R_{\rm{T}}}}}{\rm c} - {\tau _0}} \right)} \right.} \right.\\& \left. {\left. { + \frac{\gamma }{2}{{\left( {t - \frac{{2{R_{\rm{T}}}}}{\rm c} - {\tau _0}} \right)}^2}} \right)} \right]\end{aligned}$
|
(10) |
这里
|
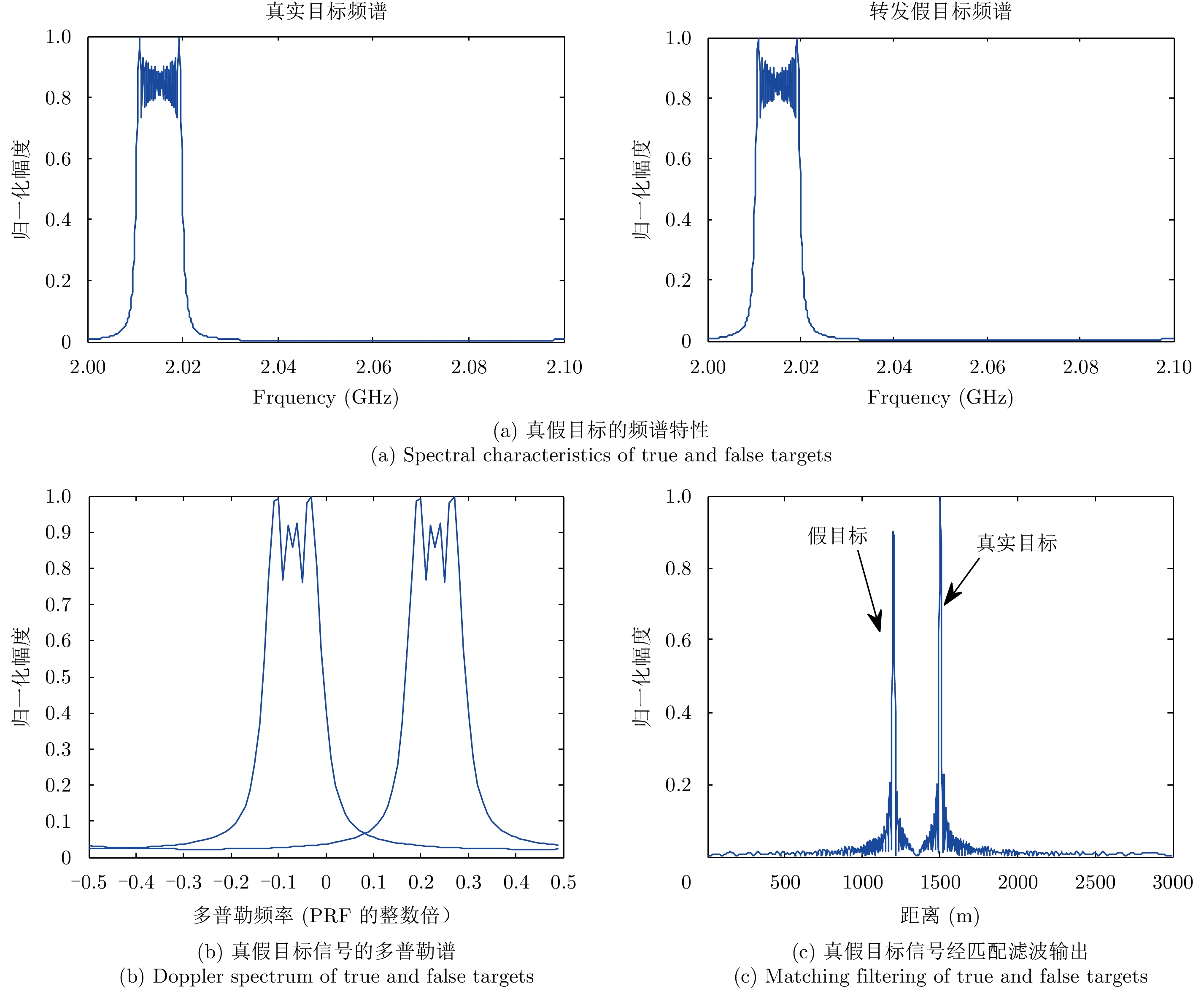
图 1 真假目标信号的频谱、多普勒普及其匹配输出 Fig.1 Spectrum, Doppler spectrum, and matched filtering of true and false targets |
从图1可以看出,要实现真假目标信号的鉴别是十分困难的。在匹配滤波前,由于移频量相对信号带宽很小,两者之间频带高度重叠,频域滤波方法无法分辩,而在多普勒域两者波形高度相似,无法分辨;在匹配滤波后,由于距离-多普勒耦合效应,原本滞后的干扰信号经匹配输出可能出现在目标回波的前方,导前的距离可由式(5)、式(6)算出。因此,无论是匹配滤波前的频域分析还是滤波后的前沿跟踪判别,均难以判别真假目标。
4 移频导前假目标的鉴别方法尽管干扰信号和目标回波具有十分相似的时频特性,但对于脉内自卫干扰而言,在时域上干扰信号存在一个显著特点:在匹配滤波前,由于其不可避免的转发延迟,干扰信号到达雷达接收机前端的时间必然滞后于真实目标回波;在匹配滤波后,由于移频的影响,干扰信号领先于真实目标回波。因此,干扰信号实际到达接收机前端与经过匹配滤波后估计到达的时间存在着差异,而真实目标回波却不存在这种差异。这种差异为真假目标的鉴别提供了物理基础。
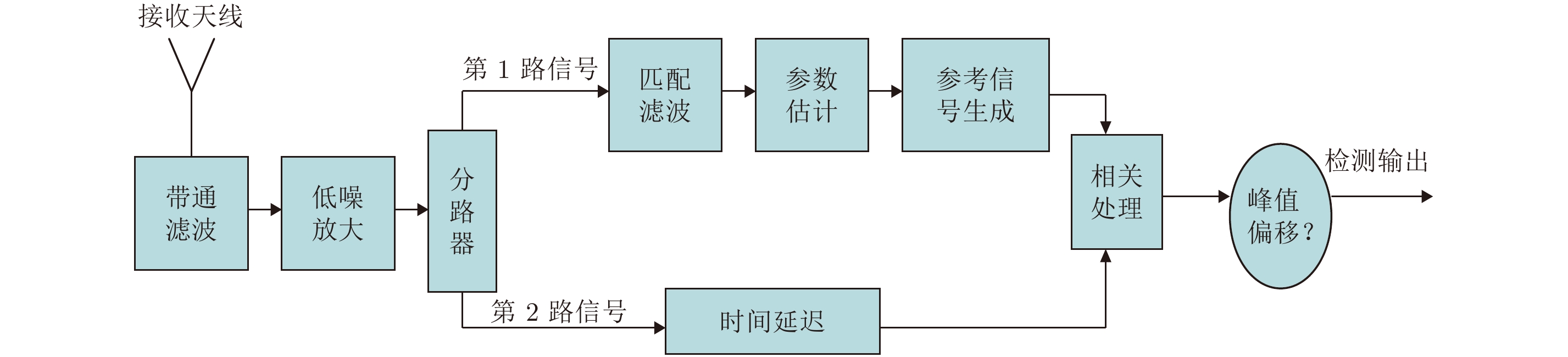
根据以上原理,本文提出了移频导前假目标的鉴别方法:在接收机前端信号分成两路,一路进行匹配滤波和参数估计[8],另一路进行延迟存贮,用于后续的相关处理。再进行匹配滤波并估计出回波信号参数后,构造相应的参考信号,在估计出的回波到达时间窗口内,将参考信号与延迟的回波进行相关处理,如果是实体目标回波,由于实际到达时间与参考信号的时间是一致的,则两个信号的相关峰值在时间零值附近;反之,如果是有源转发的信号,由于其实际到达时间晚于信号估计的到达时间,相关处理后其峰值必然偏离时间零点,偏移量与其延迟到达时间、移频量相关,根据相关峰偏移的方向和大小可以判定干扰的类型。该方法的基本原理如图2所示。
|
图 2 移频导前假目标鉴别方法流程框图 Fig.2 Diagram of preceded frequency-shift false target’s identification method |
下面对以上方法进行详细说明。
步骤1 将雷达接收到的信号进行预处理,在匹配滤波前将其分成两路。首先,对雷达接收机收到的信号进行滤波和低噪放大等预先处理,然后将收到的雷达信号分成两路。第1路进行匹配滤波、参数估计和信号生成,参数估计方法可参考文献[8]。第2路信号进行延迟,用以和以后估计出的信号进行相关处理。延迟的时间D取决于以下3个时间的总和:匹配滤波时间、参数估计时间、参考信号生成时间,若设这3个时间和为
步骤2 将第1路信号进行匹配滤波。将第1路信号进行匹配滤波,匹配滤波处理是线性调频信号最常见的处理方法,这里采用的方法与通常的匹配滤波相同。
步骤3 匹配滤波后选择一个信号,进行回波参数估计时,依据所提取出的回波参数,构造相应的参考信号。具体包括以下步骤:依据信号参数估计提供的到达时间、初始频率、调频率和信号幅度,从本振信号中经衰减、延迟,得到用于干扰检测的参考信号。
步骤4 将参考信号和步骤一得到的第2路信号进行时间对齐,然后进行相关处理。
步骤5 根据相关峰值偏移的位置量,判别是否为有源转发信号或实体目标回波:如果选择的匹配滤波输出信号进行参数估计生成的参考信号与第2路信号相关处理后的相关峰值有一个出现在零点位置,不发生偏移,则可判别生成参考信号的匹配滤波输出信号为目标实体目标回波,否则判决为有源转发形成的假目标。
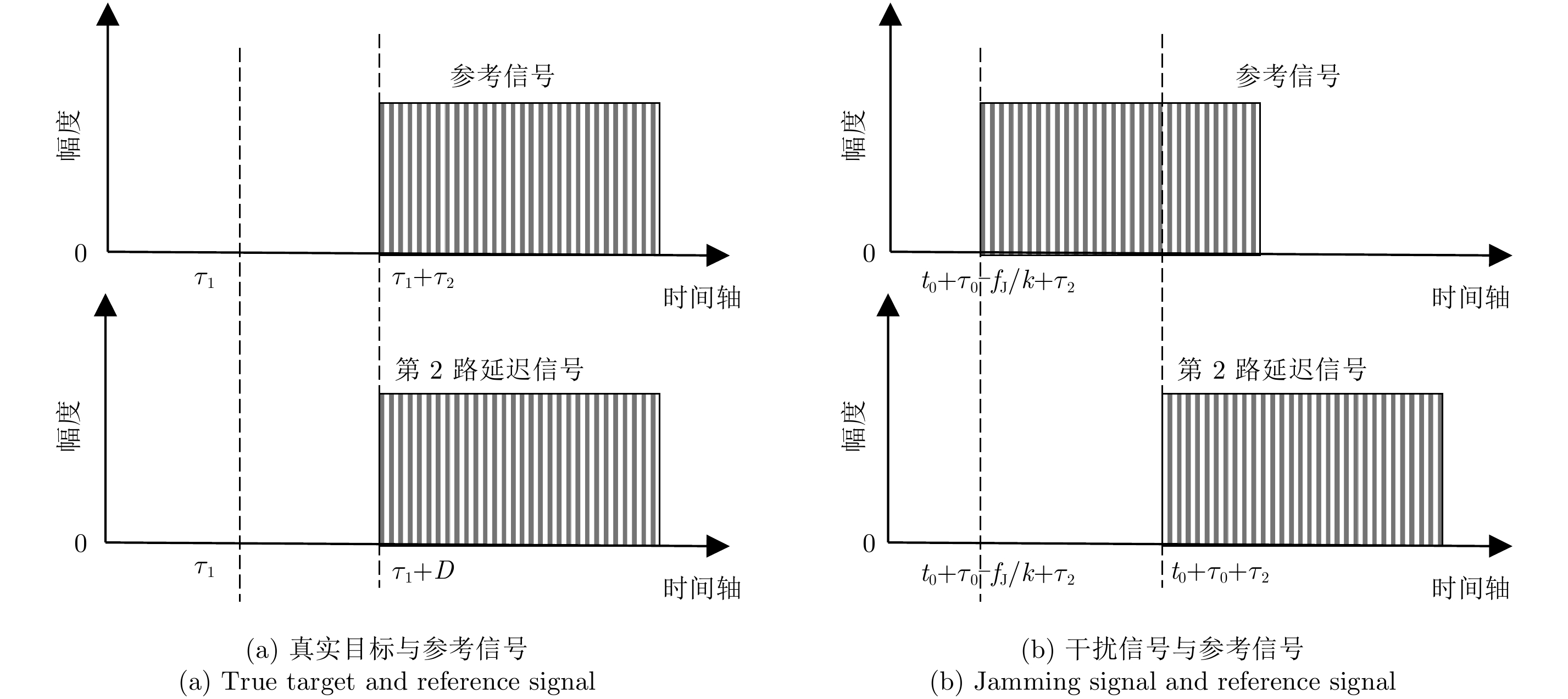
为进一步直观显示真实目标和干扰信号在进行相关处理前与参考信号的时域关系,图3分别画出了两者的关系图。
|
图 3 回波与参考信号的时域关系图 Fig.3 Diagram of time-domain relationship between echo and reference signal |
从图中可以看出,当回波为真实目标时,目标的估计到达时间与其实际到达时间是一致的,因此,时间窗口对齐后两者不存在时间差;当回波为干扰信号时,参考信号与延迟信号之间存在一个显著的时间差fJ/k,这是由于移频干扰所表现出的到达时间与其实际到达时间之间的差异导致的,进行相关处理后,这种差异将表现为相关峰在时间轴上的偏移。
5 仿真试验与分析为检验本文所提方法的有效性,进行仿真验证。设定仿真参数如下:雷达的带宽B=5 MHz,发射信号脉宽T=20 μs,干扰机的转发延迟时间
|
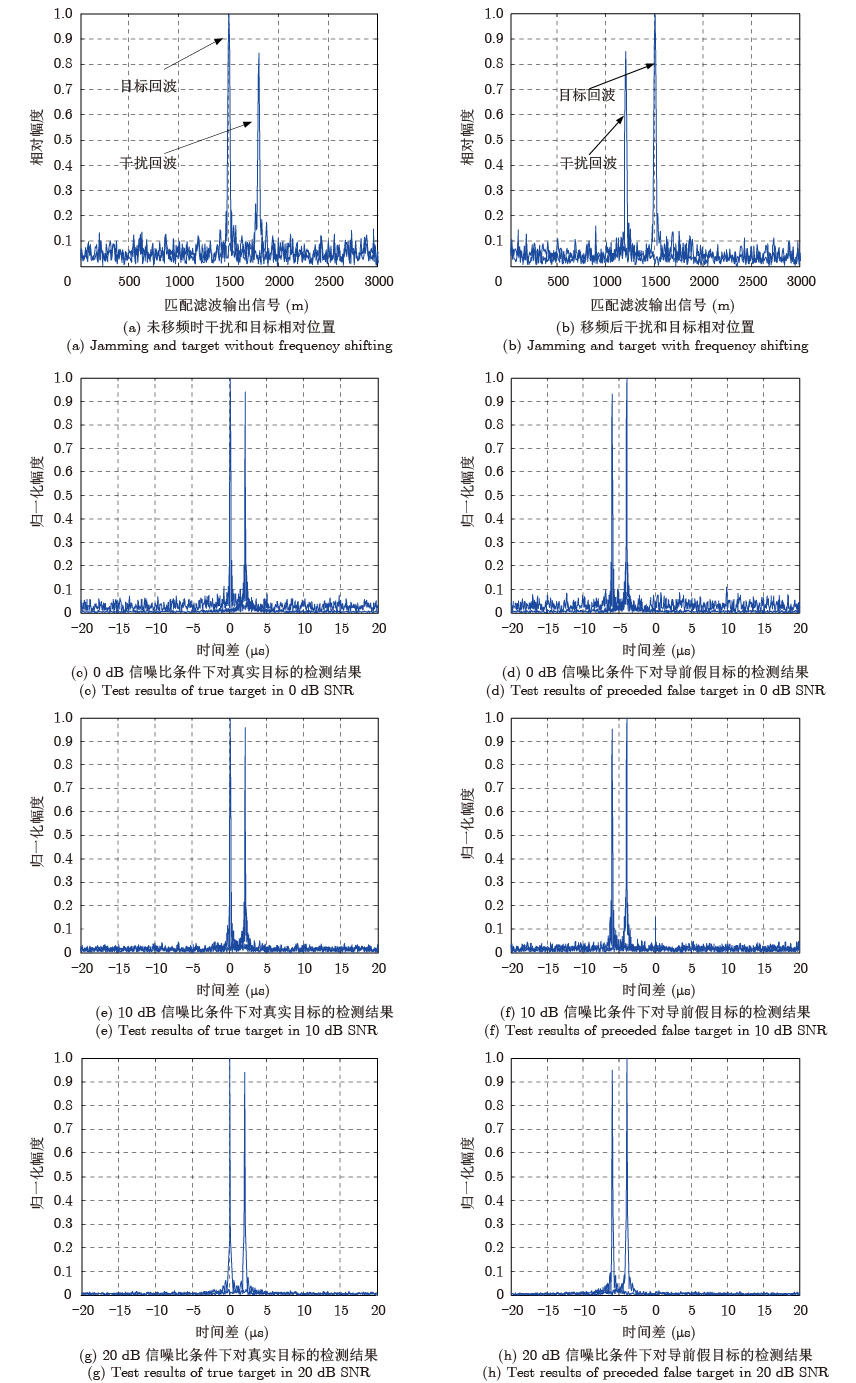
图 4 干扰和目标的相对位置及其检测结果 Fig.4 Test results of preceded false target and true target |
采用本文所提出的方法进行干扰检测,检测结果如图4(c)–图4(h)所示。从图4(c)可以看出,对于真实目标,一个相关峰处于零点,一个相关峰右偏,因此判别生成参考信号的匹配滤波输出信号为非导前有源干扰,判别结果与实际相符;图4(d)是对有源导前干扰的检测仿真图,从图中可以看出,对于有源干扰,两个相关峰值均出现了往左偏移的现象,偏移的大小与移频量和时延有关。从图4(c)–图4(h)的仿真结果可以看出,信噪比的增大只是使噪声值减小,但对于相关处理后相关峰在时间轴的偏移并不产生本质的影响。根据峰值偏移零点这一现象,可以判别其为有源导前假目标干扰,判别结果与实际相符。因此,采用本文提出的方法,可以实现对移频转发形成的前移干扰实现有效检测。
6 小结欺骗干扰信号的检测一直是雷达抗干扰的难点,特别是对于具有距离-多普勒耦合效应的线性调频信号,转发干扰信号在时频域均难以分辨。本文提出了一种新的检测方法,该方法具有如下几个基本特点:首先,在基本原理上,该方法巧妙利用转发类移频干扰所具有的不可避免的时间延迟特点,实现了移频转发形成的欺骗类干扰检测,只要干扰机具有转发延迟,该方法就能实现有效检测,与干扰机复制信号的精度无关;其次,在应用范围上,该方法适用面广,不仅适用于采用窄带信号的雷达,也适用于采用中带和宽带信号的雷达,不仅适应于导前假目标干扰,而且可以推广至对其它的移频类干扰方法检测;第三,该方法在较强的抗干扰能力,该方法无需利用多个脉冲信息,仅需利用单个脉冲即可实现检测,即使干扰机所采用的移频量在脉间捷变,本方法依然能实现干扰检测,因此,相比于前沿跟踪等抗干扰方法,该方法的适应性更强,具备较强的实际应用价值。
| [1] |
Richards M A. Fundamentals of Radar Signal Processing[M]. New York: McGraw-Hill, 2005: 67–80.
( 0) 0)
|
| [2] |
Fitzgerald R J. Effects of range-Doppler coupling on chirp radar tracking accuracy[J].
IEEE Transactions on Aerospace and Electronic Systems, 1974, AES-10(4): 528-532. DOI:10.1109/TAES.1974.307809 ( 0) 0)
|
| [3] |
刘建成, 王雪松, 刘忠, 等. 对线性调频脉压雷达的导前假目标群干扰[J].
电子与信息学报, 2008, 30(6): 1350-1353. Liu Jian-cheng, Wang Xue-song, Liu Zhong, et al.. Preceded false target groups jamming against LFM pulse compression radars[J]. Journal of Electronics & Information Technology, 2008, 30(6): 1350-1353. (  0) 0)
|
| [4] |
刘建成, 刘忠, 王雪松, 等. 基于群延迟的前移干扰研究[J].
自然科学进展, 2007, 17(1): 99-105. Liu Jian-cheng, Liu Zhong, Wang Xue-song, et al.. Study on preceded jamming based on group delay[J]. Progress in Natural Science, 2007, 17(1): 99-105. (  0) 0)
|
| [5] |
Soumekh M. SAR-ECCM using phase-perturbed LFM chirp signals and DRFM repeat jammer penalization[J].
IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 191-205. DOI:10.1109/TAES.2006.1603414 ( 0) 0)
|
| [6] |
Li Neng-jing and Zhang Yi-ting. A survey of radar ECM and ECCM[J].
IEEE Transactions on Aerospace and Electronic Systems, 1995, 31(3): 1110-1120. DOI:10.1109/7.395232 ( 0) 0)
|
| [7] |
Perez-Martinez F, Burgos-Garcia M and Asensio-Lopez A. Group delay effects on the performance of wideband CW-LFM radars[J].
IEE Proceedings-Radar, Sonar and Navigation, 2001, 148(2): 95-100. DOI:10.1049/ip-rsn:20010136 ( 0) 0)
|
| [8] |
Peleg S and Porat B. Linear FM signal parameter estimation from discrete-time observations[J].
IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(4): 607-616. DOI:10.1109/7.85033 ( 0) 0)
|




