② (中国科学院大学 北京 100190)
② (University of Chinese Academy of Sciences, Beijing 100190, China)
结合非均匀采样重建技术,方位向多通道合成孔径雷达(Synthetic Aperture Radar, SAR)能够有效克服最小天线面积限制,实现高分辨率宽幅(High-Resolution and Wide-Swath, HRWS)对地观测[1]。优良的系统性能使得多通道SAR体制受到国内外研究机构的广泛关注,并越来越多地在机载和星载平台上得到验证[2,3]。在实际SAR系统中,由于温度、天线方向图、接收机器件等误差因素,通道间往往存在不一致的幅度差异、相位误差以及时间和位置不确定性。在进行多普勒频谱重建之前,各个通道的数据必须得到精确校准,否则会严重恶化多通道数据重建性能,导致图像中出现虚假目标[4]。根据误差来源的不同,通道间特性失配主要分为幅度差异、距离向采样延时误差和相位误差。幅度误差主要来源于不一致的天线方向图。距离向采样延时误差主要是由各个通道采样时钟或者模拟-数字转换设备不一致造成的。相位误差主要来源于系统热性能的不一致、天线飞行姿态等因素,是造成图像虚假目标的主要因素。
针对方位向多通道SAR系统中通道相位失配校正问题,目前已经有大量文献进行了相关研究。文献[2]在实际数据处理过程中采用了一种干涉相位直方图分析方法,补偿通道间的常数相位误差,方法简单,但是在精度上很难保证。文献[5–7]讨论了通道相位误差的多普勒维变化特性和距离向空变性,但是在算法推导和数据处理过程中并没有考虑波束斜视的影响。文献[8]从系统天线方向图与回波信号功率谱对应关系的角度出发,考虑基带多普勒中心的影响,通过方位互相关方法获取了通道间的距离向延时误差和空不变相位误差估计。在方位互相关方法中,系统基带多普勒中心的估计精度严重影响方位互相关方法的校正精度,然而基于存在多普勒模糊的单通道信号估计的多普勒中心存在较大误差。文献[9]和文献[10]从不同的角度推导了空域互相关方法,能够实现估计信号多普勒中心频率的同时校正系统相位误差,但是该方法依赖于通道间良好的相干性。文献[11]提出一种类似于空域互相关方法的相位失配时域估计方法,计算效率较高,但是循环相消的误差估计方法在通道数较多的情况下可能会造成估计误差累积。文献[12]提出一种基于多普勒谱优化的通道相位偏差估计方法,通过最优化方法获取重构多普勒频谱幅度主瓣最窄宽度对应的相位误差作为系统相位误差的最优估计。
基于信号子空间与噪声子空间的正交性,该文提出一种改进的方位向多通道SAR通道失配校正方法。与文献[4]类似,该方法同样通过特征分解方法估计系统的相位失配。但是在推导过程中考虑了基带多普勒中心的影响,在校正相位失配的同时给出系统基带多普勒中心的鲁棒估计。本文首先介绍了方位向多通道SAR信号模型,然后详细讨论了基于特征分解的多普勒中心估计方法,最后用仿真实验和C频段方位向四通道机载SAR实验数据验证了方法的有效性。
2 方位多通道HRWS SAR系统方位多通道HRWS SAR系统通过在方位向设置多个接收子孔径,采用单发多收的方式提高系统的方位空间采样率,从而有效克服单发单收SAR系统中最小天线面积限制[13]。图1展示了方位多通道HRWS SAR系统的成像几何模型。在实际工作过程中,SAR系统采用部分方位天线长度实现宽波束发射,各个接收通道同时接收场景回波信号,从而实现方位向的宽波束覆盖。在发射端部分天线阵元工作,在接收端全部天线阵元工作,将导致整个天线阵面的温度不均匀,造成通道特性变化。通常采用整个天线孔径结合波束展宽技术实现宽波束发射。一方面,采用全孔径发射能够实现较高的系统发射功率,从而可以实现较高的系统信噪比;另一方面,采用波束展宽技术能够实现宽波束覆盖,进一步提高方位向空间分辨率。
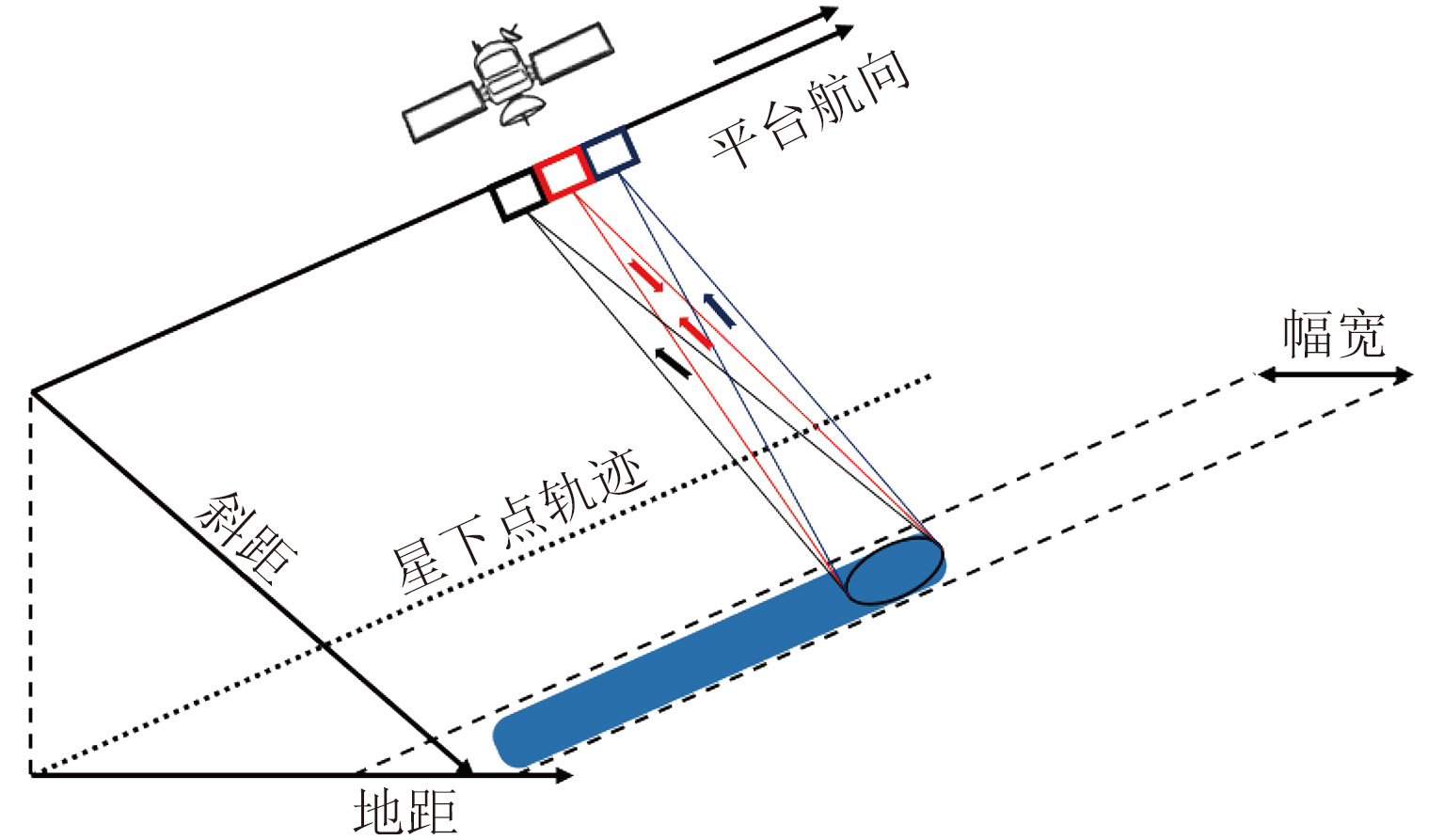
|
图 1 方位向多通道HRWS SAR系统 Fig.1 Multichannel in azimuth HRWS SAR system |
在单基SAR体制下,通过给各个通道补偿一个与孔径间隔有关的固定相位,收发分置的多通道信号可以等效为虚拟孔径的自发自收信号[14]。在理想模型下,将多通道信号变换到方位多普勒域:
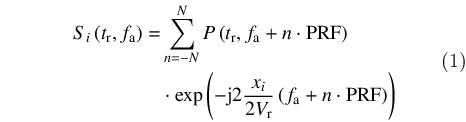
|
其中
以上分析的是理想情况下的方位多通道信号模型,并没有考虑通道失配的影响。受多种因素的干扰,实际方位多通道SAR系统中存在多种通道间幅度、相位误差。本文重点讨论斜视模型下方位多通道SAR系统相位误差的估计与校正。实测数据处理经验表明,机载多通道系统中,飞行姿态(主要是偏航和俯仰)造成通道间相位失配的重要因素。文献[6]讨论了固定天线姿态导致的距离向空变相位误差,并且采用距离向分块处理的方式校正变化的相位误差特性。在方位向,变化的天线姿态会引起变化的相位误差。在天线姿态精确控制的星载SAR系统中,空变的相位误差可以通过计算精确标定。在机载多通道SAR处理过程中,通常采用两维分块的方式进行相位误差校正,认为每个数据块中相位误差固定。基于以上讨论,本文重点对基本的固定相位误差估计与校正进行研究。相对于参考通道,假设通道i中存在固定相位误差
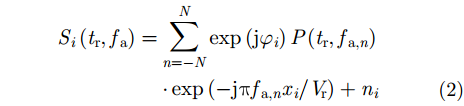
|
多通道联合信号可以表示为矩阵形式如式(3),
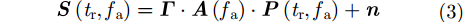
|
其中,
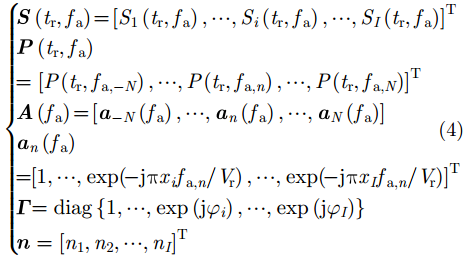
|
其中符号
特征分解的思想最初应用在阵列信号处理中,用来确定信号波达方向角的同时估计系统增益-相位误差[15]。文献[4]将类似的处理思路应用到方位多通道SAR信号处理中,实现抑制多普勒模糊的同时估计各个通道的相位失配。本文讨论波束偏离正侧视情况下,多通道SAR系统的基带多普勒中心估计和相位失配校正方法。多通道SAR回波信号在多普勒单元fa处的统计协方差矩阵可以表示为:
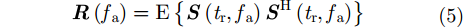
|
其中
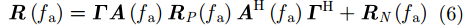
|
其中
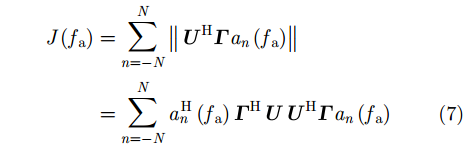
|
其中U表示噪声子空间。算法的基本原理是通过最优化的方法获取代价函数
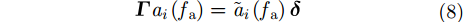
|
其中,
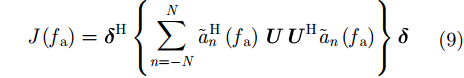
|
在处理方位向多通道SAR数据的过程中,通常选择一个参考通道,估计并补偿其他通道与参考通道之间的相位差异来实现匹配的通道传输特性。因此,需要对最优化过程施加限定条件
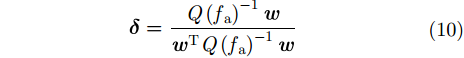
|
其中,定义
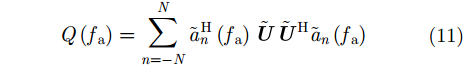
|
在实际数据处理过程中,按照上述算法逐个多普勒单元进行最优化处理,得到一个随多普勒频率变化的相位误差序列
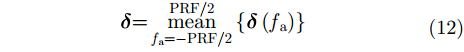
|
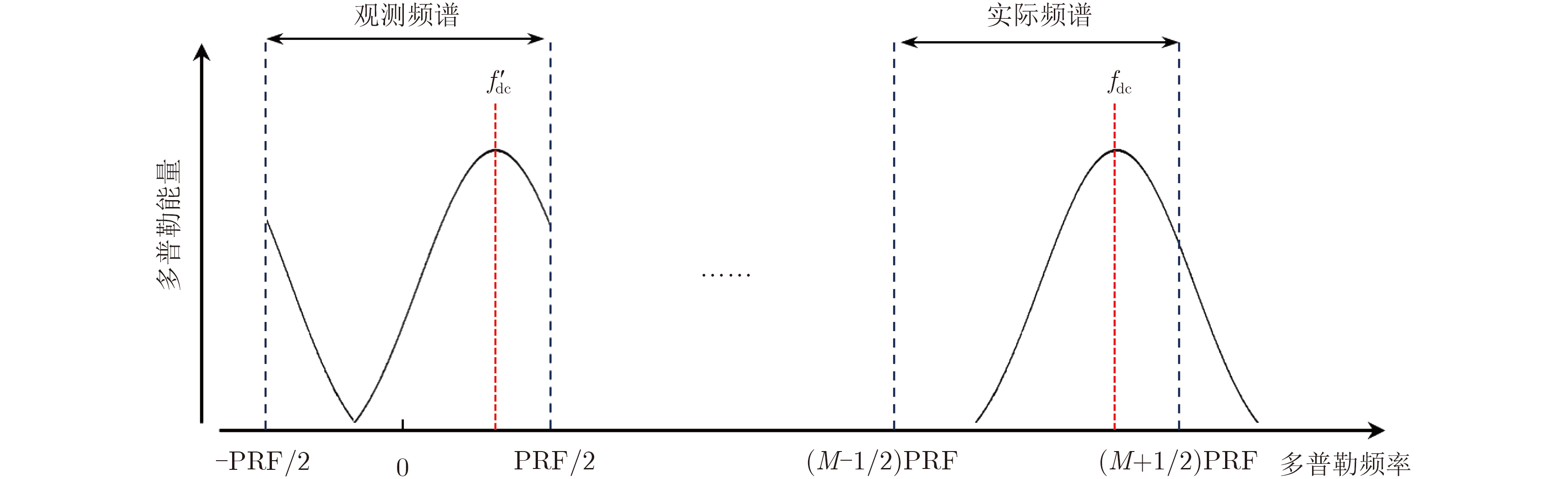
在系统运行过程中,SAR接收机在方位向以PRF采集回波信号。根据离散傅里叶变换理论,离散采样信号的频谱相当于将连续信号频谱在多普勒空间复制了无穷多次,SAR系统仅观测[–PRF/2, PRF/2]之间的部分。当天线波束指向偏离正侧视方向时,回波信号的多普勒历程较正侧视条件下偏移fdc,如图2所示。其中
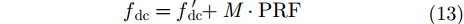
|
|
图 2 斜视情况多普勒频谱 Fig.2 Doppler spectrum in squint situation |
在成像过程中,精确的距离徙动校正依赖于信号准确的多普勒历程[17]。当波束指向偏离正侧视时,R. Lanari等人[18]提出通过在方位时域乘以与多普勒中心有关的线性相位,补偿多普勒频谱偏移带来的影响。但是在方位多通道HRWS SAR系统中,单一通道数据的多普勒频谱混叠限制了传统多普勒中心估计算法的应用。本文接下来分析天线波束斜视对相位误差估计的影响,给出一种新的方位多通道SAR基带多普勒中心估计方法。如图2所示,假设系统基带多普勒中心为正(当基带多普勒中心为负值时,讨论是类似的)。考虑多普勒频谱偏移带来的影响,导向矢量分为两部分:
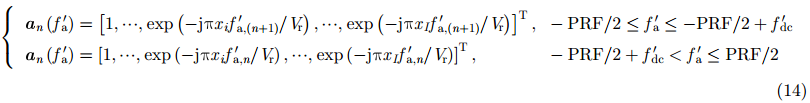
|
其中,
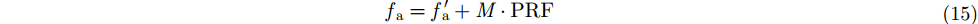
|
相应地,代价函数式(9)分为两部分:
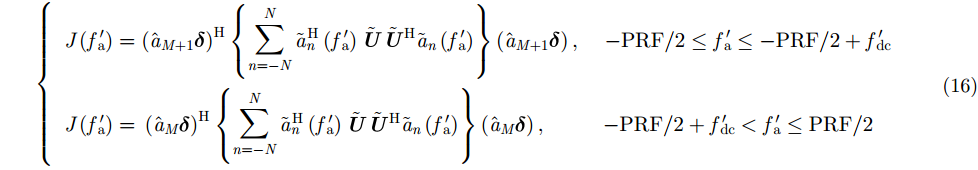
|
其中,
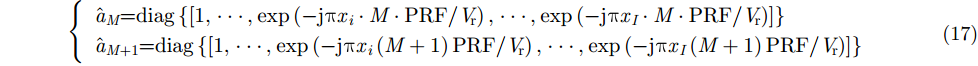
|
对比式(16)与式(9)可以发现,由于天线波束偏离正侧视导致多普勒频谱偏移,输出误差相位在频率
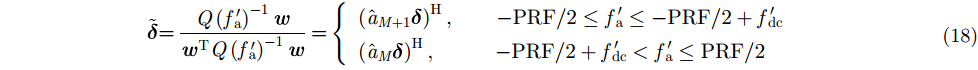
|
因此,确定输出相位变化的精确位置能够有效估计多通道SAR系统基带多普勒中心。为了获取更加准确的估计结果,我们对随多普勒频率变化的输出误差相位
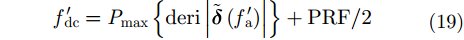
|
其中,
接下来进一步讨论多通道SAR系统通道相位误差估计。如式(18)所示,当SAR系统存在斜视时,输出误差相位在
观察式(18)可以发现,最优化输出相位项包含了多普勒模糊数M产生的相位项
因此,波束指向偏离正侧视指向时的通道相位误差可以表示为
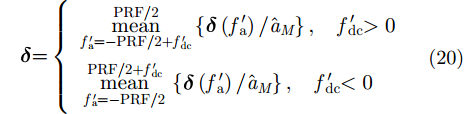
|
为了验证算法的有效性,我们分别进行了星载点目标仿真实验和机载多通道SAR实验数据处理。首先,我们设计了星载模型下的点目标仿真实验,实验参数由表1给出。
| 表 1 星载仿真实验参数 Tab.1 System parameters of simulated spaceborne experiment |
在仿真实验中,我们设置了沿方位向均匀排列的4个通道。在合成孔径时间较短的中低轨SAR系统中,采用直线轨道模型进行仿真。综合考虑系统多普勒带宽和脉冲重复频率的选择,在系统中设置了2个冗余通道,即每个多普勒单元包含2个模糊分量。同时,我们设置通道1为参考通道,在通道2、通道3和通道4中分别设置了非线性相关的相位误差,参数由表2给出。
| 表 2 仿真实验相位误差设置 Tab.2 Phase mismatch set in simulated experiment |
图3展示了仿真实验结果。图3(a)给出的是沿多普勒频率变化的相位失配估计结果。可以发现,当系统天线波束指向偏离正侧视时,3个通道的相位误差输出出现了不同程度的跳变。由于相位跳变的影响,在
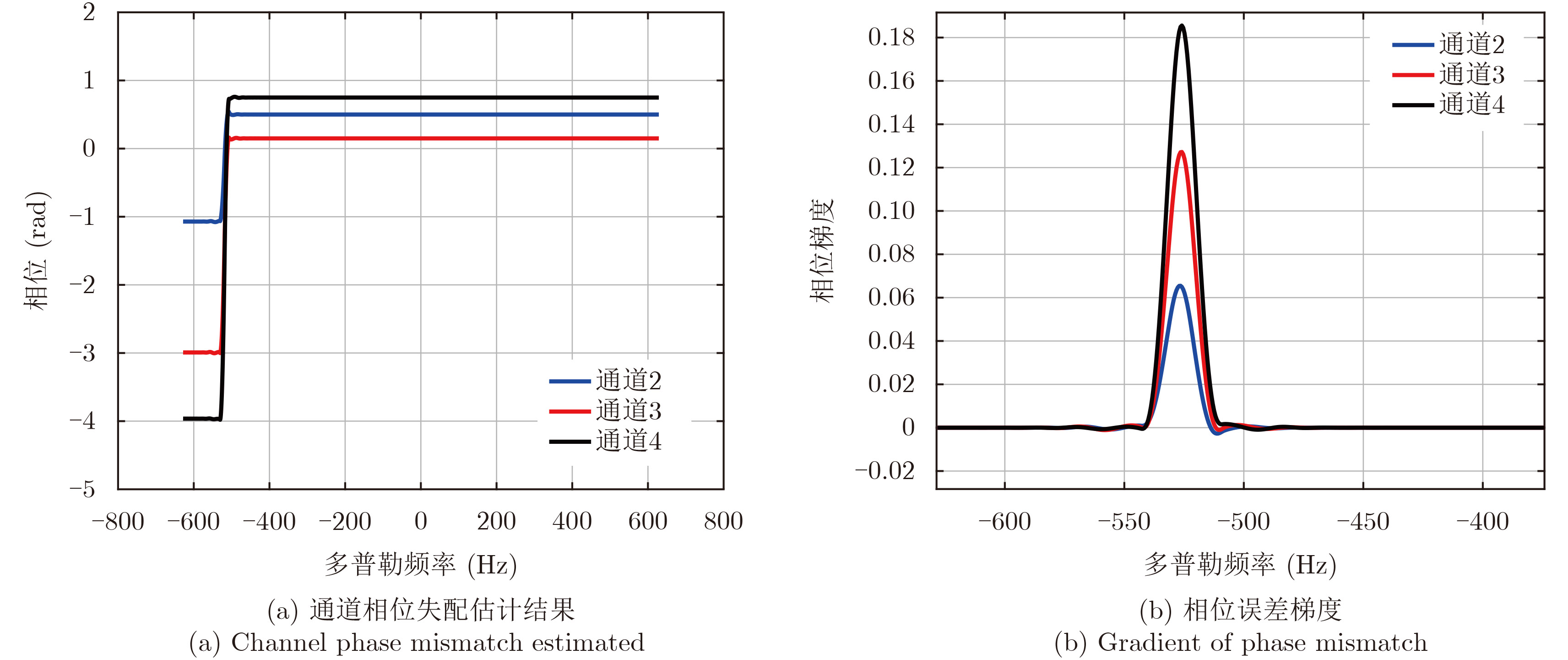
|
图 3 仿真实验结果 Fig.3 Experimental results of simulation |
| 表 3 仿真实验相位误差和基带多普勒中心估计结果 Tab.3 Estimation of phase mismatch and baseband Doppler centroid in simulated experiment |
接下来,我们将算法应用到国产C波段方位四通道机载SAR实验数据处理中,主要系统参数在表4中给出。在发射端,为了保证较高的发射功率,使用全孔径天线发射脉冲信号;在接收端,在方位向将整个天线孔径均匀分为4个通道同时接收场景回波。由于机载SAR回波信号具有较高的采样率,需要首先对原始回波数据进行重采样用以获取混叠的多通道数据。
| 表 4 C波段方位向四通道机载SAR实验参数 Tab.4 Experimental parameters of C-band azimuth four channel airborne SAR system |
需要指出的是,该机载SAR系统采用了PRF地速跟踪技术。在方位多通道SAR系统中,方位采样的空间均匀性是影响系统性能(包括系统输出信噪比、方位模糊比)的重要因素,应该优化系统参数来保证良好的空间采样均匀性。为了实现每个通道空间上均匀采样(而不是获得均匀的时间采样),系统设置PRF随着飞行速度的变化实时调整。为了得到模糊的通道数据,我们对原始回波数据在方位向进行重采样,每隔6个空间采样脉冲保留一个采样脉冲,等价于将系统PRF降低为原来的1/6。重采样之后的数据每个多普勒频率单元模糊3次,构成的方位向四通道系统存在一个冗余通道。重采样过程在图4中表示,其中,红色圆点表示原始脉冲信号,黑色圆点表示重采样后的脉冲信号。
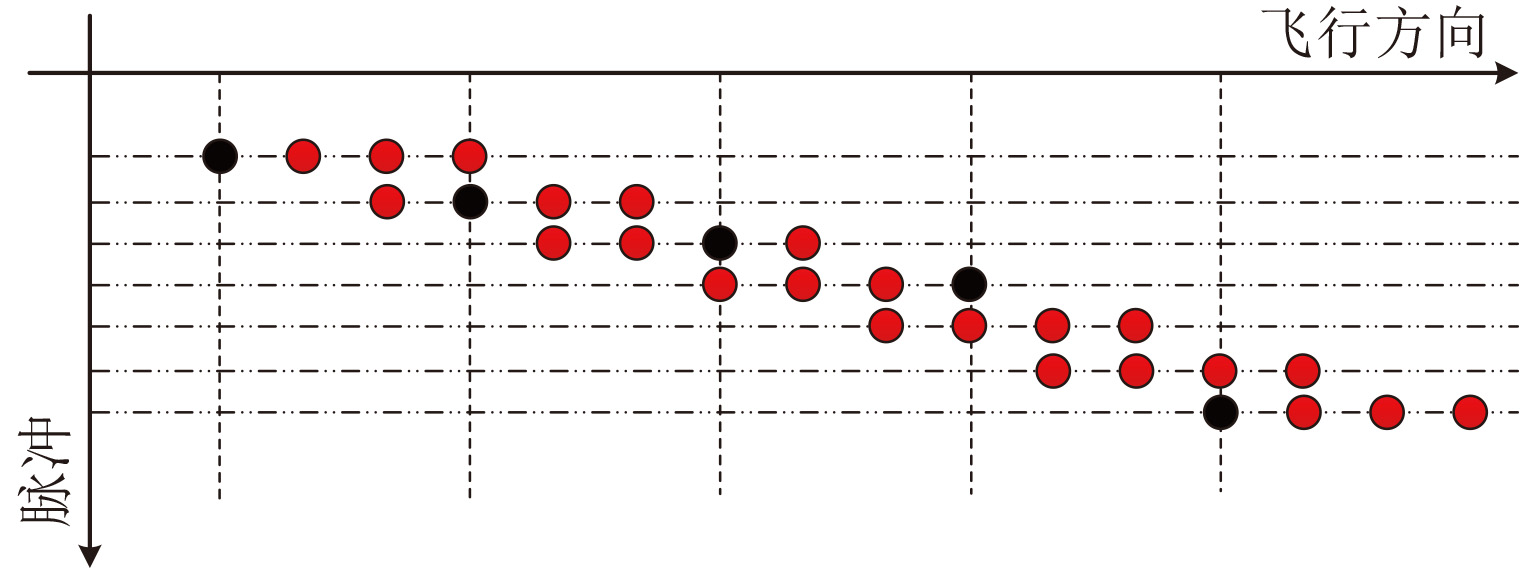
|
图 4 数据重采样过程(红色实心圆点表示原始多通道数据,黑色实心圆点表示重采样之后的多通道数据) Fig.4 Process of resampling original experimental data (red solid dots represent original experimental data, and black solid dots represent resampled data) |
图5中展示了机载实验数据处理结果。与仿真结果类似,由于波束斜视的影响,误差相位在40 Hz附近出现跳变。为了给出更好的基带多普勒中心指示,图5(b)给出了相位梯度计算结果。表5给出了机载实验数据的基带多普勒中心和通道相位失配估计结果。
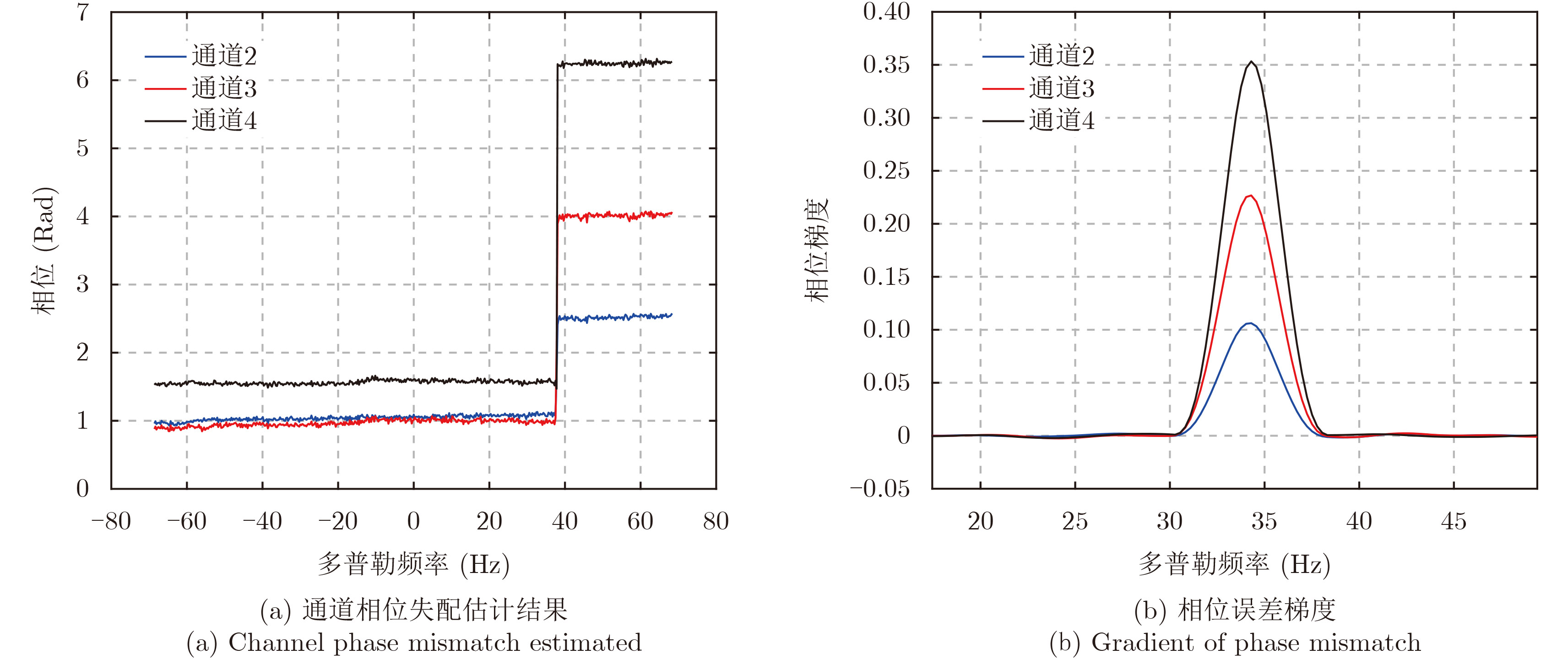
|
图 5 机载SAR实验数据处理结果 Fig.5 Experimental results using airborne SAR data |
| 表 5 C波段四通道机载SAR实验数据处理结果 Tab.5 Experimental results of C-band four channel airborne SAR system |
为了验证实验结果的正确性,基于获取的基带多普勒中心和通道相位失配估计结果,对实验数据进行了进一步成像处理。图6展示了实验数据成像结果。图6(a)展示了重采样之前满足奈奎斯特采样定理的单通道数据的成像结果。将获取的参考图像与多通道数据处理图像进行对比分析,可以有效体现通道误差造成的影响,同时能够为通道一致性校正获取的最优性能提供参照。从图6(a)中可以看出,数据包含了丰富的地物信息,包括农田、学校、高速公路和部分山地。成像结果显示,回波中包含了高速公路上运动的车辆,在图像上呈现为散焦状态,并且在方位向偏离目标的实际位置。
图6(b)展示了方位四通道机载SAR实验数据经过多通道重建处理,但是没有进行通道误差校正的成像结果。很明显,通道间失配严重影响了多通道数据的重建性能。场景中的静止建筑物和运动车辆都出现了明显的虚假目标。由于周围地物虚假目标的影响,散射较弱的高速路面和道路中间清晰的隔离带变得模糊,给自动化的道路提取造成了很大的困难。针对运动的车辆,图6(b)中出现了对称的虚假目标。由于多普勒历程的差异,可以发现散焦的运动目标存在不同的距离徙动弯曲。虚假目标来自高频部分,受方位天线方向图的加权,能量较真实目标弱很多,除此之外,虚假目标无法精确聚焦,在图像中能量更加分散。上述因素均会导致散射较弱的道路和山地对应的虚假目标淹没在周围地物当中,没有明显体现出来。
图6(c)展示了经过通道一致性校正和多通道信号重建处理的成像结果。可以发现大部分虚假目标得到了有效抑制,整体图像质量获得了很大提升。对比图6(b)和图6(c),两个结果均经过多通道数据重建,图6(b)中的虚假目标来自通道间误差。值得注意的是,重建滤波器能够有效抑制静止地物的虚假目标,而对运动目标无法进行有效重建。因此在获取的图像中仍然保留了运动车辆的虚假目标。方位向多通道高分辨率宽幅模式下的SAR运动目标检测与成像已经引起了广泛关注[19],也是我们下一步重点研究的方向之一。

|
图 6 C波段四通道机载SAR实验数据成像结果 Fig.6 Imaging results of the C-band four channel airborne SAR experimental data |
基于回波数据协方差矩阵的特征分解原理,本文提出了一种适用于方位多通道条带SAR成像的基带多普勒中心估计和相位失配校正方法。该方法以特征分解算法为基础,考虑波束指向偏离正侧视带来的多普勒中心影响,利用最优化方法估计系统的通道相位误差和基带多普勒中心。仿真星载点目标实验表明算法能够精确估计系统的基带多普勒中心和通道间相位误差。将算法应用于C波段方位向四通道机载SAR实验数据处理,获取了良好的通道一致性校正和重建处理结果,验证了算法的有效性。
| [1] |
Gebert N, Krieger G, and Moreira A. High resolution wide swath SAR imaging with digital beamforming-performance analysis, optimization, system design[C]. Proceedings of the 6th European Conference on Synthetic Aperture Radar, Dresden, Germany, July 2006: 341–344.
( 0) 0)
|
| [2] |
Gebert N, de Almeida F, and Krieger G. Airborne demonstration of multichannel SAR imaging[J].
IEEE Geoscience and Remote Sensing Letters, 2011, 8(5): 963-967. DOI:10.1109/LGRS.2011.2144563 ( 0) 0)
|
| [3] |
Kim J H, Younis M, Prats-Iraola P, et al. First spaceborne demonstration of digital beamforming for azimuth ambiguity suppression[J].
IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(1): 579-590. DOI:10.1109/TGRS.2012.2201947 ( 0) 0)
|
| [4] |
Li Zhenfang, Bao Zheng, Wang Hongyang, et al. Performance improvement for constellation SAR using signal processing techniques[J].
IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(2): 436-452. DOI:10.1109/TAES.2006.1642562 ( 0) 0)
|
| [5] |
Zhang Lei, Xing Mengdao, Qiu Chengwei, et al. Adaptive two-step calibration for high resolution and wide-swath SAR imaging[J].
IET Radar, Sonar & Navigation, 2010, 4(4): 548-559. ( 0) 0)
|
| [6] |
Zhang Shuangxi, Xing Mengdao, Xia Xianggen, et al. Multichannel HRWS SAR imaging based on range-variant channel calibration and multi-Doppler-direction restriction ambiguity suppression[J].
IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(7): 4306-4327. DOI:10.1109/TGRS.2013.2281329 ( 0) 0)
|
| [7] |
张磊, 全英汇, 邢孟道, 等. 一种子空间投影的高分辨宽测绘带SAR成像通道均衡方法[J].
电子与信息学报, 2010, 32(1): 1-6. Zhang Lei, Quan Yinghui, Xing Mengdao, et al. An SSP based channel calibration for high-resolution and wide-swath SAR imagery[J]. Journal of Electronics & Information Technology, 2010, 32(1): 1-6. DOI:10.3724/SP.J.1146.2008.01821 (  0) 0)
|
| [8] |
Feng Jin, Gao Canguan, Zhang Yi, et al. Phase mismatch calibration of the multichannel SAR based on azimuth cross correlation[J].
IEEE Geoscience and Remote Sensing Letters, 2013, 10(4): 903-907. DOI:10.1109/LGRS.2012.2227107 ( 0) 0)
|
| [9] |
Liu Yanyang, Li Zhenfang, Wang Zhibin, et al. On the baseband Doppler centroid estimation for multichannel HRWS SAR imaging[J].
IEEE Geoscience and Remote Sensing Letters, 2014, 11(12): 2050-2054. DOI:10.1109/LGRS.2014.2318511 ( 0) 0)
|
| [10] |
Li Jianbin, Li Xiaoping, Lin Mingfu, et al. Maximum-likelihood-based Doppler centroid estimation algorithm for MC-HRWS SAR system[J].
Electronics Letters, 2014, 50(22): 1630-1631. DOI:10.1049/el.2014.2723 ( 0) 0)
|
| [11] |
刘艳阳, 李真芳, 杨桃丽, 等. 一种单星方位多通道高分辨率宽测绘带SAR系统通道相位偏差时域估计新方法[J].
电子与信息学报, 2012, 34(12): 2913-2919. Liu Yanyang, Li Zhenfang, Yang Taoli, et al. A novel channel phase bias estimation method for spaceborne along-track multi-channel HRWS SAR in time-domain[J]. Journal of Electronics & Information Technology, 2012, 34(12): 2913-2919. DOI:10.3724/SP.J.1146.2012.00562 (  0) 0)
|
| [12] |
王志斌, 刘艳阳, 李真芳, 等. 基于多普勒谱优化的HRWS SAR系统通道相位偏差估计算法[J].
电子与信息学报, 2016, 38(12): 3026-3033. Wang Zhibin, Liu Yanyang, Li Zhenfang, et al. Phase bias estimation algorithm for HRWS SAR system in azimuth based on Doppler spectrum optimization[J]. Journal of Electronics & Information Technology, 2016, 38(12): 3026-3033. DOI:10.11999/JEIT161038 (  0) 0)
|
| [13] |
Gebert N. Multi-channel azimuth processing for high-resolution wide-swath SAR imaging[D]. [Ph.D. dissertation], German Aerospace Center, 2009: 20, 22.
( 0) 0)
|
| [14] |
Krieger G, Gebert N, and Moreira A. Unambiguous SAR signal reconstruction from nonuniform displaced phase center sampling[J].
IEEE Geoscience and Remote Sensing Letters, 2004, 1(4): 260-264. DOI:10.1109/LGRS.2004.832700 ( 0) 0)
|
| [15] |
Friedlander B and Weiss A J. Eigenstructure methods for direction finding with sensor gain and phase uncertainties[C]. Proceedings of International Conference on Acoustics, Speech, and Signal Processing, California, USA, April 1988: 2681–2684.
( 0) 0)
|
| [16] |
Guo Xiaojiang, Gao Yesheng, Wang Kaizhi, et al. Improved channel error calibration algorithm for azimuth multichannel SAR systems[J].
IEEE Geoscience and Remote Sensing Letters, 2016, 13(7): 1022-1026. DOI:10.1109/LGRS.2016.2561961 ( 0) 0)
|
| [17] |
Cumming I G and Wong F H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Norwood: Artech House, 2005: 194–200.
( 0) 0)
|
| [18] |
Lanari R, Zoffoli S, Sansosti E, et al. New approach for hybrid strip-map/spotlight SAR data focusing[J].
IEE Proceedings-Radar, Sonar and Navigation, 2001, 148(6): 363-372. DOI:10.1049/ip-rsn:20010662 ( 0) 0)
|
| [19] |
Baumgartner S V and Krieger G. Simultaneous high-resolution wide-swath SAR imaging and ground moving target indication: Processing approaches and system concepts[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(11): 5015-5029. DOI:10.1109/JSTARS.2015.2450019 ( 0) 0)
|




