前视阵列合成孔径雷达(Forward-looking Array Synthetic Aperture Radar，前视阵列SAR)始于20世纪90年代，最初用于解决前视雷达的左右模糊难题并提高跨航向分辨率，实现了飞行路线前下方扇形观测区域的2维成像。据此，德国宇航局设计了基于视景增强的新型区域成像雷达(Sector Imaging Radar for Enhanced Vision, SIREV)^[1]。目前，SIREV已完成理论研究、前视成像算法设计、计算机仿真与样机研制等工作，并进行了多次飞行实验。在2维成像基础上，结合平台沿航向运动形成的虚拟合成孔径，德国宇航局的Reigber A博士提出了前视阵列SAR 3维成像的概念^[2]。受天线孔径长度限制，该系统主要适用于Ka、Ku等高频段雷达的低空近距离对地观测，尤其是在地物匹配制导、飞行器自主导航和降落等场合具有独特优势。目前，前视阵列SAR 3维成像研究已经取得了许多成果，主要集中在阵列稀疏和超分辨、成像算法优化和设计等方面^[3–5]。

然而，由于阵元数多和分辨率高，该系统数据量十分巨大，给传输、存储和处理带来了难题。现有的稀疏采样方法主要集中在跨航向阵列上，通过阵列天线稀疏排布有效减少系统数据量，同时简化了阵列天线设计和降低系统成本^[5–7]。例如，韦顺军等提出散射源跨航向稀疏条件下接收天线的非均匀稀布^[5]，吕岚等人提出基于模拟退火法的阵列天线非均匀稀布方法^[6]。但是，由于回波在跨航向的稀疏度十分有限，以上跨航向稀疏采样方法在降低回波数据量方面的性能十分有限。

分析表明，由于高频段雷达的穿透性很弱，前视阵列SAR无法穿透观测地表，仅能获取观测地表的回波并3维成像。从3维空间的角度分析，观测地表仅占据了3维空间的一小部分，它在3维空间中是稀疏的^[8]。由于散射源的稀疏性是波束穿透性弱造成的，而跨航向与波束视线方向是近似垂直的，跨航向上散射源的稀疏性通常并不明显。而在高度向或沿航向上，波束视线方向与它们都不是垂直的。据此，刘向阳等人提出了距离向和沿航向联合稀疏采样并稀疏3维成像的方法，大大减少了回波数据量^[8]。然而，由于采用了压缩感知稀疏重构方法实现稀疏成像，它在信噪比较低时的性能会显著降低，导致3维图像质量下降。实际上，由于接收阵元尺寸小和高频段信号衰减损耗大，当前前视阵列SAR的信噪比通常较低，如何实现低信噪比下前视阵列SAR稀疏3维成像十分迫切。

受检测前跟踪算法的启发，本文充分利用前视阵列SAR中稀疏系数矢量中的结构化信息，提出基于Hough变换的正交匹配追踪(Orthogonal Matching Pursuit, OMP)重构算法，以提高压缩感知信号重构质量和获取高质量的3维图像。本文组织结构如下：第2节回顾前视阵列SAR的回波模型和信号处理流程；第3节提出低信噪比下基于Hough变换的压缩感知稀疏重构算法；第4节通过仿真实验验证以上算法的性能；第5节对本文进行简要小结。

前视阵列SAR系统的观测模型如图1所示，载机在观测条带后上方水平匀速运动，高度为H，速度为v。接收和发射天线分离，接收天线为均匀、稀布的阵列天线且全部阵元同时接收回波，其阵面垂直于载机飞行方向和高度向，阵元间隔为d，阵元数为N，则阵列长度为L=Nd；发射天线位于接收阵列天线中心的正下方 $\delta h$ 处，并采用无栅瓣的密布阵天线，且分时、按需方式扫描每个子测绘带。由于各个子测绘带的成像方法相同，下面均以一个子测绘带为例进行分析。另外，发射和接收波束均指向前下方，其前视角为 $\theta $ 。其中，载机飞行方向为沿航向，以x轴表示；接收阵列方向为跨航向，以y轴表示；地面高程方向为高度向，以z轴表示；波束视线方向为距离向。

图 1(Fig. 1)

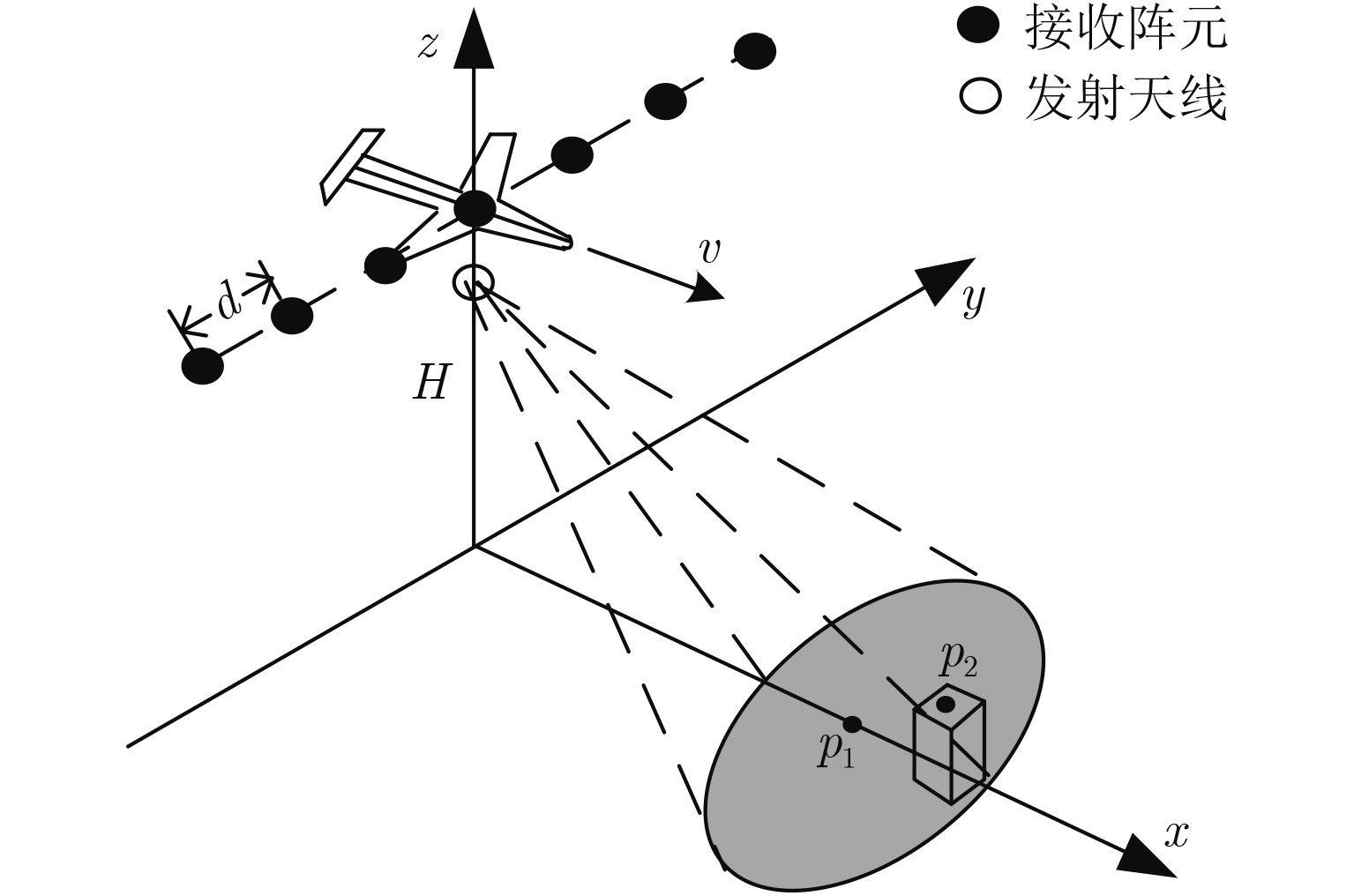
图 1 前视阵列SAR对地观测模型 Fig.1 The ground observation model for forward-looking array SAR

根据文献[8]方案，平台在沿航向运动过程中，发射和接收阵列天线每隔一定时间(不固定)完成一次回波发射和接收。其中，发射天线发送线性调频脉冲信号，每个脉冲的信号带宽均为$\Delta B$，但载频在区间[ ${f_{\rm{c}}} - B/2 - \Delta B/2$ , ${f_{\rm{c}}}{\rm{ + }}B/2 - \Delta B/2$ ]上随机变化且服从均匀分布。其中，B表示合成信号总带宽($\Delta B$小于B，约为其十分之一左右)，决定了该系统的距离分辨率；f_c表示该系统的中心频率。接收阵列天线同时接收地面回波信号，实现一次回波接收。而且，发射天线的沿航向发射间隔并不是固定的，服从区间[x_min, x_max]上的均匀分布，其中x_min表示最小采样间隔，它大于等于距离不模糊对应的沿航向最小采样间隔；x_max表示最大采样间隔，它取决于该系统所要求的稀疏采样率，即稀疏采样的采样比。

根据地面的体(或面)散射模型^[9]，散射地面可以看作是由许许多多小尺寸的点散射源构成的，其总的回波信号可以表示为：

其中，$\Omega $表示3维空间； ${\sigma _p}$ 表示点散射源P的散射系数； ${w_{\rm{a}}}( \cdot )$ 和 ${w_{\rm{r}}}( \cdot )$ 分别表示沿航向天线方向图和发射脉冲的窗函数；c表示电磁波传播速度； ${\lambda _n}$ 表示第n个发射脉冲的波长； $\gamma $ 表示发射脉冲的调频率，这里假定它们是相同的；t表示距离向快时间； ${R_{{\rm{tr}}}}({x_n},\,{y_k})$ 表示在沿航向位置x_n处，散射源P(位置为 $\left( {{x_p},{y_p},{z_p}} \right)$ )到发射天线 $\left( {{x_n},0,H - \delta h/2} \right)$ 和第k个接收阵元 $\left( {{x_n},kd - L/2,H + \delta h/2} \right)$ 的双程距离，它表示为：

需要强调的是，虽然这里用点散射源来模拟地面的回波模型，并不是说地面上仅包括少数几个点散射源，也不是说地面回波是常规意义上少数几个点散射源的回波。而是由于系统分辨率的限制，复杂的地面回波可以等价为数量有限的点散射源的回波，只不过相邻点散射源的间隔小于该系统的分辨率，称为回波的小平面单元模型^[9]。

对于每个沿航向位置x_n处的2维回波来说，由于距离向和跨航向仍采用了传统奈奎斯特采样方式，利用接收阵列的波束形成可以实现跨航向高分辨，利用脉冲的脉冲压缩可以实现距离向高分辨，形成一组沿航向的2维图像序列，如式(3)所示：

其中，sinc(·)表示辛格函数； ${A_k} \approx \sqrt {1 - {{(\lambda {f_k}/4{\rm{{{π}} }})}^2}} $ ; f_k表示跨航向波束(无量纲)；R_c表示场景中心斜距(常量)； $R({x_n},\;{x_p}) = \sqrt {{{({x_n} - {x_p})}^2} + {{(H - {z_p})}^2}} $ 。需要说明的是，在成像过程中，采用Chirp-Z变换来快速实现跨航向几何校正，其变标因子为 $\beta = {\lambda _n}R({x_n},{x_p})/\lambda {R_{\rm c}}$ ，详见文献[8]。由式(3)可见，经过上述成像处理后，跨航向位置相同的每个散射源的信号都被压缩到同一个跨航向位置上，后续的信号处理可以在一个单独的跨航向位置上分别完成，实现了信号的降维处理。

为了得到地面的3维图像，还需要沿航向的匹配滤波。但是，在沿航向方向上，每个散射源的回波跨越了多个距离门，沿航向聚焦处理还需要校正散射源的沿航向距离徙动，该距离徙动公式可以近似表示为：

其中， ${x'\!\!_n} \!=\! {x_n} \!+\! \left( {H \!-\! {z_p}} \right)\tan {\theta _0}$ , ${R_p} \!=\! \left( {H \!-\! {z_p}} \right)/\cos {\theta _0}$ 。式(4)中，1次项称作沿航向距离走动，2次和3次项称作沿航向距离弯曲。然而，由于采用了频率合成方式，每个脉冲的距离分辨率( ${\rm c}/2\Delta B$ )较低，而毫米波雷达合成孔径较短，因此距离弯曲量小于距离粗分辨率，距离弯曲校正可以忽略，采用文献[8]的方法校正时域距离走动校正即可满足沿航向成像要求。

完成沿航向时域距离走动校正后，同一散射源在不同脉冲图像中的信息被拉回到同一个距离单元。将快时间t数字化表示为t_m，校正后的回波信号可以表示为：

其中， ${x'\!\!_p} = {x_p} - \left( {H - {z_p}} \right)\tan {\theta _0}$ 。这样，沿航向聚焦处理即可以获取散射源的3维图像。然而，沿航向采样位置是非均匀且稀疏的，如何沿航向聚焦成为稀疏3维成像的关键。

由于sinc函数的局部性，由式(5)可以推断，每个跨航向上每个距离门回波序列 $S\left( {{x_n},\,{t_m},\,{f_k}} \right)$ 仅对应于一小段3维空间的散射源回波，这与常规2维SAR显著不同。它对应的散射源的3维空间范围为：

其中，由于沿航向与跨航向波束f_k是近似正交的，沿航向回波处理在跨航向波束方向无分辨能力，式(6)的第2个不等式在后续沿航向处理时不会得到改善，因此后面的讨论只关注第1个不等式。根据式(6)的第1个不等式，每个跨航向上每个距离门的回波序列 $S\left( {{x_n},\,{t_m},\,{f_k}} \right)$ 仅对应于高度向和沿航向2维空间的一小段空间，这一小段2维空间中包含多少个散射源，与地表2维地形、距离向和沿航向分辨率等都有关。图2给出了某个跨航向上距离向和沿航向2维回波对应的散射空间，其中，蓝色区域表示了某个距离门对应的散射空间区域，绿色实线表示这个散射区域附近的一小段散射地面(其它位置不会产生雷达回波信号)。严格来说，这一小段散射地面上也包含许许多多的散射源。然而，由于雷达分辨率有限，一个分辨单元内的许多个散射源是可以用一个散射源来等价的，因此散射源的数量就取决于这一小段散射地面所占据的2维分辨单元的数量。假定图2蓝色区域中每个矩形框就表示一个分辨单元，散射源数量就是绿色实线所穿过的矩形框的数量。可见，散射地面仅占据了数量有限的分辨单元，而且这一数量也远远小于沿航向采样脉冲的数量。

图 2(Fig. 2)

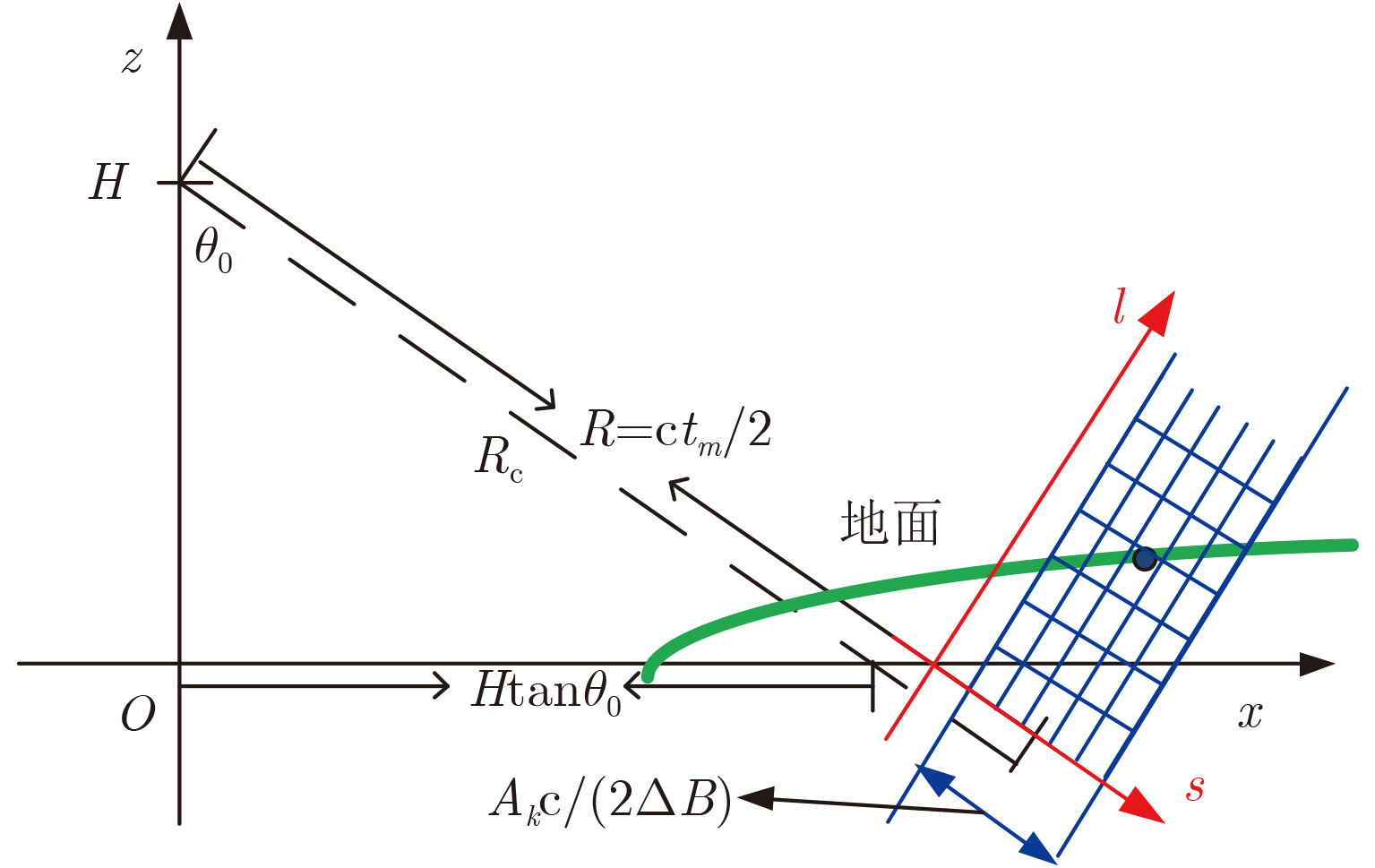
图 2 某个距离门散射源的空间位置示意图 Fig.2 The diagram of the space position of scatterers in a range cell

因此，根据式(5)的散射源回波模型，每个 $\left( {{t_m},\,{f_k}} \right)$ 处的沿航向回波 $S\left( {{x_n},\,{t_m},\,{f_k}} \right)$ 可以改写为有限个散射源的能量和形式，如式(7)所示：

其中，J表示散射源的数量，且这些散射源都位于式(6)确定的一个有限的2维空间范围内。然而，由于散射源位置是未知的，需要在式(6)确定的空间中搜索并检测出这些散射源。

为了搜索出散射源的位置，将式(6)对应的2维空间栅格化为图2中蓝色区域对应的矩形网格，每个网格对应于一个可能的散射源，而且每个网格在距离向的间隔小于距离向分辨率，在斜距离向(斜距离向垂直于距离向和跨航向)的间隔小于沿航向分辨率在斜距离向的投影。将上述2维网格按照先距离向(s轴)再斜距离向(l轴)的顺序构造一个1维散射系数矢量 ${{V}_{m,k}}$ 和一个2维回波矩阵 ${{A}_{m,k}}$ 。对于 ${{V}_{m,k}}$ ，如果该位置有散射源，该元素的值就是散射源的散射系数，否则该元素的值就是零。对于 ${{A}_{m,k}}$ ，该矩阵的列矢量就是根据该散射源的位置、N个沿航向采样位置以及式(5)确定的点回波矢量，且每个列矢量都进行了归一化。因此，如果将 $\left( {{t_m},\,{f_k}} \right)$ 处的N个沿航向回波信号表示为1维信号矢量 ${{S}_{m,k}}$ ，式(7)还可以改写为：

其中， ${{N}_{m,k}}$ 表示第m个距离单元第k个跨航向位置处的沿航向噪声回波矢量， $m = 1,2, ·\!·\!· ,M$ , $k = 1,2, ·\!·\!· ,K$ 。为了保证较高的准确性，通常在一个相对较大的空间中搜索散射源，再加上沿航向的稀疏采样， ${{V}_{m,k}}$ 的维数通常大于采样数N。而且，由于散射地面仅占据了待搜索2维空间中数量有限的分辨单元，散射系数矢量 ${{V}_{m,k}}$ 也是稀疏的，且散射源数量J也远小于N。同时，如文献[8]所述，矩阵 ${{A}_{m,k}}$ 是随距离门缓慢变化的，且其列向量也满足一定的不相关特性。因此，式(8)可以看作一个压缩感知稀疏重构问题，这样散射源的检测问题转化为压缩感知稀疏重构问题。

如果能够对每个跨航向和距离向的信号矢量 ${{S}_{m,k}}$ 依次进行稀疏重构，则可以根据它们对应的2维空间进一步构造完整的3维空间，进而得到整个3维空间的散射系数，实现3维成像。因此，前视阵列SAR 3维成像问题转化为M×K个压缩感知稀疏重构问题，如何稀疏重构成为稀疏3维成像的关键。因此，以上3维成像流程可以概括为图3所示。

然而，受毫米波器件功率小和接收阵元增益低等影响，前视阵列SAR回波信号的信噪比通常较低。压缩感知重构算法通常在高信噪比情况下具有较好的恢复性能，低信噪比下压缩感知的恢复性能大大下降，进而影响到稀疏3维成像的质量。现有研究成果表明，将先验信息和稀疏性相结合，通过压缩感知算法的改进，可以提高压缩感知稀疏重构的质量^[10,11]，例如：块结构压缩感知、树结构压缩感知等。由图2可知，每个 $\left( {{t_m},\,{f_k}} \right)$ 位置处的沿航向序列 ${{S}_{m,k}}$ 仅对应于3维空间中一小段2维空间中散射源的回波。在这一小段2维空间中，散射源的数量是有限的，而且这些散射源的位置在沿航向和高度向2维空间中是连续或间断连续的(在Layover情况下)。然而，由于这些散射源的具体位置在检测前是未知的，无论是先沿距离向再沿斜距离向排列，还是先沿斜距离向再沿距离向排列，这些散射源在散射系数矢量的位置都不是连续的，不满足块结构压缩感知的条件。充分利用散射源在2维空间的位置连续性有望进一步提高低信噪比下压缩感知的恢复性能，但尚缺少有效的方法。

图 3(Fig. 3)

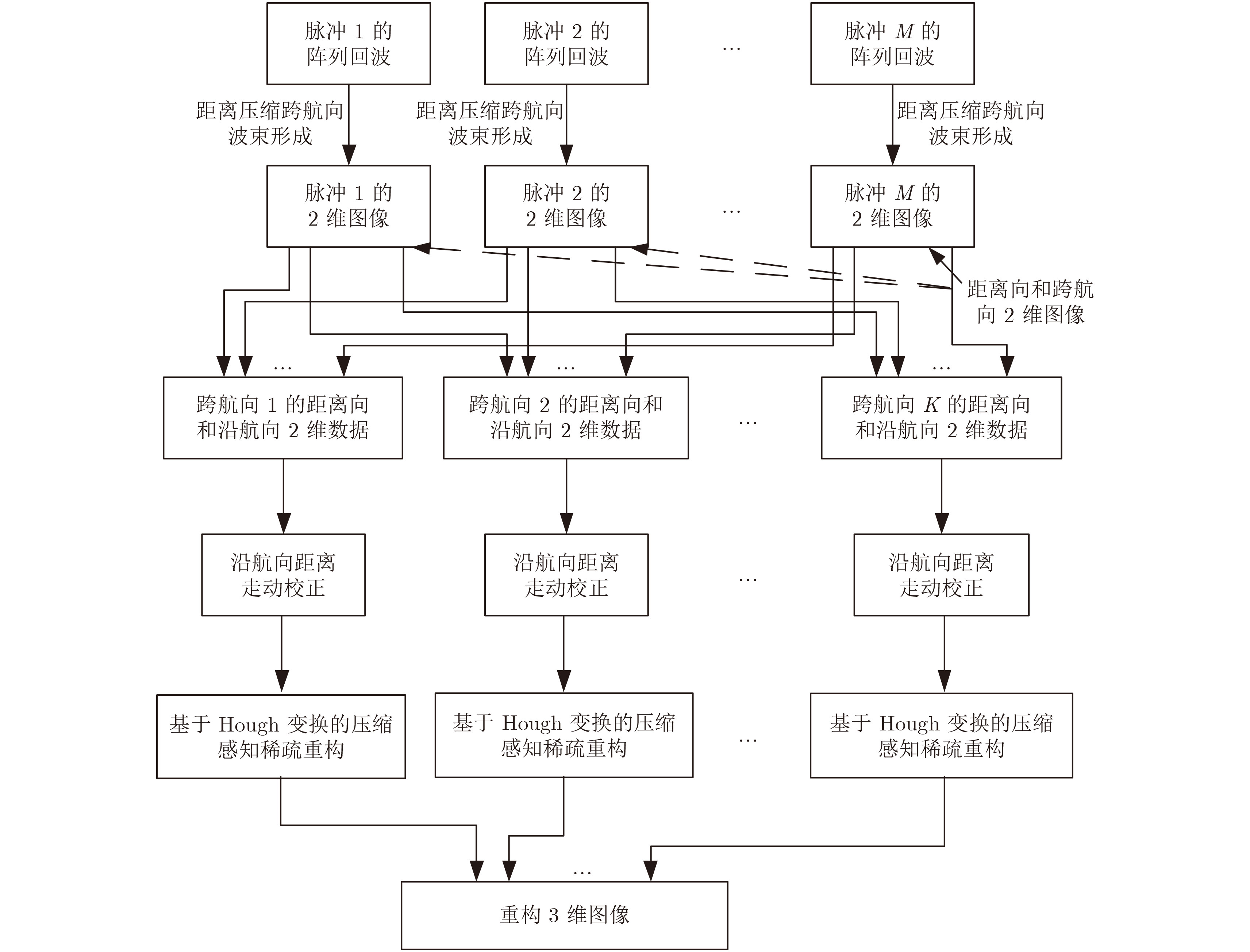
图 3 前视阵列SAR稀疏3维成像流程图 Fig.3 Flow chart of sparse three-dimensional imaging for forward-looking array SAR

贪婪类压缩感知算法是压缩感知信号重构的常用算法，例如正交匹配追踪(OMP)、压缩采样匹配追踪(Compressive Sampling Matching Pursuit, CoSaMP)等，它们具有运算量小的优点，尤其适用于数据量大或实时性强的情况。这些算法都试图在每个迭代步骤中挑选出一个或多个概率最高的散射源。在信噪比较低情况下，其挑选出错误散射源的概率大大增加，因此贪婪类压缩感知算法在低信噪比下的恢复性能大大降低。根据本文中散射源的分布特性，一个可行的方法是：在每次迭代时，不从迭代结果中直接选择一个或多个概率最高的散射源，而是先对散射源进行变换，再从变换域中选出最优的结果，然后映射到原始的散射系数矢量，找到对应的概率最高的散射源，再进一步迭代。例如，在迭代中将散射系数矢量变换到距离向和斜距离向2维空间，那么散射源的连续性就可以表现出来。由于这些散射源仅仅对应于一小块空间，当地面起伏不是特别剧烈时，它们在这个变换后的距离向和斜距离向2维空间中表现为一段直线段。如果能直接检测这些直线段，将降低错误检测的概率。

如果将迭代时变换后的2维空间看作一个2维图像，该问题就转化为图像中的直线检测问题。Hough变换是数字图像处理中一种成熟的直线或圆的检测和提取方法。它通过将图像域中的一条直线或圆变换成参数域中的一个峰值，进而根据参数域中的峰值提取出图像域中对应的直线和圆^[12]。而且，Hough变换受噪声干扰和曲线间断等因素的影响较小。该算法的详细信息请参看文献[12]，在此不再赘述。

因此，将Hough变换融入OMP算法，新的压缩感知重构算法可以概括为：

步骤1  初始化：信号余量 ${{{r}}_0} = {S}$ ，恢复信号 ${{V}_{{0}}} = {\bf{0}}$ ，原子集 ${{{Γ}}_{{0}}} = \varnothing $ ，感知矩阵 ${{{Θ}}_0} = {A}$ , i=1；

步骤2  计算余量 ${{r}_{i - 1}}$ 与感知矩阵 ${{{Θ}}_{i - 1}}$ 每一列的内积 ${{g}_i} = {{Θ}}_{i - 1}^{\rm{T}}{{r}_{i - 1}}$ ，上标T表示共轭转置；

步骤3  将g_i反向映射到距离向和斜距离向2维空间，得到2维矩阵G_i，然后对G_i进行2维Hough变换得到变换矩阵J_i；

步骤4  找出J_i中绝对值最大的元素max(J_i)。如果max(J_i)<T_f，则转到步骤7；否则根据max(J_i)找出g_i中对应元素的位置，即 ${{{Ω}}_i} =$ $ {\arg _{Ω} }\left( {{{g}_i}{\rm{ = IHT}}\left( {\max ({{J}_i})} \right)} \right)$ ，其中 ${\rm{IHT}}( \cdot )$ 表示逆Hough变换；

步骤5  更新原子集和感知矩阵，令 ${{{Γ}}_i} = {{{Γ}}_{i - 1}} \cup $ $ {a}\{ {{{Ω}}_i}\} $ , ${{{Θ}}_i} = {{{Θ}}_{i - 1}} \cap {a}\{ {{{Ω}}_i}\} $ ，然后利用最小二乘法计算并恢复出信号的近似解 ${{V}_i} = {\left( {{{Γ}}_i^{\rm{T}}{{{Γ}}_i}} \right)^{ - 1}}{{Γ}}_i^{\rm{T}}{S}$ ；

步骤6  更新余量 ${{r}_i} = {S} - {{{Γ}}_i}{{V}_i}$ , i=i+1；如果i<I_max(最大迭代次数)，转到步骤2，否则转到步骤7；

步骤7  将 ${{{Γ}}_i}$ 设置为感知矩阵，S为信号，K为稀疏度，利用OMP算法求解稀疏系数向量 ${{V}_{{\rm{out}}}}$ 。

下面通过仿真实验验证该压缩感知重构的性能，仿真参数如下：在仿真地面回波时，每个分辨单元至少放置4个独立的散射源，这些散射源均匀分布在地表上，它们的后向散射系数服从复高斯分布且相互独立。发射天线位于接收天线阵的正下方，距离接收天线阵0.5 m。在仿真载机时，载机的飞行长度约为80 m，相邻脉冲的间隔服从[0.02, 0.18]区间上的均匀分布(单位为m)，共仿真了800个脉冲的回波。该系统在沿航向方向的稀疏度约为1/10，接收机的回波信噪比为0 dB，其它仿真参数如表1所示。

表 1(Tab. 1

表 1 前视阵列SAR系统仿真参数 Tab. 1 Simulation parameters for forward-looking array SAR system 参数 数值 中心波长(mm) 3 脉冲带宽(MHz) 100 脉冲时宽(μs) 1 采样频率(MHz) 120 合成总带宽(GHz) 1 平台速度(m/s) 50 场景中心斜距(km) 1 发射天线高度(m) 499.75 接收天线高度(m) 500.25 跨航向天线长度(m) 6 接收阵元间距(cm) 3 波束中心俯仰角(°) 60 波束中心方位角(°) 0 沿航向合成孔径长度(m) 30 子测绘带波束宽度(°) 3 距离向分辨率(m) 0.15 沿航向分辨率(m) 0.2 跨航向分辨率(m) 0.5

表 1 前视阵列SAR系统仿真参数 Tab.1 Simulation parameters for forward-looking array SAR system

首先分析沿航向稀疏重构的性能。假定稀疏度为10且散射系数服从复高斯分布，图4给出了完全重构和60%重构条件下的性能。其中，每个样本下进行了1000次蒙特卡洛仿真；60%重构是指以真实稀疏度的60%为稀疏度的稀疏重构，如果重构系数的位置全部位于真实稀疏系数之中，则认为成功重构。可见，本文方法优于OMP和CoSaMP方法，尤其在信噪比仅为0 dB时，本文方法在60%重构条件下仍然能以98.5%的概率精确重构。对于60%稀疏重构，由于本文中散射源位置是连续的，采用插值方法可以重构其它未知散射源。而且，下面的稀疏3维成像实验均采用60%稀疏重构。

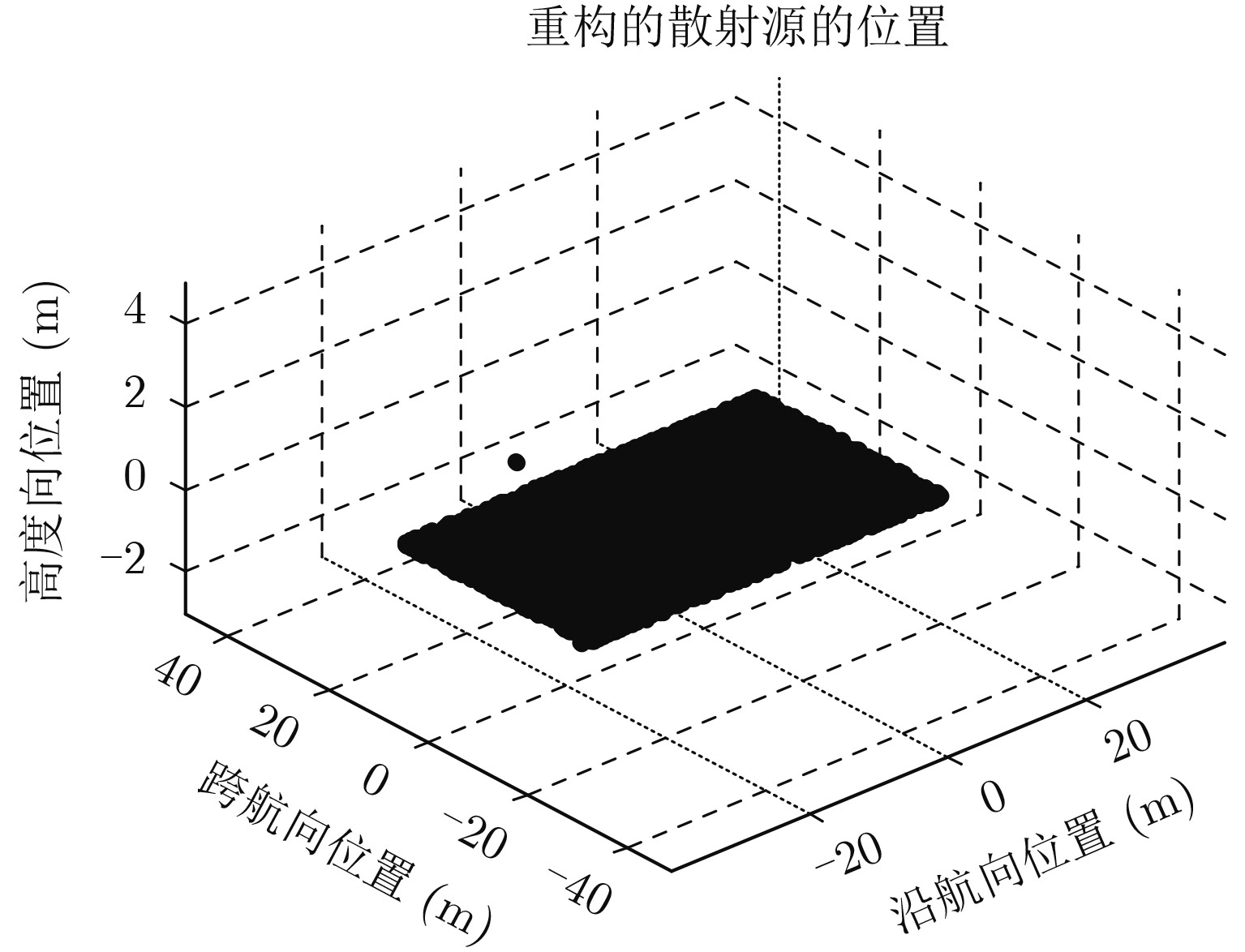
其次，观察水平地表情况下3维成像的结果，其中仿真的地表高度为零。图5给出了重构地表的散射源位置信息，其高度误差均值小于0.1 m。由于没有层叠情况，最大迭代次数I_max取为1。

图 4(Fig. 4)

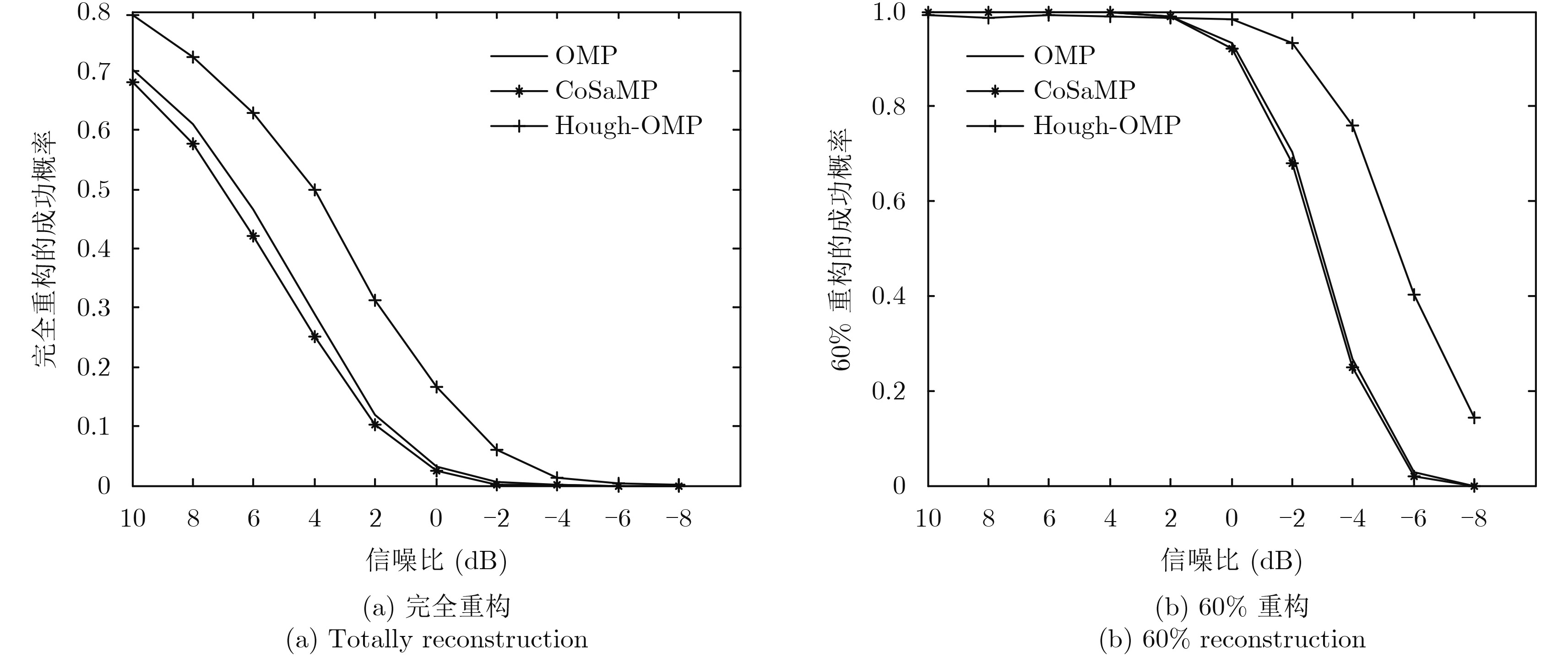
图 4 3种压缩感知算法重构性能的比较 Fig.4 Reconstruction performance comparison of three compressive sensing algorithms

图 5(Fig. 5)

图 5 水平地表的3维图像 Fig.5 Three-dimensional image of horizontal ground

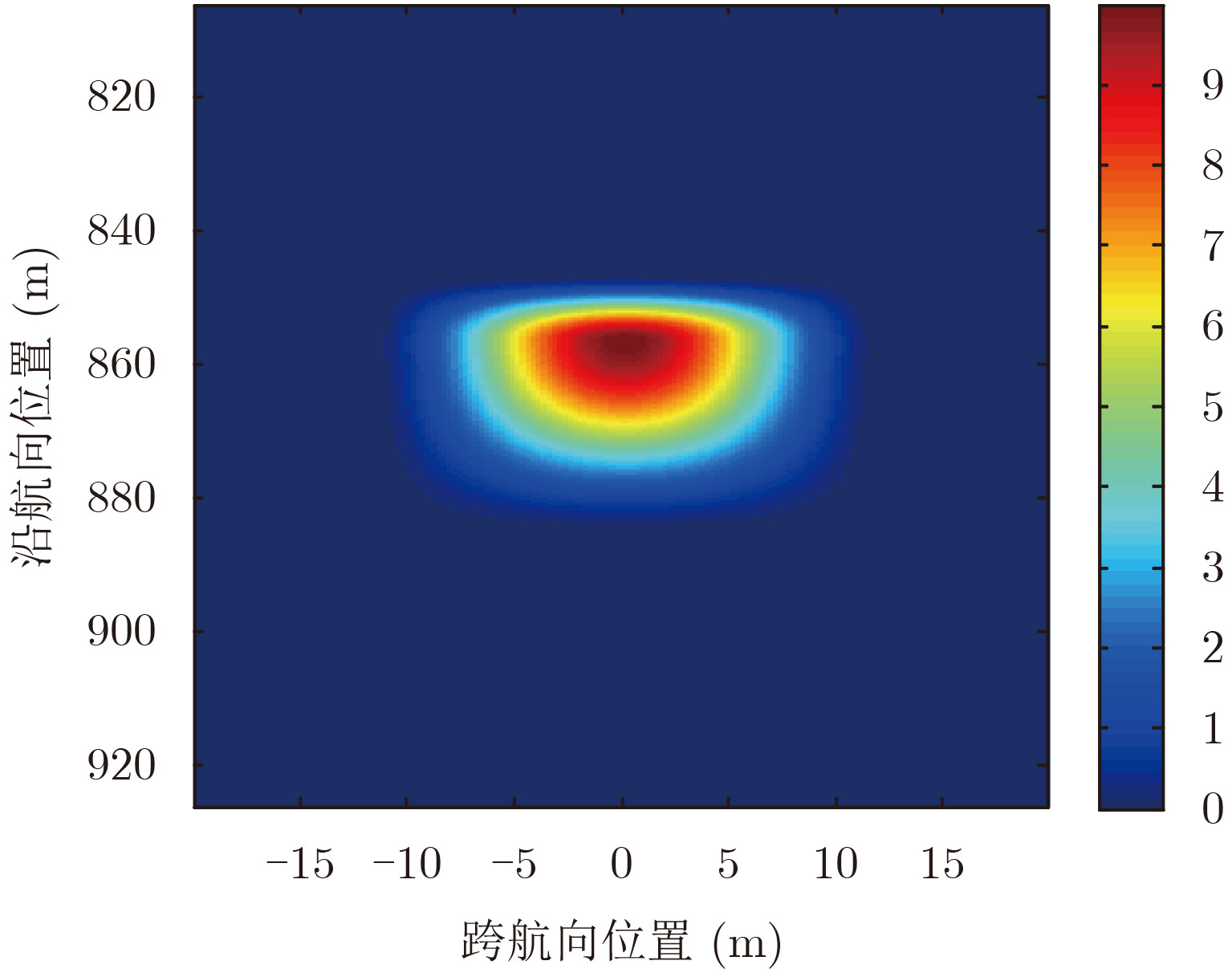
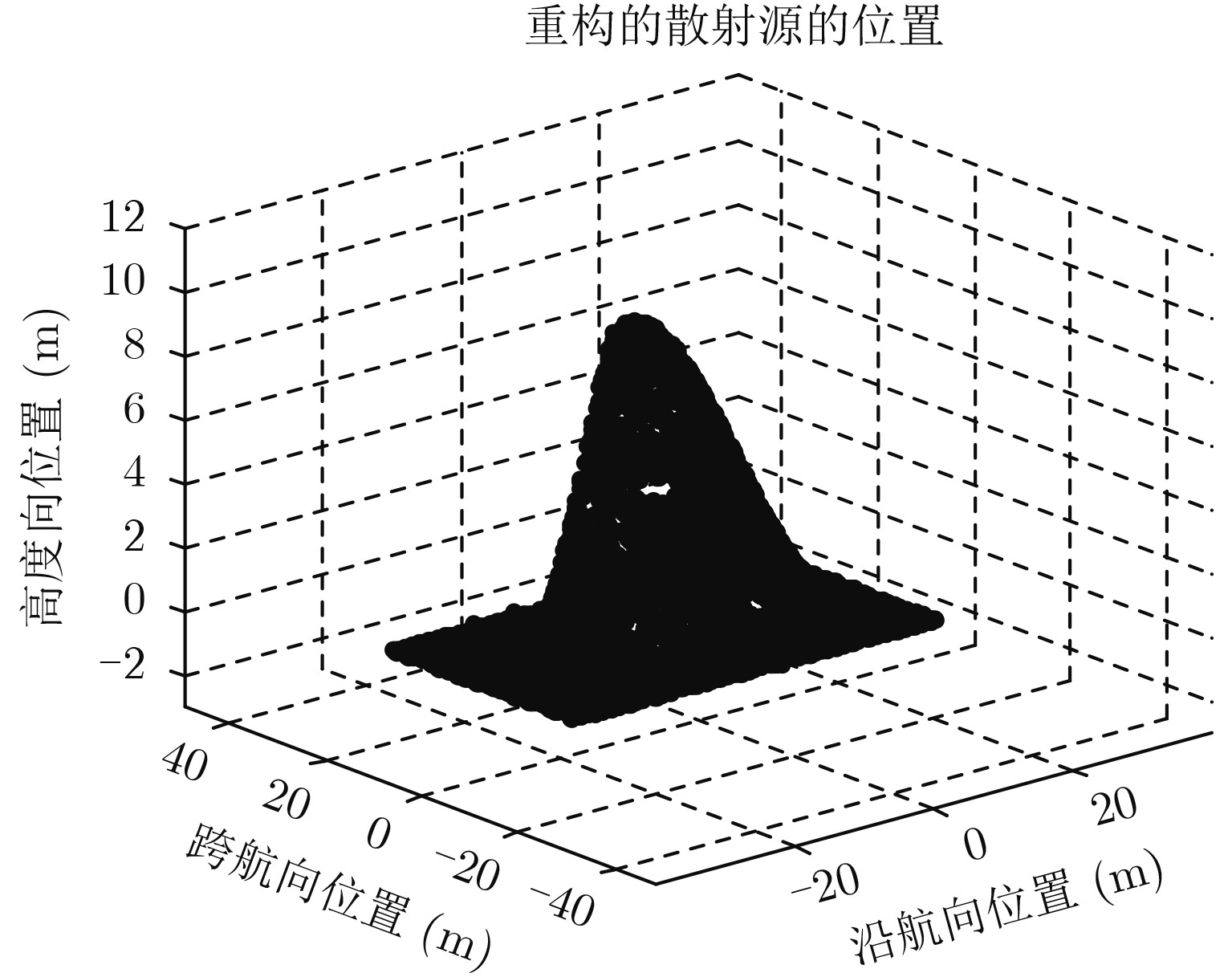
然后，通过一组起伏地形情况下3维成像结果进一步验证本文方法。图6给出了仿真地形的高度图，该地形为一个对称的山包，山包高度为10 m，不存在层叠。图7给出了重构的地表散射源位置图，可见本文方法有效实现了起伏地形的3维成像。

图 6(Fig. 6)

图 6 起伏地表的高度图 Fig.6 Height map of undulating ground

图 7(Fig. 7)

图 7 起伏地形下的3维图像 Fig.7 Three-dimensional image of undulating ground

以上仿真实验结果表明，即使回波的信噪比仅有0 dB，采用60%稀疏重构和基于Hough变换的压缩感知方法也能够有效地恢复出大部分的地表散射信息，进而实现3维成像。

对于压缩感知稀疏恢复来说，稀疏解虽然不是连续的，但它们对应的某个更高维空间的信号在某些方向上是连续的，充分利用这一特性可以有效提高压缩感知信号恢复的质量。论文利用这一方法解决了低信噪比下前视阵列SAR稀疏3维成像问题。实验结果表明，即使回波信噪比仅有0 dB，本文方法仍可以有效实现前视阵列SAR稀疏3维成像。