随着任意数字波形发射器、固态发射机、高速处理器等雷达先进技术的快速发展，现代认知雷达能够利用目标和环境的先验信息，并基于某种准则(信干噪比，检测概率等)来自适应地设计雷达发射波形和接收滤波器，以提高系统对目标的探测、识别和分类的能力^[1–10]。针对杂波环境下点目标检测的问题，文献[6]利用目标多普勒和杂波多普勒的先验信息，提出了一种以最大化输出信干噪比(Signal-to-Interference-plus-Noise Ratio, SINR)为准则的雷达发射波形与接收滤波器联合设计方法。针对Multiple-Input Multiple-Output (MIMO)雷达系统中信号相关杂波环境下的目标检测问题，文献[8]基于恒模约束和相似性约束，研究了空时序列与接收滤波器联合设计问题。利用先验已知的杂波、噪声统计信息，文献[9]提出了一种基于最小均方误差(Minimum Mean Square Error, MMSE)准则的发射信号与接收滤波器联合设计技术，以此最小化目标散射系数估计的均方误差。文献[10]研究了杂波背景下扩展目标距离敏感的问题，通过最大化识别特征和目标之间的互信息来优化雷达发射波形，增强了雷达对扩展目标的识别能力。

上述基于认知雷达的发射-接收联合设计方法均要求目标或者杂波先验信息精确已知，然而需要指出的是，实际应用中这些信息可能是不精确的，因此按照上述的方法设计的波形可能会导致系统性能的急剧恶化。为了解决该问题，近年来，稳健的发射-接收联合设计^[11–15]技术已经得到大力发展。通过假定目标多普勒位于某个特定的区间内，文献[11,12]分别讨论了单基地雷达和MIMO雷达在信号相关杂波背景下的点目标检测问题，并分别提出了一种基于半正定松弛(Semi-Definite Relaxation, SDR)与随机化理论的稳健慢时间发射接收联合设计方法，以对抗不确定的目标多普勒平移。文献[13]利用了广义丁克尔巴赫算法来优化雷达波形和多普勒滤波器组，解决了目标多普勒未知下的稳健目标检测问题。针对MIMO雷达系统未知角度的目标检测问题，文献[14]提出了一种以信号相关杂波环境下的W-SINR为准则的发射接收联合设计方法。文献[15]研究了一种稳健的慢时间发射结合设计方法，能有效对抗不确定的杂波2阶统计信息，改善W-SINR值。需要说明的是，以上很多设计方法都是基于SDR相关技术实现的，因而均具有较高的计算复杂度，大大限制了其实际应用场景。

本文主要针对单基地雷达对运动点目标在信号相关杂波背景下的检测问题，基于杂波2阶统计信息的不确定度分析^[12]，以W-SINR为优化准则，研究了一种稳健的慢时间恒模发射序列与接收滤波器设计方法，并提出了一种高效的序列迭代优化算法。该算法将该非凸高维优化问题转化为多个1维子问题求解，并分别利用丁赫尔巴赫迭代算法快速得到最优解；实验结果表明，相比SDR类算法，提出的算法在较少的时间内能够实现更高的W-SINR值，同时具有对抗杂波2阶统计信息不确定的能力。

考虑单基地雷达连续发射N个脉冲，每个脉冲在其相应脉冲重复间隔(Pulse Repetition Interval, PRI)内经匹配滤波后采样^[6,8]，则N维观测列向量为 ${{v}} = {\left[ {v\left( 1 \right){\rm{ }}\; v\left( 2 \right){\rm{ }} \cdots {\rm{ }}\; v\left( N \right)} \right]^{\rm{T}}} \in {{\rm{C}}^N}$ ，其中 ${\left( \cdot \right)^{\rm{T}}}$ 表示转置操作。取当前PRI下的观测向量描述如下^[6]：

其中， $ \odot $ 表示Hadamard积， $s = {\left[ {s\left( 1 \right)\;s\left( 2 \right) \ldots s\left( N \right)} \right]^{\rm{T}}}$ 为N个脉冲的码字序列， ${\alpha _ \rm {T}}$ 是与目标相关的复参数， ${f_{\rm{T}}}$ 是目标的归一化多普勒频率， ${{p}}\left( {{f_{\rm{T}}}} \right){\rm{ = }}$ ${\Big[ {1\;{{\rm e}^{{\rm j}2{{π}} {f_{\rm{T}}}}}{\rm{ }}\; ·\!·\!· \;{{\rm e}^{{\rm j}2{{π}} {f_{\rm{T}}}\left( {N - 1} \right)}}} \Big]^{\rm{T}}}$ 是频率向量，c和n分别是杂波项和噪声项，其中n是高斯白噪声，其协方差矩阵为 ${\rm{E}}\left[ {{{n}}{{{n}}^{\rm{H}}}} \right] = \sigma _{\rm{n}}^2{{{I}}_N}$ ，其中 ${\rm{E}}\left[ \cdot \right]$ 表示求期望， $\sigma _{\rm{n}}^2$ 为噪声功率， ${{{I}}_N}$ 表示N维单位矩阵， ${\left( \cdot \right)^{\rm{H}}}$ 表示共轭转置操作。

若将杂波向量c建模为杂波块的叠加，则可表述为：

其中， ${\alpha _{\left( {k,l} \right)}}$ 和 ${\alpha _{\rm{T}}}$ 都是零均值非相关的随机变量，且方差分别为 $\sigma _{\left( {k,l} \right)}^2 = {\rm E}\left[ {{{\left| {{\alpha _{\left( {k,l} \right)}}} \right|}^2}} \right]$ 和 $\sigma _{\rm{T}}^2 = {\rm E}\left[ {{{\left| {{\alpha _{\rm{T}}}} \right|}^2}} \right]$ ; ${f_{\left( {k,l} \right)}}$ 表示第k个距离环上第l个杂波的归一化多普勒频率。与文献[12]类似，本文同样假设 ${f_{\left( {k,l} \right)}}$ 是一个均匀分布的随机变量，且其中心多普勒频率为 ${\overline f _{\left( {k,l} \right)}}$ ，则

其中 ${\varepsilon _{\left( {k,l} \right)}}$ 控制了 ${f_{\left( {k,l} \right)}}$ 的不确定度。

${{{J}}_k} \in {{\rm{C}}^{N \times N}}$ 表示转移矩阵，其第 $\left( {n,m} \right)$ 个元素定义为：

基于先前的假设，杂波c的均值为0，协方差矩阵可描述为^[12]：

其中， ${\rm{diag}}\left( {{s}} \right)$ 表示由向量s中元素组成的对角矩阵， ${{{M}}_{\left( {k,l} \right)}}{\rm{ = }}\sigma _{\left( {k,l} \right)}^2{{Φ}}_{{\varepsilon _{\left( {k,l} \right)}}}^{{{\overline f }_{\left( {k,l} \right)}}}$ 为杂波频率协方差矩阵且有 ${{Φ}}_{{\varepsilon _{\left( {k,l} \right)}}}^{{{\overline f }_{\left( {k,l} \right)}}}{\rm{ = E}}\left[ {{{p}}\left( {{f_{\left( {k,l} \right)}}} \right){{p}}{{\left( {{f_{\left( {k,l} \right)}}} \right)}^{\rm{H}}}} \right]$ ，其第 $\left( {n,m} \right)$ 个元素定义为：

本文讨论稳健的雷达发射序列与接收滤波器联合设计问题，旨在最大化杂波多普勒2阶统计信息不确定时的W-SINR。假设慢时间观测向量v经过滤波器 ${{w}} \in {{\rm{C}}^N}$ ( ${{w}} \ne 0$ 且独立于杂波干扰和噪声过程)后输出的 ${\rm{SINR = }}\rho \left( {{{s},{w}}} \right)$ 为：

其中， $\left| \cdot \right|$ 表示取模， ${{{w}}^{\rm{H}}}{{{Σ}}_{\rm{c}}}\left( {{s}} \right){{w}}{\rm{ = E}}\left[ {{{\left| {{{{w}}^{\rm{H}}}{{c}}} \right|}^2}} \right]$ 和 $\sigma _{\rm{n}}^{\rm{2}}\left\| {{w}} \right\|_2^2{\rm{ = E}}\left[ {{{\left| {{{{w}}^{\rm{H}}}{{n}}} \right|}^2}} \right]$ 分别表示杂波和噪声滤波输出的功率。由式(5)可知杂波协方差矩阵 ${{{Σ}}_{\rm{c}}}\left( {{s}} \right)$ 由矩阵 ${{{M}}_{\left( {k,l} \right)}}$ 计算得到，而 ${{{M}}_{\left( {k,l} \right)}}$ 取决于杂波功率 $\sigma _{\left( {k,l} \right)}^2$ 、归一化多普勒频率 ${f_{\left( {k,l} \right)}}$ 以及不确定参数 ${\varepsilon _{\left( {k,l} \right)}}\left( {k = 1, ·\!·\!· ,N;l = 1, ·\!·\!· ,L} \right)$ 等信息。从实际应用考虑，这些信息均很难精确获得，因此杂波多普勒的2阶统计量 ${{{M}}_{\left( {k,l} \right)}}$ 会存在不确定度，可用以下二次约束表示：

其中， ${\widehat{{M}}_{\left( {k,l} \right)}}{\rm{ = }}\sigma _{\left( {k,l} \right)}^2{{Φ}}_{{\varepsilon _{\left( {k,l} \right)}}}^{{{\overline f }_{\left( {k,l} \right)}}}$ 为基于先验信息的估计值， ${\left\| \cdot \right\|_2}$ 表示2-范数， ${\delta _{\left( {k,l} \right)}}$ 决定了矩阵 ${{{M}}_{\left( {k,l} \right)}}$ 的不确定度大小。

另外，由于实际应用中雷达发射端非线性放大器的限制^[16]，本文考虑恒模发射序列。则恒模约束下的W-SINR优化问题描述如下：

其中， $\rho \left( {{{s},{w}},{{{M}}_{\left( {1,1} \right)}}, ·\!·\!· ,{{{M}}_{\left( {N,L} \right)}}} \right)$ 与 $\rho \left( {{{s},{w}}} \right)$ 等价，表示输出SINR, s_i表示序列s的第i个码字；“ $\underline \succ $ ”是广义的矩阵不等号：对任意矩阵 ${{A}} \in {{\rm{H}}^N},{{A}}\underline \succ {0}$ 表示矩阵A是一个半正定矩阵。

对问题P₀，首先分析其内部优化，其优化结果是在s, w一定时求最小的SINR值(即W-SINR)，以及其对应的一组杂波多普勒协方差矩阵M_(k,l), k $ 1,2, ·\!·\!· ,N;l = 1,2, ·\!·\!· ,L$ 。该内部优化可等价于最大化干扰能量P_c：

基于式(5)，P_inner是一个最大和问题，其可以等价于N×L个最大化问题P_(k,l)(k=1, ···, N, $l=1,\, ·\!·\!·, \, L $ )的和，每个最大化问题可描述为：

根据矩阵理论^[17]，约束 ${\left\| {{{{M}}_{\left( {k,l} \right)}} - {{\widehat{{M}}}_{\left( {k,l} \right)}}} \right\|_2} \le {\delta _{\left( {k,l} \right)}}$ 可导出以下不等式：

其中， ${\lambda _i}\left( {{{{M}}_{\left( {k,l} \right)}} -\!\! {{\widehat{{M}}}_{\left( {k,l} \right)}}} \right)$ 表示矩阵 ${{{M}}_{\left( {k,l} \right)}} - {\widehat{{M}}_{\left( {k,l} \right)}}$ 的第i个特征值。由于 ${{\rm{P}}_{\left( {k,l} \right)}}$ 的目标函数在变量范围 ${\widehat {{M}}_{\left( {k,l} \right)}} - {\delta _{\left( {k,l} \right)}}{{{I}}_N}\underline \prec {{{M}}_{\left( {k,l} \right)}}\underline \prec {\widehat{{M}}_{\left( {k,l} \right)}}{\rm{ + }}{\delta _{\left( {k,l} \right)}}{{{I}}_N}$ 内单增^[12]，故在 ${{{M}}_{{\rm{opt}}\left( {k,l} \right)}}{\rm{ = }}{\widehat {{M}}_{\left( {k,l} \right)}}{\rm{ + }}{\delta _{\left( {k,l} \right)}}{{{I}}_N}$ 时 ${{\rm{P}}_{\left( {k,l} \right)}}$ 取得最优。则考虑此时的杂波协方差矩阵 ${{{\mathord{\stackrel \frown {Σ} } }}_{\rm{c}}}\left( {{s}} \right)$ 和W-SINR $\mathord{\stackrel \frown \rho } \left( {{{s},{w}}} \right)$ 分别表述为：

将以上两式代入问题P₀，则优化问题重述为：

由式(15)可知，问题P₁是一个NP-hard问题，没有最优解。本文介绍一种序列迭代优化算法(ISO)来逐步优化SINR值，最终得到一个较好的次优解。具体而言，已知第n–1次迭代中码子 ${{{s}}^{\left( {n - 1} \right)}}$ ，可根据最小无失真相应(Minimum Variance Distortionless Response, MVDR)理论求解 ${{w}}_{{\rm{opt}}}^{\left( {n - 1} \right)}$ ；第n次迭代中，已知 ${{{w}}^{\left( {n - 1} \right)}}$ ，为最大化输出信噪比，可借助于模式搜索的思想，将求解 ${{s}}_{{\rm{opt}}}^{\left( n \right)}$ 的高维优化问题转化为N个求解 ${\bar s_{{\rm{opti}}}}$ 的1维分式规划问题，以此循环反复，直到满足退出条件。

首先对固定序列 ${{{s}}^{\left( n \right)}}$ 的优化问题进行讨论，基于MVDR理论^[18]，式(15)可以简化为：

其有闭式解：

对固定滤波器权向量 ${{{w}}^{\left( {n - 1} \right)}}$ ，式(15)可以简化成以下形式^[1]：

其中矩阵 ${{{Σ}}_{\rm{t}}}\left( {{{{w}}^{\left( {n - 1} \right)}}} \right)$ 和 ${{{Σ}}_{\rm{I}}}\left( {{{{w}}^{\left( {n - 1} \right)}}} \right)$ 分别表示为：

且 ${\left( \cdot \right)^ * }$ 表示取共轭。

借助于文献[19]介绍的模式搜索思想，本文通过依次优化序列s中每个元素来实现对s优化，其中优化每个码字时我们假设其余N–1个码字保持不变，则第n次迭代的优化问题 ${\rm{P}}_{{s}}^{\left( n \right)}$ 能化简成N个1维优化问题，相应于第i个码字其优化问题 ${\rm{P}}_{{{\bar s}_i}}^{\left( n \right)}$ 可表述为：

其中， $i = 1,2, ·\!·\!· ,N$ , ${\bar{{s}}} = {\left[ {{s_1}\;{s_2}\; ·\!·\!· {\rm{ }}{s_{i - 1}}\;{{\bar s}_i}\;{s_{i + 1}} ·\!·\!· {\rm{ }}{s_N}} \right]^{\rm{T}}}$ 且有

重述矩阵 ${{Σ}_{\rm{t}}}\left( {{{{w}}^{\left( {n - 1} \right)}}} \right)$ 和 ${Θ}\left( {{{{w}}^{\left( {n - 1} \right)}}} \right)$ 分别为：

其中， ${{{a}}_p} \!=\!\! {\left[ {{\alpha _{p,1}}\,{\alpha _{p,2}}\, ·\!·\!·\,{\alpha _{p,{{N}}}}} \right]^{\rm{T}}}$ 且 ${{b}_p} \!\!=\!\! {\left[ {{\beta _{p,1}}\,{\beta _{p,2}} ·\!·\!· {\beta _{p,{N}}}} \right]^{\rm{T}}}$ $ \in {{\rm{C}}^N},p = 1,2, ·\!·\!· ,N$ ，因此 ${\bar {{s}}^{\rm{H}}}{{Σ}_{\rm{t}}}\left( {{{{w}}^{\left( {n - 1} \right)}}} \right)\bar{{s}}$ 和 ${\bar{{s}}^{\rm{H}}}{Θ}\left( {{{{w}}^{\left( {n - 1} \right)}}} \right)\bar{{s}}$ 可以表述为^[19]：

其中， $\Re \left( \cdot \right)$ 表示取实部， ${a_{3,i}} = {a_{0,i}}/N + {a_{2,i}}$ , ${b_{3,i}} = {b_{0,i}}/N + {b_{2,i}}$ ，且 ${a_{r,i}},{b_{r,i}}\left( {r = 0,1,2} \right)$ 都为常数，可由下式计算得到^[19]：

最终，问题 ${\rm{P}}_{{{\bar s}_i}}^{\left( n \right)}$ 可以等价转换为以下分式规划问题

利用文献[19]中介绍的丁克尔巴赫方法能快速求解该问题。

表1总结了本文所提算法的整体流程，具体而言，每步迭代都需要计算式(17)和求解N个计算复杂度为O(N²)的优化问题 ${\rm{P}}_{{{\bar s}_i}}^{\left( n \right)},i = 1,2, ·\!·\!· ,N$ 。因此，可考虑以 $\left( {{{w}},{s_1}, ·\!·\!· ,{s_N}} \right)$ 为顺序循环优化这些变量。

表 1(Tab. 1

表 1 稳健的发射-接收联合设计算法 Tab. 1 Algorithm for the robust transmit-receive design 输入： ${{{s}}_0},\xi ,\sigma _{\left( {k,l} \right)}^2,{f_{\left( {k,l} \right)}},{\varepsilon _{\left( {k,l} \right)}},{\delta _{\left( {k,l} \right)}},k = 1,2, ·\!·\!· ,N,l = 1,2, ·\!·\!· ,L$ 输出：P1的最优解 $\left( {{{{s}}_{{\rm{opt}}}},{{{w}}_{{\rm{opt}}}}} \right)$ (1) 由式(11)得到 ${{{M}}_{{\rm{opt}}\left( {k,l} \right)}}$ 然后根据式(13)计算 $ \widehat{ {Σ} _{\rm{c}}}\left( {{s}} \right)$ ； (2) 对于 $n = 0,i = 0$ 然后初始化序列 ${{{s}}^{\left( 0 \right)}} = {{{s}}_0}$ ； (3) 由式(17)计算 ${{{w}}^{\left( 0 \right)}}$ ，根据式(14)计算 ${\stackrel \frown {\rho}} _0{\rm{ = }}\mathord{\stackrel \frown {\rho}} \left( {{{{s}}^{\left( 0 \right)}},{{{w}}^{\left( 0 \right)}}} \right)$ ； (4) n=n+1； (5) 根据式(19)和式(22)分别计算矩阵 ${{Σ}_{\rm{t}}}\left( {{{{w}}^{\left( {n - 1} \right)}}} \right)$ 和 ${Θ}\left( {{{{w}}^{\left( {n - 1} \right)}}} \right)$ ； (6) i=i+1； (7) 根据式(26)和式(27)分别计算 ${a_{r,i}},{b_{r,i}}\left( {r = 0,1,2} \right)$ ； (8) 在可行域内随机产生初始码字 ${s_{i,0}}$ ； (9) 解式(28)并得到最优解 ${s_{{\rm{opti}}}}$ ； (10) 如果i=N，输出 ${{{s}}^{\left( n \right)}} = {\left[ {{s_{{\rm{opt1}}}}\;{s_{{\rm{opt}}2}}\; ·\!·\!· {\rm{ }}{s_{{\rm{opt}}N}}} \right]^{\rm{T}}}$ ，否则返回步骤(6)； (11) 由式(17)计算 ${{{w}}^{\left( n \right)}}$ ，根据式(14)计算 ${\mathord{\stackrel \frown {\rho}} _n}{\rm{ = }}\mathord{\stackrel \frown {\rho}} \left( {{{{s}}^{\left( n \right)}},{{{w}}^{\left( n \right)}}} \right)$ ； (12) 如果 $\left| {{{\mathord{\stackrel \frown {\rho}} }_n} - {{\mathord{\stackrel \frown {\rho}} }_{n - 1}}} \right| \le \xi $ ( $\xi $ 是一个用来控制收敛的自定义参数)， 　　输出 ${{{s}}_{{\rm{opt}}}}{\rm{ = }}{{{s}}^{\left( n \right)}},{{{w}}_{{\rm{opt}}}}{\rm{ = }}{{{w}}^{\left( n \right)}}$ ；否则返回步骤(4)，直到收敛。

表 1 稳健的发射-接收联合设计算法 Tab.1 Algorithm for the robust transmit-receive design

由此可推算，ISO在每步迭代中求解 ${{{s}}^{\left( n \right)}}$ 的计算复杂度为O(N³)，而结合随机化方法的SDR类算法每步求解 ${{{s}}^{\left( n \right)}}$ 的复杂度为 ${\rm{O}}\left( {{N^{3.5}}{\rm{ + }}{N^2}L} \right)$ ^[8]，其中N为序列长度，L为随机化次数，因此，通过理论分析可知，ISO相对于SDR类算法具有更低的计算复杂度。

本文针对优化所得最大W-SINR及计算时间两方面对所提算法性能进行评估。考虑初始序列选用线性调频编码序列，码字表示为 $s\left( n \right) = 1/\sqrt N {{\rm e}^{{\rm j}{{π}} \left( {2n + {n^2}} \right)/N}}$ , $n = 1,2, ·\!·\!· ,N$ ，长度N=20，且假设算法迭代的退出条件参数设为 ${ξ} {\rm{ = }}{10^{ - 3}}$ 。另外本文注明，仿真中涉及到的计算时间分析皆基于计算机(3.5 GHz内核i3处理器以及4 GB运行内存)和Matlab 2012a环境运行得到。

考虑目标位于k=0距离环上，其归一化多普勒频移 ${f_{\rm{T}}} = - 0.4$ ，信噪比(Signal-to-Noise Ratio, SNR)为 ${\rm{SN}}{{\rm{R}}_{\rm{t}}}{\rm{ = }}{\left| {{\alpha _{\rm{T}}}} \right|^2}/\sigma _{\rm{n}}^{\rm{2}}$ =10 dB。假设c是一个位于k=6距离环上的海杂波，其中心多普勒频率为 ${\bar f_{\rm{s}}} = - 0.15$ ，多普勒不确定度 ${\varepsilon _{\left( {6,1} \right)}}{\rm{ = }}0.7$ ，杂噪比(Clutter-to-Noise Ratio, CNR) CNR_s= $ {\left| {{\alpha _{6,1}}} \right|^2}\sigma _{\rm{n}}^{\rm{2}}$ =30 dB。另外，设矩阵 ${{{M}}_{\left( {k,l} \right)}}$ 的不确定度大小为 ${\delta _{\left( {6,1} \right)}}{\rm{ = }}0.01{\lambda _0}$ ，其中 ${\lambda _0}{\rm{ = }}\mathop {\min }\nolimits_{\left( {k,l} \right)} {\lambda _{\max }}\left( {{{{M}}_{\left( {k,l} \right)}}} \right)$ 。

文献[8]讨论的是干扰参数精确已知时的SINR优化问题，但就其算法而言，文中考虑恒模约束的SOA2-CMC算法能有效解决本文所述问题P₁，而其仅考虑能量约束的SOA2-EC算法则表示不考虑任何其他约束和不确定信息的理想SINR优化情况，给出了SINR优化值上界。其中，SOA2-CMC是基于SDR和随机化方式的算法。作为对比，本文针对以上两种算法在相同场景下进行仿真，对SDR的求解可借助于凸优化工具箱(cvx)^[20]，随机化次数可取100。

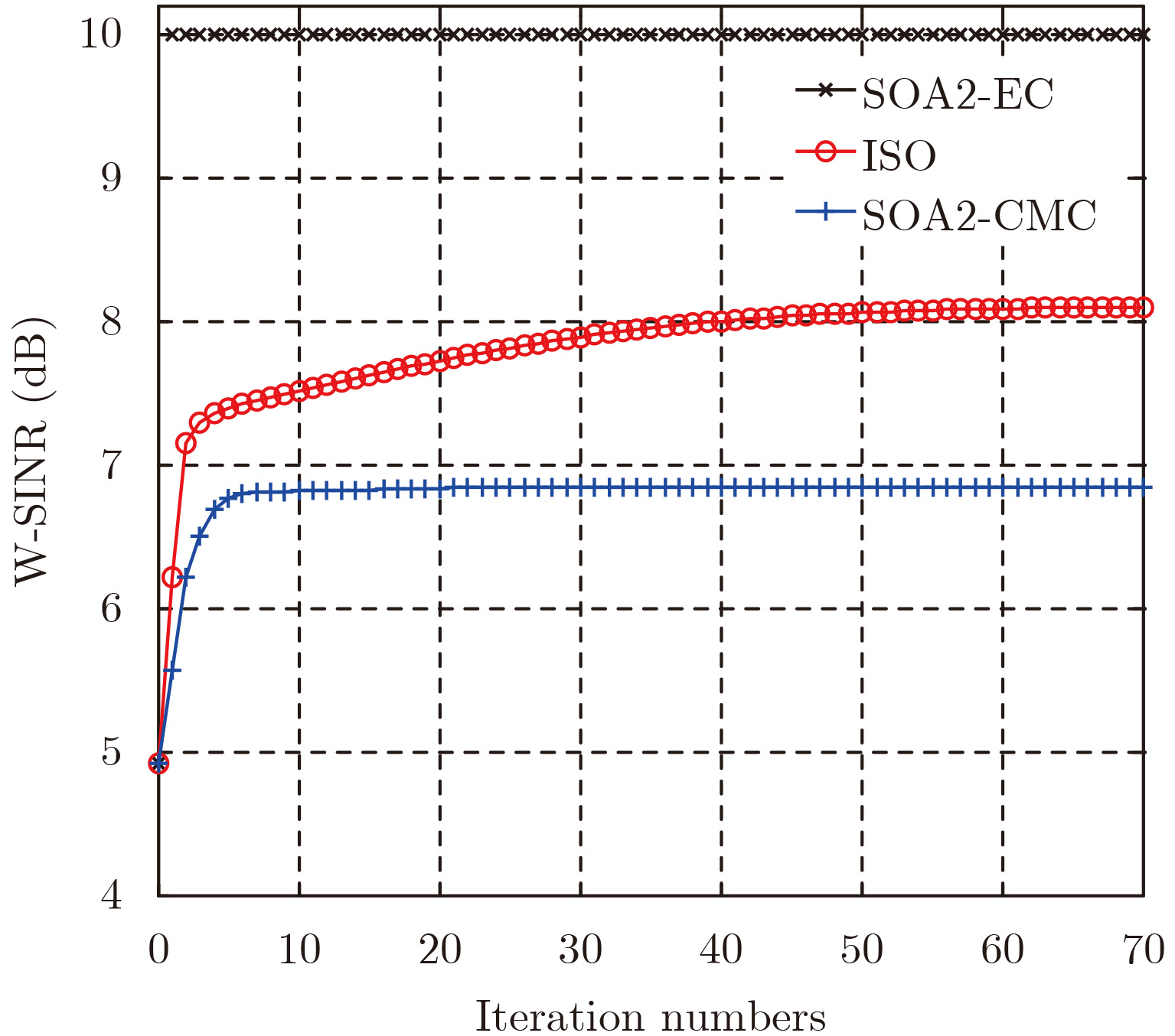
图1针对ISO, SOA2-CMC和SOA2-EC算法分别呈现了其相应W-SINR随迭代次数变化的曲线，其中为避免SOA2-CMC算法的随机性，可取其100次蒙特卡洛实验平均的结果。仿真说明，ISO和SOA2-CMC均能有效改善W-SINR值。其中，ISO能使W-SINR优化至8.09 dB，而SOA2-CMC仅能达到6.84 dB。另外，由于不确定的杂波统计特性以及发射序列的恒模约束，ISO与SOA2-CMC相对于SOA2-EC描述的理想情况都呈现一定的SINR损失。

图 1(Fig. 1)

图 1 W-SINR随迭代次数变化曲线(SOA2-EC, ISO和SOA2-CMC) Fig.1 W-SINR versus iteration number for SOA2-EC, ISO and SOA2-CMC

表2就迭代次数和计算时间两方面对SOA2-EC, ISO以及SOA2-CMC算法性能做了总结。相对于SOA2-CMC, ISO算法拥有更短的计算时间，更接近理想情况SOA2-EC的用时。具体来讲，ISO经过73步迭代用时0.220 s便达到收敛条件，而SOA2-CMC和SOA2-EC分别需要45步迭代用时23.920 s和4步迭代用时0.005 s。综上我们指出，相对于SOA2-CMC, ISO能大大减少计算量且能实现更加令人满意的W-SINR值。

表 2(Tab. 2

表 2 收敛条件 $\left| {{{\mathord{\stackrel \frown {ρ} } }_{n}} - {{\mathord{\stackrel \frown{{ρ}} } }_{{n} - {1}}}} \right| \!\!\le\!\! {10^{ - 3}}$ 下3种算法的迭代次数和计算时间 Tab. 2 Iteration number and computation time (in seconds) of all the three algorithms with the exit condition $\left| {{{\mathord{\stackrel \frown{{ρ}}} }_n} - {{\mathord{\stackrel \frown{{ρ}} } }_{{n} - {1}}}} \right| \le {{10}^{ - 3}}$ 算法 迭代次数 计算时间(s) SOA2-EC 4 0.005 ISO 73 0.220 SOA2-CMC 45 23.920

表 2 收敛条件 $\left| {{{\mathord{\stackrel \frown {ρ} } }_{n}} - {{\mathord{\stackrel \frown{{ρ}} } }_{{n} - {1}}}} \right| \!\!\le\!\! {10^{ - 3}}$ 下3种算法的迭代次数和计算时间 Tab.2 Iteration number and computation time (in seconds) of all the three algorithms with the exit condition $\left| {{{\mathord{\stackrel \frown{{ρ}}} }_n} - {{\mathord{\stackrel \frown{{ρ}} } }_{{n} - {1}}}} \right| \le {{10}^{ - 3}}$

考虑距离-多普勒平面的联合分析，定义慢时间互模糊函数(Cross-Ambiguity Function, CAF)如下^[6]：

其中， $k = 0,1, ·\!·\!· ,N - 1$ 是延时单元， $f \in \left[ { - 0.5,0.5} \right]$ 是归一化多普勒频率，则 ${\rm{g}}\left( {k,f} \right)$ 表示不同距离环、多普勒单元信号滤波后的输出功率。

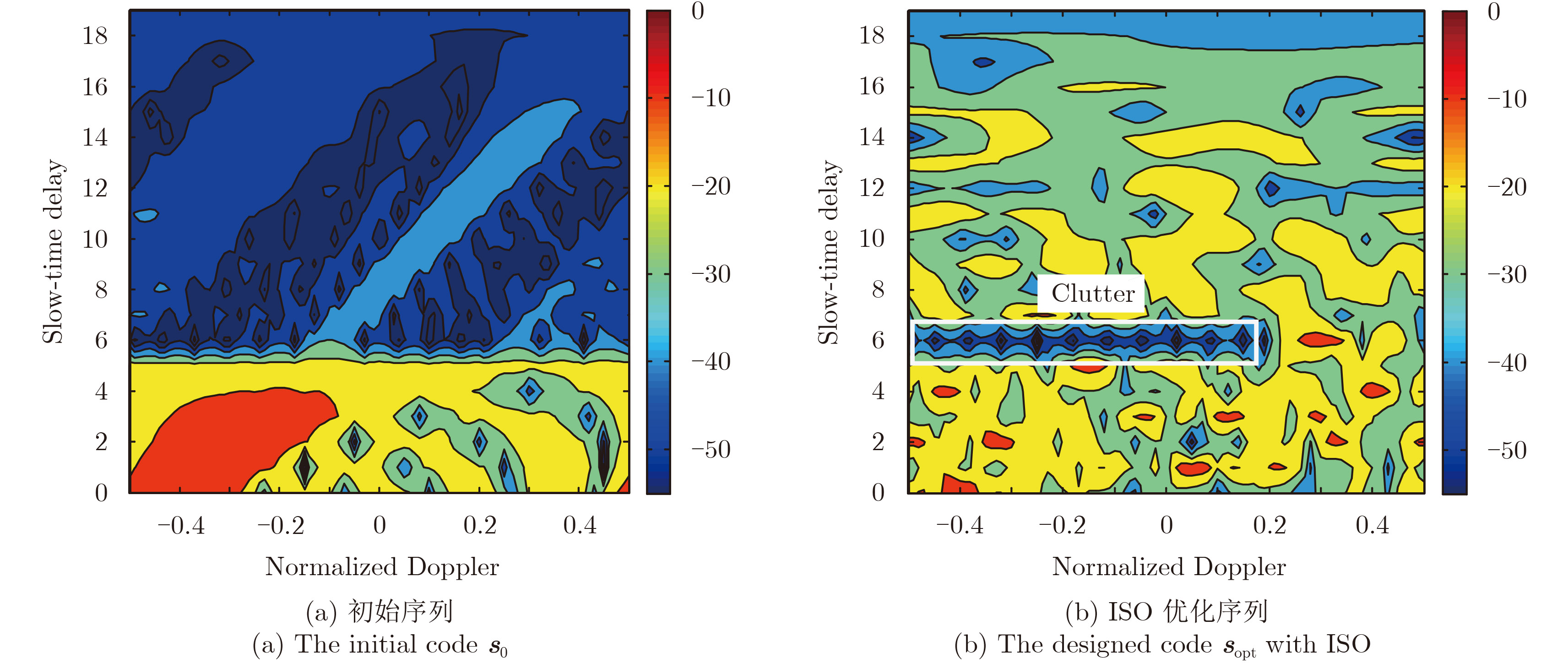
图2(a)、图2(b)分别是初始序列 ${{{s}}_0}$ 和基于ISO算法优化序列 ${{{s}}_{{\rm{opt}}}}$ 的CAF等高图，由此可知，序列 ${{{s}}_{{\rm{opt}}}}$ 的CAF在k=6, –0.5<f<0.2范围内有较低的值，且在2维平面上形成一个较为明显的杂波抑制带，这一特性说明，ISO算法能通过控制CAF形状来实现对信号相关杂波的有效抑制。

图 2(Fig. 2)

图 2 互模糊函数(CAF)等高图 Fig.2 Contour maps of CAF

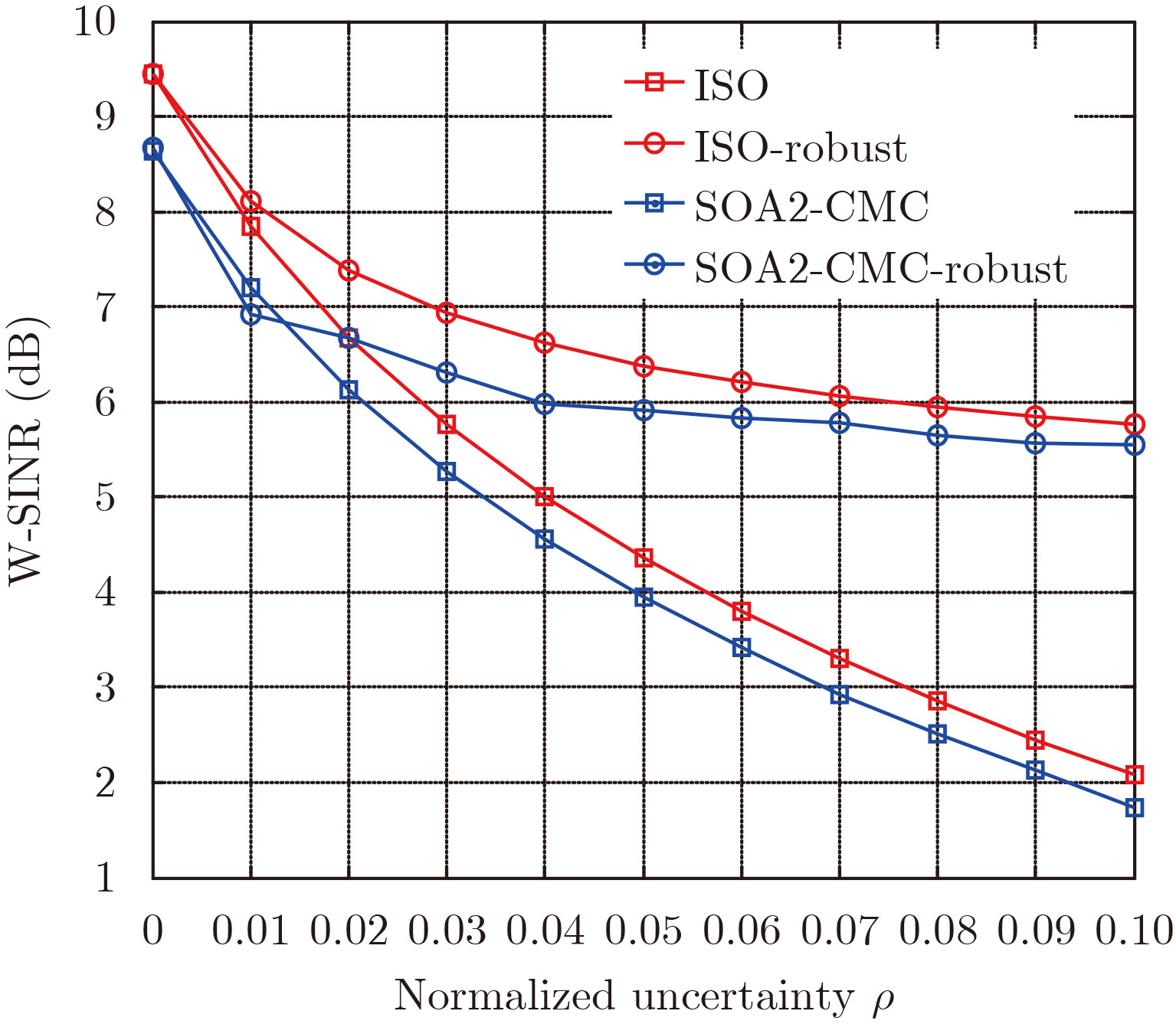
最后，本文对稳健性进行仿真，以评估系统在不确定杂波多普勒统计信息下的适应能力。考虑分别对ISO和SOA2-CMC进行两种情况下的设计：不考虑稳健性且忽略杂波多普勒失配的常规设计 $(\delta {\rm{ = }}0)$ ；考虑W-SINR优化的稳健设计 $(\delta \ne 0)$ 。图3描述的是ISO和SOA2-CMC两种算法W-SINR随着归一化不确定度 $\rho $ 的变化曲线，其中归一化不确定度 $\rho {\rm{ = }}\delta /{\lambda _0}$ ，且取 ${\rho _{\left( {6,1} \right)}} = \left[ {0\;0.01{\rm{ }} ·\!·\!· {\rm{ }}0.10} \right]$ 。结果说明，无论哪种算法，稳健设计所能实现的W-SINR都明显高于常规设计，且不确定度越大，稳健设计的优势就越明显，其中 ${\rho _{\left( {6,1} \right)}} = 0.10$ 时，基于ISO的稳健性设计相对常规设计能实现3.7 dB的W-SINR增益，且相对于SOA2-CMC具有更高的W-SINR值，这进一步证明了ISO在优化效果上的优势。另外，相较于ISO平稳的下降趋势，SOA2-CMC在该仿真参数下性能不太稳定，在 ${\rho _{\left( {6,1} \right)}} = 0.01$ 时不能体现出稳健设计的优势，这与参数选择有关，可见SOA2-CMC对参数较为敏感。基于以上说明，我们指出本算法能有效对抗杂波信息的不准确性，使系统具有更强的适应能力。

图 3(Fig. 3)

图 3 基于常规设计和稳健设计的W-SINR随归一化不确定度的变化曲线(ISO和SOA2-CMC) Fig.3 W-SINR against the normalized uncertainty size for ISO and SOA2-CMC, associated with the nominal design and the robust design

本文讨论了单基地雷达系统在信号相关杂波背景下稳健的发射-接收联合设计问题，以对抗不确定的杂波多普勒统计信息。首先，以W-SINR为优化准则，建立了恒模约束下稳健的发射-接收联合设计优化模型；然后，提出了一种序列迭代优化算法，以实现目标函数的快速连续优化；最后，通过仿真实例证明了本文算法的优越性。结果显示，ISO与SOA2-CMC都有对抗不确定杂波信息的能力，其中ISO相较于SOA2-CMC具有更低的计算复杂度和更好的W-SINR优化效果。为丰富并完善研究内容，未来的研究工作主要将围绕发射波形的复合约束展开，例如添加相似性约束等^[12]。