② (国防科学技术大学理学院 长沙 410073)
② (School of Science, National University of Defense Technology, Changsha 410073, China)
20世纪60年代以来,极化雷达经历了从非全极化测量体制到全极化测量体制的转变,从分时全极化测量体制到同时全极化测量体制的发展[1,2]。相比于分时全极化测量体制,同时全极化测量体制雷达能够在一个脉冲周期内实现目标极化散射特性的有效测量[3],其核心思想是同时发射两路正交波形,并对两路正交回波进行同时接收。然而,在工程中满足完全正交的波形难以找到,因此,设计具有良好正交性的波形对于同时全极化测量体制雷达具有重要的意义。
针对上述问题,国内外学者对同时全极化测量雷达的发射波形设计进行了深入的研究。Giuli等人在1993年提出了利用两路同时发射的正交波形进行极化散射矩阵测量的理论方法,并且以峰值旁瓣比(Peak Sidelobe Level, PSL)和波形隔离度(Isolation, I)等指标定量分析了正负斜率线性调频波形的极化测量性能[2]。Babur等人针对调频连续波波形进行了深入的研究,设计了准正交的调频连续波波形[4]。调频类波形由于样式较为简单,易被敌方截获,同时不能较好地适应各种不同的应用场景,在一定程度上限制了其应用。随着数字信号处理技术的发展,编码波形凭借其较好的抗截获性能以及较高的波形设计效率等优势逐渐进入人们的视野。特别是随着现代优化理论与方法的飞速发展,使得设计具有较低峰值旁瓣比和波形隔离度的正交编码波形成为可能。Deng等人在2004年首先利用模拟退火算法设计出了具有较好自相关和正交性能的正交多相编码波形,并进行了性能分析[5]。电子科技大学的刘波等人利用遗传算法深入研究了正交多相编码波形和正交离散频率编码波形的设计问题,分析了码长和相位编码数对波形相关性能的影响[6]。Gao等人基于距离-多普勒准则分析了正交离散频率编码的波形设计问题[7]。Kansas大学的Z.Wang等人提出了一种基于重叠正交频分复用(Interleaved Orthogonal Frequency Division Multiplexing, Interleaved OFDM)的正交编码波形设计方法[8]。然而,在被测目标高速运动以及存在较大加速度的情况下,上述正交编码波形的性能会发生退化,如回波脉压输出的旁瓣增加以及编码波形的正交性能下降等。
为了充分考虑由目标运动产生的多普勒效应对同时全极化测量波形性能的影响,本文在Deng, Khan等人工作的基础上,采用灵活的子序列分块编码方法,增加编码波形设计的自由度,综合考虑波形的自相关和互相关性能设计联合代价函数,利用遗传算法(Genetic Algorithm, GA)对正交多相编码波形进行优化设计。
2 多相编码波形表示
|
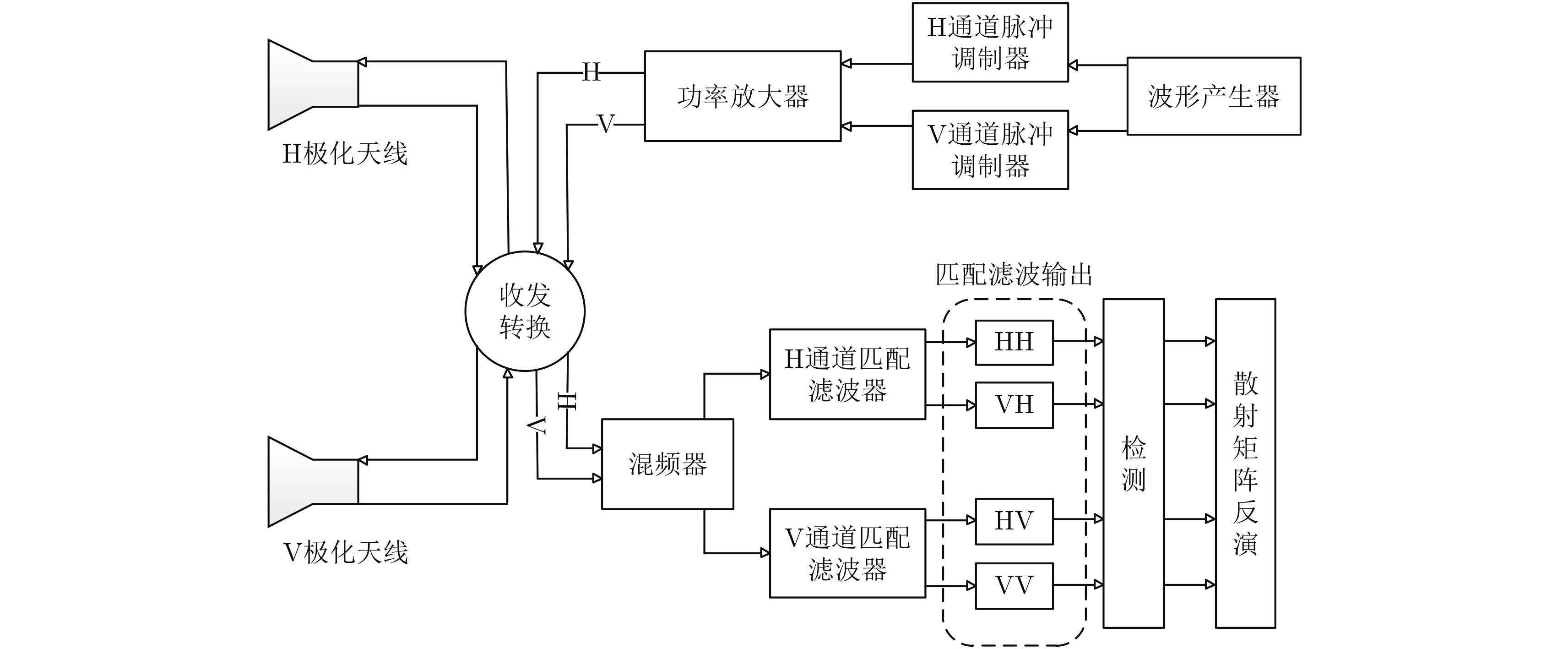
图 1 同时全极化测量雷达信号处理流程图 Fig.1 Signal processing flow chart of simultaneous full-polarization radar |
从图1可以看出,同时全极化测量体制雷达通过双极化通道同时发射两路分别为H(水平)极化和V(垂直)极化的波形,并在接收端对两路极化信号进行同时全极化接收,经过匹配滤波检测之后,对目标的极化散射矩阵进行反演。在窄带条件下,对于点目标,天线的接收信号可以表示为[10]:
|
${{e}_{\rm r}}(t) = \left[ \begin{array}{l}{e_{\rm rh}}(t)\\{e_{\rm rv}}(t)\end{array} \right] = {{R}^{\rm T}} \cdot {S} \cdot {T}\left[ \begin{array}{l}{e_{\rm h}}(t)\\{e_{\rm v}}(t)\end{array} \right]$
|
(1) |
其中R和T分别表示天线的接收和发射方向图,表征着收发天线的空域极化特性,上标T表示矩阵的转置运算;eh(t)和ev(t)分别表示H极化通道和V极化通道的发射信号;S表示目标的极化散射矩阵。接收信号经过匹配滤波之后的输出为:
|
$\begin{array}{l}\left[ {\begin{array}{*{20}{l}}{{o_{\rm hh}} \ \ {o_{\rm hv}}}\\{{o_{\rm vh}} \ \ {o_{\rm vv}}}\end{array}} \right] = \left[ {\begin{array}{*{20}{l}}{{e_{\rm rh}}(t) \otimes {h_{\rm h}}(t) \ \ {e_{\rm rh}}(t) \otimes {h_{\rm v}}(t)}\\{{e_{\rm rv}}(t) \otimes {h_{\rm h}}(t) \ \ {e_{\rm rv}}(t) \otimes {h_{\rm v}}(t)}\end{array}} \right]\\ \quad\quad\quad\quad\quad\quad\!\!\!\! = {{R}^{\rm T}} \cdot \hat {S} \cdot {T} \left[ {\begin{array}{*{20}{l}}{{m_{\rm hh}} \ \ {m_{\rm hv}}}\\{{m_{\rm vh}} \ \ {m_{\rm vv}}}\end{array}} \right]\end{array}$
|
(2) |
其中
极化测量正交多相编码波形可以表示为:
|
$\left\{ \begin{array}{l}{s_{\rm h}}(t) = \sum\limits_{n = 1}^N {\alpha \left[ {t - \left( {n - 1} \right){\tau _0}} \right]{{\rm e}^{{\rm j}{\phi _{\rm h}}(n)}}} \\{s_{\rm v}}(t) = \sum\limits_{n = 1}^N {\alpha \left[ {t - \left( {n - 1} \right){\tau _0}} \right]{{\rm e}^{{\rm j}{\phi _{\rm v}}(n)}}} \end{array} \right.$
|
(3) |
其中:
|
$\alpha (t) = \left\{ \begin{array}{l}\frac{1}{{\sqrt {N{\tau _0}} }},\ {\rm{ }}0 \le t \le {\tau _0}\\0 , \;\;\;\;\;\; \quad { {其他}}\end{array} \right.$
|
(4) |
N表示码长,
|
$\left\{ {0,\frac{{2{{π}} }}{M},2 \cdot \frac{{2{{π}} }}{M}, \cdots ,(M - 1) \cdot \frac{{2{{π}} }}{M}} \right\}$
|
(5) |
对于一个包含两组码长为N,相位编码数为M的多相编码信号集可以用矩阵表示为:
|
${S}(N,M) = \left[ \begin{array}{l}{\phi _{\rm h}}(1) \ {\rm{ }}{\phi _{\rm h}}(2){\rm{ }} \ \cdots {\rm{ }} \ {\phi _{\rm h}}(N)\\{\phi _{\rm v}}(1) \ {\rm{ }}{\phi _{\rm v}}(2){\rm{ }} \ \cdots \ {\rm{ }}{\phi _{\rm v}}(N)\end{array} \right]$
|
(6) |
矩阵中的元素只能从集合式(5)中取值。根据信号的自相关和互相关函数定义[11],可以得到多相编码信号的非周期自相关函数和互相关函数分别为:
|
$\,\,\, R({\phi _p},k) = \left\{ \begin{array}{l}\frac{1}{N}\sum\limits_{n = 1}^{N - k} {\exp\left\{ {{\rm j}\left[ {{\phi _p}(n) - {\phi _p}(n + k)} \right]} \right\}} ,\;\; \quad \ 0 < k \le (N - 1)\\\frac{1}{N}\sum\limits_{n = - k + 1}^N {\exp\left\{ {{\rm j}\left[ {{\phi _p}(n) - {\phi _p}(n + k)} \right]} \right\}} , \;\; - (N - 1) \le k \le 0\end{array} \right.{\rm{ }}p = {\rm h},{\rm v}$
|
(7) |
|
$\!\!\!\!\!\!\!\!\!\! C({\phi _{\rm h}},{\phi _{\rm v}},k) = \left\{ \begin{array}{l}\frac{1}{N}\sum\limits_{n = 1}^{N - k} {\exp\left\{ {{\rm j}\left[ {{\phi _{\rm h}}(n) - {\phi _{\rm v}}(n + k)} \right]} \right\}} ,\;\; \quad \ 0 < k \le (N - 1)\\\frac{1}{N}\sum\limits_{n = - k + 1}^N {\exp\left\{ {{\rm j}\left[ {{\phi _{\rm h}}(n) - {\phi _{\rm v}}(n + k)} \right]} \right\}} , \;\; - (N - 1) \le k \le 0\end{array} \right.$
|
(8) |
需要指出的是,传统的多相编码波形设计方法没有考虑目标运动产生的多普勒频移对波形性能的影响,Khan等人在2006年提出了一种对多相编码信号进行分块编码处理的波形设计方法[12,13],考虑了目标运动产生的多普勒频移,设计的波形相比于传统的多相编码波形具有更好的多普勒容限,但是其设计方法在码长较长时性能改善较小,波形的自相关和互相关性能相比传统的多相编码波形甚至出现了退化。
本文在Khan等人工作的基础之上,为了进一步增加波形设计的自由度,以获得更好的多普勒容限和正交性能,对多相编码波形采用了如下更为灵活的分块方式。将每行序列等间隔的分为G个子序列,则每个子序列的长度为N/G,将每个子序列的编码相位进一步设计为:
|
$\left. {\begin{array}{*{20}{l}}{{\phi _p}(m,n) \in \left\{ {\frac{{{{(2m - G)}^2} + 2 \cdot {G^2}}}{{2 \cdot {G^2}}} \cdot \left[ {0,\frac{{2{{π}} }}{M},2 \cdot \frac{{2{{π}} }}{M}, \cdots ,(M - 1) \cdot \frac{{2{{π}} }}{M}} \right]} \right\}}\\\quad\quad\quad\quad {p = {\rm h},{\rm v}; \ m = 1,2, \cdots ,G; \ n = 1,2, \cdots ,\frac{N}{G}}\end{array}} \right\}$
|
(9) |
其中
对于传统的码长为N的M相编码,每一个码元的相位有M种取值,故其总的搜索空间为Q1=MN。对于本文的分块多相编码而言,将N长的多相码分为G个子序列,每个子序列中的单个码元共有M种相位取值,故对于每一个子序列而言其搜索空间为MN/G,根据式(9)可以看出,每个子序列的相位取值空间并不相同,故码长为N的分块多相编码的总搜索空间为Q2=(MN/G)G,所以有如下等式成立:
|
${Q_2} = {({M^{N/G}})^G} = {M^N} = {Q_1}$
|
(10) |
故本文的分块编码波形与传统的多相编码波形总的搜索空间相同,即本文的分块编码波形设计方法仅仅增加了波形设计的自由度,而并未增加波形设计的复杂度。在此基础上可以将多相编码信号集的矩阵写成:
|
${S}(N,M) = \left[ \begin{array}{l}{\phi _{\rm h}}(1,1){\rm{ }} \ \cdots \ {\rm{ }}{\phi _{\rm h}}\left( {1,\frac{N}{G}} \right){\rm{ }} \ \cdots \ {\rm{ }}{\phi _{\rm h}}(G,1) \ \cdots \ {\rm{ }}{\phi _{\rm h}}\left( {G,\frac{N}{G}} \right)\\{\phi _{\rm v}}(1,1){\rm{ }} \ \cdots \ {\rm{ }}{\phi _{\rm v}}\left( {1,\frac{N}{G}} \right){\rm{ }} \ \cdots \ {\rm{ }}{\phi _{\rm v}}(G,1) \ \cdots \ {\rm{ }}{\phi _{\rm v}}\left( {G,\frac{N}{G}} \right)\end{array} \right]$
|
(11) |
综上,得到了进行分块编码处理的多相编码信号矩阵。
3 多普勒优化分析当目标高速运动时,会导致在接收端对信号进行匹配滤波接收时出现失配,严重时会出现漏检的现象。假设目标相对雷达接收端的径向速度与加速度为分别为v0和a,则信号不同时刻脉内多普勒频偏可以表示为:
|
${f_{\rm d}}(n) = \frac{{2v(n)}}{{{\lambda _0}}} = 2 \frac{{{v_0} + a \displaystyle\frac{{n - 1}}{{N - 1}}N{\tau _0}}}{{{\lambda _0}}}$
|
(12) |
其中
|
${\phi _{\rm d}}(n) = 2{{π}} {f_{\rm d}}(n)\frac{{n - 1}}{{N - 1}}N{\tau _0}$
|
(13) |
由式(13)可以得到最大的多普勒相位偏移为
|
$\begin{array}{*{20}{l}}\begin{array}{l}\Delta {\phi _{\rm d}}(n + 1) - \Delta {\phi _{\rm d}}(n) \\\quad ={\phi _{\rm d}}(n + 2) - 2{\phi _{\rm d}}(n + 1) + {\phi _{\rm d}}(n)\end{array}\\\begin{array}{l} \quad = \frac{{2{π}N{\tau _0}}}{{N - 1}}\left[ {(n + 1){f_{\rm d}}(n + 2)} \right.\\\quad \quad \ \left. { - 2n{f_{\rm d}}(n + 1) + (n - 1){f_{\rm d}}(n)} \right]\end{array}\end{array}$
|
(14) |
将式(12)带入式(14)可以得到:
|
$\Delta {\phi _{\rm d}}(n + 1) - \Delta {\phi _{\rm d}}(n) = \frac{{8{{π}} a{{(N{\tau _0})}^2}}}{{{\lambda _0}(N - 1)^2}}$
|
(15) |
根据式(15)可以发现,在假设目标为匀加速运动的情况下,给定发射端的多相编码波形的载波频率、码长和脉宽,则目标回波的多普勒相移差为等差序列。这也就意味着,当目标为匀速或者匀加速运动时,若能够测得某些时刻的多普勒相移,则可以根据上述结论推出整个码周期任意时刻的多普勒相位偏移,从而可以得出多相编码波形所需要的最大多普勒容限,即设计的发射波形所需满足的条件。在考虑目标的运动时,由于回波存在多普勒相移,需要对式(7)和式(8)进行修正,修正后的结果如下所示:
|
$R({v_0},a,{\phi _p},k) = \\
\left\{ \begin{array}{l}\frac{1}{N}\sum\limits_{n = 1}^{N - k} {\exp\left\{ {{\rm j}\left[ {{\phi _p}(n) - {\phi _p}(n + k) - {\phi _{\rm d}}(n + k)} \right]} \right\}} ,\;\;\quad \ 0 < k \le (N - 1)\\\frac{1}{N}\sum\limits_{n = - k + 1}^N {\exp\left\{ {{\rm j}\left[ {{\phi _p}(n) - {\phi _p}(n + k) - {\phi _{\rm d}}(n + k)} \right]} \right\}} ,\;\; - (N - 1) \le k \le 0\end{array} \right.{\rm{ }}p = {\rm h},{\rm v}$
|
(16) |
|
$\!\!\!\!\!\!\!\!\!\! C({v_0},a,{\phi _{\rm h}},{\phi _{\rm v}},k) = \\
\left\{ \begin{array}{l}\frac{1}{N}\sum\limits_{n = 1}^{N - k} {\exp\left\{ {{\rm j}\left[ {{\phi _{\rm h}}(n) - {\phi _{\rm v}}(n + k) - {\phi _{\rm d}}(n + k)} \right]} \right\}} ,\;\; \quad \ 0 < k \le (N - 1)\\\frac{1}{N}\sum\limits_{n = - k + 1}^N {\exp\left\{ {{\rm j}\left[ {{\phi _{\rm h}}(n) - {\phi _{\rm v}}(n + k) - {\phi _{\rm d}}(n + k)} \right]} \right\}} ,\;\; - (N - 1) \le k \le 0\end{array} \right.$
|
(17) |
根据式(2),同时全极化测量雷达的极化散射矩阵测量精度取决于信号的互相关特性,即正交性;另外根据雷达信号处理理论,为了提高雷达的检测性能,降低旁瓣对弱小检测目标的影响,发射波形的自相关性能也十分重要。所以本文以最小化自相关函数峰值旁瓣比(PSL)和波形隔离度(I)[2],以及自相关函数旁瓣能量和互相关函数能量为优化指标,设计的代价函数如式(18)所示:
|
$\begin{aligned}F = & {w_1} \cdot \left( {\rm PS{L_h} + PS{L_v}} \right) + {w_2} \cdot I\\ & + {w_3} \cdot \left( \rm{AWS{L_h} + AWS{L_v}} \right) + {w_4} \cdot {\rm CWSL}\end{aligned}$
|
(18) |
其中:
|
$\left\{ {\begin{array}{*{20}{l}}{{\rm{PS}}{{\rm{L}}_{\rm{h}}} = \mathop {{\rm{max}}}\limits_{\forall k,k \ne 0} \left[ {20\log \frac{{R({v_0},a,{\phi _{\rm{h}}},k)}}{{R({v_0},a,{\phi _h},0)}}} \right]}\\{{\rm{PS}}{{\rm{L}}_{\rm{v}}} = \mathop {{\rm{max}}}\limits_{\forall k,k \ne 0} \left[ {20\log \frac{{R({v_0},a,{\phi _{\rm{v}}},k)}}{{R({v_0},a,{\phi _{\rm{v}}},0)}}} \right]}\\{I = \mathop {{\rm{max}}}\limits_{\forall k} \left[ {20\log \frac{{C({v_0},a,{\phi _{\rm{h}}},{\phi _{\rm{v}}},k)}}{{{\rm{max}}\left[ {R({v_0},a,{\phi _{\rm{h}}},0),R({v_0},a,{\phi _{\rm{v}}},0)} \right]}}} \right]}\\{{\rm{AWS}}{{\rm{L}}_{\rm{h}}} = \sum\limits_{k = - (N - 1)}^{N - 1} {{{\left| {R({v_0},a,{\phi _{\rm{h}}},k)} \right|}^2}} - {{\left| {R({v_0},a,{\phi _{\rm{h}}},0)} \right|}^2}}\\{{\rm{AWS}}{{\rm{L}}_{\rm{v}}} = \sum\limits_{k = - (N - 1)}^{N - 1} {{{\left| {R({v_0},a,{\phi _{\rm{v}}},k)} \right|}^2}} - {{\left| {R({v_0},a,{\phi _{\rm{v}}},0)} \right|}^2}}\\{{\rm{CWSL}} = \sum\limits_{k = - (N - 1)}^{N - 1} {{{\left| {C({v_0},a,{\phi _{\rm{h}}},{\phi _{\rm{v}}},k)} \right|}^2}} }\end{array}} \right.$
|
(19) |
另外
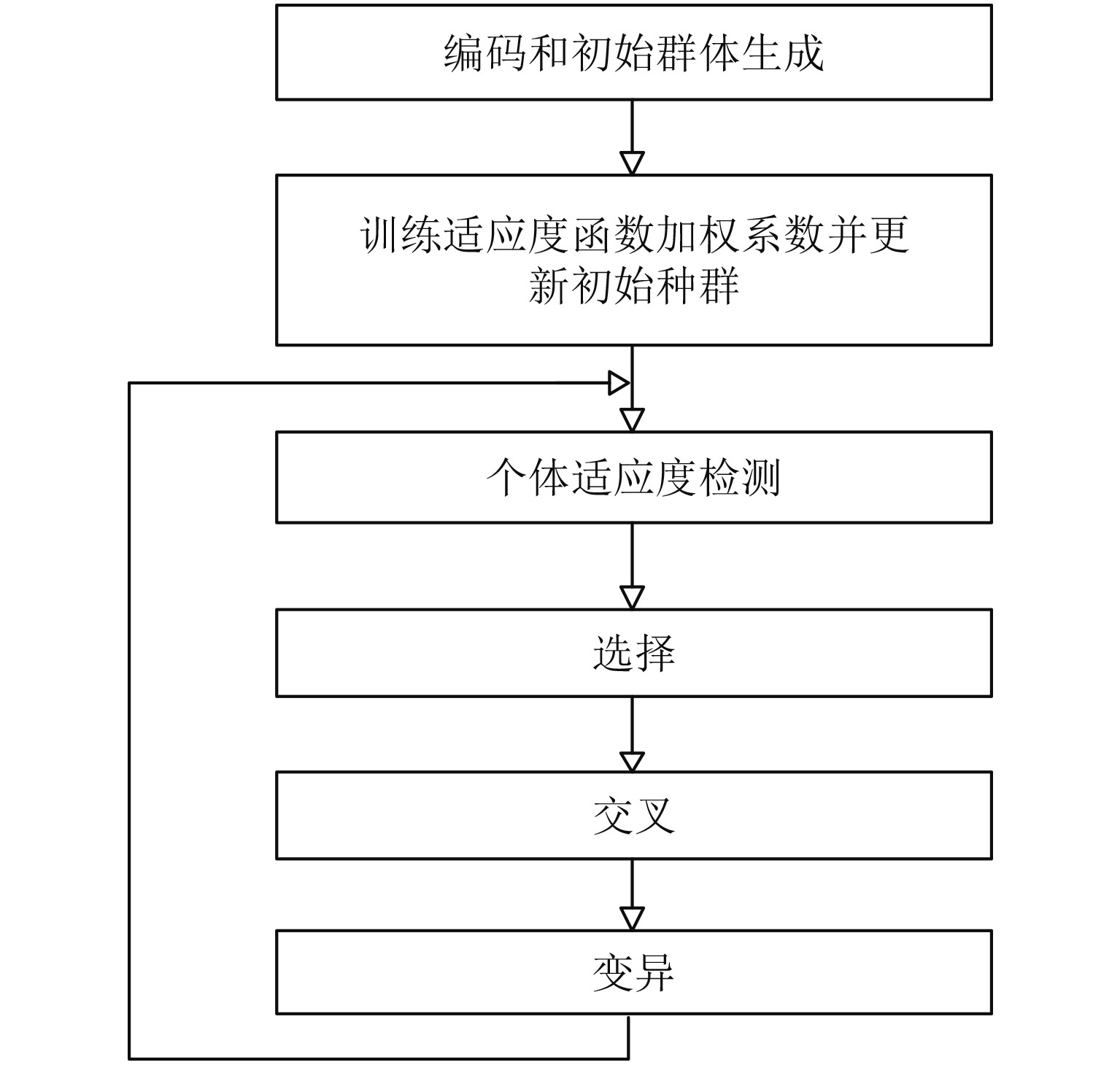
最小化代价函数式(18)是一个非线性多变量的NP问题,全局搜索算法的计算量随着码长的增加呈指数增加;传统的贪婪算法计算量小,但常会陷入局部最优解,所以传统的算法并不适用于此类优化问题。遗传算法是模拟自然界生物进化的“适者生存”原理而设计的,是一种针对多参数,多目标同时优化的快速算法,是解决问题的鲁棒算法。针对本文式(18)的优化问题,可以将其直接作为遗传算法中的适应度函数,利用遗传算法优化寻找适应度函数最大的编码波形。算法处理的流程如图2所示:
|
图 2 GA算法流程图 Fig.2 Flow chart of GA algorithm |
利用GA算法优化设计多相编码波形的步骤[14]如下所示:
(1) 参数编码:就本文所优化的问题而言,当给定多相编码的可用相位数M时,则可以直接使用M进制的序列来进行编码,然后根据给定的G,利用式(9)来计算出每个码元对应的相位。
(2) 初始群体的生成以及尺度因子W的赋值:由于遗传算法的需要,必须产生一些由若干初始解构成的初始群体,本文的初始解是随机产生的。利用初始解估算出适应度函数各个约束条件的数量级,两两相除得到数量级差异,然后以此来调整尺度因子W。
(3) 选择算子:根据个体适应度函数采用轮盘赌方法进行个体选择。
(4) 交叉:交叉是产生新个体的重要手段,本文采用的是单点交叉方式。
(5) 变异:变异操作是逐位进行的,目的是充分挖掘个体多样性。
5 仿真实验与结果分析根据上文提出的算法,本文基于Matlab对算法进行了性能分析,其中仿真的输入参数如表1所示:
| 表 1 编码波形优化设计主要参数 Tab.1 Main parameters for optimization of poly-phase codes |
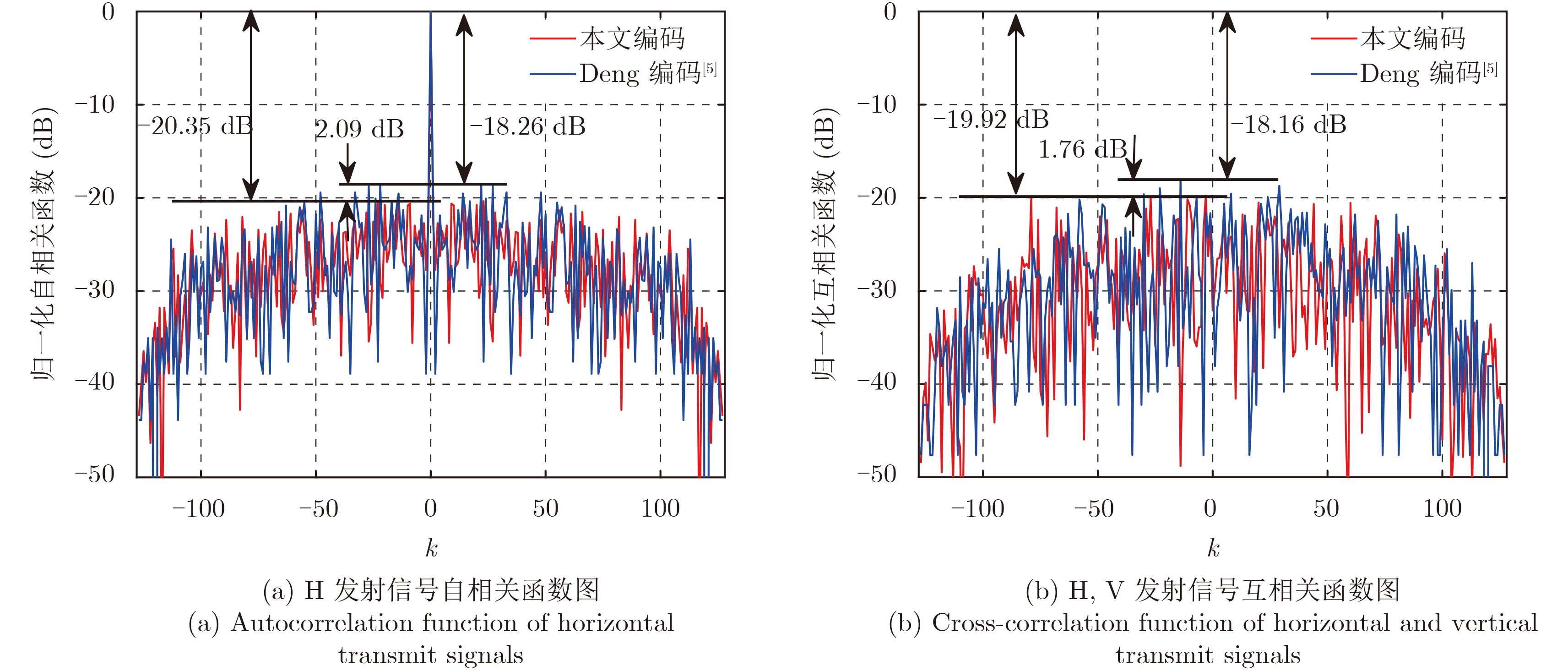
根据上述仿真参数可以得到码长N=B·T=128,利用上述数据进行仿真得到结果如下所示。图3所示为目标与接收端相对静止时接收端匹配滤波的输出结果,其中图3(a)和图3(b)分别为信号的自相关函数和两路极化信号的互相关函数。从图中可以看出,本文的优化编码相比于Deng等人[5]提出的编码,自相关函数的峰值旁瓣比和互相关函数的波形隔离度均有一定性能的提升,性能改善约为2 dB左右。
|
图 3 静止目标仿真结果图 Fig.3 Simulation results of stationary target |
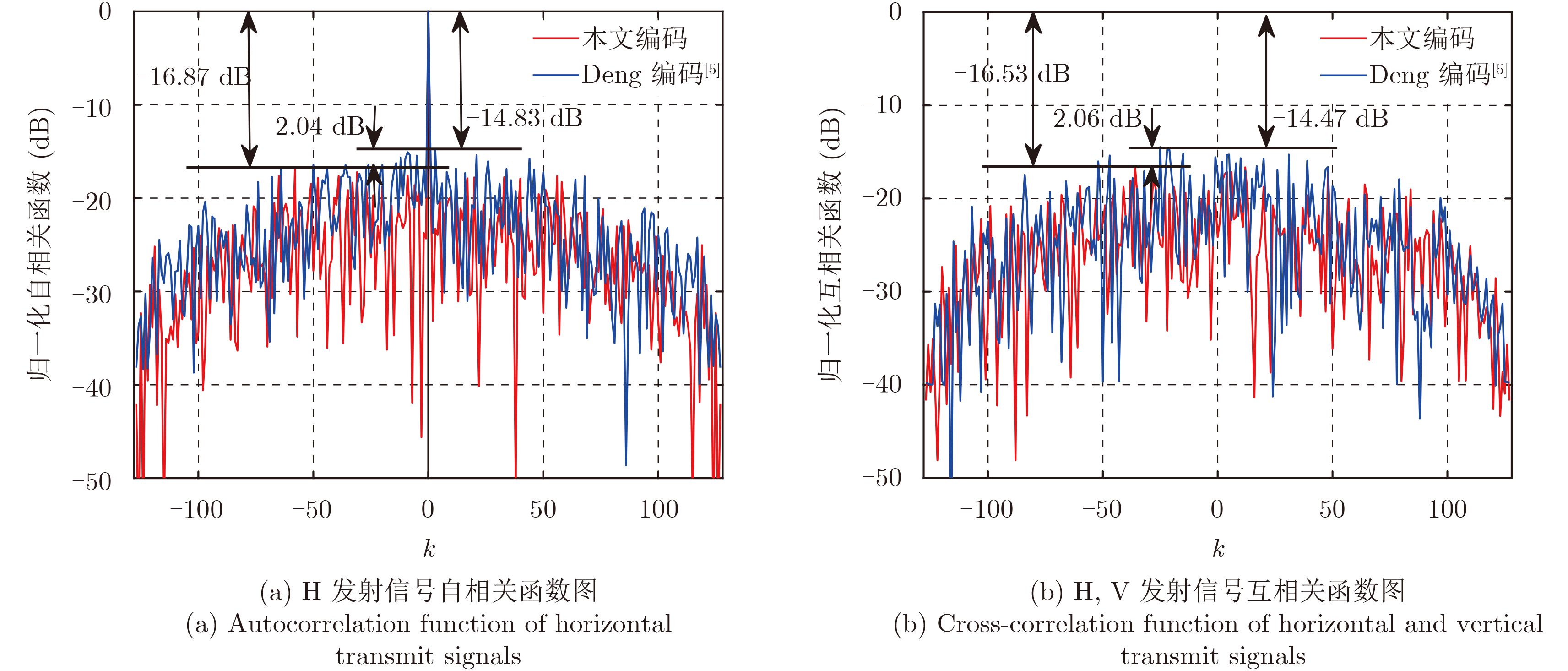
图4所示为目标相对于接收端做匀速运动时的仿真结果。当v0T=0.38时,相比于图3可以明显的看出信号的自相关和正交性能都出现了一定程度的退化,性能退化的程度与v0和T的绝对取值无关,而是与二者的乘积相关,同时本文的优化编码的性能退化程度要小于Deng等人[5]提出的编码。
|
图 4 匀速运动(v0T=0.38)目标仿真结果图 Fig.4 Simulation results of uniform motional (v0T=0.38) target |
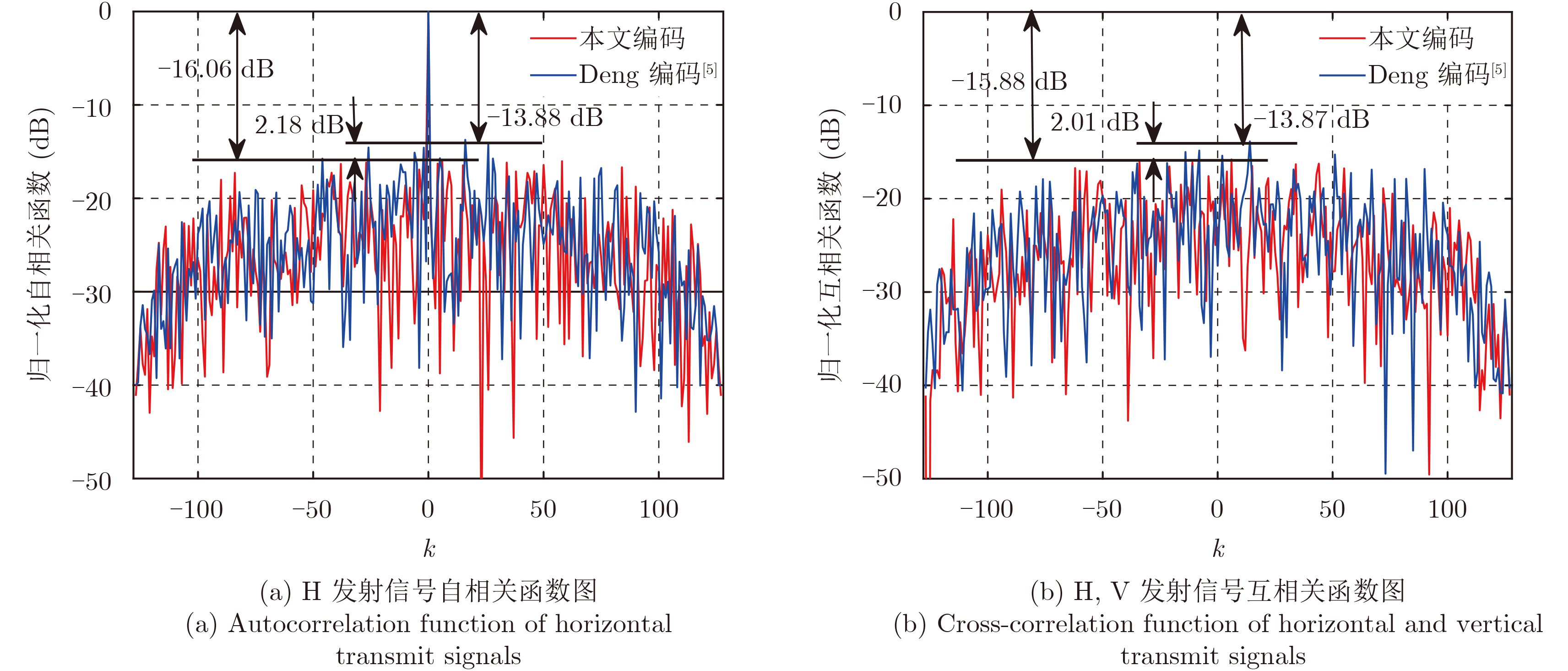
图5所示为目标相对于接收端做匀加速运动时的仿真结果图。同样相比于图3,当aT 2=0.55时,两种编码波形的匹配输出信号的性能出现了退化,退化的程度与a和T 2的乘积相关,与二者的绝对取值无关。同样可以看出,本文编码的自相关峰值旁瓣比和正交性能相比于Deng等人[5]提出的编码约有2 dB左右的性能提升。
|
图 5 匀加速运动(aT 2=0.55)目标仿真结果图 Fig.5 Simulation results of uniformly accelerated motional (aT 2=0.55) target |
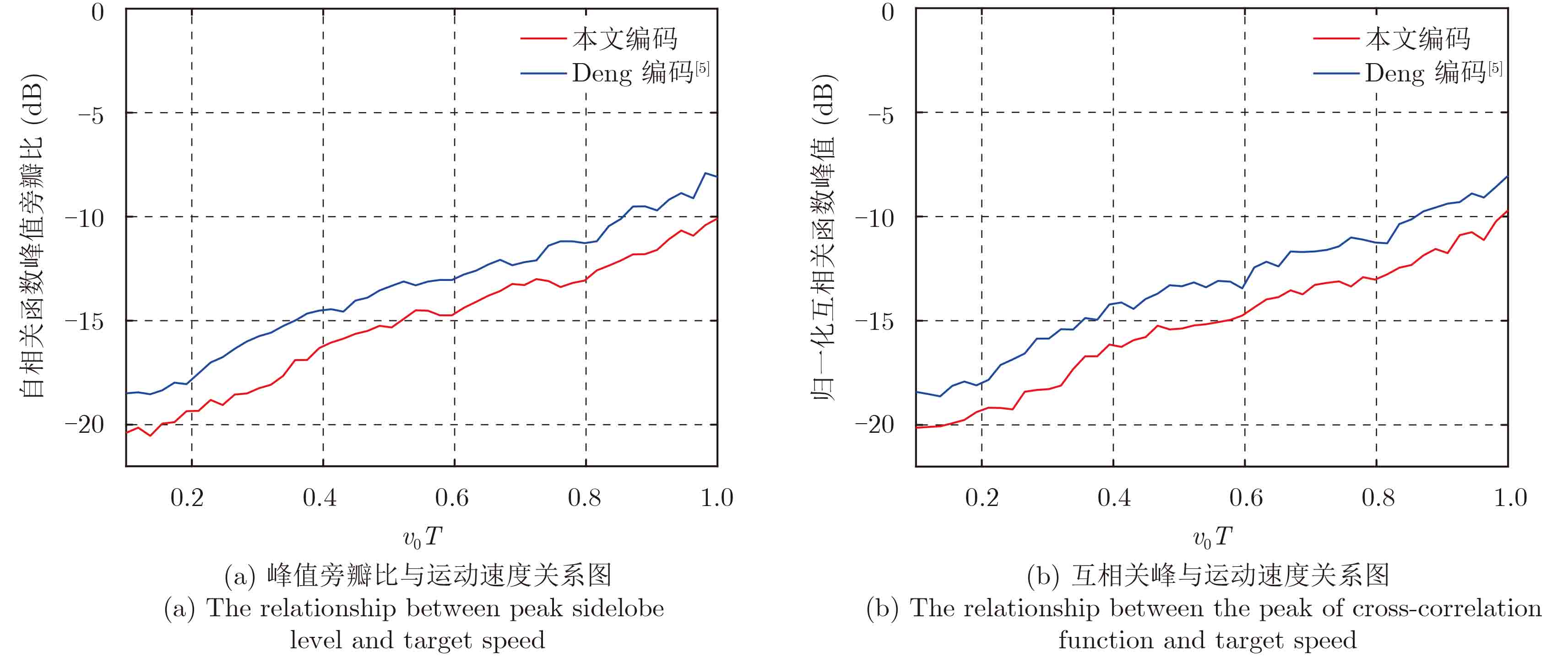
图6所示为接收端匹配滤波输出信号的峰值旁瓣比和互相关峰值随着目标运动速度增加而变化的关系图。从图6中可以看出随着目标回波多普勒相移的增加,两种信号的自相关和正交性能都出现了一定程度的下降,但是本文的编码信号的性能下降更慢,相同条件下的性能优于Deng编码,即多普勒容限要优于Deng编码[5]。
|
图 6 相关函数随目标运动速度增加变化仿真结果图 Fig.6 Simulation results of variation chart of correlation function with increase of speed |
上文分析了在码长为N=128时本文算法与Deng等人[5]算法的性能差别,为了充分挖掘算法的性能,进一步改变仿真参数,对比Deng[5]以及Khan[12]等人算法性能结果如表2,表3所示。其中PSL = (PSLh + PSLv), GA算法参数同表1,信号带宽B=1 MHz:
| 表 2 N=40时算法仿真结果(dB) Tab.2 Simulation results of N=40 (dB) |
| 表 3 N=512时算法仿真结果(dB) Tab.3 Simulation results of N=512 (dB) |
综合上述不同码长情况下的仿真结果可以看出,在码长较短时,若目标处于静止状态,则本文算法与Deng等人的算法性能几乎没有差别,但是优化波形的正交特性优于Khan编码[12];随着目标运动速度的增加,本文编码与Khan编码的自相关性能几乎相同,但是要优于Deng编码,而正交性能方面,本文编码为三者之中性能最佳的编码。随着码长的增加,波形的自相关性能和正交性能均有一定程度的提升,文献[15]指出,编码波形的自相关性能和互相关性能随码长的增加呈指数关系变化。在长码长时从仿真结果可以看出,无论目标处于静止、匀速运动或匀加速运动状态,本文优化编码的自相关和正交性能相比于Deng编码[5]都得到了改善,性能提升约为1.5~2 dB,另外Khan本人也指出其算法在码长较长时性能恶化较严重[12],这里就不在分析其长码时的性能。
6 结束语针对同时全极化测量雷达,本文提出了一种正交多相编码波形优化设计方法,深入分析了多普勒频移对极化测量的影响,并以此为基础,基于分块编码的方式,针对不同的目标运动状态,利用遗传算法对代价函数进行优化。最终设计得到了具有更好自相关与互相关性能的编码波形,相比于Deng, Khan等人[5,12]提出的编码波形性能得到了改善,在长码长时约有1.5~2 dB左右的性能提升,同时该波形的多普勒容限也有一定的改善。
但是需要指出的是,本文采用的分块编码方式为等间隔划分子块,如果采用不等间隔划分可以获得更大的波形设计自由度,使得编码更加灵活。另外,增加波形的码长也可以使信号的自相关和正交性能有很大的提升,但是通过文中对算法总搜索空间的分析可以看到,码长的增加会使搜索空间大小呈指数规律上升,因此,搜索空间的快速膨胀给设计性能更为优异的多相编码波形带来了新的挑战。另外本文针对单目标代价函数对波形进行了优化设计,实际应用中除了波形的自相关以及互相关性能外,例如不同波形对应的目标检测概率也是我们所关心的问题[16],而针对多代价函数的优化相比于单目标代价函数优化也更为复杂,因此如何更为高效的设计复杂的编码波形将是下一步研究工作的重点。
| [1] |
Melvin L S and Banner G P. Radars for the detection and tracking of ballistic missiles, satellites, and planets[J].
Lincoln laboratory Journal, 2000, 12(2): 217-244. ( 0) 0)
|
| [2] |
Giuli D, Fossi M and Facheris L. Radar target scattering matrix measurement through orthogonal signals[J].
Radar and Signal Processing, IEE Proceeding F, 1993, 140(4): 233-242. ( 0) 0)
|
| [3] |
李永祯, 王雪松, 曾永虎, 等. 宽带雷达目标的瞬态极化时频分布表征[J].
雷达科学与技术, 2004, 2(6): 321-326. Li Yong-zhen, Wang Xue-song, Zeng Yong-hu, et al.. Time-Frequency Distribution Characterization of Radar Targets’ Instantaneous Polarization Scattering[J]. Radar Science and Technology, 2004, 2(6): 321-326. (  0) 0)
|
| [4] |
Babur G, Krasnov O, Yarovoy A, et al.. Nearly Orthogonal Waveforms for MIMO FMCW Radar[J].
IEEE Transactions onAerospace and Electronic Systems, 2013, 49(3): 1426-1437. DOI:10.1109/TAES.2013.6557996 ( 0) 0)
|
| [5] |
Deng H. Polyphase code design for orthogonal netted radar systems[J].
IEEE Trans on Signal Processing, 2004, 52(11): 3126-3135. DOI:10.1109/TSP.2004.836530 ( 0) 0)
|
| [6] |
Liu B. Orthogonal Discrete Frequency-Coding Waveform Set Design with Minimized Autocorrelation Sidelobes[J].
IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(4): 1650-1657. DOI:10.1109/TAES.2009.5310326 ( 0) 0)
|
| [7] |
Gao C, Teh K C and Liu A. Orthogonal Frequency Diversity Waveform with Range-Doppler Optimization for MIMO Radar[J].
IEEE Signal Processing Letters, 2014, 21(10): 1201-1205. DOI:10.1109/LSP.2014.2329944 ( 0) 0)
|
| [8] |
Wang Z, Tigrek F, Krasnov O, et al.. Interleaved OFDM Radar for Simultaneous Polarimetric Measurement[J].
IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 2085-2099. DOI:10.1109/TAES.2012.6237580 ( 0) 0)
|
| [9] |
Brunkow D A, George J, Bring V N, et al.. Recent data system and antenna upgrades to the CSU-CHILL radar[C]. AMS 32nd Conference on Radar Meteorology, Albuquerque, New Mexico, USA, 2005.
( 0) 0)
|
| [10] |
Xiao Jin-jun and Arye Nehorai. Joint Transmitter and Receiver Polarization Optimization for Scattering Estimation in Clutter[J].
IEEE Transaction on Signal Processing, 2009, 57(10): 4142-4147. DOI:10.1109/TSP.2009.2022887 ( 0) 0)
|
| [11] |
Nadav Levanon and Eli Mozeson. Radar Signals[M]. Hoboken, New Jersey: John Wiley & Sons, 2004: 101–103.
( 0) 0)
|
| [12] |
Khan H A and Edwards D J. Doppler problems in orthogonal MIMO radar[C]. IEEE Conference on Radar, Verona, NY, USA, April 24–27, 2006, Vol. 1: 24–27.
( 0) 0)
|
| [13] |
Frank R L. Polyphase Complementary-Codes[J].
IEEE Transactions on Information Theory, 1980, 26: 641-647. DOI:10.1109/TIT.1980.1056272 ( 0) 0)
|
| [14] |
Lei Y J, Zhang S W, Li X W, et al.. MATLAB GA Algorithm Toolbox and It’s Applications[M]. Xi’an: Xidian Press, 2005: 66–70.
( 0) 0)
|
| [15] |
刘波. MIMO雷达正交波形设计及信号处理研究[D]. [博士论文], 电子科技大学, 2008.
Liu Bo. Study on orthogonal waveform design and signal processing for MIMO radar[D]. [Ph.D. dissertation], University of Electronic Science and Technology of China, 2008. (  0) 0)
|
| [16] |
王璐璐, 王宏强, 王满喜, 等. 雷达目标检测的最优波形设计综述[J].
雷达学报, 2016, 5(5): 487-498. Wang Lulu, Wang Hongqiang, Wang Manxi, et al.. An Overview of Radar Waveform Optimization for Target Detection[J]. Journal of Radars, 2016, 5(5): 487-498. (  0) 0)
|




