不同发射波形下多机协同探测雷达系统信号建模与性能分析

引用本文

杨海峰, 谢文冲, 王永良. 不同发射波形下多机协同探测雷达系统信号建模与性能分析[J]. 雷达学报, 2017, 6(3): 267-274. DOI: 10.12000/JR16142.

Yang Haifeng, Xie Wenchong, Wang Yongliang. Modeling and analysis of multiple aews coordinated detection radar system with different transmit waveform[J]. Journal of Radars, 2017, 6(3): 267-274. DOI: 10.12000/JR16142.

基金项目

国家自然科学基金青年基金(61501505, 61501506)，湖北省自然科学基金(2015CFB607)

通信作者

王永良 ylwangkjld@163.com

作者简介

杨海峰(1986–)，男，籍贯湖北省汉川市，现为空军预警学院信息与通信工程专业博士研究生，主要研究方向为空时自适应检测、阵列信号处理。E-mail: 18672954451@163.com;
谢文冲(1978–)，男，籍贯山西省万荣县，2008年获国防科技大学信号与信息处理专业工学博士学位，现为空军预警学院雷达兵器运用工程军队重点实验室副教授，已在国内外刊物及学术会议上发表学术论文近百篇，主要研究方向为机载雷达信号处理、空时自适应信号处理等。E-mail: xwch1978@aliyun.com;
王永良(1965–)，男，籍贯浙江省嘉兴市，教授，博士生导师，中国科学院院士，现为空军预警学院教授，主要研究方向为雷达信号处理、空时2维信号处理等，已发表论文270余篇，学术专著3部。E-mail: ylwangkjld@163.com

文章历史

收稿日期：2016-12-06
改回日期：2017-05-10
网络出版：2017-06-12

Contents Abstract Full text Figures/Tables PDF

不同发射波形下多机协同探测雷达系统信号建模与性能分析

杨海峰, 谢文冲, 王永良

(空军预警学院武汉 430019)

收稿日期：2016-12-06；改回日期：2017-05-10；网络出版：2017-06-12

基金项目：国家自然科学基金青年基金(61501505, 61501506)，湖北省自然科学基金(2015CFB607)

作者简介：杨海峰(1986–)，男，籍贯湖北省汉川市，现为空军预警学院信息与通信工程专业博士研究生，主要研究方向为空时自适应检测、阵列信号处理。E-mail: 18672954451@163.com;
谢文冲(1978–)，男，籍贯山西省万荣县，2008年获国防科技大学信号与信息处理专业工学博士学位，现为空军预警学院雷达兵器运用工程军队重点实验室副教授，已在国内外刊物及学术会议上发表学术论文近百篇，主要研究方向为机载雷达信号处理、空时自适应信号处理等。E-mail: xwch1978@aliyun.com;
王永良(1965–)，男，籍贯浙江省嘉兴市，教授，博士生导师，中国科学院院士，现为空军预警学院教授，主要研究方向为雷达信号处理、空时2维信号处理等，已发表论文270余篇，学术专著3部。E-mail: ylwangkjld@163.com

通信作者：王永良 ylwangkjld@163.com

摘要：多机协同探测雷达系统利用目标在不同机载雷达间的径向速度差异实现目标的有效检测，该系统已成为当前机载雷达领域的研究热点。该文首先建立了不同发射波形条件下多机协同探测雷达系统的信号模型，并给出了基于广义似然比(Generalized Likelihood Ratio Test, GLRT)准则的自适应检测器及其渐进统计分布特性，最后通过计算机仿真分析了3种特定发射波形下的运动目标检测性能。仿真结果表明多机协同探测雷达系统中发射波形的变化会严重影响雷达系统的运动目标检测性能，且相同发射波形的雷达系统对不同运动速度的目标检测性能也存在区别。

关键词：多机协同探测雷达系统发射波形信号建模目标检测

Modeling and Analysis of Multiple AEWs Coordinated Detection Radar System with Different Transmit Waveform

Yang Haifeng, Xie Wenchong, Wang Yongliang

(Air Force Early Warning Academy, Wuhan 430019, China)

Foundation Item: The China National Science Foundation (61501505, 61501506), HuBei Provincial Natural Science Foundation (2015CFB607)

Abstract: Differences in target radial velocities of different airborne radar are used for target detection in a multiple Airborne Early Warnings (AEWs) coordinated detection radar system; this subject is currently a popular research topic. In this paper, a collaborative detection radar system model comprised of multiple AEWs with different transmit waveforms is constructed. The Generalized Likelihood Ratio Test (GLRT) based adaptive detector is then proposed and the approximated statistical characters of the detector are analyzed. Finally, the moving target detection performances of three selected transmit waveforms are analyzed by computer simulation; results show that the detection performance of the collaborative detection radar system is influenced by the transmit waveform, and that the detection performances of different velocity targets are different with the same transmit waveform.

Key words: Multiple AEWs coordinated detection radar system Transmit waveform Signal modeling Target detection

1 引言

传统机载预警雷达发射并接收自身信号，然后利用目标与杂波不同的性质进行检测。但当目标落入主瓣杂波区时，机载预警雷达不能有效检测目标。为解决该问题，可通过多架预警机雷达的协同，利用目标在不同预警机之间的径向速度差异实现目标有效检测。文献[1]建立了多基地机载雷达协同探测模型，推导了集中式和分布式的似然比检测器，并指出分布式检测器可降低对通信带宽的需求且目标检测性能相对集中式检测器下降较少。文献[2]进一步分析了多基地机载雷达广义似然比(Generalized Likelihood Ratio Test, GLRT)检测器和自适应匹配滤波检测器的性能，并得出其性能随基地数增多而增强的结论。文献[3]通过不同频段的机载雷达和带通滤波器实现频率分集功能，从而使得多机协同探测雷达系统能够分离来自不同雷达的信号，提高了目标的输出信干噪比(Signal-to-Interference-plus-Noise Ratio, SINR)。但多机协同探测雷达系统在搜索模式中会出现脉冲追赶的问题^[4]，文献[5]提出可将集中式多输入多输出(Multiple-Input Multiple-Output, MIMO)雷达和分布式MIMO雷达进行结合，利用MIMO雷达全向发射的特点来避免这个问题。但由于集中式MIMO(Collocated MIMO, CMIMO)雷达在发射端不能获得发射相干增益，这导致CMIMO雷达与分布式MIMO (Distributed MIMO, DMIMO)雷达组合的雷达系统(the combination of the Collocated MIMO radar and Distributed MIMO radar, CMIMO-DMIMO)的目标检测性能弱于相控阵(Phased Array, PA)雷达和DMIMO雷达组合的雷达系统(the combination of the Phased Array radar and Distributed MIMO radar, PA-DMIMO)^[6]。

对于多机协同探测雷达系统，每部雷达的杂波分布均不相同。且在实际任务中，往往只需要对部分区域进行探测，因此可通过合理选择发射波形来取得发射波束宽度和发射相干增益间的平衡^[7]。此外，根据目标和杂波特性，可通过设计发射波形来提高雷达的目标检测性能^[8,9]。为此，本文在文献[10–13]的基础上，结合MIMO雷达的特点，建立了不同发射波形的多机协同探测雷达系统信号模型。此外，本文还进一步给出了该模型下GLRT检测器的数学表达式及其渐进统计分布特性。仿真结果证明该模型对多机协同探测雷达系统的发射波形设计具有较大的实用价值。

2 接收回波信号模型

本节在机载PA雷达和机载MIMO雷达的基础上，建立了多机协同探测系统在不同发射波形情况下的信号模型。雷达接收的信号一般由目标、杂波和噪声组成。由于噪声特性与发射波形无关，因此本节重点给出目标和杂波的信号模型。

2.1 目标模型

假设共有P架预警机进行协同探测，每架预警机的天线均采用半波长等距均匀线阵，阵元数均为M。假设目标相对每部机载预警雷达的归一化角度分别为 ${\theta _1},{\theta _2}, ·\!·\!· ,{\theta _P}$ ，目标相对每部机载预警雷达的空域导向矢量可表示为 ${{{t}}_1},{{{t}}_2}, ·\!·\!· ,{{{t}}_P} \in {{\mathbb{C}}^{M \times 1}}$ ，其中 ${{{t}}_i} = {\left[\begin{array}{*{20}{c}} \!\! 1 & {{{\rm e}^{{\rm j}2{{π}} {\theta _i}}}} & ·\!·\!· & {{{\rm e}^{{\rm j}2{{π}} (M - 1){\theta _i}}}} \end{array}\!\!\right]^{\rm{T}}}$ , $i = 1,2, ·\!·\!· ,P$ ，上标T表示转置操作， $\mathbb{C}$ 表示复数域。每部机载预警雷达发射的信号分别为 ${{{S}}_1},{{{S}}_2}, ·\!·\!· ,{{{S}}_P} \in {{\mathbb{C}}^{M \times L}}$ ，其中L表示离散基带波形的信号长度。则第p部雷达接收的目标信号可表示为：

${{{T}}_p} = \sum\limits_{i = 1}^P {{\alpha _{pi}}({{{r}}_{pi}} \otimes {{{t}}_p}){{t}}_i^{\mathop{\rm H}\nolimits} {{{S}}_i}} \in {{\mathbb{C}}^{MK \times L}}$

(1)

其中， ${\alpha _{pi}}$ 为目标复散射系数， $ \otimes $ 表示Kronecker积，上标H表示共轭转置。 ${{{r}}_{pi}} \in {{\mathbb{C}}^{K \times 1}}$ 表示目标在雷达i和雷达p组成的双基地系统中的时域导向矢量，其具体形式为 ${{{r}}_{pi}} = {\left[\begin{array}{*{20}{c}} \!\!1 \;\; {{{\rm e}^{{\rm j}2{{π}} {f_{pi}}}}} \;\; ·\!·\!· \;\; {{{\rm e}^{{\rm j}2{{π}} (K - 1){f_{pi}}}}} \end{array}\right]^{\rm{T}}}$ ，其中K表示雷达一个相干处理间隔(Coherent Processing Interval, CPI)中的脉冲个数，f_pi表示目标在雷达i与雷达p组成的双基地系统中的归一化多普勒频率。

2.2 杂波模型

机载预警雷达由于雷达下视，因此面临不可避免的杂波问题。杂波是雷达波束照射范围内所有地面分辨单元散射的雷达信号，每个地面散射单元称为杂波块。某一距离对应的杂波可以看成是该等距离环中所有杂波块散射的回波信号之和。下面以第p部雷达接收与第i部雷达发射构成的双基地系统为例，给出多机协同探测雷达系统的杂波信号模型。为简化表述，将第p部雷达接收和第i部雷达发射构成的双基地系统记为路径pi。

路径pi中的杂波回波为等距离环中所有杂波块回波之和，其示意图如图1。当不考虑距离模糊影响时，路径pi中第n个杂波块的散射信号可表示为：

${{C}}_{pi}^n = \alpha _{pi}^n \left({{r}}_{{\rm t},pi}^n \otimes {{r}}_{{\rm s},pi}^n \right){\left({{t}}_{pi}^n\right)^{\mathop{\rm H}\nolimits} }{{{S}}_i} \in {{\mathbb{C}}^{MK \times L}}$

(2)

式中， $\alpha _{pi}^n$ 表示第n个杂波块的复散射系数， ${{t}}_{pi}^n$ 表示第i部雷达的空域导向矢量，其具体形式为 ${{t}}_{pi}^n = {[\begin{array}{*{20}{c}} 1 & {{{\rm e}^{{\rm j}2{{π}} \theta _{pi}^n}}} & ·\!·\!· & {{{\rm e}^{{\rm j}2{{π}} (M - 1)\theta _{pi}^n}}} \end{array}]^{\rm{T}}}$ ，其中 $\theta _{pi}^n$ 表示杂波块n相对于第i部雷达的归一化角度。 ${{r}}_{{\rm s},pi}^n = {[\begin{array}{*{20}{c}} 1 & {{{\rm e}^{{\rm j}2{{π}} \psi _{pi}^n}}} & ·\!·\!· & {{{\rm e}^{{\rm j}2{{π}} (M - 1)\psi _{pi}^n}}} \end{array}]^{\rm T}}$ 表示第p部雷达对应于杂波块n的空域导向矢量，其中 $\psi _{pi}^n$ 表示杂波块n相对第p部雷达的归一化角度。 ${{r}}_{{\rm t},pi}^n$ 表示杂波块n在路径pi下的时域导向矢量，具体表达式为 ${{r}}_{{\rm t},pi}^n = {[\begin{array}{*{20}{c}} 1 & {{{\rm e}^{{\rm j}2{{π}} f_{pi}^n}}} & ·\!·\!· & {{{\rm e}^{{\rm j}2{{π}} (K - 1)f_{pi}^n}}} \end{array}]^{\rm{T}}}$ ，其中 $f_{pi}^n$ 表示杂波块n的归一化多普勒频率。

假设路径pi的等距离环上包含N_pi个杂波块，则路径pi的杂波信号可表示为：

${{{C}}_{pi}} = \sum\limits_{n = 1}^{{N_{pi}}} {\alpha _{pi}^n({{r}}_{{\rm t},pi}^n \otimes {{r}}_{{\! \rm s},pi}^n){{({{t}}_{pi}^n)}^{\mathop{\rm H}\nolimits} }{{{S}}_i}} $

(3)

雷达p接收到的杂波信号可表示为不同发射信号对应的杂波回波的叠加，即

$\begin{aligned}{{{C}}_p} = & \sum\limits_{i = 1}^P {{{{C}}_{pi}}} \\ = & \sum\limits_{i = 1}^P {\sum\limits_{n = 1}^{{N_{pi}}} {\alpha _{pi}^n \left({{r}}_{{\rm t},pi}^n \otimes {{r}}_{\!{\rm s},pi}^n \right){{\left({{t}}_{pi}^n \right)}^{\mathop{\rm H}\nolimits} }{{{S}}_i}} } \\ = & \sum\limits_{i = 1,i \ne p}^P {\sum\limits_{n = 1}^{{N_{pi}}} {\alpha _{pi}^n \left({{r}}_{{\rm t},pi}^n \otimes {{r}}_{{\! \rm s},pi}^n \right){{\left({{t}}_{pi}^n \right)}^{\mathop{\rm H}\nolimits} }{{{S}}_i}} } \\ & + \sum\limits_{n = 1}^{{N_{pp}}} {\alpha _{pp}^n \left({{r}}_{{\rm t},pp}^n \otimes {{r}}_{{\! \rm s},pp}^n \right){{\left({{t}}_{pp}^n \right)}^{\mathop{\rm H}\nolimits} }{{{S}}_p}} \end{aligned}$

(4)

从式(4)可看出，等式右侧第2项表示路径pp的杂波回波，等式右侧第1项表示路径pi的杂波回波，其中 $i = 1,2, ·\!·\!· ,P$ 且 $i \ne p$ 。因此，雷达p接收到的杂波信号可表示成1个单基地系统和P–1个双基地雷达系统接收到的杂波回波的叠加。

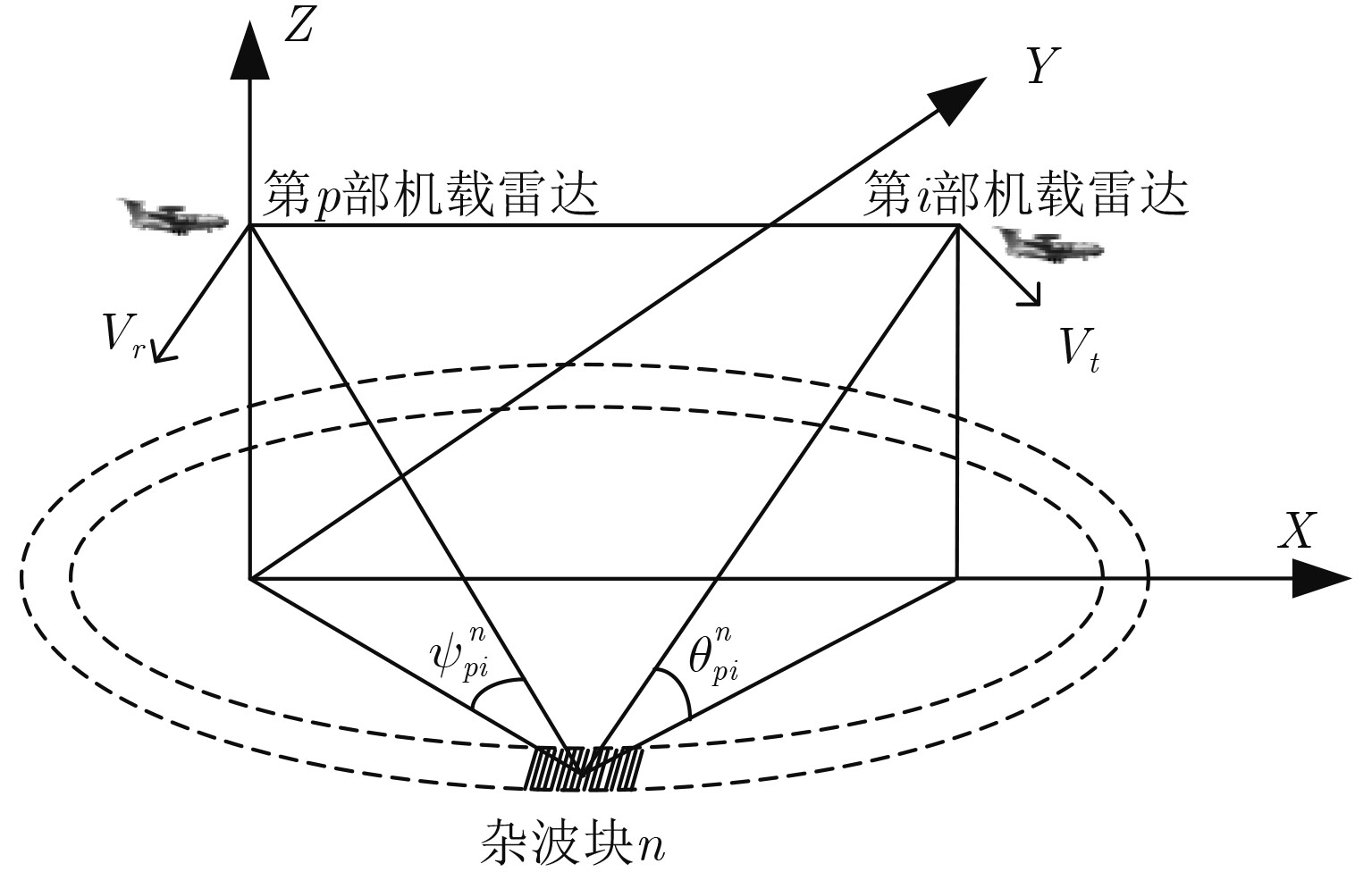
图 1 双机协同探测杂波回波示意图 Fig.1 Clutter echo of bistatic airborne radar

2.3 接收信号的数据模型

根据式(1)和式(4)，可将第p部雷达的接收数据写为：

${{{X}}_p} = {{{T}}_p} + {{{C}}_p} + {{{N}}_p}$

(5)

其中，N_p表示第p部机载雷达的噪声信号。本文采用文献[14]的噪声模型，即N_p的每一列独立同分布，且为均值为 ${{0}_{MK \times 1}}$ ，方差为 ${{R}}_p^n$ 的复高斯随机向量。

为了在后续处理中能够对来自不同机载雷达的信号进行分离，采用矩阵列向量化操作，利用发射信号的差异进行分选。对式(5)采用矩阵列向量化操作以后得

$\begin{aligned}{{{x}}_p} = & \sum\limits_{i = 1}^P {\left[ {{{\left({{t}}_i^{\mathop{\rm H}\nolimits} {{{S}}_i}\right)}^{\mathop{\rm T}\nolimits} } \otimes ({{{r}}_{pi}} \otimes {{{t}}_p})} \right]{\alpha _{pi}}} \\ & + \sum\limits_{i = 1}^P {\sum\limits_{n = 1}^{{N_{pi}}} {\left[ {{{\left[{{\left({{t}}_{pi}^n \right)}^{\mathop{\rm H}\nolimits} }{{{S}}_i}\right]}^{\mathop{\rm T}\nolimits} } \otimes \left({{r}}_{{\rm t},pi}^n \otimes {{r}}_{{\rm s},pi}^n \right)} \right]\alpha _{pi}^n} } \\ & + {{{n}}_p} \in {{\mathbb{C}}^{MKL \times 1}}\end{aligned}$

(6)

其中， ${{{n}}_p}{\rm{ = }}{\mathop{\rm vec}\nolimits} ({{{N}}_p})$ ，其服从均值为 ${{0}_{LMK \times 1}}$ ，方差为 ${{{I}}_L} \otimes {{R}}_p^n$ 的复高斯分布。 ${\mathop{\rm vec}\nolimits} ( \cdot )$ 表示矩阵列向量化操作。式(6)中杂波加噪声分量为：

${{{b}}_p} = \sum\limits_{i = 1}^P {\sum\limits_{n = 1}^{{N_{pi}}} {\left[ {{{[{{({{t}}_{pi}^n)}^{\mathop{\rm H}\nolimits} }{{{S}}_i}]}^{\mathop{\rm T}\nolimits} } \otimes ({{r}}_{{\rm t},pi}^n \otimes {{r}}_{{\rm s},pi}^n)} \right]\alpha _{pi}^n} } + {{{n}}_p}$

(7)

则杂波加噪声的理想协方差矩阵可表示为：

${{{R}}_p} = {\mathop{\rm E}\nolimits} \left({{{b}}_p}{{b}}_p^{\mathop{\rm H}\nolimits} \right)$

(8)

由于杂波和噪声不相关，且不同杂波块的复散射系数相互独立，因此式(8)可表示为：

$\begin{align} & {{R}_{p}}=\left\{ \text{E}\sum\limits_{i=1}^{P}{\sum\limits_{n=1}^{{{N}_{pi}}}{{{\left| \alpha _{pi}^{n} \right|}^{2}}\left[ {{\left[ {{\left( t_{pi}^{n} \right)}^{\text{H}}}{{S}_{i}} \right]}^{\text{T}}}\otimes \left( r_{\text{t},pi}^{n}\otimes r_{\text{s},pi}^{n} \right) \right]}} \right. \\ & \left. \cdot {{\left[ {{\left[ {{\left( t_{pi}^{n} \right)}^{\text{H}}}{{S}_{i}} \right]}^{\text{T}}}\otimes \left( r_{\text{t},pi}^{n}\otimes r_{\text{s},pi}^{n} \right) \right]}^{\text{H}}} \right\}+\text{E}\left( {{n}_{p}}n_{p}^{\text{H}} \right) \\ & =\text{ E}\left\{ \sum\limits_{i=1}^{P}{\sum\limits_{n=1}^{{{N}_{pi}}}{{{\left| \alpha _{pi}^{n} \right|}^{2}}R_{\text{T},pi}^{n}\otimes R_{\text{t},pi}^{n}\otimes R_{\text{s},pi}^{n}}} \right\}+\text{E}\left( {{n}_{p}}n_{p}^{\text{H}} \right) \\ \end{align}$

(9)

其中 ${{R}}_{{\rm{T}},pi}^n \!\!=\!\! {\left[{\left({{t}}_{pi}^n \right)^{\mathop{\rm H}\nolimits} }\!\!{{{S}}_i}\right]^{\mathop{\rm T}\nolimits} }\!\!\!{\left[{\left({{t}}_{pi}^n \right)^{\mathop{\rm H}\nolimits} }{{{S}}_i}\right]^*}$ , ${{R}}_{{\rm t},pi}^n \!\!=\!\! {{r}}_{{\rm t},pi}^n{\left({{r}}_{{\rm t},pi}^n \right)^{\mathop{\rm H}\nolimits} }$ , ${{R}}_{{\rm s},pi}^n = {{r}}_{{\rm s},pi}^n{\left({{r}}_{{\rm s},pi}^n \right)^{\mathop{\rm H}\nolimits} }$ 。在实际系统中杂波加噪声协方差矩阵通常是未知的，需要利用一定数量训练样本对R_p进行估计。

3 检测器设计

目标检测是雷达系统的一项重要功能^[15–17]，GLRT准则被广泛地应用到雷达自适应检测器设计中^[1–3]。本节根据第2节的信号模型，给出多机协同探测雷达系统的GLRT检测器。

令 ${{{a}}_p} = {\left[ {\begin{array}{*{20}{c}} {{\alpha _{p1}}} & {{\alpha _{p2}}} & ·\!·\!· & {{\alpha _{pP}}} \end{array}} \right]^{\mathop{\rm T}\nolimits} }$ ，

$\begin{aligned}{{{H}}_p} = & \left[ {{{\left({{t}}_1^{\mathop{\rm H}\nolimits} {{{S}}_1} \right)}^{\mathop{\rm T}\nolimits} } \otimes \left({{{r}}_{p1}} \otimes {{{t}}_p} \right) \;{{\left({{t}}_2^{\mathop{\rm H}\nolimits} {{{S}}_2}\right)}^{\mathop{\rm T}\nolimits} } \otimes \left({{{r}}_{p2}} \otimes {{{t}}_p}\right)} \right.\\& \quad \left. { ·\!·\!· \,{{\left({{t}}_P^{\mathop{\rm H}\nolimits} {{{S}}_P} \right)}^{\mathop{\rm T}\nolimits} } \otimes \left({{{r}}\!_{pP}} \otimes {{{t}}_p} \right)} \right]\end{aligned}$

(10)

则式(6)可改写为：

${{{x}}_p} = {{{H}}_p}{{{a}}_p} + {{{b}}_p}$

(11)

此时多机协同系统的接收数据可表示为：

${{x}} = \sum\limits_{p = 1}^P {\left({{{H}}_p}{{{a}}_p} + {{{b}}_p}\right)} $

(12)

目标检测问题等效于二元假设检验，即在有目标假设H₁和没有目标假设H₀中进行判别。两种假设下的信号模型可分别表示为：

$\left. \begin{aligned} {H_0}\!:{{x}} = & \sum\limits_{p = 1}^P {{{{b}}_p}} , {{{x}}_{p,l}} = {{{b}}_p}, \; l = 1,2, ·\!·\!· ,L, \; \\ & \quad\ \ p \!=\! 1,2, ·\!·\!· ,P\\ {H_1}\!:{{x}} = & \sum\limits_{p = 1}^P {\left({{{H}}_p}{{{a}}_p} + {{{b}}_p}\right)} , {{{x}}_{p,l}} \!=\! {{{b}}_p},\; \\ & \quad \ \ l = 1,2, ·\!·\!· ,L, \; p = 1,2, ·\!·\!· ,P\end{aligned} \right\}$

(13)

其中， ${{{x}}_{p,l}}$ 表示第p部雷达的第l个训练样本。两种条件下的联合概率密度函数(Probability Density Function, PDF)可表示为：

$\begin{aligned}f({{x}}|{{R}},{{a}},{H_b}) = & \prod\limits_{p = 1}^P {f({{{x}}_p}|{{{R}}_p},{{{a}}_p},{H_b})} \\ = & \prod\limits_{p = 1}^P {\left\{ {{{\left[ {{\pi^{N(L + 1)}}}{\det\,\!\!^{L+1}}({{{R}}_p}) \right]}^{- 1}}} \right.} \\& \times \exp \left\{ { - {\mathop{\rm tr}\nolimits} \left({{{R}}_p}^{\!\!\! - 1}{{{\tilde{R}}}_p}\right)} \right. \\&- {\rm tr} \Big[ {{{{R}}_p}^{\!\!\! - 1}\left({{{x}}_p} - b{{{H}}_p}{{{a}}_p}\right)} \\& \cdot {\left. {\left. {{{({{{x}}_p} - b{{{H}}_p}{{{a}}_p})}^{\mathop{\rm H}\nolimits} }} \right]} \right\}} \biggr\}, \ b = 0,1\end{aligned}$

(14)

其中， ${{\widetilde{R}}_{p}}=\text{ }\sum\nolimits_{l=1}^{L}{}{{x}_{p,l}}x_{p,l}^{\text{H}}$ , $\det ( \cdot )$ 表示矩阵的行列式， ${\mathop{\rm tr}\nolimits} ( \cdot )$ 表示矩阵的迹。GLRT检测器可表示为：

$\begin{aligned}{t_{{\rm{GLRT}}}} = & \frac{{\mathop {\max }\limits_{{{R}},{{a}}} f({{x}}|{{R}},{{a}},{H_1})}}{{\mathop {\max }\limits_{{R}} f({{x}}|{{R}},{H_0})}} \\ = & \prod\limits_{p = 1}^P {\frac{{\mathop {\max }\limits_{{{{R}}_p},{{{a}}_p}} f({{{x}}_p}|{{{R}}_p},{{{a}}_p},{H_1})}}{{\mathop {\max }\limits_{{{{R}}_p}} f({{{x}}_p}|{{{R}}_p},{H_0})}}} \end{aligned}$

(15)

取式(14)的自然对数后求R_p的导数，并令其等于零可得R_p的最大似然估计(Maximum Likelihood Estimate, MLE)为：

${\widehat {{R}}_p} = \frac{{{{{\tilde{{R}}}}_p} + ({{{x}}_p} - b{{{H}}_p}{{{a}}_p}){{({{{x}}_p} - b{{{H}}_p}{{{a}}_p})}^{\mathop{\rm H}\nolimits} }}}{{L + 1}}, \;b = 0,1$

(16)

将式(16)代入到式(14)可得

$\begin{aligned}& f({{x}}|\widehat {{R}},{{a}},{H_b}) \\ & \ \ = \prod\limits_{p = 1}^P {\left\{ {{{\left[{{{π}} ^{N(L + 1)}}{{\det \, }^{L + 1}}({{\widehat {{R}}}_p})\right]}^{ - 1}}\!\! \exp (L + 1)} \right\}} , \\ & \quad\ \, b =\! 0,1\end{aligned}$

(17)

则最大化a_p等效于最小化 $\det ({\widehat {{R}}_p})$ ，即最小化式(18)

$\begin{aligned}\det ({\widehat {{R}}_p}) \\ = & \det \left[ {\frac{{{{{\tilde{{R}}}}_p} + ({{{x}}_p} - b{{{H}}_p}{{{a}}_p}){{({{{x}}_p} - b{{{H}}_p}{{{a}}_p})}^{\mathop{\rm H}\nolimits} }}}{{L + 1}}} \right] \\= & \det \left[ {\frac{{{{{\tilde{{R}}}}_p}}}{{(L + 1)}}} \right] \\ & \cdot \left[ {1 + {{({{{x}}_p} - b{{{H}}_p}{{{a}}_p})}^{\mathop{\rm H}\nolimits} }{\tilde{{R}}}_p^{ - 1}({{{x}}_p} - b{{{H}}_p}{{{a}}_p})} \right],\; \\ & \quad\quad b = 0,1\end{aligned}$

(18)

对式(18)求a_p的导数，并令其等于零可得a_p的MLE为：

${\widehat {{a}}_p} = {\left({{H}}_p^{\mathop{\rm H}\nolimits} {\tilde{{R}}}_p^{ - 1}{{{H}}_p}\right)^{ - 1}}{{H}}_p^{\mathop{\rm H}\nolimits} {\tilde{{R}}}_p^{ - 1}{{{x}}_p}$

(19)

将式(16)和式(19)代入到式(15)可得GLRT检测器为：

$\begin{aligned}& {t_{{\rm{GLRT}}}} = \\ & \prod\limits_{p = 1}^P \!\!{\frac{{{{x}}_p^{\mathop{\rm H}\nolimits} {\tilde{{R}}}_p^{ - 1}{{{H}}_p}{{\left({{H}}_p^{\mathop{\rm H}\nolimits} {\tilde{{R}}}_p^{ - 1}{{{H}}_p}\right)}^{ - 1}}{{H}}_p^{\mathop{\rm H}\nolimits} {\tilde{{R}}}_p^{ - 1}{{{x}}_p}}}{{1 \!\!+\!\! {{x}}_p^{\mathop{\rm H}\nolimits} {\tilde{{R}}}_p^{ - 1}{{{x}}_p} \!\!-\!\! {{x}}_p^{\mathop{\rm H}\nolimits} {\tilde{{R}}}_p^{ - 1}{{{H}}_p}{{({{H}}_p^{\mathop{\rm H}\nolimits} {\tilde{{R}}}_p^{ - 1}{{{H}}_p})}^{ - 1}}\!\!{{H}}_{\! p}^{\mathop{\rm H}\nolimits} \!\!{\tilde{{R}}}_p^{ - 1}{{{x}}_p}}}} \end{aligned}$

(20)

4 检测器渐进统计特性分析

式(20)的GLRT检测器为一个求和项的形式，因此很难得到GLRT检测器检测概率和虚警概率的解析表达式。渐进统计特性是衡量检测器性能的重要指标^[18]，本节对式(20)的渐进统计特性进行分析，即分析R_p, $p = 1,2, ·\!·\!· ,P$ 已知时检测器的统计特性。

当协方差矩阵已知时，式(20)可改写为：

${\bar t_{{\rm{GLRT}}}} = \prod\limits_{p = 1}^P {{{x}}_p^{\mathop{\rm H}\nolimits} {{R}}_p^{ - 1}{{{H}}_p}{{\left({{H}}_p^{\mathop{\rm H}\nolimits} {{R}}_p^{ - 1}{{{H}}_p}\right)}^{ - 1}}{{H}}_p^{\mathop{\rm H}\nolimits} {{R}}_p^{ - 1}{{{x}}_p}} $

(21)

式(21)可进一步改写为：

${\bar t_{{\rm{GLRT}}}} = {{{y}}^{\mathop{\rm H}\nolimits} }{{y}}$

(22)

其中

$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! {{y}} = {\left[ {\begin{array}{*{20}{c}}{{{y}}_1^{\mathop{\rm T}\nolimits} } & {{{y}}_2^{\mathop{\rm T}\nolimits} } & ·\!·\!· & {{{y}}_P^{\mathop{\rm T}\nolimits} }\end{array}} \right]^{\mathop{\rm T}\nolimits} }$

(23)

${{{y}}_p} \!=\! {\left({{H}}_p^{\mathop{\rm H}\nolimits} {{R}}_p^{ - 1}{{{H}}_p}\right)^{ - 1/2}}{{H}}_p^{\mathop{\rm H}\nolimits} {{R}}_p^{ - 1}{{{x}}_p}, \; p \!=\! 1,2, ·\!·\!· ,P$

(24)

由于x_p在H₀假设下服从均值为零，方差为R_p的复高斯分布，则y_p在H₀假设下服从均值为零，方差为 ${{I}_{LMK}}$ 的复高斯分布。因此在H₀假设下 ${{y}}_p^{\mathop{\rm H}\nolimits} {{{y}}_p}$ 服从自由度为P的中心复卡方分布。由于 ${{\bar{t}}_{\text{GLRT}}}={{y}^{\text{H}}}y=\sum\nolimits_{p=1}^{P}{}y_{p}^{\text{H}}{{y}_{p}}$ ，即 ${\bar t_{{\rm{GLRT}}}}$ 在H₀假设下服从自由度为P ²的中心复卡方分布，其表达式为：

$\left. {{{\bar t}_{{\rm{GLRT}}}}} \right|{H_0} \ {{\text ~}} \ {\mathbb{C}}\chi _{{P^2}}^2$

(25)

在H₁假设下x_p服从均值为 ${{{H}}_p}{{{a}}_p}$ ，方差为R_p的复高斯分布，则y_p在H₁假设下服从均值为 ${({{H}}_p^{\mathop{\rm H}\nolimits} {{R}}_p^{ - 1}{{{H}}_p})^{1/2}}{{{a}}_p}$ ，方差为 ${{I}_{LMK}}$ 的复高斯分布，则在H₁假设下 ${\bar t_{{\rm{GLRT}}}}$ 服从非中心参数为ρ= $\sum\nolimits_{p=1}^{P}{}a_{p}^{\text{H}}H_{p}^{\text{H}}R_{p}^{-1}{{H}_{p}}{{a}_{p}}$ ，自由度为P ²的非中心复卡方分布，即

$\left. {{{\bar t}_{{\rm{GLRT}}}}} \right|{H_1} \ {{\sim}} \ {\mathbb{C}}\chi _{{P^2}}^2 \left(\sum\limits_{p = 1}^P \!{{{a}}_p^{\mathop{\rm H}\limits} {{H}}_p^{\mathop{\rm H}\limits} {{R}}_p^{ - 1}{{{H}}_p}{{{a}}_p}} \right)$

(26)

根据文献[19]可知协方差矩阵已知时GLRT检测器的检测概率和虚警概率分别为：

${\rm{PD = 1}} - \frac{{{{\mathop{\rm e}\nolimits} ^{ - \eta - \rho }}{\eta ^{{P^2} - 1}}}}{{({P^2} - 1)!}}{_0}{F_1}({P^2};\rho \eta )$

(27)

和

${\rm{PFA = 1}} - \frac{{{{\mathop{\rm e}\nolimits} ^{ - \eta - \rho }}{\eta ^{{P^2} - 1}}}}{{({P^2} - 1)!}}$

(28)

其中 $\eta $ 表示检测门限。式(27)中 ${}_0{F_1}({P^2};\rho \eta )$ 为广义超几何函数(Generalized hypergeometric function)，具体表达式为：

${}_0{{\mathop{ F}\nolimits} _1}(b;x) = \sum\limits_{n = 0}^\infty {\frac{1}{{{{(b)}_n}}}} \frac{{{x^n}}}{{n!}}$

(29)

其中 ${(b)_n} = b(b + 1) ·\!·\!· (b + n - 1)$ 。

根据式(27)可看出，检测器的检测概率由检测门限 $\eta $ 、机载雷达数目P和非中心参数 $\rho $ 决定，同时根据式(10)可知，非中心参数 $\rho $ 由发射波形决定。因此，式(27)给出了不同波形之间的积累增益对多机协同雷达探测系统检测性能的影响。此外，根据式(28)可知，多机协同雷达探测系统的虚警概率由检测门限 $\eta $ 、机载雷达数目P决定，其不受发射波形的影响。

5 仿真实验

雷达发射相同的波形可获得相干合成增益和强指向性的波束，发射正交波形则可获得更多的系统自由度和全向发射的波束。对于多机协同探测雷达系统，为了避免脉冲追赶问题和提高目标检测性能，需要根据任务需求来选择合适的发射波形。为比较不同发射波形对目标检测性能的影响，本节选用3种不同的发射波形进行比较，分别是PA雷达(所有雷达发射全相干波形)，PA-DMIMO雷达^[6](每部机载预警雷达采用PA体制，且不同机载预警雷达发射的信号相互正交)和CMIMO-DMIMO雷达^[6](每部机载预警雷达采用CMIMO雷达，且不同机载预警雷达发射的信号相互正交)。

本节通过计算机仿真来比较不同发射波形对目标检测性能的影响。计算机仿真采用蒙特卡洛方法，虚警概率设置为10^–3，检测门限和检测概率均通过10⁵次实验得到。

假设3架预警机进行协同探测，每部机载雷达均可接收所有机载雷达发射的信号，且每部机载雷达的阵元数为4，脉冲数为4，波形采样点数为12。为避免机载雷达与目标距离不同导致的功率差异问题，本实验将3架预警机放置在以目标为圆心的同心圆上。此外，在实际作战环境中，目标通常位于敌方区域。为保证预警机的安全，预警机通常位于我方区域，所以本实验将预警机设置在目标的同一侧，即 $({30^ \circ },{90^ \circ },{150^ \circ })$ 这3个位置，圆的半径设置为100 km，其位置示意图如图2所示。

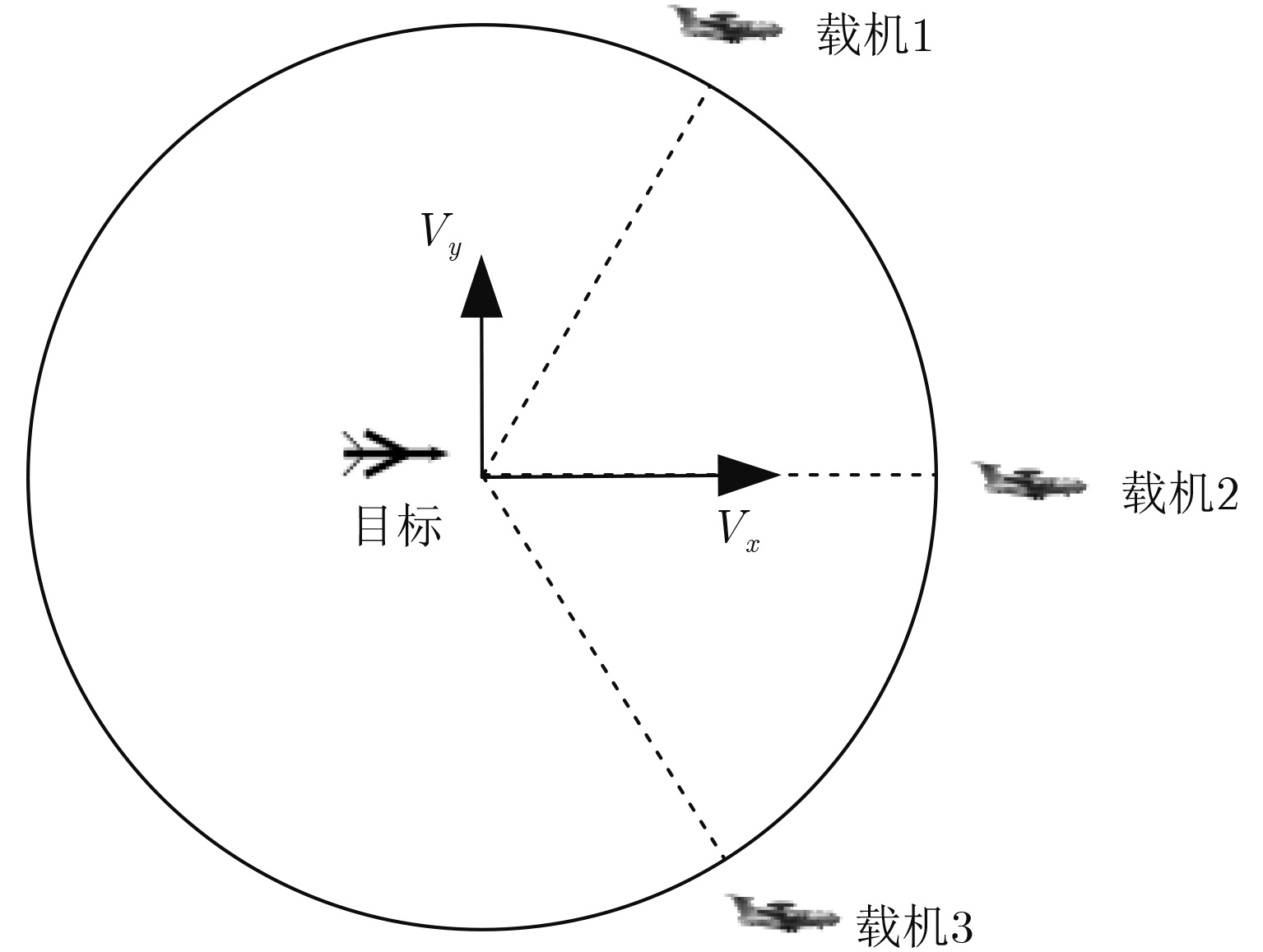
图 2 天线和目标位置示意图 Fig.2 Locations of antenna and target

载机高度均为8000 m，速度均为140 m/s。发射信号波长为0.23 m，脉冲重复频率为2434.8 Hz，杂噪比(Clutter to Noise Ratio, CNR)为60 dB。设置目标速度分别为(50, –100) m/s, (100, 100) m/s和(100, 60) m/s，其中目标速度的差异体现了目标是否进入杂波区，具体情况如表1。表1中符号√表示目标落入该路径的杂波区，路径“pi”表示第p部机载雷达接收到第i部机载雷达的发射信号。

表 1 3种雷达体制下目标落入杂波区的情况 Tab.1 Relationship between target and clutter of three radar systems with specific target velocity

从图3中可看出当收发路径数增加且杂波和噪声协方差矩阵已知时，CMIMO-DMIMO雷达的目标检测性能在SNR小于–7 dB区域的目标检测性能弱于PA-DMIMO雷达，这是因为PD-DMIMO雷达在发射端能够获得发射相干增益，而CMIMO-DMIMO不能获得发射相干增益。在SNR大于–7 dB区域CMIMO-DMIMO雷达的目标检测性能优于PA-DMIMO雷达，这是由于CMIMO-DMIMO雷达杂波分布在发射域、接收域和多普勒域的3维空间上^[10]，而PA-DMIMO雷达的杂波分布在接收域和多普勒域的2维平面上，因此目标在PA-DMIMO雷达中更可能落入多条收发路径杂波区。同时，图3中PA雷达完全不能检测目标，这是因为PA雷达不具有波形分集特性，因此其多条收发路径的杂波叠加到一起，导致不能检测目标。

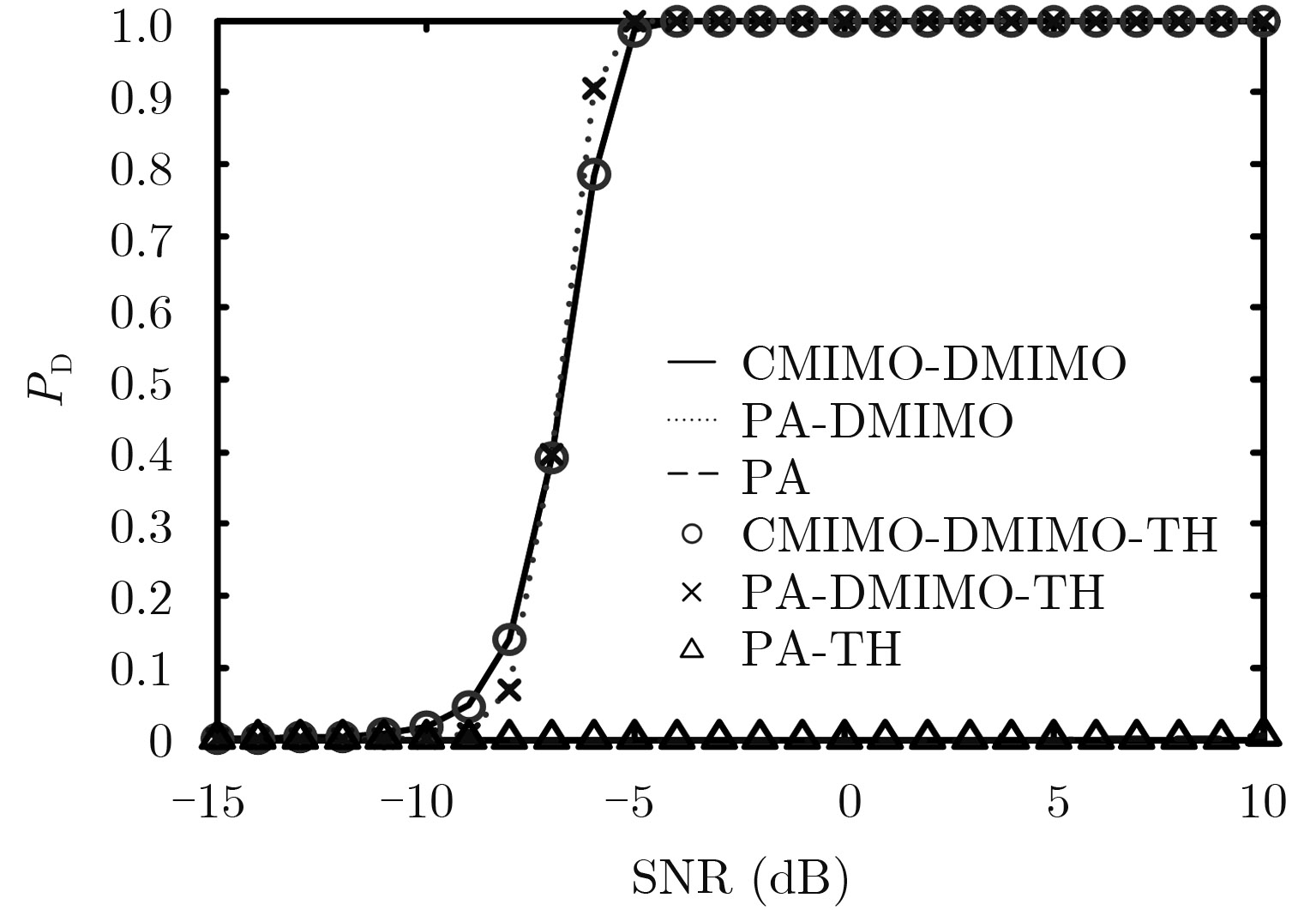
图 3 协方差矩阵已知且目标速度为(50, –100) m/s时的检测性能曲线 Fig.3 PD versus SNR for known covariance matrix with target velocity (50, –100) m/s

从图4中可看出，不同发射波形的检测性能差异较大。其中PA雷达性能最差，这是由于所有机载雷达均发射相干波束，接收天线不能区分不同发射天线的信号，使得不同路径的杂波叠加，导致无法有效检测目标。而对于CMIMO-DMIMO雷达和PA-DMIMO雷达，不同发射天线发射的信号相互正交，因此这两种体制雷达可利用信号的正交特性来分离不同路径的杂波。此外，PA-DMIMO雷达能获得发射相干增益，而CMIMO-DMIMO雷达为全向发射，不能获得发射相干增益，因此PA-DMIMO雷达性能优于CMIMO-DMIMO雷达。

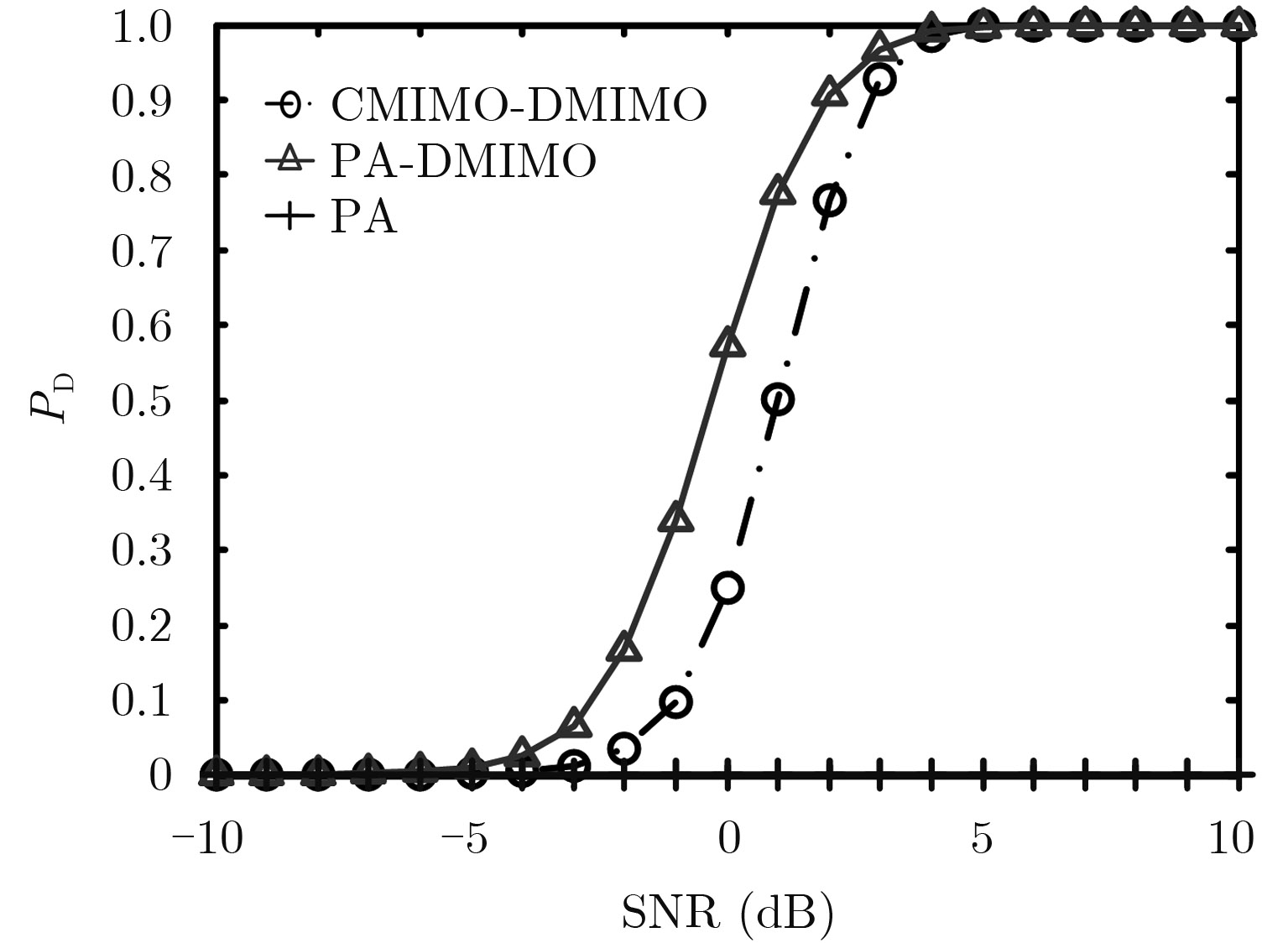
图 4 目标速度为(50, –100) m/s时的检测性能曲线 Fig.4 PD versus SNR with target velocity (50, –100) m/s

从图5中可看出当目标速度为(100, 100) m/s时，PA-DMIMO雷达的检测性能与CMIMO-DMIMO雷达的检测性能差异变小。这是由于PA-DMIMO雷达的杂波分布在接收域和多普勒域的2维平面上，而CMIMO-DMIMO雷达的杂波分布在发射域、接收域和多普勒域的3维空间上^[10]，因此PA-DMIMO雷达的检测性能对目标速度变化更为敏感。需要注意的是图5中PA-DMIMO雷达在低SNR区域的检测概率高于CMIMO-DMIMO雷达，这是由于当SNR较低时，由于PA-DMIMO雷达具有更高的发射相干增益，因此其检测概率相对更高。如表1所示，对于CMIMO-DMIMO雷达，速度为(100, 100) m/s的目标不会落入任何路径的杂波区内，而对于PA-DMIMO雷达目标则会同时落入4条路径的杂波区。因此当SNR较高时，PA-DMIMO雷达的发射相干得益已无法弥补目标落入杂波区带来的检测性能损失，此时CMIMO-DMIMO雷达的检测性能优于PA-DMIMO雷达。

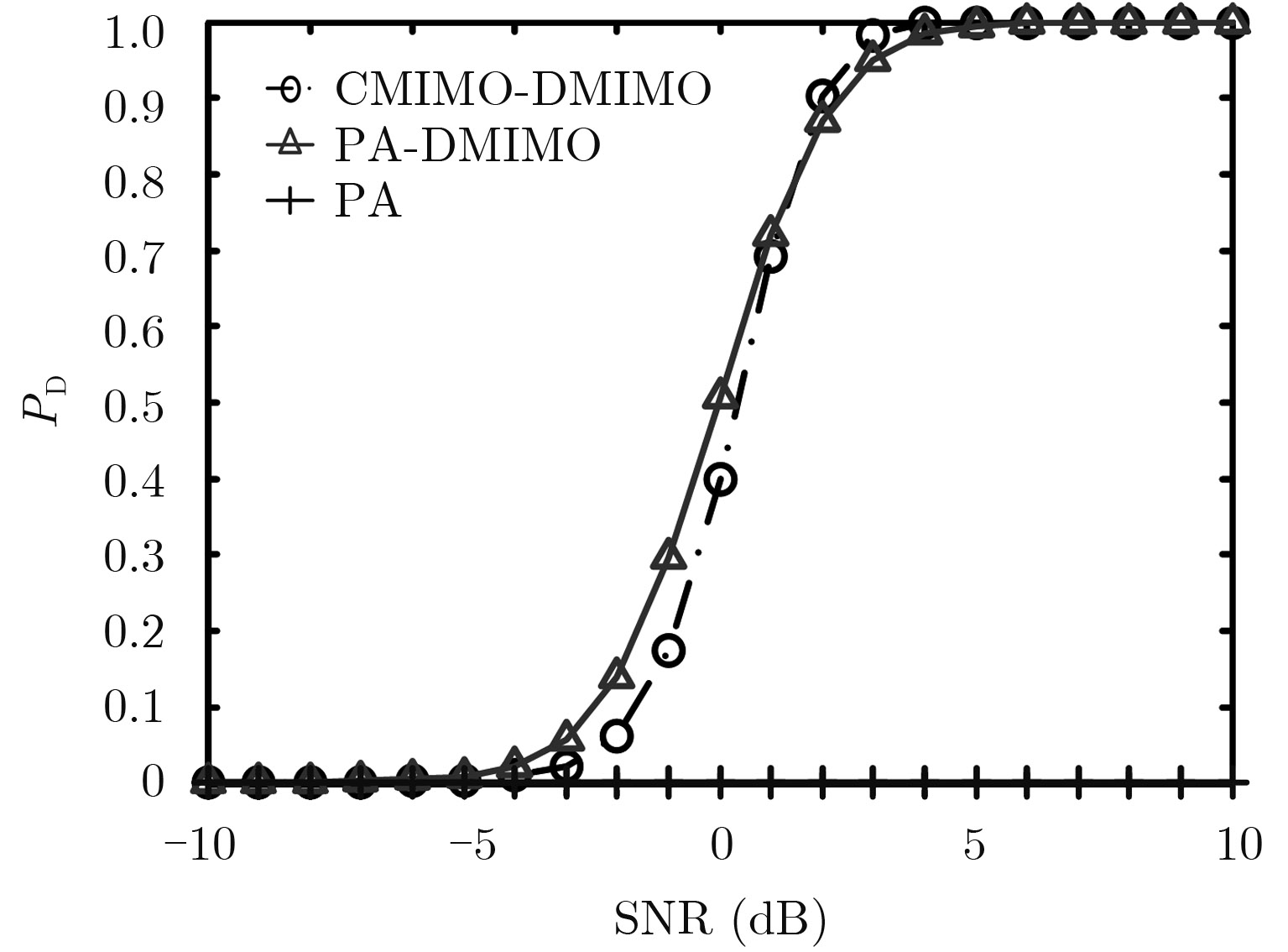
图 5 目标速度为(100, 100) m/s时的检测性能曲线 Fig.5 PD versus SNR with target velocity (100, 100) m/s

图6中PA-DMIMO雷达的检测性能较差，这是由于PA-DMIMO雷达中速度为(100, 60) m/s的目标进入6条路径的杂波区，因此其性能下降较大。而CMIMO-DMIMO雷达由于杂波3维分布的特点，使得目标进入杂波区可能性减少(未进入任何一条路径的杂波区内)，所以其性能变化不明显。

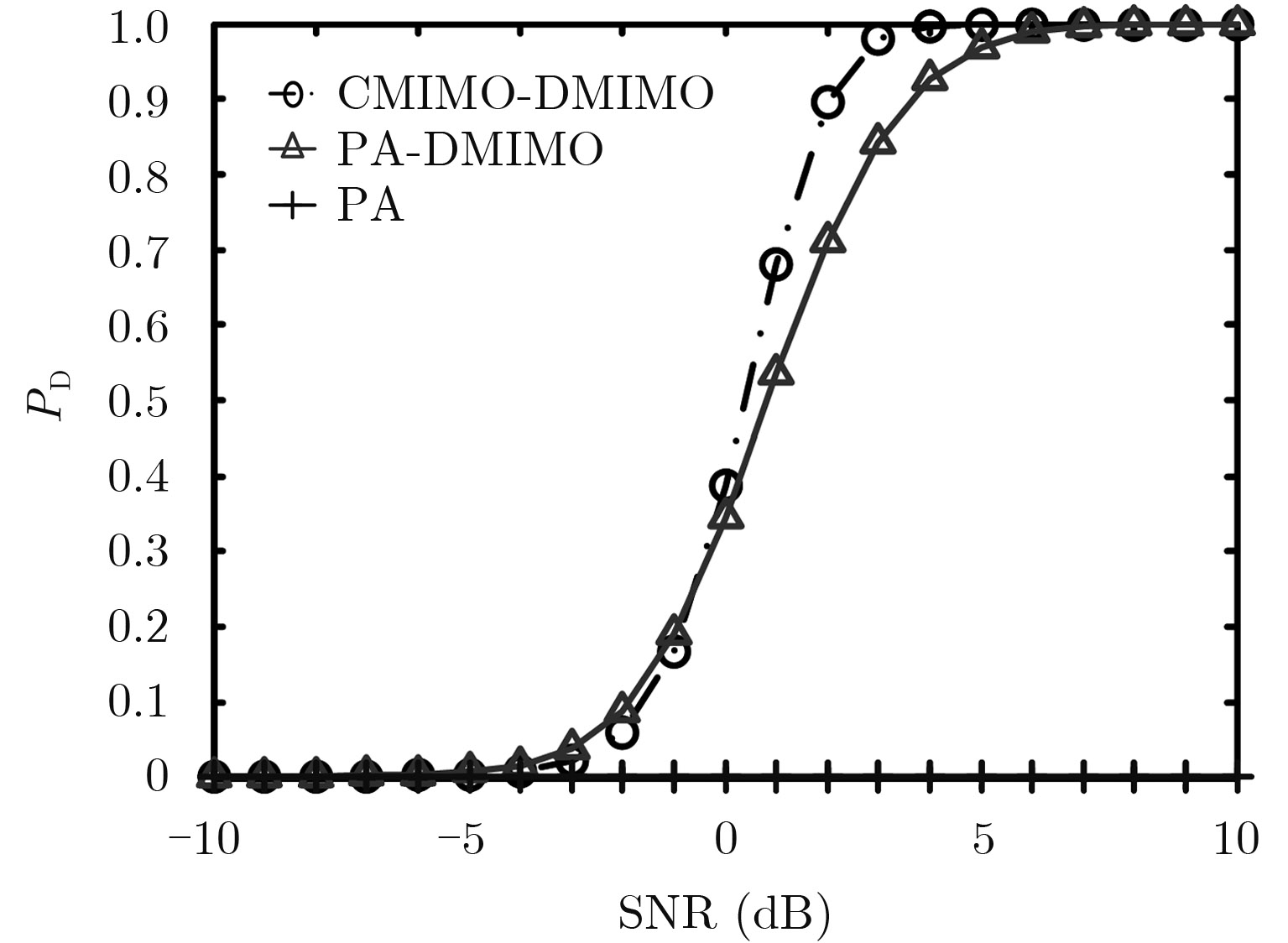
图 6 目标速度为(100, 60) m/s时的检测性能曲线 Fig.6 PD versus SNR with target velocity (100, 60) m/s

为进一步分析不同目标速度情况下发射波形对检测性能的影响，下面设置SNR为0 dB，分别仿真不同体制雷达在目标速度变化时的检测性能曲线。

从图7和图8中可看出，不同发射波形对不同速度目标的检测性能不同。其中PA雷达由于杂波的叠加导致几乎无法检测到目标。而PA-DMIMO雷达和CMIMO-DMIMO雷达的目标检测性能则随目标速度的变化而变化。其中，当目标在x轴速度为零时(如图7所示)，PA-DMIMO雷达检测性能要优于CMIMO-DMIMO雷达，这是由于PA-DMIMO雷达能获得相干增益的原因。而当目标在y轴速度为零时(如图8所示)，CMIMO-DMIMO雷达的目标检测性能接近于PA-DMIMO雷达，其原因是由于CMIMO-DMIMO雷达杂波分布特性带来的得益。

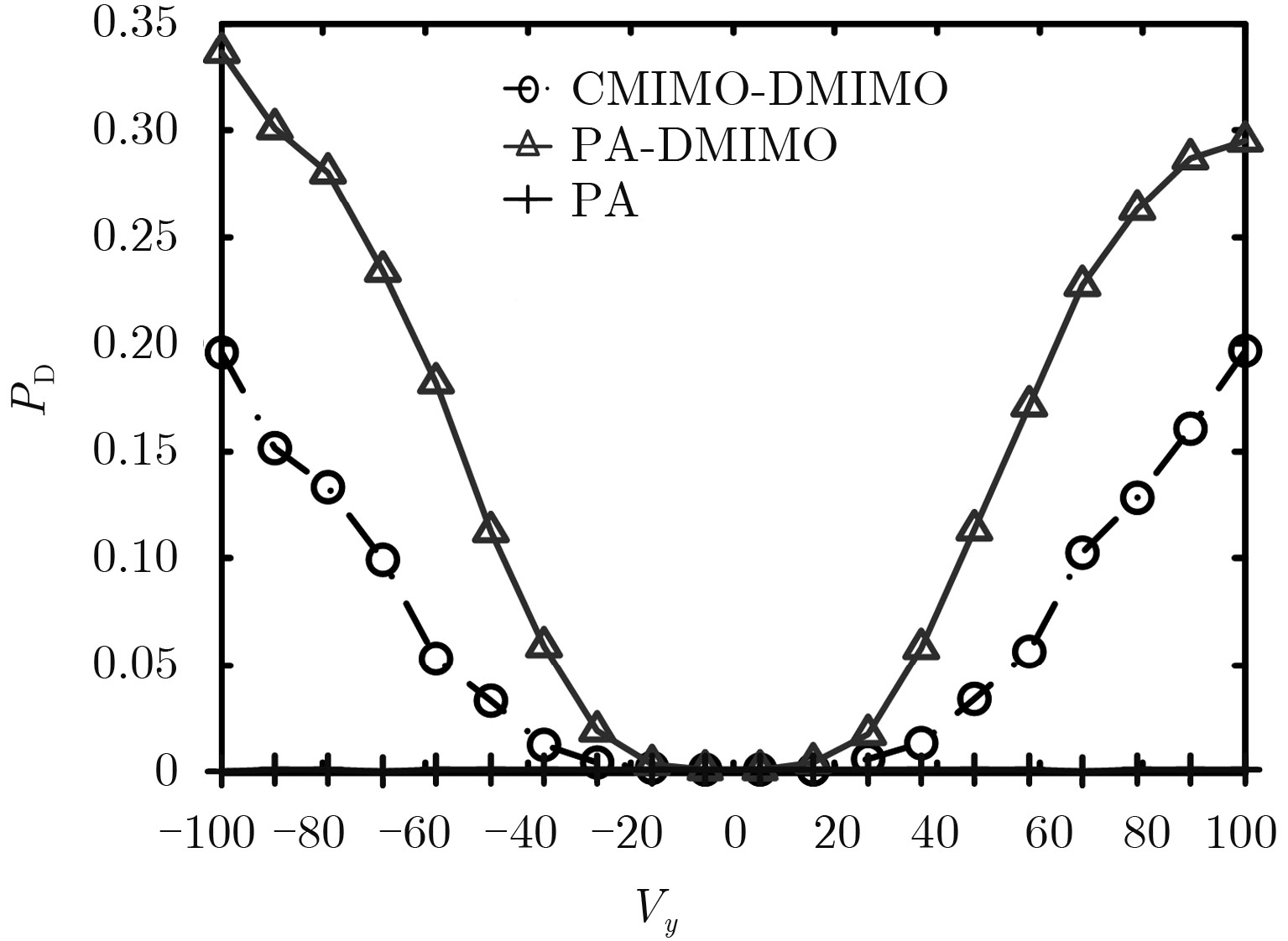
图 7 目标速度在x轴方向为零，检测概率与目标y轴速度变化的关系 Fig.7 Relationship between PD and the y-target velocity when the x-target velocity is 0 m/s

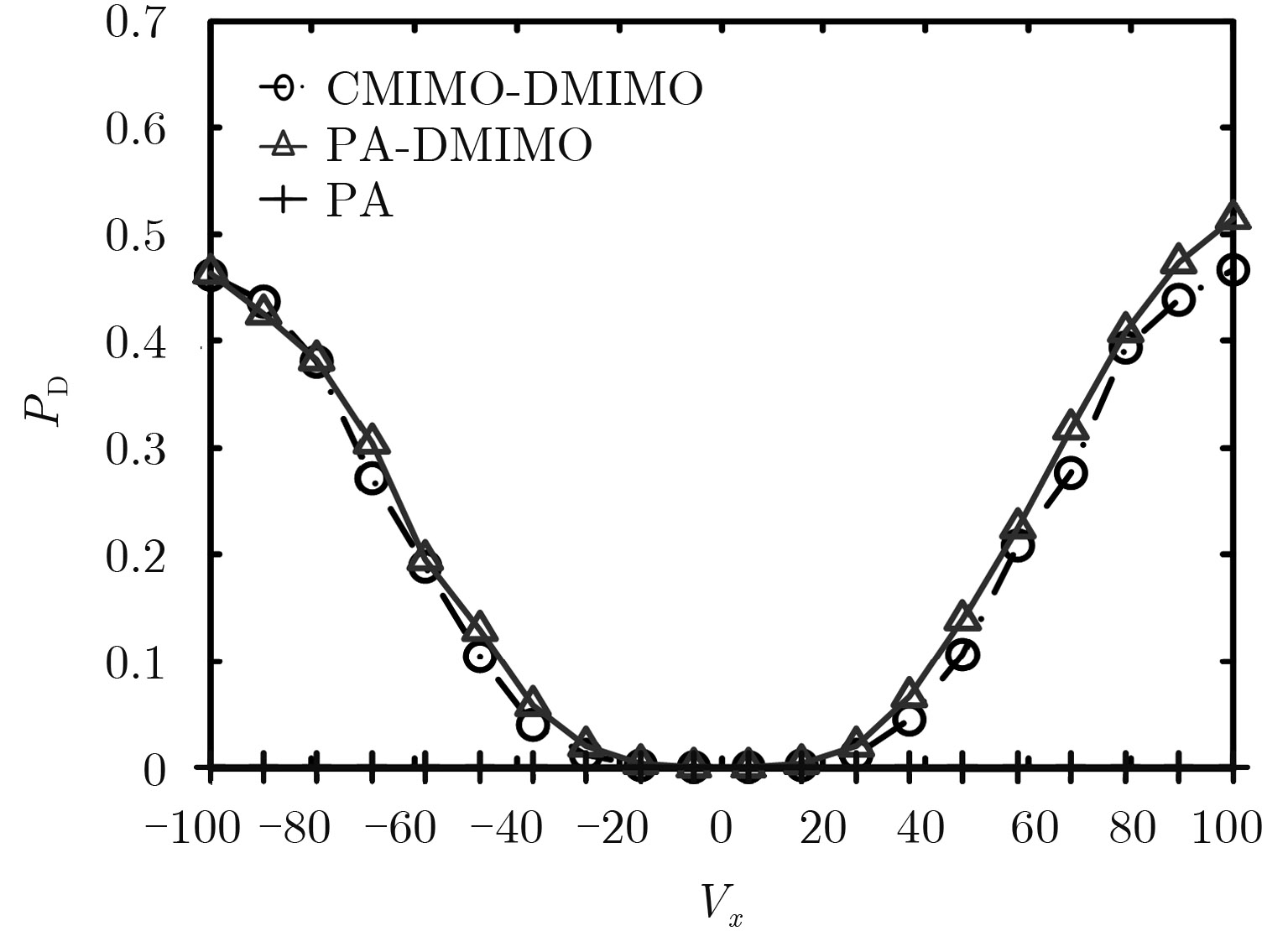
图 8 目标速度在y轴方向为零，检测概率与目标x轴速度变化的关系 Fig.8 Relationship between PD and the x-target velocity when the y-target velocity is 0 m/s

6 结论

本文建立了基于不同发射波形的多机协同探测机载雷达系统的杂波模型，然后在该模型的基础上给出了GLRT检测器及其检测概率和虚警概率的渐进表达式。研究结果表明，多机协同探测机载雷达系统中发射波形对目标检测性能有很大影响。其中，当采用全相干发射波形时，虽然能获得发射相干增益和强指向性波束，但同时会出现杂波回波叠加问题以及脉冲追赶问题。当单个发射天线发射相干波形且不同发射天线之间的信号相互正交时，可获得较强指向性波束和发射相干增益，但仍面临脉冲追赶问题。而当采用全正交发射波形时，通过信号的全向发射避免了脉冲追赶问题且杂波进一步分集，但其无法获得发射相干增益。因此，发射波形同时影响了发射相干增益、发射波束宽度及杂波分布特性，在实际工作中需要根据任务的实际需求来设计发射波形。

参考文献

[1]	Goodman N A and Bruyere D. Optimum and decentralized detection for multistatic airborne radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(2): 806-813.DOI:10.1109/TAES.2007.4285374(0)
[2]	Bruyere D and Goodman N. Adaptive detection and diversity order in multistatic radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(4): 1615-1623.DOI:10.1109/TAES.2008.4667736(0)
[3]	Jung B W, Adve R S, Chun J, et al..Detection performance using frequency diversity with distributed sensors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(3): 1800-1813.DOI:10.1109/TAES.2011.5937266(0)
[4]	Willis N J. Bistatic Radar[M]. Mendham, NJ, USA: SciTech Publishing, 2005. (0)
[5]	Chernyak V. Multisite radar systems composed of MIMO radars[J]. IEEE Aerospace and Electronic Systems Magazine, 2014, 29(12): 28-37.DOI:10.1109/MAES.2014.7015713(0)
[6]	Yang Haifeng, Liu Weijian, Xie Wenchong, et al..General signal model of MIMO radar for moving target detection[J]. IET Radar, Sonar & Navigation, 2017, 11(4): 570-578.(0)
[7]	Xu Haisheng, Wang Jian, Yuan Jian, et al..Colocated MIMO radar transmit beamspace design for randomly present target detection[J]. IEEE Signal Processing Letters, 2015, 22(7): 828-832.DOI:10.1109/LSP.2014.2371241(0)
[8]	Tang Bo, Naghsh M M and Tang Jun. Relative entropy-based waveform design for MIMO radar detection in the presence of clutter and interference[J]. IEEE Transactions on Signal Processing, 2015, 63(14): 3783-3796.DOI:10.1109/TSP.2015.2423257(0)
[9]	Jiu Bo, Liu Hongwei, Wang Xu, et al..Knowledge-based spatial-temporal hierarchical MIMO radar waveform design method for target detection in heterogeneous clutter zone[J]. IEEE Transactions on Signal Processing, 2015, 63(3): 543-554.DOI:10.1109/TSP.2014.2366714(0)
[10]	张西川, 谢文冲, 张永顺, 等. 任意波形相关性的机载MIMO雷达杂波建模与分析[J]. 电子与信息学报, 2011, 33(3): 646-651. Zhang Xichuan, Xie Wenchong, Zhang Yongshun, et al..Modeling and analysis of the clutter on airborne MIMO radar with arbitrary waveform correlation[J]. Journal of Electronics & Information Technology, 2011, 33(3): 646-651.(0)
[11]	张西川, 张永顺, 谢文冲, 等. 机载相干MIMO雷达杂波自由度估计研究[J]. 电子与信息学报, 2011, 33(9): 2125-2131. Zhang Xichuan, Zhang Yongshun, Xie Wenchong, et al..Research on the estimation of clutter rank for coherent airborne MIMO radar[J]. Journal of electronics & Information Technology, 2011, 33(9): 2125-2131.(0)
[12]	Xie Wenchong, Zhang Baihua, Wang Yongliang, et al..Range ambiguity clutter suppression for bistatic STAP radar[J]. EURASIP Journal on Advances in Signal Processing, 2013, 2013: 75DOI:10.1186/1687-6180-2013-75(0)
[13]	Xie Wenchong, Zhang Xichuan, Wang Yongliang, et al..Estimation of clutter degrees of freedom for airborne multiple-input multiple-output-phased array radar[J]. IET Radar, Sonar & Navigation, 2013, 7(6): 652-657.(0)
[14]	Xu Luzhou, Li Jian and Stoica P. Target detection and parameter estimation for MIMO radar systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 927-939.DOI:10.1109/TAES.2008.4655353(0)
[15]	Liu Weijian, Wang Yongliang, Liu Jun, et al..Adaptive detection without training data in colocated MIMO radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(3): 2469-2479.DOI:10.1109/TAES.2015.130754(0)
[16]	Gao Yongchan, Liao Guisheng and Liu Weijian. High-resolution radar detection in interference and nonhomogeneous noise[J]. IEEE Signal Processing Letters, 2016, 23(10): 1359-1363.DOI:10.1109/LSP.2016.2597738(0)
[17]	Liu Weijian, Liu Jun, Zhang Chen, et al..Performance prediction of subspace-based adaptive detectors with signal mismatch[J]. Signal Processing, 2016, 123: 122-126.DOI:10.1016/j.sigpro.2015.12.021(0)
[18]	Xu Jia, Dai Xizeng, Xia Xianggen, et al..Optimizations of multisite radar system with MIMO radars for target detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(4): 2329-2343.DOI:10.1109/TAES.2011.6034636(0)
[19]	Ross S M. Introduction to Probability Models[M]. Fifth Edition, New York, USA: Academic Press, 2014. (0)