1 引言
全极化SAR通过交替发射一组正交的极化波,并同时接收来自这两个极化通道的回波来测量目标完整的极化信息。为了提取正确的目标极化信息和保障极化SAR测量的可重复性,需要对极化SAR数据定标。
由于不需要额外的布置人造目标,基于分布式目标的定标方法[1,2,3,4,5,6]被普遍地用于估计串扰和交叉极化通道不平衡。这类定标算法一般用观测的目标协方差矩阵来估计失真参数。由于这些失真参数随距离向变化,所以实践中一般都用等斜距的像素来估计观测的目标的协方差矩阵[4, 7]。然而实际应用定标算法时,均要求所用到的分布式目标满足一定假设。简单地用同一距离门处的像素来估计观测的目标协方差矩阵难免会包含不满足假设的目标,例如地形起伏较大的地物或不含极化信息的饱和像素等。为了获得更稳定的失真参数估计,需要滤除不满足定标算法假设的目标(以下简称这种目标为离群目标)。为此,本文采用截断协方差矩阵的方法来剔除离群目标。
全文安排如下:第2节介绍了基于分布式目标的极化SAR定标算法和球形截断实高斯分布的基础理论。在第3节中,我们先将球形截断方法推广到圆对称复高斯分布的情况,并论证了将球形截断协方差矩阵用于极化定标的可行性。然后,我们阐述了将球形截断方法用于极化定标的具体实现步骤。第4节给出了实际机载SAR数据的实验结果。最后在第5节给出结论。
2 背景知识
2.1 基于分布式目标的极化定标算法
线性全极化SAR系统测量模型可以表示为[1, 5]:
|
$\left[\!\! {\begin{array}{*{20}{c}}
{{O_{{\rm{HH}}}}} \!\!&\!\!{{O_{{\rm{HV}}}}}\\
{{O_{{\rm{VH}}}}}\!\!&\!\!{{O_{{\rm{VV}}}}}
\end{array}} \!\!\right]\!\! =\!\! \left[\!\!{\begin{array}{*{20}{c}}
{{R_{{\rm{HH}}}}}\!\!&\!\!{{R_{{\rm{HV}}}}}\\
{{R_{{\rm{VH}}}}}\!\!&\!\!{{R_{{\rm{VV}}}}}
\end{array}} \!\!\right]\left[\!\! {\begin{array}{*{20}{c}}
{{S_{{\rm{HH}}}}}\!\!&\!\!{{S_{{\rm{HV}}}}}\\
{{S_{{\rm{VH}}}}}\!\!&\!\!{{S_{{\rm{VV}}}}}
\end{array}}\!\! \right]\left[{\begin{array}{*{20}{c}}
{{T_{{\rm{HH}}}}}\!\!&\!\!{{T_{{\rm{HV}}}}}\\
{{T_{{\rm{VH}}}}}\!\!&\!\!{{T_{{\rm{VV}}}}}
\end{array}} \!\!\right], $
|
或
|
${{{O}}} = {{{RST}}}$
|
(1) |
其中,
O和
S分别为目标散射矩阵的测量值和实际值,
R和
T分别表示SAR系统接收端和发射端的失真。
定义中间变量
|
$\begin{array}{l}
\\
\left. \begin{array}{l}
Y = {T_{{\rm{VV}}}}{R_{{\rm{VV}}}}\\
k = {{{R_{{\rm{HH}}}}} \mathord{\left/
{\vphantom {{{R_{{\rm{HH}}}}} {{R_{{\rm{VV}}}}}}} \right.
} {{R_{{\rm{VV}}}}}}\\
u = {{{R_{{\rm{VH}}}}} \mathord{\left/
{\vphantom {{{R_{{\rm{VH}}}}} {{R_{{\rm{HH}}}}}}} \right.
} {{R_{{\rm{HH}}}}}}\\
w = {{{R_{{\rm{HV}}}}} \mathord{\left/
{\vphantom {{{R_{{\rm{HV}}}}} {{R_{{\rm{VV}}}}}}} \right.
} {{R_{{\rm{VV}}}}}}\\
\alpha = {{{T_{{\rm{HH}}}}{R_{{\rm{VV}}}}} \mathord{\left/
{\vphantom {{{T_{{\rm{HH}}}}{R_{{\rm{VV}}}}} {{T_{{\rm{VV}}}}}}} \right.
} {{T_{{\rm{VV}}}}}}{R_{{\rm{HH}}}}\\
v = {{{T_{{\rm{VH}}}}} \mathord{\left/
{\vphantom {{{T_{{\rm{VH}}}}} {{T_{{\rm{VV}}}}}}} \right.
} {{T_{{\rm{VV}}}}}}\\
z = {{{T_{{\rm{HV}}}}} \mathord{\left/
{\vphantom {{{T_{{\rm{HV}}}}} {{T_{{\rm{HH}}}}}}} \right.
} {{T_{{\rm{HH}}}}}}
\end{array} \right\}
\end{array}$
|
(2) |
其中,
u,
v,
w,
z表示极化通道间的串扰;\[\alpha \]和
k分别表示交叉极化通道不平衡和同极化通道不平衡;
Y表示VV通道的增益和相位延迟。利用式(2),式(1)可以写成矢量形式:
|
$\begin{aligned}
\left[{\begin{array}{*{20}{c}}
{{O_{{\rm{HH}}}}}\\
{{O_{{\rm{VH}}}}}\\
{{O_{{\rm{HV}}}}}\\
{{O_{{\rm{VV}}}}}
\end{array}} \right] =&Y\left[{\begin{array}{*{20}{c}}
1&w&v&{vw}\\
u&1&{vu}&v\\
z&{zw}&1&w\\
{zu}&z&u&{\:\:\:1\:\:\:}
\end{array}} \right]\\
&\cdot \left[{\begin{array}{*{20}{c}}
{\:\alpha }&0&0&0\\
0&\alpha&0&0\\
0&0&{\:\:1\:\:}&0\\
0&0&0&1
\end{array}} \right]\\
&\cdot \left[{\begin{array}{*{20}{c}}
{\:{k^2}}&0&0&0\\
0&k&0&0\\
0&0&k&0\\
0&0&0&{\:\:1\:\:}
\end{array}} \right]\left[{\begin{array}{*{20}{c}}
{{S_{{\rm{HH}}}}}\\
{{S_{{\rm{VH}}}}}\\
{{S_{{\rm{HV}}}}}\\
{{S_{{\rm{VV}}}}}
\end{array}} \right]
\end{aligned}$
|
(3) |
通过引入下列矩阵函数
|
$\begin{aligned}
&{{{X}}}\left( {u, v, w, z} \right)\mathop {\rm{ = }}\limits^\Delta \left[{\begin{array}{*{20}{c}}
1&w&v&{vw}\\
u&1&{vu}&v\\
z&{zw}&1&w\\
{zu}&z&u&{\, \, \, 1\, \, \, }
\end{array}} \right], \\
&\widetilde {{{X}}}\left( {u, v, w, z} \right)\mathop {\rm{ = }}\limits^\Delta \left[{\begin{array}{*{20}{c}}
1&{-w}&{-v}&{vw}\\
{-u}&1&{vu}&{ - v}\\
{ - z}&{zw}&1&{ - w}\\
{zu}&{ - z}&{ - u}&{\:\:\:1\:\:\:}
\end{array}} \right], \quad \\
&{{{A}}}\left( \alpha \right)\mathop {\rm{ = }}\limits^\Delta \left[{\begin{array}{*{20}{c}}
{\:\alpha }&0&0&0\\
0&\alpha&0&0\\
0&0&{\:\:1\:\:}&0\\
0&0&0&1
\end{array}} \right], \\
&{{{K}}}\left( k \right)\mathop {\rm{ = }}\limits^\Delta \left[{\begin{array}{*{20}{c}}
{\:{k^2}}&0&0&0\\
0&k&0&0\\
0&0&k&0\\
0&0&0&{\:\:1\:\:}
\end{array}} \right]
\end{aligned}
$
|
(4) |
我们可以将式(3)简写为:
|
$\underline {{{O}}} = Y{{{X}}}\left( {u, v, w, z} \right){{{A}}}\left( \alpha \right){{{K}}}\left( k \right)\underline {{{S}}}$
|
(5) |
其中几个带下划线的符号表示相应矩阵的矢量化,例如
$ \underline {{{S}}} $$ \mathop {\rm{ = }}\limits^\Delta $${\left[{{S_{{\rm{HH}}}}\;{S_{{\rm{VH}}}}\;{S_{{\rm{HV}}}}\;{S_{{\rm{VV}}}}} \right]^{\rm T}}$(上标“T”表示矢量或矩阵的转置运算)。
基于分布式目标的定标算法要求观测数据中包含能够用来估计失真参数的冗余信息。为此,通常假设目标满足:(1)互易性,即有${S_{\rm HV}} = {S_{\rm VH}}$;(2)同极化和交叉极化通道不相关[3](或目标满足方位对称性[1])。对于后向散射SAR来说,分布式目标都满足互易性[8]。然而,并非所有的分布式目标都满足方位对称性。本文假设待定标的分布式目标满足假设(2),至于如何保证该假设成立,不在本文讨论范围之内,感兴趣的读者可以参考文献[9]。
由式(5)可得,观测散射矢量的协方差矩阵为:
|
$\begin{aligned}{{{{C}}}\!_{\underline {{{O}}} }} =&{{{X}}}\left( {u, v, w, z} \right){{{A}}}\left( \alpha \right){{{K}}}\left( k \right){{{{C}}}_{\underline {{{S}}} }}{{{{K}}}^{\rm H}}\left( k \right)\\
&\cdot{{{{A}}}^{\rm H}}\left( \alpha \right){{{{X}}}^{\rm H}}\left( {u, v, w, z} \right)|Y\, {|^2}
\end{aligned}$
|
(6) |
其中,上标“H”表示矢量(或矩阵)的共轭转置运算,矩阵
${{{{C}}}_{\underline {{{O}}} }}\mathop {\rm{ = }}\limits^\Delta {\rm{E}}\left\{ {\underline {{{O}}}\;{{\underline {{{O}}} }^{\rm H}}} \right\}$和
${{{{C}}}_{\underline {{{S}}} }}\mathop {\rm{ = }}\limits^\Delta {\rm{E}}\left\{ {\underline {{{S}}}\;{{\underline {{{S}}} }^{\rm H}}} \right\}$分别为观测的和实际的目标协方差矩阵。当分布式目标满足互易性和方位对称性时,
|
${{{{C}}}_{\underline {{{S}}} }} = \left[{\begin{array}{*{20}{c}}
{\sigma _{{\rm{HH}}}^{}}&0&0&\rho \\
0&{\sigma _ \times ^{}}&{\sigma _ \times ^{}}&0\\
0&{\sigma _ \times ^{}}&{\sigma _ \times ^{}}&0\\
{{\rho ^ * }}&0&0&{\sigma _{{\rm{VV}}}^{}}
\end{array}} \right]$
|
(7) |
式中,
$\sigma _{{\rm{HH}}}^{} = {\rm{E}}\left\{ {S_{{\rm{HH}}}^{}S_{{\rm{HH}}}^ * } \right\}, \sigma _{{\rm{VV}}}^{} = {\rm{E}}\left\{ {S_{{\rm{VV}}}^{}S_{{\rm{VV}}}^ * } \right\}, \sigma _ \times ^{} = $${\rm{E}}\left\{ {S_{{\rm{VH}}}^{}S_{{\rm{VH}}}^ * } \right\}$以及
$\rho = {\rm{E}}\left\{ {S_{{\rm{HH}}}^{}S_{{\rm{VV}}}^ * } \right\}$。可以看到,
${{{{C}}}_{\underline {{{S}}} }}$中有若干个为零的元素,以及几个相等的元素。利用
${{{{C}}}_{\underline {{{S}}} }}$的这些冗余信息,我们能够估计失真参数
u,
v,
w,
z和\[\alpha \](详情见附录)。随后,我们可以得到部分标定的散射矢量
|
${\underline {{{S}}} ^{\rm D}} = {{{{A}}}^{ - 1}}\left( \alpha \right){{{{X}}}^{ - 1}}\left( {u, v, w, z} \right)\underline {{{O}}} = Y{{{K}}}\left( k \right)\underline {{{S}}}$
|
(8) |
完整的定标,一般还需要利用人造目标(例如三面角反射器)来估计
Y和
k。本文只讨论利用分布式目标得到部分标定的散射矢量
${\underline {{{S}}} ^{\rm D}}$,至于如何估计
Y和
k并非本文重点,感兴趣的读者可以参考文献[
1]。
2.2 球形截断实高斯分布及其协方差矩阵
假设矢量${{{x}}} = {\left[{{x_{\, 1}}\, \, \, {x_{\, 2}}\, \, \, \cdots \, \, \, {x_{\, \nu }}} \right]^{\rm T}} \in \mathbb {R}{^\nu }$服从$\nu $维零均值实高斯分布,即
|
${p_{{{x}}}}\left( {{{x}}} \right) = \frac{1}{{{{\left( {2{{\pi}} } \right)}^{\nu /2}}|{{{{C}}}_{{{x}}}}\, {|^{\, 1/2}}}}\exp \left( { - \frac{1}{2}{{{{x}}}^{\rm T}} {{C}}_{{x}}^{ - 1}{{{x}}}} \right)$
|
(9) |
其中实对称正定矩阵
${{{C}}_{{{x}}}} = {\rm{E}}\left\{ {{{{x}}}\, {{{{x}}}^{\rm T}}} \right\}$为
x的协方差矩阵,定义
$\nu $维欧式空间中以原点为圆心、
$\sqrt \tau $为半径的球
|
${\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)= \left\{ {{{{x}}} \in \mathbb {R}{^\nu }\mid {{{{x}}}^{\rm T}}{{{x}}}\le \tau } \right\}$
|
(10) |
这样,我们可以定义
x在球
${\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)$内截断的概率密度函数
|
$\begin{array}{l}
{p_{{{{x}}}|{{{x}}}\, \in \, {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}\left( {{{x}}} \right) = \left\{ \begin{array}{l}
{{{p_{{{x}}}}\left( {{{x}}} \right)} \mathord{\left/
{\vphantom {{{p_{{{x}}}}\left( {{{x}}} \right)} {{V_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}}}}\right.
} {{V_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}}} \quad {{{x}}} \in {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right);\\
0, \quad \quad \quad \quad \quad \ \;{{{x}}}\notin {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right),
\end{array} \right.\\
\quad \quad \quad \quad \quad \quad \quad \quad {V_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}} = {\rm{P}}\left[{{{{x}}} \in {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)} \right]
\end{array}$
|
(11) |
式(11)中,
${\rm{P}}\left[{\, \cdot \, } \right]$表示事件·发生的概率。利用式(11),我们可以定义球形截断实高斯分布的1阶和2阶原点矩
|
${ \overset{\frown} {{\mu}} }\! {_{{{x}}}}\mathop {\rm{ = }}\limits^\Delta {\rm{E}}\left\{ {{{{x}}}|{{{x}}} \in {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)} \right\} \quad \;$
|
(12) |
|
${ \overset{\frown} {{C}} }\!\! {_{{{x}}}}\mathop {\rm{ = }}\limits^\Delta {\rm{E}}\left\{ {{{{x}}}\, {{{{x}}}^{\rm T}}{\Big {|}}{{{x}}} \in {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)} \right\}$
|
(13) |
容易证明1阶矩${ \overset{\frown} {{μ}} }\!\!{_{{{x}}}} \equiv {{{0}}}$,因而2阶原点矩矩阵${\overset{\frown} {{C}_{{x}}} }$即球形截断实高斯分布所对应的协方差矩阵。文献[10]中证明了${\overset{\frown} {{C}_{{x}}} }$与${{{{C}}}_{{{x}}}}$有相同的特征矢量。这个结论是后文中几个结论的前提,为便于读者参考,我们在此给出证明。由于${{{{C}}}_{{{x}}}}$为实对称正定矩阵,我们可以将其表示为:
|
$\begin{aligned}
{{{{C}}}\!_{{{x}}}} =&\left[{{{{{u}}}_1}\, \, \, {{{{u}}}_2}\, \, \, \cdots \, \, \, {{{{u}}}_\nu }} \right]{\rm{diag}}\left( {{\lambda _{\, 1}}, {\lambda _{\, 2}}, \cdots, {\lambda _{\, \nu }}} \right)\\
& \cdot {\left[{{{{{u}}}_1}\, \, \, {{{{u}}}_2}\, \, \, \cdots \, \, \, {{{{u}}}_\nu }} \right]^{\rm T}} = {{{U}}}\!{{{Λ}}}\!{{{{U}}}^{\rm T}}
\end{aligned}$
|
(14) |
其中,
$\left\{ {{\lambda _{\:m}}} \right\}_{m = 1}^\nu $为实特征值,
$\left\{ {{{{{u}}}_m}} \right\}_{m = 1}^\nu $是特征矢量。函数
${\rm{diag}}\left( \cdot \right)$表示以其参数为对角元的对角阵。由此,我们可以得到
|
${ \overset{\frown} {{C}}}\!\!{_{{{x}}}} = V_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}^{ - 1}\int_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)} {{{{x}}}\, {{{{x}}}^{\rm T}}\, {p_{{{x}}}}\left( {{{x}}} \right){\rm{d}}{{{x}}}} \\
\quad \ \ = \frac{1}{{{V_{{\cal B}_{\mathbb {R}}^{\nu}\left( \tau \right)}}{{\left( {2{{\pi}} } \right)}^{\nu /2}}|{{{{C}}}\!_{{{x}}}}\, {|^{\, 1/2}}}}\!\!\!\!\!\!{\begin{array}{*{20}{c}} \\
\end{array}\int_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}\!\!\!{{{x}}}\, {{{{x}}}^{\rm T}}\\
\quad \ \ \ \ \ \cdot \exp \left( { - \frac{1}{2}{{{{x}}}^{\rm T}}{{{C}}}_{{{x}}}^{ - 1}{{{x}}}}
\right){\rm{d}}{{{x}}}\\
\ \ \;\mathop {\rm{ = }}\limits^{t{\rm{ = }}{{{{U}}}^{\rm{T}}}{{x}}} {{{U}}}\left\{ {\frac{1}{{{V_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}{{\left( {2{{\pi}} } \right)}^{\nu /2}}}}\!\!\!\!\!\!{{\begin{array}{*{20}{c}}\\
\end{array}}\int_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}}\!\! {{{t}}}\, {{{{t}}}^{\rm T}}\right.\\
\quad \ \ \ \ \ \left.\cdot {\exp \left( { - \frac{1}{2}{{{{t}}}^{\rm T}}{{{{Λ}}}^{ - 1}}{{{t}}}} \right){\rm{d}}{{{t}}}} \right\}{{{{U}}}^{\rm T}}\\
\quad \ \ = {{{U}}}{\rm{diag}}\left( {{{ \overset{\frown} \lambda}_{\, 1}}, {{ \overset{\frown} \lambda}_{\, 2}}, \cdots, {{ \overset{\frown} \lambda}_{\, \nu }}} \right){{{{U}}}^{\rm T}}
$
|
(15) |
其中
|
$\begin{aligned}
{ \overset{\frown} \lambda}\!\!{_m} \!=\!&\frac{1}{{{V_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}{{\left( {2{{\pi}} } \right)}^{\nu /2}}}}\!\!\!\!\!\!\!{\begin{array}{*{20}{c}}\\
\end{array}\int _{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}\!\!\!t_m^2 \cdot \exp \!\!\left( \!\!{ - \frac{1}{2}\sum\limits_{m = 1}^\nu {\lambda _m^{ - 1}t_m^2} }\!\! \right){\rm{d}}{{{t}}}, \\
& \quad m = 1, 2, \cdots, \nu
\end{aligned}$
|
(16) |
为
${{ \overset{\frown} {{C}}_{{x}}}}$的实特征值。
3 基于球形截断协方差矩阵的极化SAR定标方法
由于理论的协方差矩阵未知,为了构造定标方程,我们用样本协方差矩阵来估计。为了保证式(6)成立,用于估计样本协方差矩阵的所有像素所经历的失真必须相同。对于窄波束SAR系统来说,可以假设系统失真只随距离向变化而不随方位向变化[3]。因此,在实践中,对于每个距离门,一般选取与之等斜距的所有像素(即1条方位线)或者与当前距离门相邻的若干条方位线中的所有像素来估计样本协方差矩阵。需要注意,由于失真参数随距离向变化,定标过程中需要单独处理每个距离门。后续讨论中,除非特殊指明,讨论范围都限定在当前距离门处。
假设在某个待考察距离门处有L个经历了相同失真的像素,它们对应的散射矢量的观测值${\underline {{{O}}} ^\ell }$与实际值${\underline {{{S}}} ^\ell }$的关系如下:
|
$\begin{aligned}
{\underline {{{O}}} ^\ell } = Y&{{{X}}}\left( {u, v, w, z} \right){{{A}}}\left( \alpha \right){{{K}}}\left( k \right){\underline {{{S}}} ^\ell }, \qquad \\
&\ell \in {\cal L} {\rm{ = }}\left\{ {1, 2, \cdots, L} \right\}
\end{aligned}$
|
(17) |
于是样本协方差矩阵的实际值和测量值分别为:
|
${{\widehat{C}}_{\underline{S}}}={{\left( L-1 \right)}^{-1}}\sum\limits_{\ell \in \mathcal{L}}{{{\underline{S}}^{\ell }}{{\underline{S}}^{\ell \text{H}}}}\ $
|
(18) |
|
${{\widehat{C}}_{\underline{O}}}={{\left( L-1 \right)}^{-1}}\sum\limits_{\ell \in \mathcal{L}}{{{\underline{O}}^{\ell }}{{\underline{O}}^{\ell \text{H}}}}\ $
|
(19) |
通过将
${\widehat {{{C}}}\!_{\underline {{{O}}} }}$作为
${{{{C}}}\!_{\underline {{{O}}} }}$的估计值,并假设
${\widehat {{{C}}}\!_{\underline {{{S}}} }}$具有
${{{{C}}}\!_{\underline {{{S}}} }}$的形式,我们就可以用定标算法估计失真参数。然而,这样不加筛选的使用全部可用样本,最后估计得到的失真参数的不确定度会比较大(见实验结果部分)。这是由于样本集
${\cal L}$中可能存在不满足定标算法所用假设的像素(以下简称离群样本),这些像素会导致
${\widehat {{{C}}}\!_{\underline {{{S}}} }}$偏离
${{{{C}}}\!_{\underline {{{S}}} }}$形式。为了滤除离群样本以得到可靠的极化失真参数估计值,我们在常规定标算法中引入球形截断协方差矩阵。
3.1 分布式目标的球形截断协方差矩阵
对于分布式目标,其统计特性可以用零均值圆对称复高斯分布来描述[11]。圆对称复高斯分布的定义要求协方差矩阵非奇异,而${{{{C}}}\!_{\underline {{{S}}} }}$为奇异阵,所以不能直接定义散射矢量$\underline {{{S}}}$的分布。从而,我们无法直接定义其球形截断协方差矩阵。为此,我们引入矢量${{{s}}}\mathop = \limits^\Delta {{{P}}}\underline {{{S}}} = {\left[{{S_{{\rm{HH}}}}\, \, \, \sqrt 2 {S_{{\rm{VH}}}}\, \, \, {S_{{\rm{VV}}}}} \right]^{\rm T}}$,其中
|
${{{P}}}\mathop {\rm{ = }}\limits^\Delta \left[{\begin{array}{*{20}{c}}
1&0&0&0\\
0&{{{1\, } \mathord{\left/
{\vphantom {{1}\!\! {\sqrt \!\!2 }}} \right.
} {\sqrt 2 }}}&{{{1} \mathord{\left/
{\vphantom {{1\!\!} {\sqrt\!\! 2 }}} \right.
} {\sqrt 2 }}}&0\\
0&0&0&1
\end{array}} \right]$
|
(20) |
记
s的协方差矩阵为
${{{{C}}}\!_{{{s}}}}\mathop {\rm{ = }}\limits^\Delta {\rm{E}}\left\{ {{{{s}}}\, {{{{s}}}^{\rm H}}} \right\}$,易得
|
${{{{C}}}\!_{{{s}}}} = {\rm{E}}\left\{ {{{{s}}}{{{{s}}}^{\rm H}}} \right\} = {\rm{E}}\left\{ {{{{P}}}\underline {{{S}}}\;{{\underline {{{S}}} }^{\rm H}}{{{{P}}}^{\rm H}}} \right\} = {{{P}}}{{{{C}}}_{\underline {{{S}}} }}{{{{P}}}^{\rm H}}$
|
(21) |
将式(7)带入式(21)可得
|
${{{{C}}}\!_{{{s}}}} = \left[{\begin{array}{*{20}{c}}
{\sigma _{{\rm{HH}}}^{}}&0&\rho \\
0&{2\sigma _ \times ^{}}&0\\
{{\rho ^ * }}&0&{\sigma _{{\rm{VV}}}^{}}
\end{array}} \right]$
|
(22) |
因为行列式
$|{{{{C}}}\!_{{s}}}\, |\, = 2\sigma _ \times ^{}\left( {\sigma _{{\rm{HH}}}^{}\sigma _{{\rm{VV}}}^{} - {\rho ^2}} \right) > 0$,所以
${{{{C}}}\!_{{{s}}}}$非奇异。于是我们可以定义
s的概率密度函数
|
${p_{{{s}}}}\left( {{{s}}} \right) = \frac{1}{{{{{\pi}} ^\nu }|{{{{C}}}\!_{{{s}}}}\, |}}\exp \left( { - {{{{s}}}^{\rm H}}{{{C}}}\!_{{{s}}}^{ - 1}{{{s}}}} \right)$
|
(23) |
仿照实高斯分布的情况,我们定义复数空间的“球”
|
${\cal B}_{\mathbb {C}}^{\nu} \left( \tau \right) = \left\{ {{{{s}}} \in \mathbb {C}{^\nu }|{{{{s}}}^{\rm H}}{{{s}}}\le \tau } \right\}$
|
(24) |
以及
s在
${\cal B}_{\mathbb {C}}^{\nu} \left( \tau \right)$内截断的概率密度函数
|
$\begin{array}{l}
{p_{{{{s}}}|{{{s}}}\, \in \, {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}\left( {{{s}}} \right) = \left\{\!\! \begin{array}{l}
{{{p_{{{s}}}}\left( {{{s}}} \right)} \mathord{\left/
{\vphantom {{{p_{{{s}}}}\left( {{{s}}} \right)} {{V_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}}}} \right.
} {{V_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}}}, \quad {{{s}}} \in {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right);\\
0, \quad \quad \quad \quad \quad \quad {{{s}}} \notin {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right),
\end{array} \right.\\
\quad \quad \quad \quad \quad \quad \quad \ \ {V_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}} = {\rm{P}}\left[{{{{s}}} \in {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)} \right]
\end{array}$
|
(25) |
利用式(25)可以定义复圆高斯矢量
s的球形截断分布的1阶、2阶原点矩
|
${ \overset{\frown} {{μ}} }\!\!{_{{{s}}}}\mathop {\rm{ = }}\limits^\Delta {\rm{E}}\left\{ {{{{s}}}|{{{s}}} \in {\cal B}_{\mathbb {C}}^{\nu} \left( \tau \right)} \right\} \quad \ $
|
(26) |
|
${ \overset{\frown} {{C}} }\!\!{_{{{s}}}}\mathop {\rm{ = }}\limits^\Delta {\rm{E}}\left\{ {{{{s}}}\, {{{{s}}}^{\rm H}}|{{{s}}} \in {\cal B}_{\mathbb {C}}^{\nu} \left( \tau \right)} \right\}$
|
(27) |
在附录B中我们将证明
${{ \overset{\frown} {{C}}}\!\!_{{{s}}}}$就是协方差矩阵(等价于证明
${ \overset{\frown} {{μ}}\!\!_{{{s}}} } \equiv {{{0}}}$),并且
${{ \overset{\frown} {{C}}}\!\!_{{{s}}}}$与
${{{{C}}}\!_{{{s}}}}$有相同的特征矢量。
利用s的截断分布,我们可以定义$\underline {{{S}}}$的截断协方差矩阵
|
${{ \overset{\frown} {{C}}}\!\!_{\underline {{{S}}} }}\mathop {\rm{ = }}\limits^\Delta {\rm{E}}\left\{ {\underline {{{S}}} {{\underline {{{S}}} }^{\rm H}}|{{{s}}} \in {\cal B}_{\mathbb {C}}^{\nu} \left( \tau \right)} \right\}$
|
(28) |
容易验证,
${{ \overset{\frown} {{C}}}\!\!_{{{S}}}}$与
${{{{C}}}_{{{s}}}}$有下面的对应关系:
|
${{ \overset{\frown} {{C}}}\!\!_{\underline {{{S}}} }} = {{{{P}}}^{\rm H}}{{ \overset{\frown} {{C}}}\!\!_{{{s}}}}{{{P}}}$
|
(29) |
3.2 基于球形截断协方差矩阵的定标方法
由于定标算法要求${{{{C}}}\!_{\underline {{{S}}} }}$具有式(7)的形式,我们考察截断后${{ \overset{\frown} {{C}}}\!\!_{\underline {{{S}}} }}$的形式。由文献[12],协方差矩阵Cs的3个特征矢量有如下解析形式:
|
$\left. \begin{aligned}
{{{{v}}}_{\, 1}}&= \frac{1}{{1 + |\, a{|^2}}}\left[{\begin{array}{*{20}{c}}
a\\
{\, 0\, }\\
1
\end{array}} \right]\\
\quad {{{{v}}}_{\, 2}}&= \frac{1}{{1 + |b{|^2}}}\left[{\begin{array}{*{20}{c}}
b\\
{\, 0\, }\\
1
\end{array}} \right]\quad \\
{{{{v}}}_{\, 3}}&= \left[{\begin{array}{*{20}{c}}
{\, 0\, }\\
1\\
{\, 0\, }
\end{array}} \right]
\end{aligned} \right\}$
|
(30) |
其中
|
$ \begin{aligned}
&a = \frac{{2\rho }}{{{\sigma _{{\rm{VV}}}} - {\sigma _{{\rm{HH}}}} + \sqrt {{Δ}} }}, \\
&b = \frac{{2\rho }}{{{\sigma _{{\rm{VV}}}}- {\sigma _{{\rm{HH}}}} - \sqrt {{Δ}}, }}\\
&{{Δ}}= {\left( {\sigma _{VV}^{} - {\sigma _{{\rm{HH}}}}} \right)^2} + 4{\rho ^2} \quad \quad
\end{aligned}$
|
(31) |
从前面的讨论可知
v1,
v2和
v3也是
${ \overset{\frown} {{C}}}\!\!{_{{{s}}}}$的特征矢量。假设
v1,
v2和
v3分别对应特征值
${ \overset{\frown} \lambda }\!\!{_{\, 1}}$,
${ \overset{\frown} \lambda }\!\!{_{\, 2}}$和
${ \overset{\frown} \lambda }\!\!{_{\, 3}}$,则利用Hermitian矩阵的谱表示可以得到
|
$\begin{array}
&{{ \overset{\frown} {{C}}}_{{{s}}}} \; = {{ \overset{\frown} \lambda }_{\, 1}}{{{{v}}}_1}{{{v}}}_1^{\rm H} + {{ \overset{\frown} \lambda }_{\, 2}}{{{{v}}}_2}{{{v}}}_2^{\rm H} + {{ \overset{\frown} \lambda }_{\, 3}}{{{{v}}}_3}{{{v}}}_3^{\rm H}\\
= \frac{{{{ \overset{\frown} \lambda }_{\, 1}}}}{{1 + |\, a{|^2}}}\left[{\begin{array}{*{20}{c}}
{|\, a{|^2}}&0&a\\
0&0&0\\
{{a^ * }}&0&1
\end{array}} \right] \\
\ \ \, + \frac{{{{ \overset{\frown} \lambda }_{\, 2}}}}{{1 + |b{|^2}}}\left[{\begin{array}{*{20}{c}}
{|\, b{|^2}}&0&b\\
0&0&0\\
{{b^ * }}&0&1
\end{array}} \right] \ \\
+ {{ \overset{\frown} \lambda }_{\, 3}}\left[{\begin{array}{*{20}{c}}
0&0&0\\
0&1&0\\
0&0&0
\end{array}} \right] \quad \quad \ \\
= \left[{\begin{array}{*{20}{c}}
{{ \overset{\frown} \sigma}_{{\rm{HH}}}^{}}&0&{\overset{\frown} \rho}\\
0&2\!{{\overset{\frown} \sigma} _x} \!\!&0\\
{{{\overset{\frown} \rho}^ * }}&0&{{ \overset{\frown} \sigma}_{{\rm{VV}}}^{}} \quad
\end{array}} \right]
\end{array}$
|
(32) |
通过将式(32)代入式(29),易得
${{\overset{\frown} {{C}}}\!\!\!_{\underline {{{S}}} }}$具有式(7)的形式。因此,球形截断后,
${{\overset{\frown} {{C}}}\!\!\!_{\underline {{{S}}} }}$依然满足定标算法的要求。
下面将球形截断协方差矩阵引入极化定标算法。首先,我们定义球形截断样本协方差矩阵的观测值和实际值
|
${{\widehat{\overset{\frown }{\mathop{C}}\,}}_{\underline{O}}}={{\left( M-1 \right)}^{-1}}\sum\limits_{\ell \in \mathcal{L}}{{{\prod }_{B_{\mathbb{C}}^{\nu }\left( \tau \right)}}}\left( P{{\underline{S}}^{\ell }} \right){{\underline{O}}^{\ell }}{{\underline{O}}^{\ell \text{H}}}$
|
(33) |
|
${{\widehat{\overset{\frown }{\mathop{C}}\,}}_{\underline{S}}}={{\left( M-1 \right)}^{-1}}\sum\limits_{\ell \in \mathcal{L}}{{{\prod }_{B_{\mathbb{C}}^{\nu }\left( \tau \right)}}}\left( P{{\underline{S}}^{\ell }} \right){{\underline{S}}^{\ell }}{{\underline{S}}^{\ell \text{H}}}$
|
(34) |
其中
|
${{{Π}} _{{\cal B}_{\mathbb {C}}^{\nu} \left( \tau \right)}}\left( {{{{P}}}{{\underline {{{S}}} }^\ell }} \right) = \left\{\!\! {\begin{array}{*{20}{c}}
{1, }&{{{{P}}}{{\underline {{{S}}} }^\ell } \in {\cal B}_{\mathbb {C}}^{\nu} \left( \tau \right)} \quad \ \;\\
{0, }&{{{{P}}}{{\underline {{{S}}} }^\ell } \notin {\cal B}_{\mathbb {C}}^{\nu} \left( \tau \right)} \quad \quad
\end{array}} \right.$
|
(35) |
|
$M = \sum\limits_{\ell \in {\cal L}} {{{{Π}} _{{\cal B}_{\mathbb {C}}^{\nu} \left( \tau \right)}}\left( {{{{P}}}{{\underline {{{S}}} }^\ell }} \right)} \quad \quad \quad \quad \quad \quad \quad \ \quad \ $
|
(36) |
因为
${\widehat {\overset{\frown} {{C}}}_{\underline {{{S}}} }}$是球形截断协方差矩阵
${{\overset{\frown} {{C}}}_{\underline {{{S}}} }}$的估计,所以我们可以认为其具有式(7)的形式。于是,将
${\widehat {\overset{\frown} {{C}}}_{\underline {{{O}}} }}$作为
${{{{C}}}\!_{\underline {{{O}}} }}$的估计值,我们就能得到失真参数的估计值。
实际处理中,${\underline {{{S}}} ^\ell }$未知。为了利用式(33)计算${\widehat {\overset{\frown} {{C}}}_{\underline {{{O}}} }}$,我们尚需估计示性函数${{{Π}} _{{\cal B}_{\mathbb {C}}^{\nu} \left( \tau \right)}}\left( {{{{P}}}{{\underline {{{S}}} }^\ell }} \right)$。根据文献[4],当串扰比较小时有
|
$\begin{align}
& ||{{\underline{O}}^{\ell }}|{{|}^{2}}\approx |Y{{|}^{2}}(|k{{|}^{4}}|\alpha {{|}^{2}}|S_{\text{HH}}^{\ell }{{|}^{2}}+|k{{|}^{2}}|\alpha {{|}^{2}}\cdot |S_{\text{VH}}^{\ell }{{|}^{2}} \\
& +|k{{|}^{2}}|S_{\text{HV}}^{\ell }{{|}^{2}}+|S_{\text{VV}}^{\ell }{{|}^{2}}) \\
\end{align}$
|
(37) |
另外,由于|
k|和|\[\alpha \]|的数值都接近1,式(37)可以进一步近似为
|
$\begin{aligned}
|\!|{\underline {{{O}}} ^\ell }|\!|{^2}&\!\approx\!\! \, \, |Y\, \, |{^2}\Big( {|S_{{\rm{HH}}}^\ell{|^2} \!\!+\!\! |S_{{\rm{VH}}}^\ell {|^2} \!\!+\!\! |S_{{\rm{HV}}}^\ell {|^2} \!\!+\!\! |S_{{\rm{VV}}}^\ell {|^2}} \Big)\\
&= \!|Y\, \, |{^2}|\!|\, {{{P}}}{\underline {{{S}}} ^\ell }\, |\!|{^2}
\end{aligned}$
|
(38) |
因此,我们可以近似地用
${{{Π}} _{{\cal B}_{\mathbb {C}}^{\nu} \left( \eta \right)}}\left( {{{\underline {{{O}} } }^\ell }} \right)$来估计
${{{Π}} _{{\cal B}_{\mathbb {C}}^{\nu} \left( \tau \right)}}\left( {{{{P}} }{{\underline {{{S}} } }^\ell }} \right)$。即,我们可以用
|
${{\widehat{\overset{\frown }{\mathop{C}}\,}}_{\underline{O}}}\approx {{\left( {{M}^{\prime }}-1 \right)}^{-1}}\sum\limits_{\ell \in \mathcal{L}}{\prod }\text{ }\left( {{\underline{O}}^{\ell }}\in B_{\mathbb{C}}^{\nu }\left( \eta \right) \right){{\underline{O}}^{\ell }}{{\underline{O}}^{\ell \text{H}}}$
|
(39) |
来计算
${\widehat {\overset{\frown} {{C}}}\!_{\underline {{{O}}} }}$,其中
|
$M^\prime =\sum\limits_{\ell \in {\cal L}} {{Π}} {\left( {{{\underline {{{O}}} }^\ell } \in {\cal B}_{\mathbb {C}}^{\nu} \left( \eta \right)} \right)}$
|
(40) |
从式(39)可以看出,我们仍需给出选择合适的阈值作球半径的方法。由于在绝对定标工作尚未完成前|
Y|是未知的,
$|\!|{\underline {{{O}}} ^\ell }|\!|{^2}$的具体数值并不具备明确的物理意义。为了避免直接用具体的阈值做半径,本文采用
$|\!|{\underline {{{O}}} ^\ell }|\!|{^2}$的经验累积分布的分位数来间接地进行截断操作。定义
$|\!|{\underline {{{O}}} ^\ell }|\!|{^2}$的经验累积分布如下
|
$ F\left( \eta \right) \!=\! F\left(\! {|\!|{{\underline {{{O}} } }^\ell }|\!|{^2}\!≤\eta } \!\right)\\
\quad \quad \ \mathop = \limits^\Delta \left\{ \!\!\!\!\begin{array}{l}
0, \quad \quad \ \eta < {\min _\ell }|\!|{\underline {{{O}}} ^\ell }|\!|{^2}\\
{{M^\prime } \mathord{\left/
{\vphantom {{M^\prime } L}} \right.
} L}, \ {\min _\ell }|\!|{\underline {{{O}}} ^\ell }|\!|{^2}\!≤\!\eta\!≤\! {\max _\ell }|\!|{\underline {{{O}}} ^\ell }|\!|{^2}\\
1, \quad \quad \ \eta \, > {\max _\ell }|\!|{\underline {{{O}}} ^\ell }|\!|{^2}
\end{array} \right.$
|
(41) |
而其\[\beta \]-上分位数
${\eta _\beta }$则可以表示为:
|
$F\left( {{\eta _\beta }} \right) = 100\left( {1 - \beta } \right)\%, \quad \quad \beta \in \left[{0, \, \, 1} \right]$
|
(42) |
我们可以通过选取不同的\[\beta \],并利用
${\eta _\beta } = {F^{ - 1}}\left( {1 - \beta } \right)$得到其对应的阈值
${\eta _\beta }$。这样,我们可以用式(39)来估计
${\widehat {\overset{\frown} {{C}}}_{\underline {{{O}}} }}$。
假设待估计的参数为x(x可以是u, v, w, z和\[\alpha \]中的任意一个),并记此时x的估计值为$\hat x\left( \beta \right)$。为了评价失真参数估计的稳健性,我们可以用Bootstrap的方法[13]来估计失真参数的标准误差${\rm{SE}}\left[{\hat x\left( \beta \right)} \right]$。当\[\beta \]增大时,${\eta _\beta }$会变小,截断样本协方差矩阵也会逐渐趋于稳定。相应地,标准误差${\rm{SE}}\left[{\hat x\left( \beta \right)} \right]$也会随着\[\beta \]的增大而渐进地趋于零。然而,当\[\beta \]取值过大时,阈值${\eta _\beta }$会过小,这一方面会造成样本数量不足,另一方面会导致截取出的样本集中信噪比低的像素的比例增多。这两方面因素都会导致定标算法的精度的下降[3]。作为折衷,我们定义最优的\[\beta \]如下:
|
${\beta _{{\rm{opt}}}} = \mathop {\min }\limits_{\beta \in {[0, {\beta _{\rm max}}]}} {\rm{SE}}\left[{\hat x\left( \beta \right)} \right]≤{\rm{S}}{{\rm{E}}_{{\rm{tol}}}}\, $
|
(43) |
当\[\beta \]=\[\beta \]
opt时,我们既有效地降低失真参数估计的不确定度,又保障定标算法的精度。如果将此时的失真参数估计用于极化定标,就能得到比较可靠的定标结果。注意,为了防止样本过小,我们人为地限定了
${\beta _{\rm \max }} = 0.2$。
综上,我们将基于球形截断协方差矩阵的定标算法流程总结在表 1中。
表 1(Tab. 1)
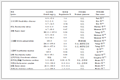
表 1 基于球形截断协方差矩阵的极化定标算法流程Tab. 1Algorithm for Polarimetric Calibration Using Spherically Truncated Covariance Matrix
| 输入: 像素集合$\left\{ {{{\underline {{{O}}} }^\ell }|\ell \in {\cal L} {\rm{ = }}\left\{ {1,2, \cdots ,L} \right\}} \right\}$
|
| 输出: \[\beta \]opt及失真参数估计值$\hat x\left( {{\beta _{{\rm{opt}}}}} \right)$ |
初始化: \[\beta \]=0, \[\delta \]\[\beta \]=1/L, \[\beta \]max=0.2, SEtol=0.0165,
根据式(41)计算$F\left( \eta \right)$ |
| $ {\rm{left = 0,right}} = \left\lceil {{\beta _{\max }}/\delta \beta } \right\rceil $ |
| ${\rm{WHILE}}\left( {{\rm{left}} < {\rm{right}}} \right)$ |
| ${\rm{middle}} = 0.5\left( {{\rm{left}} + {\rm{right}}} \right),\beta = {\rm{middle}} \times \delta \beta $ |
| 计算阈值${\eta _\beta } = {F^{ - 1}}\left( {1 - \beta } \right)$ |
| 利用(39)计算球形截断样本协方差矩阵${\widehat {\overset{\frown} C}_{\underline {{{O}}} }}$ |
| 利用定标算法(见附录${{Euclid}{A}}$)估计失真参数$\hat x\left( \beta \right)$ |
| 利用Bootstrap方法估计失真参数标准误差${\rm{SE}}\left[ {\hat x\left( \beta \right)} \right]$ |
| ${\rm{IF}}\left( {{\rm{SE}}\left[ {\hat x\left( \beta \right)} \right]≤{\rm{S}}{{\rm{E}}_{{\rm{tol}}}}} \right)$ |
| right=middle–1 |
| ELSE |
| left=middle+1 |
| END IF |
| END WHILE |
| ${\beta _{{\rm{opt}}}} = \beta, \ \hat x = \hat x\left( {{\beta _{{\rm{opt}}}}} \right)$ |
|
表 1 基于球形截断协方差矩阵的极化定标算法流程
Tab.1 Algorithm for Polarimetric Calibration Using Spherically Truncated Covariance Matrix |
4 实验结果及分析
图 1为中国科学院电子学研究所的机载P波段全极化SAR系统于2010年11月采集的山西长治地区的全极化图像。该图像尺寸为2028×1024,距离向和方位向分辨率都为1.2 m。场景内容包括自然地物、人造建筑物以及若干人造点目标。平台移动方向为从左到右,近距为图像下侧。本文利用该数据来验证所提方法。
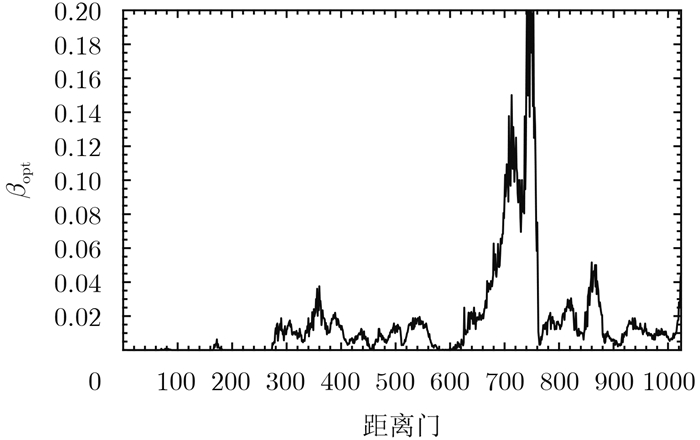
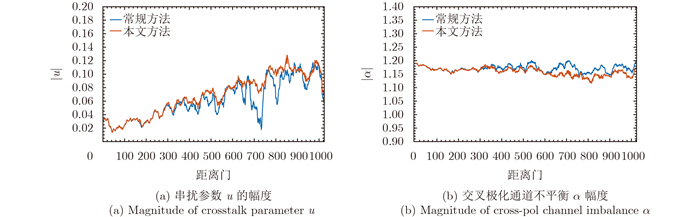
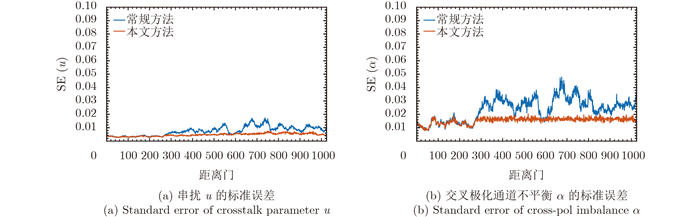
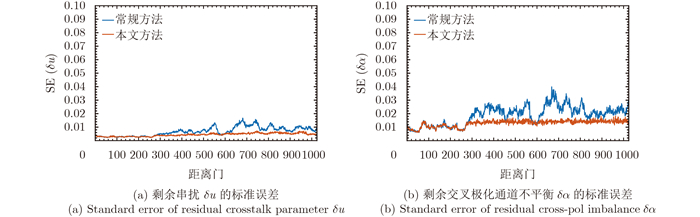
去除同极化交叉极化相关系数大于0.5的像素和总功率最大的10%的像素,我们得到如图 2所示的全局掩模。本文将仅以该掩模筛选样本的定标方法用于对照,后文简称其为常规方法。在全局掩模的基础上,我们再利用截断协方差矩阵的方法筛选样本。取SEtol=0.0165并利用表 1中的算法估计\[\beta \]opt。图 3给出\[\beta \]opt的估计结果,从中可以看出,只有少部分距离门处\[\beta \]opt为0,这表明在大部分距离门处,截断协方差矩阵方法都可以降低失真参数的标准误差。图 4比较了常规方法和本文方法估计的失真参数结果。从图 4可以看出,常规方法和本文方法的差异比较显著。然而,仅凭图 4并不能判断两种方法孰优孰劣。图 5给出了这两种方法得到的失真参数估计的标准误差。从图 5则可以明显的看出本文方法所估计的失真参数标准误差更小。因此,本文方法提高了极化定标的稳健性。注意,本文只给出了串扰u的结果,其它串扰参数的实验结果与之类似。
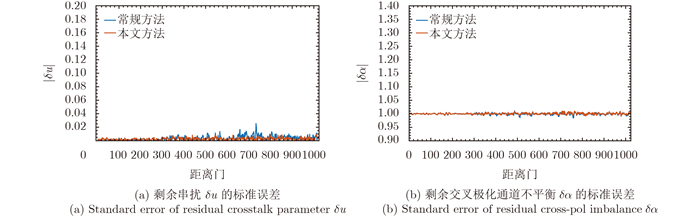
最后,为了验证定标方法的精度,我们在图 6和图 7给出了常规方法和本文方法定标完成后的剩余极化失真的估计值及相应的标准误差。从图 6可以看出,两种方法,定标完的剩余失真都比较小。然而,从图 7可以看出,本文方法剩余失真的标准误差更小。另外,注意到图 5和图 7很差异甚小,这说明无论选用哪种方法得到的失真参数估计来定标,都不能减小失真参数的不确定度。因此,为了降低失真参数的不确定度,我们必须在估计失真参数时对样本进行筛选。
5 总结
本文在传统极化定标算法的实践中引入了球形截断协方差矩阵,并从理论上证明了球形截断不会导致极化SAR定标所依赖的假设不成立。实际机载极化SAR的定标实验结果表明,利用球形截断协方差矩阵估计的失真参数有效地降低了失真参数估计的标准误差。因此,基于球形截断协方差矩阵的极化SAR定标方法是一个稳健的定标方法。
附录A
本节给出了用观测的平均协方差矩阵来估计失真参数的具体细节[6]。注意,与文献[6]不同,本文沿用文献[4]中失真参数的定义及符号。令
|
${{{W}}} = {\left| {Y{Y_0}} \right|^2}{{{A}}}\left( \alpha \right){{{K}}}\left( k \right){{{{C}}}_{\underline {{{S}}} }}{{{{K}}}^{\rm H}}\left( k \right){{{{A}}}^{\rm H}}\left( \alpha \right)$
|
(A-1) |
其中,
${Y_0}\mathop {\rm{ = }}\limits^\Delta \left( {1 - uw} \right)\left( {1 - vz} \right)$。式(7)代入式(A-1),我们有
|
$\left.\begin{array}{l}
{W_{11}} = \:|{Y_0}Y\;{|^{\:2}}|k{|^{\:4}}|\alpha {|^{\:2}}{\sigma _{11}}\\
{W_{14}} = \:|{Y_0}Y\;{|^{\:2}}\alpha {k^2}\rho \\
{W_{44}} = \:|{Y_0}Y\;{|^{\:2}}{\sigma _{44}}\\
{W_{22}} = \:|{Y_0}Y\;{|^{\:2}}|k{|^{\:2}}{\sigma _ \times }|\alpha {|^{\:2}}\\
{W_{33}} = \:|{Y_0}Y\;{|^{\:2}}|k{|^{\:2}}{\sigma _ \times }\\
{W_{23}} = \:|{Y_0}Y\;{|^{\:2}}|k{|^{\:2}}{\sigma _ \times }\:\alpha
\end{array}\right\}$
|
(A-2) |
和
|
${W_{21}} = 0, \quad {W_{31}} = 0, \quad {W_{24}} = 0, \quad {W_{34}} = 0$
|
(A-3) |
另一方面,根据式(6),对${{{{C}}}\!_{\underline {{{O}}} }}$左乘$\widetilde {{{X}}}\left( {u, v, w, z} \right)$(其定义在式(4)中)和右乘${\widetilde {{{X}}}^{\rm{H}} }\left( {u, v, w, z} \right)$,我们可得W的估计
|
${{{W}}} = \widetilde {{{X}}}\left( {u, v, w, z} \right){{{{C}}}\!_{\underline {{{O}}} }}{\widetilde {{{X}}}^{\rm{H}} }\left( {u, v, w, z} \right)$
|
(A-4) |
推导中用到了等式
$\widetilde {{{X}}}\left( {u, v, w, z} \right){{{X}}}\left( {u, v, w, z} \right) = {Y_0}$。将式(A-4)展开可得
|
$\begin{array}{*{35}{l}}
{{W}_{21}} & =\;\,{{C}_{21}}-v{{C}_{41}}-{{v}^{*}}{{C}_{23}}-u{{C}_{11}}-{{w}^{*}}{{C}_{22}} \\
{} & \;\;+u{{w}^{*}}{{C}_{12}}+u{{v}^{*}}{{C}_{13}}+uv{{C}_{31}}+{{v}^{*}}{{w}^{*}}{{C}_{24}}+v{{w}^{*}}{{C}_{42}}+|v{{|}^{\,2}}{{C}_{43}} \\
{} & \;-u{{v}^{*}}{{w}^{*}}{{C}_{14}}-uv{{w}^{*}}{{C}_{32}}-u|v{{|}^{\,2}}{{C}_{33}}-{{w}^{*}}|v{{|}^{\,2}}{{C}_{44}}+u{{w}^{*}}|v{{|}^{\,2}}{{C}_{34}} \\
{{W}_{31}} & =\;\,{{C}_{31}}-w{{C}_{41}}-{{w}^{*}}{{C}_{32}}-z{{C}_{11}}-{{v}^{*}}{{C}_{33}} \\
{} & \;\;+z{{v}^{*}}{{C}_{13}}+z{{w}^{*}}{{C}_{12}}+zw{{C}_{21}}+{{v}^{*}}{{w}^{*}}{{C}_{34}}+{{v}^{*}}w{{C}_{43}}+|w{{|}^{\,2}}{{C}_{42}} \\
{} & \;\;-z{{w}^{*}}{{v}^{*}}{{C}_{14}}-zw{{v}^{*}}{{C}_{23}}-z|w{{|}^{\,2}}{{C}_{22}}-{{v}^{*}}|w{{|}^{\,2}}{{C}_{44}}+z{{v}^{*}}|w{{|}^{\,2}}{{C}_{24}} \\
{{W}_{24}} & =\;\,{{C}_{24}}-u{{C}_{14}}-{{u}^{*}}{{C}_{23}}-{{z}^{*}}{{C}_{22}}-v{{C}_{44}} \\
{} & \;\;+v{{z}^{*}}{{C}_{42}}+u{{z}^{*}}{{C}_{12}}+{{u}^{*}}{{z}^{*}}{{C}_{21}}+uv{{C}_{34}}+{{u}^{*}}v{{C}_{43}}+|u{{|}^{\,2}}{{C}_{13}} \\
{} & \;\;-v{{u}^{*}}{{z}^{*}}{{C}_{41}}-vu{{z}^{*}}{{C}_{32}}-{{z}^{*}}|u{{|}^{\,2}}{{C}_{11}}-v|u{{|}^{\,2}}{{C}_{33}}+v{{z}^{*}}|u{{|}^{\,2}}{{C}_{31}} \\
{{W}_{34}} & =\;\,{{C}_{34}}-z{{C}_{14}}-{{z}^{*}}{{C}_{32}}-{{u}^{*}}{{C}_{33}}-w{{C}_{44}} \\
{} & \;\;+w{{u}^{*}}{{C}_{43}}+z{{u}^{*}}{{C}_{13}}+{{z}^{*}}{{u}^{*}}{{C}_{31}}+wz{{C}_{24}}+w{{z}^{*}}{{C}_{42}}+|z{{|}^{\,2}}{{C}_{12}} \\
{} & \;\;-w{{z}^{*}}{{u}^{*}}{{C}_{41}}-wz{{u}^{*}}{{C}_{23}}-{{u}^{*}}|z{{|}^{\,2}}{{C}_{11}}-w|z{{|}^{\,2}}{{C}_{22}}+w{{u}^{*}}|z{{|}^{\,2}}{{C}_{21}} \\
\end{array}$
|
|
$\begin{array}{*{20}{l}}
{W_{34}}&\!\!\!\!=\!{C_{34}} \!-\! z{C_{14}} \!-\! {z^*}{C_{32}} \!-\! {u^*}{C_{33}} \!-\! w{C_{44}}\\
&+\! w{u^*}{C_{43}} \!+\! z{u^*}{C_{13}} \!+\! {z^*}{u^*}{C_{31}} \!+\! wz{C_{24}}\\
&+\! w{z^*}{C_{42}} \!+\! |z{|^{\, 2}}{C_{12}}\:\: \!-\! w{z^*}{u^*}{C_{41}} \!-\! wz{u^*}{C_{23}}\\
&-\! {u^*}|z{|^{\, 2}}{C_{11}} \!-\! w|z{|^{\, 2}}{C_{22}} \!+\! w{u^*}|z{|^{\, 2}}{C_{21}}
\end{array} $
|
(A-5) |
注意,这里为了简化记号,
Cij表示矩阵
${{{{C}}}\!_{\underline {{{O}}} }}$的第
i行、第
j列的元素。联立式(A-3)和式(A-5)可以建立以下的非线性方程组:
|
${{{f}}}\left( {{{x}}} \right) = {{0}} $
|
(A-6) |
其中
|
$\begin{aligned}
{{{x}}} =&\left[{{\mathop{\rm Re}\nolimits} \left( u \right), {\mathop{\rm Re}\nolimits} \left( v \right), {\mathop{\rm Re}\nolimits} \left( w \right), {\mathop{\rm Re}\nolimits} \left( z \right), } \right.\\
& \ {\left. {{\rm{Im}}\left( u \right), {\rm{Im}}\left( v \right), {\rm{Im}}\left( w \right), {\rm{Im}}\left( z \right)} \right]^{\rm{T}}}
\end{aligned} \quad \ \ $
|
(A-7) |
|
$\begin{aligned}
{{{f}}}({{{x}}})\! =\!&\left[{{\rm{Re}}({W_{21}}), {\rm{Re}}({W_{31}}), {\rm{Re}}({W_{24}}), {\rm{Re}}({W_{34}}), } \right.\\
&\ \ {\left. {{\rm{Im}}({W_{21}}), {\rm{Im}}({W_{31}}), {\rm{Im}}({W_{24}}), {\rm{Im}}({W_{34}})} \right]^{\rm{T}}}
\end{aligned}$
|
(A-8) |
利用Newton迭代法求解式(A-6),即可得串扰的估计值。利用式(A-4)矫正串扰,可以得到
W。这样,由式(A-2)可得
|
$\alpha = \sqrt {{W_{22}}/{W_{33}}} \cdot \exp \left\{ {{\rm j}{\rm{Arg}}\left( {{W_{23}}} \right)} \right\}$
|
(A-9) |
感兴趣的读者可能注意到,除了失真参数的定义有区别外,这里给出的算法细节与原始文献[
6]中算法仍然有差别。在文献[
6]中,串扰的估计和通道不平衡的估计杂糅在一起,迭代过程中的参数更新也很复杂。并且,文献[
6]的作者虽然声称需要更新\[\alpha \],但是并未给出其更新的方法。本文将串扰的估计和通道不平衡的估计分成两个独立的步骤,这将极大地简化算法实现。另外,文献[
6]中的方法估计得到的部分失真参数并不与其定义相对应(差了一个比例因子)
[14],而本文的方法所估计的失真参数直接对应了其定义。
附录B
此处,我们将证明${{\overset{\frown} {{C}}}\!\!_{{{s}}}}$就是协方差矩阵,并且${{\overset{\frown} {{C}}}\!\!_{{{s}}}}$与${ {{C}}}\!_{{{s}}}$有相同的特征矢量。由于这个结论对任意服从圆对称零均值复高斯分布的随机矢量都成立,我们对一个任意的服从圆对称零均值复高斯分布的随机矢量证明以上结论。不妨假设复矢量${{{z}} } = {\left[{{z_1}\, \, \, {z_2}\, \, \, \cdots \, \, \, {z_\nu }} \right]^{\rm T}}$服从$\nu $维零均值复圆高斯分布,即
|
${p_{{{z}}}}\left( {{{z}}} \right) = \frac{1}{{{{{\pi}} ^\nu }|{{{{C}}}_{{{z}}}}\, |}}\exp \left( { - {{{{z}}}^{\rm H}}{{{C}}}\!_{{{z}}}^{ - 1}{{{z}}}} \right)$
|
(B-1) |
其中,
${{{{C}}}\!_{{{z}}}} = {\rm{E}}\left\{ {{{{z}}}{{{{z}}}^{\rm H}}} \right\}$为
z的协方差矩阵,而圆对称性则要求下面两式成立:
|
${\rm{E}}\left\{ {{\mathop{\rm Re}\nolimits} \left\{ {{{z}}} \right\}{\mathop{\rm Re}\nolimits} \left\{ {{{{{z}}}^{\rm H}}} \right\}} \right\} = {\rm{E}}\left\{ {{\mathop{\rm Im}\nolimits} \left\{ {{{z}}} \right\}{\mathop{\rm Im}\nolimits} \left\{ {{{{{z}}}^{\rm H}}} \right\}} \right\} \quad \quad \quad \quad $
|
(B-2) |
|
${\rm{E}}\left\{ {{\mathop{\rm Im}\nolimits} \left\{ {{{z}}} \right\}{\mathop{\rm Re}\nolimits} \left\{ {{{{{z}}}^{\rm H}}} \right\}} \right\} = - {\rm{E}}\left\{ {{\mathop{\rm Re}\nolimits} \left\{ {{{z}}} \right\}{\mathop{\rm Im}\nolimits} \left\{ {{{{{z}}}^{\rm H}}} \right\}} \right\}$
|
(B-3) |
仿照实高斯分布的情况,我们定义
$\nu $维复数空间的“球”
|
${\cal B}_{\mathbb {C}}^{\nu} \left( \tau \right) = \left\{ {{{{z}}} \in \mathbb {C}{^\nu }|{{{{z}}}^{\rm H}}{{{z}}}\le\tau } \right\}$
|
(B-4) |
以及
z在
${\cal B}_{\mathbb {C}}^{\nu}
\left( \tau \right)$内截断的概率密度函数
|
$\begin{array}{l}
{p_{{{{z}}}|{{{z}}}\, \in \, {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}\left( {{{z}}} \right) = \left\{ \begin{array}{l}
{{{p_{{{z}}}}\left( {{{z}}} \right)} \mathord{\left/
{\vphantom {{{p_{{{z}}}}\left( {{{z}}} \right)} {{V_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}}}} \right.
} {{V_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}}}, \quad {{{z}}} \in {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right);\\
0, \quad \quad \quad \quad \quad \quad {{{z}}}\notin {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right),
\end{array} \right.\\
\quad \quad \quad \quad \quad \quad \quad \quad {V_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}} = {\rm{P}}\left[{{{{z}}} \in {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)} \right]
\end{array}$
|
(B-5) |
利用式(B-5)我们可以定义球形截断复圆高斯分布的1阶和2阶原点矩
|
${{\overset{\frown} {{μ}}}_{{{z}}}}\mathop {\rm{ = }}\limits^\Delta {\rm{E}}\left\{ {{{{z}}}|{{{z}}} \in {\cal B}_{\mathbb {C}}^{\nu} \left( \tau \right)} \right\} \quad \ $
|
(B-6) |
|
${{\overset{\frown} {{C}}}_{{{z}}}} \mathop {\rm{ = }}\limits^\Delta {\rm{E}}\left\{ {{{{z}}}\, {{{{z}}}^{\rm H}}|{{{z}}} \in {\cal B}_{\mathbb {C}}^{\nu} \left( \tau \right)} \right\}$
|
(B-7) |
式(B-1)有如下等价的实数形式
[15]:
|
${p_{{{z}}}}\left( {{{z}}} \right) \!\!=\!\! {p_{{{y}}}}\!\left( {{{y}}} \right)\!\! =\!\! \frac{1}{{{{\left( {2{{\pi}} } \right)}^\nu }|{{{{C}}}_{{{y}}}}\, {|^{\, 1/2}}}}\exp\!\! \left( \!\!{ \!-\! \frac{1}{2}{{{{y}}}^{\rm T}}\!{{{C}}}\!_{{{y}}}^{ - 1}{{{y}}}} \!\!\right)$
|
(B-8) |
其中
|
$\begin{aligned}
{{{y}}} =&\left[{{\mathop{\rm Re}\nolimits} \{ {z_1}\}, {\mathop{\rm Re}\nolimits} \{ {z_2}\}, \cdots, {\mathop{\rm Re}\nolimits} \{ {z_\nu }\}, } \right.\\
&\ {\left. {{\mathop{\rm Im}\nolimits} \{ {z_1}\}, {\mathop{\rm Im}\nolimits} \{ {z_2}\}, \cdots, {\mathop{\rm Im}\nolimits} \{ {z_\nu }\} } \right]^{\rm T}}
\end{aligned} \quad $
|
(B-9) |
|
${{{{C}}}_{{{y}}}} = \frac{1}{2}\left[{\begin{array}{*{20}{r}}
{{\mathop{\rm Re}\nolimits} \left\{ {{{{{C}}}_{{{z}}}}} \right\}}&{-{\mathop{\rm Im}\nolimits} \left\{ {{{{{C}}}_{{{z}}}}} \right\}}\\
{{\mathop{\rm Im}\nolimits} \left\{ {{{{{C}}}_{{{z}}}}} \right\}}&{{\mathop{\rm Re}\nolimits} \left\{ {{{{{C}}}_{{{z}}}}} \right\}}
\end{array}} \right]$
|
(B-10) |
另外,复数空间的球
${\cal B}_{\mathbb {C}}^{\nu} \left( \tau \right)$也等价于实欧式空间的球
${\cal B}_{\mathbb {R}}^{2\nu}\left( \tau \right) = \left\{ {{{{y}}} \in \mathbb {R} {^{2\nu }}|{{{{y}}}^{\rm T}}{{{y}}} ≤ \tau } \right\}$。因此,式(B-5)也有等价的实数形式:
|
$\begin{array}{l}
{p_{{{{y}}}|{{{y}}}\, \in \, {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}\left( {{{y}}} \right) = \left\{ \begin{array}{l}
{{{p_{{{y}}}}\left( {{{y}}} \right)} \mathord{\left/
{\vphantom {{{p_{{{y}}}}\left( {{{y}}} \right)} {{V_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}}}} \right.
} {{V_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}}}}, \quad {{{y}}} \in {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right);\\
0, \quad \quad \quad \quad \quad \quad {{{y}}} \notin {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right),
\end{array} \right.\\
\quad \quad \quad \quad \quad \quad \quad \quad {V_{{\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)}} = {\rm{P}}\!\left[{{{{y}}} \in {\cal B}_{\mathbb {R}}^{\nu} \left( \tau \right)} \right]
\end{array}$
|
(B-11) |
定义其1阶矩和2阶矩如下:
|
${{\overset{\frown} {{μ}}}_{{{y}}}}\mathop {\rm{ = }}\limits^\Delta {\rm{E}}\left\{ {{{{y}}}|{{{y}}} \in {\cal B}_{\mathbb {R}}^{2\nu}\left( \tau \right)} \right\} \quad \ $
|
(B-12) |
|
${{\overset{\frown} {{C}}}_{{{y}}}} \mathop {\rm{ = }}\limits^\Delta {\rm{E}}\left\{ {{{{y}}}\, {{{{y}}}^{\rm T}}|{{{y}}} \in {\cal B}_{\mathbb {R}}^{2\nu}\left( \tau \right)} \right\}$
|
(B-13) |
容易验证
|
${{\overset{\frown} {{μ}}}_{{{y}}}} =\! \left[\!\! {\begin{array}{*{20}{c}}
{{\mathop{\rm Re}\nolimits} \left\{ {{{\overset{\frown} {{μ}}}_{{{z}}}}} \right\}}\\
{{\mathop{\rm Im}\nolimits} \left\{ {{{\overset{\frown} {{μ}}}_{{{z}}}}} \right\}}
\end{array}}\!\! \right], \ \!\!{{\overset{\frown} {{C}}}_{{{y}}}} = \!\frac{1}{2}\left[\!\! {\begin{array}{*{20}{r}}
{{\mathop{\rm Re}\nolimits} \left\{ {{{\overset{\frown} {{C}}}_{{{z}}}}} \right\}}\!\!&\!\!{-{\mathop{\rm Im}\nolimits} \left\{ {{{\overset{\frown} {{C}}}_{{{z}}}}} \right\}}\\
{{\mathop{\rm Im}\nolimits} \left\{ {{{\overset{\frown} {{C}}}_{{{z}}}}} \right\}}\!\!&\!\!{{\mathop{\rm Re}\nolimits} \left\{ {{{\overset{\frown} {{C}}}_{{{z}}}}} \right\}} \
\end{array}} \!\!\right]$
|
(B-14) |
由于矢量y服从零均值实高斯分布,所有由2.2节的结论可知${{\overset{\frown} {{μ}}}_{{{y}}}} \equiv {{{0}}}$且${{\overset{\frown} {{C}}}_{{{y}}}}$与Cy特征矢量相同。由${{\overset{\frown} {{μ}}}_{{{y}}}} \equiv {{{0}}}$直接能得到${{\overset{\frown} {{μ}}}_{{{z}}}} \equiv {{{0}}}$,也就说明${{\overset{\frown} {{C}}}_{{{s}}}}$就是协方差矩阵。接下来我们将证明${{\overset{\frown} {{C}}}_{{{z}}}}$与Cz也有相同的特征矢量。首先,我们先考察Cz与Cy的特征矢量的关系。因为Cz为Hermitian矩阵,所以它有$\nu$个实特征值$\left\{ {{\gamma _m}} \right\}_{m = 1}^\nu$和与之对应的$\nu$个特征矢量$\left\{ {{{{{v}}}_m}} \right\}_{m = 1}^\nu$。记${{{V}}} = \left[{{{{{v}}}_1}\, \, \, {{{{v}}}_2}\, \, \, \cdots \, \, \, {{{{v}}}_\nu }} \right]$, ${{{Γ}}} = {\rm{diag}}\left( {{\gamma _{1}}, } \right.$$\left. {{\gamma _{2}}, \cdots, {\gamma _{\nu }}} \right)$,则有${{{{C}}}_{{{z}}}}{{{{V}}} } = {{{Γ}}}{{{V}}}$以及${{{{{V}}} }^{\rm H}}{{{{C}}}_{{{z}}}} = $$ {{{Γ}}}{{{{V}}}^{\rm H}}$。从而有
|
$\left.\begin{array}{c}
{{{{C}}}_{{{z}}}}{{{V}}} = {{Γ}}{{{V}}}\Rightarrow \left\{ {\begin{array}{*{20}{c}}
{{\mathop{\rm Re}\nolimits} \left\{ {{{{{C}}}_{{{z}}}}} \right\}{\mathop{\rm Re}\nolimits} \left\{ {{{V}}} \right\} - {\mathop{\rm Im}\nolimits} \left\{ {{{{{C}}}_{{{z}}}}} \right\}{\mathop{\rm Im}\nolimits} \left\{ {{{V}}} \right\} = {{Γ}}{\mathop{\rm Re}\nolimits} \left\{ {{{V}}} \right\}}\\
{{\mathop{\rm Re}\nolimits} \left\{ {{{{{C}}}_{{{z}}}}} \right\}{\mathop{\rm Im}\nolimits} \left\{ {{{V}}} \right\} + {\mathop{\rm Im}\nolimits} \left\{ {{{{{C}}}_{{{z}}}}} \right\}{\mathop{\rm Re}\nolimits} \left\{ {{{V}}} \right\} = {{Γ}}{\mathop{\rm Im}\nolimits} \left\{ {{{V}}} \right\}}
\end{array}} \right.\\
{{{{V}}}^{\rm H}}{{{{C}}}_{{{z}}}} = {{Γ}}{{{{V}}}^{\rm H}}\Rightarrow \left\{ {\begin{array}{*{20}{c}}
{{\mathop{\rm Re}\nolimits} \left\{ {{{{{C}}}_{{{z}}}}} \right\}{\mathop{\rm Re}\nolimits} \left\{ {{{V}}} \right\} - {\mathop{\rm Im}\nolimits} \left\{ {{{{{C}}}_{{{z}}}}} \right\}{\mathop{\rm Im}\nolimits} \left\{ {{{V}}} \right\} = {{Γ}}{\mathop{\rm Re}\nolimits} \left\{ {{{V}}} \right\}}\\
{{\mathop{\rm Re}\nolimits} \left\{ {{{{{C}}}_{{{z}}}}} \right\}{\mathop{\rm Im}\nolimits} \left\{ {{{V}}} \right\} + {\mathop{\rm Im}\nolimits} \left\{ {{{{{C}}}_{{{z}}}}} \right\}{\mathop{\rm Re}\nolimits} \left\{ {{{V}}} \right\} = {{Γ}}{\mathop{\rm Im}\nolimits} \left\{ {{{V}}} \right\}}
\end{array}} \right.
\end{array}\right\} \quad \quad $
|
(B-15) |
令
|
${{{Q}}} = \left[{\begin{array}{*{20}{r}}
{{\mathop{\rm Re}\nolimits} \left\{ {{{V}}} \right\}}&{-{\mathop{\rm Im}\nolimits} \left\{ {{{V}}} \right\}}\\
{{\mathop{\rm Im}\nolimits} \left\{ {{{V}}} \right\}}&{{\mathop{\rm Re}\nolimits} \left\{ {{{V}}} \right\}}
\end{array}} \right]$
|
(B-16) |
利用式(B-15),容易验证
${{{{Q}}}^{\rm H}}{{{{C}}}_{{{y}}}}{{{Q}}} = {2^{ - 1}}$$ \cdot {\rm{diag}}\left( {{\gamma _{\, 1}}, {\gamma _{\, 2}}, \cdots, {\gamma _{\, \nu }}, {\gamma _{\, 1}}, {\gamma _{\, 2}}, \cdots, {\gamma _{\, \nu }}} \right)$。类似地,Hermitian矩阵
${{\overset{\frown} {{C}}}_{{{z}}}}$也有
$\nu$个实特征值
$\left\{{\mathop \gamma\limits^\frown _m}\right\}_{m = 1}^\nu $和与之对应的
$\nu$个特征矢量
$\left\{{\mathop {{υ}}\limits^\frown _m}\right\}_{m = 1}^\nu $。记
${\overset{\frown} {{V}}} = [{\overset{\frown} {{v}}_1} \; {\overset{\frown} {{v}}_2}···{\overset{\frown} {{v}}_\nu}]$,
${\overset{\frown} {{Γ}}} = {\rm{diag}}\left( {\overset{\frown} \gamma_1}, \; {\overset{\frown}\gamma_2}, ···, {\overset{\frown} \gamma_\nu} \right)$,则有
${{\overset{\frown} {{C}}}_{{{z}}}} {\overset{\frown} {{V}}}={\overset{\frown} {{Γ}}}{\overset{\frown} {{V}}}$,以及
${{\overset{\frown} {{V}}}^{\rm H} {\overset{\frown} {{C}}}\!\!_{{{z}}}={\overset{\frown} {{Γ}}}{\overset{\frown} {{V}}}^{\rm H}}$。仿照前面,若令
|
${\overset{\frown} {{Q}}}= \left[{\begin{array}{*{20}{r}}
{{\mathop{\rm Re}\nolimits} \left\{ {\overset{\frown} {{V}}} \right\}}&{-{\mathop{\rm Im}\nolimits} \left\{ {\overset{\frown} {{V}}} \right\}}\\
{{\mathop{\rm Im}\nolimits} \left\{ {\overset{\frown} {{V}}} \right\}}&{{\mathop{\rm Re}\nolimits} \left\{ {\overset{\frown} {{V}}} \right\}}
\end{array}} \right]$
|
(B-17) |
容易验证
${{\overset{\frown }{\mathop{Q}}\,}^{\text{H}}}\overset{\frown }{\mathop{C}}\,{{}_{y}}\overset{\frown }{\mathop{Q}}\,={{2}^{-1}}\text{diag}\left( {{\overset{\frown }{\mathop{\gamma }}\,}_{1}},\ {{\overset{\frown }{\mathop{\gamma }}\,}_{2}},\ \cdots ,\ {{\overset{\frown }{\mathop{\gamma }}\,}_{\nu }},{{\overset{\frown }{\mathop{\gamma }}\,}_{1}},\ \right.$
$\left. { \; {\overset{\frown} \gamma_2}, \; ···, \;{\overset{\frown} \gamma_\nu}} \right)$。因为
${{\overset{\frown} {{C}}}_{{{y}}}}$与
Cy特征矢量相同,所以
${\overset{\frown} {{Q}}} = {{{Q}}}$。因此,
${\overset{\frown} {{V}}} = {{{V}}}$,即
${{\overset{\frown} {{C}}}_{{{z}}}}$与
Cz特征矢量相同。


 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)




