② (中国科学院空间信息与应用系统重点实验室 北京 100190)
③ (中国科学院大学 北京 100049)
④ (民政部国家减灾中心 北京 100124)
⑤ (民政部卫星减灾应用中心 北京 100124)
② (Key Laboratory of Technology in Geo-spatial Information Processing and Application System, Beijing 100190, China)
③ (University of Chinese Academy of Science, Beijing 100049, China)
④ (National Disaster Reduction Center of China, MCA, Beijing 100124, China)
⑤ (Satellite Disaster Reduction Application Center, MCA, Beijing 100124, China)
极化合成孔径雷达SAR系统通过天线发射两组极化方向正交的电磁波,获得照射地物4个不同收发极化组合下的后向散射回波。该系统在保持单通道SAR系统全天候全天时的优势之外,还拥有了包含于极化通道相对关系中更为丰富的信息量,在覆盖地物分类,变化检测以及目标提取方面具有广泛的应用[1–3]。
但是,由于极化SAR观测维度的增加及系统复杂性的提高,使得其在观测链路中受到一些误差源额外影响。在这些误差源影响下,各极化通道之间相对关系将无法真实反映观测地物散射特征,从而影响到后续的应用处理。实际中,这类散射特性失真通过极化定标处理进行补偿。最初的定标算法主要针对于收发天线内部的极化畸变,包括通道间的串扰以及两组天线自身的不平衡度[4–7]。其中,串扰是指在不同极化方式间发生能量转移的变极化效应,不平衡度反映的是系统发射和接收两种不同极化电磁波的增益差别。目前,针对其他不同的误差源,如飞行平台姿态波动,地表起伏以及法拉第旋转等,定标算法有了进一步的发展[8–10]。但这些误差源在模型中基本可以用串扰和不平衡度来衡量。因而,串扰和不平衡度是用于衡量定标算法性能的常用指标。最新发展的全极化SAR卫星,如Radarsat-2, ALOS-2及Sentinal-1等都给出了定标后数据残余串扰及不平衡度的指标要求[11–13]。
研究系统误差源在具体数据应用中的影响,有助于设计合理化的系统指标并选取合适的定标方案。地物分类,作为极化SAR数据应用的一个重要方向,对图像所反映的散射特性真实性有较高的要求。极化数据失真将导致图像像素类别的错误判决。Lee等人最初在文献[14]提出了一种非监督极化图像分类算法。该算法结合了Cloude分解以及基于协方差矩阵参数化模型的Wishart分类器。该方法可以在不需要人工干预下,得到具有散射机理解释的分类结果。后续的研究人员在此基础上做了诸多开发改进[15–18],但大部分方法仍需要Cloude分解提供的特征参量作为初始类别的依据。针对极化失真因子对该方法分类结果的影响,前人进行了研究[19–21]。其中,Wang Y等人对有代表性的场景,在给定极化失真下的Cloude分解参量变化进行统计分析,指出一些特定目标(如建筑等)分解参量(如熵值)会出现较大偏离;Wang C等人证明了定标误差对单纯Wishart分类器不存在影响,并通过实测数据的半物理仿真实验,给出了针对不同地物Cloude分解各参量随极化失真因子的变化情况,指出了串扰是最有决定性的因子。因此,本文重点考察系统天线间的串扰对Cloude分解中获得的散射特征及后续图像地物分类的影响。我们首先在下一节中从理论上推导串扰作用下的地物散射特性变化,然后利用不同类别地物实际极化SAR图像,通过半物理仿真验证散射特性的变化趋势,并给出图像分类结果的变化情况,给出针对不同地物的定标指标参考范围。
2 模型推导及理论分析极化SAR数据包含媒介在4个极化维度上的后向散射系数。在水平和垂直线极化正交基下,数据可用下述散射矩阵形式表述[22]:
| ${{S}} = \left[ {\begin{array}{*{20}{c}}{{S_{{\rm{hh}}}}} & {{S_{{\rm{hv}}}}}\\{{S_{{\rm{vh}}}}} & {{S_{{\rm{vv}}}}}\end{array}} \right]$ | (1) |
S 矩阵中的元素表示不同通道的后向散射系数,由水平极化和垂直极化在发射端和接收端的不同组合,一共有4个不同的极化通道,我们用下标表示参量所对应的极化通道,例如,Svh表示的是以水平极化(h)发射,垂直极化(v)接收的雷达波照射下的后向散射系数。考虑媒介散射的互易性,极化信息可以用缩减的3维复向量来表示:
| ${{{k}}_{3{\rm{l}}}} = {\left[ {\begin{array}{*{20}{c}}{{S_{{\rm{hh}}}}} & {\sqrt 2 \frac{{{S_{{\rm{hv}}}} + {S_{{\rm{vh}}}}}}{2}} & {{S_{{\rm{vv}}}}}\end{array}} \right]^{\rm{T}}}$ | (2) |
上标T为矩阵转置操作。极化信息还可以通过3维Pauli特征向量表示:
| ${{{k}}_{3{\rm{P}}}} = \frac{1}{{\sqrt 2 }}{\left[ {{S_{{\rm{hh}}}} + {S_{{\rm{vv}}}},{S_{{\rm{hh}}}} - {S_{{\rm{vv}}}},{S_{{\rm{hv}}}} + {S_{{\rm{vh}}}}} \right]^{\rm{T}}}$ | (3) |
k 3l与 k 3P中包含的信息量一致,都是常用的极化单视复数据格式。为了减小相干斑对图像影响,极化数据通常要进行多视处理。多视处理后,Pauli特征向量 k 3P通过非相干平均得到极化相干矩阵 T 3:
| ${{{T}}_3} = \left\langle {{{k}_{3{\rm{P}}}}{{k}_{3{\rm{P}}}}\!\!\!\!\!^{\rm{H}}} \right\rangle = \left[ {\begin{array}{*{20}{c}}{{T_{11}}} & {{T_{12}}} & {{T_{13}}}\\{{T_{21}}} & {{T_{22}}} & {{T_{23}}}\\{{T_{31}}} & {{T_{32}}} & {{T_{33}}}\end{array}} \right]$ | (4) |
其中,上标H表示复共轭转置; T 3矩阵中,对角线元素T11, T22和T33均为正实数,其他元素满足:
| ${T_{12}} = {T_{21}}\!\!\!^*, \ {T_{13}} = {T_{31}}\!\!\!^*, \ {T_{23}} = {T_{32}}\!\!\!^*$ | (5) |
Cloude分解是基于对相关矩阵 T 3特征值分析的一类极化分解方法。对 T 3进行特征值分解可以得到
| ${{{T}}_3} = {\lambda _1}{{e}_1}{{e}_1}\!\!^{\rm{H}} + {\lambda _2}{{e}_2}{{e}_2}\!\!^{\rm{H}} + {\lambda _1}{{e}_3}{{e}_3}\!\!^{\rm{H}}$ | (6) |
其中,
| $H = \mathop \sum \limits_{i = 1}^3 - {P_i}{\rm{lo}}{{\rm{g}}_3}{P_i}$ | (7) |
其中
| ${P_i} =\frac{{{\lambda _i}}}{{\mathop \sum \limits_j {\lambda _j}}}$ | (8) |
该参数值在0到1之间变化,表示媒质散射的随机性,在散射类别较为丰富的区域,熵值较大。Cloude分解的另一维分量从特征向量中提取得到。特征向量 ei 可以参数化为如下形式:
| ${{e}_i} = {{\rm e}^{i{\phi _i}}}{\left[ {\begin{array}{*{20}{c}}{{\rm{cos}}{\alpha _i}} & {{\rm{sin}}{\alpha _i}{\rm{cos}}{\beta _i}{{\rm e}^{i{{δ} _i}}}} & {{\rm{sin}}{\alpha _i}{\rm{sin}}{\beta _i}{{\rm e}^{i{\gamma _i}}}}\end{array}} \right]^{\rm{T}}}$ | (9) |
| $ \alpha = {P_1}{\alpha _1} + {P_2}{\alpha _2} + {P_3}{\alpha _3}$ | (10) |
H和
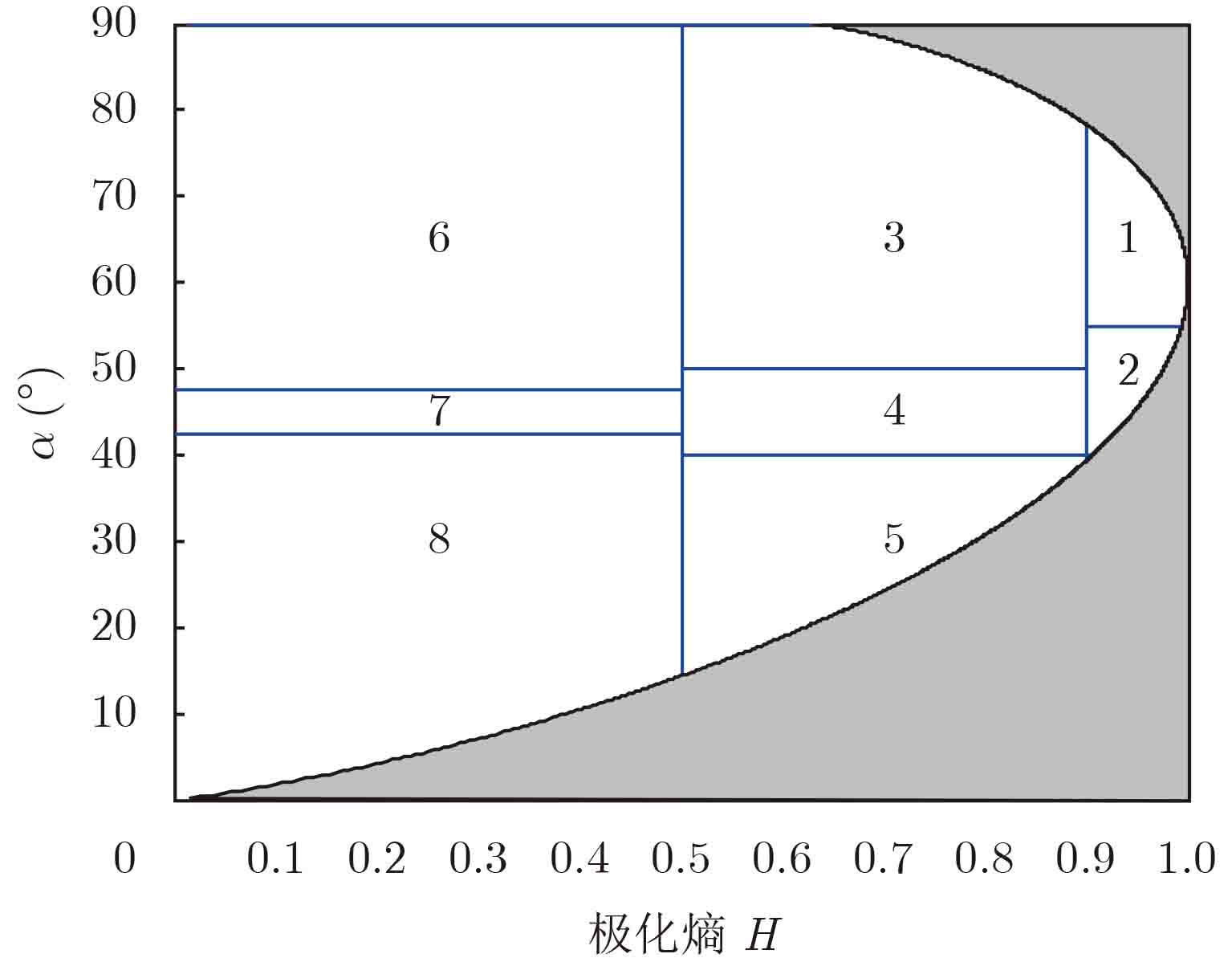
|
图 1 H-
|
下面我们加入系统误差源,以考察串扰误差对Cloude分解特征量对应地物散射机理的影响。
以目标的散射矩阵作为极化散射特性的表征时,PolSAR的观测模型通常可以表示如下:
| $\begin{array}{l}\!\!\!\! {M} = A{{\rm e}^{{\rm j}\varphi }}{{R}^{\rm{T}}}{ST} + {N} = A{{\rm e}^{{\rm j} \varphi }}\left[ {\begin{array}{*{20}{c}}1 & {{\delta _2}}\\{{\delta _1}} & {{f_1}}\end{array}} \right]\\\ \ \ \ \ \cdot \!\! \left[ {\begin{array}{*{20}{c}} {{S_{{\rm{hh}}}}} & {{S_{{\rm{hv}}}}}\\{{S_{{\rm{vh}}}}} & {{S_{{\rm{vv}}}}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}1 & {{\delta _3}}\\{{\delta _4}} & {{f_2}}\end{array}} \right] \!+\! \left[ {\begin{array}{*{20}{c}}{{n_{{\rm{hh}}}}} & {{n_{{\rm{hv}}}}}\\{{n_{{\rm{vh}}}}} & {{n_{{\rm{vv}}}}}\end{array}} \right]\end{array}$ | (11) |
式中,
M
表示的是散射矩阵测量值,A表示绝对幅度,
首先,我们忽略不平衡度和加性噪声的影响,将噪声矩阵 N 设为零,不平衡度f1和f2均等于1。此外,4组串扰参数在模型中地位相同,为简化分析,各串扰参数被认为相等,
| ${\delta _1} = {\delta _2} = {\delta _3} = {\delta _4} = \delta $ | (12) |
故观测模型可以简化为:
| ${{M}} = \left[ {\begin{array}{*{20}{c}}1 & \delta \\\delta & 1\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{S_{{\rm{hh}}}}} & {{S_{{\rm{hv}}}}}\\{{S_{{\rm{vh}}}}} & {{S_{{\rm{vv}}}}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}1 & \delta \\\delta & 1\end{array}} \right]$ | (13) |
将目标各通道散射元素用1维向量的形式描述后,模型可以重新描述为:
| $\left[ {\begin{array}{*{20}{c}}{{M_{{\rm{hh}}}}}\\{{M_{{\rm{hv}}}}}\\{{M_{{\rm{vh}}}}}\\{{M_{{\rm{vv}}}}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}1 & \delta & \delta & {{\delta ^2}}\\\delta & 1 & {{\delta ^2}} & \delta \\\delta & {{\delta ^2}} & 1 & \delta \\{{\delta ^2}} & \delta & \delta & 1\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{S_{{\rm{hh}}}}}\\{{S_{{\rm{hv}}}}}\\{{S_{{\rm{vh}}}}}\\{{S_{{\rm{vv}}}}}\end{array}} \right]$ | (14) |
其中,Mij 为各极化通道的后向散射系数观测值,其下标定义与前述一致。观测数据的Pauli特征向量为:
| $\begin{split}& \!\!\!\!\!\!\!\!\!\! {{ {k}}_{3{\rm{PM}}}} = \frac{1}{{\sqrt 2 }}{\left[ {{M_{{\rm{hh}}}} + {M_{{\rm{vv}}}},{M_{{\rm{hh}}}} - {M_{{\rm{vv}}}},{M_{{\rm{hv}}}} + {M_{{\rm{vh}}}}} \right]^{\rm{T}}}\\& \ \ = \! \! \frac{1}{{\sqrt 2 }}\!\! \left[ {\begin{array}{*{20}{c}} {\!\!\!\!\!\!\! 1 + {\delta ^2}} \ \ \ \ \ 0 \ \ \ \ \ \ \ {2\delta }\\ 0 \ \ \ \ {1 - {\delta ^2}} \ \ \ \ \ 0 \\{\ \ \ 2\delta } \ \ \ \ \ \ \ 0 \ \ \ \ \ \ {1 + {\delta ^2}}\end{array}} \right] \!\!\! \left[ {\begin{array}{*{20}{c}}{{S_{{\rm{hh}}}} \!+\! {S_{{\rm{vv}}}}}\\{{S_{{\rm{hh}}}} \!-\! {S_{{\rm{vv}}}}}\\{{S_{{\rm{hv}}}} \!+\! {S_{{\rm{vh}}}}}\end{array}} \right]\end{split}$ | ((15)) |
结合式(4),可以推导得到观测得到相关矩阵 T 3M与理论值 T 3之间的关系,即相关矩阵形式下的观测模型。
| $\begin{array}{*{20}{l}}\begin{array}{l}\!\!\! {{T}_{3{\rm{M}}}} = {{k}_{3{\rm{PM}}}}{{k}_{3{\rm{PM}}}}\!\!\!\!\!\!\!\!^{\rm{H}} \ \ = \left[ {\begin{array}{*{20}{c}}{1 + {\delta ^2}} & 0 & {2\delta }\\0 & {1 - {\delta ^2}} & 0\\{2\delta } & 0 & {1 + {\delta ^2}}\end{array}} \right]\\\;\;\;\;\;\;\;\; \cdot {{k}_{3{\rm{P}}}}{{k}_{3{\rm{P}}}}\!\!\!\!\!^{\rm H} \ {\left[ {\begin{array}{*{20}{c}}{1 + {\delta ^2}} & {0} & {2\delta }\\0 & {1 - {\delta ^2}} & {0}\\{2\delta } & {0} & {1 + {\delta ^2}}\end{array}} \right]^{\rm{H}}}\end{array}\\\begin{array}{l}\;\;\;\;\;\; = \left[ {\begin{array}{*{20}{c}}{1 + {\delta ^2}} & 0 & {2\delta }\\0 & {1 - {\delta ^2}} & 0\\{2\delta } & 0 & {1 + {\delta ^2}}\end{array}} \right]\\\;\;\;\;\;\;\;\; \cdot {{T}_3}{\left[ {\begin{array}{*{20}{c}}{1 + {\delta ^2}} & {0} & {2\delta }\\0 & {1 - {\delta ^2}} & {0}\\{2\delta } & {0} & {1 + {\delta ^2}}\end{array}} \right]^{\rm{H}}}\end{array}\end{array}$ | (16) |
由观测散射向量获得的相关矩阵 T 3M,可以同样通过特征值获得对应的散射熵值。下面我们就先从理论上分析一下 T 3与 T 3M特征值差异,考察观测过程中的串扰误差对散射熵产生的影响。由定理[24]可知,特征值和积特性满足:
| $\mathop \sum \limits_{i = 1}^3 {\lambda _i} = {\rm{trace(}}{{T}}{\rm{)}}, \quad \quad\quad \prod\limits_{i = 1}^3 {{\lambda _i} = \det ({{T}})} $ | (17) |
其中, trace(·)为矩阵迹,det(·)为矩阵行列式。将式(17)根据相关矩阵理论值和观测值展开后,做因式分解后可以得到:
| $\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \ \, \, {\rm{trace(}}{{{T}}_3}{\rm{)}} = {T_{11}} + {T_{22}} + {T_{33}}$ | (18) |
| $\begin{aligned}\ \, \, \det ({{T}_3}) = & {T_{11}}{T_{22}}{T_{33}} - {T_{11}}{T_{23}}{T_{32}} - {T_{12}}{T_{21}}{T_{33}} \\& +{T_{12}}{T_{23}}{T_{31}} + {T_{13}}{T_{21}}{T_{32}} - {T_{13}}{T_{22}}{T_{31}}\end{aligned}$ | (19) |
| $\begin{aligned}{\rm{trace}}({{T}_{3{\rm{M}}}}) = & (1 + {\delta ^2} + {\delta ^{*2}} + {\delta ^2}{\delta ^{*2}} + 4\delta {\delta ^*}){T_{11}}\\ & + (1 - {\delta ^2} - {\delta ^{*2}} + {\delta ^2}{\delta ^{*2}}){T_{22}}\\ & + (1 + {\delta ^2} + {\delta ^{*2}} + {\delta ^2}{\delta ^{*2}} + 4\delta {\delta ^*}){T_{33}}\\& + (2\delta {\delta ^{*2}} + 2{\delta ^2}{\delta ^*} + 2\delta + 2{\delta ^*}){T_{13}}\\ & + (2\delta {\delta ^{*2}} + 2{\delta ^2}{\delta ^*} + 2\delta + 2{\delta ^*}){T_{31}}\end{aligned}$ | (20) |
| $\begin{aligned}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\ \, \, \det ({{T}_{3{\rm{M}}}}) = & {(1 - \delta )^3}{(1 + \delta )^3}{(1 - {\delta ^*})^3}\\& \cdot {(1 + {\delta ^*})^3}\det ({{T}_3})\end{aligned}$ | (21) |
在trace(
T
3M)中,由于实际地物中T13与T31相对于其他相关矩阵元素要小得多,分析时可以近似忽略。另外可以发现,det(
T
3M)与det(
T
3)之间比例仅取决于串扰量,与矩阵自身变化无关。由于对各特征值进行统一的尺度处理并不改变对应的Pi
值及熵值,因此可以将
T
3M各特征值均除以(1 – $\delta $)·
| $\begin{array}{l}\mathop \sum \limits_{i = 1}^3 {\lambda _{i{\rm{MN}}}} = \frac{{1 + {\delta ^2} + {\delta ^{*2}} + {\delta ^2}{\delta ^{*2}} + 4\delta {\delta ^*}}}{{1 - {\delta ^2} - {\delta ^{*2}} + {\delta ^2}{\delta ^{*2}}}}{T_{11}} + {T_{22}} + \frac{{1 + {\delta ^2} + {\delta ^{*2}} + {\delta ^2}{\delta ^{*2}} + 4\delta {\delta ^*}}}{{1 - {\delta ^2} - {\delta ^{*2}} + {\delta ^2}{\delta ^{*2}}}}{T_{33}}\\\quad\quad\quad\quad\! = \left( {1 + \frac{{2{\delta ^2} + 2{\delta ^{*2}} + 4\delta {\delta ^*}}}{{1 - {\delta ^2} - {\delta ^{*2}} + {\delta ^2}{\delta ^{*2}}}}} \right){T_{11}} + {T_{22}} + \left( {1 + \frac{{2{\delta ^2} + 2{\delta ^{*2}} + 4\delta {\delta ^*}}}{{1 - {\delta ^2} - {\delta ^{*2}} + {\delta ^2}{\delta ^{*2}}}}} \right){T_{33}}\\\quad\quad\quad\quad\! = \left( {1 + \frac{{2{{(\delta + {\delta ^*})}^2}}}{{(1 - \delta )(1 + \delta )(1 - {\delta ^*})(1 + {\delta ^*})}}} \right){T_{11}} + {T_{22}}+ \left( {1 + \frac{{2{{(\delta + {\delta ^*})}^2}}}{{(1 - \delta )(1 + \delta )(1 - {\delta ^*})(1 + {\delta ^*})}}} \right){T_{33}}\\\quad\quad\quad\quad\!= \left( {1 + \frac{{8{\rm{real(}}\delta {{\rm{)}}^2}}}{{{{\left| {1 - \delta } \right|}^2}{{\left| {1 + \delta } \right|}^2}}}} \right){T_{11}} + {T_{22}} + \left( {1 + \frac{{8{\rm{real(}}\delta {{\rm{)}}^2}}}{{{{\left| {1 - \delta } \right|}^2}{{\left| {1 + \delta } \right|}^2}}}} \right){T_{33}}\end{array}$ | (22) |
故3组特征值在乘积值不变条件下,累和增大,因此 T 3M特征值相对差异要比 T 3特征值大,由熵的特性可知,式(7)中各Pi 值越接近,熵值越大;相反各Pi 值差异越大,熵值越小;而在本文讨论的范畴中,Pi 值差异大小反映的即是相关矩阵特征值的相对差异。因此在串扰作用下地物的散射熵值将出现一致性减小。
3 实验结果下面根据实测数据,验证理论分析的结果,并进一步展示串扰误差对分类结果的影响。
选取4组有明显差异场景类型的Radarsat-2数据,对其添加不同程度的串扰,分析其散射熵值变化,以及
| 表 1 数据情况说明 Tab.1 The description of datasets |

|
图 2 各场景数据的Pauli分解伪彩合成图 Fig.2 The Pauli decomposition maps for all datasets |
Radarsat-2数据经过定标处理,可以认为各通道的原始复数据反映的是地物后向散射系数的真实值,即模型式(13)中的
S
各元素。然后对每一组图像添加强度逐次增强的串扰量,强度分别为–40 dB, –35 dB, –30 dB, –25 dB, –20 dB, –15 dB, –10 dB, –5 dB,其相位为
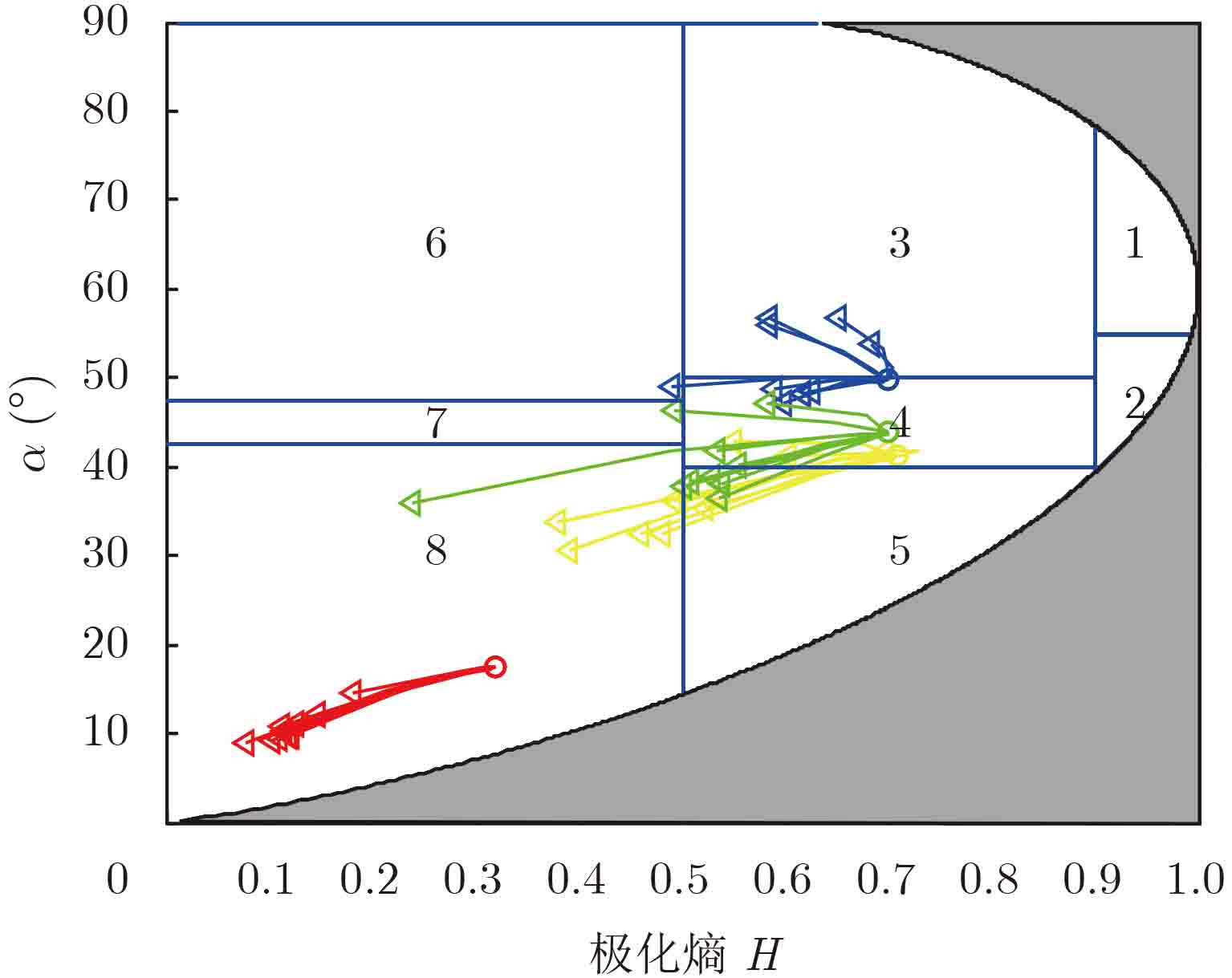
|
图 3 不同串扰下的中心散射机制在H-$\alpha $平面上变化,红色代表城区图像,黄色代表农田图像,蓝色代表入海口图像,绿色代表丛林图像 Fig.3 The changing of scattering center on the H-$\alpha $ plane under different crosstalk, red represents the urban area, yellow represents the agricultural field, blue represents the estuary scene, and green represents the forest area |
进一步,我们对各类地物进行

|
图 4 不同串扰下的
|
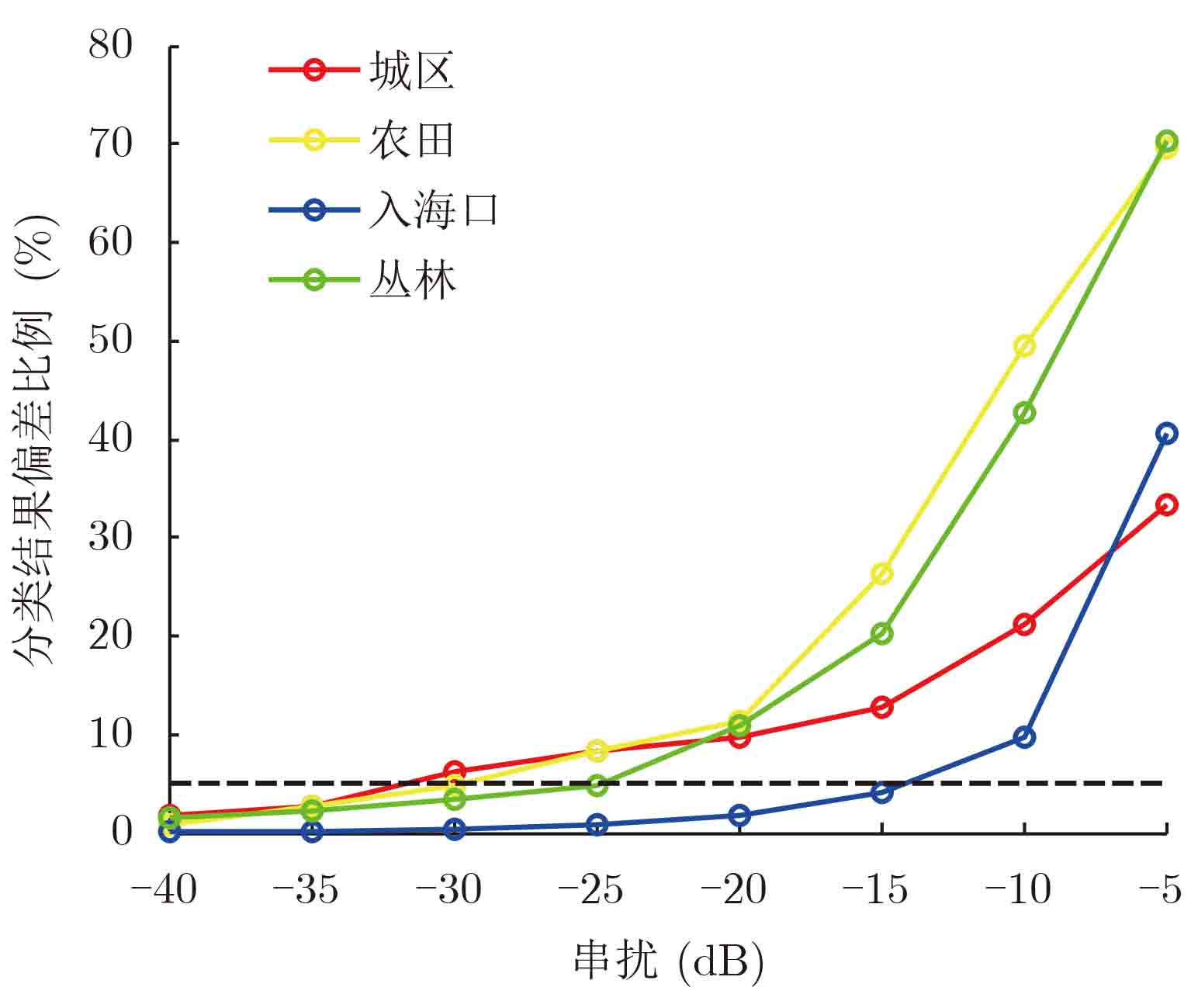
|
图 5 不同串扰下的
|
本文给出了相关矩阵表示下的极化SAR观测模型,推导了系统串扰对相关矩阵特征值的影响,进而得出在串扰强度逐渐增加的情况下,Cloude分解获得分类特征量极化熵将逐渐减小的结论。并且,利用多种不同类型地物的实际极化图像进行实验分析。在多次模拟强度逐渐增强的随机串扰实验结果中,4类地物的地物中心散射机制均一致性向熵值减小方向偏移,验证了理论分析结果。同时,实验还分析了串扰量对基于Cloude分解的
| [1] |
Akbari V, Anfinsen S, Doulgeris A, et al. Polarimetric SAR change detection with the complex Hotelling-Lawley trace statistic[J].
IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(7): 3953-3966. DOI:10.1109/TGRS.2016.2532320 ( 0) 0)
|
| [2] |
Doulgeris A. An automatic U-distribution and Markov Random Field segmentation algorithm for PolSAR images[J].
IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(4): 1819-1827. DOI:10.1109/TGRS.2014.2349575 ( 0) 0)
|
| [3] |
Tao D, Doulgeris A and and Brekke C. A segmentation-based CFAR detection algorithm using truncated statistics[J].
IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(3): 2887-2898. ( 0) 0)
|
| [4] |
Whitt M, Ulaby F, Polatin P, et al. A general polarimetric radar calibration technique[J].
IEEE Transactions on Antennas and Propagation, 1991, 39(1): 62-67. DOI:10.1109/8.64436 ( 0) 0)
|
| [5] |
Freeman A. SAR calibration: an overview[J].
IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(6): 1107-1121. DOI:10.1109/36.193786 ( 0) 0)
|
| [6] |
Quegan S. A unified algorithm for phase and cross-talk calibration of polarimetric data-theory and observations[J].
IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(1): 89-99. DOI:10.1109/36.285192 ( 0) 0)
|
| [7] |
Sarabandi K, Pierce L, Dobson M, et al. Polarimetric calibration of SIR-C using point and distributed target[J].
IEEE Transactions on Geoscience and Remote Sensing, 1995, 33(4): 858-866. DOI:10.1109/36.406672 ( 0) 0)
|
| [8] |
Freeman A. Calibration of linearly polarized polarimetric SAR data subject to Faraday rotation[J].
IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(8): 1617-1624. DOI:10.1109/TGRS.2004.830161 ( 0) 0)
|
| [9] |
Sabry R, Vachon P and Cole M. Prediction of polarimetric-SAR field-orientation rotation due to topographical slope variation for squint operations[J].
IEEE Geoscience and Remote Sensing Letters, 2011, 8(3): 570-574. DOI:10.1109/LGRS.2010.2092410 ( 0) 0)
|
| [10] |
Hu Dingsheng, Qiu Xiaolan, Hu Donghui, et al. Improved airborne PolSAR calibration algorithm based on time-variant attitude compensation[J].
International Journal of Remote Sensing, 2015, 36(12): 3184-3195. DOI:10.1080/2150704X.2015.1054042 ( 0) 0)
|
| [11] |
Touzi R, Hawkins R and Cote S. High-precision assessment and calibration of polarimetric RADARSAT-2 sar using transponder measurements[J].
IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(1): 487-503. DOI:10.1109/TGRS.2012.2201946 ( 0) 0)
|
| [12] |
Azcueta M, d’Alessandro M, Zajc T, et al. ALOS-2 preliminary calibration assessment[C]. IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 2015: 4117–4120.
( 0) 0)
|
| [13] |
Geudtner D, Torres R, Snoeij P, et al. Sentinel-1 mission capabilities and SAR system calibration[C]. IEEE Radar Conference (RadarCon13), Ottawa, Canada, 2013: 1–4.
( 0) 0)
|
| [14] |
Lee J, Grunes M, Ainsworth T, et al. Unsupervised classification using polarimetric decomposition and the complex Wishart classifier[J].
IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2249-2258. DOI:10.1109/36.789621 ( 0) 0)
|
| [15] |
Benz U and Pottier E. Object based analysis of polarimetric SAR data in alpha-entropy-anisotropy decomposition using fuzzy classification by eCognition[C]. International Geoscience and Remote Sensing Symposium, Sydney, Austrilia, 2001, 3: 1427–1429.
( 0) 0)
|
| [16] |
Cao F, Hong W, Wu Y, et al. An unsupervised segmentation with an adaptive number of clusters using the Span/H/alpha/A space and the complex Wishart clustering for fully polarimetric SAR data analysis[J].
IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3454-3467. DOI:10.1109/TGRS.2007.907601 ( 0) 0)
|
| [17] |
Yu P, Qin A and Clausi D. Unsupervised polarimetric SAR image segmentation and classification using region growing with edge penalty[J].
IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(4): 1302-1317. DOI:10.1109/TGRS.2011.2164085 ( 0) 0)
|
| [18] |
Dabboor M, Collins M, Karathanassi V, et al. An unsupervised classification approach for polarimetric SAR data based on the Chernoff distance for complex Wishart distribution[J].
IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(7): 4200-4213. DOI:10.1109/TGRS.2012.2227755 ( 0) 0)
|
| [19] |
Correia A, Freitas C, and Mura J. Evaluation of the influence of the polarimetric calibration process on the H/A/alpha decomposition[C]. IEEE International Geoscience and Remote Sensing Symposium, Honolulu, Hawaii, USA, 2010: 2039–2042.
( 0) 0)
|
| [20] |
Wang Y, Ainsworth T and Lee J. Assessment of system polarization quality for polarimetric SAR imagery and target decomposition[J].
IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(5): 1755-1771. DOI:10.1109/TGRS.2010.2087342 ( 0) 0)
|
| [21] |
Wang C, Yu W, Wang Y, et al. Polarimetric calibration requirements on several classification schemes for land application of polarimetric synthetic aperture radar[J].
IET Radar, Sonar & Navigation, 2013, 7(2): 113-122. ( 0) 0)
|
| [22] |
Lee J and Potter E. Polarimetric Radar Imaging From Basic to Application[M]. New York: CSC Press, 2009: 53–84.
( 0) 0)
|
| [23] |
Cloude S and Pottier E. A review of target decomposition theorems in radar polarimetry[J].
IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(2): 498-518. DOI:10.1109/36.485127 ( 0) 0)
|
| [24] |
数学手册编写组. 数学手册[M]. 北京: 人民教育出版社, 1979: 117–120.
Mathematical Manual drafting group. Mathematical Manual[M]. Beijing: People’s Education Press, 1979: 117–120. (  0) 0)
|




