② (中国电子科技集团公司第二十九研究所电磁空间作战与应用重点实验室 成都 610036)
③ (电子科技大学通信与信息工程学院 成都 611731)
② (CETC Key Laboratory of Electromagnetic Domain Operation, No.29 Research Institute of CETC, Chengdu 610036, China)
③ (School of Communication and Information Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China)
目标定位广泛应用在雷达、声呐、通信和导航中,包括获取目标的距离、位置、速度等信息。本文考虑利用频控阵MIMO雷达获取目标的角度、距离和幅度信息。近年来,多输入多输出(Multiple-Input Multiple-Output, MIMO)系统吸引了众多学者和科研团队的广泛关注。受最先进的通信理论启发,特别是MIMO系统和空时编码技术[1, 2],在2003年的第37届、2004年的第38届“信号、系统与计算机”的Asilomar会议以及2004年的IEEE雷达会议上专题讨论了MIMO雷达系统及其相关理论问题[3, 4, 5],从此MIMO雷达的概念被正式提出。相比相控阵雷达,MIMO雷达除了提高了目标检测的可靠性和探测隐身目标的能力外,MIMO雷达具有更高的分辨特性、更好的目标参数估计性能、抗干扰能力以及更好的目标识别能力等等。
此外,在多天线系统中,频控阵(Frequency Diverse Array, FDA)被认为是一种很有潜力的技术。在2006年的IEEE国际雷达会议上,P. Antonik等人首次提出频控阵雷达的概念[6]。在FDA中,相邻阵元存在一个较小的频率增量,该频率增量相对时间而言是恒定的,且远远小于载频,于是发射信号在频域上部分重叠。P. Antonik指出FDA波束形成器的波束扫描角随着距离而变化,结果频控阵雷达的波束具有角度和距离依赖性,这为目标的距离和角度参数联合定位提供可能。结合MIMO雷达[7, 8],文献[9]提出了一种基于频控阵的MIMO雷达技术,该文考虑了将波形复用和FDA应用到了双站雷达系统中,通过仿真验证了FDA雷达获取目标的距离和角度是可能的。为了实现距离和角度估计,王文钦博士[10]提出了频控阵的发射子孔径设计方案,其本质上是将发射阵列划分成多个子阵,并利用凸优化理论优化发射方向图矩阵。结合空时自适应处理(Space Time Adaptive Processing, STAP),许京伟博士[11]提出了基于频率分集阵列STAP雷达的距离模糊杂波分离与抑制方法,该方法利用频率分集阵列发射导向矢量的距离角度2维依赖性,通过空间频率域子空间投影实现距离模糊杂波的分离。文献[12]提出使用两脉冲的频控阵估计目标的距离和角度,第1个脉冲利用传统的相控阵估计目标的角度信息,再利用第2个脉冲通过频率增量估计出距离信息。
本文在研究FDA-MIMO雷达基础上,结合稀疏迭代技术,解决FDA-MIMO雷达中的角度、距离及幅度估计问题。FDA-MIMO的发射波束不仅与目标的方位角有关,同时也与目标的距离有关。在建立FDA-MIMO系统模型的基础上,首先将迭代自适应方法引入到FDA-MIMO雷达中,研究基于迭代自适应方法的FDA-MIMO雷达参数估计;接着提出一种基于稀疏迭代的加权最小化方法,该方法利用加权lq范数(0 < q≤1)做为目标函数,并通过迭代优化估计目标的距离、角度及幅度信息。最后仿真验证本文给出的稀疏迭代方法的有效性。
2 频控阵MIMO雷达信号模型考虑窄带频控阵MIMO雷达系统模型,其阵列由N个发射天线和M个接收天线构成。N个不同的发射天线上发射的信号x(t)表示为:

|
其中,E是发射能量,
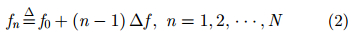
|
其中,
在频控阵MIMO雷达中,发射信号s(t)
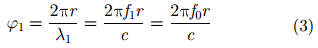
|
其中,λ1表示第1个发射阵元上的载波波长。类似地,第n个天线到目标的相位为:
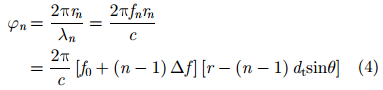
|
其中,dt表示发射阵列的阵元间隔,
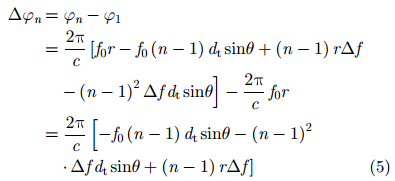
|
以第1个阵元作为参考阵元,可得频控阵MIMO雷达的发射阵列的导向向量为:
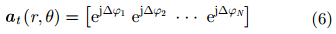
|
于是,频控阵MIMO雷达模型的阵列因子(Array Factor, AF)定义为:

|
其中,相位项Φ0定义为:
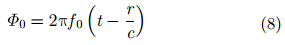
|
当雷达系统发射的波形信号照射到L个散射体上,假设第l个散射体位于远场、且角度和距离为
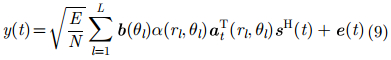
|
其中,
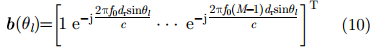
|
其中,dr是接收阵列的阵元间隔。
式(9)经采样处理转换成离散信号,并将感兴趣的目标场景划分成P个距离单元和K个角度单元,可能的目标位置完全与离散单元匹配,则在单次快拍的情况下接收信号的矩阵形式为:
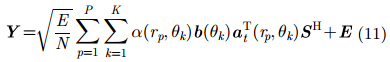
|
其中,E为加性噪声,
堆积接收信号,即将接收信号表示成向量形式y=vec(Y),式(11)转化为:

|
其中,vec表示将矩阵元素按列排成一个列向量,从而将矩阵向量化。α表示目标的距离、角度和幅度信息,V包含了阵列的导向矢量,其分别为:
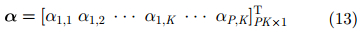
|
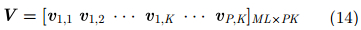
|
其中,V的列向量为:
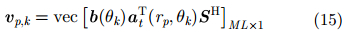
|
在式(12),接收信号y和导向矩阵V是已知的,α是未知的。本文利用式(12),通过稀疏迭代的方法同时估计出目标的距离、角度和幅度信息。
3 基于稀疏迭代的多维参数联合估计方法正如文献[13]所述,频控阵在MIMO雷达中的一个重要应用潜力是对目标的距离和角度进行2维联合估计。文献[14]考虑了将迭代自适应方法(Iterative Adaptive Approaches, IAA)应用在MIMO雷达成像中,但在文献[14]中,接收信号模型中引入了转移矩阵以表示目标的距离信息,本文式(9)中没有引入转移矩阵,通过利用频控阵MIMO导向向量的距离依赖性,联合估计目标的距离、角度和幅度信息。本小节在介绍IAA的基础上,将加权q范数最小化方法[15]扩展至频控阵MIMO雷达中进行估计目标参数。
3.1 迭代自适应方法令

|
其中,P表示距离维。同样,定义数据协方差矩阵为:
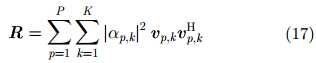
|
IAA最小化如下的加权均方目标函数:
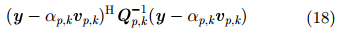
|
最小化式(18)可得到如下的目标参数估计:
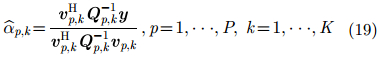
|
由于
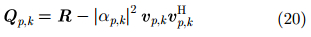
|
并利用矩阵的逆特性,可得
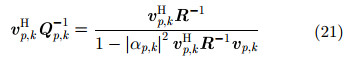
|
因此,式(19)中
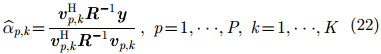
|
由于式(17)中R依赖于
Step 1 初始化:
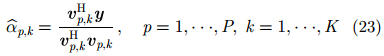
|
Step 2 根据式(17),求解R;
Step 3 根据式(22),
Step 4 增加迭代数k,重复迭代Step 2和Step 3,直到满足一定的停止准则,或者循环达到一定的次数时停止迭代。
在实际中,雷达系统仅需照射有限的角度区域(如-30°~30°)[14],不需要覆盖整个区域(-90°~90°)。但当扫描单元数K减少时,式(17)中R可能不满足条件,由于R可逆的条件是P·K ≥ML。为了解决该问题,文献[14]考虑使用对角矩阵

|
其中,

|
其中,
针对静止目标,IAA和IAA-R在快拍数据比较少的情况下,特别是在单次快拍时,相比DAS估计,IAA和IAA-R能获得较好的目标估计和有效的旁瓣压缩。但在真实的目标位置附近,IAA和IAA-R还是获得了一些虚假目标。针对该问题,下面给出了一种基于q范数的多维参数估计。
3.2 基于稀疏迭代的加权q范数最小化方法基于稀疏迭代的加权q范数最小化方法解决如下的目标函数:
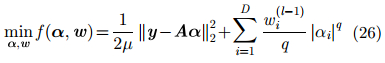
|
其中,μ是一个正数,
首先,对于优化问题式(26),参数a通过复数求导得到。求导式(26)中的目标函数,并置参数a的复数导数为零,可得
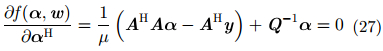
|
其中,
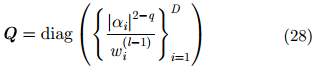
|
于是求解式(27),可得参数α的估计值为:
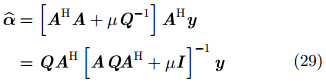
|
其中,IML表示单位向量。观测式(29)可知,估计项
其次,在获得
提出的方法利用DAS估计做为目标参数的初始化估计,通过迭代方法改进DAS估计,以获得更高的分辨率。具体步骤如下:
Step 1 初始化:迭代次数l=1,目标参数为式(23);
Step 2 计算加权和μ,其分别表示如下:

|
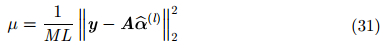
|
其中,ε2是一个正数,其目的是确保
Step 3 利用式(29)更新目标参数;
Step 4 迭代Step 2和Step 3,直到一定的迭代次数。
本方法求得了未知量的数学表达式,并通过多次迭代求解,提供了更加精确的估计,故不需借助内点法(如凸优化软件CVX等)求解;文献[17]证明在没有噪声的情况下,lq范数代替l1范数时利用更少的测量便可重建信号。后面的仿真中证明,在有噪声的情况下,迭代加权的lq范数方法用更少迭代,也能够获得更加精确的估计。
4 仿真与分析本小节通过仿真实验验证提出方法的性能。在仿真中,考虑频控阵MIMO雷达系统的发射天线和接收天线数分别为N=M=12,天线阵列按均匀线阵布置,且收发天线间隔为半波长。发射信号选用加权CAN序列[18],序列长度L=32,接收快拍数为1。载频频率f0=10 GHz,频率增量Δf=3 MHz。感兴趣的目标
考虑4个目标位于不同距离和角度位置,具体参数为:
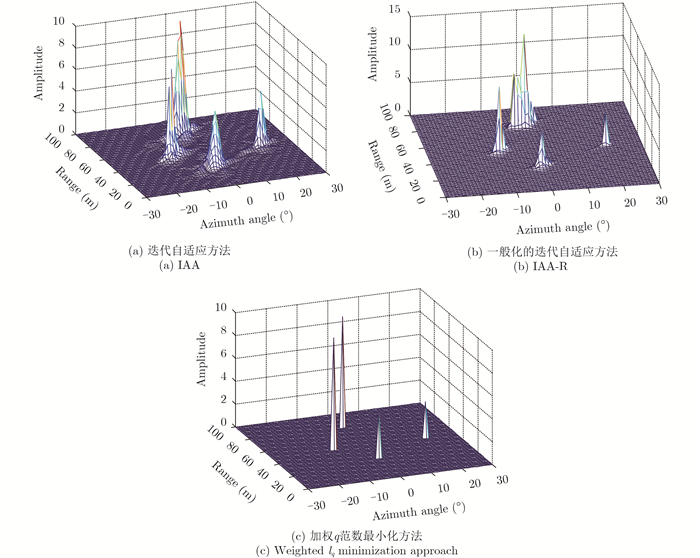
|
图 1 4个不同目标的估计结果 Fig.1 The estimation results using different approaches (L=4) |
考虑21个目标位于不同距离和角度的估计。图 2显示了不同方法的距离和角度估计结果,其中,图 2(a)显示了真实目标的距离和角度的位置信息,所有目标的幅度为10;图 2(b)-图 2(d)分别显示了DAS, IAA和IAA-R的估计结果。IAA和IAA-R的迭代次数为100次。由仿真结果可知,IAA和IAA-R估计性能要优于DAS估计,IAA-R估计性能要优于IAA;对比IAA和IAA-R,目标位于-20 时估计性能要优于其它目标位置,但都在真实的目标位置附近获得了虚假目标,也没能准确地估计到目标幅度。图 2(e)和图 2(f)分别显示了本文提出的方法经过20次迭代后得到的3维和2维(距离和角度)仿真结果,其中,q=0.8。如图显示,本文提出的方法除了获得了21个目标准确的距离和角度信息外,也获得了目标的幅度信息。
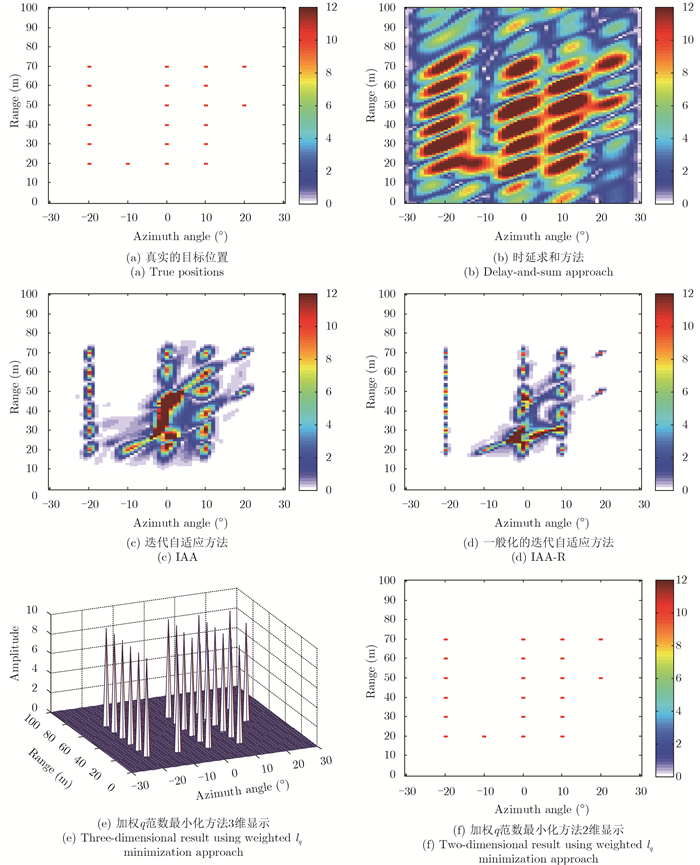
|
图 2 21个不同目标的估计结果 Fig.2 The estimation results using different approaches (L=21) |
图 3显示了本文提出的方法在不同信噪比情况下,获得精确的目标估计结果时不同q值与迭代次数之间的关系图。由图 3可知,在获得精确的目标估计结果时,本文提出的方法随着q值增加,相应地迭代次数也增加。当SNR=20 dB时,q=0.1时获得精确的目标估计时所需迭代次数为7,比q=0.9时所需迭代次数28次减少了1/4。这也证明了文献[17]中提到的lq范数代替l1范数时,可以利用更少的迭代便可重建信号。
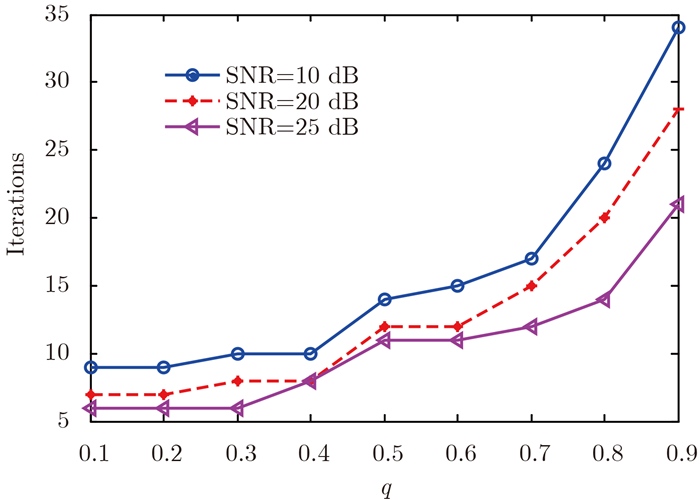
|
图 3 迭代次数与q值之间的关系 Fig.3 Relation between iterations and q |
本文给出了一种窄带频控阵MIMO雷达系统的模型,提出了将稀疏迭代的方法应用到频控阵MIMO雷达中,利用频控阵的发射导向矢量的距离和角度依赖性,结合稀疏迭代方法,在接收端通过单次快拍有效估计到目标的距离、角度以及幅度信息。结果表明,相比DAS估计、IAA和IAA-R,本文提出的方法除了获得了多个目标准确的距离和角度信息外,也获得了所有的目标幅度信息。
| [1] |
Paulraj A, Gore D, Nabar R, et al. An overview of MIMO communications—A key to gigabit wireless[J].
Proceedings of the IEEE, 2004, 92(2): 198-218. ( 0) 0)
|
| [2] |
Tarokh V, Seshadri N, Calderbank A R. Space-time codes for high data rate wireless communication: Performance criterion and code construction[J].
IEEE Transactions on Information Theory, 1998, 44(2): 744-765. ( 0) 0)
|
| [3] |
Bliss D W and Forsythe K W. Multiple-Input Multiple-Output (MIMO) radar and imaging: Degrees of freedom and resolution[C]. Proceeding 37th Asilomar Conference on Signal, System and Computers, Pacific Grove, CA, 2003, 1: 54–59.
( 0) 0)
|
| [4] |
Rabideau D and Parker P. Ubiquitous MIMO multifunction digital array radar[C]. Proceeding 37th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, 2003, 1: 1057–1064.
( 0) 0)
|
| [5] |
Fishler E, Haimovich A, Blum R, et al. . MIMO radar: An idea whose time has come[C]. Proceedings of the 2004 IEEE Radar Conference, Philadelphia, Pennsylvania, 2004: 71–78.
( 0) 0)
|
| [6] |
Antonik P, Wicks M C, Griffiths H D, et al. . Frequency diverse array radars[C]. 2006 IEEE Conference on Radar, Verona, New York, USA, 2006: 215–217.
( 0) 0)
|
| [7] |
巩朋成, 邵振海, 涂光鹏, 等. 基于发射方向图合成的低PAPR宽带MIMO雷达波形设计[J].
中国科学:信息科学, 2013, 43(3): 429-444. Gong Peng-cheng, Shao Zhen-hai, Tu Guang-peng, et al. Low PAPR waveform design based on transmit beampattern synthesis for wideband MIMO radars[J]. SCIENCE CHINA Information, 2013, 43(3): 429-444. DOI:10.1360/112012-503 (  0) 0)
|
| [8] |
Gong P, Shao Z, Tu G, et al. Transmit beampattern design based on convex optimization for MIMO radar systems[J].
Signal Processing, 2014, 94(1): 195-201. ( 0) 0)
|
| [9] |
Sammartino P F, Baker C J, Griffiths H D. Frequency diverse MIMO techniques for radar[J].
IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 201-222. ( 0) 0)
|
| [10] |
Wang W Q, So H C. Transmit subaperturing for range and angle estimation in frequency diverse array radar[J].
IEEE Transactions on Signal Processing, 2014, 62(8): 2000-2011. ( 0) 0)
|
| [11] |
许京伟, 廖桂生. 前视阵FDA-STAP雷达距离模糊杂波抑制方法[J].
雷达学报, 2015, 4(4): 386-392. Xu Jing-wei, Liao Gui-sheng. Range-ambiguous clutter suppression for forward-looking frequency diverse array space-time adaptive processing radar[J]. Journal of Radars, 2015, 4(4): 386-392. DOI:10.12000/JR15101 (  0) 0)
|
| [12] |
Wang W Q, Shao H Z. Range-angle localization of targets by a double-pulse frequency diverse array radar[J].
IEEE Journal of Selected Topics in Signal Processing, 2014, 8(1): 106-114. DOI:10.1109/JSTSP.2013.2285528 ( 0) 0)
|
| [13] |
王文钦, 邵怀宗, 陈慧. 频控阵雷达:概念、原理与应用[J].
电子与信息学报, 2016, 38(4): 1000-1011. Wang Wen-qin, Shao Huai-zong, Chen Hui. Frequency diverse array radar: Concept, principle and application[J]. Journal of Electronics & Information Technology, 2016, 38(4): 1000-1011. DOI:10.11999/JEIT151235 (  0) 0)
|
| [14] |
Roberts W, Stoica P, et al. Iterative adaptive approaches to MIMO radar imaging[J].
IEEE Journal of Selected Topics in Signal Processing, 2010, 4(1): 5-20. ( 0) 0)
|
| [15] |
Gong P, Shao Z. Target estimation by iterative reweighted lq minimization for MIMO radar[J].
Signal Processing, 2014, 101: 35-41. ( 0) 0)
|
| [16] |
Candès E J, Wakin M B, Boyd S P. Enhancing sparsity by reweighted l1 minimization[J].
Journal of Fourier Analysis and Applications, 2008, 14(5/6): 877-905. ( 0) 0)
|
| [17] |
Chartrand R. Exact reconstruction of sparse signals via nonconvex minimization[J].
IEEE Signal Processing Letter, 2007, 14(10): 707-710. ( 0) 0)
|
| [18] |
He H, Stoica P, Li J. Designing unimodular sequence sets with good correlations-including an application to MIMO radar[J].
IEEE Transactions on Signal Processing, 2009, 57(11): 4391-4405. ( 0) 0)
|




