1 引言
拖曳式雷达有源诱饵(Towed Radar Active Decoy,TRAD)作为一种载机外干扰源,通过施放与载机回波相似的非相干/相干干扰信号,使得雷达接收的目标回波和干扰信号互相干涉混叠,引起雷达观测的不确定,致使目标跟踪失效,进而使导弹命中概率急剧下降。目前,TRAD已成为空战中飞机目标的重要保护手段[1, 2, 3]。
由于TRAD在现代战争中具有比较好的作战效果,20世纪80年代中期以来,美、法等国家掀起了研制TRAD的热潮。目前,欧美国家公开报道的拖曳式雷达诱饵主要有ALE-50,ALE-55,Ariel,Sky Buzzer,BO2D等,其典型干扰样式是转发式干扰、噪声压制干扰和调制应答式干扰。但现役大量装备的拖曳式有源诱饵多为第1代诱饵(如ALE-50等),这也是唯一经过实战检验的诱饵[4],其基本功能是通过对雷达发射脉冲进行直接放大转发或简单调制放大转发而实现信号的转发或应答。因此本文从实际需求出发,主要研究转发式拖曳诱饵干扰的对抗问题。
目前,国内外关于拖曳式诱饵干扰的研究主要集中在干扰原理分析、性能仿真和效果评估等[5, 6, 7, 8, 9]方面,而关于干扰鉴别与抑制方法的研究较少。由于TRAD能够逼真地模拟目标的运动等特性,使得二者在时域、频域和空域上的差异都较小,常规的信号处理方法难以对其进行检测和分辨,无法抑制诱饵干扰。而极化描述了电磁波的矢量性,是幅度、频率、相位以外的一个重要基本参量,利用雷达目标和有源电子干扰在极化特性上的差异进行真假鉴别与抑制方法的研究日益增多[5, 10, 11]。然而,极化信息用于拖曳式诱饵干扰的鉴别与抑制方法研究尚少见诸报道。
事实上,目标回波信号的极化与雷达发射信号极化密切相关,而有源拖曳式诱饵干扰信号的极化与雷达发射极化无关,即二者合成信号为一个固定极化信号和一个与目标变极化效应相关的信号的矢量叠加,这与当无干扰条件下仅为与目标变极化效应相关的信号极化存在差异,可以通过极化编码等方式加以检测与抑制。本文研究了利用极化信息进行抑制机载拖曳式诱饵干扰的方法,给出了转发式诱饵干扰和雷达目标在单脉冲极化雷达测角系统中的不同极化通道响应函数,提出了一种转发式诱饵干扰的存在性检测与抑制方法,并结合典型干扰场景仿真验证了该方法的有效性。
2 全极化雷达回波模型及极化散射矩阵(PSM)的估计
2.1 目标的全极化雷达回波模型及其PSM的估计
对于极化散射矩阵为${{S}} = \left[{\begin{array}{*{20}{c}}
{{S_{{\rm{HH}}}}} & {{S_{{\rm{HV}}}}}\\
{{S_{{\rm{VH}}}}} & {{S_{{\rm{VV}}}}}
\end{array}} \right] = $
$\left[{\begin{array}{*{20}{c}}
{{S_{{\rm{HH}}}}} & {{S_{{\rm{HV}}}}}\\
{{S_{{\rm{HV}}}}} & {{S_{{\rm{VV}}}}}
\end{array}} \right]$
的目标而言,当雷达以某一极化方式为${{{P}}_i} = {\left[{{P_{i{\rm{H}}}},{P_{i{\rm{V}}}}} \right]^{\rm{T}}}\left( {i = 1,·\!·\!·,N} \right)$的脉冲信号激励目标时,对于水平极化(H)接收天线而言,空间特定位置雷达目标的和、差通道信号为[10, 11, 12]:
|
$\left. \begin{aligned}
{\Sigma _{{\rm{H}}{{\rm{P}}_i}}} & \!\!= \!\!a{{h}}_{\rm{H}}^{\rm{T}}{{S}}{{{P}}\!_i}f({\theta _0} \!+\! {\theta _S})e(t) \!+\! a{{h}}_{\rm{H}}^{\rm{T}}{{S}}{{{P}}\!_i}f({\theta _0} \!-\! {\theta _S})e(t)\\
& \!\!=\!\! a\!\left(\! {{S_{{\rm{HH}}}}{P_{i{\rm{H}}}} \!+\! {S_{{\rm{HV}}}}{P_{i{\rm{V}}}}} \!\right)\!\left[{f({\theta _0} \!-\! {\theta _S}) \!+\! f({\theta _0} \!+\! {\theta _S})} \right]\!\!e(t)\\
{\Delta _{{\rm{H}}{{\rm{P}}_i}}}& \!\!=\!\! a{{h}}_{\rm{H}}^{\rm{T}}{{S}}{{{P}}\!_i}f({\theta _0} \!+\! {\theta _S})e(t) \!-\! a{{h}}_{\rm{H}}^{\rm{T}}{{S}}{{{P}}\!_i}f({\theta _0} \!-\! {\theta _S})e(t)\\
& \!\!=\!\! a\!\left(\! {{S_{{\rm{HH}}}}{P_{i{\rm{H}}}} \!+\! {S_{{\rm{HV}}}}{P_{i{\rm{V}}}}} \!\right)\!\left[{f({\theta _0} \!+\! {\theta _S}) \!-\! f({\theta _0} \!-\! {\theta _S})} \right]\!\!e(t)\\
& \ \ \ \quad \ \ i = 1,·\!·\!· ,N
\end{aligned} \!\!\right\}$
|
(1) |
其中,
a为与雷达发射功率、天线增益、雷达与目标距离等因素有关的一个常量因子;
${{h}} _{\rm{H}}^{} = {\left[{1,0} \right]^{\rm{T}}}$为接收天线的极化方式;
$f(\theta )$为单脉冲雷达天线的电压方向图,
θ为来波偏离雷达视线(天线瞄准轴)的角度(为方便讨论,这里只考虑一个方位),
θ0为单脉冲雷达两个天线波束最大方向偏离天线瞄准方向的夹角,
θS为目标偏离雷达视线的角度;
e(
t)为与雷达发射信号波形有关的调制信号波形(时延、频移调制等)。由于
${\theta _S}$很小,有
$f({\theta _0} \pm {\theta _S}) \approx f({\theta _0}) \mp f'({\theta _0}){\theta _S}$[1, 4, 13],则有,
|
$\left. \begin{aligned}
{\Sigma _{{\rm{H}}{{\rm{P}}_i}}} & \approx 2af({\theta _0})e(t)\left( {{S_{{\rm{HH}}}}{P_{i{\rm{H}}}} + {S_{{\rm{HV}}}}{P_{i{\rm{V}}}}} \right)\\
{\Delta _{{\rm{H}}{{\rm{P}}_i}}}& \approx - 2af'({\theta _0}){\theta _S}e(t)\left( {{S_{{\rm{HH}}}}{P_{i{\rm{H}}}} + {S_{{\rm{HV}}}}{P_{i{\rm{V}}}}} \right)\\
& \quad \quad \ i = 1,·\!·\!·,N
\end{aligned} \right\}$
|
(2) |
对于垂直极化接收天线(V)而言,雷达目标的和差通道信号为:
|
$\left. \begin{aligned}
{\Sigma _{{\rm{V}}{{\rm{P}}_i}}} & \!=\! a\left(\! {{S_{{\rm{VH}}}}{P_{i{\rm{H}}}} \!\!+\!\! {S_{{\rm{VV}}}}{P_{i{\rm{V}}}}} \right)\!\left[{f({\theta _0} \!\!-\!\! {\theta _S}) \!\!+\!\! f({\theta _0} \!\!+\!\! {\theta _S})} \right]\!e(t)\\
& \approx\! 2af({\theta _0})e(t)\left( {{S_{{\rm{VH}}}}{P_{i{\rm{H}}}} \!\!+\!\! {S_{{\rm{VV}}}}{P_{i{\rm{V}}}}} \right)\\
{\Delta _{{\rm{V}}{{\rm{P}}_i}}}& \!\!=\!\! a\left( {{S_{{\rm{VH}}}}{P_{i{\rm{H}}}} \!\!+\!\! {S_{{\rm{VV}}}}{P_{i{\rm{V}}}}} \right)\left[{f({\theta _0} \!\!+\!\! {\theta _S}) \!\!-\!\! f({\theta _0} \!\!-\!\! {\theta _S})} \right]\!e(t)\\
& \approx \!-\! 2af'({\theta _0}){\theta _S}e(t)\left( {{S_{{\rm{VH}}}}{P_{i{\rm{H}}}} \!+\! {S_{{\rm{VV}}}}{P_{i{\rm{V}}}}} \right)\\
& \quad \quad \ i = 1,\cdots ,N
\end{aligned} \!\!\right\}$
|
(3) |
因此,选择任意的两组极化方式$\left( {{{{P}}\!_i},{{{P}}\!_j},\ i \ne j} \right)$ 的脉冲信号激励目标时,对式(2)、式(3)中的和通道信号进行匹配滤波(消除e(t)的影响)、幅相标定(消除$2a{{\rm e}^{{\rm j}\alpha }}f({\theta _0})$的影响)以后,可以得到如下关系式:
|
$\left. \begin{array}{l}
\Sigma _{{\rm{H}}{{\rm{P}}\!_i}}^{\prime } = {S_{{\rm{HH}}}}{P_{i{\rm{H}}}} + {S_{{\rm{HV}}}}{P_{i{\rm{V}}}}\\
\Sigma _{{\rm{V}}{{\rm{P}}\!_i}}^{\prime } = {S_{{\rm{VH}}}}{P_{i{\rm{H}}}} + {S_{{\rm{VV}}}}{P_{i{\rm{V}}}}\\
\Sigma _{{\rm{H}}{{\rm{P}}\!_j}}^{\prime } = {S_{{\rm{HH}}}}{P_{j{\rm{H}}}} + {S_{{\rm{HV}}}}{P_{j{\rm{V}}}}\\
\Sigma _{{\rm{V}}{{\rm{P}}\!_j}}^{\prime } = {S_{{\rm{VH}}}}{P_{j{\rm{H}}}} + {S_{{\rm{VV}}}}{P_{j{\rm{V}}}}\\
\quad \quad \quad \; i \ne j
\end{array} \right\}$
|
(4) |
式中,
$\Sigma _{{\rm{H}}{{\rm{P}}\!_i}}^{\prime }$,
$\Sigma _{{\rm{V}}{{\rm{P}}\!_i}}^{\prime }$分别为发射第
i个极化状态时,H极化与V极化接收和通道经过匹配滤波、幅相标定后的数据,
$\Sigma _{{\rm{H}}{{\rm{P}}\!_j}}^{\prime }$,
$\Sigma _{{\rm{V}}{{\rm{P}}\!_j}}^{\prime }$分别为发射第
j个极化状态时,H极化与V极化接收和通道经过匹配滤波、幅相标定后的数据。
进而可以估计得到目标的PSM为:
|
$\begin{array}{l}
{S_{{\rm{HH}}}}\! = \!\frac{{{P_{i{\rm{V}}}}\Sigma _{{\rm{H}}{{\rm{P}}_j}}^{\prime } \!\!-\!\! {P_{j{\rm{V}}}}\Sigma _{{\rm{H}}{{\rm{P}}_i}}^{\prime }}}{{{P_{j{\rm{H}}}}{P_{i{\rm{V}}}}\!\! -\!\! {P_{i{\rm{H}}}}{P_{j{\rm{V}}}}}},\!{S_{{\rm{HV}}}} \!= \!\!\frac{{{P_{i{\rm{H}}}}\Sigma _{{\rm{H}}{{\rm{P}}_j}}^{\prime } \!\!-\!\! {P_{j{\rm{H}}}}\Sigma _{{\rm{H}}{{\rm{P}}_i}}^{\prime }}}{{{P_{j{\rm{V}}}}{P_{i{\rm{H}}}} \!\!-\!\! {P_{i{\rm{V}}}}{P_{j{\rm{H}}}}}},\\
{S_{{\rm{VV}}}} \!= \!\frac{{{P_{j{\rm{H}}}}\Sigma _{{\rm{V}}{{\rm{P}}_i}}^{\prime } \!\!-\!\! {P_{i{\rm{H}}}}\Sigma _{{\rm{V}}{{\rm{P}}_j}}^{\prime }}}{{{P_{i{\rm{V}}}}{P_{j{\rm{H}}}} \!\!-\!\! {P_{j{\rm{V}}}}{P_{i{\rm{H}}}}}},\ i \ne j
\end{array}$
|
(5) |
也即通过任意一对脉冲信号,可估计出目标的PSM值为:
|
$\eqalign{
& {S_{i,j}} = \left[ \matrix{
{{{P_{i{\rm{V}}}}\Sigma _{{\rm{H}}{{\rm{P}}_j}}^\prime - {P_{j{\rm{V}}}}\Sigma _{{\rm{H}}{{\rm{P}}_i}}^\prime } \over {{P_{j{\rm{H}}}}{P_{i{\rm{V}}}} - {P_{i{\rm{H}}}}{P_{j{\rm{V}}}}}}{{{P_{i{\rm{H}}}}\Sigma _{{\rm{H}}{{\rm{P}}_j}}^\prime - {P_{j{\rm{H}}}}\Sigma _{{\rm{H}}{{\rm{P}}_i}}^\prime } \over {{P_{j{\rm{V}}}}{P_{i{\rm{H}}}} - {P_{i{\rm{V}}}}{P_{j{\rm{H}}}}}} \hfill \cr
{{{P_{i{\rm{H}}}}\Sigma _{{\rm{H}}{{\rm{P}}_j}}^\prime - {P_{j{\rm{H}}}}\Sigma _{{\rm{H}}{{\rm{P}}_i}}^\prime } \over {{P_{j{\rm{V}}}}{P_{i{\rm{H}}}} - {P_{i{\rm{V}}}}{P_{j{\rm{H}}}}}}{{{P_{j{\rm{H}}}}\Sigma _{{\rm{V}}{{\rm{P}}_i}}^\prime - {P_{i{\rm{H}}}}\Sigma _{{\rm{V}}{{\rm{P}}_j}}^\prime } \over {{P_{i{\rm{V}}}}{P_{j{\rm{H}}}} - {P_{j{\rm{V}}}}{P_{i{\rm{H}}}}}} \hfill \cr} \right] \cr
& = S,\quad i \ne j \cr} $
|
(6) |
2.2 存在拖曳式诱饵干扰下的雷达全极化回波模型及其等效PSM的估计
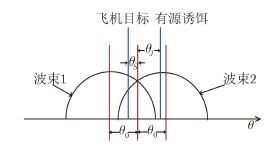
机载拖曳式有源诱饵在使用过程中,由于它与载机的航速、航向及雷达散射特征基本相同,雷达无法从角度、距离和速度上将目标与诱饵进行分辨,因此雷达会将目标与诱饵当作一个目标进行处理,造成测角偏差,并最终失去对目标的攻击能力。设有源诱饵的极化方式为${{{h}}_{\rm{J}}} = {\left[{{H_{{\rm{JH}}}},{H_{{\rm{JV}}}}} \right]^{\rm{T}}}$,$\left\| {{{{h}}_{\rm{J}}}} \right\| = 1$,不妨设有源诱饵和目标的几何关系如图 1所示。其中,θS表示飞机目标与瞄准轴的夹角,θJ表示有源诱饵与瞄准轴的夹角。
当雷达以极化方式为 ${{{P}}_i} = {\left[{{P_{i{\rm{H}}}},{P_{i{\rm{V}}}}} \right]^{\rm{T}}}\left( {i = } \right.$${1,·\!·\!·,N}$的脉冲信号激励目标时,对于水平极化接收天线而言,此时雷达的和、差通道信号为:
|
$\begin{align}
& {{\Sigma }_{\text{H}{{\text{P}}_{i}}}}=a\left( {{S}_{\text{HH}}}{{P}_{i\text{H}}}+{{S}_{\text{HV}}}{{P}_{i\text{V}}} \right)\left[ f({{\theta }_{0}}-{{\theta }_{S}})+f({{\theta }_{0}}+{{\theta }_{S}}) \right] \\
& \cdot e(t)+b{{H}_{\text{JH}}}\left[ f({{\theta }_{0}}-{{\theta }_{J}})+f({{\theta }_{0}}+{{\theta }_{J}}) \right]J(t) \\
& \approx 2af({{\theta }_{0}})e(t)\left( {{S}_{\text{HH}}}{{P}_{i\text{H}}}+{{S}_{\text{HV}}}{{P}_{i\text{V}}} \right)+2b{{H}_{\text{JH}}}f({{\theta }_{0}})J(t), \\
& {{\Delta }_{\text{H}{{\text{P}}_{i}}}}=a\left( {{S}_{\text{HH}}}{{P}_{i\text{H}}}+{{S}_{\text{HV}}}{{P}_{i\text{V}}} \right)\left[ f({{\theta }_{0}}+{{\theta }_{S}})-f({{\theta }_{0}}-{{\theta }_{S}}) \right] \\
& \cdot e(t)+b{{H}_{\text{JH}}}\left[ f({{\theta }_{0}}+{{\theta }_{J}})-f({{\theta }_{0}}-{{\theta }_{J}}) \right]J(t) \\
& \approx -2a{f}'({{\theta }_{0}}){{\theta }_{S}}e(t)\left( {{S}_{\text{HH}}}{{P}_{i\text{H}}}+{{S}_{\text{HV}}}{{P}_{i\text{V}}} \right)-2b{{H}_{\text{JH}}}{f}'({{\theta }_{0}}){{\theta }_{J}}J(t), \\
& \ i=1,\cdots ,N \\
\end{align}$
|
(7) |
其中,
b为与诱饵干扰功率、雷达发射功率、天线增益、雷达与目标距离等因素有关的一个常量因子,
θJ表示有源诱饵与瞄准轴的夹角,
J(
t)为有源诱饵干扰的信号形式。
对于垂直极化接收天线而言,雷达目标的和差通道信号为:
|
$\begin{align}
& {{\Sigma }_{\text{V}{{\text{P}}_{i}}}}=a\left( {{S}_{\text{VH}}}{{P}_{i\text{H}}}+{{S}_{\text{VV}}}{{P}_{i\text{V}}} \right)\left[ f({{\theta }_{0}}-{{\theta }_{S}})+f({{\theta }_{0}}+{{\theta }_{S}}) \right]\cdot \\
& e(t)+b{{H}_{\text{JV}}}\left[ f({{\theta }_{0}}-{{\theta }_{J}})+f({{\theta }_{0}}+{{\theta }_{J}}) \right]J(t) \\
& \approx 2af({{\theta }_{0}})e(t)\left( {{S}_{\text{VH}}}{{P}_{i\text{H}}}+{{S}_{\text{VV}}}{{P}_{i\text{V}}} \right)+2b{{H}_{\text{JV}}}f({{\theta }_{0}})J(t), \\
& {{\Delta }_{\text{V}{{\text{P}}_{i}}}}=a\left( {{S}_{\text{VH}}}{{P}_{i\text{H}}}+{{S}_{\text{VV}}}{{P}_{i\text{V}}} \right)\left[ f({{\theta }_{0}}+{{\theta }_{S}})-f({{\theta }_{0}}-{{\theta }_{S}}) \right]n \\
& \cdot e(t)+b{{H}_{\text{JV}}}\left[ f({{\theta }_{0}}+{{\theta }_{J}})-f({{\theta }_{0}}-{{\theta }_{J}}) \right]J(t) \\
& \approx -2a{f}'({{\theta }_{0}}){{\theta }_{S}}e(t)\left( {{S}_{\text{VH}}}{{P}_{i\text{H}}}+{{S}_{\text{VV}}}{{P}_{i\text{V}}} \right)-2b{{H}_{\text{JV}}}{f}'({{\theta }_{0}}){{\theta }_{J}}J(t) \\
& i=1,\cdots ,N \\
\end{align}$
|
(8) |
对于转发式有源诱饵而言,不妨设干扰信号与雷达发射调制信号波形存在如下关系:
其中,
G为转发增益。因此,依然选择任意的两组极化方式
$\left( {{{{P}}_i},{{{P}}_j},\ i \ne j} \right)$脉冲信号激励目标时的雷达接收信号,对其和通道信号进行匹配滤波、幅相标定以后,此时得到如下关系式:
|
$\left.\begin{array}{l}
\Sigma _{{\rm{H}}{{\rm{P}}_i}}^{\prime } = {S_{{\rm{HH}}}}{P_{i{\rm{H}}}} + {S_{{\rm{HV}}}}{P_{i{\rm{V}}}} + \frac{{bG}}{a}{H_{{\rm{JH}}}}\\
\Sigma _{{\rm{V}}{{\rm{P}}_i}}^{\prime } = {S_{{\rm{VH}}}}{P_{i{\rm{H}}}} + {S_{{\rm{VV}}}}{P_{i{\rm{V}}}} + \frac{{bG}}{a}{H_{{\rm{JV}}}}\\
\Sigma _{{\rm{H}}{{\rm{P}}_j}}^{\prime } = {S_{{\rm{HH}}}}{P_{j{\rm{H}}}} + {S_{{\rm{HV}}}}{P_{j{\rm{V}}}} + \frac{{bG}}{a}{H_{{\rm{JH}}}}\\
\Sigma _{{\rm{V}}{{\rm{P}}_j}}^{\prime } = {S_{{\rm{VH}}}}{P_{j{\rm{H}}}} + {S_{{\rm{VV}}}}{P_{j{\rm{V}}}} + \frac{{bG}}{a}{H_{{\rm{JV}}}}\\
\quad \quad \quad \quad \ i \ne j
\end{array} \right\}$
|
(10) |
此时,仍按式(5)和式(6)计算出此时的等效PSM(记为列矢量)为:
|
$\begin{aligned}
{{{S}}_{i,j}} & = \left[\begin{array}{l}
{S_{{\rm{HH}}}} + \frac{{{P_{i{\rm{V}}}} - {P_{j{\rm{V}}}}}}{{{P_{j{\rm{H}}}}{P_{i{\rm{V}}}} - {P_{i{\rm{H}}}}{P_{j{\rm{V}}}}}}\frac{{bG}}{a}{H_{{\rm{JH}}}}\\
{S_{{\rm{HV}}}} + \frac{{{P_{i{\rm{H}}}} - {P_{j{\rm{H}}}}}}{{{P_{j{\rm{V}}}}{P_{i{\rm{H}}}} - {P_{i{\rm{V}}}}{P_{j{\rm{H}}}}}}\frac{{bG}}{a}{H_{{\rm{JH}}}}\\
{S_{{\rm{VV}}}} + \frac{{{P_{j{\rm{H}}}} - {P_{i{\rm{H}}}}}}{{{P_{i{\rm{V}}}}{P_{j{\rm{H}}}} - {P_{j{\rm{V}}}}{P_{i{\rm{H}}}}}}\frac{{bG}}{a}{H_{{\rm{JV}}}}
\end{array} \right]\\
& = \left[\begin{array}{l}
{S_{{\rm{HH}}}}\\
{S_{{\rm{HV}}}}\\
{S_{{\rm{VV}}}}
\end{array} \right] + \frac{{bG}}{a}\left[\begin{array}{l}
\frac{{{P_{i{\rm{V}}}} - {P_{j{\rm{V}}}}}}{{{P_{j{\rm{H}}}}{P_{i{\rm{V}}}} - {P_{i{\rm{H}}}}{P_{j{\rm{V}}}}}}{H_{{\rm{JH}}}}\\
\frac{{{P_{i{\rm{H}}}} - {P_{j{\rm{H}}}}}}{{{P_{j{\rm{V}}}}{P_{i{\rm{H}}}} - {P_{i{\rm{V}}}}{P_{j{\rm{H}}}}}}{H_{{\rm{JH}}}}\\
\frac{{{P_{j{\rm{H}}}} - {P_{i{\rm{H}}}}}}{{{P_{i{\rm{V}}}}{P_{j{\rm{H}}}} - {P_{j{\rm{V}}}}{P_{i{\rm{H}}}}}}{H_{{\rm{JV}}}}
\end{array} \right]\\
& = {{S}} + {{{S}}_{\rm{J}}}\left( {i,j} \right),\ i \ne j
\end{aligned}$
|
(11) |
其中
|
${{{S}}_{\rm{J}}}\left( {i,j} \right) = \frac{{bG}}{a}\left[\begin{array}{l}
\frac{{{P_{i{\rm{V}}}} - {P_{j{\rm{V}}}}}}{{{P_{j{\rm{H}}}}{P_{i{\rm{V}}}} - {P_{i{\rm{H}}}}{P_{j{\rm{V}}}}}}{H_{{\rm{JH}}}}\\
\frac{{{P_{i{\rm{H}}}} - {P_{j{\rm{H}}}}}}{{{P_{j{\rm{V}}}}{P_{i{\rm{H}}}} - {P_{i{\rm{V}}}}{P_{j{\rm{H}}}}}}{H_{{\rm{JH}}}}\\
\frac{{{P_{j{\rm{H}}}} - {P_{i{\rm{H}}}}}}{{{P_{i{\rm{V}}}}{P_{j{\rm{H}}}} - {P_{j{\rm{V}}}}{P_{i{\rm{H}}}}}}{H_{{\rm{JV}}}}
\end{array} \right]$
|
也即对于任意一对脉冲,估计出的PSM值与目标PSM真实值存在显著差异,且互不相同,这为有源诱饵存在的检测、鉴别与抑制提供了依据和支撑。
3 TRAD的存在性检测与抑制算法
3.1 极化检测特征量的设计
由式(5)、式(6)和式(11)可知,假设雷达的发射信号为由N个不同极化方式的子脉冲组成的极化调制脉冲信号,
|
${{{E}}_{\rm{T}}} = \left\{ {{{{P}}_1},{{{P}}_2},·\!·\!· ,{{{P}}_N}} \right\}$
|
(12) |
其中,
${{{P}}_1},{{{P}}_2},\cdots ,{{{P}}_N}$表示
N个不同极化方式的子脉冲,子脉冲脉宽为
${\tau\! _{_P}}$,发射信号脉冲宽度为
${T_P} = N{\tau\! _{_P}}$。接收时,双正交极化(不妨设水平/垂直极化,H/V)通道同时接收,根据子脉冲的双正交极化通道接收信号可以反演出目标的极化散射矩阵(PSM),而且对子脉冲对应回波进行两两组合可反演得到
$M = \left( {N(N - 1)} \right)/2$组PSM估计值。
当没有干扰时,考虑到此时为跟踪状态,雷达接收回波的信噪比较高,因此目标PSM的M组估计值精度较高,一致性好;而存在有源诱饵干扰时,计算M组PSM的估计值与目标真实PSM值相差较大,且互不相同。因此,可以借鉴极化聚类中心和极化散度[14]的概念来刻画此种差异,设计有源诱饵存在性检测的鉴别量。
若M组PSM估计值记为列矢量为${{{S}}_k} = $
$
{\left[\!{\begin{array}{*{20}{c}}
{{S_{{\rm{HH}}k}}} & {{S_{{\rm{HV}}k}}} & {{S_{{\rm{VV}}k}}}
\end{array}} \!\right]^{\rm T}}$,$k = 1,·\!·\!·,M$,那么PSM的聚类中心定义为:
|
$\overline {{S}}\!\! =\! \frac{1}{M}\!\sum\limits_{k = 1}^M \!{{{{S}}_k}}\! = \!\frac{1}{M}\!\!{\left[\!\!\! {\begin{array}{*{20}{c}}
{\sum\limits_{k = 1}^M {{S_{{\rm{HH}}k}}} } & \! {\sum\limits_{k = 1}^M {{S_{{\rm{HV}}k}}} } & \! {\sum\limits_{k = 1}^M {{S_{{\rm{VV}}k}}} }
\end{array}} \!\!\!\!\right]^{\rm{T}}}$
|
(13) |
PSM的分布散度定义为:
|
${{Δ} _S} = \frac{1}{M}\sum\limits_{k = 1}^M {\left( {{{{S}}_k} - \overline {{S}}} \right)} {\left( {{{{S}}_k} - \overline {{S}}} \right)^{\rm{H}}}$
|
(14) |
其中,上标“H”表示共轭转置。
在没有干扰时,PSM的聚类中心为$\overline {{S}} = {\left[{{S_{{\rm{HH}}}},{S_{{\rm{HV}}}},{S_{{\rm{VV}}}}} \right]^{\rm T}} = {{S}}$,分布散度为${{Δ} _S} = 0$;存在拖曳式有源干扰时,PSM的聚类中心为:
|
$\overline {{S}} = {{S}} + \frac{1}{M}\sum\limits_{k = 1}^M {{{{S}}_{\rm{J}}}\left( k \right)} $
|
(15) |
其分布散度为:
|
$\begin{aligned}
{{Δ} _S} = & \frac{1}{M}\sum\limits_{k = 1}^M {\left[{{{{S}}_{\rm{J}}}\left( k \right) - \frac{1}{M}\sum\limits_{k = 1}^M {{{{S}}_{\rm{J}}}\left( k \right)} } \right]} \\
& \cdot {\left[{{{{S}}_{\rm{J}}}\left( k \right) - \frac{1}{M}\sum\limits_{k = 1}^M {{{{S}}_{\rm{J}}}\left( k \right)} } \right]^{\rm{H}}} > 0
\end{aligned}$
|
(16) |
因此,可以根据PSM值分布散度的相对大小来检验是否存在转发式拖曳式诱饵干扰信号,即:
|
$\eta = \frac{{{{Δ}_S}}}{{{{\overline {{S}}}^{\rm{H}}}\overline {{S}}}} = \left\{ \begin{array}{l}
\ge {{{T}}_{\rm{h}}},\begin{array}{*{20}{c}}
& \!\!\!{{存在干扰}}
\end{array}\\
< {{{T}}_{\rm{h}}},\!\!\!\begin{array}{*{20}{c}}
& {{不存在干扰}}
\end{array}
\end{array} \right.$
|
(17) |
其中,
Th为鉴别门限,与子脉冲的个数、干信比等因素有关,经统计分析一般可取值为0.2。
3.2 极化抑制算法
前面给出了干扰存在性的检验方法,在此基础上,根据雷达各个子脉冲的接收回波的极化特性的差异,可以滤除干扰信号,并进行单脉冲测角处理,给出正确的角度测量值。
由式(7)、式(8)和式(9)可知,对于任一对子脉冲而言,对差通道信号进行匹配滤波、幅相标定以后,此时得到如下关系式:
|
$\left. \begin{aligned}
\Delta _{{\rm{H}}{{\rm{P}}_i}}^{\prime} \approx & - \frac{{f'({\theta _0})\left( {{S_{{\rm{HH}}}}{P_{i{\rm{H}}}} + {S_{{\rm{HV}}}}{P_{i{\rm{V}}}}} \right)}}{{f({\theta _0})}}{\theta _S}\\
& - \frac{{bG{H_{{\rm{JH}}}}f{'}({\theta _0})}}{{af({\theta _0})}}{\theta _J}\\
\Delta _{{\rm{V}}{{\rm{P}}_i}}^{\prime} \approx & - \frac{{f'({\theta _0})\left( {{S_{{\rm{VH}}}}{P_{i{\rm{H}}}} + {S_{{\rm{VV}}}}{P_{i{\rm{V}}}}} \right)}}{{f({\theta _0})}}{\theta _S}\\
& - \frac{{bG{H_{{\rm{JV}}}}f{'}({\theta _0})}}{{af({\theta _0})}}{\theta _J}\\
& \quad i = 1,·\!·\!· ,N
\end{aligned} \right\}$
|
(18) |
根据经典单脉冲测角方法,此时测角值为:
|
$\left.\begin{array}{l}
\frac{{\Delta _{{\rm{H}}{{\rm{P}}_i}}^{\prime}}}{{\Sigma _{{\rm{H}}{{\rm{P}}_i}}^{\prime}}} \!\!=\!\! - \!\frac{{f{'}({\theta _0})}}{{f({\theta _0})}}\frac{{\left( {{S_{{\rm{HH}}}}{P_{i{\rm{H}}}} \!+\! {S_{{\rm{HV}}}}{P_{i{\rm{V}}}}} \right){\theta _S} \!+\! \displaystyle\frac{{bG{H_{{\rm{JH}}}}}}{a}{\theta _J}}}{{{S_{{\rm{HH}}}}{P_{i{\rm{H}}}} \!+ \! {S_{{\rm{HV}}}}{P_{i{\rm{V}}}} \!+\! \displaystyle\frac{{bG{H_{{\rm{JH}}}}}}{a}}}\\
\frac{{\Delta _{{\rm{V}}{{\rm{P}}_i}}^{\prime}}}{{\Sigma _{{\rm{V}}{{\rm{P}}_i}}^{\prime}}} \!\!=\!\! - \!\frac{{f{'}({\theta _0})}}{{f({\theta _0})}}\frac{{\left( {{S_{{\rm{VH}}}}{P_{i{\rm{H}}}} \!+\! {S_{{\rm{VV}}}}{P_{i{\rm{V}}}}} \right){\theta _S} \!+\! \displaystyle\frac{{bG{H_{{\rm{JV}}}}}}{a}{\theta _J}}}{{{S_{{\rm{VH}}}}{P_{i{\rm{H}}}} \!+\! {S_{{\rm{VV}}}}{P_{i{\rm{V}}}} \!+\! \displaystyle\frac{{bG{H_{{\rm{JV}}}}}}{a}}}
\end{array} \!\!\!\! \right\}$
|
(19) |
也就是说,实际的测角值将是${\theta _S},\ {\theta _J}$的加权平均值,但通过上述的研究可以发现,根据式(10)有
|
$\Sigma _{{\rm{H}}{{\rm{P}}_i}}^{\prime} \!-\! \Sigma _{{\rm{H}}{{\rm{P}}_j}}^{\prime} \!=\! {S_{{\rm{HH}}}}\left( {{P_{i{\rm{H}}}} \!-\! {P_{j{\rm{H}}}}} \right) \!+\! {S_{{\rm{HV}}}}\left( {{P_{i{\rm{H}}}} \!-\! {P_{j{\rm{H}}}}} \right)$
|
(20) |
同样,根据式(18)有
|
$\Delta _{{\rm{H}}{{\rm{P}}_i}}^{\prime}\! \!-\!\! \Delta _{{\rm{H}}{{\rm{P}}_j}}^{\prime}\!\! =\!\! \frac{{f'({\theta _0})}}{{f({\theta _0})}}\!{\theta _S}\!\left[{{S_{{\rm{HH}}}}\!\left(\! {{P_{j{\rm{H}}}} \!\!-\!\! {P_{i{\rm{H}}}}}\! \right) \!\!+\!\! {S_{{\rm{HV}}}}\left( {{P_{j{\rm{V}}}} \!-\! {P_{i{\rm{V}}}}} \right)} \right]$
|
(21) |
根据式(20)、式(21),目标角度值可以由式(22)得到
|
${\hat \theta _{\rm H}} = \frac{{\Delta _{{\rm{H}}{{\rm{P}}_i}}^{\prime} - \Delta _{{\rm{H}}{{\rm{P}}_j}}^{\prime}}}{{\Sigma _{{\rm{H}}{{\rm{P}}_i}}^{\prime} - \Sigma _{{\rm{H}}{{\rm{P}}_j}}^{\prime}}}$
|
(22) |
于是有
|
${\hat \theta _{\rm H}} = - \frac{{f'({\theta _0})}}{{f({\theta _0})}}{\theta _S},\ \ i \ne j$
|
(23) |
同理,可以得到
|
${\hat \theta _{\rm V}} = \frac{{\Delta _{{\rm{V}}{{\rm{P}}_i}}^{\prime} - \Delta _{{\rm{V}}{{\rm{P}}_j}}^{\prime}}}{{\Sigma _{{\rm{V}}{{\rm{P}}_i}}^{\prime} - \Sigma _{{\rm{V}}{{\rm{P}}_j}}^{\prime}}} = - \frac{{f'({\theta _0})}}{{f({\theta _0})}}{\theta _S},\ \ i \ne j$
|
(24) |
由式(23),式(24)可见,经过不同子脉冲信息的融合,可以得到目标角度的精确测量值,且该值与子脉冲的极化状态无关。
4 仿真实验与结果分析
假设在我方跟踪阶段敌方战机发现被锁定后投放拖曳式诱饵进行对抗,我方雷达测角方式为比幅单脉冲测角,敌方拖曳式诱饵工作方式为直接放大转发。发射的子脉冲${{{P}}_1},{{{P}}_2},·\!·\!· ,{{{P}}_N}$均为线极化,可以统一由${{{P}}_k} = {\left[{\cos \left( {\frac{{k\pi }}{N}} \right),\sin \left( {\frac{{k\pi }}{N}} \right)} \right]^{\rm T}}$,$k = 0,1,2,·\!·\!·,N - 1$表示,相位差${\eta _k} = 0$。雷达发射信号的中心频率${f_0} = 10 \; {\rm GHz}$,目标为某飞机在某姿态角下的散射矩阵为${{S}} \!=\! \left[{\begin{array}{*{20}{c}}
1 \! & \! {0.2\! +\! {\rm j}0.45}\\
{0.2\! + \!{\rm j}0.45} \! & \! {0.7}
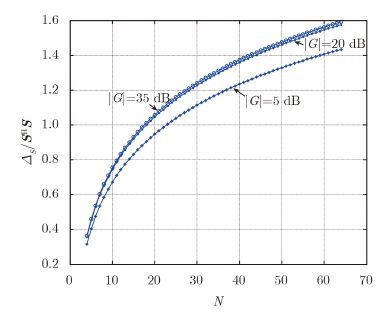
\end{array}} \right],$$\;b/a = 1$,天线的主瓣宽度4°。图 2给出鉴别量$\eta $随发射信号子脉冲个数N的变化曲线。
从图 2可见,随着子脉冲数N的增大,$\eta $的值单调增加,这意味着作为判断干扰存在与否的鉴别量性能也随着子脉冲数的增加而改善。这个结论在直观上可以这样理解:对于N=4和N=8这两种情况,发射子脉冲的极化按照${{{P}}_k} = {\left[{\cos \left( {\frac{{k\pi }}{N}} \right),\sin \left( {\frac{{k\pi }}{N}} \right)} \right]^{\rm T}}$,$k = 0,1,2,·\!·\!·,N - 1$的取法,N=4的情况显然包含在N=8中,即后者多包含了${{{P}}_k} \!=\! {\left[\! {\cos \left(\! {\frac{{k\pi }}{N}}\! \right),\sin \!\left( \!{\frac{{k\pi }}{N}} \!\right)}\! \right]^{\rm T}}$,k=1,3,5,7四组极化,这必然导致散度值的增加。另外观察图 2的|G|=5,|G|=20,|G|=35三条曲线可以发现,随着转发增益|G|的增大,相应的$\eta $值也随之增大,但是从|G|=20到|G|=35增加的幅度并不十分明显。图 3给出了N=16时,$\eta $随|G|增大的渐进过程。由图 3可见,即使当|G|不是特别大时,鉴别量$\eta $的值也是十分接近极限值的,这说明,本鉴别算法适用范围是较为宽泛的。
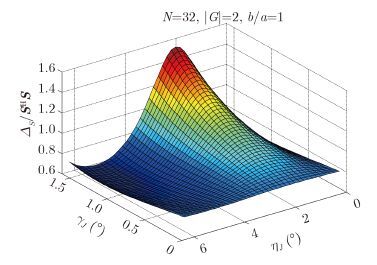
图 4仿真分析了干扰极化状态对鉴别量的影响,其中${\gamma _J} \in [0,{90^ \circ }]$,${\eta _J} \in [0,{360^ \circ }]$。 从图 4的结果可见,${\gamma _J}$,${\eta _J}$的变化对鉴别量的值影响明显,且在${\gamma _J} \in [0,{90^ \circ }]$,${\eta _J} \in [0,{360^ \circ }]$范围内存在峰值和谷值。这意味着对于干扰方可以通过控制不同极化通道的幅度比将鉴别量的值减小到最小,以此提高干扰性能。但是即使是在鉴别量值最小的时刻,本文设定的门限依然有效。
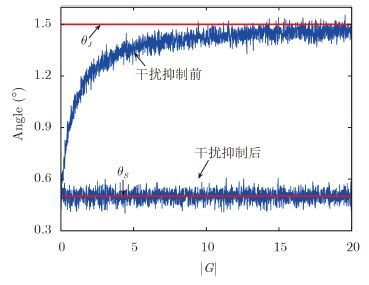
最后,在判定存在拖曳式干扰后,采用本文所提出的办法进行抑制。图 5给出了测角值随干扰转发增益|G|的变化曲线,其中θS=0.5°,θJ=1.5°,信噪比为10 dB,干扰抑制之前的角度测量值取所有子脉冲组合测角的均值。由图 5可见,在未采用抑制算法之前,随着转发增益的增大,角度测量值将逐渐离开真实值过渡到θJ,采用本文算法后,角度测量值在真实值附近波动,表明拖曳式诱饵干扰得到了有效的抑制。
5 结束语
机载拖曳式有源干扰是对抗防空导弹的有效手段,对导弹末制导构成了严峻挑战。本文研究了利用极化信息鉴别机载拖曳式有源转发干扰的方法,并给出了抑制该类型干扰的算法,理论分析和计算机仿真均证实了本文算法的正确性和有效性。本文的研究工作对于雷达系统优化设计、干扰系统优化设计等应用领域有着一定的参考价值。

 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)




