② (西安电子科技大学 西安 710071)
③ (中国人民解放军95890部队 武汉 430000)
② (Xidian University, Xi'an 710071, China)
③ (Unit 95890 of PLA, Wuhan 430000, China)
纵观空时自适应信号处理(Space Time Adaptive Processing,STAP)[1-3]技术40多年的发展历程,STAP技术作为一种信号处理技术,由于可以通过对载机平台运动的补偿实现最优杂波抑制。因而自从20世纪70年代Brennan等人首先将最优处理器应用到机载雷达中以来,STAP技术便成为国际上研究的热点。然而,STAP技术用于实际系统时,其主要困难在于对杂波协方差矩阵求逆的运算量巨大,所以研究降维准最优处理方法成为STAP的核心内容。现有的固定结构降维STAP算法主要包括:Klemm先后提出的空时级联处理[4]和辅助通道法[5],保铮等提出的m路多普勒通道进行联合自适应处理的方法(m Doppler Time,mDT)[6],Wang等人提出的局域联合处理的算法(Joint Domain Localized,JDL)[7]和王永良等提出的空时相邻多波束算法(Space Time Multiple Beam,STMB)[8]等。
多输入多输出(Multiple-Input Multiple-Output,MIMO)雷达[9, 10]因其具有探测性能好、反隐身、抗干扰及反侦察能力强等优势,受到国内外研究人员的高度关注。传统相控阵雷达中天线发射相干波形,可形成窄发射波束。而MIMO雷达中发射非相干(或正交)波形,因此形成宽(或全方向)发射波束。文献[11, 12]等对机载MIMO雷达STAP技术的研究表明:MIMO雷达发射正交信号产生的分集特性,扩展了其杂波抑制处理的系统自由度,这为设计MIMO体制下高性能的杂波抑制技术带来了机遇。
由于扩展了系统处理的自由度,MIMO雷达STAP技术在高维协方差矩阵求逆时运算量的问题更加突出。若R为QNK×QNK维方阵,则对其求逆需要的运算量为O[(QNK)3]量级,需要进行降维处理才能达到实时处理的要求。因此,针对MIMO雷达的降维STAP算法[13, 14]成为国内外一个研究的热点。上述针对相控阵的STAP降维方法经过修改后可用于MIMO雷达系统,形成了各种MIMO雷达收发联合(Joint Transmitter-Receiver,JTR)自适应的降维算法,以降低算法的运算量。通过分析不难发现,上述的方法可以用一个统一的理论框架来进行描述,现有的大多数的MIMO雷达STAP降维算法都可以归于这一框架内。本文在研究机载MIMO雷达杂波抑制的收发联合自适应的降维STAP(Joint Transmitter-Receiver Space Time Adaptive Processing,JTR-STAP)算法的基础上,提出了MIMO雷达JTR-STAP处理的统一理论框架结构,并建立了3种收发联合自适应降维STAP处理结构,最后给出了3种适用于MIMO体制的降维STAP处理算法。
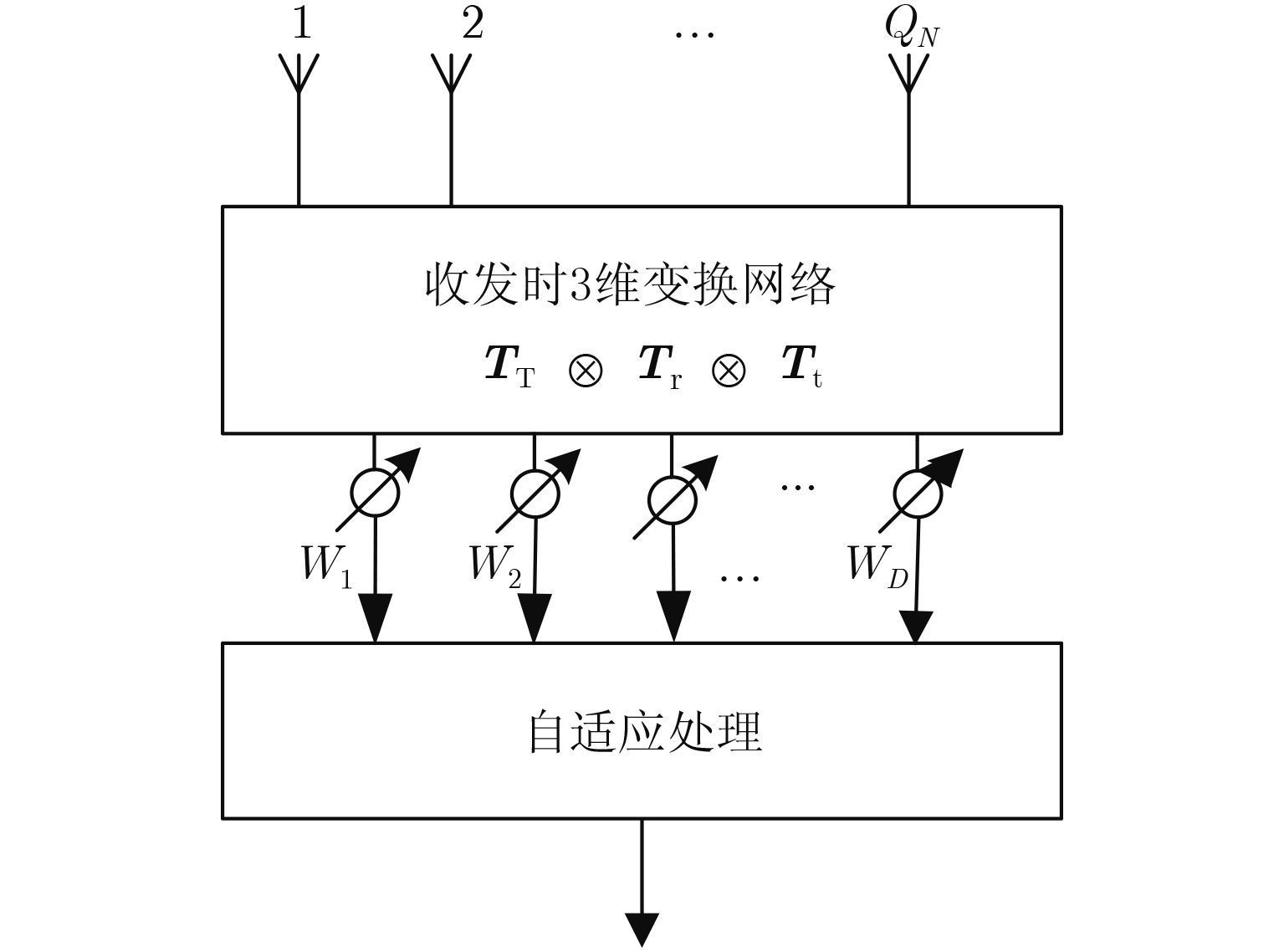
2 降维JTR-STAP算法的统一理论框架机载MIMO雷达收发联合的降维空时自适应处理(JTR-STAP)算法的统一框架结构如图 1所示,JTR-STAP通过使用与杂波数据无关的线性变换矩阵来降低MIMO雷达的系统自由度,从而达到减少计算量和训练数据样本数量的目的,同时利用MIMO雷达的发射波形分集的特点从发射空域、接收空域和时域同时降维,实现“收发时”3个域的联合STAP处理。JTR-STAP即充分发挥MIMO雷达的波形分集在杂波抑制中的优势,又充分利用了现有的相控阵的接收端STAP处理的技术,实现了机载MIMO雷达杂波抑制性能的大幅提升[15]。本文STAP算法设计的思路在于从发射和接收端同时形成凹口进行杂波抑制。
|
图 1 降维JTR-STAP算法的统一框架结构 Fig.1 The unified frame structure of reduced dimensional JTR-STAP algorithm |
依据MIMO STAP收发时域联合自适应的原理,总结相控阵雷达STAP处理算法的结构模型,将机载MIMO雷达JTR-STAP算法的统一理论框架描述如下。
机载MIMO雷达进行降维STAP处理时,发射阵列空域、接收阵列空域和时间域的联合降维变换矩阵T 可表述为:
| $T={{T}_{\text{T}}}\otimes {{T}_{\text{r}}}\otimes {{T}_{\text{t}}}\in {{\mathbb{C}}^{QNK\times D}}$ | (1) |
其中,${{T}_{\text{T}}}\in {{\mathbb{C}}^{K\times {{K}_{D}}}},{{T}_{\text{r}}}\in {{\mathbb{C}}^{N\times {{N}_{D}}}},{{T}_{\text{t}}}\in {{\mathbb{C}}^{Q\times {{Q}_{D}}}}$分别为时域、接收空域和发射空域的1维变换矩阵,D=KDNDQD,代表了对“收发时”3域上的联合降维处理。由T 对全空时杂波采样数据矢量X进行降维变换后的空时数据
| ${{Y}} = {{{T}}^{\rm{H}}}{{{X}} = }\left( {{{{T}}_{\rm{T}}} \otimes {{{T}}_{\rm{r}}} \otimes {{{T}}_{\rm{t}}}} \right){{X}}$ | (2) |
则联合降维变换后的空时导向矢量变为:
| ${{{S}}_{\rm{Z}}} = {{{T}}^{\rm{H}}}{{{S}} = }\left( {{{T}}_{\rm{T}}^{\rm{H}}{{{S}}_{\rm{T}}}} \right) \otimes \left( {{{T}}_{\rm{r}}^{\rm{H}}{{{S}}_{\rm{r}}}} \right) \otimes \left( {{{T}}_{\rm{t}}^{\rm{H}}{{{S}}_{\rm{t}}}} \right)$ | (3) |
其中,$S=S\left( {{f}_{d,l}},{{\psi }_{0}} \right)={{S}_{\text{T}}}\left( {{f}_{dk}} \right)\otimes {{S}_{\text{r}}}\left( {{\psi }_{0}} \right)\otimes {{S}_{\text{t}}}\left( {{\psi }_{0}} \right)$表示主波束指向(锥角为${\psi _0}$)上对应第l个待检测多普勒通道的空时导向矢量。为了便于书写,此处省略相应参数符号。
采样数据协方差矩阵变为:
| ${{{R}}_{\rm{Z}}} = {{{T}}^{\rm{H}}}{{RT}}$ | (4) |
根据线性约束最小方差(Linear Constrain Mininum Variance,LCMV)准则可知,在统一降维处理结构下计算时空2维自适应权${{{{W}}}_{\rm{Z}}} \in \mathbb {C} ^{{Q_D}{N_D}{K_D} \times 1}$的优化模型为
| $ \left. \begin{array}{l} \min {\rm{ }}{{W}}_{\rm{Z}}^{\rm{H}}{{{T}}^{\rm{H}}}{{RT}}{{{W}}_{\rm{Z}}}\\ {\rm s.t}. \ \,{\rm{ }}{{W}}_{\rm{Z}}^{\rm{H}}{{{S}}_{\rm{Z}}} = 1 \end{array} \right\}$ | (5) |
式(5)体现了机载MIMO雷达发射、接收和时域3维空间上的联合优化处理,称之为收发联合降维STAP(JTR-STAP)算法统一框架。求解式(5)可以得
| $\begin{align} & {{W}_{\text{Z}}}=\mu {{\left[ {{T}^{\text{H}}}RT \right]}^{-1}}{{S}_{\text{Z}}} \\ & =\mu {{\left[ {{\left( T_{\text{T}}^{\text{H}}\otimes T_{\text{r}}^{\text{H}}\otimes T_{\text{t}}^{\text{H}} \right)}^{\text{H}}}R\left( T_{\text{T}}^{{}}\otimes T_{\text{r}}^{{}}\otimes T_{\text{t}}^{{}} \right) \right]}^{-1}} \\ & \cdot \left( T_{\text{T}}^{\text{H}}{{S}_{\text{T}}}\otimes T_{\text{r}}^{\text{H}}{{S}_{\text{r}}}\otimes T_{\text{t}}^{\text{H}}{{S}_{\text{t}}} \right) \\ \end{align}$ | (6) |
其中,μ为常数。
则JTR-STAP处理后第l个待检测多普勒通道的输出为:
| $z\left( {{f}_{d,l}} \right)=W_{\text{Z}}^{\text{H}}Y$ | (7) |
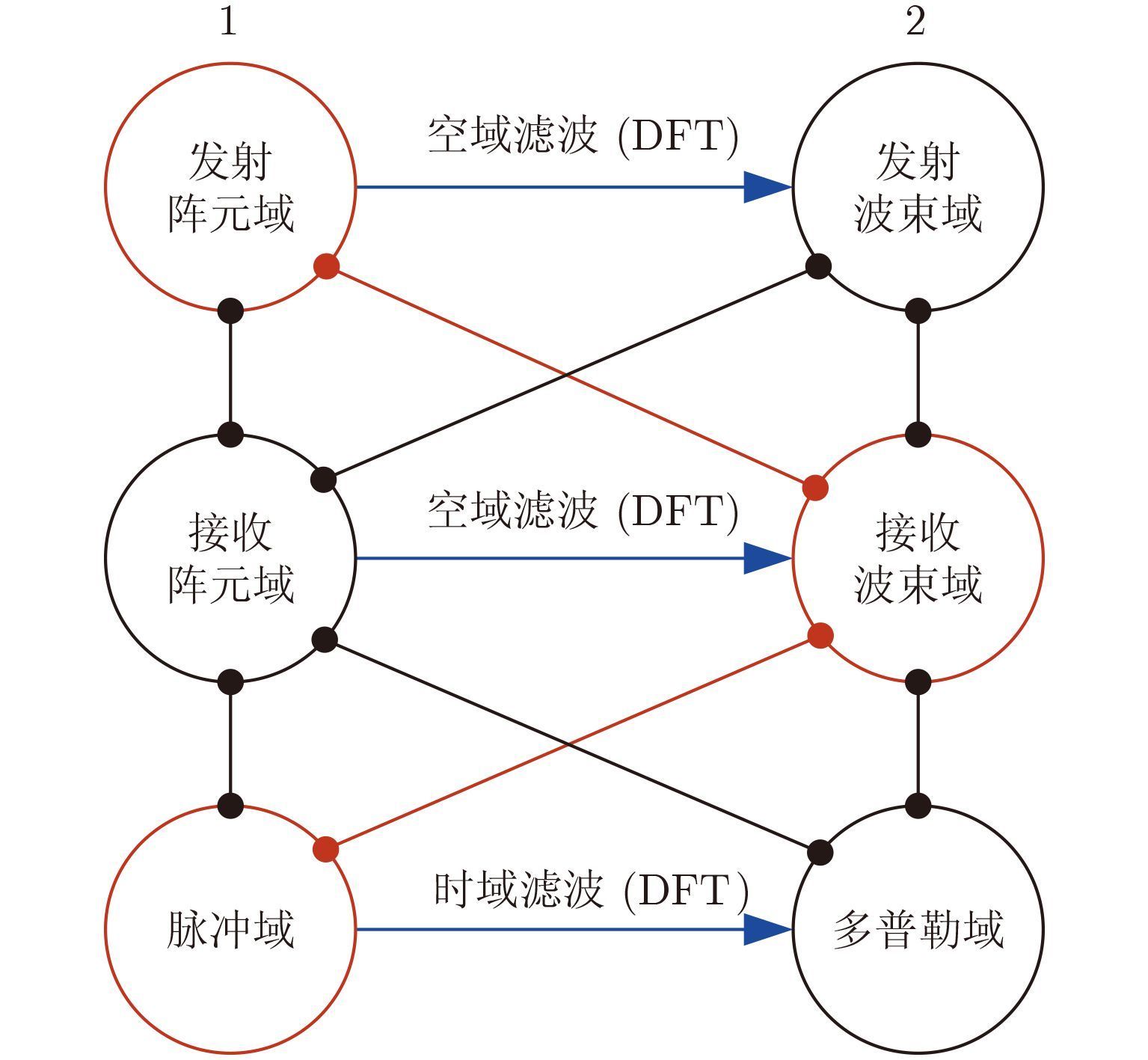
式(6)中包含了对发射阵列的降维变换矩阵Tt和接收阵列的降维变换矩阵Tr。因此式(6)即为收发联合空时变换自适应处理器权值计算的统一表达式。降维STAP处理的关键在于如何选择合适的降维矩阵T,使得机载MIMO雷达在保持其杂波抑制优势的前提下,降低MIMO STAP算法的复杂度和运算量。基于这一思路,依据JTR-STAP算法的统一框架,可以构建多种联合自适应处理算法。在固定结构降维STAP算法中,由于收发阵列可分别对应阵元域和波束域,时间上的脉冲又可分为脉冲域和多普勒域,对“收发时”3个域进行排列组合即可以得到固定结构降维的8大处理域,具体如图 2所示。图 2中用数字符号代表某一处理域,如“1-2-1”代表“发射阵元-接收波束-多普勒域”。由于波束域是经阵元域进行傅氏变换得到的,多普勒域是经过脉冲域进行傅氏变换得到的,因此这8大处理域相互紧密联系,在物理概念上是完全统一的,经适当变换,可以互相转换,其处理模型可以由式(6)统一描述。
|
图 2 机载MIMO雷达收发联合降维空时域及其组合相互关系 Fig.2 The JTR reduced dimensional space time domain and their relationship for airborne MIMO radar |
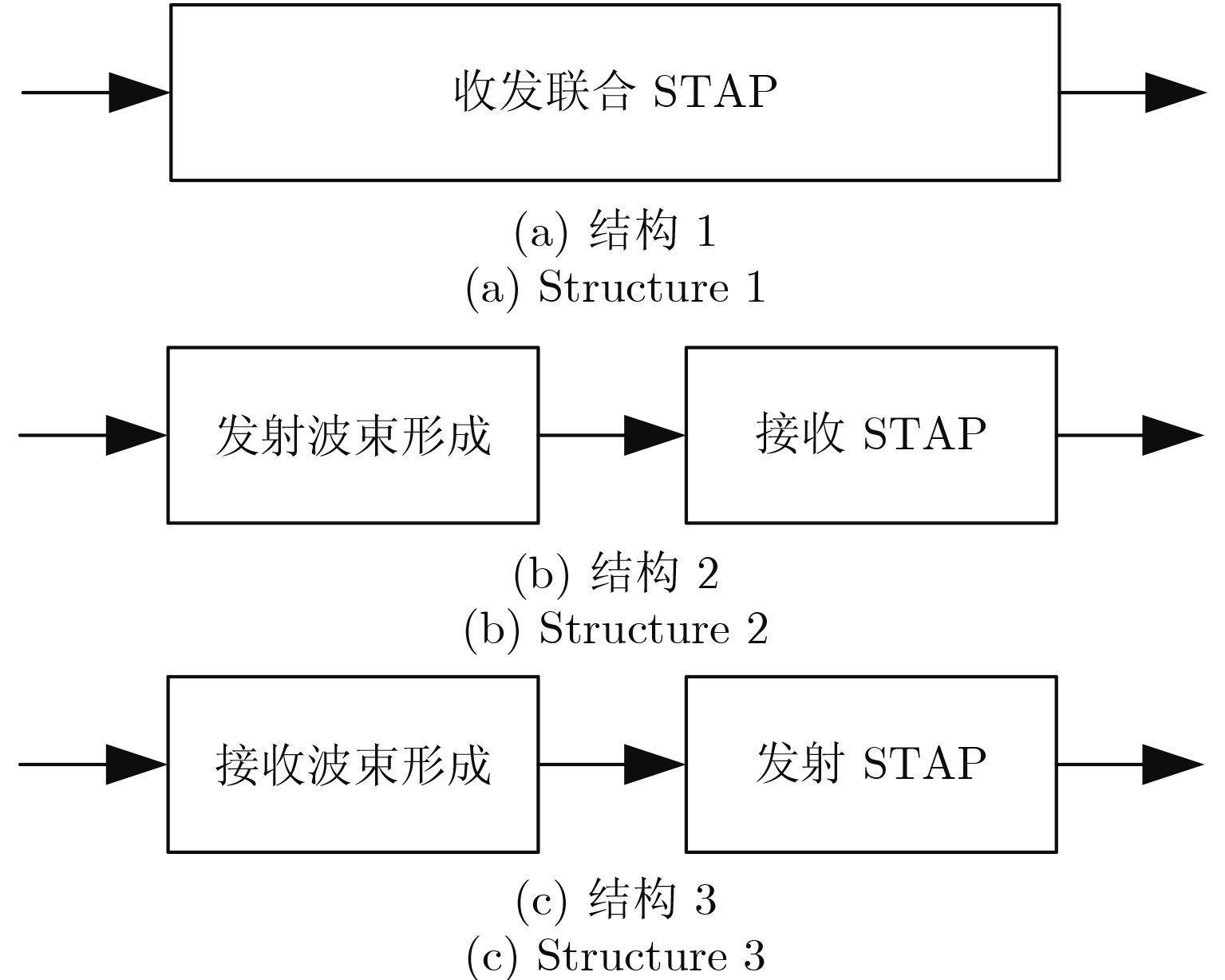
依据上节给出的MIMO STAP统一框架,建立JTR-STAP算法的3种处理结构,分别为 (如图 3所示):
|
图 3 MIMO STAP的3种联合自适应结构 Fig.3 Three joint adaptive structures of MIMO STAP method |
(1)收发联合自适应处理结构;(2)先发射波束形成再接收STAP的联合处理结构;(3)先接收波束形成再发射STAP的联合处理结构。
4 不同处理结构下的降维JTR-STAP算法 4.1 收发联合自适应的降维JTR-STAP算法该类结构下的JTR-STAP算法主要包含了收发联合自适应的mDT处理(JTR-mDT)、收发联合自适应的JDL处理(JTR-JDL)、收发联合自适应广义相邻多波束(JTR-STMB) 3种典型的收发联合自适应处理算法。
4.1.1 收发联合自适应的 mDT 处理(JTR-mDT)依据传统相控阵雷达中的mDT算法的思想,MIMO STAP中的mDT法首先对QN个收发通道分别进行多普勒滤波,然后选取与待检测多普勒通道相邻的KD–1个多普勒通道进行自适应处理,此处定义该方法为收发联合的mDT方法(JTR-mDT)。该方法属于发射阵元-接收阵元-多普勒处理,其降维变换统一关系为图 2所示的1-1-1→1-2-1。由统一框架式(1)可得该算法“收发时”3域上的联合降维变换矩阵为:
| $\left. \begin{aligned} & {{T}} = {{{T}}_{\rm{T}}} \otimes {{{T}}_{\rm{s}}} \otimes {{{T}}_{\rm{t}}} \in \mathit{\mathbb{C}}{^{QNK \times QN{K_D}}}\\ & {{{T}}_{\rm{T}}} \!= \left[{{{\tilde {{T}}}_{{\rm{T}},l - \left( {{K_D} - 1} \right)/2}} \ \!\cdot \! \cdot \! \cdot {{{T}}_{{\rm{T}},l}} \ \!\cdot \! \cdot \! \cdot {{\tilde {{T}}}_{{\rm{T}},l + \left( {{K_D} - 1} \right)/2}}} \right] \\ & \quad \quad \ \ \in {\mathbb {C}^{K \times {{K_D}}}}\\ & {{{T}}_{\rm{r}}} = {{{I}}\!_N} \in \mathbb {C}{^{N \times N}}\\ & {{{T}}_{\rm{t}}} = {{{I}}\!_Q} \in \mathbb {C} {^{Q \times Q}} \end{aligned}\!\!\right\} $ | (8) |
其中,${{{T}}_{{\rm{t}},l}} = {{{H}}\!_q} \circ {{{S}}_{\rm{t}}}\left( {{f\!_{d,l}}} \right)$表示第l个待检测多普勒通道时域权。${{\tilde {{T}}}_{{\rm{t}},m}} = {{{H}}\!_q} \circ {{{S}}_{\rm{t}}}\left( {{f\!_{d,l - m}}} \right)$(m=±1,±2,···,±$ \left( {{K\!_D} - 1} \right)/2$)表示主通道左右第m个辅助多普勒通道的时域权,此处设${K\!_D}$为奇数。Hq为时域静态的权,“$ \circ $”表示点积。
4.1.2 收发联合自适应的 JDL 处理(JTR-JDL)收发联合自适应的JDL处理(JTR-JDL)首先将发射阵元-接收阵元-脉冲域变换为发射波束-接收波束-多普勒域,然后再选择待检测单元附近QDNDKD个局域通道进行自适应处理。其降维变换统一关系为图 2中的1-1-1→2-2-2。由统一框架式(1)可得该算法的联合降维变换矩阵为:
| $\left. \begin{align} & T={{T}_{\text{T}}}\otimes {{T}_{\text{s}}}\otimes {{T}_{\text{t}}}\in {{\mathbb{C}}^{QNK\times {{Q}_{D}}{{N}_{D}}{{K}_{D}}}} \\ & {{T}_{\text{T}}}=\left[ {{T}_{\text{T}}}_{,l-\left( {{K}_{D}}-1 \right)/2}\cdot {{T}_{\text{T},l}}\cdot {{T}_{\text{T}}}_{,l+\left( {{K}_{D}}-1 \right)/2} \right] \\ & \in {{\mathbb{C}}^{K\times {{K}_{D}}}} \\ & {{T}_{\text{r}}}=\left[ {{T}_{\text{r}}}_{,-\left( {{N}_{D}}-1 \right)/2}\cdot {{T}_{\text{r},0}}\cdot {{T}_{\text{r}}}_{,\left( {{N}_{D}}-1 \right)/2} \right] \\ & \in {{\mathbb{C}}^{N\times {{N}_{D}}}} \\ & {{T}_{\text{t}}}=\left[ {{T}_{\text{t}}}_{,-\left( {{Q}_{D}}-1 \right)/2}\cdot {{T}_{\text{t},0}}\cdot {{T}_{\text{t}}}_{,\left( {{Q}_{D}}-1 \right)/2} \right] \\ & \in {{\mathbb{C}}^{Q\times {{Q}_{D}}}} \\ \end{align} \right\}$ | (9) |
其中,Tt,i,Tr,j和TT,l–k分别表示与主波束相邻的左右第i个发射波束、第j个接收波束和第k个多普勒通道的降维权矢量。
4.1.3 收发联合自适应广义相邻多波束(JTR-STMB)收发联合自适应广义相邻多波束(JTR-STMB)同样属于统一关系图 2中的1-1-1→2-2-2变换。JTR-STMB将不同多普勒通道看作时域不同的“波束”,这些时域“波束”和空域波束一起形成空时多波束,然后再对这些空时多波束选择相应的邻近局域通道进行自适应处理。
JTR-STMB方法的空时域的降维矩阵类似于JTR-JDL方法,其表达式为:
| $\left. \begin{aligned} & {{{T}}_{\rm{T}}}\! =\!\! \left[\! {{{{T}}_{\rm{T}}}_{,l - \left( {{K_D} - 1} \right)/2} \ \!\cdot \! \cdot \! \cdot {{{T}}_{{\rm{T}},l}} \ \!\cdot \! \cdot \! \cdot {{{T}}_{\rm{T}}}_{,l + \left( {{K_D} - 1} \right)/2}} \right]\\ & \quad \quad \ \in\! \mathbb {C} {^{K \times {K_D}}}\\ & {{{T}}_{\rm{r}}}\! =\! \left[{{{{T}}_{\rm{r}}}_{,- \left( {{N_D} - 1} \right)/2} \ \!\cdot \! \cdot \! \cdot {{{T}}_{{\rm{r}},0}} \ \!\cdot \! \cdot \! \cdot {{{T}}_{\rm{r}}}_{,\left( {{N_D} - 1} \right)/2}} \right]\\ & \quad \quad \ \in \mathbb {C}{^{N \times {N_D}}}\\ & {{{T}}_{\rm{t}}}\! =\! \left[{{{{T}}_{\rm{t}}}_{,- \left( {{Q_D} - 1} \right)/2} \ \!\cdot \! \cdot \! \cdot {{{T}}_{{\rm{t}},0}} \ \!\cdot \! \cdot \! \cdot {{{T}}_{\rm{t}}}_{,\left( {{Q_D} - 1} \right)/2}} \right]\\ & \quad \quad \ \in \mathbb {C}{^{Q \times {Q_D}}} \end{aligned} \right\}$ | (10) |
由统一框架式(1)可得该算法的联合降维变换矩阵为:
| ${{T}} \!=\! {\left[\!\! \begin{array}{l} {\left( {{{{T}}_{\rm{T}}} \otimes {{{T}}_{{\rm{r}},0}} \otimes {{{T}}_{{\rm{t}},0}}} \right)^{\rm{T}}}\\ {\left( {{{{T}}_{{\rm{T}},l}} \otimes {{{{{T}}'}}\!\!_{\rm{r}}} \otimes {{{{{T}}'}}\!\!_{\rm{t}}}} \right)^{\rm{T}}} \end{array}\!\! \right]^{\rm{T}}} \!\! \!\!\in \mathbb {C}{^{QNK \times {K_D} + {N_D} + {Q_D} - 2}}$ | (11) |
其中,${{T}}_{\rm{r}}\,\!\!^\prime$与波束域降维矩阵Tr的区别在于不包含空域主波束Tr,0。${{T}}_{\rm{t}}\,\!\!^\prime$与波束域降维矩阵Tt的区别在于不包含空域主波束Tt,0。
4.2 先发射波束形成再接收STAP的级联处理为了充分利用MIMO雷达的发射分集的特点,起到从发射阵列抗干扰的作用。这里提出一种先发射波束形成再接收降维STAP的收发联合自适应处理结构(Transmit Digital BeamForming-Receive Reduced Space Time Adaptive Processing,TDBF-RRSTAP)。接收通道接收到各正交发射波形的回波数据后,在每个接收通道通过各自的匹配滤波器将各个波形回波数据进行分离,形成Q个发射通道(注:此处所指的发射通道是指在接收端因匹配分离而形成的“虚拟”发射通道,而不是发射端的各正交波形的发射通道)。TDBF-RRSTAP结构可描述为:
(1) 在每个接收通道中对Q个发射通道进行自适应波束形成,其目的在于,一是对空域的某角度的干扰进行自适应置零,起到干扰抑制的作用,二是将对多路发射通道的数据进行降维处理。在每个接收通道中,发射通道经DBF后相当于对多路发射通道进行相参积累形成一路数据。N个接收通道对应形成了N个波束形成输出数据。
(2) 再在K个脉冲时间内,将第1步处理后的N路接收通道数据做降维STAP处理,实现对地杂波的抑制。此时降维STAP的算法可选择mDT,JDL,STMB等,同样在估算1级处理后的局域杂波自由度后,也可以采用传统的PC,CSM和MWF等降秩STAP算法进行2级STAP处理。
由于各接收通道的分离的发射通道的数据是相同的,因此各接收通道内的发射通道的波束形成自适应权值相同。对第1个接收通道基于SMI算法的自适应权值可表述为:
| ${{{W}}_{\rm{t}}} = \mu {{R}}_{\rm{t}}^{ - 1}{{{S}}_{\rm{t}}}\left( {{\psi _0}} \right) \in \mathbb {C} {^{Q \times 1}}$ | (12) |
其中,μm为常数,Rt表示匹配滤波分离得到的发射通道的杂波协方差矩阵,${{{S}}_{\rm{t}}}\left( {{\psi _0}} \right)$表示发射导向矢量,${\psi _0}$为主波束指向的锥角。波束形成后的数据变为:
| ${{Y}} = {{T}}_1^{\rm{H}}{{X}} \in \mathbb {C} {^{NK \times 1}}$ | (13) |
其中,${{{T}}_1} = {{{I}}\!_K} \otimes {{{I}}\!_N} \otimes {{{W}}\!_{\rm{t}}} \in \mathbb {C} {^{QNK \times NK}}$表示1级发射阵元域DBF处理后收发时域的变换矩阵。易得2级降维STAP处理的变换矩阵为:
| $\begin{aligned} {{T}} & = \left( {{{{I}}\!_K} \otimes {{{I}}\!_N} \otimes {{{W}}\!_{\rm{t}}}} \right)\left( {{{{T}}_{\rm{T}}} \otimes {{{T}}_{\rm{r}}}} \right)\\ & = {{{T}}_{\rm{T}}} \otimes {{{T}}_{\rm{r}}} \otimes {{{W}}_{\rm{t}}} \in \mathbb {C} {^{QNK \times {K_D}{N_D}}} \end{aligned}$ | (14) |
式(14)即为TDBF-RRSTAP结构的降维变换矩阵,其中时域和接收空域的变换矩阵TT,Tr可依据4.1节所述的收发联合STAP算法选取。
4.3 先接收波束形成再发射STAP的级联处理这里给出一种先接收波束形成再发射降维STAP的收发联合自适应处理结构(Receive Digital BeamForming-Transmit Reduced Space Time Adaptive Processing,RDBF-TRSTAP),该结构的处理流程与TDBF-RRSTAP不同,其采用先接收波束形成再进行发射端降维的处理结构。由于各发射通道的接收通道的数据是相同的,因此各发射通道内的接收通道的波束形成自适应权值相同,对第1个发射通道基于SMI算法的自适应权值可表述为:
| ${{{W}}\!_{\rm{r}}} = \mu {{R}}_{\rm{r}}^{ - 1}{{{S}}_{\rm{r}}}\left( {{\psi _0}} \right) \in \mathbb {C} {^{N \times 1}}$ | (15) |
其中,${{{R}}_{\rm{r}}}$表示各接收通道的杂波协方差矩阵,${{{S}}_{\rm{r}}}\!\left( {{\psi _0}} \right)$表示接收导向矢量。波束形成后的数据变为:
| ${{Y}} = {{T}}_2^{\rm{H}}{{X}} \in \mathbb {C} {^{QK \times 1}}$ | (16) |
其中,${{{T}}_2} = {{{I}}\!_K} \otimes {{{W}}_{\rm{r}}} \otimes {{{I}}\!_Q} \in \mathbb {C} {^{QNK \times QK}}$表示1级接收阵元域DBF处理后收发时域的变换矩阵。易得2级发射通道的降维STAP处理的变换矩阵为:
| ${{{T}} = }{{{T}}_{\rm{T}}} \otimes {{{W}}\!_{\rm{r}}} \otimes {{{T}}_{\rm{t}}} \in \mathbb {C} {^{QNK \times {K_D}{N_D}}}$ | (17) |
式(17)即为RDBF- TRSTAP结构的降维变换矩阵,其中时域和接收空域的变换矩阵TT,Tt同样可以依据4.1节所述的收发联合STAP算法选取。由于实际应用中发射通道个数Q一般较小,因此RDBF-TRSTAP中的1级STAP处理中可以直接利用阵元-脉冲域的方法实施。
5 仿真结果仿真实验验证机载MIMO雷达空时自适应处理抑制杂波的性能,仿真参数设定为:发射阵元M=8,接收阵元N=8,时域采样脉冲K=8,工作波长λ=0.23 m,接收阵元间距dR=0.115 m,发收阵元间距比α=10(特殊情况单独说明),载机速度V=140 km/h,载机飞行高度H=8 km,脉冲重复频率fr=2438.8 Hz,发射功率P=180 kW,输入杂噪比CNR=60 dB。本文将发射波形合成结构表述为集合{M1,M2,···,MQ},Q ≤ M,其物理意义可描述为:M个发射阵元发射的波形可合成为Q个正交波形,且M=M1+M2+···+MQ。
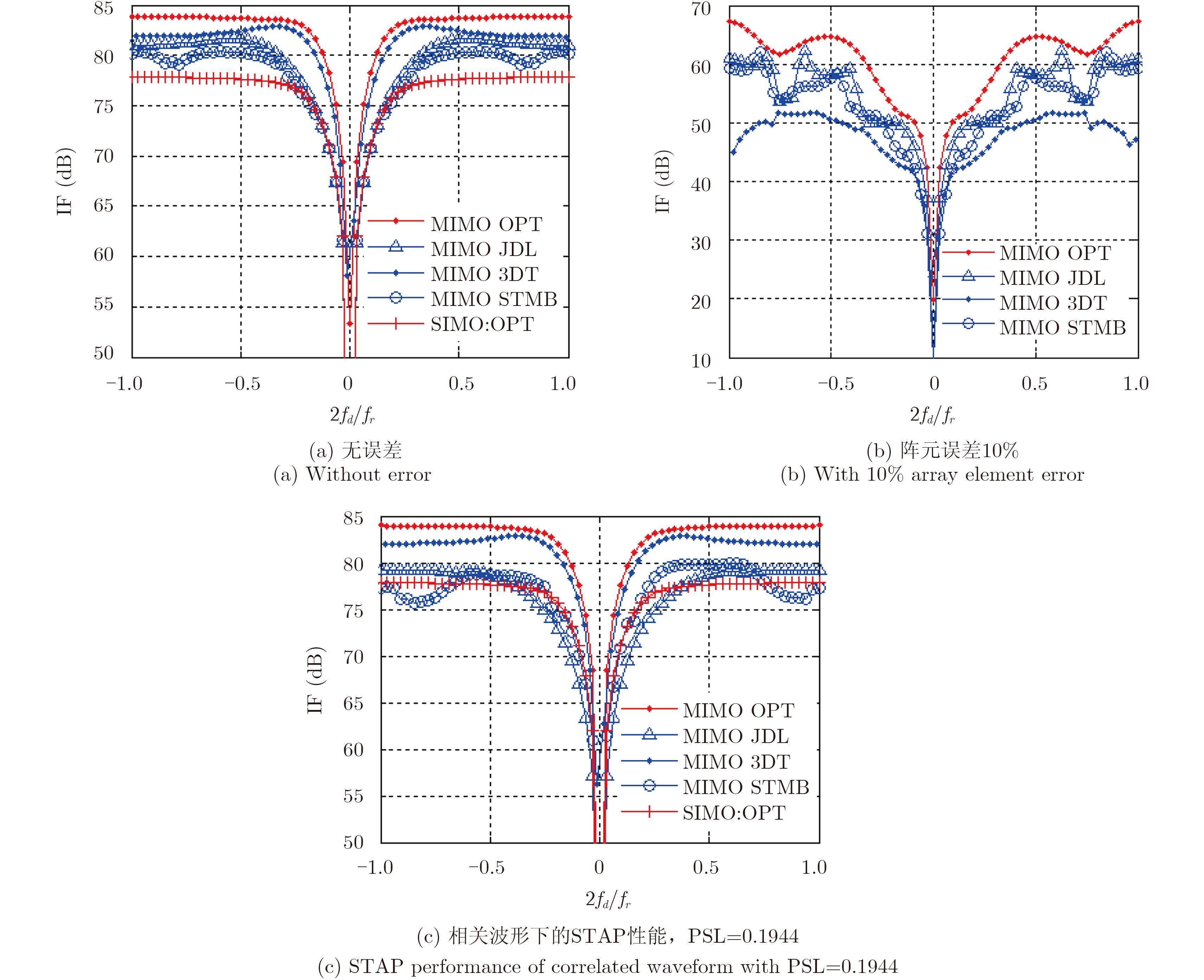
对收发联合自适应的3种MIMO STAP算法JTR-mDT算法、JTR-JDL算法、JTR-STMB算法与全空时自适应的OPT算法的性能进行了仿真对比。其中mDT的变换后通道数选为m=3。STMB算法的局域中发射通道数QD=7,接收通道数ND=7,时域通道数KD=7。MIMO雷达发射的合成结构为{4,4,4,4},作为对比的相控阵雷达(SIMO)的发射阵元数同MIMO PA雷达的总数相同即为16个。图 4对比分析了机载MIMO雷达与机载相控阵雷达系统改善因子性能。
|
图 4 4种MIMO STAP算法的性能比较 Fig.4 Comparison of performance for four MIMO STAP algorithms |
由图 4(a)可见,相同的发射阵元数量下,MIMO体制下收发联合的STAP算法的杂波抑制性能均好于传统的相控阵雷达的OPT处理的性能。这是因为MIMO雷达利用了发射正交信号产生的分集特性,扩展了其杂波抑制处理的系统自由度。分析图 4(b)可得,在加入10%阵元误差的影响下,MIMO 3DT联合自适应算法更容易受到误差因素的影响。由图 4(c)可知在相关性的影响下,此处发射波形的互相关峰值旁瓣水平(Peak Sidelobe Level,PSL)等于0.1944,各算法的性能均有下降但3DT算法性能下降不大,JDL和STMB在旁瓣杂波区性能下降约为7 dB,且主瓣杂波凹口宽度扩大,GMTI性能下降。波形正交性的退化同误差一样会影响机载MIMO雷达的杂波抑制性能。
图 5给出了理想情况下对应上述4种JTR-STAP算法的空时2维频响图,时域加70 dB Chebyshev权,空域锥削加30 dB Chebyshev权,目标位置空域角度为(90°,0°),归一化多普勒频率对应为0.5。

|
图 5 4种收发联合自适应算法的空时频响图及投影图 Fig.5 Frequency response diagram and projection drawing of four JTR adaptive algorithms |
由图 5可见,频率响应均沿机载MIMO雷达的杂波脊线形成了频响凹口,“挖掉”了对应位置分布的杂波。另外,在各JTR-STAP算法滤除杂波性能的决定下,各算法频响的凹口大小与深度均不同。对比分析可得,OPT法形成的凹口相对较小,且方向图的主瓣方向好,对目标的检测性能最好。3DT法在空域未作加权处理,因而在频响方向图的主瓣方向性较好,且杂波抑制凹口较窄,同等情况下其STAP处理性能要优于JDL法和STMB法。JDL法和STMB法在空时域均进行了加权处理,使得这两种算法的频响方向图的主瓣和主杂波区的杂波抑制凹口展宽,导致了该算法下MIMO体制机载雷达的GMTI性能受影响。
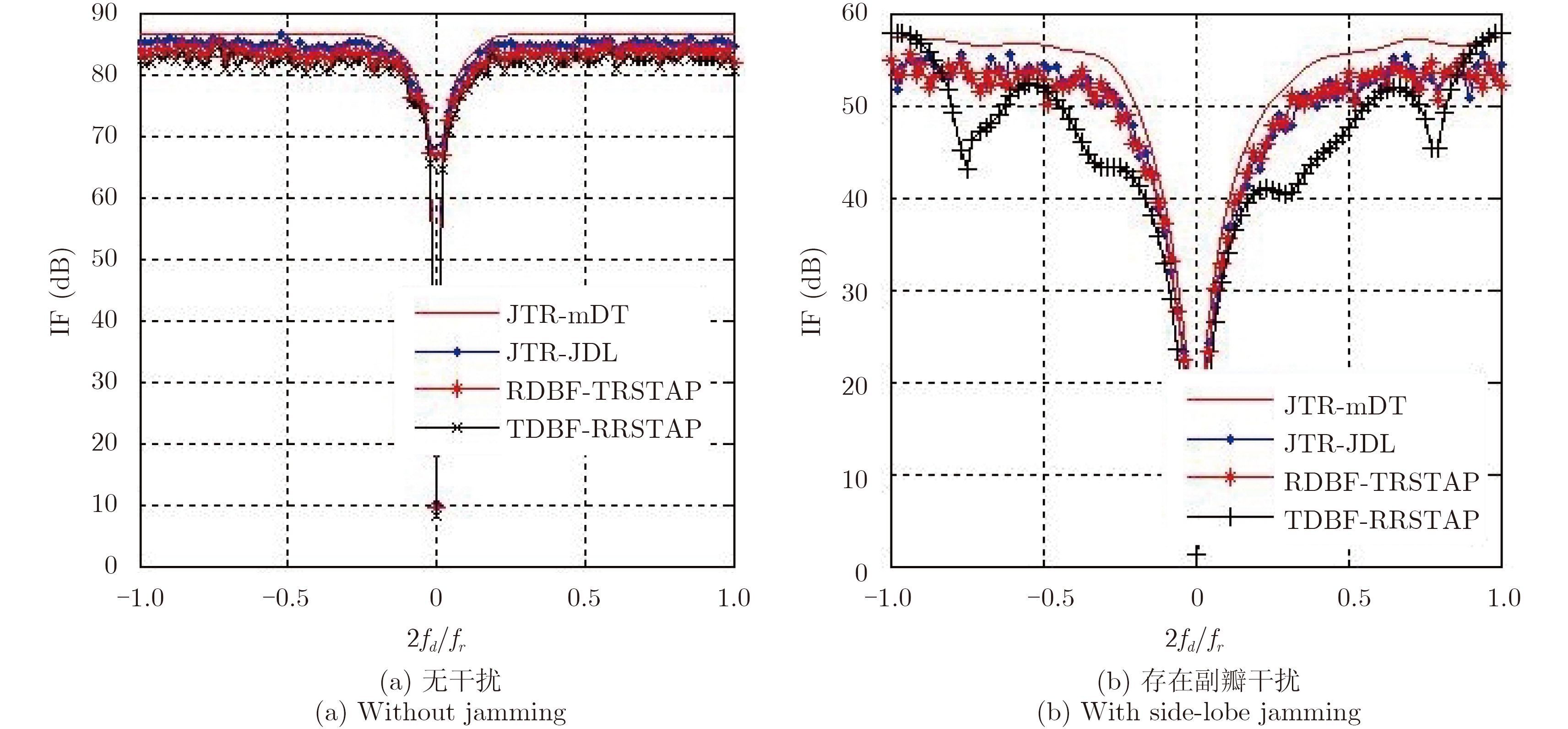
图 6分别给出了无干扰和有副瓣干扰时的杂波抑制结果,仿真过程中假设副瓣干扰方位为20°和60°。从仿真结果可以看出:无干扰时,JTR-mDT的性能要优于其它算法,TDBF-RRSTAP,RDBF-TRSTAP和JTR-JDL算法性能接近,如图 6(a)所示。当存在副瓣干扰时,JTR-mDT性能下降不大,与TDBF-RRSTAP,RDBF-TRSTAP算法均能在杂波位置形成凹口,IF曲线有所下降但仍具有较好的杂波抑制性能,如图 6(b)所示。综上可得,当不存在干扰或仅有副瓣干扰源时,由于TDBF-RRSTAP和RDBF-TRSTAP算法的运算量较小,且性能相比JTR-mDT和JTR-JDL虽然略有降低,但仍能满足检测要求,所以该情况下一般选用TDBF-RRSTAP和RDBF-TRSTAP算法。
|
图 6 降维MIMO STAP算法性能比较 Fig.6 Comparison of performance for reduced dimensional MIMO STAP algorithms |
本文提出了机载MIMO雷达JTR-STAP处理的统一框架关系,依据机载MIMO雷达杂波模型,建立了机载MIMO雷达在发射、接收和时间3大域上的联合自适应处理算法,为JTR-STAP算法的研究提供了统一的框架结构。然后依据收发时3域处理的统一框架理论,针对MIMO雷达的特点提出了固定结构降维处理的3种联合STAP处理结构,并详细论述各处理结构的原理和数学描述。通过仿真结果对比分析得出:JTR-mDT算法较JTR-JDL,JTR-STMB算法具有更好的环境适应性。然而,本文提出的机载MIMO雷达收发联合降维自适应算法的理论框架相当于仅增加了发射阵元域(发射波束域)。实际上,发射的维度是由于正交波形引入的,因此,可以将此维度视为发射波形域,而MIMO雷达的发射波形分集与灵活性正是MIMO雷达所特有的优势。迄今为止,已有一些文献[16-20]通过发射波形设计来进一步提升MIMO-STAP的性能,如何将这一部分的内容纳入本框架中是我们下一步的研究内容。
| [1] |
王永良, 彭应宁.
空时自适应信号处理[M]. 北京: 清华大学出版社, 2000 .
Wang Y L, and Peng Y N.
Space Time Adaptive Processing[M]. Beijing: Tsinghua University Press, 2000 .
( 0) 0)
|
| [2] |
Melvin W L. A STAP overview[J].
IEEE Aerospace and Electronic Systems Magazine , 2004, 19 (1) : 19-35 DOI:10.1109/MAES.2004.1263229 ( 0) 0)
|
| [3] |
Yang X, Sun Y, Zeng T, et al. Fast STAP method based on PAST with sparse constraint for airborne phased array radar[J].
IEEE Transactions on Signal Processing , 2016, 64 (17) : 4550-4561 DOI:10.1109/TSP.2016.2569471 ( 0) 0)
|
| [4] |
Klemm R. Suboptimum clutter suppression for airborne phased array radar[C]. IEE Radar Conference, London, 1982, 216:473-476.
( 0) 0)
|
| [5] |
Klemm R. Adaptive airborne MTI:An auxiliary channel approach[J].
IEE Proceedings F , 1987, 134 (3) : 269-276 ( 0) 0)
|
| [6] |
保铮, 廖桂生, 吴仁彪, 等. 相控阵机载雷达杂波抑制的时-空二维自适应滤波[J].
电子学报 , 1993, 21 (9) : 1-7 Bao Z, Liao G S, Wu R B, et al. 2-D temporal-spatial adaptive clutter suppression for phased array airborne radars[J].
Acta Electronic Sinica , 1993, 21 (9) : 1-7 ( 0) 0)
|
| [7] |
Wang H and Cai L. On adaptive spatial-temporal processing for airborne surveillance radar systems[J].
IEEE Transactions on Aerospace Electronics Systems , 1994, 30 (3) : 660-669 DOI:10.1109/7.303737 ( 0) 0)
|
| [8] |
Wang Y, Chen J, Bao Z, et al. Robust space-time adaptive processing for airborne radar in nonhomogeneous clutter environments[J].
IEEE Transactions on Aerospace Electronics Systems , 2003, 39 (1) : 70-81 DOI:10.1109/TAES.2003.1188894 ( 0) 0)
|
| [9] |
Fishler E, Haimovich A, Blum R, et al.. MIMO radar:An idea whose time has come[C]. Proceedings of the IEEE Radar Conference, 2004:71-78.
( 0) 0)
|
| [10] |
Li J and Stoica P. MIMO radar with colocated antennas[J].
IEEE Signal Processing Magazine , 2007, 24 (5) : 106-114 DOI:10.1109/MSP.2007.904812 ( 0) 0)
|
| [11] |
Chen C Y and Vaidyanathan P P. MIMO radar space-time adaptive processing using prolate spheroidal wave functions[J].
IEEE Transactions on Signal Processing , 2008, 56 (2) : 623-635 DOI:10.1109/TSP.2007.907917 ( 0) 0)
|
| [12] |
Wang G H and Lu Y L. Clutter rank of STAP in MIMO radar with waveform diversity[J].
IEEE Transactions on Signal Processing , 2010, 58 (2) : 938-943 DOI:10.1109/TSP.2009.2031301 ( 0) 0)
|
| [13] |
He J, Feng D, and Ma L. Reduced-dimension clutter suppression method for airborne multiple-input multiple-output radar based on three iterations[J].
IET Radar, Sonar & Navigation , 2015, 9 (3) : 249-254 ( 0) 0)
|
| [14] |
王珽, 赵拥军. 基于三迭代与二阶锥规划的机载MIMO雷达稳健降维STAP方法[J].
航空学报 , 2015, 36 (11) : 3706-3714 Wang T, Zhao Y J. Robust reduced-dimension STAP method for airborne MIMO radar based on TRIA and SOCP[J].
Acta Aeronautica et Astronautica Sinica , 2015, 36 (11) : 3706-3714 ( 0) 0)
|
| [15] |
Guerci J R.
Cognitive Radar-The Knowledge-Aidded Fully Adaptive Approach[M]. Boston, London: Artech House, 2010 : 91 -109.
( 0) 0)
|
| [16] |
Wang H Y, Liao G S, Li J, et al. Waveform optimization for MIMO-STAP to improve the detection performance[J].
Signal Processing , 2011, 91 (11) : 2690-2696 DOI:10.1016/j.sigpro.2011.06.005 ( 0) 0)
|
| [17] |
Wang H Y, Liao G S, Li J, et al. Robust waveform design for MIMO-STAP to improve the worst-case detection performance[J].
EURASIP Journal on Advances in Signal Processing , 2013, 52 : 1-8 ( 0) 0)
|
| [18] |
唐波, 张玉, 李科, 等. 杂波中MIMO 雷达恒模波形及接收机联合优化算法研究[J].
电子学报 , 2014, 42 (9) : 1706-1711 Tang B, Zhang Y, Li K, et al. Joint constant-envelope waveform and receiver design for MIMO radar in the presence of clutter[J].
Acta Electronica Sinica , 2014, 42 (9) : 1706-1711 ( 0) 0)
|
| [19] |
Tang B, Tang J. Joint design of transmit waveforms and receive filters for MIMO radar space time adaptive processing[J].
IEEE Transactions on Signal Processing , 2016, 64 (18) : 4707-4722 DOI:10.1109/TSP.2016.2569431 ( 0) 0)
|
| [20] |
Tang B, Li J, Zhang Y, et al. Design of MIMO radar waveform covariance matrix for clutter and jamming suppression based on space time adaptive processing[J].
Signal Processing , 2016, 121 : 60-69 DOI:10.1016/j.sigpro.2015.10.033 ( 0) 0)
|




