近年来,相比传统体制的雷达,MIMO雷达以其在检测,跟踪和参数估计更优的性能获得了大量关注。MIMO雷达分为共置天线 [1] 和分布式两种体制 [2] 。本文主要研究的是分布式MIMO雷达多目标跟踪背景下的发射站,接收站优化选择。分布式MIMO雷达属于无线传感网络的一种特殊形式。在传感器网络中,由于频谱资源,通信资源,能量资源的限制,需要通过对传感器资源进行合理的优化配置来达到更高的效率。分布式MIMO雷达也提出了对收发传感器进行优化选择的需求。
传感器选择问题作为传感器网络管理的一个重要子课题,涌现出了大量有价值的成果。文献[3– 5]提出了一系列关于一般传感器优化选择的方法。文献[3]最早提出了一个通用的凸优化选择模型来进行传感器选择。在该文中,传感器选择被建立为一个尽可能小化估计误差椭圆体积情况下的布尔变量的选择问题。通过该模型可以在满足固定传感器数量需求的情况下实现参数估计性能的性能最优选择。文献[4]通过对卡尔曼滤波器的广义推导,利用半正定松弛技术,实现了在各个传感器之间存在相关噪声下的优化选择,但是其优化模型忽略了当前时刻费歇尔信息矩阵的先验信息,所以其性能选择准则是非最优的。文献[5]用扩展卡尔曼滤波器中的卡尔曼增益的列稀疏性来表征传感器选择的有无,实现了跟踪性能和被选传感器数量的折中。
针对分布式MIMO雷达体制下的发射站接收站选择,Hana Godrich根据现有的传感器选择方法较早的关注了在分布式MIMO雷达体制下的收发站选择问题。她在文献[6]中提出了一种贪婪迭代算法,即每一次迭代中选择性能最好的传感器,在较低计算量的前提下获得了发射站和接收站的近似最优选择。然而这种方法更多的是基于对分布式MIMO雷达的性能分析下的一种直觉选择。在文献[7]中,在MIMO雷达网络在定位的应用背景下,实现了一种基于2阶椎规划(Second Order Cone Programming, SOCP)的分两步走发射站选择和功率分配方法,即在先选择发射站后再对发射功率进行分配。该方法虽然寻求联合资源分配,但是一方面优化求解过程不是联合进行,另一方面没有考虑接收站选择在MIMO雷达网络中的影响。在MIMO雷达目标跟踪应用背景下,利用后验克拉美罗下界(Posterior Cramer-Rao Lower Bound, PCRLB)作为性能指标,文献[8]中把优化问题设计为尽可能少的获取选择发射站的数量同时尽可能高的提高跟踪性能。该模型比较符合实际任务需求,但是由于其目标函数的非凸性,只能采取启发式方法进行求解,其有效性无法总能得到保证,两种代价函数之间的优化系数也没有给出一种较好的求解方案。文献[9]考虑了MIMO雷达网络在分散发射聚焦接收工作模式下的多目标接收站选择。虽然文中给出了基于凸优化的选择方案,但是文中假设发射站雷达的全向发射模式现代雷达还难以达到。
在现有的传感器选择方法中。对于一般通用的传感器选择算法,在很大程度上因为具体模型的不同,无法直接应用于分布式MIMO的传感器选择。另外一方面,现有的分布式MIMO雷达选择算法要么采用的是一种启发式的算法,要么只能选择雷达网络中发射站和接收站中的其中一种,无法保证其最优性。本文将优化多目标中跟踪性能最差的目标后验克拉美罗下界为目标函数,构建关于收发站的代价函数,利用分块坐标迭代,实现了多目标跟踪背景下分布式MIMO雷达收发站的联合选择。仿真实验,验证了本方法相比其它算法获得了更优的选择性能,并且在拥有更低计算量的情况下逼近全局搜索的最优选择。
2 系统信号模型考虑这样一个拥有
M个发射站,
N个接收站非相参分布式MIMO雷达系统。在雷达监视范围内一共存在
Q个目标。在
k时刻,第
q个目标的状态向量可以表示为
| $\tau _{m,n,k}^q = \frac{{R_{m,k}^q + R_{n,k}^q}}{\rm c} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad $ | (1) |
| $\begin{array}{l}f_{m,n,k}^q = \frac{{{f_{\rm{c}}}}}{{\rm{c}}}\left[ {\frac{{\dot x_k^q\left( {{x_{m,k}} - x_k^q} \right) + \dot y_k^q\left( {{y_{m,k}} - y_k^q} \right)}}{{R_{m,k}^q}}} \right.\\ \quad \quad \quad \quad \left. { + \frac{{\dot x_k^q\left( {{x_{n,k}} - x_k^q} \right) + \dot y_k^q\left( {{y_{n,k}} - y_k^q} \right)}}{{R_{n,k}^q}}} \right]\end{array}$ | (2) |
其中,
发射站发射一系列能量归一化的正交波形满足
| $\tilde r_{m,n}^q\left( t \right) \!=\! \tilde a_{m,n}^qh_{m,n,k}^q{\tilde s_m}\left( \!{t \!-\! \tau _{m,n,k}^q} \!\right){{\rm e}^{{\rm j}2{{π}} f_{m,n,k}^qt}} \!+\! {\tilde n_{m,n}}\left( t \right)$ | (3) |
其中,目标的RCS起伏被建模为一个复高斯随机变量
假设目标运动模型被建模为随机加速度线性运动模型,那么对于第 q个目标可以表示为:
| ${{x}}_k^q = {{Fx}}_{k - 1}^q + {{v}}_{k - 1}^q$ | (4) |
其中,
| ${{Q}} = \xi {{{I}}_2} \otimes \left[ {\begin{array}{*{20}{c}}{\frac{{\Delta {T\;^3}}}{3}} & {\frac{{\Delta {T\;^2}}}{2}}\\{\frac{{\Delta {T\;^2}}}{2}} & {\Delta T}\end{array}} \right]$ | (5) |
| ${{F}} = {{{I}}_2} \otimes \left[ {\begin{array}{*{20}{c}}1 & {\Delta T}\\0 & 1\end{array}} \right]$ | (6) |
在一般的文献中,通常会将每个接收站获得的全部采样数据传输至数据融合中心来统一进行信号级数据融合以获得目标的位置速度最优估计。但是为了降低数据传输率和时频不同步等其它问题,本文采用的是分布式非直接估计方法
[10]
,即每个接收站都对目标对应
M条反射波路径的延时和多普勒频移进行最大似然估计然后再传输至数据融合中心,而不必传输全部采样数据。在非直接参数估计中,本文定义一组关于目标的未知参数
| $\hat {{θ}} _{m,n,k}^q = \arg \mathop {\max }\limits_{\hat \tau _{m,n,k}^q,\hat f_{m,n,k}^q} \sum\limits_{m = 1}^M \int {\Big| {\tilde r_n^q\left( t \right)\tilde s_m^*\left( {t - \hat \tau _{m,n,k}^q} \right)}\Big. }\\ \quad \quad \quad \ \ \, {\Big. { {{\rm{e}}^{ - {\rm{j}}2{{π}}\hat f_{m,n,k}^qt}}} \Big|^2}{\rm{dt}}$ | (7) |
其中,
| ${{y}}_k^q = {{{h}}_k}\left( {{{x}}_k^q} \right) + {{w}}_k^q$ | (8) |
其中,
| ${{J}}_{\rm{Z}}^{ - 1}\!\left( {{{θ}} _k^q} \right) \!\!=\!\! {\left[ {{\rm{blkdiag}}\left(\! {{{{J}}_{\rm{Z}}}\left( {{{θ}} _{1,1,k}^q} \right),\! \cdots\! ,{{{J}}_{\rm{Z}}}\left( {{{θ}} _{M,N,k}^q} \right)} \right)} \right]^{ - 1}}$ | (9) |
其中,
| ${{{J}}_{\rm{Z}}}\left( {{{θ}} _{m,n,k}^q} \right) = \frac{{8{{{π}} ^2}{{\left| {a_{m,n}^q} \right|}^2}h_{m,n,k}^q}}{{{N_0}}}\left[ {\begin{array}{*{20}{c}}{\beta _m^2} & {{\xi _m}}\\{{\xi _m}} & {T_m^2}\end{array}} \right]$ | (10) |
其中,
后验克拉罗美罗下界(PCLRB)是常用的用来衡量目标跟踪性能的指标 [12] 。对于一个任意未知参数向量 a ,通过观测向量 b ,它的后验克拉罗美罗下界(PCLRB)可以表达为:
| ${{\mathbb{E}}_{{{a,b}}}}\left\{ {\left[ {{\overset{\frown} {{a}}} \left( {{b}} \right) - {{a}}} \right] {{\left[ {{\overset{\frown} {{a}}} \left( {{b}} \right) - {{a}}} \right]}^{\rm{T}}}} \right\} \succeq {{J}}_{\rm{B}}^{ - 1}$ | (11) |
其中,
| $ {{{J}}_{\rm{B}}} = - {\mathbb{E}}\left[ {\Delta _{{a}}^{{a}}\log {p_{{{a}}, {{b}}}}\left( {{a}, {{b }}} \right)} \right] $ | (12) |
其中,
| ${{{J}}_{\rm{B}}} = {{{J}}_{\rm{Z}}} + {{{J}}_{\rm{P}}}$ | (13) |
其中,
| $\left. \begin{array}{l}{{{J}}_{\rm{Z}}} = - {{\mathbb{E}}_{{a}}}\left[ {\Delta _{{a}}^{{a}}{p_{{{b|a}}}}\left( {{{b|a}}} \right)} \right]\\{{{J}}_{\rm{P}}} = - {{\mathbb{E}}_{{a}}}\left[ {\Delta _{{a}}^{{a}}{p_{{a}}}\left( {{a}} \right)} \right] \end{array} \right\}$ | (14) |
在本文的目标跟踪模型中,
| ${{P}}_k^q \!=\! {\mathbb{E}}\!\left\{ \!\!{\left[ {{\overset{\frown} {{x}}}_k^q\left( {{{Y}}_{1:k}^q} \right) \!-\! {{x}}_k^q} \right]\!\!{{\left[ {{\overset{\frown} {{x}}}_k^q\!\left( {{{Y}}_{1:k}^q} \right) \!-\! {{x}}_k^q} \right]}^{\rm{T}}}} \!\right\} \!\!\succeq\!\! {\left( {{{J}}_k^q} \right)^{ - 1}}$ | (15) |
要利用所有时刻的观测数据来计算PCRLB非常困难,文献[12]给出了BFIM
| ${{J}}_{k + 1}^q = {{D}}_k^{22} - {{D}}_k^{21}{\left( {{{J}}_k^q + {{D}}_k^{11}} \right)^{ - 1}}{{D}}_k^{12}$ | (16) |
这里为了符号简洁省略了BFIM的下标B来简化书写。式中各项可以分别表示为:
| $\left. {\begin{array}{*{20}{l}} \ \;{{{D}}_k^{11} = {{\mathbb{E}}_{{{x}}_k^q,{{x}}_{k + 1}^q}}\left[ { - \Delta _{{{x}}_k^q}^{{{x}}_k^q}\ln p\left( {{{x}}_{k + 1}^q|{{x}}_k^q} \right)} \right]}\\ \ \;{{{D}}_k^{12} = {{D}}_k^{21} = {{\mathbb{E}}_{{{x}}_k^q,{{x}}_{k + 1}^q}}\left[ { - \Delta _{{{x}}_k^q}^{{{{x}}_{k + 1}}}\ln p\left( {{{x}}_{k + 1}^q|{{x}}_k^q} \right)} \right]}\\\begin{array}{l}{{D}}_k^{22} = {{D}}_k^{22}\left( 1 \right) + {{D}}_k^{22}\left( 2 \right) \\\ \;\ \;\ \ = {{\mathbb{E}}_{{{x}}_k^q,{{x}}_{k + 1}^q}}\left[ { - \Delta _{{{x}}_{k + 1}^q}^{{{x}}_{k + 1}^q}\ln p\left( {{{x}}_{k + 1}^q|{{x}}_k^q} \right)} \right]\\\ \;\ \; \ \ \ \ \ + {{\mathbb{E}}_{{{x}}_{k + 1}^q,{{y}}_{k + 1}^q}}\left[ { - \Delta _{{{x}}_{k + 1}^q}^{{{x}}_{k + 1}^q}\ln p\left( {{{y}}_{k + 1}^q|{{x}}_k^q} \right)} \right]\end{array}\end{array}} \!\!\!\! \right\}$ | (17) |
由于本文假设目标满足线性运动模型,通过矩阵求逆引理以及一系列的变换和化简,先验费歇尔信息矩阵可以表示为:
| ${{{J}}_{\rm{P}}}\left( {{{x}}_k^q} \right) = {\left[ {{{{Q}}^q} + {{F}}{{\left( {{{J}}_{k - 1}^q} \right)}^{ - 1}}{{{F}}^{\rm{T}}}} \right]^{ - 1}}$ | (18) |
而关于量测信息的费歇尔信息矩阵为:
| $\begin{array}{l}{{{J}}_{\rm{Z}}}\left( {{{x}}_k^q} \right) = {{\mathbb{E}}_{{{x}}_k^q,{{y}}_k^q}}\left[ { - \Delta _{{{{x}}_k}}^{{{{x}}_k}}\ln p\left( {{{y}}_k^q|{{x}}_k^q} \right)} \right]\\\;\;\;\;\;\;\;\;\;\;\;\;\; = {{\mathbb{E}}_{{{x}}_k^q}}\left\{ {{{\mathbb{E}}_{{{y}}_k^q|{{x}}_k^q}}\left[ { - \Delta _{{{x}}_k^q}^{{{x}}_k^q}\ln p\left( {{{y}}_k^q|{{x}}_k^q} \right)} \right]} \right\}\\\;\;\;\;\;\;\;\;\;\;\;\;\; = {{\mathbb{E}}_{{{x}}_k^q}}\left[ {{{\left( {{{H}}_k^q} \right)}^{\rm{T}}}{{{J}}_{\rm{Z}}}\left( {{{θ}} _k^q} \right){{H}}_k^q} \right]\end{array}$ | (19) |
其中
| ${\nabla _{{{x}}_k^q}}\tau _{m,n,k}^q = \frac{1}{\rm c}\left[ {\begin{array}{*{20}{c}}{\cos \phi _{m,k}^q + \cos \varphi _{n,k}^q}\\{\sin \phi _{m,k}^q + \sin \varphi _{n,k}^q}\\0\\0\end{array}} \right]$ | (20) |
和
| ${\nabla _{{{x}}_k^q}}f_{m,n,k}^q = - \frac{{2{{π}} }}{\lambda }\left[ {\begin{array}{*{20}{c}}\begin{array}{l}\dot x_k^q\left( {\frac{1}{{R_{m,k}^q}} + \frac{1}{{R_{n,k}^q}}} \right)\\ - \frac{{\cos \phi _{m,k}^q\left( {\dot x_k^q\cos \phi _{m,k}^q + \dot y_k^q\sin \phi _{m,k}^q} \right)}}{{{{\left( {R_{m,k}^q} \right)}^2}}} - \frac{{\cos \varphi _{n,k}^q\left( {\dot x_k^q\cos \varphi _{n,k}^q + \dot y_k^q\sin \varphi _{n,k}^q} \right)}}{{{{\left( {R_{n,k}^q} \right)}^2}}}\end{array}\\\begin{array}{l}\dot y_k^q\left( {\frac{1}{{R_{m,k}^q}} + \frac{1}{{R_{n,k}^q}}} \right)\\ - \frac{{\sin \phi _{m,k}^q\left[ {\dot x_k^q\cos \phi _{m,k}^q + \dot y_k^q\sin \phi _{m,k}^q} \right]}}{{{{\left( {R_{m,k}^q} \right)}^2}}} - \frac{{\sin \varphi _{n,k}^q\left[ {\dot x_k^q\cos \varphi _{n,k}^q + \dot y_k^q\sin \varphi _{n,k}^q} \right]}}{{{{\left( {R_{n,k}^q} \right)}^2}}}\end{array}\\{\cos \phi _{m,k}^q + \cos \varphi _{n,k}^q}\\{\sin \phi _{m,k}^q + \sin \varphi _{n,k}^q}\end{array}} \right]$ | (21) |
通常来说
在本节中,分布式MIMO雷达多目标发射站接收站联合选择模型被建立。首先本文引入两组选择向量
| ${{{J}}_{\rm{Z}}}\!\left( {{{x}}_k^q,{{t}},{{r}}} \right) \!\!=\!\! \sum\limits_{m = 1}^M\! {\sum\limits_{n = 1}^N {t_m^qr_n^q \!{{\left(\! {{{H}}_{m,n,k}^q} \right)}^{\rm{T}}}\!\!\!{{{J}}_{\rm{Z}}}\!\left( {{{θ}} _{m,n,k}^q} \right)\!\!{{H}}_{m,n,k}^q} } $ | (22) |
费歇尔信息矩阵逆矩阵的迹是一个常用的用来进行优化选择的准则 [6, 7] 。由于雷达网络资源的限制,针对每一个目标只能有有限数量的发射站和接收站对其进行观察。本文通过选择发射站和接收站来获得更低的PCRLB,通常情况下也能获得更低的MSE。同时由于多目标的存在,需要平衡每个目标之间的跟踪性能。在本文的框架中以优化各个目标中跟踪性能最差的目标达到最优来实现系统整体性能的优化。于是本文给出以下优化模型
| $\left. {\begin{array}{*{20}{l}}{\mathop {\min }\limits_{{{t}},{{r}}} \;\mathop {\max }\limits_q \left[ {{\mathop{\rm tr}\nolimits} {{\left( {{{{J}}_k}} \right)}^{ - 1}}} \right]}\\\begin{array}{l}{\rm{subject\; to}}\;K_{\min }^q \le {\left( {{{u}}_1^q} \right)^{\rm{T}}}{{t}} \le K_{\max }^q,q \in {\cal Q}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;L_{\min }^q \le {\left( {{{u}}_2^q} \right)^{\rm{T}}}{{r}} \le L_{\max }^q,q \in {\cal Q}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {{{u}}_3^m} \right)^{\rm{T}}}{{t}} \le 1, \ m \in {\cal M}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {{{u}}_4^n} \right)^{\rm{T}}}{{r}} \le 1, \ n \in {\cal N}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t_m^q \in \left\{ {0,1} \right\}, \ m \in {\cal M},q \in {\cal Q}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;r_n^q \in \left\{ {0,1} \right\}, \ n \in {\cal N},q \in {\cal Q}\end{array}\end{array}} \!\!\!\!\!\!\!\right\}$ | (23) |
其中,
因为最后两个非凸约束的存在导致该优化问题不可解。所以为了有效的求解该优化问题,本文把最后两个非凸约束松弛为其对应的凸包
| ${v_l}\! \ge\! {{e}}_l^{\rm{T}}\!{\left[ {{{J}}_{{\rm P},k}^q \!+\! {{J}}_{\rm Z}^q\left( {{{x}}_k^q,{{t}},{{r}}} \right)} \right]^{ - 1}}\!{{{e}}_l}, \ l \!\in\! {\cal L},q \!\in\! {\cal Q}$ | (24) |
利用舒尔补定理,可以把优化问题转化为一个半正定规划(SemiDefinite Programming, SDP)问题 1 0
| $\left. {\begin{array}{*{20}{l}}{\mathop {\min }\limits_{{{t}},{{r}},{{v}}} \;{{{1}}^{\rm{T}}}{{v}}}\\\begin{array}{l}{\rm{subject\; to}}\!\left[\!\! {\begin{array}{*{20}{c}}{{{{J}}_{{\rm{P}},k}} + {{{J}}_{\rm{Z}}}\left( {{{x}}_k^q,{{t}},{{r}}} \right)} & {{{{e}}_l}}\\{{{e}}_l^{\rm{T}}} & {{v_l}}\end{array}} \!\!\right]\\ \quad \quad \quad \quad \ \!\succeq\! {{{0}}_{L + 1}}, \ l \in {\cal L},q \in {\cal Q}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {{{u}}_1^q} \right)^{\rm{T}}}{{t}} = {K_{\max }}, \ q \in {\cal Q}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {{{u}}_2^q} \right)^{\rm{T}}}{{r}} = {L_{\max }}, \ q \in {\cal Q}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {{{u}}_3^m} \right)^{\rm{T}}}{{t}} \le 1, \ m \in {\cal M}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {{{u}}_4^n} \right)^{\rm{T}}}{{r}} \le 1, \ n \in {\cal N}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t_m^q \in \left[ {0,1} \right],m \in {\cal M}, \ q \in {\cal Q}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;r_n^q \in \left[ {0,1} \right],n \in {\cal N}, \ q \in {\cal Q}\end{array}\end{array}} \right\}$ | (25) |
其中, e l 是 L维单位矩阵的第 l列向量。由于该转化后的优化问题关于选择 t 和 r 分别为一个凸优化问题, 所以本文直觉的选择坐标下降法(Bolck Coordinate Descent, BCD)来进行优化。坐标下降法可以描述为在每一次迭代中,本文最小化 t 或者 r 中的一个,同时保持另一个选择向量固定。通过此种方法,发射站和接收站联合选择可以总结步骤为:
1. 利用目标状态预测估计状态
2. 给定一个迭代初始可行点
3. 针对式(25)中的问题,对
(1)
(2)
(3) 如果
4. 对
(a) 令
(b) 对
(c) 对
5. 得到发射站和接收站的选择集合
其中,
在本节中,本文进行了计算机仿真实验来验证所提出的优化模型的有效性。仿真实验结果表明,本文所提出的动态规划方法使取得了比固定选择更优的性能,并且能在计算量更小的前提下获得和全局穷举搜索近似的性能。
在第1个仿真场景中,为了呈现发射站和接收站的动态选择过程,首先考虑一个规模相对较大的分布式MIMO雷达网络。12个发射站和12个接收站分别随机布置在
|
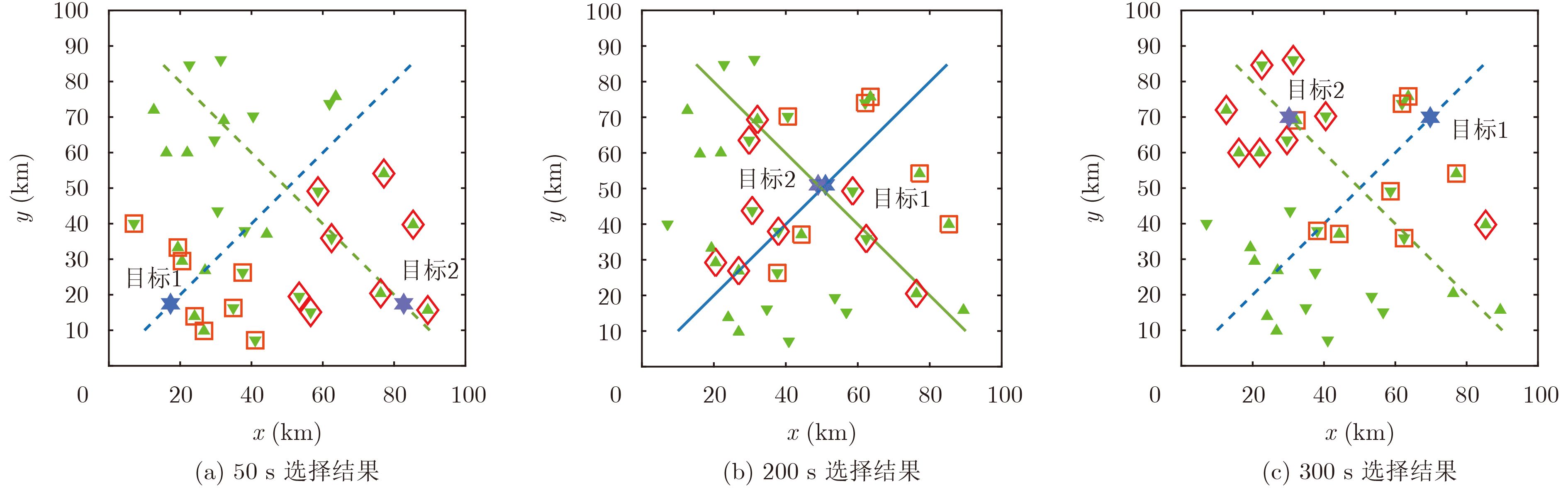
图 1 发射站接收站实时选择情况 Fig.1 Selection results of transmitters and receivers varied with time |
在
图1中,本文给出了在时刻50 s, 200 s, 300 s下针对目标1和目标2的发射站接收站动态实时选择情况,其中“
|
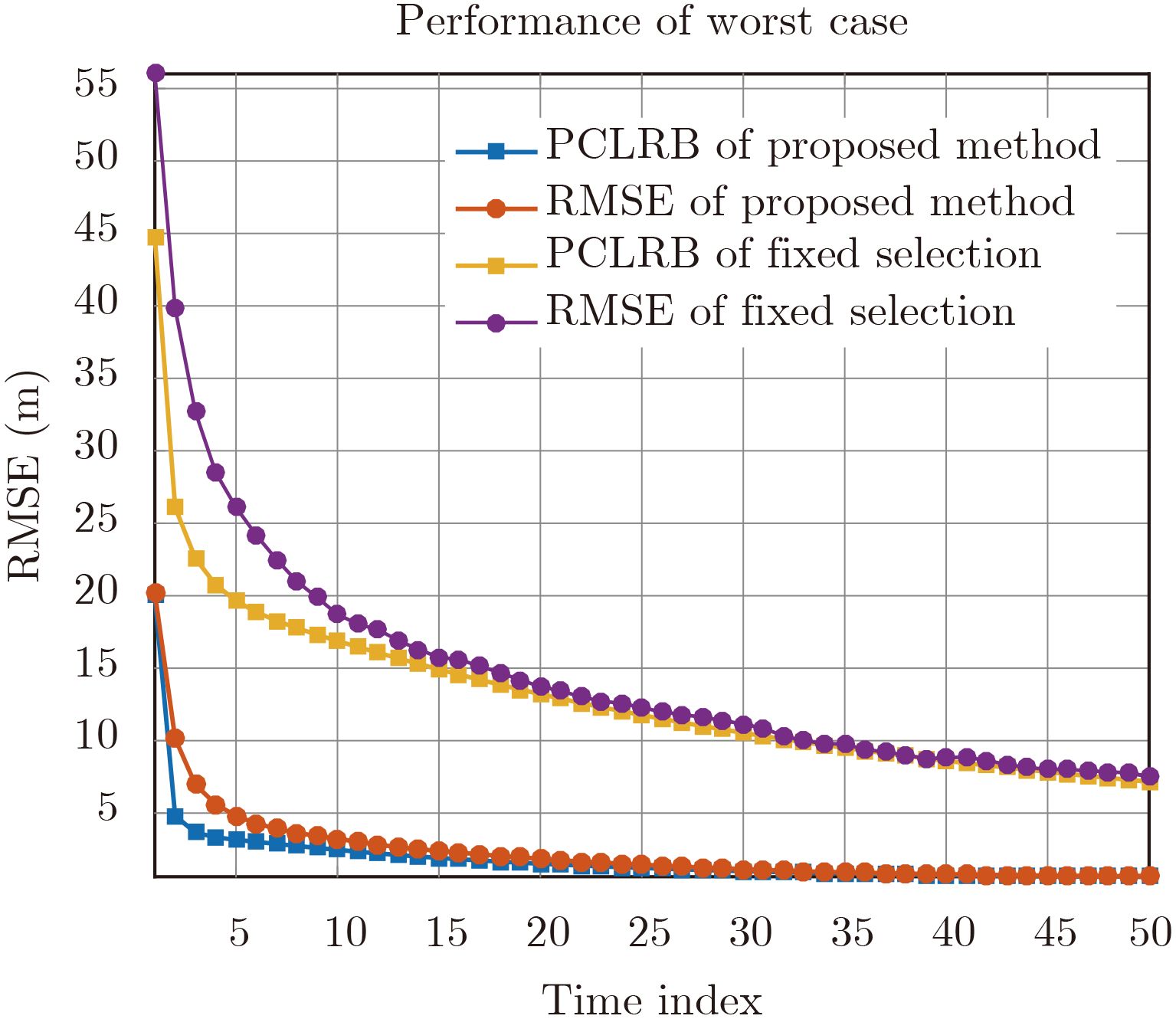
图 2 文中所提优化方法与固定选择方法的性能对比 Fig.2 Performance of proposed method and fixed selection method |
本文定义每个时刻所跟踪目标中性能最差的RMSE为:
| ${\rm{RMS}}{{\rm{E}}_k} = \mathop {\max }\limits_q \!\!{\left[\! {\sqrt {\frac{1}{{{\rm{MC}}}}\sum\limits_i^{{\rm{MC}}} {\left\| {{{x}}_k^q\left( i \right) \!\!-\!\!{\hat {{x}}}_{k|k}^q\left( i \right)} \right\|_2^2} } } \right]^{1/2}} \ \ \ \ $ | (26) |
其中,MC是蒙特卡洛仿真实验的次数。
|
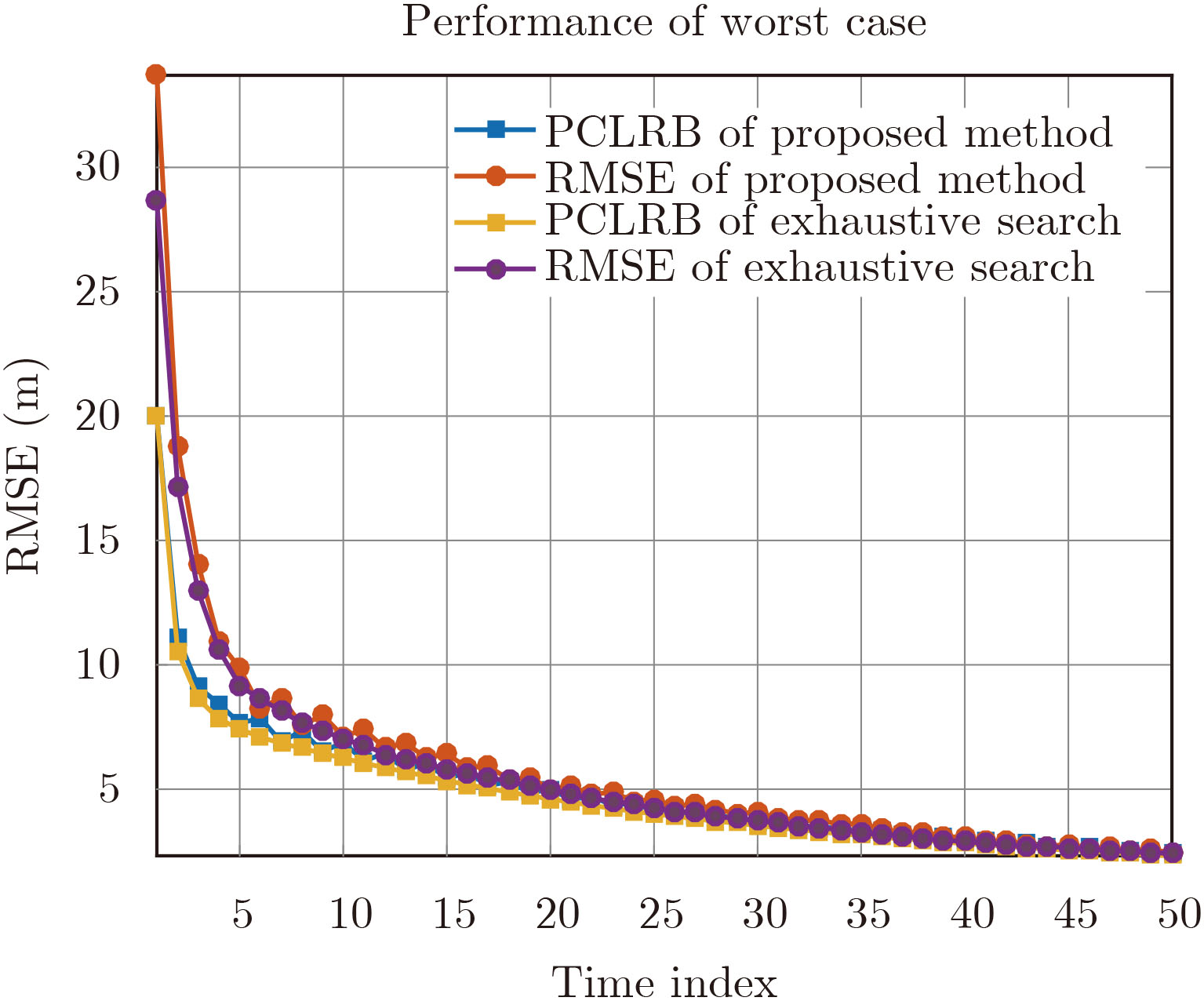
图 3 文中所提优化方法与穷举搜索选择方法的性能对比 Fig.3 Performance of proposed method and exhaustive search method |
当发射站和接收站数量较大的时候穷举搜索法因为计算量太大而变得不可行。为了验证所提方法的全局最优性,本文考虑将发射站和接收站的总数分别减少为8个和8个,各个目标被允许的发射站和接收站数目保持4个不变。同 图2一样,在给出一次完成选择方案后进行1000次蒙特卡洛仿真实验求得两种方法的RMSE。可以看到, 图3中,本文所提方法与穷举搜索有非常相近的跟踪性能。
|
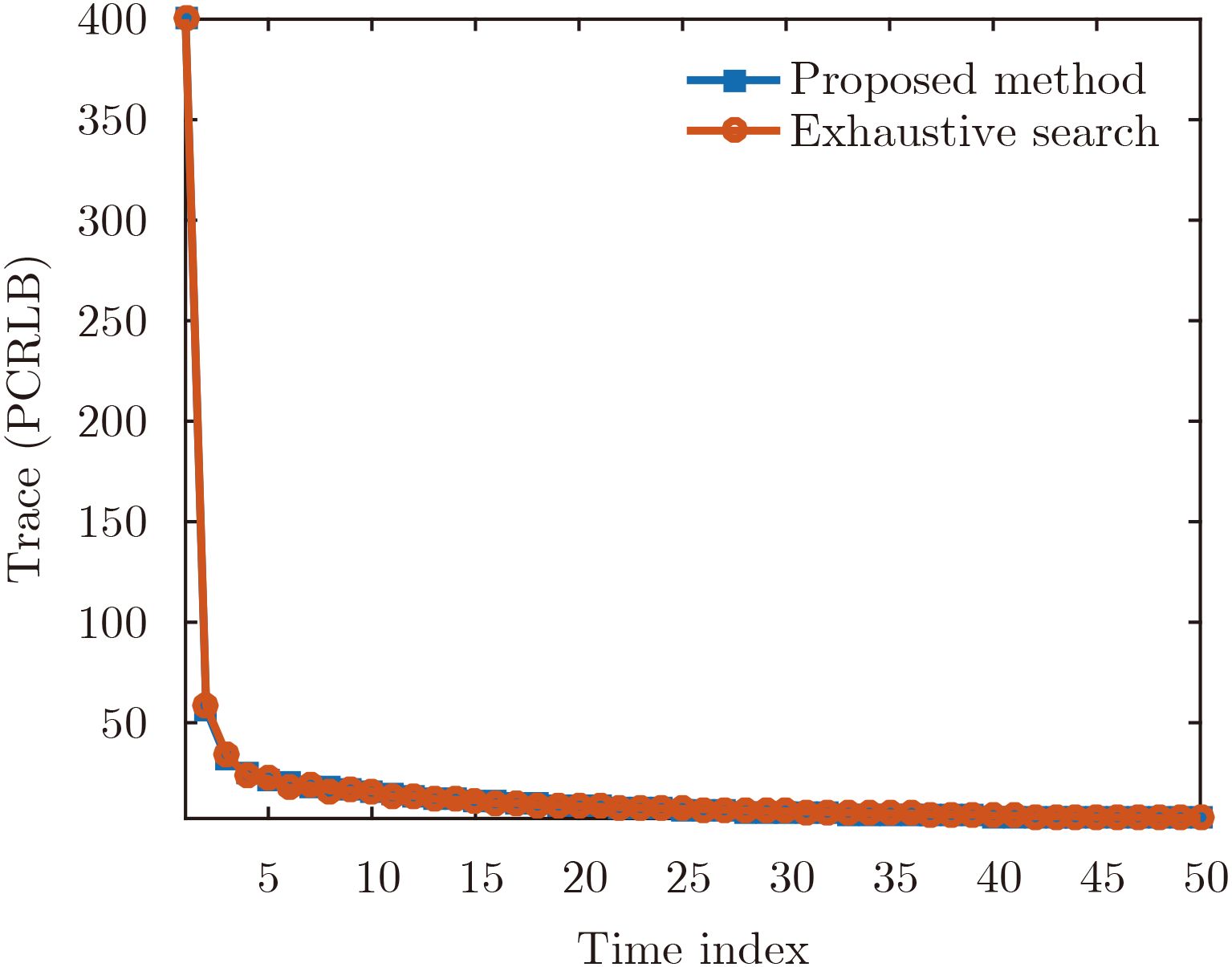
图 4 文中所提优化方法的平均PCRLB与穷举搜索选择方法对比 Fig.4 Average performance of proposed method and exhaustive search method |
为了验证算法的稳定性,在同一场景下100次重复试验下文中方法的平均PCRLB对比和由穷举搜索获得的PCRLB。 图4表明本文基于分块坐标下降方法的优化选择方法在保证稳健性的基础上取得了近乎穷举搜索的性能。
|
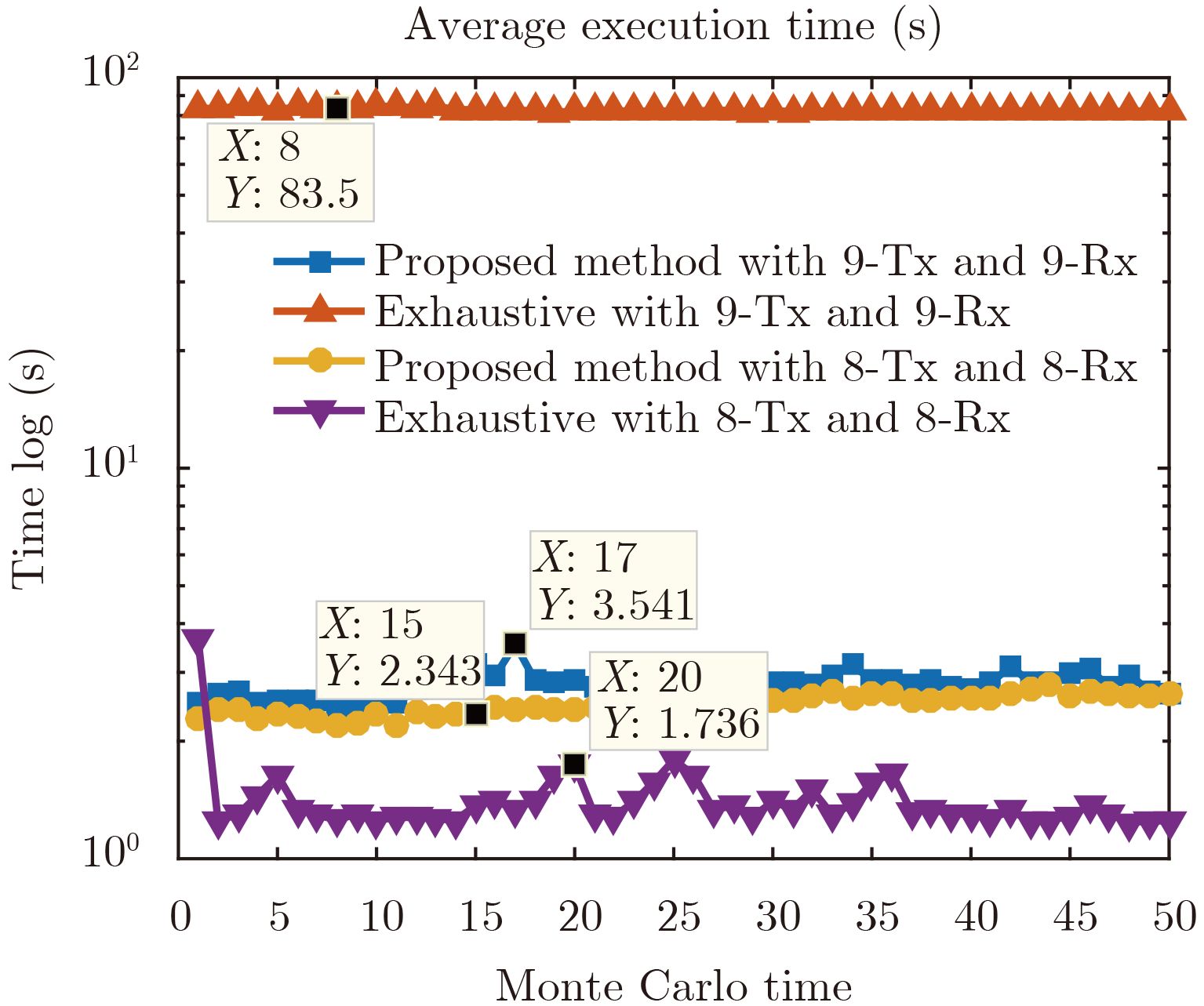
图 5 文中所提优化方法与穷举搜索法不同场景下的执行时间 Fig.5 Execution time of proposed method and exhaustive search method |
给出本文算法准确的计算量比较困难,相比于穷举搜索指数级增长的计算量
本文研究了在分布式MIMO雷达网络中,多目标跟踪背景下的发射站接收站联合选择问题。一种基于以后验卡拉美罗界为性能指标,旨在优化多目标跟踪下跟踪性能最差的目标的发射站接收站优化问题被提出。通过分块坐标下降该优化问题得以求解,实现了发射站和接收站的动态闭环选择。通过仿真实验,在每一个时刻,本文提出的方法可以利用前面时刻的先验信息形成预先规划针对每一个目标的发射站接收站选择。相比于非动态规划下的固定选择,本文的优化选择方法取得了更好的性能。于此同时,对比全局最优的穷举搜索在更小的计算量的前提下获得了近似的性能。
| [1] |
Li J and Stoica P MIMO radar with colocated antennas[J].
IEEE Signal Processing Magazine, 2007, 24(5): 106-114. DOI:10.1109/MSP.2007.904812 ( 0) 0)
|
| [2] |
Haimovich A M, Blum R S and L J Cimini MIMO Radar with Widely Separated Antennas[J].
IEEE Signal Processing Magazine, 2008, 25(1): 116-129. DOI:10.1109/MSP.2008.4408448 ( 0) 0)
|
| [3] |
Joshi S and Boyd S Sensor selection via convex optimization[J].
IEEE Transactions on Signal Processing, 2009, 57(2): 451-462. DOI:10.1109/TSP.2008.2007095 ( 0) 0)
|
| [4] |
Shen X, Liu S and Varshney P K Sensor selection for nonlinear systems in large sensor networks[J].
IEEE Transactions on Aerospace & Electronic Systems, 2014, 50(4): 2664-2678. ( 0) 0)
|
| [5] |
Masazade E, Fardad M and Varshney P K Sparsity-Promoting Extended Kalman Filtering for Target Tracking in Wireless Sensor Networks[J].
IEEE Signal Processing Letters, 2012, 19(19): 845-848. ( 0) 0)
|
| [6] |
Godrich H, Petropulu A P and Poor H V Sensor Selection in Distributed Multiple-Radar Architectures for Localization: A Knapsack Problem Formulation[J].
IEEE Transactions on Signal Processing, 2012, 60(1): 247-260. DOI:10.1109/TSP.2011.2170170 ( 0) 0)
|
| [7] |
Ma Botao, Chen Haowen, Sun Bin, et al.. A joint scheme of antenna selection and power allocation for localization in MIMO radar sensor networks[C]. IEEE International Conference on Signal Processing, Hangzhou, China, 2014: 2226–2229.
http://ieeexplore.ieee.org/document/7015390/ ( 0) 0)
|
| [8] |
Glass J D and Smith L D. MIMO radar resource allocation using posterior Cramér-Rao lower bounds[C]. IEEE Aerospace Conference, Big Sky, MT, USA, 2011: 1–9.
http://dl.acm.org/citation.cfm?id=2053918.2054178 ( 0) 0)
|
| [9] |
Xie M, Yi W, Kirubajaran T, et al.. Receive-beam allocation for multiple target tracking with distributed MIMO radar systems[C]. IEEE Radar Conference, Philadelphia, PA, USA, 2016. DOI: 10.1109/RADAR. 2016.7485153.
http://ieeexplore.ieee.org/document/7485153/ ( 0) 0)
|
| [10] |
Godrich H, Tajer A, and Poor H.V. Distributed target tracking in multiple widely separated radar architectures[C]. IEEE 7th Sensor Array and Multichannel Signal Processing Workshop (SAM), Hoboken, NJ, USA, 2012: 153–156. DOI: 10.1109/SAM. 2012.6250453.
http://ieeexplore.ieee.org/document/6250453/ ( 0) 0)
|
| [11] |
Trees H L V. Detection, Estimation, and Modulation Theory—Part I[M]. Publishing House of Electronics Industry, Beijing, China, 2003: 131–143.
( 0) 0)
|
| [12] |
Tichavsky P, Muravchik C H and Nehorai A Posterior Cramer-Rao bounds for discrete-time nonlinear filtering[J].
IEEE Transactions on Signal Processing, 1998, 46(5): 1386-1396. DOI:10.1109/78.668800 ( 0) 0)
|
| [13] |
Boyd S and Vandenberghe L. Convex Optimization[M]. Cambridge University Press, Cambridge, UK, 2004: 55–60.
( 0) 0)
|
| [14] |
Arulampalam M S, Maskell S, Gordon N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J].
IEEE Transactions on signal processing, 2002, 50(2): 174-188. DOI:10.1109/78.978374 ( 0) 0)
|
| [15] |
Nemirovski A. Interior point polynomial time methods in convex programming[OL]. . 2012.
( 0) 0)
|
| [16] |
Razaviyayn M, Hong M and Luo Z Q A unified convergence analysis of block successive minimization methods for nonsmooth optimization[J].
SIAM Journal on Optimization, 2013, 23(2): 1126-1153. DOI:10.1137/120891009 ( 0) 0)
|




