生物雷达[1]通过发射电磁波信号穿透衣物等非金属障碍物,分析接收到的回波信号,对被测主体进行非接触式的体征探测,而且可以给出生命体心肺活动的有关医学信息,具有探测距离较远,不易受到天气、光线(如昼夜)、温度等实际因素影响的优点。生物雷达在医疗监护领域譬如非接触式呼吸心跳监测[2]、心律失常检测[3]、病态呼吸模式检测[4],尤其是在婴儿猝死综合症和睡眠呼吸中止症方面有广阔的应用[5],同时在野战救护、反恐处突和应急搜索等领域有广泛的应用前景[6],成为了近年来雷达领域的研究热点。早期的生物雷达以单频连续波雷达为主,多用于生命检测[7],随后发展出的超宽带技术由于具有良好的穿透能力,辅以杂波相消,信号分离技术可实现对生命体的呼吸频率和心率的检测,从而实现诸如呼吸模式研究、心律失常检测、胸腔形变检测等更为复杂的应用[8]。
在生命特征提取的应用中,呼吸和心跳通常被建模成正弦信号进行表征,认为心率、呼吸频率等同于它们频谱函数中的基频值,需要从有限长信号中对其进行分离。常规的生物雷达信号处理方法是首先使用带通滤波器将呼吸和心跳信号进行分离,之后利用离散傅里叶变换进行心率和呼吸频率的参数提取[9]。基于多分辨率的特性,小波变换可用作滤波器,通过对小波尺度等参数的选取实现对呼吸和心跳信号的分离。文献[10]和文献[11]采用小波变换处理雷达回波信号,提取生命体征的瞬时频率和微多普勒信息。文献[12]通过计算雷达回波信号各小波系数的自相关,再求得峰值比最大的自相关序列,以此峰值计算心率。该算法能有效提取周期性信息,得到平均心率信息。由于受外界环境噪声以及监测条件变化的影响,呼吸和心跳信号所对应的小波尺度无法预先设定,小波变换并不能一直很好地用作生命体征信号的提取。因此,需要针对小波尺度的选择方法进行相应的研究。本文提出了一种以信噪比为准则的自适应小波尺度选择方法,实现了不同场景下的非接触式生命体征信号分离。
2 自适应小波尺度选择方法 2.1 频率分离与小波尺度对应关系小波变换具有多分辨率特性,可以由粗到精的逐步观察信号,通过选择适当的尺度因子,确定一组伸缩窗,同时选择恰当的母小波,则可以在时域和频域表征信号的局部特征。信号f(t)的连续小波变换(Continuous-Wavelet Transform,CWT):
| $C(a,b;f(t),\psi (t)) = \int_{ - \infty }^\infty {f(t)\frac{1}{{\sqrt a }}} {\psi ^*}\left( {\frac{{t - b}}{a}} \right){\rm{d}}t$ | (1) |
其中,ψ为母小波,a为尺度因子,b为位移因子,分别决定小波的时频窗在频域和时域的位置。小波分析中的尺度因子a的变化不仅改变小波的频谱结构,而且改变其窗口的大小和形状,较大的尺度因子对应低频段,此时重构信号频率分辨率高,时间分辨率低;反之,较小的尺度因子对应高频段,此时重构信号频率分辨率低,时间分辨率高,这就是它的多分辨率特性。对于处于不同频率带上的呼吸和心跳信号,可以利用不同的小波尺度选择进行分离。
采用小波技术提取生命体征信号需要对信号时频域都有较高的刻画,在众多母小波中,Morlet小波有以下3个特点:一是对于低频率振动信号具有很好的时间和频率定位功能,可以较好地揭示信号的振动模式;二是其傅里叶变换为Gauss函数,是一个特性较理想的带通滤波器;三是具有良好的时频局部化特性,并且对称性较好,其小波变换系数的相位信息比较规则[13-15]。所以本文选择Morlet母小波来进行时频分析。
Morlet基本小波的时域和频域表达式为:
| $g(t)=\frac{1}{\sqrt{\pi {{f}_{\text{b}}}}}{{\text{e}}^{\text{j}2\pi f{{}_{0}}t}}{{\text{e}}^{-{{t}^{2}}/-{{t}^{2}}{{f}_{\text{b}}}}}$ | (2) |
| $G(f)=\frac{1}{\sqrt{\pi {{f}_{\text{b}}}}}{{\text{e}}^{-{{\pi }^{2}}{{f}_{\text{b}}}{{(f-{{f}_{0}})}^{2}}}}$ | (3) |
a对应的Morlet小波函数的时域和频域表达式为[14]:
| ${{g}_{a}}(t)=\sqrt{\frac{1}{ak}}g\left( \frac{t}{ak} \right)$ | (4) |
| ${{G}_{a}}(f)=\sqrt{\frac{ak}{\pi f{{}_{\text{b}}}}}{{\text{e}}^{-{{\pi }^{2}}f{{}_{\text{b}}}{{(akf-{{f}_{0}})}^{2}}}}$ | (5) |
其中,fb是母小波的带宽参数,可预先设为定值,k为常数,与信号采样时间和采样点数有关。f0为小波中心频率,表征了小波的总体特性。值得注意的是实际应用中的CWT需要事先定义尺度范围a,因此,需要采用合适的方法来确定需要估计的频率分量的尺度范围。根据式(5),对于给定的a,当akf=f0时,Ga(f)的值最大,使得呼吸与心跳回波在该小波尺度下的能量达到最大即为所选尺度范围。因此,对于呼吸分量fr和心率分量fh,分别存在如下关系[13-18]:
| $\left\{ \begin{array}{*{35}{l}} {{f}_{\text{r}}}=\frac{f{{}_{0}}}{{{a}_{\text{r}}}k}=\frac{f{{}_{0}}f{{}_{\text{s}}}}{{{a}_{\text{r}}}} \\ {{f}_{\text{h}}}=\frac{f{{}_{0}}}{{{a}_{\text{h}}}k}=\frac{f{{}_{0}}f{{}_{\text{s}}}}{{{a}_{\text{h}}}} \\ \end{array} \right.$ | (6) |
其中,k表示信号采样间隔,为慢时间维的脉冲重复频率fs的导数。由式(6)可得,不同频率下的尺度选择与母小波的选择、中心频率选取及采样频率有关。在母小波中心频率f0和采样频率fs已知条件下,呼吸频率fr和心率fh对应着不同的小波尺度ar和ah。
2.2 小波尺度粗集合在式(6)的基础上,依据呼吸和心跳的频率范围可以初步确定呼吸信号和心跳信号小波尺度范围,首先假设呼吸频率范围和心率范围分别为:
| $\left\{ \begin{array}{*{35}{l}} {{\Omega }_{\text{r}}}=[f{{}_{\text{r1}}},f{{}_{\text{r2}}}] \\ {{\Omega }_{\text{h}}}=[f{{}_{\text{h1}}},f{{}_{\text{h2}}}] \\ \end{array} \right.$ | (7) |
为了方便计算机处理,在CWT的基础上通常将尺度参数a离散化,这种小波变换被称为二进小波变换(Dyadic Wavelet Transform,DWT),即将小波尺度特殊离散化a=2m。将式(7)代入式(6)可确定包含有整个呼吸频率和心率范围的整数形式的小波尺度粗集合:
| $\left\{ \begin{array}{*{35}{l}} {{A}_{\text{r}}}=\left\{ \left. {{a}_{\text{r}}} \right|{{a}_{\text{r}}}\in \left\{ \left\lfloor {{\log }_{2}}\left( \frac{f{{}_{\text{0}}}f{{}_{\text{s}}}}{f{{}_{\text{r2}}}} \right) \right\rfloor ,\left\lfloor {{\log }_{2}}\left( \frac{f{{}_{\text{0}}}f{{}_{\text{s}}}}{f{{}_{\text{r2}}}} \right) \right\rfloor +1,\cdots ,\left\lceil {{\log }_{2}}\left( \frac{f{{}_{\text{0}}}f{{}_{\text{s}}}}{f{{}_{\text{r1}}}} \right) \right\rceil \right\} \right\} \\ {{A}_{\text{h}}}=\left\{ \left. {{a}_{\text{h}}} \right|{{a}_{\text{h}}}\in \left\{ \left\lfloor {{\log }_{2}}\left( \frac{f{{}_{\text{0}}}f{{}_{\text{s}}}}{f{{}_{\text{h2}}}} \right) \right\rfloor ,\left\lfloor {{\log }_{2}}\left( \frac{f{{}_{\text{0}}}f{{}_{\text{s}}}}{f{{}_{\text{h2}}}} \right) \right\rfloor +1,\cdots ,\left\lceil {{\log }_{2}}\left( \frac{f{{}_{\text{0}}}f{{}_{\text{s}}}}{f{{}_{\text{h1}}}} \right) \right\rceil \right\} \right\} \\ \end{array} \right.$ | (8) |
其中,
令呼吸信号小波尺度最小值为
| $\left\{ \begin{array}{*{35}{l}} {{A}_{\text{r}}}=\left\{ {{r}_{1}},{{r}_{1}}+1,\cdot \cdot \cdot ,{{r}_{2}} \right\} \\ {{A}_{\text{h}}}=\left\{ {{h}_{1}},{{h}_{1}}+1,\cdot \cdot \cdot ,{{h}_{2}} \right\} \\ \end{array} \right.$ | (9) |
式(9)所示集合内每一个小波尺度均可以重构出一组信号:
| $\left\{ \begin{array}{l} {{{{S}}}_{\rm{r}}} = \{ {s_i}|i \in {{{{A}}}_{\rm{r}}}\} \\ {{{{S}}}_{\rm{h}}} = \{ {s_j}|j \in {{{{A}}}_{\rm{h}}}\} \end{array} \right.$ | (10) |
其中,Si表示小波尺度为
| $\left\{ \begin{array}{l} {{{{W}}}_{\rm{r}}} = \{ {f\!_{{s_i}}}|i \in {{{{A}}}_{\rm{r}}}\} \\ {{{{W}}}_{\rm{h}}} = \{ {f\!_{{s_j}}}|j \in {{{{A}}}_{\rm{h}}}\} \end{array} \right.$ | (11) |
其中,
| $\left\{ \begin{array}{*{35}{l}} {{S}_{\text{r}}}{{}^{\prime }}=\left\{ {{s}_{i}}{{}^{\prime }}|f{{}_{{{s}_{i}}{{}^{\prime }}}}\in {{W}_{\text{r}}}\cap {{\Omega }_{\text{r}}},i\in {{A}_{\text{r}}} \right\} \\ {{S}_{\text{h}}}{{}^{\prime }}=\left\{ {{s}_{j}}{{}^{\prime }}|f{{}_{{{s}_{j}}{{}^{\prime }}}}\in {{W}_{\text{h}}}\cap {{\Omega }_{\text{h}}},j\in {{A}_{\text{h}}} \right\} \\ \end{array} \right.$ | (12) |
从而得到的呼吸信号和心跳信号对应尺度因子范围精集合
| $\left\{ \begin{array}{l} {{{{A}}}_{\rm{r}}}\!\!^\prime = \left\{ {i|{s_i}\!^\prime \in {{{S}}}_{\rm{r}}^{\prime}} \right\}\\ {{{{A}}}_{\rm{h}}}\!\!^\prime = \left\{ {j|{s_j}\!^\prime \in {{{S}}}_{\rm{h}}^{\prime}} \right\} \end{array} \right.$ | (13) |
同样可以更新该尺度下的重构信号频率估计值集合为:
| $\left\{ \begin{array}{l} {{{{W}}}_{\rm{r}}}\!\!^\prime = \{ {f\!_{{s_i}\!^\prime }}|i \in {{{{A}}}_{\rm{r}}}\!\!^\prime \} \\ {{{{W}}}_{\rm{h}}}\!\!^\prime = \{ {f\!_{{s_j}\!^\prime }}|j \in {{{{A}}}_{\rm{h}}}\!\!^\prime \} \end{array} \right.$ | (14) |
得到最终尺度范围集合
首先给出信噪比的计算公式,假设小波尺度对应重构信号的频谱峰值频率为
| $\begin{array}{l} {\rm{SNR}} = 10{\lg} \frac{{\displaystyle \int_{{f_{\max }} - B/2}^{{f\!_{\max }} + B/2}} {\left| {P(f)} \right|} {\rm{ d}}f}{{\displaystyle \int_0^\infty {\left| {P(f)} \right|} {\rm{ d}}f - \int_{{f\!_{\max }} - B/2}^{{f_{\max }} + B/2} {\left| {P(f)} \right|} {\rm{ d}}f}} \end{array}$ | (15) |
其中,B代表信号周期图频率分辨率,由具体FFT点数和采样率决定。P(f)表示在频率为f 时的信号输出功率。则小波尺度范围
| $\left\{ \begin{array}{l} {{{{M}}}_{\rm{r}}} = \left\{ {{\rm{SN}}{{\rm{R}}_i}|i \in {{{{A}}}_{\rm{r}}}\!\!^\prime } \right\}\\ {{{{M}}}_{\rm{h}}} = \left\{ {{\rm{SN}}{{\rm{R}}_j}|j \in {{{{A}}}_{\rm{h}}}\!\!^\prime } \right\} \end{array} \right.$ | (16) |
其中,SNRi表示小波尺度
(1) 理想测量条件
理想条件一般指近距离非接触测量,大约在0.1 m左右进行探测。若已知参考呼吸频率为fr,参考心率为fh,分别与式(14)中重构频率估计值进行比较,计算其准确率:
| $\left\{ \begin{array}{*{35}{l}} {{\psi }_{\text{r}}}=\left\{ {{\varphi }_{i}}=1-\left| \frac{f{{}_{\text{r}}}-f{{}_{{{s}_{i}}{{}^{\prime }}}}}{f{{}_{\text{r}}}} \right||f{{}_{{{s}_{i}}{{}^{\prime }}}}\in {{W}_{\text{r}}}{{}^{\prime }},i\in {{A}_{\text{r}}}{{}^{\prime }} \right\} \\ {{\psi }_{\text{h}}}=\left\{ {{\theta }_{j}}=1-\left| \frac{f{{}_{h}}-f{{}_{{{s}_{j}}{{}^{\prime }}}}}{f{{}_{\text{h}}}} \right||f{{}_{{{s}_{j}}{{}^{\prime }}}}\in {{W}_{\text{h}}}{{}^{\prime }},j\in {{A}_{\text{h}}}{{}^{\prime }} \right\} \\ \end{array} \right.$ | (17) |
其中,φi和θj分别为小波尺度
| $\left\{ \begin{array}{l} {a_{{\rm{r\_ideal}}}} = \mathop {\arg }\limits_i \{ {\varphi _i} = 1\} \\ {a_{{\rm{h\_ideal}}}} = \mathop {\arg }\limits_j \{ {\theta _j} = 1\} \end{array} \right.$ | (18) |
根据式(16),可以得知
| $\left\{ \! \! \! \!\begin{array}{l} {\rm{SN}}{{\rm{R}}_{{\rm{r\_ideal}}}} \!= \! \max \left\{ {{\rm{SN}}{{\rm{R}}_i}|i \in {{{{A}}}_{\rm{r}}}\!^\prime ,{\rm{ }}i \!\ne \! {a_{{\rm{r\_ideal}}}}} \right\}\\ {\rm{SN}}{{\rm{R}}_{{\rm{h\_ideal}}}} \!= \! \max \left\{ {{\rm{SN}}{{\rm{R}}_j}|j \in {{{{A}}}_{\rm{h}}}\!\!^\prime ,{\rm{ }}j \!\ne \!{a_{{\rm{h\_ideal}}}}} \right\} \end{array} \right.$ | (19) |
| $\left\{ \begin{array}{l} {\rm{SN}}{{\rm{R}}_{{\rm{r\_ideal}}}}{\rm{ < SN}}{{\rm{R}}_{{\rm{Tr\_ideal}}}}{\rm{ < SN}}{{\rm{R}}_{{{{a}}_{{\rm{r\_ideal}}}}}}\\ {\rm{SN}}{{\rm{R}}_{{\rm{h\_ideal}}}}{\rm{ < SN}}{{\rm{R}}_{{\rm{Th\_ideal}}}}{\rm{ < SN}}{{\rm{R}}_{{{{a}}_{{\rm{h\_ideal}}}}}} \end{array} \right. \ \ \ \ \ \ \ \ $ | (20) |
(2) 边界测量条件
在给定准确度σ下,雷达系统具有一个测量边界,在该边界测量的呼吸频率和心率准确度恰好均不低于σ。已知参考呼吸频率为fr,参考心率为fh,依据式(17)计算其准确率。因为心跳比较呼吸更加难以测量,根据测量前规定的准确度σ,在保证心跳具有σ的准确度前提下,可以确信呼吸准确度也不低于σ,因此使得φi最大和θj=σ时的小波尺度即为最终选择尺度:
| $\left\{ \begin{array}{l} {a_{{\rm{r\_complex}}}} = \mathop {\arg }\limits_{} \mathop {\max }\limits_i \{ {\varphi _i}\} \\ {a_{{\rm{h\_complex}}}} = \mathop {\arg }\limits_j \{ {\theta _j} = \sigma \} \end{array} \right.$ | (21) |
根据式(16),可以得知所选尺度
| $\left\{ \begin{array}{l} {\rm{SN}}{{\rm{R}}_{{{{a}}_{{\rm{r\_complex}}}}}}{\rm{ < SN}}{{\rm{R}}_{{\rm{Tr\_complex}}}}\\ {\rm{SN}}{{\rm{R}}_{{{{a}}_{{\rm{h\_complex}}}}}}{\rm{ < SN}}{{\rm{R}}_{{\rm{Th\_complex}}}} \end{array} \right.$ | (22) |
综合两种特殊测量条件下的检测,得到适合绝大部分中间场景的呼吸尺度集合
| $\left\{ \!\!\! \begin{array}{l} {\rm{max}}\left\{\! {{\rm{SN}}{{\rm{R}}_{{{{a}}_{{\rm{r\_complex}}}}}}{\rm{,SN}}{{{R}}_{{\rm{r\_ideal}}}}} \! \right\}{\rm{ \! < \! SN}}{{\rm{R}}_{{\rm{Tr}}}}{\rm{ \! < \! SN}}{{\rm{R}}_{{{{a}}_{{\rm{r\_ideal}}}}}}\\ {\rm{max}}\left\{ \! {{\rm{SN}}{{\rm{R}}_{{{{a}}_{{\rm{h\_complex}}}}}}{\rm{,SN}}{{\rm{R}}_{{\rm{h\_ideal}}}}} \! \right\}{\rm{ \! < \! SN}}{{\rm{R}}_{{\rm{Th}}}}{\rm{ \! < \! SN}}{{\rm{R}}_{{{{a}}_{{\rm{h\_ideal}}}}}} \end{array} \right.$ | (23) |
值得注意的是,式(23)中针对两个下限取最大值的过程将会舍弃少部分边界条件下测量场景,致使该场景下的检测得不到结果,实际操作过程中这一现象的出现取决于准确度σ的预先设定。
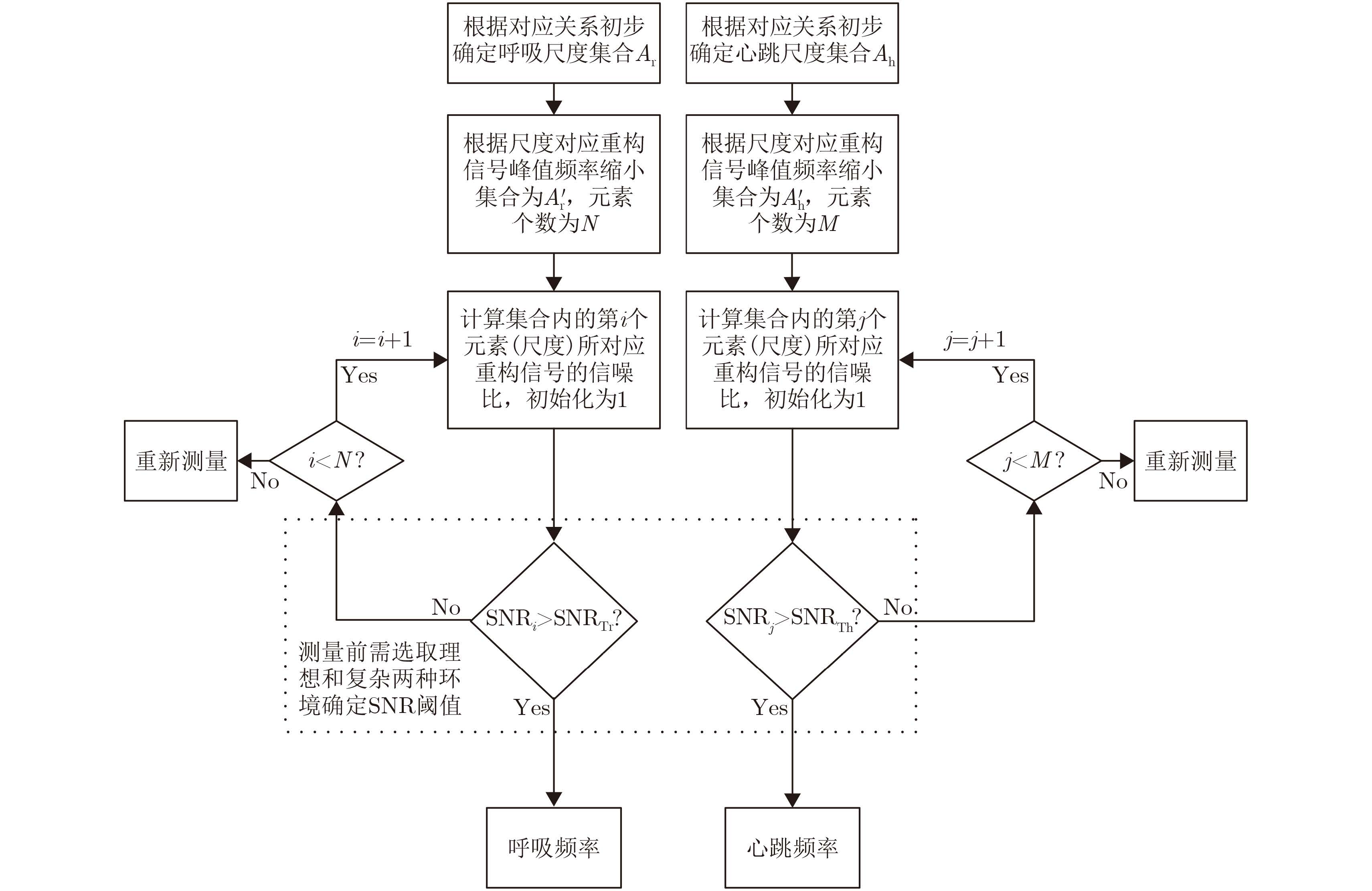
2.5 算法流程通过理想条件测量和边界条件测量,确定了信噪比阈值后,算法可以进行自适应的小波尺度选择。最终尺度集合
|
图 1 自适应小波尺度选择算法流程图 Fig.1 The flow chart of the adaptive wavelet scales selection algorithm |
实验采用的冲激超宽带雷达系统如图 2所示,天线采用Vivaldi天线,发射信号中心频率6.8 GHz,带宽2.3 GHz。

|
图 2 冲激超宽带雷达系统 Fig.2 Impulse ultra-wideband radar system |
实验设置和测试设备如图 3所示,选用了综合医疗器械DynaMap Suite-SA7925输出的呼吸数据和心跳数据作为生物雷达检测的呼吸和心跳的参考信号。

|
图 3 实验设置和测试设备 Fig.3 Experimental setup and measuring devices |
依据本文第2部分,在进行体征信号检测前,我们需要通过理想条件和边界条件的测量来确定信噪比阈值。依据算法流程,首先需要根据重构呼吸频率和心率范围,初步确定小波尺度范围Ar和Ah;然后计算落于呼吸频率和心率范围内的频率峰值,缩小尺度范围至
(1) 理想测量条件
理想条件下人体距离天线约为0.1 m,被测目标为一名健康男性。
(a) 确定小波尺度粗集合
采用二进小波变换,选择Morlet母小波中心频率参数值为8,即f0=28 Hz。雷达接收回波结果脉冲积累后以65 Hz的实际慢时间维采样频率进行采样存储,即fs=65 Hz,对于呼吸频率fr,其范围一般为0.13~0.65 Hz,心率fh一般为0.83~1.80 Hz,根据式(6),计算得:
| $\left\{ \begin{array}{l} {2^{14}} \le \frac{{256*65}}{{0.65}} \le {a_{\rm{r}}} \le \frac{{256*65}}{{0.13}} \le {2^{17}}\\ {2^{12}} \le \frac{{256*65}}{{3.0}} \le {a_{\rm{h}}} \le \frac{{256*65}}{{0.83}} \le {2^{15}} \end{array} \right.$ | (24) |
可以确定小波尺度粗集合Ar={14,15,16,17}和Ah={12,13,14,15}。
(b) 确定小波尺度精集合
计算小波尺度范围内各尺度对应重构信号的峰值频率和信噪比,如表 1所示。Ar集合中所有尺度对应重构信号的峰值频率均落于0.13~0.65 Hz呼吸频率范围内,而Ah集合中尺度14和15对应重构信号的峰值频率落于0.83~1.80 Hz心率范围外,则可更新得到小波尺度精集合
| 表 1 理想测量条件下不同小波尺度下的峰值频率与信噪比 Tab.1 The peak frequency and SNR for each different wavelet scale under ideal measuring condition |
(c) 确定信噪比阈值范围
已知呼吸频率的参考值为0.22 Hz,心跳频率参考值为1.25 Hz,比较呼吸频率最终尺度范围内
| $\left\{ \begin{array}{l} {\rm{0}}{\rm{.45 < SN}}{{\rm{R}}_{{\rm{Tr\_ideal}}}} < 3.16\\ {\rm{ - 9}}{\rm{.87 < SN}}{{\rm{R}}_{{\rm{Th\_ideal}}}} < - 4.21 \end{array} \right.$ | (25) |
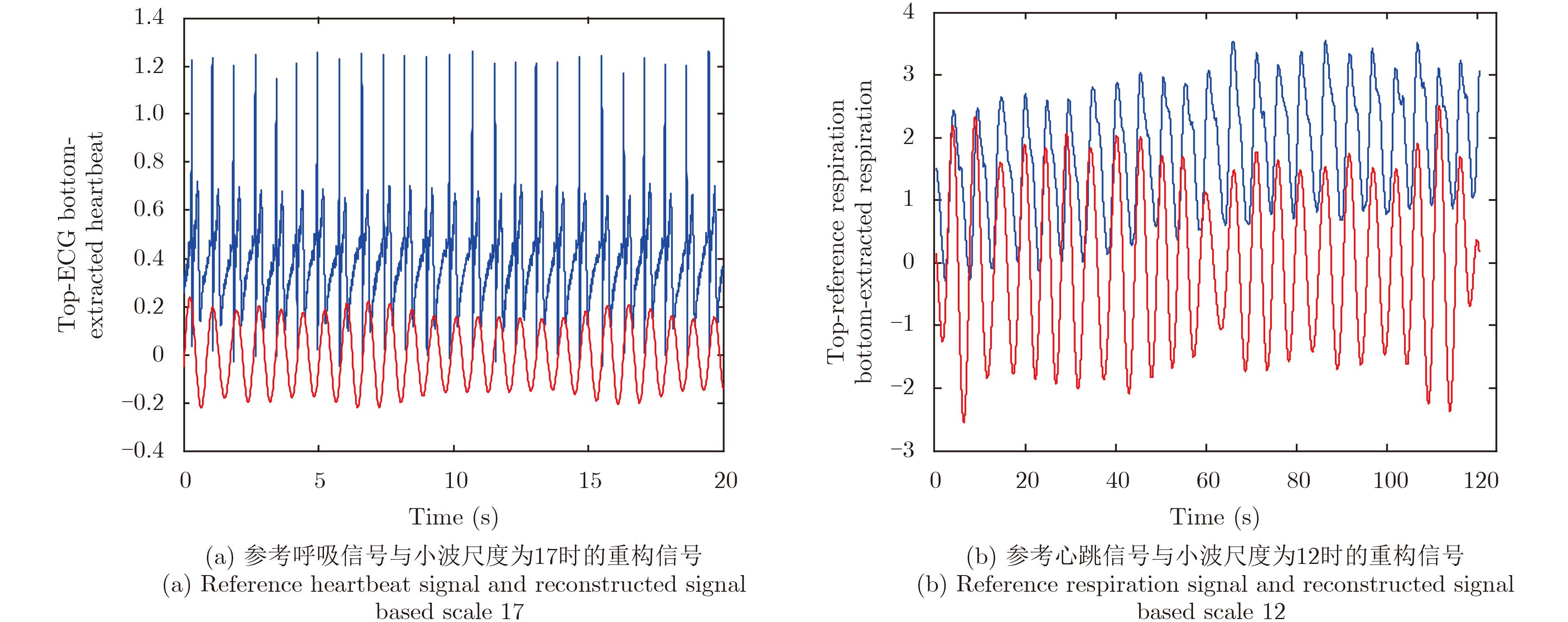
|
图 4 理想条件下的重构生命体征信号与参考信号的比较 Fig.4 The comparison between reconstructed vital sign signals and reference signals |
(2) 边界测量条件
首先设定边界条件下准确率σ=0.95,经过多次实验,对不同体型、性别和距离远近的人体进行检测,与参考信号进行比较,在保证呼吸频率和心率检测准确率均不小于95%的限制条件下,确定边界测量条件。与理想条件下的步骤类似,可以给出所选小波尺度所对应峰值频率符合限制条件下的信噪比,如表 2所示。
| 表 2 边界测量条件下求得小波尺度的峰值频率与信噪比 Tab.2 The peak frequency and SNR for each different wavelet scale under complex measuring condition |
由式(21)和式(22)可得边界测量条件下的阈值范围为:
| $\left\{ \begin{array}{l} - {\rm{4}}{\rm{.03 < SN}}{{\rm{R}}_{{\rm{Tr\_complex}}}}\\ - {\rm{9}}{\rm{.20 < SN}}{{\rm{R}}_{{\rm{Th\_complex}}}} \end{array} \right.$ | (26) |
依据式(23),由式(25)和式(26)得到测量准确度不低于95%条件下的定标阈值范围:
| $\left\{ \begin{array}{l} {\rm{ 0}}{\rm{.45 < SN}}{{\rm{R}}_{\rm{T}}}_{\rm{r}}{\rm{ < 3}}{\rm{.16}}\\ - {\rm{9}}{\rm{.20 < SN}}{{\rm{R}}_{\rm{T}}}_{\rm{h}} < - 4.21 \end{array} \right.$ | (27) |
在此范围内我们一般选取较为接近下限的值为信噪比阈值,即呼吸信号分离信噪比阈值为
改变被测场景,选取一名健康女性作为被测目标,在人体相距天线1.0 m条件下进行生物雷达呼吸心跳检测。当信噪比阈值确定后,采用提出的自适应小波尺度选择方法对测试目标的呼吸和心跳信号进行分离,呼吸频率和心率的测量准确度均不低于95%。图 5给出了实测场景下的自适应小波尺度选择后的呼吸和心跳信号分离结果,其中心跳信号选择的尺度为12,呼吸信号选择的尺度为16,测试结果证明算法较好地实现了呼吸与心跳信号小波尺度的选取,同时实现了较高准确度的呼吸和心跳检测,具有可操作性与实用性。
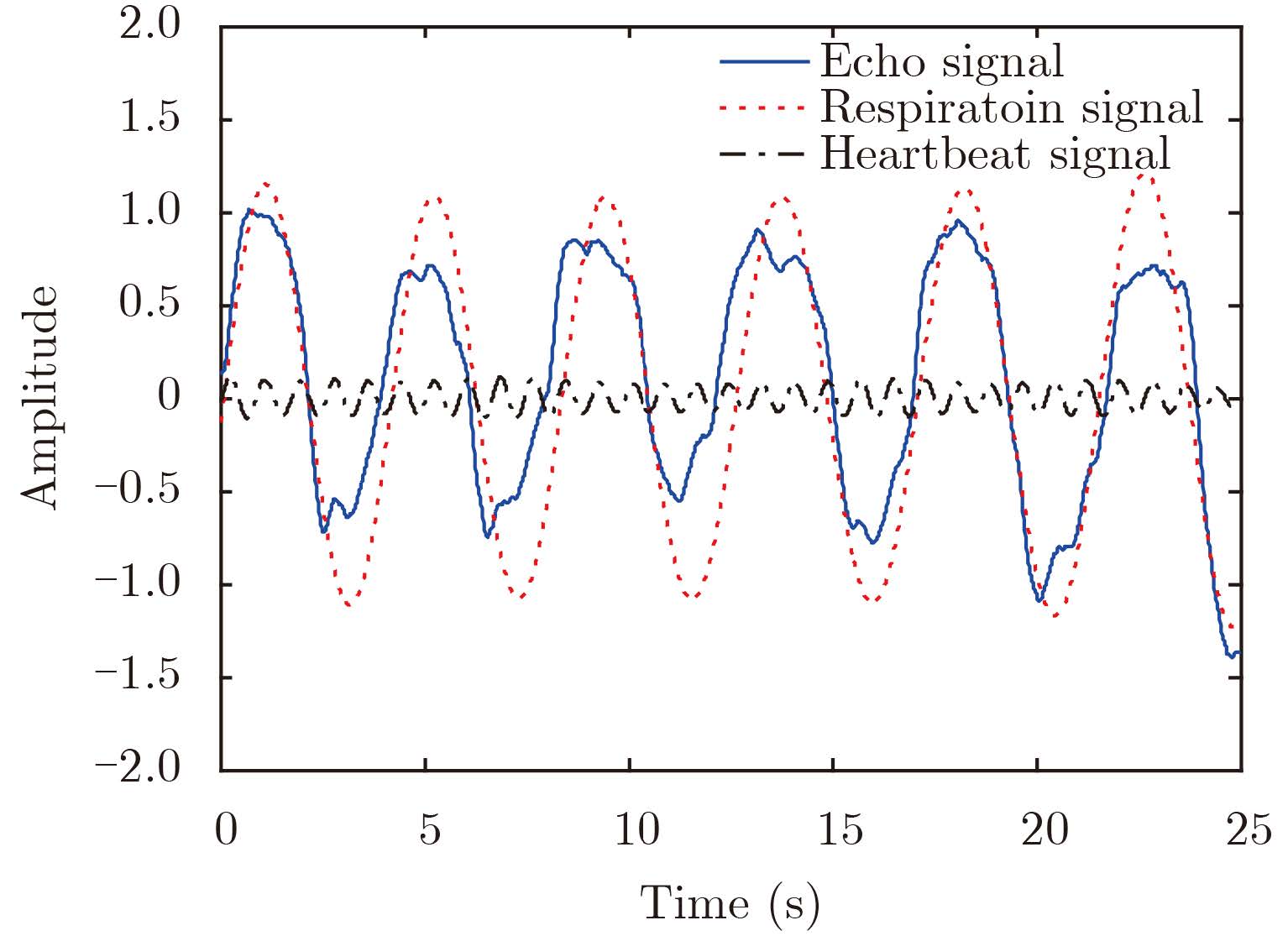
|
图 5 自适应小波尺度选择下的呼吸与心跳分离结果 Fig.5 Separation results using adaptive wavelet scales selection algorithm |
本文针对生物雷达呼吸与心跳分离方法中小波变换尺度选择不固定这一问题,从理论分析到实验验证,对实际条件下的信噪比阈值进行了确定,实现了呼吸与心跳信号的有用分离,该方法可以灵活设定准确度范围,使生物雷达系统达到较高精度的非接触测量。
| [1] |
胡巍. 基于多普勒雷达的非接触式生命体征检测技术研究[D]. [博士论文], 中国科学技术大学, 2014: 1-5.
Hu Wei. Non-contact vital sign detection based on Doppler radar[D]. [Ph.D. dissertation], University of Science and Technology of China, 2014: 1-5.
http://cdmd.cnki.com.cn/article/cdmd-10358-1014268930.htm ( 0) 0)
|
| [2] |
Li Changzhi, Lin Jenshan, and Xiao Yanming. Robust overnight monitoring of human vital signs by a non-contact respiration and heartbeat detector[C]. IEEE EMBS Annual International Conference, New York, NY, USA, 2006: 2235-2238.
( 0) 0)
|
| [3] |
Hu Wei, Zhao Zhangyan, Wang Yunfeng, et al. Noncontact accurate measurement of cardiopulmonary activity using a compact quadrature Doppler radar sensor[J].
IEEE Transactions on Biomedical Engineering , 2014, 61 (3) : 725-735 DOI:10.1109/TBME.2013.2288319 ( 0) 0)
|
| [4] |
Gu Changzhan and Li Changzhi. Assessment of human respiration patterns via noncontact sensing using Doppler multi-radar system[J].
Sensors , 2015, 15 (3) : 6383-6398 DOI:10.3390/s150306383 ( 0) 0)
|
| [5] |
Gu Changzhan. Short-Range noncontact sensors for healthcare and other emerging applications: A review[J]. Sensors, 2016, 16(8). Pii: E1169. DOI: 10.3390/s16081169.
10.3390/s16081169 ( 0) 0)
|
| [6] |
Chen Kun-Mu, Huang Yong, Zhang Jianping, et al. Microwave life-detection systems for searching humansubjects under earthquake rubble or behind barrier[J].
IEEE Transactions on Biomedical Engineering , 2000, 47 (1) : 105-114 DOI:10.1109/10.817625 ( 0) 0)
|
| [7] |
Gu Changzhan and Li Changzhi. From tumor targeting to speech monitoring: accurate respiratory monitoring using medical continuous-wave radar sensors[J].
IEEE Microwave Magazine , 2014, 15 (4) : 66-76 DOI:10.1109/MMM.2014.2308763 ( 0) 0)
|
| [8] |
Fontana R J. Recent system applications of short-pulse ultra-wideband (UWB) technology[J].
IEEE Transactions on Microwave Theory and Techniques , 2004, 52 (9) : 2087-2104 DOI:10.1109/TMTT.2004.834186 ( 0) 0)
|
| [9] |
Lazaro A, Girbau D, and Villarino R. Analysis of vital signs monitoring using an IR-UWB radar[J].
Progress In Electromagnetics Research , 2010, 100 : 265-284 DOI:10.2528/PIER09120302 ( 0) 0)
|
| [10] |
Tariq A and Ghafouri-Shiraz H. Vital signs detection using Doppler radar and continuous wavelet transform[J].
Journal of Nursing Science , 2011, 10 (5) : 285-288 ( 0) 0)
|
| [11] |
Tariq A and Ghafouri-Shiraz H. Doppler radar vital signs monitoring using wavelet transform[C]. 2010 Antennas & Propagation Conference, Loughborough, 2010: 293-296.
( 0) 0)
|
| [12] |
Morgan D and Zierdt M. Novel signal processing techniques for Doppler radar cardiopulmonary sensing[J].
Signal Processing , 2009, 89 (1) : 45-66 DOI:10.1016/j.sigpro.2008.07.008 ( 0) 0)
|
| [13] |
易丽, 何怡刚, 方葛丰, 等. 基于Morlet小波在雷达信号脉内特征提取中的应用[J].
计算机应用研究 , 2013, 30 (1) : 172-175 Yi Li, He Yigang, Fang Gefeng, et al. Application of modified Morlet wavelet in feature extraction of radar signal to intra-pulse[J].
Application Research of Computers , 2013, 30 (1) : 172-175 ( 0) 0)
|
| [14] |
薛蕙, 杨仁刚. 基于连续小波变换的非整数次谐波测量方法[J].
电力系统自动化 , 2003, 27 (5) : 49-53 Xue Hui and Yang Rengang. A novel method for non-integer harmonics measurement using continuous wavelet transform[J].
Automation of Electric Power Systems , 2003, 27 (5) : 49-53 ( 0) 0)
|
| [15] |
卢新城, 龚沈光, 周骏, 等. 基于Morlet小波的高分辨信号频谱估计[J].
武汉理工大学学报(交通科学与工程版) , 2002, 27 (5) : 61-74 Lu Xincheng, Gong Shenguang, Zhou Jun, et al. High resolution signal spectrum estimation based on Morletwavelet[J].
Journal of Wuhan University of Technology (Transportation Science & Engineering) , 2002, 27 (5) : 61-74 ( 0) 0)
|
| [16] |
Yang Yushan and Li Yuanyuan. Spectral analysis of geomagnetic data with continuous wavelet transform[C]. International Congress on Image and Signal Processing, 2009: 1-4.
http://cn.bing.com/academic/profile?id=2165345584&encoded=0&v=paper_preview&mkt=zh-cn ( 0) 0)
|
| [17] |
Rueda J L, Juarez C A, and Erlich I. Wavelet-based analysis of power system low-frequency electromechanical oscillations[J].
IEEE Transactions on Power Systems , 2011, 26 (3) : 1733-1743 DOI:10.1109/TPWRS.2010.2104164 ( 0) 0)
|
| [18] |
Ball John E and Tolley Alan. Low SNR radar signal detection using the continuous wavelet transform (CWT) and a Morlet wavelet[C]. 2008 IEEE Radar Conference, 2008: 1-6.
( 0) 0)
|
| [19] |
Lazaro Antonio, Girbau David, and Villarino Ramon. Techniques for clutter suppression in the presence of body movements during the detection of respiratory activity through UWB radars[J].
Sensors , 2014, 14 (2) : 2595-2618 DOI:10.3390/s140202595 ( 0) 0)
|




