1 引言

生命探测雷达技术是一种综合运用生物医学、电子工程、雷达信号处理等技术的新型非接触式生命检测技术^[1]，该技术利用电磁波的多普勒效应实现生命体的振动信息探测和提取^[2]，从而对人体目标进行非接触式的探测、定位、成像等。由于该技术不受环境温度、热物体和声音干扰等优点^[3]，被广泛应用于地震、坍塌、建筑物倒塌下的废墟救援^{[4, 5]}，反恐行动中对人员情况的掌握^{[6, 7]}，生物医疗中对人体呼吸心跳信号的检测^[8]等领域。

自从20世纪70年代Caro C.G和Bloice J.A将雷达技术应用于生命体非接触式检测^[9]，生命探测雷达技术就引起了科学界的广泛关注，相关科研人员对振动测量反演方法^[5]、穿墙探测杂波抑制方法^[6]、运动模态识别技术^[10]和近距离目标成像技术^[11]等研究领域开展了研究，取得了大量的研究成果。

理论上取得突破的同时，为了满足实际应用的需求，美国、英国、加拿大、中国等国家的研究者研制了多个基于多普勒原理的生命探测雷达系统^{[3, 12-14]}，但是相关的文献的内容主要集中在雷达信号处理和生命信号检测方面，并未给出具体测振性能的理论分析。然而，在实际雷达系统的研制和性能评估过程中，这一性能的分析是极其重要的。由于目前并无该性能有效的评价指标，使得生命探测雷达系统的参数设计和性能评估均很难精确地进行。

针对上述问题，本文仿照合成孔径雷达中等效噪声截面积的概念提出了微多普勒测量灵敏度的指标，用于衡量生命探测雷达系统振动测量性能。该指标将相位噪声和热噪声对测振精度的影响转化为等效平均振动幅度，然后定义目标平均振幅与相位噪声、热噪声等效平均振幅之比为相位测量信噪比，可以根据输出信噪比满足最小信噪比要求得到系统的微多普勒测量灵敏度。最后，利用本文提出的系统微多普勒测量灵敏度给出了示例系统并进行了分析，给出了该系统在不同距离处的测振性能。

2 微多普勒信号感知机理 2.1 线性近似测振模型

生命探测雷达一般可分为脉冲体制和连续波体制，两者均能很好地对微振动进行有效测量。本文提出的分析方法对两种体制均有效，但推导过程略有差异，不失一般性地，本部分先针对脉冲体制雷达进行建模分析，连续波体制雷达的分析将在第5部分给出，第5部分之前，所有的发射信号均认为是脉冲信号。

假设雷达向目标发射脉冲信号，发射信号可以写为：

${s_{\rm{T}}}\left( t \right) = {A_0}L\left( t \right){\rm{exp}}\left( {{\rm}2{\rm{\pi }}{f_{\rm{c}}}t} \right)\exp \left\{ {{\rm{j}}\phi \left( t \right)} \right\}$

(1)

其中，L(t)为发射信号的波形函数，A₀为幅度，f_c为载波频率，ϕ(t)为相位噪声。

记目标的微振动信号为M(t)，目标的振动中心与雷达的距离为R₀，则t时刻目标与雷达的距离为：

$R\left( t \right) = {R_0} + M\left( t \right)$

(2)

雷达接收到的回波信号可以写为：

$\begin{array}{*{20}{c}} {{s_{\rm{R}}}\left( t \right) = \sigma {A_0}L\left( {t - \frac{{2R\left( t \right)}}{{\rm{c}}}} \right)}\\ { \cdot {\rm{exp}}\left\{ {{\rm{j}}2\pi {f_{\rm{c}}}\left( {t - \frac{{2R\left( t \right)}}{{\rm{c}}}} \right)} \right\}}\\ { \cdot \exp \left\{ {{\rm{j}}\phi \left( {t - \frac{{2R\left( t \right)}}{{\rm{c}}}} \right)} \right\} + N\left( t \right)} \end{array}$

(3)

其中，σ是目标后向散射系数，c为光速，N(t)是热噪声。

正交解调后的基带信号可以表示为复数形式：

$\begin{array}{*{20}{c}} {{s_{\rm{R}}}\left( t \right) = {\sigma _0}{A_0}L\left( {t-\frac{{2R\left( t \right)}}{{\rm{c}}}} \right)\;\exp \left\{ {-{\rm{j}}\pi \frac{{4R\left( t \right)}}{\lambda }} \right.}\\ {\left. { + {\rm{j}}\phi \left( {t-\frac{{2R\left( t \right)}}{{\rm{c}}}} \right) - {\rm{j}}\phi \left( t \right)} \right\} + N\left( t \right)} \end{array}$

(4)

因为雷达的脉冲持续时间很短，并且脉冲重复频率远远高于目标振动信号最高频率的两倍。因此，可以按照走-停-走模型建立微弱振动信号与高分辨1维像之间的调制关系。即可以近似认为在1帧时间内，目标静止不动；在相邻两帧之间目标表面位置发生微变，该微变可以由目标所在分辨单元相位变化同步反映。记t_k表示快时间，t_m表示慢时间，则式(4)可重新写为：

$\begin{array}{*{20}{c}} {{s_{\rm{R}}}\left( {{t_{\rm{k}}}, {t_{\rm{m}}}} \right) = \sigma {A_0}L\left( {{t_{\rm{k}}}-\frac{{2R\left( {{t_{\rm{m}}}} \right)}}{{\rm{c}}}} \right)}\\ { \cdot \exp \left\{ {-{\rm{j}}\frac{{4{\rm{\pi }}R\left( {{t_{\rm{m}}}} \right)}}{\lambda } + {\rm{j}}\phi \left( {{t_{\rm{m}}}-\frac{{2{R_0}}}{{\rm{c}}}} \right)} \right.}\\ { - {\rm{j}}\phi \left( {{t_{\rm{m}}}} \right)\} + N\left( {{t_{\rm{k}}}, {t_{\rm{m}}}} \right)} \end{array}$

(5)

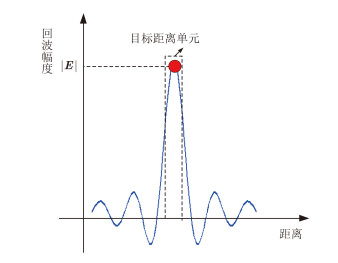
然后，对回波进行高分辨处理，得到含振动目标的高分辨1维像，如图 1所示。高分辨合成以后的目标场景1维像时域表达为：

$\begin{array}{*{20}{c}} {s\left( {{t_{\rm{k}}}, {t_{\rm{m}}}} \right) = \sigma {A_0}*{\rm{AF}}\left( {{t_{\rm{k}}}-\frac{{2\left( {{R_0} + M\left( {{t_{\rm{m}}}} \right)} \right)}}{{\rm{c}}}} \right)}\\ { \cdot \exp \left\{ {-\left( {{\rm{j}}\frac{{4{\rm{\pi }}}}{\lambda }{R_0} + {\rm{j}}\frac{{4{\rm{\pi }}}}{\lambda }M\left( {{t_{\rm{m}}}} \right) + {\rm{j}}\phi \left( {{t_{\rm{m}}}} \right)} \right.} \right.}\\ {\left. {\left. {-{\rm{j}}\phi \left( {{t_{\rm{m}}} - \frac{{2{R_0}}}{{\rm{c}}}} \right)} \right)} \right\} + N\left( {{t_{\rm{k}}}, {t_{\rm{m}}}} \right)} \end{array}$

(6)

其中，AF(t)为L(t)的距离维模糊函数。根据匹配滤波理论，$s\!\left( {{t_{\rm{k}}}, {t_{\rm{m}}}} \right)$的峰值点应出现在${t_{\rm{k}}} = \frac{{2R\left( {{t_{\rm{m}}}} \right)}}{{\rm{c}}}$处，从式(6)中不难看出，$s\!\left(\! {{t_{\rm{k}}}\! =\! \frac{{2R\left( {{t_{\rm{m}}}} \right)}}{{\rm{c}}}, {t_{\rm{m}}}}\! \right)$的相位中包含了振动的信息，通过对多个PRT的峰值位置相位分析可以提取出目标的振动。然而，式(6)的相位同时受到热噪声和相位噪声的干扰，为了验证上述振动测量方法的有效性和准确性，应对噪声对振动测量精度的影响程度进行建模分析。

在式(6)基础上提取目标单元的慢时间信号。不失一般性，设目标在振动时不发生越距离单元走动，并且忽略目标相位中心与距离单元中心的距离差异，则目标单元处的高分辨像复数测量值可以表示为：

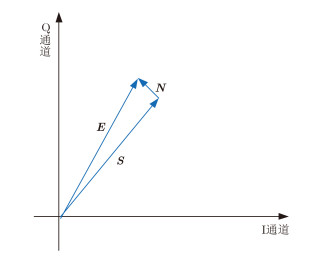
$\begin{array}{*{20}{c}} {\boldsymbol{E} = \boldsymbol{S} + \boldsymbol{N}, }\\ {\boldsymbol{S} = {S_0}\exp \left( {{\rm{j}}{\phi _0} + {\rm{j}}\frac{{4{\rm{\pi }}{R_0}}}{\lambda } + {\rm{j}}\frac{{4{\rm{\pi }}M\left( {{t_{\rm{m}}}} \right)}}{\lambda } + {\rm{j}}{\phi _n}\left( {{{\rm{t}}_{\rm{m}}}} \right)} \right), }\\ {\boldsymbol{N}{\rm{ = }}{\rm{N}}\left( {{{\rm{t}}_{\rm{m}}}} \right)} \end{array}$

(7)

其中，S₀表示目标1维像幅度，ϕ₀是目标后向散射系数σ所携带的相位，$\Delta {\phi {_\rm{n}}}\left( {{t_{\rm{m}}}} \right) = {\phi {_\rm{n}}}\left( {{t_{\rm{m}}}} \right) - {\phi {_\rm{n}}}\left( {{t_{\rm{m}}} - 2{R_0}/{\rm{c}}} \right)$是收发系统相位噪声在目标回波相位中的综合结果，是随时间变化的非白噪声。E, S, N分别表示目标所在单元总体回波以及其中的目标散射回波、接收机热噪声。目标单元的复矢量E是单元内信号复矢量S和噪声复矢量N的加和关系，如图 2所示。

假设

$\left| {4{\rm{\pi }}M\left( {{t_{\rm{m}}}} \right){\rm{ }}/\lambda } \right| \ll 1, \;\left| {\Delta {\phi _n}\left( {{{\rm{t}}_{\rm{m}}}} \right)} \right|{\rm{ }} \ll {\rm{1}}, \;\frac{{\left| {{\rm{N}}\left( {{{\rm{t}}_{\rm{m}}}} \right)} \right|}}{{\left| {{\rm{\bar S}}} \right|}} \ll {\rm{1}}$

(8)

即目标振动相位、目标上的相位噪声、热噪声与目标单元静止回波幅度的比值远远小1。针对微弱振动的测量，该假设通常是满足的。对式(7)做泰勒展开得到如下表达式：

$\begin{array}{*{20}{c}} {\boldsymbol{E} = \boldsymbol{S} + \boldsymbol{N}}\\ {\begin{array}{*{20}{c}} { = \bar S \cdot \left( {1 + {\rm{j}}\left( {\frac{{4{\rm{\pi }}M\left( {{t_{\rm{m}}}} \right)}}{\lambda } + \Delta {\phi _{\rm{n}}}\left( {{t_{\rm{m}}}} \right)} \right)} \right.}\\ {\left. { + o\left( {\frac{{4{\rm{\pi }}M\left( {{t_{\rm{m}}}} \right)}}{\lambda }} \right) + o\left( {\Delta {\phi _{\rm{n}}}\left( {{t_{\rm{m}}}} \right)} \right)} \right) + N\left( {{t_{\rm{m}}}} \right)} \end{array}} \end{array}$

(9)

其中，$\bar S = {S_0}\exp \left( {{\rm j}{\phi _0} + {\rm j}4{\rm{\pi }} {{{R_0}} \mathord{\left/ {\vphantom {{{R_0}} \lambda }} \right.} \lambda }} \right)$，表示目标静止时的1维像取值，$o\left( { \ } \right)$表示高阶无穷小量。

将目标在静止状态下的相位作为固定相位从E的相位测量结果中减去，可以得到只与目标振动和噪声相关的相位项，即

$\begin{array}{*{20}{c}} {{\phi _{\rm{M}}}\left( {{t_{\rm{m}}}} \right) = \angle \left( {{\bf{E}}/\bar S} \right) = }\\ {\angle {\rm{ }}\left( {1 + {\rm{j}}\frac{{4{\rm{\pi }}M\left( {{t_{\rm{m}}}} \right)}}{\lambda } + {\rm{j}}\Delta {\phi _{\rm{n}}}\left( {{{\rm{t}}_{\rm{m}}}} \right){\rm{ + }}\frac{{{\rm{N}}\left( {{{\rm{t}}_{\rm{m}}}} \right)}}{{{\rm{\bar S}}}}{\rm{ + }}{\rm{o}}} \right){\rm{ = }}}\\ {{{\tan }^{{\rm{-1}}}}\left( {\frac{{\frac{{{\rm{4\pi M}}\left( {{{\rm{t}}_{\rm{m}}}} \right)}}{\lambda }{\rm{ + }}\Delta {\phi _{\rm{n}}}\left( {{{\rm{t}}_{\rm{m}}}} \right){\rm{ + }}{\rm{Im}}\left( {\frac{{{\rm{N}}\left( {{{\rm{t}}_{\rm{m}}}} \right)}}{{{\rm{\bar S}}}}} \right){\rm{ + }}{\rm{Im}}\left( {{\rm{o}}} \right)}}{{{\rm{1 + Re}}\left( {\frac{{{\rm{N}}\left( {{{\rm{t}}_{\rm{m}}}} \right)}}{{{\rm{\bar S}}}}} \right){\rm{ + Re}}\left( {\rm{o}} \right)}}} \right)} \end{array}$

(10)

其中，Re(), Im()分别表示复数的实部和虚部，o是各项高阶小量的统一表示。

在式(8)的小信号条件假设下，式(10)在1阶近似的条件下可以写成：

${\phi _{\rm{M}}}\left( {{t_{\rm{m}}}} \right) \approx \frac{{4{\rm{\pi }}M\left( {{t_{\rm{m}}}} \right)}}{\lambda } + \Delta {\phi _{\rm{n}}}\left( {{{\rm{t}}_{\rm{m}}}} \right){\rm{ + }}{\rm{Im}}\left( {\frac{{{\rm{N}}\left( {{{\rm{t}}_{\rm{m}}}} \right)}}{{{\rm{\bar S}}}}} \right)$

(11)

式(11)即为微振动高分辨相位导出测振模型，它揭示了目标振动、目标回波、相位噪声、热噪声对目标单元相位测量结果的贡献。

2.2 近似模型成立条件分析

相位导出测振的模型在建立过程使用了线性近似，仿真分析近似模型成立的条件。设实际测量的相位信号为${{\overset\frown{\phi }}_{\text{M}}}\left( {{t}_{\text{m}}} \right)\left( {{t_{\rm{m}}}} \right)$，通过模型计算的相位信号为${\phi {_\rm{M}}}\left( {{t_{\rm{m}}}} \right)$，则建模误差为${\rm{RMSE = }}|{{\overset\frown{\phi }}_{\text{M}}}\left( {{t}_{\text{m}}} \right)-{{\phi {{_\rm{M}}}}{|^2}}/{|{\phi {_\rm{M}}}{|^2}}$。

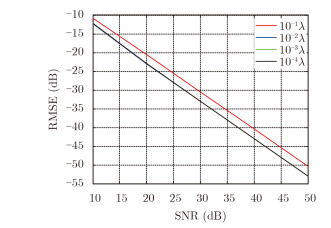
通过仿真分析不同振动幅度，建模误差RMSE和接收机信噪比SNR的关系。图 3是在振动幅度分别为10^-1λ, 10^-2λ, 10^-3λ, 10^-4λ，建模误差RMSE随信噪比SNR变化的关系图。随着信噪比SNR的增大或者振动幅度的减小，建模误差将逐渐减小，但当振动幅度小于10^-2λ时，信噪比将是影响建模误差的主要因素。从仿真结果可以看出当SNR>20 dB，振动幅度小于10^-1λ时，都能满足RMSE < -20 dB。

3 多普勒测量灵敏度 3.1 相位噪声等效平均振动幅度

式(11)中热噪声和系统相位噪声在测量相位上线性叠加，共同影响测振精度。式(11)中的$\Delta {\phi {_\rm{n}}}\left( {{t_{\rm{m}}}} \right)$是相位噪声噪声引起的，将相位噪声的平均功率记为${P_\Phi }$，则：

$\begin{matrix} {{P}_{\Phi }}=\text{E}\left( {{\left| {{\phi }_{\text{n}}}\left( {{\text{t}}_{\text{m}}} \right) \right|}^{2}} \right) \\ \text{=}\text{E}\left( {{\left| {{\phi }_{\text{n}}}\left( {{\text{t}}_{\text{m}}} \right)-{{\text{t}}_{\text{m}}}\text{-}\frac{\text{2}{{\text{R}}_{\text{0}}}}{\text{c}} \right|}^{2}} \right) \\ \text{=4}\int_{\text{-}{{\text{B}}_{\text{v}}}\text{/2}}^{{{\text{B}}_{\text{v}}}\text{/2}}{{{\text{S}}_{\Phi }}\left( {{\text{f}}_{\text{m}}} \right){{\sin }^{\text{2}}}\left( \pi {{\text{f}}_{\text{m}}}\frac{\text{2}{{\text{R}}_{\text{0}}}}{\text{c}} \right)\text{d}{{\text{f}}_{\text{m}}}} \\ \end{matrix}$

(12)

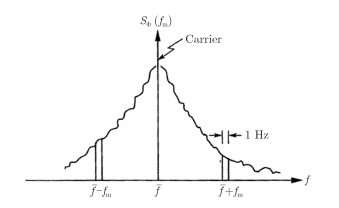
其中，${S_\Phi }\left( {{f_{\rm{m}}}} \right)$是相位噪声双边带功率谱密度，f_m是频率，B_v为信号的带宽。相位噪声的双边带功率谱的形式^[15]如图 4所示。

系统相位噪声主要取决于雷达电子系统器件水平。相位噪声对测振精度影响衡量指标可以仿造合成孔径雷达中的${\rm{NE}}{\sigma _0}$的概念^[16]，将相位噪声的影响等效平均振动幅度，记为PEA₀，则

$\begin{matrix} \text{PE}{{\text{A}}_{\text{0}}}=\frac{\lambda }{4\text{ }\!\!\pi\!\!\text{ }}\sqrt{{{P}_{\Phi }}} \\ =\frac{\lambda }{4\text{ }\!\!\pi\!\!\text{ }}\sqrt{4\int_{-{{B}_{\text{v}}}/2}^{{{B}_{\text{v}}}/2}{}{{S}_{\Phi }}\left( {{f}_{\text{m}}} \right){{\sin }^{2}}\left( \text{ }\!\!\pi\!\!\text{ }{{f}_{\text{m}}}\frac{2{{R}_{0}}}{\text{c}} \right)\text{d}{{f}_{\text{m}}}}\text{ } \\ \end{matrix}$

(13)

3.2 热噪声等效平均振动幅度

式(11)中${\mathop{\rm Im}\nolimits} \left( {\frac{{N\left( {{t_{\rm{m}}}} \right)}}{{\bar S}}} \right)$项是由接收机热噪声引起的，且与目标单元静止回波信号有关。目标单元静止回波信号与发射信号的功率、天线增益、目标距离、目标散射系数等有关。将接收到目标回波信号的平均功率记为P_S，则：

${P_{\rm{S}}} = {\rm{E}}\left( {{{\left| {\bar S} \right|}^2}} \right) = \frac{{{P_{\rm{t}}}{G_{\rm{t}}}{G_{\rm{r}}}{\lambda ^2}\sigma \beta }}{{{{\left( {4{\rm{\pi }} } \right)}^3}{R_0^4}L}}$

(14)

其中，P_t为发射机发射功率，G_t为发射天线增益，G_r为接收天线增益，σ为目标后向散射系数，λ为波长，R为目标的距离，L为系统损耗，β为信号处理增益。

热噪声的平均功率与接收机的噪声系数，热噪声的带宽有关。将热噪声的平均功率记为P_N，则：

${P_{\rm{N}}} = {\rm{E}}\left( {{{\left| {N\left( {{t_{\rm{m}}}} \right)} \right|}^2}} \right) = {\rm{k}}{T_0}{F_{\rm{n}}}{B_{\rm{n}}}$

(15)

其中，k为波尔兹曼常数，T₀为室温，F_n为接收机噪声系数，B_n为热噪声的带宽。

同理，将热噪声对测振精度影响衡量指标转化为热噪声等效平均振动幅度，记为NEA₀，则：

$\begin{matrix} \text{NE}{{\text{A}}_{\text{0}}}=\frac{\lambda }{4\text{ }\!\!\pi\!\!\text{ }}\sqrt{\text{E}\left( {{\left| \text{Im}\left( \frac{N\left( {{t}_{\text{m}}} \right)}{{\bar{S}}} \right) \right|}^{2}} \right)} \\ =\frac{\lambda }{4\text{ }\!\!\pi\!\!\text{ }}\sqrt{\frac{{{P}_{\text{N}}}}{2{{P}_{\text{S}}}}} \\ =\frac{\lambda }{4\text{ }\!\!\pi\!\!\text{ }}\sqrt{\frac{\text{k}{{T}_{0}}{{F}_{\text{n}}}{{B}_{\text{n}}}{{\left( 4\pi \right)}^{3}}R_{0}^{4}L}{2{{P}_{\text{t}}}{{G}_{\text{t}}}{{G}_{\text{r}}}{{\lambda }^{2}}\sigma \beta }} \\ \end{matrix}$

(16)

3.3 微多普勒测量灵敏度

定义式(11)中的目标平均振幅与相位噪声、热噪声等效平均振幅之比为相位测量信噪比，记为SNR_M。则相位测量的信噪比SNR_M为：

${\rm{SN}}{{\rm{R}}_{\rm{M}}} = \frac{{{{\overline M }^2}}}{{{\rm{PEA}}_0^2 + {\rm{NEA}}_0^2}}$

(17)

其中，${\overline M }$是目标平均振幅，定义为${\overline M }=$$\sqrt {\frac{\, 1 \, \, }{T}\!\int_0^T \!\!\!{{M^2}\left( {{t_{\rm{m}}}} \right){\rm{d}}{t_{\rm{m}}}} }$, T为振动持续时间。

在输出信噪比满足最小信噪比要求${\rm{SN}}{{\rm{R}}_{\rm{M}}} \ge$${\rm{SN}}{{\rm{R}}_{{\rm{min}}}}$时，定义满足${\rm{SN}}{{\rm{R}}_{\rm{M}}} = {\rm{SN}}{{\rm{R}}_{{\rm{min}}}}$时的平均振动幅度为系统微多普勒测量灵敏度${M_{\min }}$，则

${M_{\min }} = {\rm{SN}}{{\rm{R}}_{\min }} \cdot \sqrt {{\rm{NEA}}_0^2 + {\rm{PEA}}_0^2}$

(18)

4 系统设计与仿真分析

下面利用上述推导结论进行系统测量性能分析的仿真。仿真所用的雷达系统参数如表 1所示。

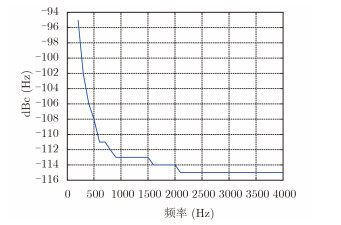
基于作者所在单位某在设计生命探测雷达在中心频率处的相噪仿真结果，可得到系统在X波段的相位噪声功率谱密度函数如图 5所示。考虑到相位噪声功率谱密度函数具有轴对称性，图 5只给出了单边的功率谱特性，另一侧的函数与图 5的函数关于纵轴对称。

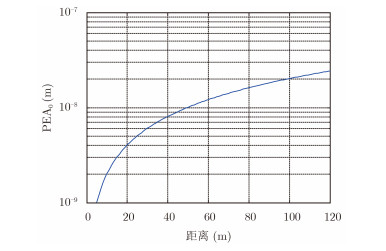
将图 5给出相位噪声指标代入到式(13)，可以计算得到PEA₀随距离变化的曲线如图 6所示。从图 6中不难看出，随着距离的增大，PEA₀逐渐增大，且增长趋于平缓，与理论结果相符。

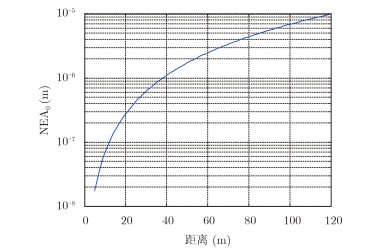
基于上述参数设计，通过式(16)计算得到NEA₀随距离变化的曲线如图 7所示。可以看出，热噪声等效平均振幅的变化特性与相位噪声的变化趋势相似，但振幅要比相位噪声等效平均振幅大两个数量级以上，因此可以得出结论：热噪声对振动测量的影响远远大于相位噪声的影响，在系统分析与设计时，应将热噪声作为重点分析的对象。

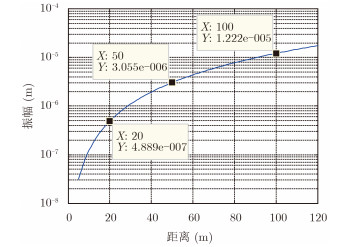
假设最终输出最小信噪比要求SNR_min=5 dB，根据式(18)计算系统的多普勒测量灵敏度随距离变化的曲线，如图 8所示。在20 m的时候能够测量到0.5 mm左右的振动，50 m时能够测量到3 mm左右的振动，100 m时能够测量到12 mm左右的振动。

从该雷达系统的分析结果看出微多普勒测量灵敏度随着距离的增大而变低，其中影响微多普勒测量灵敏度的主要因素是热噪声。

5 连续波体制雷达情况的分析

一般而言，连续波体制的雷达往往采用两种波形——单频信号和调频信号。调频连续波信号一般采用去斜处理或匹配滤波处理，其处理结果的峰值相位与相应调频方式的脉冲信号相同，因此本文提出的方法对调频连续波体制的测振雷达同样有效。下面重点讨论单频连续波的情况。

单频连续波雷达发射的信号为单频连续波，其表达式为：

${s_{\rm{T}}}\left( t \right) = {A_0}{\rm exp}\left( {{\rm j}2{\rm{\pi }} {f_{\rm{c}}}t} \right)\exp \left\{ {{\rm j}\phi \left( t \right)} \right\}$

(19)

其中，A₀为幅度，f_c为载波频率，ϕ(t)为相位噪声。与第2部分的分析类似，可以得出正交解调后的基带信号为：

$\begin{matrix} {{s}_{\text{R}}}\left( t \right)=\text{ }{{\sigma }_{0}}{{A}_{0}}\exp \left\{-\text{j }\!\!\pi\!\!\text{ }\frac{4{{R}_{0}}}{\lambda }-\text{j }\!\!\pi\!\!\text{ }\frac{4M\left( t \right)}{\lambda } \right. \\ \left. +\text{j}\phi \left( t-\frac{4{{R}_{0}}}{\lambda } \right)-\text{j}\phi \left( t \right) \right\}+N\left( t \right) \\ \end{matrix}$

(20)

与脉冲体制的雷达不同，单频连续波体制的雷达回波具有恒定的幅度且无需进行匹配滤波处理，式(20)所示的回波信号的相位直接反映了振动的信息，与式(6)的相位相同。为了便于分析，不妨对其进行等间隔采样，记采样之后的时间轴为t_m，则可重新写为：

$\begin{matrix} {{s}_{\text{R}}}\left( {{t}_{\text{m}}} \right)={{\sigma }_{0}}{{A}_{0}}\exp \left\{-\text{j }\!\!\pi\!\!\text{ }\frac{4{{R}_{0}}}{\lambda }-\text{j }\!\!\pi\!\!\text{ }\frac{4M\left( {{t}_{\text{m}}} \right)}{\lambda } \right. \\ \left. +\text{j}\phi \left( t-\frac{4{{R}_{0}}}{\lambda } \right)-\text{j}\phi \left( {{t}_{\text{m}}} \right) \right\}+N\left( {{t}_{\text{m}}} \right) \\ \end{matrix}$

(21)

此时得到的结论与(6)形式完全一致，不同的是由于单频连续波没有进行匹配滤波处理，没有距离分辨能力，在不考虑杂波的前提下其测振原理与调频连续波没有区别。

6 结束语

本文针对生命探测雷达系统设计和性能评估过程中缺少有效测振性能评价指标的问题，通过系统回波建模分析提出了微多普勒测量灵敏度的概念，并利用该概念给出了系统测振性能的具体分析方法，对生命探测雷达的系统参数设计提供了理论基础，并能很好地分析系统在不同场景、不同距离下的测振性能，对于生命探测雷达的后续研究具有重要的指导意义。