② (国防科学技术大学电子科学与工程学院 长沙 410073)
② (College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)
传统雷达只发射一种或几种波形,波形变化仅限于一定范围内的波形参数调整,灵活程度低。随着高速率信号处理、任意波形产生器等技术的不断进步,波形设计具有更大的自由度,脉间波形捷变和发射任意形状的复杂波形成为可能,为雷达波形设计的研究提供了硬件基础。
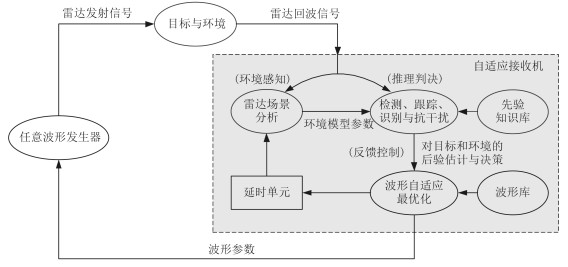
随着大量复杂电子设备的使用以及电子对抗的加剧,战场环境更加瞬息万变,传统的仅在接收机进行自适应信号处理的方法已经无法满足复杂电磁环境的需求。需要从发射信号这一源头上进行自适应优化设计,从而提高雷达系统的性能。Simon Haykin教授提出的认知雷达(Cognitive Radar)概念,就是一种全自适应的雷达系统[1],其系统原理框图如图 1所示。由雷达发射机发射的信号,经过目标和环境的调制,被雷达接收机接收,雷达对回波进行分析和处理后将实时的目标和环境信息再反馈给发射机,利用该信息或其他先验知识进行波形设计,从而发射与当前目标和环境相匹配的最优雷达波形,提高雷达系统的检测、跟踪和识别性能。基于知识的自适应波形设计是认知雷达研究的关键技术之一,得到了雷达界的广泛关注和充分研究。
|
图 1 认知雷达系统原理框图 Fig.1 Schematic diagram of cognitive radar system |
波形设计是一个约束最优化问题,通常包括一个或多个优化准则函数以及一个或多个约束条件。准则函数的选择通常与雷达任务有关[2, 3],例如采用信噪比(Signal-to-Noise Ratio, SNR)、信干噪比(Signal-to-Interference-plus-Noise Ratio, SINR)1)或检测概率作为准则函数,用于提高雷达系统的检测性能;采用参数估计的最小均方误差(Minimum Mean Square Error, MMSE)或雷达回波与目标冲激响应之间的互信息(Mutual Information, MI)作为准则函数,从而提高雷达系统的参数估计性能;采用不同类别的目标回波之间的欧氏距离或马氏距离作为准则函数,优化雷达系统的目标识别性能。约束条件通常包括发射波形的能量恒定,包络恒定,或者相似性约束(Similarity Constraint)等等。
1):本文中提到的信干噪比SINR和信杂噪比(Signal-to-Clutter-plusNoise Ratio, SCNR)不加区分,因为杂波可以认为是信号相关的干扰(Signal-Dependent Interference),所以都用SINR表示。
目标检测性能是雷达系统的重要指标之一,也是雷达进行目标跟踪和参数估计的前提条件。通过波形设计来提高雷达系统的目标检测性能是本文研究的关键问题。针对不同雷达系统、不同的目标环境和实际情况,雷达目标检测的最优波形设计包含着丰富的内容,如表 1所示。对于不同的雷达系统,如单发单收(Single-Input-Single-Output, SISO)雷达,设计一个发射机的发射信号;对于多发多收(Multiple-Input-Multiple-Output, MIMO)雷达,设计发射波形的协方差矩阵,或优化每个发射机的功率分配。根据雷达带宽与目标物理尺寸之间的相对关系,雷达检测的目标模型包括点目标模型和扩展目标模型;目标冲激响应有确定冲激响应和随机冲激响应之分。检测目标的个数可能是一个或者多个;环境中可能包含了信号相关噪声,即杂波,也可能包含了其他电子设备的有意或无意干扰信号;噪声特性可能是白噪声或者色噪声;波形设计对象可以是任意波形设计,也可以给定某种信号形式(如OFDM信号或相位编码信号)设计其参数;波形设计的结果可能是能量谱密度(Energy Spectral Density, ESD),也可以直接合成时域波形;优化准则可能同时包含多个函数;波形的约束条件也根据实际需求各有不同。因此,雷达目标检测的波形优化研究内容多样,文献层出不穷。
| 表 1 雷达目标检测的波形优化研究内容 Tab.1 Research content of radar waveform optimization for target detection |
本文将检测波形最优化研究中若干重要步骤进行分类总结梳理,回顾了其中的一些经典方法,并探讨该研究的发展趋势。
2 雷达目标检测的最优波形设计方法这一节中,我们将雷达目标检测的最优波形设计问题分为了若干类别,并对每一类的经典文献和方法进行了总结回顾,每个类别并不是完全独立的,而是可能存在一定的交叉。这是由于雷达目标检测的最优波形设计中,模型的建立与多种实际因素有关,研究中要根据目标和环境的实际情况建立合适的数学模型来进行求解。本节首先讨论了雷达目标检测的最优波形设计问题采用的准则函数和约束条件;然后分别从不同目标模型、不同环境特性和时域波形合成方法这3大类问题入手进行总结归纳,它们是最优检测波形设计中都会涉及到的不同环节的问题,通过这一节的论述,不仅可以对雷达目标检测的波形设计问题有整体宏观把握,而且对该问题中涉及到的重要细节有更加深入的认识,为该领域的研究者提供思路和借鉴。
2.1 不同准则函数与约束条件雷达目标检测的最优波形设计问题是一个约束优化问题,包含优化准则函数和约束条件两部分。优化准则函数有以下4种,一是采用检测概率作为优化准则函数,检测概率越大,目标检测性能越好,这种方法最为直接,但是需要建立检测概率与雷达波形之间的关系,在求解时较为复杂。第2种方法是采用SNR或SINR作为优化准则函数,因为通常情况下,SNR或SINR越大,检测概率越高,而且SNR或SINR更容易与发射波形建立简单的关系,从而简化了模型和求解。但需要注意的是,有些情况下检测概率不仅与SNR或SINR有关,还与其他因素如信号协防差矩阵的秩有关[4, 5],这时不能简单地采用SNR或SINR准则,而需要直接采用检测概率准则。第3种准则函数是积分旁瓣电平(Integrated Sidelobe Level, ISL),通常用于多目标检测问题,考虑到自相关函数的旁瓣较高会将相邻弱小目标的主瓣淹没,影响检测性能,因此具有较低ISL的发射波形能够较好地进行多目标检测。对于距离-多普勒2维的情况,则采用信号模糊函数作为准则函数,希望发射波形的模糊函数具有尖锐的峰值和较低的旁瓣。第4种准则函数是信息论准则中的Kullback-Leibler散度。雷达目标检测问题可以看作二元假设检验问题,原假设为目标不存在,备选假设为目标存在,原假设概率密度函数到备选假设概率密度函数的Kullback-Leibler散度越大,采用似然比检验的检测概率就越高。Kullback-Leibler散度准则多用于MIMO雷达目标检测的波形优化设计。
常用的约束条件见表 2所示。能量约束是最基本的约束条件,发射信号需要是能量或功率有限的。为了最大化发射功率,需要发射信号具有恒定的包络,也就是恒包络约束。对包络约束的适当松弛是低PAPR约束,注意到,当PAPR=0时,就是恒包络约束。文献[6]研究发现通过适当放松恒包络约束,可以获得更好性能的发射波形。相似性约束是为了保证设计的发射信号能够具有某种常用雷达信号(如线性调频信号)的良好性质,因此约束发射信号与该基准信号具有相似性。
| 表 2 常见的一些约束条件 Tab.2 Commonly used radar waveform constraints |
最优波形设计不仅与采用的优化准则函数和约束条件有关,还与目标和环境模型有关。本小节考虑不同目标模型以及相应的最优波形设计方法。
2.2.1 点目标模型与扩展目标模型根据雷达信号带宽与目标物理尺寸之间的相对关系,可以将目标分为点目标或者扩展目标。当雷达信号为窄带信号时,目标可以看作具有无限小物理尺寸的点目标,其各个方向的雷达散射系数是相同的,雷达发射波形经过目标的反射后,具有一定的时延和多普勒频移。假设雷达发射信号为
| $r(t)=\sqrt{{{E}_{\text{R}}}}s(t-\tau ){{\text{e}}^{\text{j}2\pi ({{f}_{\text{c}}}+{{f}_{\text{d}}})t}}$ | (1) |
其中,ER是回波信号能量,τ和fd分别是目标的时延和多普勒频移。
当雷达信号带宽B与c/2△L可以比拟时,其中c为光速,△L是目标在距离向的空间展布,那么目标回波将不是单色波,而是具有不同的频率响应分量,点目标模型将不再适用[7, 28]。此时,需要将目标回波看作是多个点或者是连续的点在一定扩展区域的回波的叠加,这种目标称为扩展目标。通常用时域的目标冲激响应来描述扩展目标的散射特性。对于一定的目标姿态角,目标冲激响应可以看作一个线性时不变系统,如图 2所示。目标冲激响应用
| $y(t) = s(t) * h(t) = \int_{ - \infty }^\infty {h(\tau )s(t - \tau ){\rm d}\tau } $ | (2) |
其中,*表示信号卷积。
特别地,当扩展目标可以等效为多个静止点目标的叠加时,其目标冲激响应为:
| $h(t)=\sum\limits_{i=1}^{K}{{{\alpha }_{i}}\delta (t-{{\tau }_{i}})}$ | (3) |
其中,K为等效的点目标个数,
根据扩展目标冲激响应是确定的还是随机的,可以把扩展目标进一步地分为确定目标冲激响应模型和随机目标冲激响应模型[8]。确定目标冲激响应模型中,目标冲激响应h(t)是已知的确定信号,用该目标冲激响应来描述目标特性。随机目标冲激响应模型中,目标冲激响应h(t)是能量有限的随机信号,可以看作一系列样本函数的集合
(1) h(t)的所有样本函数都是因果冲激响应,也就是说
(2)对于所有的样本函数
(3)假设
(4)假设h(t)是一个高斯随机过程。当目标包含很多个在空间内随机分布的散射中心时,该假设是成立的。这是由于接收信号的同相通道和正交通道都是高斯随机过程。
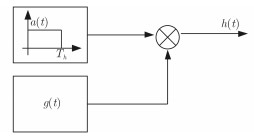
该有限持续时间随机目标冲激响应的产生框图如图 3所示。假设目标冲激响应在时间范围[0, Th]内是非零值,在这个区间外都是0。g(t)是一个复平稳随机过程。a(t)是一个长度为Th的矩形窗函数。那么,h(t)=a(t)g(t)就是一个有限时间长度的随机过程,其支撑区间为[0, Th]。由于g(t)是广义平稳的,因此h(t)在范围[0, Th]内局部平稳。
|
图 3 随机目标冲激响应模型 Fig.3 Impulse response of random target |
当噪声为白噪声时,点目标的检测概率只与发射波形的能量有关,为:
| ${P_{\rm D}} = Q\Big({Q^{ - 1}}\big({P_{\rm FA}}\big) - \sqrt {E/{s^2}} \Big)$ | (4) |
其中,PD是检测概率,
当噪声为白噪声
| ${{P}_{\text{D}}}=Q({{Q}^{-1}}({{P}_{\text{FA}}})-\sqrt{{{s}^{\text{T}}}{{C}^{-1}}s})$ | (5) |
其中,s是信号矢量,
当环境中存在杂波时,S M Kay研究了高斯点目标在杂波环境中的最优波形设计[9]。高斯点目标的冲激响应函数为
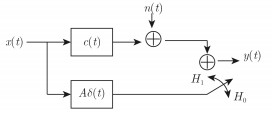
|
图 4 杂波中点目标检测的信号模型 Fig.4 Signal model for point target detection in clutter |
当发射信号具有较大的时宽带宽积时,上述检测问题在Neyman-Pearson准则下的检测概率为:
| ${{P}_{\text{D}}}={{P}_{\text{FA}}}^{1\text{ }\!\!\backslash\!\!\text{ }1+{{d}^{2}}}$ | (6) |
其中,
| $\left. \begin{array}{l} \max \int_{ - W/2}^{W/2} {\frac{{{{\left| {X(f)} \right|}^2}}}{{{S_{\rm cc}}(f){{\left| {X(f)} \right|}^2} + {S_{\rm nn}}(f)}}} {\rm d} \ f\\ \,\,{\rm{s}}.{\rm{t}}.\,\,\,\,\,\,\,\,\,\,\int_{ - W/2}^{W/2} {{{\left| {X(f)} \right|}^2}} {\rm d} \ f \le E \end{array} \right\}$ | (7) |
可见,最优波形的ESD
| ${\varepsilon _x}(f) = \max \left( {\frac{{\sqrt {{{{S_{\rm nn}}(f)} \mathord{\left/ {\vphantom {{{S_{\rm nn}}(f)} A}} \right. } A}} - {S_{\rm nn}}(f)}}{{{S_{\rm cc}}(f)}},0} \right)$ | (8) |
其中,max(x, 0)表示x和0之间的最大值,常数A由能量约束得到,即
| $\int_{ - {W \mathord{\left/ {\vphantom {W 2}} \right. } 2}}^{{W \mathord{\left/ {\vphantom {W 2}} \right. } 2}} {\max \left( {\frac{{\sqrt {{{{S_{\rm nn}}(f)} \mathord{\left/ {\vphantom {{{S_{\rm nn}}(f)} A}} \right. } A}} - {S_{\rm nn}}(f)}}{{{S_{\rm cc}}(f)}},0} \right)} {\rm d}\,f = E$ | (9) |
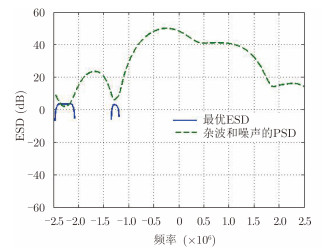
这是经典的注水法(Waterfilling)结论。采用文献[9]中雷达实例的仿真参数可以得到图 5,可见最优检测波形的ESD将能量集中在杂波和噪声功率较小的频带内。
最优波形的注水法解给出了雷达目标检测的最优波形ESD的解析表达式,但是仅得到了最优波形的ESD,要得到时域波形还需要进一步求解。该方法可以推广到扩展目标检测的情况。
2.2.3 点目标的最优检测波形扩展目标模型比点目标模型的应用更为广泛,扩展目标检测的最优波形设计研究也可以根据环境特性分为只考虑加性高斯噪声的情况[7, 29]和杂波环境中扩展目标检测的情况[4, 8, 10, 11, 30, 31]。
M R Bell推导了无杂波情况下扩展目标检测的最优波形[7],通过最大化接收机滤波器输出的SNR,得到最优波形是下面Fredholm方程的解:
| ${\lambda _{\max }}{x_{\rm opt}}(t) = \int_{ - {T \mathord{\left/ {\vphantom {T 2}} \right. } 2}}^{{T \mathord{\left/ {\vphantom {T 2}} \right. } 2}} {{x_{\rm opt}}(\tau )L(t - \tau ){\rm d}\tau } $ | (10) |
其中,λmax是最大特征值,最优波形xopt(t)是相应的特征函数,通过缩放使得其能量为给定的发射信号能量,核函数L(t)为:
| $L(t)=\int_{-\infty }^{\infty }{\frac{{{\left| H(f) \right|}^{2}}}{{{S}_{\text{nn}}}(f)}{{\text{e}}^{\text{j}2\pi ft}}\text{d}f}$ | (11) |
其中,H(f)是任意扩展目标冲激响应函数h(t)的傅里叶变换(下同)。该方法需要求解Fredholm方程,不便于应用。
杂波环境中扩展目标检测问题的信号模型如图 6所示。其中,h(t)是任意扩展目标冲激响应函数。
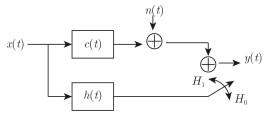
|
图 6 杂波中扩展目标检测的信号模型 Fig.6 Signal model for extended target detection in clutter |
S U Pillai等人和D A Garren等人研究了杂波环境中扩展目标检测的最优波形设计[10, 11],文献中提出了一种迭代的方法来求解匹配滤波器输出SINR最大时的最优发射波形,其中仍然没有摆脱求解积分方程的步骤,而且没有保证算法的收敛性。R A Romero推导了杂波环境中扩展目标检测的最优波形ESD的解析表达式[8],与S M Kay的方法类似,优化问题为最大化频域SINR并约束波形能量:
| $\left. {\begin{array}{*{20}{l}} {\max \int_{ - W/2}^{W/2} {\frac{{\left| {H(f)} \right|{{\left| {X(f)} \right|}^2}}}{{{S_{\rm cc}}(f){{\left| {X(f)} \right|}^2} + {S_{\rm nn}}(f)}}} {\rm d}f}\\ {{\rm{s}}.{\rm{t}}.\,\,\,\,\int_{ - W/2}^{W/2} {{{\left| {X(f)} \right|}^2}} {\rm d}f \le E} \end{array}} \right\}$ | (12) |
采用拉格朗日乘数法可以得到最优波形也满足注水法解的形式。
| ${\varepsilon _x}(f)\! =\! \max \! \Biggr(\! {\frac{{\sqrt {{{\left| {H(f)} \right|}^2}{S_{\rm nn}}(f)} }}{{{S_{\rm cc}}(f)}}\left( {A \!-\! \sqrt {\frac{{{S_{\rm nn}}(f)}}{{{{\left| {H(f)} \right|}^2}}}} } \!\right),\!0} \Biggr)$ | (13) |
其中,常数A由波形能量约束决定。
可见,最优波形ESD与目标冲激响应频谱、噪声PSD、杂波PSD以及能量约束有关。当目标冲激响应为图 3所示的随机过程时,需要将目标冲激响应频谱的模平方
| ${\varepsilon _x}(f) \!\!=\!\! \max \left( {\frac{{\sqrt {\sigma _H^2(f){S_{\rm nn}}(f)} }}{{{S_{\rm cc}}(f)}}\left( {A - \sqrt {\frac{{{S_{\rm nn}}(f)}}{{\sigma _H^2(f)}}} } \right),0} \right)$ | (14) |
其中,
上述方法可以看作S M Kay的方法[9]在扩展目标模型中的推广。同样的,该方法只给出了最优波形的ESD,没有给出时域波形的情况。
秩1目标是扩展目标模型的一种特例。假设扩展目标冲激响应是K个散射点的叠加,即式(3)所示,那么目标回波信号为:
| ${y_t}(t) = x(t) * h(t) = \sum\limits_{i = 1}^K {{\alpha _i}x(t - {\tau _i})} $ | (15) |
式(15)写成频域表示为:
| ${{\mathit{\pmb{Y}}}_{t}}=\text{diag}({{\mathit{\pmb{h}}}_{t}})\mathit{\pmb{x}}$ | (16) |
其中,
| ${{h}_{t}}={{P}_{t}}a=\left[ \begin{matrix} {{\text{e}}^{\text{j}2\pi {{f}_{-N/2}}{{\tau }_{1}}}} & \cdots & {{\text{e}}^{\text{j}2\pi {{f}_{-N/2}}{{\tau }_{K}}}} \\ \vdots & \ddots & \vdots \\ {{\text{e}}^{\text{j}2\pi {{f}_{N/2-1}}{{\tau }_{1}}}} & \cdots & {{\text{e}}^{\text{j}2\pi {{f}_{N/2-1}}{{\tau }_{K}}}} \\ \end{matrix} \right]\left[ \begin{matrix} {{\alpha }_{1}} \\ \vdots \\ {{\alpha }_{K}} \\ \end{matrix} \right]$ | (17) |
ht是目标散射矢量,可以认为是零均值复高斯随机矢量,协方差矩阵为Rht,即
文献[4]针对扩展目标中的秩1目标,推导了最大化检测概率的最优波形,证明了秩1目标最大化检测概率的最优波形与最大化SINR的最优波形是等价的,对于最大化SINR的波形优化问题,采用交替迭代发射波形和接收机滤波器的方法进行求解。进一步的,讨论了目标特性已知而环境特性未知情况下,最大化目标回波的次优发射波形设计;以及环境特性已知而目标特性未知情况下,最小化杂波回波能量的次优发射波形设计。对于大时宽带宽积的渐近情况,推导了最优波形的注水法形式,该结论是S M Kay注水法结论[9]在秩1目标情况下的推广。
2.3 不同环境特性的最优波形设计 2.3.1 环境特性建模最优波形设计与环境特性是密切相关的。雷达目标检测所处的环境通常包括:噪声、杂波(信号相关干扰)、干扰等。信道噪声或者接收机噪声通常建模为加性高斯随机过程,
杂波与实际环境关系较大,因此杂波模型比较多样化,一种简单的方式是将其看作信号相关干扰,即杂波是雷达发射波形经过随机线性时不变滤波器的输出,其冲激响应是一个广义平稳随机过程[8-11, 32]。如图 4和图 6中所示,杂波为:
| ${y_c}(t) = x(t) * c(t)$ | (18) |
该模型不允许频谱扩展,因此雷达和杂波之间不存在相对运动。通常假设c(t)的PSD是已知的,为S
特别的,也可以认为c(t)是由多个不同散射强度和时延的散射点构成的[4],杂波冲激响应函数为:
| $c(t) = \sum\limits_{l = 1}^L {{a_{c,l}}\delta (t - {\tau _l})} $ | (19) |
其中,
| ${y_c}(t) = \sum\limits_{l = 1}^L {{a_{c,l}}x(t - {\tau _l})} $ | (20) |
当杂波为相邻距离单元的回波信号时[33-35],将其建模为不同距离单元的不相关散射中心回波的叠加,当前距离单元回波与杂波和噪声的回波为:
| $\begin{align} & \mathit{\pmb{y}}={{\alpha }_{0}}\left[ \begin{matrix} {{s}_{1}} \\ \vdots \\ {{s}_{N}} \\ \end{matrix} \right]+{{\alpha }_{1}}\left[ \begin{matrix} 0 \\ {{s}_{1}} \\ \vdots \\ {{s}_{N-1}} \\ \end{matrix} \right]+\cdots +{{\alpha }_{N-1}}\left[ \begin{matrix} 0 \\ \vdots \\ 0 \\ {{s}_{1}} \\ \end{matrix} \right]+ \\ & {{\alpha }_{-1}}\left[ \begin{matrix} {{s}_{2}} \\ \vdots \\ {{s}_{N}} \\ 0 \\ \end{matrix} \right]+\cdots +{{\alpha }_{-N+1}}\left[ \begin{matrix} {{s}_{N}} \\ 0 \\ \vdots \\ 0 \\ \end{matrix} \right]+\mathit{\pmb{n}} \\ \end{align}$ | (21) |
其中,
当环境杂波为海杂波时,S P Sira将常用的复合高斯海杂波模型用于波形设计问题中[36],研究了强海杂波参数估计与最优检测波形设计问题。综上,杂波中目标检测的波形设计问题需要根据实际杂波模型来分别进行研究。
干扰样式多种多样,其分类和建模不在本文考虑范围内。本文基于目标检测的波形优化问题进行讨论,而干扰雷达系统检测性能的干扰模式通常为噪声压制干扰。因此在目标检测波形优化设计的文献中,一般简单地将干扰看作色噪声,具有某个给定的PSD。如对于窄带噪声压制干扰或相邻频带的其他电子设备干扰,其PSD在某一个或几个频带内较大,其余频带内较小,采用色噪声环境中最优波形设计相同的方法,通过最大化SINR,构造波形频谱凹口来抑制该类干扰,提高干扰环境中的雷达目标检测性能。如图 7所示[12],干扰频谱是系统频带内某个频带的噪声。
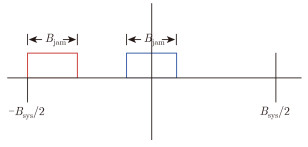
|
图 7 干扰频谱Bjam与系统带宽Bsys Fig.7 Jamming band Bjam and system bandwidth Bsys |
色噪声是与发射信号不相关的噪声,通常认为其协方差矩阵是已知的。文献[12]提出了3种抑制色噪声的波形优化方法,准则函数为最大化SINR。
| $\underset{\mathit{\pmb{s}}}{\mathop{\max }}\,\text{SINR}={{\mathit{\pmb{s}}}^{\text{H}}}{{\mathit{\pmb{C}}}^{-1}}\mathit{\pmb{s}}$ | (22) |
其中,C是噪声协方差矩阵。
方法1是简单地将最优波形矢量选为噪声协方差矩阵的最小特征值对应的特征矢量[10],即
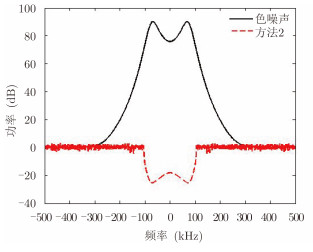
|
图 8 色噪声PSD与方法二得到的最优波形功率[13] Fig.8 Colored noise PSD and the optimal waveform power using method 2[13] |
进一步地,Li Jian等人在上述色噪声中SINR最大的波形优化问题中增加了相似性约束和恒包络约束[13],提出了SWORD(Signal Waveform's Optimal-under-Restriction Design)方法来求解该优化问题,相比于文献[12]有较大的性能提升。
2.3.3 杂波环境中的最优波形设计与色噪声不同,杂波信号回波与雷达发射波形相关,使得雷达波形设计更加复杂。早期研究中,通过设计发射信号和滤波器对来最大化信杂噪比以提高雷达目标检测性能的文献有很多[37-40]。这些算法统称为特征迭代算法[41],首先对于给定的发射信号获得最优滤波器,再利用该最优滤波器求解最优发射信号,依次迭代来求解Fredholm积分方程,这种特征迭代算法的最优性并未被证明。
文献[42]证明了不需要同时设计信号和滤波器,当已知信道PSD,噪声PSD和点目标运动的多普勒和发射信号频谱时,干扰环境中点目标检测的最优接收机是确定的,只需要进行发射波形设计,再采用与之对应的Neyman-Pearson接收机即可。
对于图 4和图 6所示的一般杂波模型,SINR的形式很容易得到,点目标模型和扩展目标模型最大化SINR的最优波形ESD都是注水法的形式,见式(8)和式(13)。最优波形将能量集中在杂波功率较小的频带内,从而抑制杂波[8, 9]。
对于式(21)所示的相邻距离单元杂波回波模型,最大化信杂噪比的波形优化准则同样可以表示为[34]:
| $\underset{\mathit{\pmb{s}}}{\mathop{\max }}\,\text{SINR}={{\mathit{\pmb{s}}}^{\text{H}}}\mathit{\pmb{C}}{{(\mathit{\pmb{s}})}^{-1}}\mathit{\pmb{s}}$ | (23) |
注意到,与式(22)不同,此时的协方差矩阵C不仅包含了噪声协方差,还包含了杂波分量,因此与信号有关,不能直接采用类似SWORD的方式进行求解。文献[34]研究了恒包络或低PAPR约束下的最优波形设计,证明了散射系数估计的MSE最小准则与最大化SINR准则是一致的。对于恒包络约束条件,采用梯度下降法可以从时域直接求解最优波形与相应的滤波器;对于低PAPR约束,仍然从频域求解最优波形的ESD,进而采用循环算法(Cyclic Algorithm)进行时域合成。
对于上述相邻距离单元杂波回波模型,M Piezzo等人将雷达网络中多部雷达的波形设计问题看作非合作博弈[33],用博弈论的方法来求解杂波中最大化SINR的最优波形。
对于一些具体问题中的杂波模型,如文献[36]中的复合高斯海杂波,通过估计杂波的时变参数,最小化其它距离单元的杂波贡献来设计相位调制波形。
2.4 时域波形合成在雷达目标检测的最优波形设计过程中,有的方法只能获得最优波形的ESD,要得到时域信号需要进一步进行时域波形合成[5, 9, 23, 15-18];有的方法可以直接设计时域最优发射波形[6, 7, 10, 12, 13, 30]。
2.4.1 最优ESD合成时域波形由于雷达目标检测的最优波形设计通常采用SINR作为优化准则函数,而SINR的频域表达式只与波形的ESD有关,与波形相位无关。在得到最优波形ESD之后,如何进行时域信号合成使得合成的时域信号ESD与最优波形ESD差距最小,是波形设计研究的重要问题之一。
Durbin方法[43]是一种简单的时域信号合成方法,它通常用于MA模型谱估计问题中,采用Durbin方法的好处是可以合成最小相位信号。首先将最优波形ESD进行傅里叶反变换,得到自相关函数,将该自相关函数带入Yule Walker方程,用Levinson算法来求出最佳线性预测系数,从而得到自相关函数的估计。将求得的自相关函数估计写成Yule Walker方程,得到的MA参数就是时域波形[9]。这里,并没有对信号进行其他约束,实际应用中通常需要信号是恒包络的,或者具有较低的PAPR。
对于恒包络信号的时域合成,一种简单的方法是计算最优ESD的傅里叶反变换,加窗获得所需要的样本数,然后加上恒包络约束。但是该方法合成的时域信号ESD与所需的最优ESD差距很大。也可以采用驻定相位原理来进行时域信号合成[15]。
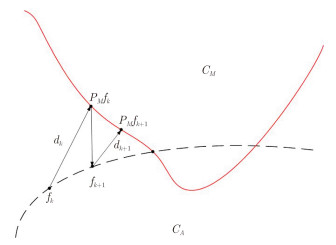
给定最优波形的ESD,求解具有恒定包络约束的时域波形问题属于相位恢复(Phase Retrieval)问题,有关相位恢复问题的综述可以参考文献[19]第2章。最早的相位恢复问题采用Gerchberg-Saxton算法(GSA)来求解,这是一种误差递减算法,通过在时域和频域之间不断投影,逐渐减小设计的信号ESD与最优波形ESD之间的误差,从而求得满足时域包络约束条件,且频域ESD与最优ESD误差最小的最优时域波形。文献[19]对传统的GSA算法进行改进,用来设计时频域样本数不相等情况下的最优时域波形。图 9为该投影过程中误差减小的示意图[18],其中,集合CM表示满足频域ESD要求的波形集合,集合CA表示满足时域恒包络约束的波形集合,注意到,两个集合可能不存在交集。
文献[15]采用最小化设计信号的频率响应与最优ESD的平方根之间的均方误差的方法来进行恒包络时域信号合成,即
| $\begin{align} & s=\arg \underset{s\in {{\mathbb{C}}^{M}}}{\mathop{\min }}\,{{\sum\limits_{n=-N/2}^{N/2-1}{\left| \sqrt{{{E}_{s}}_{,\text{opt}}({{f}_{n}})}{{\text{e}}^{\text{j}\angle S({{f}_{n}})}}-S({{f}_{n}}) \right|}}^{2}}\Delta f \\ & \text{s}.\text{t}.\left| s(m) \right|=\sqrt{E/T} \\ \end{align}$ | (24) |
其中,时域信号s的长度为M,持续时间为T,能量为E, S(fn)是信号的傅里叶变换,
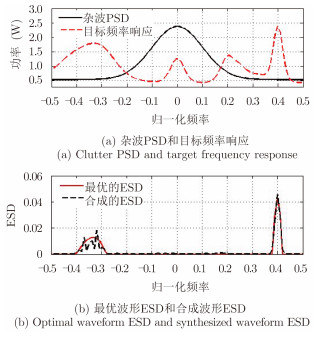
|
图 10 多目标分类的SINR最大的最优波形设计[20] Fig.10 SINR based radar waveform optimization for multiple target classification[20] |
文献[17]采用最小化设计信号的ESD与最优ESD之间的均方误差的方法来进行恒包络时域信号合成,即
| $\begin{align} & s=\arg \underset{s\in {{\mathbb{C}}^{M}}}{\mathop{\min }}\,{{\sum\limits_{n=-N/2}^{N/2-1}{\left| {{\left| S({{f}_{n}}) \right|}^{\text{2}}}-{{E}_{s}}_{,\text{opt}}({{f}_{n}}) \right|}}^{2}}\Delta f \\ & \text{s}.\text{t}.\left| s(m) \right|=\sqrt{E/T} \\ \end{align}$ | (25) |
注意到,上述几种迭代方法只能合成恒包络时域信号,当放宽恒包络约束条件,而采用低PAPR约束时,上述方法无法使用。P Stoica等人提出了一种循环算法进行时域信号合成,不仅适用于只有能量约束的波形设计,有恒包络约束的信号合成,还适用于低PAPR约束的情况[16]。
2.4.2 直接设计时域最优波形设计最优ESD进而合成时域波形的方法多少会带来一定的性能损失,因此有的文献转而从时域直接合成所需要的最优发射波形。
求解Fredholm方程的方法以及利用求解Fredholm方程的特征迭代法属于直接时域波形求解的方法[7, 10, 12],不需要经过求解最优ESD再合成时域波形。经典的SWORD法[22]也是直接从时域求解式(23)中的优化问题。
杂波环境中恒包络发射信号最优化问题[16]
| $\left. \begin{array}{*{35}{l}} \underset{s}{\mathop{\max }}\,\text{SINR}={{s}^{\text{H}}}C{{(s)}^{-1}}s \\ \text{s}.\text{t}.{{s}_{k}}={{\text{e}}^{\text{j}{{\phi }_{k}}}},\ k=1,\cdots ,M \\ \end{array} \right\}$ | (26) |
可以直接采用梯度下降法来求解。但是由于每次迭代都需要求解M个方向的梯度,因此计算复杂度比较高。
对于一般杂波模型,将离散SINR的频域表示
| ${d^2} = \sum\limits_{n = - {N \mathord{\left/ {\vphantom {N 2}} \right. } 2}}^{{N \mathord{\left/ {\vphantom {N 2}} \right. } 2} - 1} {\frac{{\left| {H({f_n})} \right|{{\left| {X({f_n})} \right|}^2}}}{{{S_{\rm cc}}({f_n}){{\left| {X({f_n})} \right|}^2} + {S_{\rm nn}}({f_n})}}} \Delta f$ | (27) |
利用离散傅里叶变换矩阵转化为如下时域表示[6, 21, 44]:
| $d{{\left( s \right)}^{2}}=\sum\limits_{n=-N/2}^{N/2-1}{\frac{{{s}^{\text{H}}}\left[ \left| H({{f}_{n}}) \right|{{\omega }_{n}}\omega _{n}^{\text{H}} \right]s}{{{s}^{\text{H}}}\left[ {{S}_{\text{cc}}}({{f}_{n}}){{\omega }_{n}}\omega _{n}^{\text{H}} \right]{{s}^{2}}+{{S}_{\text{nn}}}({{f}_{n}})}}\Delta f$ | (28) |
其中,
通过第2节对雷达目标检测的波形优化问题进行分类整理不难看出,雷达目标检测的波形优化问题一直是认知雷达及波形优化问题中人们关注的重要问题之一,已有研究已经包含了不同准则函数、约束条件、目标模型、环境特性等多个方面的最优波形设计,但是这些研究仍然存在一些不足之处,例如干扰抑制和杂波抑制的波形优化设计研究中,对于实际的具体干扰模型或者杂波模型的情况研究较少,一些通用的简化模型可能在实际应用中不足以描述环境特性,因而导致最优波形性能下降;最优波形设计算法的复杂度、实时性分析以及在实际系统应用中可能存在的问题讨论不够深入,与真正使用还存在很大的差距;发射波形最优化结合环境与目标参数估计,以及发射波形的自适应变化策略等研究不够充分。因此,我们认为目标检测的波形优化问题具有如下几点重要的发展趋势。
3.1 多目标场景的检测波形最优化已有的目标检测最优波形设计问题中,通常要判决场景中存在/不存在某一类已知的目标。由于检测概率、SINR等优化准则函数与该目标的特性(如目标冲激响应)有关,因此基于这些准则函数的波形优化都是针对该类目标的最优检测波形。当场景中可能同时存在多类待检测的目标时,最优检测波形应如何设计是下一步研究的重要内容。已有研究中采用约束或优化波形的自相关/互相关函数的方法,使相关函数具有较尖锐的主瓣和较低的旁瓣,从而在多目标场景中减小强目标回波对邻近弱目标的遮盖,是多目标场景中最优波形设计的一种思路。另外,同时利用多类目标特性来设计某种最优发射波形,或交替发射多种目标分别对应的最优检测波形等方法有待进一步研究。
3.2 多优化准则的检测波形最优化随着雷达性能的不断提高和技术的不断发展,进一步需要雷达同时具有多种模式和多种任务。因此,雷达发射波形不仅要具有较好的目标检测性能,还要具有较高的参数估计或跟踪、识别性能,从而通过一次或较少次数的观测同时完成检测、估计等任务。一些研究已经开展了多个优化准则的波形最优化设计,如同时提高检测概率和减小参数估计的克拉美罗下限[45],同时提高SINR和互信息[23],同时优化目标检测性能和相关函数特性[6, 21],同时增大马氏距离提高检测性能和减小稀疏恢复的误差[46]等。随着对多模式多任务雷达需求的加剧,未来波形优化设计将朝着多种优化准则的方向发展,将模糊函数特性、相似性约束、检测概率、参数估计性能等众多因素同时考虑在内,设计具有多种优化性能的统一的发射波形形式。
3.3 认知MIMO雷达和认知雷达网络的波形设计与资源优化配置与传统的相控阵雷达相比,MIMO雷达的每个发射天线可以发射不同的波形,具有较大系统自由度,可以获得更高的目标分辨和参数估计性能。认知MIMO雷达基于目标和环境信息,通过自适应调整MIMO雷达各天线的发射波形,适应变化的目标和环境并提高MIMO雷达性能。复杂环境中通常包括多部雷达系统,充分利用每部雷达的信息构建认知雷达网络,也是未来发展趋势之一。基于MIMO雷达和雷达网络的波形设计以及有限资源的优化配置问题是研究的热点之一,也将进一步获得更大的发展。
3.4 检测波形最优化方法在认知雷达中的应用目前开展的检测波形最优化方法与认知雷达技术中的波形自适应优化方法还存在一定的差距。检测波形最优化方法通常假设目标和环境特性已经获取,利用该信息或其他先验知识进行波形最优化。并没有将回波参数估计与发射波形设计结合起来,将整个认知雷达探测过程串联起来进行研究。在实时雷达观测过程中,如何将回波中提取的目标和环境信息提供给发射机进行最优波形设计,目标和环境特性的变化对发射波形调整的影响、波形自适应方法、波形调整的策略制定等问题,还需要进一步深入研究。
3.5 检测波形最优化方法的统一性与特殊性研究一方面,检测波形最优化方法将朝着统一化的方向发展:不同目标模型和环境特性下的检测波形最优化方法具有某些方面的共同点,其统一性研究有重要的意义;实际环境的影响、先验信息或估计误差对波形设计的影响以及非理想统计特性的影响等需要进一步开展全面、普适性的研究;并且不同的检测波形最优化方法都将朝着更加快速、稳健的方向发展。
另一方面,针对特别场景的检测波形最优化有待进一步研究,如城市环境、地海交界等特殊杂波模型下的最优检测波形;检测波形设计与其他方向的交叉结合,如基于空时自适应处理、压缩传感、贝叶斯估计等技术的检测波形设计等问题,需要针对特定问题和特定应用,研究最优波形设计算法。
4 总结本文对雷达目标检测的最优波形设计研究进行了归纳总结,将其按照一些常见的重要问题分为若干类别,分别分析了一些常用的准则函数和约束条件,点目标模型和扩展目标模型的最优检测波形设计,色噪声和杂波环境中的最优检测波形设计,最优检测波形ESD合成时域信号及直接时域波形设计等问题。通过分类梳理,有助于充分了解和掌握现有目标检测波形优化设计问题的研究现状和主要研究内容。根据现有研究,本文提出了目标检测的波形优化问题发展的趋势,为该领域的研究者提供借鉴与思路。
| [1] |
Haykin S. Cognitive radar: A way of the future[J].
IEEE Signal Processing Magazine , 2006, 23 (1) : 30-40 DOI:10.1109/MSP.2006.1593335 ( 0) 0)
|
| [2] |
黎湘, 范梅梅. 认知雷达及其关键技术研究进展[J].
电子学报 , 2012, 40 (9) : 1863-1870 Li Xiang, Fan Mei-mei. Research advance on cognitive radar and its key technology[J].
Acta Electronica Sinica , 2012, 40 (9) : 1863-1870 ( 0) 0)
|
| [3] |
Haykin S, Xue Y, and Davidson T N. Optimal waveform design for cognitive radar[C]. Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, 2008: 3-7.
( 0) 0)
|
| [4] |
Deng X, Qiu C, Cao Z, et al. Waveform design for enhanced detection of extended target in signal-dependent interference[J].
IET Radar, Sonar & Navigation , 2012, 6 (1) : 30-38 ( 0) 0)
|
| [5] |
Xin F, Wang B, Wang J, et al. Optimal waveform design with constant modulus constraint for rank-one target detection[J].
Sensors & Transducers , 2014, 163 (1) : 39-43 ( 0) 0)
|
| [6] |
Sen S. Characterizations of PAPR-constrained radar waveforms for optimal target detection[J].
IEEE Sensors Journal , 2014, 14 (5) : 1647-1654 DOI:10.1109/JSEN.2014.2299283 ( 0) 0)
|
| [7] |
Bell M R. Information theory and radar waveform design[J].
IEEE Transactions on Information Theory , 1993, 39 (5) : 1578-1597 DOI:10.1109/18.259642 ( 0) 0)
|
| [8] |
Romero R A, Bae J, Goodman N A. Theory and application of SNR and mutual information matched illumination waveforms[J].
IEEE Transactions on Aerospace and Electronic Systems , 2011, 47 (2) : 912-927 DOI:10.1109/TAES.2011.5751234 ( 0) 0)
|
| [9] |
Kay S M. Optimal signal design of Gaussian point targets in stationary Gaussian clutter/reverberation[J].
IEEE Journal of Selected Topics in Signal Processing , 2007, 1 (1) : 31-41 DOI:10.1109/JSTSP.2007.897065 ( 0) 0)
|
| [10] |
Pillai S U, Youla D C, Oh H S, et al. Optimum transmit-receiver design in the presence of signal-dependent interference and channel noise[J].
IEEE Transactions on Information Theory , 2000, 46 (2) : 577-584 DOI:10.1109/18.825822 ( 0) 0)
|
| [11] |
Garren D A, Osborn M K, Odom A C, et al. Enhanced target detection and identification via optimised radar transmission pulse shape[J].
IEE Poceedings-F Radars, Sonar and Navigation , 2001, 148 (3) : 130-138 DOI:10.1049/ip-rsn:20010324 ( 0) 0)
|
| [12] |
Bergin J S, Techau P M, and Don Carlos J E. Radar waveform optimization for colored noise mitigation[C]. IEEE International Radar Conference, Arlington, Virginia, 2005: 149-154.
( 0) 0)
|
| [13] |
Li J, Guerci J R, Xu L. Signal waveform's optimal-under-restriction design for active sensing[J].
IEEE Signal Processing Letters , 2006, 13 (9) : 565-568 DOI:10.1109/LSP.2006.874465 ( 0) 0)
|
| [14] |
Gini F, De Maio A, Patten L K.
Waveform Design and Diversity for Advanced Radar Systems[M]. London: The Instituion of Engineering and Technology, 2012 .
( 0) 0)
|
| [15] |
Jackson L B, Kay S M, Vankayalapati N. Iterative method for nonlinear FM synthesis of radar signals[J].
IEEE Transactions on Aerospace and Electronic Systems , 2010, 46 (2) : 910-917 DOI:10.1109/TAES.2010.5461666 ( 0) 0)
|
| [16] |
Goodman N A, Venkata P R, Neifeld M A. Adaptive waveform design and sequential hypothesis testing for target recognition with active sensors[J].
IEEE Journal of Selected Topics in Signal Processing , 2007, 1 (1) : 105-113 DOI:10.1109/JSTSP.2007.897053 ( 0) 0)
|
| [17] |
Gong X, Meng H, Wei Y, et al. Phase-modulated waveform design for extended target detection in the presence of clutter[J].
Sensors , 2011, 11 (7) : 7162-7177 ( 0) 0)
|
| [18] |
Pillai S U, Li K Y, and Beyer H. Reconstruction of constant envelope signals with given Fourier transform magnitude[C]. IEEE Radar Conference, Pasadena, CA, USA, 2009: 1-4.
( 0) 0)
|
| [19] |
Patten L K. On the satisfaction of modulus and ambiguity function constraints in radar waveform optimization for detection[D].[Ph.D. dissertation], Wright State University, 2009.
( 0) 0)
|
| [20] |
Wang Lu-lu, Wang Hong-qiang, and Qin Yu-liang. Adaptive waveform design for multi-target classification in signal dependent interference[C]. 19th International Conference on Digital Signal Processing, Hong Kong, China, 2014: 167-172.
( 0) 0)
|
| [21] |
Sen S. Constant-envelope waveform design for optimal target-detection and autocorrelation performances[C]. IEEE International Conference on Acoustics Speech and Signal Processing(ICASSP), Vancouver, BC, Canada, 2013: 3851-3855.
( 0) 0)
|
| [22] |
Stoica P, He H, Li J. New algorithms for designing unimodular sequences with good correlation properties[J].
IEEE Transactions on Signal Processing , 2009, 57 (4) : 1415-1425 DOI:10.1109/TSP.2009.2012562 ( 0) 0)
|
| [23] |
Zhang J D, Zhu D Y, and Zhang G. Multi-objective waveform design for cognitive radar[C]. IEEE CIE International Conference on Radar, Chengdu, China, 2011: 580-583.
( 0) 0)
|
| [24] |
Sen S. PAPR-constrained pareto-optimal waveform design for OFDM STAP radar[J].
IEEE Transactions on Geoscience and Remote Sensing , 2014, 52 (6) : 3658-3669 DOI:10.1109/TGRS.2013.2274593 ( 0) 0)
|
| [25] |
Aubry A, De Maio A, Piezzo M, et al. Knowledge-aided (poentially cognitive) transmit signal and receive filter design in signal-depended clutter[J].
IEEE Transactions on Aerospace and Electronic Systems , 2013, 49 (1) : 93-117 DOI:10.1109/TAES.2013.6404093 ( 0) 0)
|
| [26] |
De Maio A, Huang Y, Piezzo M, et al. Design of optimized radar codes with a peak to average power ratio constraint[J].
IEEE Transactions on Signal Processing , 2011, 59 (6) : 2683-2697 DOI:10.1109/TSP.2011.2128313 ( 0) 0)
|
| [27] |
Cui G, Li H, Rangaswamy M. MIMO radar waveform design with constant modulus and similarity constraints[J].
IEEE Transactions on Signal Processing , 2014, 62 (2) : 343-353 DOI:10.1109/TSP.2013.2288086 ( 0) 0)
|
| [28] |
黄培康, 殷红成, 许小剑.
雷达目标特性[M]. 北京: 电子工业出版社, 2005 .
Huang Pei-kang, Yin Hong-cheng, Xu Xiao-jian.
Radar Target Signature[M]. Beijing: Publishing House of Electronics Industry, 2005 .
( 0) 0)
|
| [29] |
Wei Y, Meng H, Liu Y, et al. Radar phase-modulated waveform design for extended target detection[J].
Tsinghua Science and Technology , 2011, 16 (4) : 364-370 DOI:10.1016/S1007-0214(11)70053-0 ( 0) 0)
|
| [30] |
Yin F, Debes C, Zoubir A M. Parametric waveform design using discrete prolate spheroidal sequences for enhanced detection of extended targets[J].
IEEE Transactions on Signal Processin , 2012, 60 (9) : 4525-4536 DOI:10.1109/TSP.2012.2202111 ( 0) 0)
|
| [31] |
Sen S, Nehorai A. Target detection in clutter using adaptive OFDM radar[J].
IEEE Signal Processing Letters , 2009, 16 (7) : 592-595 DOI:10.1109/LSP.2009.2020470 ( 0) 0)
|
| [32] |
Chen C Y, Vaidyanathan P P. MIMO radar waveform optimization with prior information of the extended target and clutter[J].
IEEE Transactions on Signal Processing , 2009, 57 (9) : 3533-3544 DOI:10.1109/TSP.2009.2021632 ( 0) 0)
|
| [33] |
Peizzo M, Aubry A, Buzzi S, et al. Non-cooperative code design in radar networks: A game-theoretic approach[J].
EURASIP Journal on Advances in Signal Processing , 2013 (1) : 1-17 ( 0) 0)
|
| [34] |
Stoica P, He H, Li J. Optimization of the receive filter and transmit sequence for active sensing[J].
IEEE Transactions on Signal Processing , 2012, 60 (4) : 1730-1740 DOI:10.1109/TSP.2011.2179652 ( 0) 0)
|
| [35] |
Aubry A, De Maio A, Iommelli S, et al.. Cognitive design of the transmitted phase code and receive filter in reverberating environment[C]. International Conference on Waveform Diversity and Design, Kauai, Hawaii, 2012: 85-90.
( 0) 0)
|
| [36] |
Sira S P, Cochran D, Papandreou-Suppappola A, et al. Adaptive waveform design for improved detection of low-RCS targets in heavy sea clutter[J].
IEEE Journal of Selected Topics in Signal Processing , 2007, 1 (1) : 56-66 DOI:10.1109/JSTSP.2007.897048 ( 0) 0)
|
| [37] |
Cohen A I. An algorithm for designing burst waveforms with quantized transmitter weights[J].
IEEE Transactions on Aerospace and Electronic Systems , 1975, 11 (1) : 56-64 ( 0) 0)
|
| [38] |
DeLong Jr D F, Hofstetter E M. Optimum radar signal-filter pairs in a cluttered environment[J].
IEEE Transactions on Information Theory , 1970, 16 (1) : 89-90 DOI:10.1109/TIT.1970.1054412 ( 0) 0)
|
| [39] |
Mesiya M F, Mclane P J. Design of optimal radar signals subject to a fixed amplitude constraint[J].
IEEE Transactions on Aerospace and Electronic Systems , 1973, 9 (5) : 679-687 ( 0) 0)
|
| [40] |
Rummler W D. A technique for improving the clutter performance of coherent pulse trains[J].
IEEE Transactions on Aerospace and Electronic Systems , 1967, 3 (6) : 898-906 ( 0) 0)
|
| [41] |
Patton L K, Rigling B D. Autocorrelation constraints in radar waveform optimization for detection[J].
IEEE Transactions on Aerospace and Electronic Systems , 2012, 48 (2) : 951-968 DOI:10.1109/TAES.2012.6178041 ( 0) 0)
|
| [42] |
Sibul L, Titlebaum E L. Signal design for detection of targets in clutter[J].
Proceedings of the IEEE , 1981, 69 (4) : 481-482 DOI:10.1109/PROC.1981.12001 ( 0) 0)
|
| [43] |
Kay S M.
Modern Spectral Estimation: Theory and Application[M]. Englewood Cliffs: NJ: Prentice-Hall, 1988 .
( 0) 0)
|
| [44] |
Sen S and Glover C W. Optimal multicarrier phase-coded waveform design for detection of extended targets[C]. IEEE Radar Conference, Ottawa, Ontario, Canada, 2013: 1-6.
( 0) 0)
|
| [45] |
Stringer J, Lamont G, and Akers G. Multi-objective evolutionary algorithm determined radar phase codes[C]. IEEE Radar Conference, Atlanta, GA, 2012: 161-166.
( 0) 0)
|
| [46] |
Sen S, Tang G, Nehorai A. Multiobjective optimization of OFDM radar waveform for target detection[J].
IEEE Transactions on Signal Processing , 2011, 59 (2) : 639-652 DOI:10.1109/TSP.2010.2089628 ( 0) 0)
|