(中国科学院电子学研究所 北京 100190)
(中国科学院大学 北京 100049)
(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)
(University of Chinese Academy of Sciences, Beijing 100049, China)
合成孔径雷达(Synthetic Aperture Radar,SAR)是一种可以通过信号处理技术合成地球表面高分辨率微波图像的主动成像雷达。它拥有全天时、全天候的成像能力。极化SAR(Polarimetric SAR,PolSAR)可以提供观测场景的一系列极化信息并已被成功应用于众多实际应用中[1, 2]。目前,星载SAR系统的局限主要在于难以同时获取具备高分辨率与宽测绘幅宽的雷达图像。而对于可以获取散射目标完备极化信息的全极化(quadrature-polarimetric,quad-pol)SAR系统而言,其可获取的测绘幅宽相比一般的SAR系统更要小一倍以上。原因在于全极化SAR系统需要将脉冲重复频率(Pulse Repetition Frequency,PRF)至少提高一倍以上以满足交替发射两种互相垂直的极化波的需要。
传统的全极化SAR系统发射水平(Horizontal,H)与垂直(Vertical,V)线性极化波,同时使用H与V极化天线进行接收。这样的设置将会在大入射角时在交叉极化(HV或VH)测量通道中产生严重的距离模糊问题,进而进一步限制有效测绘幅宽[3, 4]。另外,由于自然目标的同极化(HH或VV)散射回波能量通常比交叉极化散射回波能量高6~10 dB,需要在实际全极化SAR系统中应用复杂的接收策略来处理不同的极化通道接收到的能量,以保证接收到的回波信号均处于模拟数字转换器 (Analog to Digital,ADC) 模块的有效动态范围内[5, 6]。针对以上问题,混合极化(Hybrid-Polarity,HP)架构于文献[4, 7, 8]中提出。混合极化架构下的全极化SAR系统交替发射右旋圆极化(Right-Handed Circular,RHC)与左旋圆极化(Left-Handed Circular,LHC)波,并使用正交的线性极化天线进行接收。这样,极化SAR系统中的发射极化波与接收极化波之间将不再存在同极化与交叉极化的关系,从而能够改善前述的距离模糊问题[4]。另外,极化SAR系统接收到的信号的平均能量是相当的,因而不再需要应用复杂的接收策略。这样,基于混合极化架构的全极化SAR系统相比传统的线性全极化SAR系统将拥有更宽的测绘幅宽与更低的硬件需求[4]。
混合极化架构还能够支持简缩极化(Compact Polarimetry,CP)中的圆发线收(Circular Transmit Linear Receive,CTLR)模式[7]。简缩极化是由不同特殊双极化(dual-polarimetric,dual-pol)模式组成的一个集合概念。它要求雷达系统发射拥有相同H与V分量的极化波,如左旋、右旋圆极化波与±45°斜线极化波,并保留接收极化波间的相对相位信息[9, 10, 11, 12]。由于简缩极化具有双极化诸如双倍测绘幅宽、更低功耗与更简易系统需求[7, 9]的优点,并在许多实际应用中能够得到与全极化SAR相当的数据处理结果[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61],因而在过去的十年中广受关注。
以上这一系列优点使得混合极化架构成为未来完成极化SAR任务的潜在选择。截至目前为止已有数个极化SAR任务采用了混合极化架构。它们包括:搭载在印度Chandrayaan-1探月任务与美国月球勘测轨道飞行器(Lunar Reconnaissance Orbiter,LRO)上的两颗小型射频(mini-Radio-Frequency,mini-RF)雷达[62];搭载在印度遥感卫星RISAT-1上的C波段SAR[63];搭载在日本遥感卫星ALOS-2上的L波段SAR(实验模式)[64]。在未来,加拿大的C波段RADARSAT星座任务(RADARSAT Constellation Mission,RCM)[12, 65, 66],美国探测形变、生态结构与冰层动力学(Deformation,Ecosystem Structure,and Dynamics of Ice,DESDynI)遥感任务的L波段干涉SAR(Interferometry SAR,InSAR)系统[67, 68]与印度的第2次探月任务Chandrayaan-2[69]亦已确认将采用混合极化架构。
本文首先回顾了混合极化架构的基本原理,包括系统设计、系统模型与标定方法。然后重点讨论了混合极化架构的两点问题。其中最主要的一点是当雷达系统工作在双极化模式下时,系统的发射失真即便被准确估计出来,也无法被标定。另外一点是在混合极化架构下,发射模式通常被设定为圆极化波。在这一设置下,极化SAR系统的双极化模式即为CTLR模式。但是在简缩极化中,除了CTLR模式以外,发射45°线性极化波的π/4模式在某些应用中同样可以得到较好的结果,因而同样值得关注。针对这两点,本文将提出一种混合极化架构的改进。同时,本文也将介绍以实验验证为目的而开发的原型实验系统。
本文在接下来的部分中将详述适用于混合极化架构的极化SAR应用。由于基于混合极化架构的极化SAR系统提供的全极化数据可以直接转化为传统的线性极化基散射矩阵,因此这一部分的综述主要集中在对应的双极化应用,即简缩极化应用上。首先这一部分将介绍4个常用的简缩极化信息提取方法,即协方差矩阵扩展方法,基于Stokes矩阵的方法,特征值分解方法与基于散射模型方法。接下来再介绍由这些信息提取方法衍生出的一系列简缩极化应用。考虑到文章的篇幅,本文仅对使用简缩极化数据的非监督地物分类应用与极化干涉树高反演应用进行详细综述。
本文的结构如下。第2节分别回顾了基于混合极化架构的双、全极化SAR系统的系统设计与系统模型。第3节阐述了混合极化架构的自检特性(self-checking property)[7]以及有效标定技术。由于发射失真不能通过外定标方法进行标定,这一节还探讨了对发射失真的评估问题。第4节提出了一种混合极化架构的改进方案。第5节展示了多个数据处理算法,包括由混合极化基转换到线性极化基数据,及由全极化数据模拟简缩极化数据的算法。这一节还介绍了4个主要的简缩极化信息提取方法。第6节回顾了简缩极化应用。最后,第7节对阶段研究进行了总结。
2 混合极化架构 2.1 混合双极化架构混合极化首先于文献[7]提出以支持简缩极化中的CTLR模式。CTLR模式要求雷达系统发射一种圆极化波(右旋圆极化或左旋圆极化之一)并使用正交的线性极化基进行接收。由于简缩极化实际上是由特殊双极化模式构成的一个集合概念,因此本文将此混合极化架构称作混合双极化(Hybrid Dual-Pol,HP2)架构。混合双极化架构的系统框图如图 1(a)所示。为了生成发射所需的圆极化波,波形发生器产生的信号首先经功分器分为两路功率相等的子信号,再将其中之一相移90°。两路生成的子信号随后被馈入双线性极化天线的H与V馈电口。这一部分设计在图中已使用虚线框标出。这一部分设计的简化框图如图 1(b)所示。图中
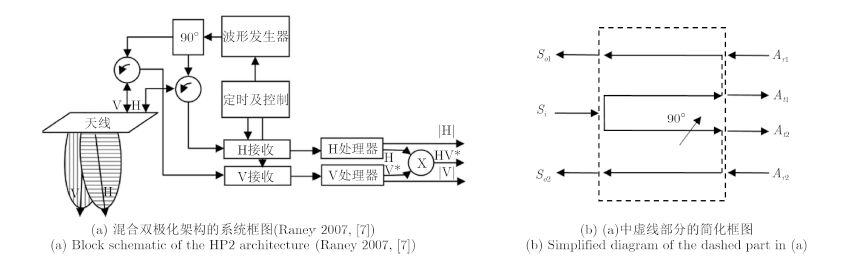
|
图 1 混合双极化架构的系统框图 (Raney 2007,文献[7]) Fig.1 Block schematic of the HP2 architecture (Raney 2007, Ref.[7]) |
可以看到,混合双极化架构中并没有过多的射频硬件。这意味着雷达系统中的损耗以及失真源将会更少。另外,由于两路接收通道均不再需要接收交叉极化信号,因此其平均信号水平应相当。这也意味着雷达系统中出现较强极化信号污染较弱极化信号(即发生系统串扰)的概率变小了[4]。
基于混合双极化架构的星载极化SAR系统的系统模型为[70]:
| $ \begin{array}{l} \left[{\begin{array}{*{20}{c}} {{M_{{\rm{RH}}}}}\\ {{M_{{\rm{RV}}}}} \end{array}} \right] = A\left( {r,\theta } \right){{\rm{e}}^{\,{\rm{j}}\phi }}\frac{1}{{\sqrt 2 }} \cdot \left[{\begin{array}{*{20}{c}} 1& {{\delta _2}}\\ {{\delta _1}}& {{f_1}} \end{array}} \right]\\ \quad \quad \quad \quad \quad \cdot \left[{\begin{array}{*{20}{c}} {\cos \varOmega }& {\sin \varOmega }\\ { - \sin \varOmega }& {\cos \varOmega } \end{array}} \right] \cdot \left[{\begin{array}{*{20}{c}} {{S_{{\rm{HH}}}}}& {{S_{{\rm{HV}}}}}\\ {{S_{{\rm{VH}}}}}& {{S_{{\rm{VV}}}}} \end{array}} \right]\\ \quad \quad \quad \quad \quad \cdot \left[{\begin{array}{*{20}{c}} {\cos \varOmega }& {\sin \varOmega }\\ { - \sin \varOmega }& {\cos \varOmega } \end{array}} \right] \\ \quad \quad \quad \quad \quad \cdot \left[{\left[{\begin{array}{*{20}{c}} 1\\ { - {\rm j}} \end{array}} \right] + \delta \left[{\begin{array}{*{20}{c}} 1\\ {\rm j} \end{array}} \right]} \right] + \left[{\begin{array}{*{20}{c}} {{N_1}}\\ {{N_2}} \end{array}} \right] \end{array} $ | (1) |
| $M=A{{\text{e}}^{\text{j}\phi }}\frac{1}{\sqrt{2}}R{{R}_{F}}S{{R}_{F}}\left[ {{k}_{\text{RHC}}}+\delta {{k}_{\text{LHC}}} \right]+N$ | (2) |
照射到目标表面的电磁场Ei可以被进一步表示为:
| ${{\bf{{{E}}}}_i} ={{R}_F}\left[{{k_{{\rm{RHC}}}} + \delta {k_{{\rm{LHC}}}}} \right] = \left[{\begin{array}{*{20}{c}} {\cos \varOmega }& {\sin \varOmega }\\ { - \sin \varOmega } & {\cos \varOmega } \end{array}} \right] \\ \quad \quad \cdot \left[{\left[{\begin{array}{*{20}{c}} 1\\ { - {\rm j}} \end{array}} \right] + \delta \left[{\begin{array}{*{20}{c}} 1\\ {\rm j} \end{array}} \right]} \right] \\ \quad \,\,= {{\rm e}^{ - {\rm j}\varOmega }}\left[{\left[{\begin{array}{*{20}{c}} 1\\ { - {\rm j}} \end{array}} \right] + \delta {{\rm e}^{\,{\rm j}2\varOmega }}\left[{\begin{array}{*{20}{c}} 1\\ {\rm j} \end{array}} \right]} \right]$ | (3) |
虽然发射失真可以如式(1)与式(2)一样直接使用单一项
| ${\bf{{{T}}}} = \left[{\begin{array}{*{20}{c}} 1 & 0\\ 0 & {{f_2}} \end{array}} \right] \cdot \left[{\begin{array}{*{20}{c}} 1 & {{\delta _4}}\\ {{\delta _3}} & 1 \end{array}} \right]$ | (4) |
| ${\bf{{{T}}}} \cdot {k_{\rm RHC}} = \alpha \left[{{\rm k_{RHC}} + \delta {k_{\rm LHC}}} \right]$ | (5) |
| $\alpha = \frac{{\left( {1 + {f_2}} \right) - {\rm j}({\delta _4} - {\delta _3})}}{2}$ | (6) |
发射失真的两种表示方法均是有效的。但由式(1)可知,即便精确知道发射失真项的大小也无法通过右乘对应逆矩阵来得到目标的真实散射矩阵。因此使用综合串扰项统一表示所有发射失真会更加简洁明了,而精确的发射失真表示可以更详细地分析不同失真源的影响。这一部分工作将在3.2节中进行回顾。
2.2 混合四极化架构文献[7]建议使用混合极化架构代替传统的线性全极化系统来构建全极化SAR系统。这样的设置下,雷达系统将交替发射左右旋圆极化波,使用H, V极化基进行相干接收。这一想法在文献[4]与[8]中被进一步详细阐述。
图 2(a)中展示了混合四极化架构(Hybrid Quad-Pol,HP4)[8]的系统框图。发射模块中的移相器相较前述混合双极化架构做了一点小的修改。为了分别发射右旋与左旋圆极化波,信号的相位分别相移+90°与-90°。这一部分设计同样在图 2(a)中使用虚线标注出来了,并在图 2(b)中展示了其简化框图。如果移相器固定相移+90°或-90°,则得到的系统设计即为混合双极化架构。因此CTLR模式可以视作基于混合四极化架构的极化SAR系统的对应双极化模式。后文将使用混合极化架构一词来指代本节介绍的混合四极化架构。
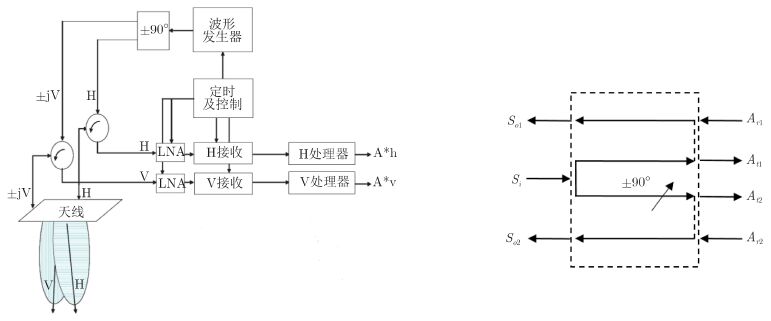
|
图 2 混合四极化架构的系统框图 (Raney 2008, 文献[8]) Fig.2 Block schematic of the HP4 architecture (Raney 2008, Ref.[8]) |
混合四极化架构同样继承了前文所述混合双极化架构的各优点。首先,发射与接收极化之间同样不再存在同或交叉极化的关系。根据文献[4]中的推导结果,这一特性可以有效减小距离模糊,从而使得基于混合极化架构的极化SAR系统拥有更宽的测绘幅宽。另外,由于接收通道的平均信号能量应是相同的,因此不再需要复杂的接收策略来调整不同回波信号的接收增益[5, 6]。这样,相比传统的线性极化系统,基于混合极化架构的极化SAR系统的系统设计更简单。这意味着通过混合极化架构,雷达的成本得以降低并且能够更好地保证标定与测试的鲁棒性。
由于不再需要根据不同的雷达回波改变接收机的接收增益,基于混合极化架构的星载极化SAR系统的系统模型与考虑了FR效应的标准极化系统模型相似[73]:
| ${{\mathbf{M}}_{\text{HP4}}}=A{{\text{e}}^{\text{j}\phi }}\mathbf{R}{{\mathbf{R}}_{F}}{{\mathbf{S}}_{\text{HP4}}}{{\mathbf{R}}_{F}}\mathbf{T}+\mathbf{N}$ | (7) |
| ${{\bf{{{S}}}}_{\rm HP4}} = \left[{\begin{array}{*{20}{c}} {{S_{{\rm{RH}}}}}& {{S_{{\rm{LH}}}}}\\ {{S_{{\rm{RV}}}}}& {{S_{{\rm{LV}}}}} \end{array}} \right] \\ \quad \,\,\quad = \left[{\begin{array}{*{20}{c}} {{S_{{\rm{HH}}}} - {\rm j}{S_{{\rm{HV}}}}}& {{S_{{\rm{HH}}}} + {\rm j}{S_{{\rm{HV}}}}}\\ {{S_{{\rm{VH}}}} - {\rm j}{S_{{\rm{VV}}}}}& {{S_{{\rm{VH}}}} + {\rm j}{S_{{\rm{VV}}}}} \end{array}} \right]$ | (8) |
由基于混合极化架构的极化SAR系统获得的测试数据同样可以首先转化为线性极化基,再直接应用标准极化系统模型进行后续的定标与数据处理。
3 失真的标定与评估基于混合极化架构的极化SAR获取的全极化数据可以直接转化为传统的线性极化基,因此可以直接应用标准的极化定标技术进行数据标定工作。混合极化架构在定标方面剩下的问题是如何标定获取的双极化数据,即简缩极化数据的标定。
3.1 简缩极化数据的标定 3.1.1 自检定标方法基于混合极化架构的极化SAR系统的两路接收通道的平均信号能量应是相等的,因此当回波信号的H与V分量相等时,相应的接收信号的1阶与2阶统计特性也应是相等的。在实践中,当雷达垂直观测地表时能够满足此条件。假设没有发射失真,则不满足此判定标准的误差可被测量与补偿[7, 74].
对于月球探测而言,由于既无法在月球表面放置定标器,月球表面又没有亚马逊热带雨林,无法使用对地遥感中常用的定标方法。因此在mini-RF探月任务中使用了上述的混合极化架构定标方法[62, 75]。在其在轨定标实验中,航天器被人为调整使得雷达天线能够对准月球的天底点。测得的V-H通道间增益与相位差分别为-2.55 dB±0.25 dB与-138°。这一测试结果较好地吻合了端到端的系统测试得到的预期结果-2.14 dB±0.25 dB与-135.9°±1.5°。两者存在细微差别的主要原因在于实际发射的极化波并非是完美的圆极化波,而是轴比(Axial,Ratio,AR)为2.46 dB±0.15 dB的椭圆极化波。
3.1.2 基于全极化系统的定标方法基于混合极化架构的极化SAR系统既可以工作在双极化模式下,又可以工作在全极化模式下。因此雷达系统如果能够如星载SAR一般,在整个数据获取阶段保证系统的稳定性,则系统的误差可以通过在各数据获取阶段的开始与(/或)结尾使用全极化模式来得到[70]。
3.1.3 法拉第旋转角的标定方法对于工作在低频段的星载极化SAR,还需要考虑FR效应的影响。除了使用电离层总电子含量(Total Electron Content,TEC)图来估计FR角大小的方法外[76],FR角还可以通过理论上HH-VV相位差接近零的裸土后向散射估计[18]。 裸土的识别是通过不受FR影响的一致性系数m来完成的:
| $\mu = \frac{{2{\mathop{\rm Im}\nolimits} \left\langle {{M_{{\rm{RH}}}}M_{{\rm{RV}}}^*} \right\rangle }}{{\left\langle {{M_{{\rm{RH}}}}M_{{\rm{RV}}}^*} \right\rangle + \left\langle {{M_{{\rm{RH}}}}M_{{\rm{RV}}}^*} \right\rangle }} \\ \quad \! \cong 2\frac{{{\mathop{\rm Re}\nolimits} \left( {{S_{{\rm{HH}}}}S_{{\rm{VV}}}^*} \right) - {{\left| {{S_{{\rm{HV}}}}} \right|}^2}}}{{{{\left| {{S_{{\rm{HH}}}}} \right|}^2} + 2{{\left| {{S_{{\rm{HV}}}}} \right|}^2} + {{\left| {{S_{{\rm{VV}}}}} \right|}^2}}}$ | (9) |
对于裸土散射(即表面散射)而言,m是正数且趋近于1。对于2次散射而言,m是负数且趋近于-1,其中间值(零值附近)代表着体散射。体散射与表面散射之间的阙值估计为0.35,而体散射与2次散射之间的阙值估计为-0.2。通过识别出的裸土,FR角可通过以下公式计算得到:
| ${Ω} \! = \frac{1}{2}\arctan \left(\! {2\frac{{{\mathop{\rm Re}\nolimits} \left\langle {{M_{{\rm{RH}}}}M_{{\rm{RV}}}^*} \right\rangle }}{{\left\langle {{M_{{\rm{RV}}}}M_{{\rm{RV}}}^*} \right\rangle - \left\langle {{M_{{\rm{RH}}}}M_{{\rm{RH}}}^*} \right\rangle }}} \!\right)\!\!\bmod \frac{\pi }{4}$ | (10) |
在文献[77]中,My-Linh等人首先针对CTLR模式提出了基于定标器的定标方法。由于发射失真无法被标定,雷达系统的发射被认为是完美的(即无误差的)。该方法使用了包括两个0°与45°的二面角与一个0°三面角的3个定标器来标定接收的通道失衡与通道串扰,FR角和系统增益。
文献[78]中,Chen与Quegan研究了针对工作在CTLR模式下的低波段星载SAR系统基于定标器的定标方法。在其研究中共分析了6种包含由数量不等的主动与被动定标器组成的定标策略。首先可以确认的一点是,使用4个定标器的定标策略比仅使用3个定标器的定标策略准确性更高。但这会在实际部署中增加花费与复杂程度。另外一点结论是,在所有被动定标器中首选网格三面角(gridded trihedral)定标器。相比二面角与三面角定标器,它的平均极化噪声(Average Polarimetric Noise,APN)更低且对瞄准精度不敏感。文献[78]最终推荐的定标策略包括2个区分HH与VV通道的网格三面角定标器以及2个能够区分HV与VH通道的主动定标器。
在文献[79]中,陈琳等人提出来一项针对所有双极化SAR系统的通用定标算法。该算法仅使用了1个三面角与2个0°与45°二面角。这一方法中未考虑FR的影响。经验证,此通用定标算法对所有双极化模式,包括传统的线性双极化模式以及简缩极化中的CTLR模式与p/4模式均有效。最终该算法的有效性在配置了p/4模式与CTLR模式发射/接收设置的地基SAR系统上得以验证[34]。
3.2 发射失真的评估在上述章节中,本文已讨论了混合极化架构在工程实现中的难点:双极化模式下的发射失真并不能简单通过乘上一对应逆矩阵消除。因此应当对发射失真产生的影响进行完整的评估。在文献[71]中,Guo等人采用了最大归一化误差(Maximum Normalized Error,MNE)指标对发射失真做了定量评估。对于基于混合双极化架构的极化SAR系统而言,MNE的定义为:
| ${\rm{MNE}} = {\left\| {{\bf{{PD}}} - {{\bf{{P}}}_0}} \right\|_2}$ | (11) |
| ${\bf{{P}}} = \left( {\begin{array}{*{20}{c}} {p_h^t} & 0 & {p_v^t} & 0 \\ 0 & {p_h^t} & 0 & {p_v^t} \end{array}} \right)\quad \quad \quad \quad \,\,$ | (12) |
| ${\bf{{D}}} = {\left[{\left[{\begin{array}{*{20}{c}} {\cos {Ω} } & {\sin {Ω} }\\ { - \sin {Ω} } & {\cos {Ω} } \end{array}} \right] \cdot {{\bf{{X}}}_t}} \right]^{\rm T}} \otimes {\bf{{I}}}$ | (13) |
| ${{\bf{{P}}}_0} = \left( {\begin{array}{*{20}{c}} 1 & 0 & {\rm j} & 0\\ 0 & 1 & 0 & {\rm j} \end{array}} \right)\quad \quad \quad \quad \quad \quad \,\,$ | (14) |
这一评估方法可以用来评估由FR、通道失衡以及通道串扰等多重误差源综合产生的影响。但是为了单独评估各误差源的影响,下文将分别仿真由各误差源单独引起的MNE变化。
3.2.1 法拉第旋转角根据式(3),当FR是发射中唯一的失真,即发射的是完美圆极化波时,FR角直接变为一项可被省略的加性相位项。如果发射极化波是非完美的,则FR将会如式(3)所示,对综合串扰d产生影响。
3.2.2 通道失衡假设发射中唯一存在的失真为通道失衡,即
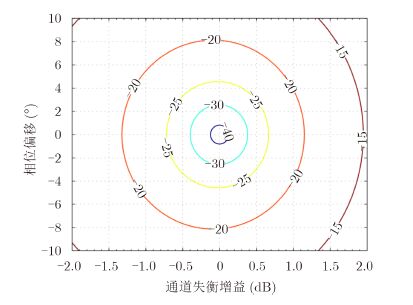
|
图 3 由通道失衡引起的MNE变化 Fig.3 MNE evaluation due to channel imbalance |
为了简便,假设通道串扰满足
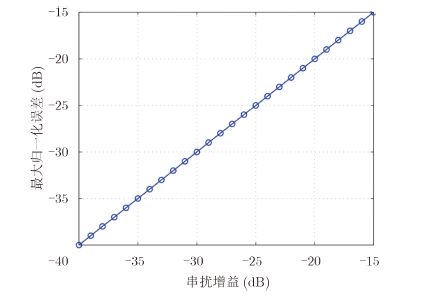
|
图 4 由通道串扰增益引起的MNE变化 Fig.4 MNE evaluation due to crosstalk gain |
可以看到,MNE随着通道串扰增益按比例以分贝级增长。为了维持MNE小于-20 dB,发射的通道串扰需要小于-20 dB。
3.2.4 入射角发射波的非圆性(non circularity)同样会随着入射角的变化而变化[65]。在文献[65]中,Touzi与Charbonneau估计RCM发射极化波的AR的变化范围会在1.4 dB(在0°波束扫描角50 km范围内)到3 dB(ScanSAR模式下,350 km幅宽)之间。为了估计这一影响,发射Jones矢量被设置为[81]:
| $\left[{\begin{array}{*{20}{c}} {p_h^t}\\ {p_v^t} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {\cos \phi }& { - \sin \phi }\\ {\sin \phi }& {\cos \phi } \end{array}} \right] \cdot \left[{\begin{array}{*{20}{c}} {\cos \tau }\\ {{\rm j}\sin \tau } \end{array}} \right]$ | (15) |
这里仅考虑椭圆率,因此方向角被设为
|
图 5 由椭圆率引起的MNE变化 Fig.5 MNE evaluation due to the change in ellipticity |
如前所述,混合极化架构在工程实现中,定标方面的主要难点是:当工作在双极化模式下时,即使能够通过不同的外定标方法精确得到发射失真的大小,也无法对发射失真进行标定。因此在大部分的混合极化系统相关文章中,发射失真是被忽略的。但是正如3.3节所述,发射失真一定会对基于混合极化架构的极化SAR产生影响。
在3.3节中使用了用来测量极化系统极化纯度的通用度量MNE来评估发射失真。与此同时,发射失真也可以通过它们所产生的结果,即发射极化波的失真大小来度量。在这一观点下,可以使用AR来量化发射失真。对于完美圆极化而言AR=0 dB,而AR=+∞则表示的是线性极化波。据报道,两颗探月小型射频雷达的AR大约为2.5 dB[62]。而即将发射的RCM雷达系统在最坏情况下的AR约在1.5 dB到3.0 dB之间[65]。印度的第2次探月任务规划其所使用的雷达系统AR小于2.0 dB[69]。据研究,AR与MNE在数值上并非是一一对应的。如要保证前述
为了克服上述问题,需要在基于混合极化架构的极化SAR系统中应用内定标技术。然而传统的内定标回路将会增加雷达系统所需的射频器件数量。这不仅会导致系统成本的增加,同时还将增加系统中潜在的失真源的数量。因此本文采取另一种方案,仅修改混合极化架构中的发射模块。修改后得到的改进型混合极化架构的系统框图如图 6(a)所示。修改后的发射模块同样在图 6(a)中使用虚线标注出来了,并在图 6(b)中展示了其简化框图。对比图 1(b)与图 2(b)中所示的系统设计,原始的±90°移相器由2个高精度可调衰减器与360°移相器代替。在图 6(b)中,这两个器件分别被表示为“A”与“P”。
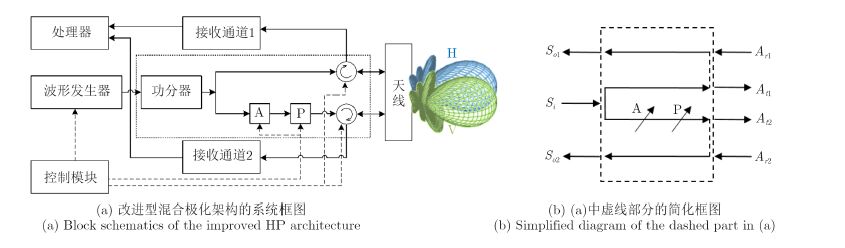
|
图 6 改进型混合极化架构的系统框图 Fig.6 Block schematic of the improved HP architecture |
应用这一直观的改进,可以使用预失真的方法来修正发射失真:首先,调节衰减器与移相器,使得两路发射通道拥有相等的能量与期望的相位差(例如对于圆极化而言,90°或-90°)。接下来使用之前章节介绍的定标方法测定发射失真大小。然后,继续调节衰减器与移相器以补偿测定的失真。这样,就可以将发射失真降低到一能够被接受的水平上。
利用这两个高精度可调衰减器与移相器,基于改进型混合极化架构的极化SAR系统同时还可以产生任意的发射极化波。考虑到降低FR效应与消除观测中的旋转选择性(rotational selectivity),原始的基于混合极化架构的极化SAR系统通常使用圆极化波作为发射极化波。然而其他发射设置同样值得进一步的研究与应用。例如,文献[29]发现p/4模式的数据可以应用基于模型的目标分解方法,从而获得比CTLR模式更好的极化分解结果。类似的算法同样可以应用到p/4模式下的简缩极化干涉SAR(PolSAR interferometry,PolInSAR)数据处理中并且得到较好的目标分解结果[31]。
类似于最初的混合极化架构,改进型混合极化架构同样能够支持全极化模式。通过转换衰减器与移相器,改进型混合极化架构可以交替产生互相正交的极化对。虽然基于改进混合极化架构的极化SAR理论上可以生成任意的极化对,但是为了保留拥有更宽测绘幅宽的优势,最终采用的发射极化基需与接收极化基(即H与V极化基)不同[4]。
4.2 系统模型2.1节与2.2节中介绍的系统模型同样适用于基于改进型混合极化架构的极化SAR系统。但是需要注意的是,当工作在双极化模式下时,式(1)与式(2)中发射极化波带有综合串扰项d的Jones矢量需要相应做出调整。例如,若发射采用的是传统的H与V极化波,或者前述的斜线性极化波,则该项需调整为[79]:
| ${\rm{H}}\;{\rm{极化波}}\quad \quad \quad \quad \left[ {\matrix{ {{{\rm{T}}_{\rm{H}}}} \cr {{{\rm{T}}_{\rm{V}}}} \cr } } \right]{\rm{ = }}\left[ {\matrix{ {\rm{1}} \cr \delta \cr } } \right]$ | (16) |
| ${\rm{V极化波}}\quad \quad \quad \quad \left[ {\matrix{ {{{\rm{T}}_{\rm{H}}}} \cr {{{\rm{T}}_{\rm{V}}}} \cr } } \right]{\rm{ = }}\left[ {\matrix{ \delta \cr {\rm{1}} \cr } } \right]$ | (17) |
$\pi$ /4线性极化波
| $\left[ \begin{matrix} {{T}_{\text{H}}} \\ {{T}_{\text{V}}} \\ \end{matrix} \right]=\left[ \begin{matrix} 1 \\ 1 \\ \end{matrix} \right]+\delta \left[ \begin{matrix} 1 \\ -1 \\ \end{matrix} \right]$ | (18) |
而对于全极化模式,式(7)中的2×2矩阵SHPA需要根据采用的发射与接收极化基做出相应的调整。
4.3 原型系统图 7展示的是包含发射与接收模块的改进混合极化架构原型系统。矢量网络分析仪(Vector Network Analyzer,VNA)被用于测量原型系统各通道的幅度与相位特征。通过相应的控制程序可以实现对原型系统中的不同器件的控制。该程序还可以通过网络与VNA进行通信实现数据的自动采集。最后,该程序集成了前述的预失真功能。据估算,利用预失真方法可以将理想双极化天线产生的圆极化波的AR控制在1 dB以内。

|
图 7 使用VNA测试的改进混合极化架构的原型系统 Fig.7 Prototype system of the improved HP architecture measured by a VNA |
另一个需要探讨的问题是不同天线的使用问题。最初的混合极化架构建议利用同一个双线性极化天线来发射和接收极化波。但是同样可以使用两个互相垂直的单极化天线来代替双线性极化天线。如果不使用相同的天线进行发射与接收,则需要多达4个单极化天线。在后续的研究中,拟采用这一包含4个单极化天线的天线设置方案。这样的设置方案主要拥有成本低与隔离度高这两项点优点。但是与此同时,这样的设置会因为采用两个不同天线同时发射或者接收,而产生视差问题(parallax problem)。具体问题仍需进一步研究。
利用这一原型系统,可以首先验证预失真方法,并开展更多不同简缩极化模式的相关实验、分析发射失真对雷达观测产生的实际影响。改进混合极化架构的数据分析问题可以采用Sabry与Vanchon[82]针对一般简缩极化与全极化SAR研发的数据分析框架。
5 数据处理方法根据雷达极化的基本理论[81],任意全极化数据均可以直接转换成其他发射/接收设置下的极化数据,包括双极化模式数据。因此通过基于混合极化架构的极化SAR系统采集到的全极化数据可以直接转化为传统的线性全极化数据。这样便可以直接应用为传统极化SAR研发的一系列数据分析方法。
混合极化架构对应的双极化模式,即简缩极化模式是最近十年才提出的。其数据处理方法以及应用仍值得回顾。由于前文介绍的改进型混合极化架构同时可以产生CTLR模式以及p/4模式的数据,因此在接下来的两节中将主要介绍它们对应的数据处理方法以及应用。
5.1 简缩极化数据仿真截至目前为止,仅有印度的RISAT-1与日本的ALOS-2卫星有能力提供实际的简缩极化数据。其中,后者以实验模式进行的简缩极化模式数据获取并未公开。因此目前绝大部分简缩极化研究仍是基于所谓的模拟(simulated)简缩极化数据展开的。模拟简缩极化数据指的是前文所述由全极化数据直接转化得到的相应双极化数据。文献[7]中的附录部分列举了由线性全极化数据转化模拟CTLR模式数据的方法。该方法利用的是传统线性全极化数据的协方差矩阵C3。类似地,也可使用相干矩阵T3模拟简缩极化数据[83]。文献[11]中展示了所有3种主要简缩极化模式由2×2散射矩阵元素构成的散射矢量与协方差矩阵。这一转化过程同样可以直接使用最新的PolSAR Pro 5.0软件[84]来完成。
需要注意的一点是,虽然本文将这种转化得到的数据称为模拟数据,但是由于使用的数据是真实数据,转化得到的数据同样也是真实数据。另外,由于转化得到的简缩极化数据与全极化数据本质上使用的是同一组数据,因此基于这两组数据之间的对比是可重复的。
5.2 基本数据产品简缩极化数据的基本数据产品包括2×2协方差矩阵C2 与Stokes矢量
| ${{\bf{{C}}}_2}{\rm{ = }}\left\langle {{{\bf{{k}}}_{{\rm{CP}}}} \cdot {\bf{{k}}}_{\rm CP}^{*{\rm T}}} \right\rangle = \frac{1}{2}\left[{\begin{array}{*{20}{c}} {{g_0} + {g_1}}& {{g_2} - {\rm j}{g_3}}\\ {{g_2} + {\rm j}{g_3}}& {{g_0} - {g_1}} \end{array}} \right]$ | (19) |
根据文献[11],3种主要简缩极化模式的协方差矩阵均由以下3项相加构成:第1项包含的是仅与SHH和SVV有关的元素,第2项包含|SHH|2元素,而最后一项包含的是交叉极化相关项。基于互易假设SVH=SHV与反射对称假设
| $\frac{{\left\langle {{{\left| {{S_{{\rm{HV}}}}} \right|}^2}} \right\rangle }}{{\left\langle {{{\left| {{S_{{\rm{HH}}}}} \right|}^2}} \right\rangle + \left\langle {{{\left| {{S_{{\rm{VV}}}}} \right|}^2}} \right\rangle }} = \frac{{1 - \left| \rho \right|}}{4}$ | (20) |
| $\rho \equiv \frac{{\left\langle {{S_{{\rm{HH}}}} \cdot S_{{\rm{VV}}}^*} \right\rangle }}{{\sqrt {\left\langle {{{\left| {{S_{{\rm{HH}}}}} \right|}^2}} \right\rangle \cdot \left\langle {{{\left| {{S_{{\rm{VV}}}}} \right|}^2}} \right\rangle } }}$ | (21) |
Nord等人进一步将这一限制条件发展为:
| $\frac{{\left\langle {{{\left| {{S_{{\rm{HV}}}}} \right|}^2}} \right\rangle }}{{\left\langle {{{\left| {{S_{{\rm{HH}}}}} \right|}^2}} \right\rangle + \left\langle {{{\left| {{S_{{\rm{VV}}}}} \right|}^2}} \right\rangle }} = \frac{{1 - \left| \rho \right|}}{N}$ | (22) |
| $N = \frac{{{{\left| {{S_{{\rm{HH}}}} - {S_{{\rm{VV}}}}} \right|}^2}}}{{{{\left| {{S_{{\rm{HV}}}}} \right|}^2}}}$ | (23) |
利用这些限制条件,可以通过迭代解出|SHV|2这样,伪全极化数据中的其他未知项便可通过计算得到。除此方法之外,还有基于散射分解模型[48, 85]或C2的特征值或极化度(Degree of Polarization,DoP)的重建算法[86, 87]。文献[87]中详细对比、评估了这些算法。
这一类信息提取方法的优点在于一旦得到了伪全极化数据,则可以直接应用传统全极化SAR的数据分析方法。但是极化SAR中大部分的应用需要的是得到观测场景的散射特性,而不是事先对它们做出一定的假设。因此这一类方法的应用实际上是非常受限的。
5.3.2 基于Stokes矢量的方法简缩极化数种的极化信息还可以从SV中直接进行提取。通过SV可以进一步得到一系列包含不同极化特性的子参数[7, 62, 88]:
前文所述的极化度DoP:
| $m = \frac{{\sqrt {g_1^2 + g_2^2 + g_3^2} }}{{{g_0}}}$ | (24) |
线性极化度mL:
| ${m_L} = \frac{{\sqrt {g_1^2 + g_2^2} }}{{{g_0}}}$ | (25) |
线性极化比
| ${\mu _L} = \frac{{{g_0} - {g_1}}}{{{g_0} + {g_1}}}$ | (26) |
圆极化度mC:
| ${m_C} = \frac{{{g_3}}}{{{g_0}}}$ | (27) |
圆极化比(Circular Polarization Ratio,CPR)
| ${\mu _C} = \frac{{{g_0} - {g_3}}}{{{g_0} + {g_3}}}$ | (28) |
后向散射场的两个线性电矢量间的相对相位
| $\delta = {\tan ^{ - 1}}\left[{\frac{{{g_3}}}{{{g_2}}}} \right],\;\;\;\; - {180^ \circ } < \delta \le - {180^ \circ }$ | (29) |
除去这6个子参数,SV中还能提取另外两个非常重要的参量:从简缩地表随机体散射(Random Volume over Ground,RVoG)散射模型中提取出的目标参数
在文献[84]中,简缩RVoG散射模型的形式如下:
| ${\bf{{g}}} = {g_0}\left( {1 - m} \right)\left( {\begin{array}{*{20}{c}} 1\\ 0\\ 0\\ 0 \end{array}} \right) + {g_0}m\left( {\begin{array}{*{20}{c}} 1\\ {\sin 2{\alpha _s}\cos \phi }\\ { \pm \sin 2{\alpha _s}\sin \phi }\\ { \mp \cos 2{\alpha _s}} \end{array}} \right)$ | (30) |
| ${\alpha _s} = \frac{1}{2}{\tan ^{ - 1}}\left( {\frac{{\sqrt {g_1^2 + g_2^2} }}{{ \mp {g_3}}}} \right)$ | (31) |
| $\phi = \arg \left( {{g_1} \pm {\rm j}{g_2}} \right)\quad \quad \quad \quad $ | (32) |
根据著名的Born-Wolf电磁波分解式[82],SV同样可以被分解为一个完全极化分量与一个完全去极化分量。其中完全极化项可以进一步写成由庞加莱参数,即方向角y与椭圆率角c构成的形式:
| ${\bf{{g}}} = {g_0}\left( {1 - m} \right)\left( {\begin{array}{*{20}{c}} 1\\ 0\\ 0\\ 0 \end{array}} \right) + m{g_0}\left( {\begin{array}{*{20}{c}} 1\\ {\cos 2\psi \sin 2\chi }\\ { \pm \sin 2\psi \cos 2\chi }\\ { \mp \sin 2\chi } \end{array}} \right)$ | (33) |
对比式(30)与式(33)所表示的分解模型,可以发现
| $\cos 2{\alpha _s} = \sin 2{c} $ | (34) |
与著名的H/alpha分解算法类似,C2 同样可以直接使用特征值分解算法进行分解[40, 84, 91]:
| ${{\bf{{C}}}_2} \!=\! \left[{{{\bf{{U}}}_2}} \right]\left(\!\! {\begin{array}{*{20}{c}} {{\lambda _1}}\!\!& \!\!0\\ 0 \!\!& \!\!{{\lambda _2}} \end{array}} \!\!\right){\left[{{{\bf{{U}}}_2}} \right]^{ - 1}},\;\;{{\bf{{U}}}_2} \!=\! \left(\!\! {\begin{array}{*{20}{c}} {{{\bf{{u}}}_1}}& {{{\bf{{u}}}_2}} \end{array}} \!\!\right)$ | (35) |
| ${H_w} = - \sum\limits_{i = 1}^2 {{p_i}{{\log }_2}{p_i}} $ | (36) |
| $\alpha = \sum\limits_{i = 1}^2 {{p_i}{\alpha _i}} \quad \quad \quad \ \ $ | (37) |
| ${p_i} = \frac{{{\lambda _i}}}{{{\lambda _1} + {\lambda _2}}}\quad \quad \quad \quad \quad \quad \quad \quad $ | (38) |
| ${{\bf{{u}}}_i} = {{\rm e}^{{\rm j}{\phi _i}}}{\left( {\begin{array}{*{20}{c}} {\cos {\alpha _i}}& {\sin {\alpha _i}{{\rm e}^{{\rm j}{\delta _i}}}} \end{array}} \right)^{\rm T}}$ | (39) |
| ${{\bf{{C}}}_2} = \left( {\begin{array}{*{20}{c}} 1& 0 \\ 0& m \end{array}} \right),\;\;\;\;{\rm{or}}\\ {{\bf{{C}}}_2} = \left( {\begin{array}{*{20}{c}} m& 0\\ 0& 1 \end{array}} \right),\;\;\;\;0 \le m \le 1$ | (40) |
已确认的是,本方法仅对简缩极化中的双圆极化(Dual Circular Polarization,DCP或CC)模式有效。该模式要求雷达系统发射正交的圆极化波,并使用正交的圆极化基进行接收[10]。但是由于CTLR模式与CC模式间的散射矢量存在以下关系[91]:
| ${{\bf{{k}}}_{{\rm{CL}}}} = \frac{1}{2}\left( {\begin{array}{*{20}{c}} 1& 1 \\ { - {\rm j}}& {\rm j} \end{array}} \right){{\bf{{k}}}_{{\rm{CC}}}}$ | (41) |
通过著名的Freeman-Durden分解算法可以将全极化数据分解为3种基于物理散射模型的理想散射分量[92]:
| ${{{{C}}}_3} = \frac{{{f\!_v}}}{8}\left( {\begin{array}{*{20}{c}} 3& 0 & 1\\ 0& 2 & 0\\ 1& 0 & 3 \end{array}} \right) + {f\!_d}\left( {\begin{array}{*{20}{c}} {{{\left| \alpha \right|}^2}}& 0 & \alpha \\ 0& 0 & 0\\ {{\alpha ^*}}& 0 & 1 \end{array}} \right) \\ \quad \quad \,\,+ {f\!_s}\left( {\begin{array}{*{20}{c}} {{{\left| \beta \right|}^2}}& 0& \beta \\ 0& 0 & 0\\ {{\beta ^*}}& 0 & 1 \end{array}} \right)$ | (42) |
类似地,协方差矩阵同样可以表示为这3种散射分量的和[93, 94]:
| $\pi {\rm{/4 \ 模式}} \quad \quad \quad {{\bf{{C}}}_2} = \frac{{{f\!_v}}}{8}\left( {\begin{array}{*{20}{c}} {\rm{2}}& {\rm{1}}\\ {\rm{1}}& {\rm{2}} \end{array}} \right) + {f\!_d}\left( {\begin{array}{*{20}{c}} {{{\left| \alpha \right|}^2}}& \alpha \\ { - {\alpha ^*}}& 1 \end{array}} \right) + {f\!_s}\left( {\begin{array}{*{20}{c}} {{{\left| \beta \right|}^2}}& \beta \\ { - {\beta ^*}}& 1 \end{array}} \right) \quad \quad \quad \quad \quad \ $ | (43) |
| ${\rm{CTLR \ 模式}} \quad \quad {{\bf{{C}}}_2} = \frac{{{f\!_v}}}{4}\left( {\begin{array}{*{20}{c}} {\rm{1}}& {\rm{0}}\\ {\rm{0}}& {\rm{1}} \end{array}} \right) + {f\!_d}\left( {\begin{array}{*{20}{c}} {{{\left| \alpha \right|}^2}}& {{\rm j}\alpha }\\ { - {\rm j}{\alpha ^*}}& 1 \end{array}} \right) + {f\!_s}\left( {\begin{array}{*{20}{c}} {{{\left| \beta \right|}^2}}& {{\rm j}\beta }\\ { - {\rm j}{\beta ^*}}& 1 \end{array}} \right) \quad \quad \quad \quad $ | (44) |
雷达极化中最重要的应用之一是地物的分类与监测。简缩极化所带来的宽测绘幅宽优势可以提升星载极化SAR系统的这一能力。与此同时,这一项优势还可以降低星载极化SAR系统获取同一场景相干时序雷达图像所需的时间间隔。但是由于通过简缩极化获取的极化信息本就是非完备的,因此简缩极化数据处理的研究目标是在同一个后向散射分类策略下获得与全极化SAR类似的数据处理结果。
6.1.1 基于Stokes矢量的分类算法利用前文所述的m与
| $\left[{\begin{array}{*{20}{c}} {{P_D}}\\ {{P_V}}\\ {{P_S}} \end{array}} \right]{\rm{ = }}\left[{\begin{array}{*{20}{c}} {\frac{1}{2}{g_0}m\left( {1 \pm \sin \delta } \right)}\\ {{g_0}\left( {1 - m} \right)}\\ {\frac{1}{2}{g_0}m\left( {1 \mp \sin \delta } \right)} \end{array}} \right]$ | (45) |
类似地,各散射类的能量还可以通过基于m-c或m-as参数的分解算法得到:
| $\left[\!\!\! {\begin{array}{*{20}{c}} {{P_D}}\\ {{P_V}}\\ {{P_S}} \end{array}} \!\!\!\right]\!\!{\rm{ = }}\!\!\left[\!\!\! {\begin{array}{*{20}{c}} {\frac{1}{2}{g_0}m\left( {1 + \sin 2\chi } \right)}\\ {{g_0}\left( {1 - m} \right)}\\ {\frac{1}{2}{g_0}m\left( {1 - \sin 2\chi } \right)} \end{array}}\!\!\! \right]\!\!{\rm{ = }}\!\!\left[\!\!\! {\begin{array}{*{20}{c}} {\frac{1}{2}{g_0}m\left( {1 + \sin 2{\alpha _s}} \right)}\\ {{g_0}\left( {1 - m} \right)}\\ {\frac{1}{2}{g_0}m\left( {1 - \sin 2{\alpha _s}} \right)} \end{array}} \!\!\!\right]$ | (46) |
图 8中展示了这些算法得到的分类结果。这里使用的数据是四视旧金山NASA/JPL AIRSAR L波段的全极化数据。对应的模拟左旋圆极化CTLR模式数据是通过欧空局(European Space Agency,ESA)PolSAR Pro 5.0软件转化得到的。由于数据本身已经是四视的,因此空间平均步骤仅使用了5×5矩形窗滤波器进行滤波。可以看到,两幅分类图近乎相同。而且所有分类图中,体散射类均明显被高估了。根据Cloude等人[63]的研究结果,这可能是简缩极化固有的特点。其原因在于简缩极化模式下,森林地区的散射熵会比全极化模式高。
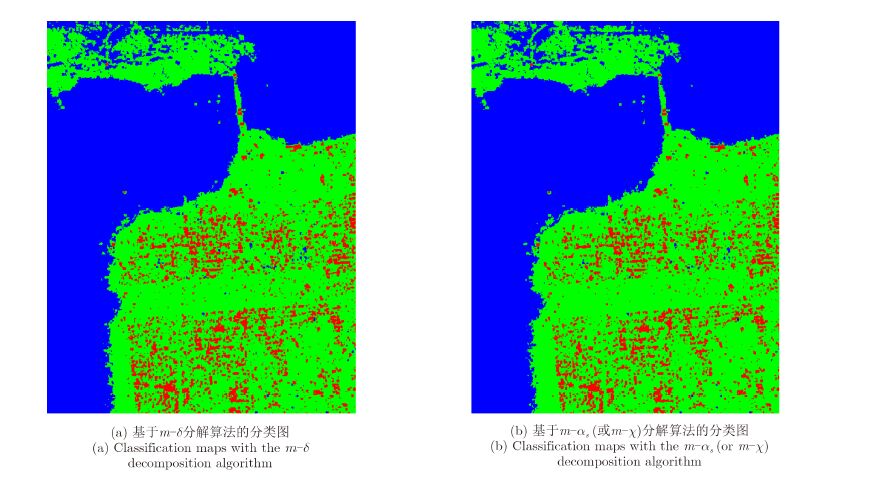
|
图 8 基于不同分解算法的分类图 Fig.8 Classification maps with different decomposition algorithms |
另一类非监督分类方法是利用前述特征值分解算法(或简缩H/alpha分解算法)得到的简缩极化信息。文献[40]中建议不同PSM间的最佳边界值为:
低熵与中熵区域间的边界值为H=0.65,而中熵与高熵区域间的边界值为H=0.96。
在低熵区域内,多次散射类与偶极子散射类间的边界值为a=42°,而偶极子散射类与表面散射类间的边界值为a=48°。
在中熵区域内,多次散射类与植被散射类间的边界值大约为a=40°,而植被散射类与表面散射类间的边界值为a=51°。
在高熵区域内,几乎所有PSM均为植被散射类。多次散射类与植被散射类间的边界值为a=34.5°,而植被散射类与表面散射类间的边界值为a=51°。
图 9中展示的是对前文使用的数据的分类结果。

|
图 9 缩极化H/alpha分类结果 Fig.9 Compact H/alpha classification results |
由于不可缺少的空间平均步骤,前两小节得到的分类结果均难以保证图像的细节与纹理特征。为了提升分类结果,需要进一步利用CTLR模式数据的统计特性。与全极化SAR的散射矢量相同,CTLR模式的散射矢量服从复高斯分布[39]。因此,同样可以在CTLR模式数据中应用Wishart分类器。
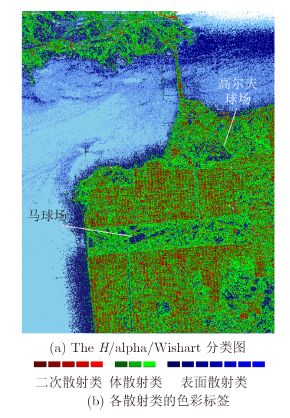
文献[33, 39]与文献[38]结合了Wishart分类器与简缩极化H/alpha分解算法和基于Stokes参数的分解算法。图 10中展示的是利用Zhang等人[40]建议的H/alpha平面边界值得到的分类结果。可以看到,引入了Wishart分类器后,图像的细节与纹理特征均较好地得以保留。
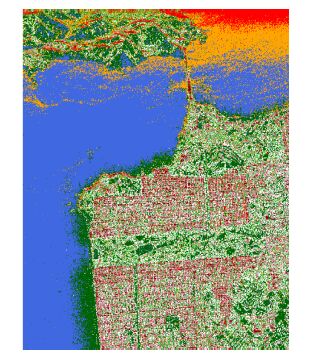
|
图 10 简缩H/alpha/Wishart分类算法的分类结果 Fig.10 The classification maps of the compact H/alpha/Wishart algorithm with the same color labels as in Fig. 9(a). |
对于第2种分类方法,我们增加了两步提纯步骤,即排除没有明确PSM的像素与利用总功率(span)的聚类步骤,以保证初始Wishart类的可靠性[38]。分类结果如图 11所示。
|
图 11 m/chi/Wishart分类算法的分类结果 Fig.11 Classification results of the m/chi/Wishart algorithm |
简缩极化干涉SAR技术是目前简缩极化领域的一个研究热点。简缩极化干涉SAR系统通过一次单基线干涉或者重轨干涉可以获得目标场景中每个分辨单元的2个目标散射矢量。基线两端获得的简缩极化目标散射矢量分别用
| ${{\bf{{J}}}_4} = \left[{\begin{array}{*{20}{c}} {{{\bf{{J}}}_{11}}}& {{{\bf{{J}}}_{12}}}\\ {{\bf{{J}}}_{12}^{*T}}& {{{\bf{{J}}}_{22}}} \end{array}} \right]$ | (47) |
简缩极化干涉SAR数据处理方法主要有两种,一是将简缩极化干涉SAR数据重建成伪全极化干涉SAR数据[24, 25],重建思想与第5.3.1节相似,一旦重建得到伪全极化干涉SAR数据,传统的全极化干涉SAR数据处理方法都可以使用;另外一个非常重要也是经典的数据处理方法是,不进行信息重建,直接对简缩极化干涉SAR数据进行处理。本节仅回顾了第2种数据处理方法中两个经典的简缩极化干涉SAR应用。
6.2.1 森林树高反演树高反演是简缩极化干涉SAR技术的一个典型的应用。大多数的树高反演方法都是基于RVoG模型的。该模型是一种能够表征不同极化状态的复干涉相干系数随垂直结构参数变化规律的二层结构模型。这二层包括一个地表层和一个均匀体散射层。树高反演过程包括:根据相干系数拟合直线、根据拟合直线与单位圆的交点计算地表相位、计算代表树高信息的体散射去相干等。树高反演过程中,最重要的步骤便是直线的拟合及体散射去相干的正确估计。无论哪种树反演方法,都是基于简缩极化干涉SAR的复相干系数做处理。复相干系数为:
| $\gamma \; ({\omega _1},{\omega _2}) = \frac{{\omega _1^{\rm{H}}{{\bf{{J}}}\!_{12}}{\omega _2}}}{{\sqrt {\omega _1^{\rm{H}}{{\bf{{J}}}\!_{11}}{\omega _1}\omega _2^{\rm{H}}{{\bf{{J}}}\!_{22}}{\omega _2}} }}$ | (48) |
在参考文献[21, 22]中,是通过求得接收天线在所有极化状态下的复相干来计算简缩极化干涉复相干的轨迹。基于求得的复相干轨迹拟合出一条直线,然后再运用三阶段反演方法进行树高估计。详细步骤如下:
(1) 变换接收天线的极化状态(式(48)中w1,w2),计算不同极化状态下的复相干,并根据复相干分布拟合直线。
(2) 计算拟合直线与单位圆的两个交点,正确选择其中一个表示地表相位
(3) 选择距离地表相位最远的复相干系数表示树高的体散射相干系数
(4) 应用查表法(Look-Up Table,LUT)技术最终求得森林的树高以及森林消光系数。
参考文献[26]中的树高反演方法不同于参考文献[21, 22]。在文献[26]中,不计算简缩极化干涉复相干轨迹,而是通过计算几个复相干进行直线拟合,用于直线拟合的复相干包括:两个接收通道的各自复相干,无约束最优相干和最大相位分离复相干。最大相位分离复相干用于估计地表相位及初步估计体散射去相干,然后通过计算简缩极化干涉相干区域的边界来修正体散射去相干,获得了精确的地表相位及体散射去相干后,采用查表法进行树高及消光系数的估计。
6.2.2 简缩极化干涉SAR目标分解参考文献[28]与文献[30]提出了基于简缩极化干涉SAR数据的目标分解方法。该方法将全极化中 Freeman-Durden三分量目标分解方法应用到简缩极化干涉SAR数据中[25]。类似于5.3.4节的内容,该方法将简缩极化干涉SAR的协方差矩阵J2分解为对应表面散射、2次散射与体散射的3个矩阵之和。
| $\pi {\rm{/4 \ 模式}} \quad \quad \quad \ {{\bf{{J}}}_2} = \frac{{{f\!_{cv}}}}{8}\left[{\begin{array}{*{20}{c}} {\rm{2}}& {\rm{1}}\\ {\rm{1}}& {\rm{2}} \end{array}} \right] + {f\!_{cd}}\left[{\begin{array}{*{20}{c}} {{{\left| \alpha \right|}^2}}& \alpha \\ { - {\alpha ^*}}& 1 \end{array}} \right] + {f\!_{cs}}\left[{\begin{array}{*{20}{c}} {{{\left| \beta \right|}^2}}& \beta \\ { - {\beta ^*}}& 1 \end{array}} \right] \quad \quad \quad \quad \quad \ $ | (49) |
| ${\rm{CTLR \ 模式}} \quad \quad {{\bf{{J}}}_2} = \frac{{{f\!_{cv}}}}{4}\left[{\begin{array}{*{20}{c}} {\rm{1}}& {\rm{0}}\\ {\rm{0}}& {\rm{1}} \end{array}} \right] + {f\!_{cd}}\left[{\begin{array}{*{20}{c}} {{{\left| \alpha \right|}^2}}& {\rm j\alpha }\\ { - {\rm j}{\alpha ^*}}& 1 \end{array}} \right] + {f\!_{cs}}\left[{\begin{array}{*{20}{c}} {{{\left| \beta \right|}^2}}& {\rm j\beta }\\ { - {\rm j}{\beta ^*}}& 1 \end{array}} \right] \quad \quad \quad \quad $ | (50) |
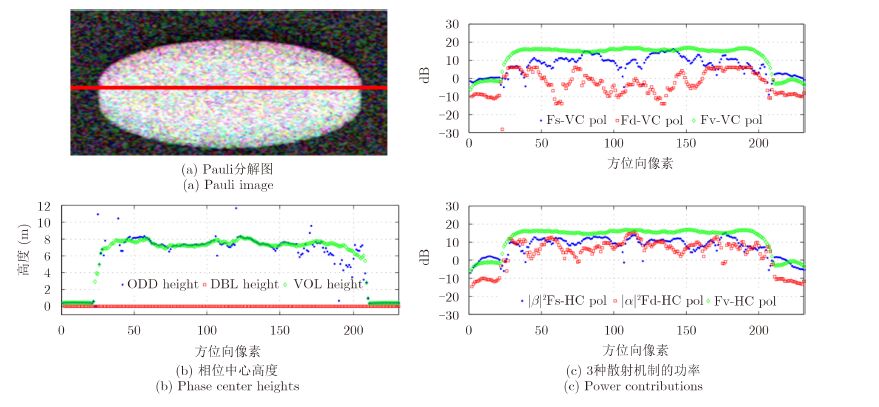
该算法的验证使用的是由PolSARProSim软件生成的仿真数据。根据10 m的森林树高,生成了仿真L波段全极化干涉SAR数据。仿真场景的Pauli图如图 12(a)所示。途中红线代表下文分析所取的一条方位线数据。将仿真的全极化SAR数据转换成简缩极化SAR数据,获得简缩极化干涉互相关矩阵J2。分解结果如图 12(c)所示。图中Odd,DBL与VOL分别代表奇次散射类、2次散射类与体散射类,VC与HC分别表示发射圆极化并使用V或H线性极化接收。通过对简缩极化干涉SAR数据进行目标分解,各散射机制的功率信息及散射相位中心高度信息都能被获得,此外该目标分解结果与全极化干涉目标分解结果[95]非常吻合,这也验证了简缩极化干涉SAR在目标分解方面的应用潜能。
|
图 12 仿真数据的Pauli分解图 Fig.12 Simulated dataset Pauli decomposition image |
除了前文介绍的这两类主要简缩极化应用以外,还有一些受益于宽测绘幅宽优势的简缩极化应用,包括土壤湿度估计[17, 18, 19, 20],冰山[43, 44, 45]、溢油[46, 47, 48, 49, 50, 51, 52, 53]与船舶检测[42, 45, 52, 53, 54, 55],农作物分类[56, 57, 58, 59, 60, 61]与海冰监测[12, 13, 14, 85, 86]等。调研结果表明,可以在这些应用领域内通过简缩极化数据得到与全极化数据性能相似的数据处理结果。
7 结束语本文全面地回顾了基于混合极化架构的极化SAR的原理与应用。混合极化架构实际上首先是一种强调使用两路信号通道合成发射极化波的极化SAR系统设计方案。雷达系统理论上可以产生任意极化波,包括简缩极化所需的圆极化波与斜线性极化波(即±45°极化波)。也就是说,这一特性使得基于混合极化架构的极化SAR系统可以工作在不同的简缩极化模式下。而简缩极化模式相比传统线性双极化模式,可以得到更好的分类结果。另外,如果最终采用的发射极化波拥有相等的H与V分量,则极化SAR系统可以额外拥有独特的自我检测标定特性。这一系统设计方案还强调接收极化基需与发射极化不同。这样,极化SAR系统的距离模糊问题可以得到改善,进而进一步增加雷达系统在全极化模式下的测绘幅宽大小。这一系统设计方案所需求的射频器件也较少,因而能够保证保证系统的成本更低、鲁棒性更好。最后,得益于更宽的测绘幅宽,基于混合极化架构的极化SAR系统可以在更短的时间间隔内获取同一目标场景的相干雷达图像。
本文同时指出了混合极化架构在工程实现中的难点,即工作在双极化模式时,发射失真无法被标定。另外,混合极化架构所采用的发射极化总是圆极化的。但是在某些应用中,使用其他极化波进行发射能够得到更好的结果。为了克服这些难点,本文提出了一个混合极化架构的改进版本。在改进型混合极化架构下,可以应用预失真技术修正发射失 真。相比拥有额外内定标回路的雷达系统,本文提出的改进型混合极化架构需要的射频器件更少。另外,基于改进型混合极化架构的极化SAR系统可以发射任意极化波,从而可以进一步支持π/4模式以及使用其他互相正交的发射极化基的全极化模式。本文最后展示了基于此改进型混合极化架构的原型系统。原型系统的相关实验验证与测试工作仍在进行中。
1 IntroductionSynthetic Aperture Radar (SAR) is an active imaging radar, which produces high-resolution microwave images of the earth's surface via signal processing technologies. It has all-day and all-weather imaging capability. Polarimetric SAR (PolSAR) offers additional polarimetric information of the observed scene and has already been successfully applied in a multitude of practical applications[1, 2]. The limitation of current spaceborne SAR systems is mainly the acquisition of radar images with both high-resolution and wide-swath coverage. As for fully, or quadrature polarimetric polarimetric (quad-pol) SAR systems, which could obtain the complete backscattering characterization of scatterers, the available swath width is at least halved compared with conventional SAR systems due to the doubled Pulse Repetition Frequency (PRF) for interleaved transmission of two orthogonal polarizations.
Conventional quad-pol SAR systems operate with Horizontal (H) and Vertical (V) linear polarizations in both transmission and reception. This configuration will give rise to severe range ambiguities in the cross-polarized (HV or VH) measurement channels, which will further limit the swath coverage particularly at larger incidence[3, 4]. Meanwhile, since the like-polarized (HH or VV) returns from natural terrain are generally 6~10 dB higher than the cross-polarized (HV or VH) returns, complex reception strategies are applied in practical radar systems to keep both measured returns within the valid dynamic range of the Analog to Digital Converter (ADC) module[5, 6]. On account of these drawbacks, a new PolSAR architecture called the Hybrid-Polarity (HP) architecture, has been proposed in Refs. [4, 7, 8] in recent years. By transmitting interleaved Right-Handed Circular (RHC) and Left-Handed Circular (LHC) polarized waves and receiving on orthogonal linear polarizations, the range ambiguity performance of the HP architecture based PolSAR system is improved for having no like- or cross-polarized relationship between the transmitting and receiving polarizations[4]. Meanwhile, the mean signal level in either receiving path is also balanced, which implies that no complex reception strategies are more needed. Thereby, PolSAR systems based on the HP architecture will have wider swath coverage and lower hardware requirement than conventional linearly-polarized PolSAR systems[4].
The HP architecture can also support the Circular Transmit Linear Receive (CTLR) mode[7] of Compact Polarimetry (CP), a collection of special dual-polarimetric (dual-pol) modes, which requires the transmission of polarizations with equivalent H and V components, such as RHC and LHC polarizations and the ±45° slant linear polarizations, and retains the relative phase of the received polarizations[9, 10, 11, 12]. CP has attracted wide attentions in the past ten years for having the potential to produce comparable results in many applications as those derived from quad-pol SARs[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61] while maintaining the advantages of dual-pol SARs such as doubled swath width, low power consumption and low system complexity[7, 9].
These advantages make the HP architecture a potential choice for future PolSAR missions. To date, several launched PolSAR missions have adopted the HP architecture: the two mini-Radio-Frequency (mini-RF) radars onboard the Indian Chandrayaan-2-1 moon mission and the American Lunar Reconnaissance Orbiter (LRO)[62], the C-band SAR onboard the Indian remote sensing satellite RISAT-1[63], the L-band SAR onboard the Japanese remote sensing satellite ALOS-2 (experimental mode)[64]. Future SAR missions including the Canadian C-band RADARSAT Constellation Mission (RCM)[12, 65, 66], the American L-band Interferometry SAR (InSAR) system of the Deformation, Ecosystem Structure, and Dynamics of Ice (DESDynI) mission[67, 68]; and the second moon mission of Indian Space Research Organization (ISRO) Chandrayaan-2[69] have also confirmed to adopt the HP architecture.
In this paper, we will first review the basic principles of the HP architecture including system designs, system models, and calibration methods. Two implementation difficulties of the HP architecture will be discussed. The major one is that when operating under the dual-pol mode, the distortions in transmit cannot be calibrated, even if their actual values can be precisely measured with specific calibration methods. The other one is that the transmission in the HP architecture are usually configured as circular polarization. Under this configuration, the dual-pol mode corresponds the CTLR mode. However, beside the CTLR mode, other CP modes with different transmit polarization such as the π/4 mode, which radiates 45° linearly-polarized waves with respect to either H and V orientations, may also produce favorable results in certain applications and deserves consideration. To deal with these two problems, an improved version of the HP architecture will be proposed in this paper. The prototype system developed for experimental validation will also be introduced.
In the next part of this paper, applications suitable for the HP architecture based PolSAR will be illustrated. Since the quad-pol data provided by HP architecture based SAR systems can be directly transformed into conventional linearly-polarized scattering matrix, this part of review will mainly focus on the corresponding dual-pol applications, i.e. CP applications. Four CP information retrieval methodologies, including the covariance matrix expansion method, the Stokes vector based method, the eigenvalue decomposition method, and the scattering model based method will be first introduced. Suitable applications stemmed from these methodologies will be reviewed next. Considering the length of the paper, only investigations on unsupervised classification of land and terrains using CP data and Compact PolSAR interferometry for tree height inversion will be reviewed in detail.
The organization of this paper is given as follows. In Section 2, the system designs and system models of the HP architecture based dual-pol and quad-pol SAR systems are reviewed, respectively. In Section 3, the self-checking property[7] of the HP architecture and calibration techniques are illustrated. Assessment of the transmit distortions, which cannot be calibrated using external calibration methods, are also discussed. In Section 4, an improved version of the HP architecture is proposed. In Section 5, several data processing algorithms including the transformation of HP quad-pol data to linear quad-pol data, and the simulation of CP data with quad-pol data are introduced. Four major CP information retrieval methodologies are also illustrated in this section. In Section 6, investigations on CP applications are reviewed. Conclusions are finally made in Section 7.
2 Hybrid-polarity Architecture 2.1 Hybrid dual-pol architectureThe HP architecture was first proposed in Ref. [7] to support the CTLR mode of CP, which requires the transmission of single circular polarization (either RHC or LHC) and simultaneously receiving on two orthogonal linear polarizations. Since CP is actually a collection of special dual-pol modes, this HP architecture is referred as the Hybrid Dual-Pol (HP2) architecture in this paper. The block schematic of the HP2 architecture is shown in Fig. 1(a). In order to produce circular polarization for transmission, the signal flow generated by the waveform generator is split in two with a power splitter and one of the sub-signal flow is phase shifted 90° afterwards. This part of design is highlighted with a dashed frame in Fig. 1(a). The two sub-signal flows are used to feed the H- and V-elements of a dual-linearly-polarized antenna. The outlined part of the HP2 architecture could be simplified as Fig. 1(b), with

|
Fig.1 Block schematic of the HP2 architecture (Raney 2007, Ref. [7]) |
As we can see, very few RF hardware is required in the HP2 architecture, which implies fewer losses and fewer sources of potential distortion sources in the radar system. Besides, since neither receive channel is disadvantaged by being cross-polarized, the mean signal level in both channels should be similar. This means also that there will be less chance of having a stronger polarization affect a weaker polarization, i.e. having a strong crosstalk within the radar system[4].
The system model of the HP2 architecture based spaceborne PolSAR system is[70]:
| $ \begin{array}{l} \left[{\begin{array}{*{20}{c}} {{M_{{\rm{RH}}}}}\\ {{M_{{\rm{RV}}}}} \end{array}} \right] = A\left( {r, \theta } \right){{\rm{e}}^{\, {\rm{j}}\phi }}\frac{1}{{\sqrt 2 }} \cdot \left[{\begin{array}{*{20}{c}} 1& {{\delta _2}}\\ {{\delta _1}}& {{f_1}} \end{array}} \right]\\ \quad \quad \quad \quad \quad \cdot \left[{\begin{array}{*{20}{c}} {\cos \varOmega }& {\sin \varOmega }\\ { - \sin \varOmega }& {\cos \varOmega } \end{array}} \right] \cdot \left[{\begin{array}{*{20}{c}} {{S_{{\rm{HH}}}}}& {{S_{{\rm{HV}}}}}\\ {{S_{{\rm{VH}}}}}& {{S_{{\rm{VV}}}}} \end{array}} \right]\\ \quad \quad \quad \quad \quad \cdot \left[{\begin{array}{*{20}{c}} {\cos \varOmega }& {\sin \varOmega }\\ { - \sin \varOmega }& {\cos \varOmega } \end{array}} \right] \\ \quad \quad \quad \quad \quad \cdot \left[{\left[{\begin{array}{*{20}{c}} 1\\ { - {\rm j}} \end{array}} \right] + \delta \left[{\begin{array}{*{20}{c}} 1\\ {\rm j} \end{array}} \right]} \right] + \left[{\begin{array}{*{20}{c}} {{N_1}}\\ {{N_2}} \end{array}} \right] \end{array} $ | (1) |
| $M=A{{\text{e}}^{\text{j}\phi }}\frac{1}{\sqrt{2}}R{{R}_{F}}S{{R}_{F}}\left[ {{k}_{\text{RHC}}}+\delta {{k}_{\text{LHC}}} \right]+N$ | (2) |
The electric field Ei incident on the surface could be further derived as:
| ${{\bf{{{E}}}}_i} ={{R}_F}\left[{{k_{{\rm{RHC}}}} + \delta {k_{{\rm{LHC}}}}} \right] = \left[{\begin{array}{*{20}{c}} {\cos \varOmega }& {\sin \varOmega }\\ { - \sin \varOmega } & {\cos \varOmega } \end{array}} \right] \\ \quad \quad \cdot \left[{\left[{\begin{array}{*{20}{c}} 1\\ { - {\rm j}} \end{array}} \right] + \delta \left[{\begin{array}{*{20}{c}} 1\\ {\rm j} \end{array}} \right]} \right] \\ \quad \, \, = {{\rm e}^{ - {\rm j}\varOmega }}\left[{\left[{\begin{array}{*{20}{c}} 1\\ { - {\rm j}} \end{array}} \right] + \delta {{\rm e}^{\, {\rm j}2\varOmega }}\left[{\begin{array}{*{20}{c}} 1\\ {\rm j} \end{array}} \right]} \right]$ | (3) |
Although the distortions in transmission can be simply represented with one single term
| ${\bf{{{T}}}} = \left[{\begin{array}{*{20}{c}} 1 & 0\\ 0 & {{f_2}} \end{array}} \right] \cdot \left[{\begin{array}{*{20}{c}} 1 & {{\delta _4}}\\ {{\delta _3}} & 1 \end{array}} \right]$ | (4) |
| ${\bf{{{T}}}} \cdot {k_{\rm RHC}} = \alpha \left[{{\rm k_{RHC}} + \delta {k_{\rm LHC}}} \right]$ | (5) |
| $\alpha = \frac{{\left( {1 + {f_2}} \right) - {\rm j}({\delta _4} - {\delta _3})}}{2}$ | (6) |
Either expressions of the transmit distortions is applicable. But as we can see in Eq. (1), even if the distortion terms on transmit are explicitly known, the real scattering matrix of the target can still not be obtained through multiplying a corresponding inverse matrix. Therefore, it will be more concise by using the general crosstalk term. But the explicit formulation of the transmit distortions allows us to assess the influences of different distortion sources in detail, respectively. This part of work will be reviewed in Subsection 3.2.
2.2 Hybrid quad-pol architectureAs an alternative to conventional linearly-polarized quad-pol SAR systems, it was suggested in Ref. [7] to use the HP architecture to configure a quad-pol SAR system. The transmitted polarizations would be RHC and LHC, interleaved, and the receive polarizations would be coherent H and V polarizations. This idea was further elaborated in Ref. [4] and Ref. [8].
The block schematic of the Hybrid Quad-Pol (HP4)[8] architecture is shown in Fig. 2(a). The transmit module is similar to the introduced HP2 architecture, with a small modification in the phase shifter. The phase of the signal flow will be shifted between +90° and -90° for RHC and LHC polarization transmission, respectively. This part of design is also outlined in Fig. 2(a) and simplified in Fig. 2(b). If the phase shifter is fixed at either +90° or -90°, the resulting system design is the HP2 architecture. Therefore, the CTLR mode can be regarded as the corresponding dual-pol mode of the HP4 architecture based PolSAR system. In the following text, we will use the phrase “HP architecture” to indicate an HP4 architecture, which can also operate under dual-pol mode.

|
Fig.2 Block schematic of the HP4 architecture (Raney 2008, Ref. [8]) |
The advantages of the HP2 architecture denoted in previous subsection is also inherited by the HP4 architecture. First, there are also no like- or cross-polarized relationship between the transmitted and received polarization. According to the deductions made in Ref. [4], this feature will lead to a better range ambiguity performance, which implies that an HP4 architecture based quad-pol SAR system can have a wider swath coverage, particularly at higher incident angles than conventional linear quad-pol SAR systems.
Moreover, since the mean signal level in both receive channels are similar, conventional complex reception strategies to adjust the receiver gain for different returns[5, 6] are also no longer needed. Therefore, comparing with conventional linearly-polarized PolSAR systems, the system design of the HP4 architecture based PolSAR system is much simpler, which in turn implies a less costly radar and more robust calibration and measurement reliability.
Since there is no need to toggle the gain of receivers between either radar returns, the system model of the HP4 architecture based spaceborne PolSAR system is similar to the standard polarimetric system model concerning the FR effect[73]:
| ${{\mathbf{M}}_{\text{HP4}}}=A{{\text{e}}^{\text{j}\phi }}\mathbf{R}{{\mathbf{R}}_{F}}{{\mathbf{S}}_{\text{HP4}}}{{\mathbf{R}}_{F}}\mathbf{T}+\mathbf{N}$ | (7) |
| ${{\bf{{{S}}}}_{\rm HP4}} = \left[{\begin{array}{*{20}{c}} {{S_{{\rm{RH}}}}}& {{S_{{\rm{LH}}}}}\\ {{S_{{\rm{RV}}}}}& {{S_{{\rm{LV}}}}} \end{array}} \right] \\ \quad \, \, \quad = \left[{\begin{array}{*{20}{c}} {{S_{{\rm{HH}}}} - {\rm j}{S_{{\rm{HV}}}}}& {{S_{{\rm{HH}}}} + {\rm j}{S_{{\rm{HV}}}}}\\ {{S_{{\rm{VH}}}} - {\rm j}{S_{{\rm{VV}}}}}& {{S_{{\rm{VH}}}} + {\rm j}{S_{{\rm{VV}}}}} \end{array}} \right]$ | (8) |
Since the data derived from HP4 architecture based PolSAR system could be transformed into conventional linear basis, standard algorithms developed for polarimetric calibration could be directly applied on the HP4 architecture based PolSAR systems. The calibration issue left for the HP architecture is the calibration of data obtained through HP2 architecture based PolSAR systems, i.e. the calibration of CP data.
3.1 Calibration of CP data 3.1.1 Self-checking calibration methodSince the mean signal level in both receive path of the HP architecture based PolSAR system is expected to be balanced, the first- and second-order statistics of the return signals should be identical when the H and V backscatter coefficients are equal. In practice, this criterion is achieved when the radar views at an incident angle that is normal to the mean slope of the illuminated terrain. The discrepancies, which do not meet this criterion, can be measured and compensated[7, 74].
This unique calibration strategy of the HP architecture has been adopted by the lunar mini-RF programs[62, 75]. Since there are no Amazon rain forests, nor specially placed radar reflectors available on the Moon, standard calibration techniques used by Earth orbiters were not applicable. During the on-orbit calibration experiment, the spacecraft was rolled to align the mini-RF radar antenna in a nadir-pointing orientation towards the Moon to cooperate the calibration experiment. The V-H gain balance and V-H phase balance were counted to be -2.55 dB±0.25 dB and -138°±2.7°, respectively. These results compare well with the predictions made through an end-to-end system measurement, which were -2.14 dB±0.25 dB and -135.9°±1.5°, correspondingly. The small difference between these two strategies was mainly due to the actual imperfect transmitted circular polarization, which was measured having an Axial Ratio (AR) of 2.46 dB±0.15 dB.
3.1.2 Quad-pol based calibration methodAn HP architecture based PolSAR system can operate under both quad-pol mode and dual-pol mode. Therefore, if such system is stable during the data-taking stage, as is the case for spaceborne SARs, the discrepancies within the system could be directly obtained by operating quad-pol mode at the beginning and/or the end of the data-taking stage[70].
3.1.3 Calibration of faraday rotationAs for spaceborne PolSAR systems operating with low frequency microwaves, the FR effect must also be taken into consideration. Beside the usage of Total Electron Content (TEC) maps[76], FR angles can also be estimated through backscatters from bare surfaces, where the HH-VV phase difference is close to zero[18]. The identification of bare surfaces was made by the conformity coefficient m, which is FR independent:
| $\mu = \frac{{2{\mathop{\rm Im}\nolimits} \left\langle {{M_{{\rm{RH}}}}M_{{\rm{RV}}}^*} \right\rangle }}{{\left\langle {{M_{{\rm{RH}}}}M_{{\rm{RV}}}^*} \right\rangle + \left\langle {{M_{{\rm{RH}}}}M_{{\rm{RV}}}^*} \right\rangle }} \\ \quad \! \cong 2\frac{{{\mathop{\rm Re}\nolimits} \left( {{S_{{\rm{HH}}}}S_{{\rm{VV}}}^*} \right) - {{\left| {{S_{{\rm{HV}}}}} \right|}^2}}}{{{{\left| {{S_{{\rm{HH}}}}} \right|}^2} + 2{{\left| {{S_{{\rm{HV}}}}} \right|}^2} + {{\left| {{S_{{\rm{VV}}}}} \right|}^2}}}$ | (9) |
| ${Ω} \! = \frac{1}{2}\arctan \left(\! {2\frac{{{\mathop{\rm Re}\nolimits} \left\langle {{M_{{\rm{RH}}}}M_{{\rm{RV}}}^*} \right\rangle }}{{\left\langle {{M_{{\rm{RV}}}}M_{{\rm{RV}}}^*} \right\rangle - \left\langle {{M_{{\rm{RH}}}}M_{{\rm{RH}}}^*} \right\rangle }}} \!\right)\!\!\bmod \frac{\pi }{4}$ | (10) |
In Ref.[77], Truong-Loï et al. first proposed a calibrator based calibration method for the CTLR mode. Since the transmit distortions could not be corrected, the transmission of the radar system is considered perfect. Three calibrators, including two dihedrals at 0° and 45° and a trihedral at 0° are utilized to measure and correct the channel imbalance and cross-talk in reception, FR angle and system gain.
In Ref. [78], Chen and Quegan also investigated several calibrator-based calibration strategies for spaceborne low-frequency SAR systems operating with CTLR mode. In their investigation, six different calibration schemes, containing different mixtures of passive and active radar calibrators, were proposed and carefully investigated. First, it was established that calibration strategies involving four calibrators will yield a more accurate estimation of the radar system parameters than those using just three calibrators. However, the augment in cost and complexity in deployment deserves careful consideration. Second, among the three passive calibrators, gridded trihedral is the most preferred against the dihedral and trihedral, because of its much lower Average Polarimetric Noise (APN) and insensitivity to pointing accuracy. The mostly recommended calibration scheme concludes two gridded trihedrals that select for the HH and VV channels, and two active calibrators that select for the HV and VH channels.
In Ref. [79], Chen at al. proposed a general calibration algorithm for all dual-pol SAR systems using only one trihedral and two dihedrals, 0° and 45° in rotation angle. The FR effect is not considered in this method. This method is applicable for all dual-pol modes including the conventional linear dual mode, the CTLR mode, and the p/4 mode of CP. The effectiveness of this algorithm has been verified with a ground-based SAR system with p/4 mode and CTLR mode transmit/receive configurations[34].
3.2 Assessment of the transmit distortionsIn previous section, we have discussed one major implementation difficulty of the HP architecture: the transmit distortions in its corresponding dual-pol mode cannot be corrected by simply multiplying a corresponding inverse matrix. Therefore, the influence of such distortions requires careful assessment. In Ref. [71], Guo et al. adopted the Maximum Normalized Error (MNE)[80]for quantitative evaluation. In the case with the HP2 architecture based PolSAR system, MNE is defined as:
| ${\rm{MNE}} = {\left\| {{\bf{{PD}}} - {{\bf{{P}}}_0}} \right\|_2}$ | (11) |
| ${\bf{{P}}} = \left( {\begin{array}{*{20}{c}} {p_h^t} & 0 & {p_v^t} & 0 \\ 0 & {p_h^t} & 0 & {p_v^t} \end{array}} \right)\quad \quad \quad \quad \, \, $ | (12) |
| ${\bf{{D}}} = {\left[{\left[{\begin{array}{*{20}{c}} {\cos {Ω} } & {\sin {Ω} }\\ { - \sin {Ω} } & {\cos {Ω} } \end{array}} \right] \cdot {{\bf{{X}}}_t}} \right]^{\rm T}} \otimes {\bf{{I}}}$ | (13) |
| ${{\bf{{P}}}_0} = \left( {\begin{array}{*{20}{c}} 1 & 0 & {\rm j} & 0\\ 0 & 1 & 0 & {\rm j} \end{array}} \right)\quad \quad \quad \quad \quad \quad \, \, $ | (14) |
This evaluation campaign can be used to assess the influence of transmit distortions caused by multiple sources, including FR, channel imbalance and crosstalk in transmission, and incident angle. However, in order to assess the influence caused by each distortion source alone, the corresponding MNE changes of each distortion source is simulated, respectively.
3.2.1 Faraday rotationAccording to Eq. (3), when FR is the only distortion in transmit, i.e. the circular polarization transmitted is perfect, the FR angle simply becomes an additional phase term, and can be omitted in the following data processing steps. On the other hand, if the transmit polarization is imperfect, the FR will have an influence on the general crosstalk d, which is already shown in Eq. (3).
3.2.2 Channel imbalance Assuming that the only existent distortion in transmission is channel imbalance, i.e.

|
Fig.3 MNE evaluation due to channel imbalance |
For the sake of simplicity, the crosstalk is here assumed

|
Fig.4 MNE evaluation due to crosstalk gain |
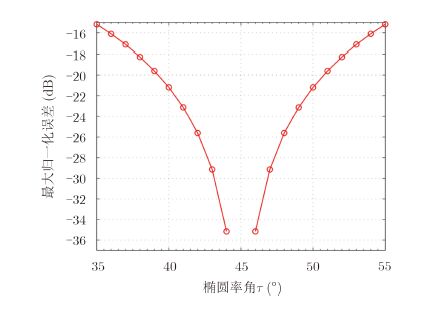
It is admitted that the non-circularity of the transmitted wave also increases with the change of incidence angle[65]. In Ref. [65], Touzi and Charbonneau estimated that the AR of the transmitted polarization with RCM may vary between 1.4 dB (within 50 km at 0° beam scan angle) and 3.0 dB for the most raising beams of the 350 km ScanSAR swath. Such AR variations correspond to an elliptical polarization whose ellipticity varies between 35° and 41°. To evaluate such influence, the transmit Jones vector is set as[81]:
| $\left[{\begin{array}{*{20}{c}} {p_h^t}\\ {p_v^t} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {\cos \phi }& { - \sin \phi }\\ {\sin \phi }& {\cos \phi } \end{array}} \right] \cdot \left[{\begin{array}{*{20}{c}} {\cos \tau }\\ {{\rm j}\sin \tau } \end{array}} \right]$ | (15) |
In this case, only ellipticity is taken into consideration and the orientation angle is set as

|
Fig.5 MNE evaluation due to the change in ellipticity |
As introduced in previous sections, the HP architecture has one major implementation difficulty within the calibration issue: the transmit distortions can not be calibrated when working under the dual-pol mode, even if the values of transmit distortions can be precisely obtained through various external calibration methods. Therefore, those transmit distortions are always neglected in most HP system related papers. But as is shown in Subsection 3.2, transmit distortions will surely have certain influence on the HP architecture based PolSAR system.
In Subsection 3.2, the transmit distortions are evaluated by MNE, which is a generic metric defined to measure the polarization purity of a PolSAR system. On the other hand, the transmit distortions can also be quantified by their outcomes, which is the distortion of transmitted polarizations. Under this point of view, AR is used to quantify transmit distortions. As for a perfect circularly polarized wave AR=0 dB, and AR=+∞ is for a linearly-polarized wave. It is reported that the transmitted polarization in the two Lunar Mini-RF radars have an AR on the order of 2.5 dB[62]. Besides, it is expected that AR may vary between 1.4 dB and 3 dB in the worst case of the upcoming RCM radar system[65], and the radar system of the second moon mission of ISRO is designed to have an AR of less than 2 dB[69]. According to our research, AR and MNE values are not one to one related. But AR should be less than 1.8 dB to fulfill the aforementioned
In order to overcome this flaw, internal calibration techniques should be built in the HP architecture based PolSAR systems. But conventional internal calibration loops may greatly increase the RF hardware required in the radar system, which implies an augment in cost and potential distortion sources. Alternatively, we have just modified the transmit module of the HP architecture. The block schematic of the resulting improved HP architecture is shown in Fig. 6(a). The modified transmit module is also outlined and simplified in Fig. 6(b). Comparing with the system designs shown in Fig. 1(b) and Fig. 2(b), the original ±90° phase shifter is replaced by two high-accuracy variable attenuator and 360° -covering phase shifter, denoted by “A” and “P”, respectively.

|
Fig.6 Block schematic of the improved HP architecture |
With these improvements, a pre-distortion technique can be used to correct the transmit distortions. First, the attenuator and phase shifter are tuned so that the two transmit path have balanced power level and wanted phase difference (for example +90° or -90° for circular polarizations). Next, the transmit distortions are measured with calibration methods introduced in previous section. Then, we can further tune the attenuator and phase shift to compensate those distortions. Thereby, the transmit distortions can be mitigated to an acceptable level.
With the two high-accuracy tunable attenuator and phase shifter, the PolSAR system based on the improved HP architecture can also generate arbitrary transmit polarizations. Original HP architecture based PolSAR systems usually operate with circularly-polarized transmissions with the consideration of mitigated FR effect and having no rotational selectivity upon the observation. But other transmit configurations also deserve further researches and applications. For example, Ref. [29] founded that with p/4 mode data, better decomposition results can be derived than those derived from CTLR mode data utilizing model-based decomposition algorithms[29]. Similar algorithms can also be applied to p/4 mode compact PolSAR interferometry (PolInSAR) data and produce promising target decomposition results[31].
Similar to the original HP architecture, the improved HP architecture can also support quad-pol mode. By switching the attenuator and the phase shifter, the improved HP architecture can produce interleaved orthogonal polarization pairs. Although arbitrary transmit polarization pairs can be generated, but in order to retain the advantage of having a wider swath coverage, the adopted transmit polarization pairs should differ from the receive polarization basis, i.e. H and V polarizations.
4.2 System modelThe system model introduced in Subsection 2.1 and Subsection 2.2 also suits for the improved HP architecture based PolSAR system. When operating under dual-pol mode, the Jones vector of the transmitted polarization with general transmit distortion term d in Eq. (1) and Eq. (2) should be adjusted accordingly. For example, if traditional H and V transmission, or the aforementioned slant linear polarization are utilized in transmission, those term should be adjusted as[79]:
| ${\rm{H \ transmission}} \quad \quad \quad \quad \left[{\begin{array}{*{20}{c}} {{T_H}}\\ {{T_V}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} 1\\ \delta \end{array}} \right]$ | (16) |
| ${\rm{V \ transmission}} \quad \quad \quad \quad \left[{\begin{array}{*{20}{c}} {{T_H}}\\ {{T_V}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} \delta \\ 1 \end{array}} \right]$ | (17) |
| $ \quad \;\pi /4 \; {\rm{linear \; polarization \; transmission}}\\ \quad \quad \quad \quad \ \left[{\begin{array}{*{20}{c}} {{T_H}}\\ {{T_V}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} 1\\ 1 \end{array}} \right] + \delta \left[{\begin{array}{*{20}{c}} 1\\ { - 1} \end{array}} \right] \quad \quad \quad \quad \quad \quad $ | (18) |
As for the quad-pol mode, the 2×2 matrix SHPA in Eq. (7) should be adjusted according to the utilized transmit and receive polarization pairs.
4.3 Prototype systemAs is shown in Fig. 7, our research team has already built a prototype system consisting the transmit and receive modules of the proposed improved HP architecture. A Vector Network Analyzer (VNA) is utilized to measure the magnitude and phase characteristics of the prototype system. Besides, we have also developed a program to control the attenuators, phase shifter and switches within the prototype system and communicate VNA through network. The pre-distortion related functions are also built in the program. It is estimated that the AR of the circular polarized wave transmitted by an ideal dual-linearly polarized antenna can be maintained within 1 dB with the pre-distortion technique.

|
Fig.7 Prototype system of the improved HP architecture measured by a VNA |
Another issue to be discussed is the usage of different antennas. In original HP architecture, it is suggested to utilize one dual-linearly polarized antenna for both transmit and receive. But we can also use two orthogonal single polarized antennas to replace one dual-linearly-polarized antenna. If different antennas are used for transmitting and receiving, then up to four single polarized antennas are required. In this research program, we have adopted this antenna configuration including four single polarized antennas. This configuration has the advantage of lower cost and better isolation, but suffers from parallax problem due to the boresight separation between two different antennas. Whether this trade is favorable still requires further verification.
Utilizing this prototype system, we will first validate the expected pre-distortion feature. Next, we will implement further experiments on different CP modes and assess actual influence of the transmit distortions on different radar observations. As for the analysis of data obtained from the improved HP architecture based PolSAR system, the unified data analysis framework for general compact and quad-pol SARs developed by Sabry and Vachon[82] can be applied.
5 Data Processing MethodologiesAccording to basic radar polarimetry theories[81], any quad-pol data can be directly transformed into other polarimetric data with different transmit/receive configuration, including dual-pol mode data. Therefore, quad-pol data derived from the HP architecture based PolSAR system can be directly transformed into conventional linear quad-pol data. Thereby, analyzing tools developed for conventional PolSAR can be similarly applied to HP architecture based quad-pol SARs.
On the other hand, the corresponding dual-pol modes, i.e. CP modes, of the HP architecture based PolSAR was newly introduced in the past ten years. Corresponding data processing methodologies and applicable applications still deserves to be reviewed. In the following two sections, data processing methodologies and the applications based on both CTLR mode and p/4 data are introduced, since those data could be derived from the proposed improved HP architecture.
5.1 CP data simulationTo date, only RISAT-1 and ALOS-2 are capable of providing CP data. ALOS-2 has acquired CP data with experimental mode, and those data are still not made public for the research community. Therefore, most CP researches are still based on simulated CP data, which is the dual-pol data directly transformed from corresponding quad-pol data. As is illustrated above, any quad-pol data can be used to transform other polarimetric data, including dual-pol data. An example of transmitting linear quad-pol data to CTLR mode data is shown in the Appendix of Ref. [7]. This formulation utilized the covariance matrix C3 of conventional linear quad-pol data. Similarly, one can use the coherency matrix T3 of conventional linear quad-pol data to simulate CP data[83]. In Ref. [11], the scattering vectors and covariance matrices of all three CP modes composed by the elements of the 2×2 Sinclair matrix are also shown. This transformation process could also be carried out in the newest PolSAR Pro 5.0 software[84].
It is important to note that though the transformed CP data is called as “simulated CP data”, but since the quad-pol data used for transformation is real, the generated CP data is real. Moreover, this transformation also makes the comparison between CP and quad-pol repeatable, since same data is used in either cases.
5.2 Fundamental data productsThe fundamental data products of the CP data include the 2×2 covariance matrix C2 and the Stokes vector (SV)
| ${{\bf{{C}}}_2}{\rm{ = }}\left\langle {{{\bf{{k}}}_{{\rm{CP}}}} \cdot {\bf{{k}}}_{\rm CP}^{*{\rm T}}} \right\rangle = \frac{1}{2}\left[{\begin{array}{*{20}{c}} {{g_0} + {g_1}}& {{g_2} - {\rm j}{g_3}}\\ {{g_2} + {\rm j}{g_3}}& {{g_0} - {g_1}} \end{array}} \right]$ | (19) |
According to Ref. [11], the covariance matrix C2 of the three main CP modes can all be expressed as a sum of three terms: one only contains elements which have dependency with SHH and SVV, one contains |SHH|2 elements, and another term is consist of only co-polarization correlations. Based on the reciprocity assumption, i.e. SVH=SHV, and the reflection symmetry assumption, i.e.
| $\frac{{\left\langle {{{\left| {{S_{{\rm{HV}}}}} \right|}^2}} \right\rangle }}{{\left\langle {{{\left| {{S_{{\rm{HH}}}}} \right|}^2}} \right\rangle + \left\langle {{{\left| {{S_{{\rm{VV}}}}} \right|}^2}} \right\rangle }} = \frac{{1 - \left| \rho \right|}}{4}$ | (20) |
| $\rho \equiv \frac{{\left\langle {{S_{{\rm{HH}}}} \cdot S_{{\rm{VV}}}^*} \right\rangle }}{{\sqrt {\left\langle {{{\left| {{S_{{\rm{HH}}}}} \right|}^2}} \right\rangle \cdot \left\langle {{{\left| {{S_{{\rm{VV}}}}} \right|}^2}} \right\rangle } }}$ | (21) |
This constraint is further developed by Nord et al.[11] as:
| $\frac{{\left\langle {{{\left| {{S_{{\rm{HV}}}}} \right|}^2}} \right\rangle }}{{\left\langle {{{\left| {{S_{{\rm{HH}}}}} \right|}^2}} \right\rangle + \left\langle {{{\left| {{S_{{\rm{VV}}}}} \right|}^2}} \right\rangle }} = \frac{{1 - \left| \rho \right|}}{N}$ | (22) |
| $N = \frac{{{{\left| {{S_{{\rm{HH}}}} - {S_{{\rm{VV}}}}} \right|}^2}}}{{{{\left| {{S_{{\rm{HV}}}}} \right|}^2}}}$ | (23) |
Utilizing these constraints, the value of |SHV|2 can be derived though an iterative solving process. Thus, other unknowns of the pseudo quad-pol data could be calculated. There are also some other reconstruction algorithms, which are either based on the scattering decomposition models[48, 85] or the eigenvalues of the C2, or Degree of Polarization (DoP)[86, 87]. Detailed assessment and comparisons of these approaches could be found in Ref. [87].
This kind of retrieval method has the advantage that, once the pseudo quad-pol data is obtained, all analysis tools developed for quad-pol SARs could be directly applied. However, the objective in many applications of PolSARs is to ascertain the scattering properties of the scene, rather than to presume them at the outset, and to realize image classification over an unconstrained variety of scene characteristics. Therefore, the application of this methodology is in fact restricted.
5.3.2 Stokes vector based methodPolarimetric information contained in CP data could also directly extracted from SV, from which various child parameters containing different polarimetric features could be generated[7, 62, 88]:
The aforementioned DoP:
| $m = \frac{{\sqrt {g_1^2 + g_2^2 + g_3^2} }}{{{g_0}}}$ | (24) |
The degree of linear polarization mL:
| ${m_L} = \frac{{\sqrt {g_1^2 + g_2^2} }}{{{g_0}}}$ | (25) |
The linear polarization ratio
| ${\mu _L} = \frac{{{g_0} - {g_1}}}{{{g_0} + {g_1}}}$ | (26) |
The degree of circular polarization mC:
| ${m_C} = \frac{{{g_3}}}{{{g_0}}}$ | (27) |
The Circular Polarization Ratio (CPR)
| ${\mu _C} = \frac{{{g_0} - {g_3}}}{{{g_0} + {g_3}}}$ | (28) |
The relative phase between the two linear E-vectors of the backscattered field:
| $\delta = {\tan ^{ - 1}}\left[{\frac{{{g_3}}}{{{g_2}}}} \right], \;\;\;\; - {180^ \circ } < \delta \le - {180^ \circ }$ | (29) |
Besides these six child parameters, other two very important parameters derived from SV are: the target parameter
In Ref. [83], the compact RVoG scattering model is formed as:
| ${\bf{{g}}} = {g_0}\left( {1 - m} \right)\left( {\begin{array}{*{20}{c}} 1\\ 0\\ 0\\ 0 \end{array}} \right) + {g_0}m\left( {\begin{array}{*{20}{c}} 1\\ {\sin 2{\alpha _s}\cos \phi }\\ { \pm \sin 2{\alpha _s}\sin \phi }\\ { \mp \cos 2{\alpha _s}} \end{array}} \right)$ | (30) |
| ${\alpha _s} = \frac{1}{2}{\tan ^{ - 1}}\left( {\frac{{\sqrt {g_1^2 + g_2^2} }}{{ \mp {g_3}}}} \right)$ | (31) |
| $\phi = \arg \left( {{g_1} \pm {\rm j}{g_2}} \right)\quad \quad \quad \quad $ | (32) |
According to the well-known Born and Wolf wave decomposition[81], SV could also be decomposed into a completely polarized and a completely depolarized wave component, in which the polarized term could be further written as a function of the polarization ellipse parameters, i.e. the orientation angle y and the ellipticity angle c:
| ${\bf{{g}}} = {g_0}\left( {1 - m} \right)\left( {\begin{array}{*{20}{c}} 1\\ 0\\ 0\\ 0 \end{array}} \right) + m{g_0}\left( {\begin{array}{*{20}{c}} 1\\ {\cos 2\psi \sin 2\chi }\\ { \pm \sin 2\psi \cos 2\chi }\\ { \mp \sin 2\chi } \end{array}} \right)$ | (33) |
Comparing the decomposition models in Eq. (30) and Eq. (33), we can conclude that
| $\cos 2{\alpha _s} = \sin 2{c} $ | (34) |
Similar to the famous H/alpha decomposition algorithm, C2 could also be directly decomposed with the eigenvalue decomposition[40, 83, 91]:
| ${{\bf{{C}}}_2} \!=\! \left[{{{\bf{{U}}}_2}} \right]\left(\!\! {\begin{array}{*{20}{c}} {{\lambda _1}}\!\!& \!\!0\\ 0 \!\!& \!\!{{\lambda _2}} \end{array}} \!\!\right){\left[{{{\bf{{U}}}_2}} \right]^{ - 1}}, \;\;{{\bf{{U}}}_2} \!=\! \left(\!\! {\begin{array}{*{20}{c}} {{{\bf{{u}}}_1}}& {{{\bf{{u}}}_2}} \end{array}} \!\!\right)$ | (35) |
| ${H_w} = - \sum\limits_{i = 1}^2 {{p_i}{{\log }_2}{p_i}} $ | (36) |
| $\alpha = \sum\limits_{i = 1}^2 {{p_i}{\alpha _i}} \quad \quad \quad $ | (37) |
| ${p_i} = \frac{{{\lambda _i}}}{{{\lambda _1} + {\lambda _2}}}\quad \quad \quad \quad \quad \quad \quad \quad $ | (38) |
| ${{\bf{{u}}}_i} = {{\rm e}^{{\rm j}{\phi _i}}}{\left( {\begin{array}{*{20}{c}} {\cos {\alpha _i}}& {\sin {\alpha _i}{{\rm e}^{{\rm j}{\delta _i}}}} \end{array}} \right)^{\rm T}}$ | (39) |
The boundary curves of the derived
| ${{\bf{{C}}}_2} = \left( {\begin{array}{*{20}{c}} 1& 0 \\ 0& m \end{array}} \right), \;\;\;\;{\rm{or}}\\ {{\bf{{C}}}_2} = \left( {\begin{array}{*{20}{c}} m& 0\\ 0& 1 \end{array}} \right), \;\;\;\;0 \le m \le 1$ | (40) |
It is established that this method is only applicable to CP data under the dual circular polarization (DCP, or CC) mode, which transmits circular polarization, and receives in orthogonal circular polarizations[10]. But since the scattering vectors of the CTLR mode and CC mode are linearly related through the following equation[91]:
| ${{\bf{{k}}}_{{\rm{CL}}}} = \frac{1}{2}\left( {\begin{array}{*{20}{c}} 1& 1 \\ { - {\rm j}}& {\rm j} \end{array}} \right){{\bf{{k}}}_{{\rm{CC}}}}$ | (41) |
In the famous Freeman-Durden decomposition, quad-pol SAR data can be decomposed into three canonical scattering components utilizing three physically based scattering models[92]:
| $\begin{aligned} {C_3} = \frac{{f\!_v}}{8}\left( {\begin{array}{*{20}{c}} 3 & 0 & 1\\ 0 & 2 & 0\\ 1 & 0 & 3 \end{array}} \right) + f{\!_d}\left( {\begin{array}{*{20}{c}} {{{\left| \alpha \right|}^2}}& 0 & \alpha \\ 0 & 0 & 0\\ {{\alpha ^*}}& 0 & 1 \end{array}} \right) + f{\!_s}\left( {\begin{array}{*{20}{c}} {{{\left| \beta \right|}^2}} & 0 & \beta \\ 0 & 0 & 0\\ {{\beta ^*}}& 0 & 1 \end{array}} \right) \end{aligned} $ | (42) |
Similarly, the
| $\pi {\rm{/4 \ mode}} \quad \quad \quad {{\bf{{C}}}_2} = \frac{{{f\!_v}}}{8}\left( {\begin{array}{*{20}{c}} {\rm{2}}& {\rm{1}}\\ {\rm{1}}& {\rm{2}} \end{array}} \right) + {f\!_d}\left( {\begin{array}{*{20}{c}} {{{\left| \alpha \right|}^2}}& \alpha \\ { - {\alpha ^*}}& 1 \end{array}} \right) + {f\!_s}\left( {\begin{array}{*{20}{c}} {{{\left| \beta \right|}^2}}& \beta \\ { - {\beta ^*}}& 1 \end{array}} \right) \quad \quad \quad \quad \quad \ $ | (43) |
| ${\rm{CTLR \ mode}} \quad \quad {{\bf{{C}}}_2} = \frac{{{f\!_v}}}{4}\left( {\begin{array}{*{20}{c}} {\rm{1}}& {\rm{0}}\\ {\rm{0}}& {\rm{1}} \end{array}} \right) + {f\!_d}\left( {\begin{array}{*{20}{c}} {{{\left| \alpha \right|}^2}}& {{\rm j}\alpha }\\ { - {\rm j}{\alpha ^*}}& 1 \end{array}} \right) + {f\!_s}\left( {\begin{array}{*{20}{c}} {{{\left| \beta \right|}^2}}& {{\rm j}\beta }\\ { - {\rm j}{\beta ^*}}& 1 \end{array}} \right) \quad \quad \quad \quad $ | (44) |
For both modes, there are up to 5 unknowns (or 10 real unknowns) in
One of the most important applications in radar polarimetry is arguably terrain and land-use classification and surveillance. The advantage of wide swath coverage of CP will surely enhance this ability of spaceborne PolSAR systems and provide time series or stacks of coherent radar images in a shorter time interval. But as the polarimetric information received through CP are naturally incomplete, our research goal of CP data processing is to strive for quantitative backscatter classification of the same finesse as those derived from quad-pol SAR systems.
6.1.1 Stokes vector based classification algorithmsUtilizing the m and d parameter shown in previous section, Charbonneau et al. first demonstrated a decomposition strategy of double-bounce, volumetric and surface scattering based on the decomposition of total power (g0) with trigonometric functions[12]. The derived powers of each scattering category are:
| $\left[{\begin{array}{*{20}{c}} {{P_D}}\\ {{P_V}}\\ {{P_S}} \end{array}} \right]{\rm{ = }}\left[{\begin{array}{*{20}{c}} {\frac{1}{2}{g_0}m\left( {1 \pm \sin \delta } \right)}\\ {{g_0}\left( {1 - m} \right)}\\ {\frac{1}{2}{g_0}m\left( {1 \mp \sin \delta } \right)} \end{array}} \right]$ | (45) |
Similarly, the powers of each scattering category derived from m-c or m-as parameters based decomposition algorithms are:
| $\left[{\begin{array}{*{20}{c}} {{P_D}}\\ {{P_V}}\\ {{P_S}} \end{array}} \right]{\rm{ = }}\left[{\begin{array}{*{20}{c}} {\frac{1}{2}{g_0}m\left( {1 + \sin 2\chi } \right)}\\ {{g_0}\left( {1 - m} \right)}\\ {\frac{1}{2}{g_0}m\left( {1 - \sin 2\chi } \right)} \end{array}} \right] \\ \quad \quad \quad \!\!\quad = \left[{\begin{array}{*{20}{c}} {\frac{1}{2}{g_0}m\left( {1 + \sin 2{\alpha _s}} \right)}\\ {{g_0}\left( {1 - m} \right)}\\ {\frac{1}{2}{g_0}m\left( {1 - \sin 2{\alpha _s}} \right)} \end{array}} \right]$ | (46) |
A demonstration of the classification results derived from these algorithms is given in Fig. 8. The utilized dataset is the well-known four-look NASA/JPL AIRSAR L-band dataset over San Francisco. Corresponding CTLR mode data with LHC transmission is transformed through PolSAR Pro 5.0 software developed by the European Space Agency (ESA). Since the dataset is already four-look, the spatial averaging process is implemented with a 5×5 boxcar filter. As we can see, the two classification map are almost identical, and the volume category is obvious overestimated in either classification map. According to Cloude et al.[83], this might be a common feature of CP, due to higher scattering entropy (than quad-pol SAR) in forest environments.

|
Fig.8 Classification maps with different decomposition algorithms |
Another unsupervised classification strategy is to utilize the CP information derived from the aforementioned eigenvalue decomposition, or the compact H/alpha decomposition. The optimum boundaries between the PSMs are suggested as[40]:
The boundary between low-entropy zones and medium-entropy zones is set as H=0.65, and the boundary between medium-entropy zones and high-entropy zones is set as H=0.96.
In low-entropy zones, the boundary between multiple and dipole scattering types is a=42°, and the boundary between dipole and surface scattering types is a=48°.
In medium-entropy zones, the boundary between multiple and vegetation scattering types is about a=40°, and the boundary between vegetation and surface scattering types is a=51°.
In high-entropy zones, nearly all the PSMs are vegetation scattering. The boundary between multiple and vegetation scattering types is a=34.5°, and the boundary between vegetation and surface scattering types is a=51°.
The classification results of the same dataset used in previous subsection is demonstrated in Fig. 9.

|
Fig.9 Compact H/alpha classification results |
Due to the indispensable spatial averaging process, the classification results presented in previous two subsections can hardly guarantee the details and texture features of the image. In order to improve those classification results, statistical property of the CTLR mode data could be further utilized. One main statistical property of such data is that its scattering vectors do obey the multivariate complex Gaussian distribution, just like the scattering vectors of quad-pol SAR data[39]. Therefore, we could also implement the famous Wishart classifier on the CTLR mode data.
In Refs. [33, 39] and Ref. [38], the Wishart classifier is combined with the compact H/alpha decomposition algorithm and the Stokes parameter based decomposition algorithms. In Fig. 10, we have presented the classification results of the former scheme with the H/alpha plane boundaries suggested by Zhang et al.[40]. We can see that the details and texture features of the image are surely well preserved.

|
Fig.10 The classification maps of the compact H/alpha/Wishart algorithm with the same color labels as in Fig. 9(a) |
As for the latter classification scheme, we have added two steps of refining process, i.e. excluding pixels with no clear defined PSMs and cluster merging process utilizing span (the total power), to ensure the reliability of the initial Wishart classes[38]. The classification results are shown in Fig. 11.

|
Fig.11 Classification results of the m/chi/Wishart algorithm |
Compact PolInSAR is also one of the research hotspot within CP technologies. Compact PolInSAR system can measure two target scattering vectors of each resolution element in the scene from two slightly different look angle in a single-pass or repeated-pass interferometric configuration. The compact polarimetric scattering vectors measured at ends 1 and 2 of the baseline, can be expressed as
| ${{\bf{{J}}}_4} = \left[{\begin{array}{*{20}{c}} {{{\bf{{J}}}_{11}}}& {{{\bf{{J}}}_{12}}}\\ {{\bf{{J}}}_{12}^{*T}}& {{{\bf{{J}}}_{22}}} \end{array}} \right]$ | (47) |
There are two main directions to process compact PolInSAR data. One is to reconstruct the quad PolInSAR data from the compact PolInSAR[24, 25], similar to the covariance matrix expansion method introduced in Subsection 5.3.1. Another important and more typical one is to process compact PolSAR dataset directly. Once pseudo-quad-pol data is reconstructed, conventional PolInSAR methodologies can be applied. Therefore, we will only review the two typical compact PolInSAR applications stemmed from the latter research direction in this subsection.
6.2.1 Forest height estimationOne typical application of compact PolInSAR technique is the estimation of forest heights. All methods of forest heights inversion are based on the RVoG model, which is modeled as the combination of a ground contribution and a volume only contribution. The inversion consists of fitting a line through the coherences, computing the topographical phase which is the intersection of fitting line with the unit circular and computing the volume only coherence which provides the vegetation height. The key step is therefore to fit line and find the correct volume only coherence. No matter which methods, their theory basis all are the complex coherence of compact PolInSAR data, which can be expressed as
| $\gamma \; ({\omega _1}, {\omega _2}) = \frac{{\omega _1^{\rm{H}}{{\bf{{J}}}_{12}}{\omega _2}}}{{\sqrt {\omega _1^{\rm{H}}{{\bf{{J}}}_{11}}{\omega _1}\omega _2^{\rm{H}}{{\bf{{J}}}_{22}}{\omega _2}} }}$ | (48) |
In Refs. [21, 22], the compact polarimetric coherence locus associated with all the polarization states of the receiving antenna (a two-parameter space) were computed. Based on the coherence locus, a straight line was fitted, and then the three-stage inversion method was applied to estimate the tree heights. Detailed steps are listed as following:
(1) Synthesize many interferometric coherence values by varying the polarization of the receive antennas (varying w1, w2 of Eq. (48)) and identify the fitting line.
(2) Identify the two intersection points between the fitting line and the circle. Choose between the two the one that is associated with the topographical phase
(3) Select the interferometric coherence that is furthest from the ground coherence as
(4) Apply the Look-Up Table (LUT) technique to find the tree height and the attenuation.
The tree heights inversion procedure in Ref. [26] is different from those in Refs. [21, 22]. In Ref. [26], the compact polarimetric coherence locus was not computed, instead, only several coherences were computed to fit the straight line. The coherence used to fit the straight line included two receiving channel coherences, unconstrained optimal coherences and maximum phase separation coherences. The maximum phase separation coherences were used to estimate the topographical phase and initial volume decorrelation. Then volume decorrelation estimation was updated with coherence boundary extraction method. After obtaining the ground phase and the accurate volume only coherence, LUT technique was used to find the tree heights and the attenuations.
6.2.2 Compact PolInSAR target decompositionIn Refs. [28, 30] a target decomposition method utilizing compact PolInSAR data is proposed. The Freeman-Durden decomposition technique was applied to the compact PolInSAR data[25]. The complex cross-correlation matrix of compact PolInSAR was decomposed into three 2×2 scattering matrices corresponding to the surface, double-bounce, and volume scattering.
| $\pi {\rm{/4 \ mode}} \quad \quad \quad {{\bf{{J}}}_2} = \frac{{{f\!_{cv}}}}{8}\left[{\begin{array}{*{20}{c}} {\rm{2}}& {\rm{1}}\\ {\rm{1}}& {\rm{2}} \end{array}} \right] + {f\!_{cd}}\left[{\begin{array}{*{20}{c}} {{{\left| \alpha \right|}^2}}& \alpha \\ { - {\alpha ^*}}& 1 \end{array}} \right] + {f\!_{cs}}\left[{\begin{array}{*{20}{c}} {{{\left| \beta \right|}^2}}& \beta \\ { - {\beta ^*}}& 1 \end{array}} \right] \quad \quad \quad \quad \quad \ $ | (49) |
| ${\rm{CTLR \ mode}} \quad \quad {{\bf{{J}}}_2} = \frac{{{f\!_{cv}}}}{4}\left[{\begin{array}{*{20}{c}} {\rm{1}}& {\rm{0}}\\ {\rm{0}}& {\rm{1}} \end{array}} \right] + {f\!_{cd}}\left[{\begin{array}{*{20}{c}} {{{\left| \alpha \right|}^2}}& {{\rm j}\alpha }\\ { - {\rm j}{\alpha ^*}}& 1 \end{array}} \right] + {f\!_{cs}}\left[{\begin{array}{*{20}{c}} {{{\left| \beta \right|}^2}}& {{\rm j}\beta }\\ { - {\rm j}{\beta ^*}}& 1 \end{array}} \right] \quad \quad \quad \quad $ | (50) |
The algorithm was validated with simulated data derived from PolSARProSim program. One simulated L-band PolInSAR forest dataset was generated corresponding to 10 m forest heights. Fig. 12(a) is the Pauli image of the simulated scenario: here we analyzed an image transect indicated by the red line. We transformed the simulated quad-pol data to compact- pol data, and then constructed the compact-pol cross-correlation observable matrix J2. Decomposing results are shown in Fig. 12(c). The phrase ODD, DBL, and VOL stands for odd-bounce scattering, double-bounce scaffering, and volume scaffering, respectively, and VC and HC stands for circular polarization in transmission and receiving in linear (vertical or horizontal) polarization. According to the compact PolInSAR target decomposition, the amplitude and phase of each scattering mechanism were obtained. In addition, the decomposition results quite agreed with fully PolInSAR decomposition[95], which demonstrated that the compact PolInSAR also has the potential for target decomposition.

|
Fig.12 Simulated dataset Pauli decomposition image |
Beside the two main applications introduced in previous subsections, other wide-swath-bene-fitted applications, such as soil moisture estimation[17, 18, 19, 20], iceberg[43, 44, 45], oil-spill[46, 47, 48, 49, 50, 51, 52, 53] and ship detection[42, 45, 52, 53, 54, 55, crop classification[56, 57, 58, 59, 60, 61] and sea ice surveillance[12, 13, 14, 85, 86] have also been carefully investigated in the latest researches. According to their investigations, comparable data processing results could be obtained with CP data comparing with those derived from quad-pol SAR data.
7 ConclusionIn this paper, we have fully reviewed the principles and applications of the HP architecture based PolSAR. As we can see, the HP architecture is actually a PolSAR system design scheme, which firstly emphasis the synthesis of transmit polarizations with two separated signal channels. Thereby, any polarization can be generated theoretically, including the circular polarizations and the slant linear polarizations required in compact polarimetry. In other words, this feature makes an HP architecture based PolSAR system possible to operate under different CP modes, which can produce classification results superior than conventional linear dual-pol modes. Moreover, if the adopted transmit polarizations have equal H and V components, as is the case with all CP modes, the HP architecture based PolSAR system will have a unique self-calibration feature. Secondly, this design scheme also emphasis that the transmitted polarization should differ from the receiving polarization basis. Thus, the range ambiguity performance of the HP architecture based PolSAR system can be improved and the swath coverage of the HP architecture based PolSAR system can be further broadened, particularly at higher incident angles, when operating under quad-pol mode. Last but not least, this design scheme actually requires very few RF hardware, which implies a less costly and more robust PolSAR system. Besides, shorter repetition intervals, in which coherent radar images are obtained, can also be reached by HP architecture based PolSAR systems due to the advantage of wider swath coverage.
Meanwhile, this paper has also pointed out the implementation difficulties of the HP architecture, i.e. the transmit distortions cannot be calibrated when the HP architecture based PolSAR system works under the dual-pol mode. Besides, the polarization adopted for transmission is also always circular. Since PolSAR data acquired with other transmit polarization may also produce favorable results in certain applications, this configuration is also regarded as one problem. In order to overcome these problems, we have proposed an improved version of the HP architecture. With the improved HP architecture, a pre-distortion technique can be applied to correct the transmit distortions. Comparing with radar systems with extra internal calibration loops, the proposed improved version requires less RF hardware. Besides, instead of just transmitting circular polarizations, a PolSAR system based on the improved HP architecture can operate with arbitrary transmit polarization configurations. This feature implies that the improved HP architecture can also support the π/4 mode and other quad-pol modes with different orthogonal transmit polarization pairs. At last, we have illustrated a prototype system based on the improved HP architecture. Associated experimental verifications are still in progress.
| [1] |
Moreira A, Prats-Iraola P, Younis M, et al. A tutorial on synthetic aperture radar[J].
IEEE Geoscience and Remote Sensing Magazine , 2013, 1 (1) : 6-43 DOI:10.1109/MGRS.2013.2248301 ( 0) 0)
|
| [2] |
Ouchi K. Recent trend and advance of synthetic aperture radar with selected topics[J].
Remote Sensing , 2013, 5 (2) : 716-807 DOI:10.3390/RS5020716 ( 0) 0)
|
| [3] |
Curlander J C and McDonough R N.
Synthetic Aperture Radar: Systems and Signal Processing[M]. New York, NY, USA: John Wiley & Sons, Inc., 1991 : 303 -305.
( 0) 0)
|
| [4] |
Raney R K, Freeman A, and Jordan R L. Improved range ambiguity performance in quad-pol SAR[J].
IEEE Transactions on Geoscience and Remote Sensing , 2012, 50 (2) : 349-356 DOI:10.1109/TGRS.2011.2121075 ( 0) 0)
|
| [5] |
Freeman A. A new system model for radar polarimeters[J].
IEEE Transactions on Geoscience and Remote Sensing , 1991, 29 (5) : 761-767 DOI:10.1109/36.83991 ( 0) 0)
|
| [6] |
Touzi R, Livingstone C E, Lafontaine J R C, et al. Consideration of antenna gain and phase patterns for calibration of polarimetric SAR data[J].
IEEE Transactions on Geoscience and Remote Sensing , 1993, 31 (6) : 1132-1145 DOI:10.1109/36.317449 ( 0) 0)
|
| [7] |
Raney R K. Hybrid-polarity SAR architecture[J].
IEEE Transactions on Geoscience and Remote Sensing , 2007, 45 (11) : 3397-3404 DOI:10.1109/TGRS.2007.895883 ( 0) 0)
|
| [8] |
Raney R K. Hybrid-quad-pol SAR[C]. 2008 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Boston, USA, 2008, 4: IV-491-IV-493. doi: 10.1109/ IGARSS.2008.4779765.
( 0) 0)
|
| [9] |
Souyris J C, Imbo P, Fjørtoft R, et al. Compact polarimetry based on symmetry properties of geophysical media: The p/4 mode[J].
IEEE Transactions on Geoscience and Remote Sensing , 2005, 43 (3) : 634-646 DOI:10.1109/TGRS.2004.842486 ( 0) 0)
|
| [10] |
Stacy N and Preiss M. Compact polarimetric analysis of X-band SAR data[C]. 6th European Conference on Synthetic Aperture Radar (EUSAR), Dresden, Germany, 2006.
( 0) 0)
|
| [11] |
Nord M E, Ainsworth T L, Lee J S, et al. Comparison of compact polarimetric synthetic aperture radar modes[J].
IEEE Transactions on Geoscience and Remote Sensing , 2009, 47 (1) : 174-188 DOI:10.1109/TGRS.2008.2000925 ( 0) 0)
|
| [12] |
Charbonneau F J, Brisco B, Raney R K, et al. Compact polarimetry overview and applications assessment[J].
Canadian Journal of Remote Sensing , 2010, 36 (Suppl. 2) : S298-S315 DOI:10.5589/M10-062 ( 0) 0)
|
| [13] |
Dabboor M and Geldsetzer T. Towards sea ice classification using simulated RADARSAT Constellation Mission compact polarimetric SAR imagery[J].
Remote Sensing of Environment , 2014, 140 : 189-195 DOI:10.1016/J.RSE.2013.08.035 ( 0) 0)
|
| [14] |
Geldsetzer T, Arkett M, Zagon T, et al. All-season compact-polarimetry C-band SAR observations of sea ice[J].
Canadian Journal of Remote Sensing , 2015, 41 (5) : 485-504 DOI:10.1080/07038992.2015.1120661 ( 0) 0)
|
| [15] |
Geldsetzer T, Charbonneau F, Arkett M, et al. Ocean wind study using simulated RCM compact-polarimetry SAR[J].
Canadian Journal of Remote Sensing , 2015, 41 (5) : 418-430 DOI:10.1080/07038992.2015.1104635 ( 0) 0)
|
| [16] |
Denbina M and Collins M J. Wind speed estimation using C-band compact polarimetric SAR for wide swath imaging modes[J].
ISPRS Journal of Photogrammetry and Remote Sensing , 2016, 113 : 75-85 DOI:10.1016/J.ISPRSJPRS.2016.01.002 ( 0) 0)
|
| [17] |
Williams M L. Potential for surface parameter estimation using compact polarimetric SAR[J].
IEEE Geoscience and Remote Sensing Letters , 2008, 5 (3) : 471-473 DOI:10.1109/LGRS.2008.918012 ( 0) 0)
|
| [18] |
Truong-Loï M L, Freeman A, Dubois-Fernandez P C, et al. Estimation of soil moisture and Faraday rotation from bare surfaces using compact polarimetry[J].
IEEE Transactions on Geoscience and Remote Sensing , 2009, 47 (11) : 3608-3615 DOI:10.1109/TGRS.2009.2031428 ( 0) 0)
|
| [19] |
Ouellette J D, Johnson J T, Kim S, et al. A simulation study of compact polarimetry for radar retrieval of soil moisture[J].
IEEE Transactions on Geoscience and Remote Sensing , 2014, 52 (9) : 5966-5973 DOI:10.1109/TGRS.2013.2294133 ( 0) 0)
|
| [20] |
Ponnurangam G G, Jagdhuber T, Hajnsek I, et al. Soil moisture estimation using hybrid polarimetric SAR data of RISAT-1[J].
IEEE Transactions on Geoscience and Remote Sensing , 2016, 54 (4) : 2033-2049 DOI:10.1109/TGRS.2015.2494860 ( 0) 0)
|
| [21] |
Angelliaume S, Dubois-Fernandez P, and Souyris J C. Compact PolInSAR for vegetation characterisation[C]. 2007 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Barcelona, Spain, 2007: 1136-1138. doi: 10.1109/IGARSS.2007.4423003.
( 0) 0)
|
| [22] |
Dubois-Fernandez P C, Souyris J C, Angelliaume S, et al. The compact polarimetry alternative for spaceborne SAR at low frequency[J].
IEEE Transactions on Geoscience and Remote Sensing , 2008, 46 (10) : 3208-3222 DOI:10.1109/TGRS.2008.919143 ( 0) 0)
|
| [23] |
Wilsen C B, Sarabandi K, and Lin Y C. The effect of tree architecture on the polarimetric and interferometric radar responses[C]. 1998 IEEE Geoscience and Remote Sensing Symposium (IGARSS), Seattle, WA, USA, 1998, 3: 1499-1501. doi: 10.1109/IGARSS.1998.691536.
( 0) 0)
|
| [24] |
Lavalle M. Full and compact polarimetric radar interferometry for vegetation remote sensing[D]. [Ph.D. dissertation], Université Rennes 1, 2009: 95-128.
( 0) 0)
|
| [25] |
Lavalle M, Solimini D, Pottier E, et al. Compact polarimetric SAR interferometry[J].
IET Radar, Sonar & Navigation , 2010, 4 (3) : 449-456 DOI:10.1049/IET-RSN.2009.0049 ( 0) 0)
|
| [26] |
谈璐璐, 杨立波, 杨汝良. 合成孔径雷达简缩极化干涉数据的
植被高度反演技术研究[J].
电子与信息学报 , 2010, 32 (12) : 2814-2819 Tan L L, Yang L B, and Yang R L. Investigation on vegetation height retrieval technique with compact PolInSAR data[J].
Journal of Electronics & Information Technology , 2010, 32 (12) : 2814-2819 ( 0) 0)
|
| [27] |
Arnaubec A, Roueff A, Dubois-Fernandez P C, et al. Vegetation height estimation precision with compact PolInSAR and homogeneous random volume over ground model[J].
IEEE Transactions on Geoscience and Remote Sensing , 2014, 52 (3) : 1879-1891 DOI:10.1109/TGRS.2013.2256362 ( 0) 0)
|
| [28] |
Guo S, Li Y, Yin Q, et al.. Applying the Freeman-Durden decomposition to compact polarimetric SAR Interferometry[C]. 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, Canada, 2014: 3486-3489. doi: 10.1109/IGARSS.2014.6947233.
( 0) 0)
|
| [29] |
Guo S L, Li Y, and Hong W. Model-based target decomposition with p/4 mode compact polarimetry data[J].
Science China: Information Sciences , 2016, 59 (16) : 062307 DOI:10.1007/s11432-015-5478-4 ( 0) 0)
|
| [30] |
郭胜龙, 李洋, 尹嫱, 等. 基于简缩极化干涉SAR数据的森林垂直参数反演[J].
电子信息学报 , 2016, 38 (1) : 71-79 Guo S L, Li Y, Yin Q, et al. Vertical parameters estimation of forest with compact polarimetric SAR interferometry data[J].
Journal of Electronics & Information Technology , 2016, 38 (1) : 71-79 ( 0) 0)
|
| [31] |
郭胜龙, 李洋, 杨士林, 等. 基于模型的p/4模式简缩极化干涉数据目标分解[J].
电子信息学报 , 2015, 37 (1) : 22-28 Guo S L, Li Y, Yang S L, et al. Model-based target decomposition with p/4 mode compact polarimetric SAR interferometric data[J].
Journal of Electronics & Information Technology , 2015, 37 (1) : 22-28 ( 0) 0)
|
| [32] |
Ainsworth T L, Kelly J P, and Lee J S. Classification comparisons between dual-pol, compact polarimetric and quad-pol SAR imagery[J].
ISPRS Journal of Photogrammetry and Remote Sensing , 2009, 64 (5) : 464-471 DOI:10.1016/J.ISPRSJPRS.2008.12.008 ( 0) 0)
|
| [33] |
Chen L, Cao F, and Hong W. Unsupervised classification for compact polarimetric SAR data using m-d decomposition, SPAN and the Wishart classifier[C]. The 2nd Asian-Pacific Conference on Synthetic Aperture Radar (APSAR) 2009, Xian, China, 2009: 742-745. doi: 10.1109/APSAR. 2009. 5374214.
( 0) 0)
|
| [34] |
Chen L. Investigation on the models and methods of compact polarimetric SAR information processing[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2013: 45-60, 69-74, 75-98.
( 0) 0)
|
| [35] |
Cloude S R, Goodenough D G, and Chen H. Compact polarimetry for C-band land-use classification: a pre-study for the Canadian Radar Constellation Mission (RCM)[C]. SPIE Remote Sensing. International Society for Optics and Photonics, Edinburgh, United Kingdom, 2012: 853606- 853606-14. doi: 10.1117/12.973704.
( 0) 0)
|
| [36] |
Panigrahi R and Mishra A K. Unsupervised classification of scattering behaviour using hybrid-polarimetry[J].
IET Radar, Sonar & Navigation , 2013, 7 (3) : 270-276 DOI:10.1049/IET-RSN.2012.0207 ( 0) 0)
|
| [37] |
Turkar V, De S, Rao Y S, et al.. Comparative analysis of classification accuracy for RISAT-1 compact polarimetric data for various land-covers[C]. 2013 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, VIC, Australia, 2013: 3586-3589. doi: 10.1109/IGARSS.2013.6723605.
( 0) 0)
|
| [38] |
Chen S, Guo S, Li Y, et al. Unsupervised classification for hybrid polarimetric SAR data based on scattering mechanisms and Wishart classifier[J].
Electronics Letters , 2015, 51 (19) : 1530-1532 DOI:10.1049/EL.2015.1627 ( 0) 0)
|
| [39] |
Guo S, Tian Y, Li Y, et al.. Unsupervised classification based on H/alpha decomposition and Wishart classifier for compact polarimetric SAR[C]. 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 2015: 1614-1617. doi: 10.1109/IGARSS.2015. 7326093.
( 0) 0)
|
| [40] |
Zhang H, Xie L, Wang C, et al. Investigation of the capability of decomposition of compact polarimetric SAR[J].
IEEE Geoscience and Remote Sensing Letters , 2014, 11 (4) : 868-872 DOI:10.1109/LGRS.2013.2280456 ( 0) 0)
|
| [41] |
Aghabalaei A, Maghsoudi Y, and Ebadi H. Forest classification using extracted PolSAR features from compact polarimetry data[J].
Advances in Space Research , 2016, 57 (9) : 1939-1950 DOI:10.1016/J.ASR.2016.02.007 ( 0) 0)
|
| [42] |
Touzi R and Vachon P W. RCM polarimetric SAR for enhanced ship detection and classification[J].
Canadian Journal of Remote Sensing , 2015, 41 (5) : 473-484 DOI:10.1080/07038992.2015.1110010 ( 0) 0)
|
| [43] |
Denbina M and Collins M J. Iceberg detection using compact polarimetric synthetic aperture radar[J].
Atmosphere-Ocean , 2012, 50 (4) : 437-446 DOI:10.1080/07055900.2012.733307 ( 0) 0)
|
| [44] |
Denbina M and Collins M J. Iceberg detection using analysis of the received polarization ellipse in compact polarimetry[C]. 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, Canada, 2014: 266-269. doi: 10.1109/IGARSS.2014.6946408.
( 0) 0)
|
| [45] |
Denbina M, Collins M J, and Atteia G. On the detection and discrimination of ships and icebergs using simulated dual-polarized RADARSAT constellation data[J].
Canadian Journal of Remote Sensing , 2015, 41 (5) : 1-17 DOI:10.1080/07038992.2015.1104630 ( 0) 0)
|
| [46] |
Salberg A B, Rudjord O, and Solberg A H S. Oil spill detection in hybrid-polarimetric SAR images[J].
IEEE Transactions on Geoscience and Remote Sensing , 2014, 52 (10) : 6521-6533 DOI:10.1109/TGRS.2013.2297193 ( 0) 0)
|
| [47] |
Li Y, Zhang Y, Chen J, et al. Improved compact polarimetric SAR quad-pol reconstruction algorithm for oil spill detection[J].
IEEE Geoscience and Remote Sensing Letters , 2014, 11 (6) : 1139-1142 DOI:10.1109/LGRS.2013.2288336 ( 0) 0)
|
| [48] |
Yin J, Moon W, and Yang J. Model-based pseudo-quad-pol reconstruction from compact polarimetry and its application to oil-spill observation[J].
Journal of Sensors , 2015 DOI:10.1155/2015/734848 ( 0) 0)
|
| [49] |
Nunziata F, Migliaccio M, and Li X. Sea oil slick observation using hybrid-polarity SAR architecture[J].
IEEE Journal of Oceanic Engineering , 2015, 40 (2) : 426-440 DOI:10.1109/JOE.2014.2329424 ( 0) 0)
|
| [50] |
Li Y, Lin H, Zhang Y, et al. Comparisons of circular transmit and linear receive compact polarimetric SAR features for oil slicks discrimination[J].
Journal of Sensors , 2015 DOI:10.1155/2015/631561 ( 0) 0)
|
| [51] |
Li H, Perrie W, He Y, et al. Analysis of the polarimetric SAR scattering properties of oil-covered waters[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing , 2015, 8 (8) : 3751-3759 DOI:10.1109/JSTARS.2014.2348173 ( 0) 0)
|
| [52] |
Shirvany R, Chabert M, and Tourneret J Y. Ship and oil-spill detection using the degree of polarization in linear and hybrid/compact dual-pol SAR[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing , 2012, 5 (3) : 885-892 DOI:10.1109/JSTARS.2012.2182760 ( 0) 0)
|
| [53] |
Yin J, Yang J, Zhou Z S, et al. The extended bragg scattering model-based method for ship and oil-spill observation using compact polarimetric SAR[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing , 2015, 8 (8) : 3760-3772 DOI:10.1109/JSTARS.2014.2359141 ( 0) 0)
|
| [54] |
Atteia G E and Collins M J. On the use of compact polarimetry SAR for ship detection[J].
ISPRS Journal of Photogrammetry and Remote Sensing , 2013, 80 : 1-9 DOI:10.1016/J.ISPRSJPRS.2013.01.009 ( 0) 0)
|
| [55] |
Yin J and Yang J. Ship detection by using the M-Chi and M-Delta decompositions[C]. IEEE International Geoscience and Remote Sensing Symposium (IGARSS) 2014, Quebec City, Canada, 2014: 2738-2741. doi: 10.1109/IGARSS. 2014.6947042.
( 0) 0)
|
| [56] |
Ballester-Berman J D and Lopez-Sanchez J M. Time series of hybrid-polarity parameters over agricultural crops[J].
IEEE Geoscience and Remote Sensing Letters , 2012, 9 (1) : 139-143 DOI:10.1109/LGRS.2011.2162312 ( 0) 0)
|
| [57] |
Brisco B, Li K, Tedford B, et al. Compact polarimetry assessment for rice and wetland mapping[J].
International Journal of Remote Sensing , 2013, 34 (6) : 1949-1964 DOI:10.1080/01431161.2012.730156 ( 0) 0)
|
| [58] |
Lopez-Sanchez J M, Vicente-Guijalba F, Ballester-Berman J D, et al. Polarimetric response of rice fields at C-band: Analysis and phenology retrieval[J].
IEEE Transactions on Geoscience and Remote Sensing , 2014, 52 (5) : 2977-2993 DOI:10.1109/TGRS.2013.2268319 ( 0) 0)
|
| [59] |
Yang Z, Li K, Liu L, et al. Rice growth monitoring using simulated compact polarimetric C band SAR[J].
Radio Science , 2014, 49 (12) : 1300-1315 DOI:10.1002/2014RS005498 ( 0) 0)
|
| [60] |
Uppala D, Kothapalli R V, Poloju S, et al. Rice crop discrimination using single date RISAT1 hybrid (RH, RV) polarimetric data[J].
Photogrammetric Engineering & Remote Sensing , 2015, 81 (7) : 557-563 DOI:10.14358/PERS.81.7.557 ( 0) 0)
|
| [61] |
Xie L, Zhang H, Wu F, et al. Capability of rice mapping using hybrid polarimetric SAR data[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing , 2015, 8 (8) : 3812-3822 DOI:10.1109/JSTARS.2014.2387214 ( 0) 0)
|
| [62] |
Raney K, Spudis P D, Bussey B, et al. The lunar mini-RF radars: Hybrid polarimetric architecture and initial results[J].
Proceedings of the IEEE , 2011, 99 (5) : 808-823 DOI:10.1109/JPROC.2010.2084970 ( 0) 0)
|
| [63] |
Misra T and Kirankumar A S. RISAT-1: Configuration and performance evaluation[C]. 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 2014: 1-4. doi: 10.1109/URSIGASS.2014.6929612.
( 0) 0)
|
| [64] |
Kankaku Y, Osawa Y, Suzuki S, et al.. The overview of the L-band SAR onboard ALOS-2[C]. 2009 Proceedings of Progress in Electromagnetics Research Symposium (PIERS), Moscow, Russia, 2009: 735-738.
( 0) 0)
|
| [65] |
Touzi R and Charbonneau F. Requirements on the calibration of hybrid-compact SAR[C]. 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, Canada, 2014: 1109-1112. doi: 10.1109/IGARSS.2014.6946623.
( 0) 0)
|
| [66] |
Thompson A A. Overview of the RADARSAT constellation mission[J].
Canadian Journal of Remote Sensing , 2015, 41 (5) : 401-407 DOI:10.1080/07038992.2015.1104633 ( 0) 0)
|
| [67] |
Raney R K. DESDynI adopts hybrid polarity SAR architecture[C]. 2009 IEEE Radar Conference, Pasadena, USA, 2009: 1-4. doi: 10.1109/RADAR.2009.4977046.
( 0) 0)
|
| [68] |
Donnellan A, Rosen P, Graf J, et al.. Deformation, ecosystem structure, and dynamics of ice (DESDynI)[C]. 2008 IEEE Aerospace Conference, Big Sky, MT, USA, 2008: 1-13. doi: 10.1109/AERO.2008.4526249.
( 0) 0)
|
| [69] |
Putrevu D, Das A, Vachhani J G, et al. Chandrayaan-2 dual-frequency SAR: Further investigation into lunar water and regolith[J].
Advances in Space Research , 2016, 57 (2) : 627-646 DOI:10.1016/J.ASR.2015.10.029 ( 0) 0)
|
| [70] |
Freeman A, Dubois-Fernandez P, and Truong-Lo M L. Compact polarimetry at longer wavelengths-calibration[C]. 7th European Conference on Synthetic Aperture Radar (EUSAR), Friedrichshafen, Germany, 2008: 1-4.
( 0) 0)
|
| [71] |
Guo S, Zhang J, Li Y, et al. Effects of polarization distortion at transmission and faraday rotation on compact polarimetric SAR system and decomposition[J].
IEEE Geoscience and Remote Sensing Letters , 2015, 12 (8) : 1700-1704 DOI:10.1109/LGRS.2015.2420116 ( 0) 0)
|
| [72] |
Tan H and Hong J. Correction of transmit crosstalk in reconstruction of quad-pol data from compact polarimetry data[J].
IEEE Geoscience and Remote Sensing Letters , 2015, 12 (5) : 1051-1055 DOI:10.1109/LGRS.2014.2377491 ( 0) 0)
|
| [73] |
Freeman A. Calibration of linearly polarized polarimetric SAR data subject to Faraday rotation[J].
IEEE Transactions on Geoscience and Remote Sensing , 2004, 42 (8) : 1617-1624 DOI:10.1109/TGRS.2004.830161 ( 0) 0)
|
| [74] |
Raney R K. Comments on hybrid-polarity SAR architecture[C]. 2007 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Barcelona, Spain, 2007: 2229-2231. doi: 10.1109/IGARSS.2007.4423282.
( 0) 0)
|
| [75] |
McKerracher J R, Sequeira H B, Raney R K, et al.. Mini-RF calibration, a unique approach to on-orbit synthetic aperture radar system calibration[C]. The 41st Lunar and Planetary Science Conference, Woodlands, TX, USA, 2010: 2352-2353.
( 0) 0)
|
| [76] |
Wright P A, Quegan S, Wheadon N S, et al. Faraday rotation effects on L-band spaceborne SAR data[J].
IEEE Transactions on Geoscience and Remote Sensing , 2003, 41 (12) : 2735-2744 DOI:10.1109/TGRS.2003.815399 ( 0) 0)
|
| [77] |
Truong-Lo M L, Dubois-Fernandez P, Pottier E, et al.. Potentials of a compact polarimetric SAR system[C]. 2010 IEEE Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 2010: 742-745. doi: 10.1109/IGARSS.2010.5649036.
( 0) 0)
|
| [78] |
Chen J and Quegan S. Calibration of spaceborne CTLR compact polarimetric low-frequency SAR using mixed radar calibrators[J].
IEEE Transactions on Geoscience and Remote Sensing , 2011, 49 (7) : 2712-2723 DOI:10.1109/TGRS.2011.2109065 ( 0) 0)
|
| [79] |
Chen L, Zhang J J, Li Y, et al. General calibration algorithm for single-transmitting-dual-receiving polarimetric SAR system[J].
Journal of Radars , 2012, 1 (3) : 323-328 DOI:10.3724/SP.J.1300.2012.20062 ( 0) 0)
|
| [80] |
Wang Y, Ainsworth T L, and Lee J S. Assessment of system polarization quality for polarimetric SAR imagery and target decomposition[J].
IEEE Transactions on Geoscience and Remote Sensing , 2011, 49 (5) : 1755-1771 DOI:10.1109/TGRS.2010.2087342 ( 0) 0)
|
| [81] |
Lee J S and Pottier E.
Polarimetric Radar Imaging: From Basics to Applications[M]. 2009 : 27 -28.
( 0) 0)
|
| [82] |
Sabry R and Vachon P W. A unified framework for general compact and quad polarimetric SAR data and imagery analysis[J].
IEEE Transactions on Geoscience and Remote Sensing , 2014, 52 (1) : 582-602 DOI:10.1109/TGRS.2013.2242479 ( 0) 0)
|
| [83] |
Cloude S R, Goodenough D G, and Chen H. Compact decomposition theory[J].
IEEE Geoscience and Remote Sensing Letters , 2012, 9 (1) : 28-32 DOI:10.1109/LGRS.2011.2158983 ( 0) 0)
|
| [84] |
PolSAR Pro 5.0 Software, European Space Agency. [OL].https://earth.esa.int/web/polsarpro/home, 2016.10.13.
( 0) 0)
|
| [85] |
Eltoft T, Doulgeris A P, and Grahn J. Model-based polarimetric decomposition of Arctic sea ice[C]. 10th European Conference on Synthetic Aperture Radar (EUSAR), Berlin, Germany, 2014.
( 0) 0)
|
| [86] |
Espeseth M M, Brekke C, and Anfinsen S N. Hybrid-polarity and reconstruction methods for sea ice with L-and C-Band SAR[J].
IEEE Geoscience and Remote Sensing Letters , 2016, 13 (3) : 467-471 DOI:10.1109/LGRS.2016.2519824 ( 0) 0)
|
| [87] |
Espeseth M M. Synthetic aperture radar compact polarimetry for sea ice surveillance[D]. [Master dissertation], The Arctic University of Norway, 2015: 85-124.
( 0) 0)
|
| [88] |
Raney R K. Dual-polarized SAR and stokes parameters[J].
IEEE Geoscience and Remote Sensing Letters , 2006, 3 (3) : 317-319 DOI:10.1109/LGRS.2006.971746 ( 0) 0)
|
| [89] |
Raney R K, Cahill J T S, Patterson G, et al.. The m-chi decomposition of hybrid dual-polarimetric radar data[C]. 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 2012: 5093-5096. doi: 10.1109/IGARSS.2012.6352465.
( 0) 0)
|
| [90] |
Raney R K, Cahill J T S, Patterson G, et al. The m-chi decomposition of hybrid dual-polarimetric radar data with application to lunar craters[J].
Journal of Geophysical Research: Planets , 2012, 117 (E12) DOI:10.1029/2011JE003986 ( 0) 0)
|
| [91] |
Guo R, Liu Y B, Wu Y H, et al. Applying H/a decomposition to compact polarimetric SAR[J].
IET Radar, Sonar & Navigation , 2012, 6 (2) : 61-70 DOI:10.1049/IET-RSN.2011.0007 ( 0) 0)
|
| [92] |
Freeman A and Durden S L. A three-component scattering model for polarimetric SAR data[J].
IEEE Transactions on Geoscience and Remote Sensing , 1998, 36 (3) : 963-973 DOI:10.1109/36.673687 ( 0) 0)
|
| [93] |
Liu M, Zhang H, and Wang C. Three-component scattering model for compact polarimetric SAR data[J].
Chinese Journal of Radio Science , 2012, 27 (2) : 365-371 ( 0) 0)
|
| [94] |
Guo R, He W, Zhang S, et al. Analysis of three-component decomposition to compact polarimetric synthetic aperture radar[J].
IET Radar, Sonar & Navigation , 2014, 8 (6) : 685-691 DOI:10.1049/IET-RSN.2013.0114 ( 0) 0)
|
| [95] |
Ballester-Berman J D and Lopez-Sanchez J M. Applying the Freeman-Durden decomposition concept to polarimetric SAR interferometry[J].
IEEE Transactions on Geoscience and Remote Sensing , 2010, 48 (1) : 466-479 DOI:10.1109/TGRS.2009.2024304 ( 0) 0)
|




