② (国防科学技术大学电子信息系统复杂电磁环境效应国家重点实验室 长沙 410073))
② (State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System, National University of Defense Technology, Changsha 410073, China)
电磁波的极化现象以及雷达目标的变极化效应早在20 世纪50 年代就已经受到学术界的广泛关注。在随后的几十年中,雷达极化问题的研究引起了美、俄、英、法、意、日等发达国家浓厚的研究兴趣,积累了一大批基础性研究成果并逐渐迈入实用阶段。极化特性是雷达目标电磁散射的基本属性之一,日益受到学术界和工业部门的广泛关注[1, 2]。单基地雷达目标极化特性研究已经取得很大进展[3],通过电磁计算和暗室测量数据研究目标极化特性是一个重要手段[4, 5],需要注意的是极化坐标系与实际雷达测量之间的差异[6, 7]。
双/多基地雷达是近年来的研究热点,特别是无源双基地雷达和双基地SAR研究如火如荼,但是对目标的双基地散射特性研究不够,特别是极化特性。Cécile Titin-Schnaider长期从事双基地极化基础理论研究[8, 9, 10, 11],最开始研究了全极化双基地雷达观测条件下的最优极化问题(接收功率最大或最小),采用二阶矩Kennaugh矩阵描述随机结构,得到无约束条件下的矢量最优化问题。他将Huynen理论扩展到双基地模式下,得到的散射矩阵通常不再对称,他还从双基地Kennaugh矩阵提取了一组特征参数,研究了这些参数的幅度分布特性。类似于单基地雷达,他进一步研究了这些参数的物理意义,并通过电磁计算数据得到了验证,但是其研究对象相对简单,仅为对称的圆柱体。复杂目标、地海杂波的双基地极化散射特性研究与测量还需进一步深入开展。
基于第三方照射源的无源雷达是一种典型的双基地雷达。近20年来,利用广播电视、通讯基站、导航和通信卫星、无线局域网络等信号的无源雷达受到研究者广泛关注并成为新型探测技术的研究重点,国内外己成功研制了多种试验系统,获得了大量实测数据,无源相关定位雷达的基础理论与关键技术取得了突破性进展[12]。无源雷达采用不同极化接收天线能够获得不一样的探测性能[13, 14, 15],对直达波的抑制具有改善作用,不同的极化组合效果不一样,实际应用中需通过测试来选择,但是目标的双基地极化散射特性还不明确,存在随机性,需要针对特定目标进行研究,研究其空间分布特性、统计特性、极化特性等,从而指导目标检测门限设计。
为此,本文以无源双基地雷达常规试验中观测的飞机目标为研究对象,通过电磁计算的方法研究该目标在数字电视广播这一频段的双基地全极化散射特性,可为全极化双基地雷达飞机目标探测试验的开展(接收天线极化选择、检测门限设计等)提供参考。
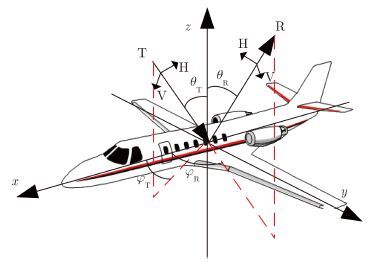
2 双基地散射计算模型目标电磁散射计算坐标系约定如图 1所示,以目标质心为坐标原点,x轴指向机头,y轴指向左侧机翼,z轴与x,y轴构成右手直角坐标系。入射矢量与z轴夹角定义为俯仰角,取值范围0°~180°,入射矢量在xoy平面内顺时针方向转到x轴的角度为方位角,取值范围0°~360°,散射矢量与z轴夹角定义为俯仰角,取值范围0°~180°,散射矢量在xoy平面内顺时针方向转到x轴的角度为方位角,取值范围0°~360°。由于飞机目标为轴对称目标,因此计算时取入射俯仰角(0°~180°)、入射方位角(0°~180°),接收俯仰角(0°~180°)、接收方位角(0°~360°),得到水平和垂直极化入射条件下的水平极化和垂直极化散射电场分量,即全极化散射矩阵,包含了后向散射和非后向散射。极化坐标系的定义如下:入射矢量Ei与H极化、V极化构成直角坐标系,H极化位于入射矢量与目标轴z轴构成的平面内;散射矢量Es与接收H极化、V极化构成直角坐标系,且H极化位于散射矢量与目标轴z轴构成的平面内。论文选择的计算频率为682 MHz,该频率为数字电视地面广播(Digital Television Terrestrial Broadcasting,DTTB)信号的中心频率,目标为全尺寸波音737机型,材料为金属,采用的电磁计算软件为成熟的商用软件CST,采用方法为快速多层多极子算法,计算数据的统计结果可以指导基于DTTB信号的双极化无源雷达空中目标探测试验,也可以为该P波段内的其它双基地雷达提供参考。
|
图 1 目标坐标系示意图 Fig.1 Geometry ordinates of target |
电波入射方向矢量为:
| ${{E}_{\rm{i}}} = \big( {\sin {\theta _{\rm{T}}}\cos {\varphi _{\rm{T}}},\sin {\theta _{\rm{T}}}\sin {\varphi _{\rm{T}}},\cos {\theta _{\rm{T}}}} \big)$ | (1) |
电波散射方向矢量为:
| ${{E}_{\rm{s}}} = \big( {\sin {\theta _{\rm{R}}}\cos {\varphi _{\rm{R}}},\sin {\theta _{\rm{R}}}\sin {\varphi _{\rm{R}}},\cos {\theta _{\rm{R}}}} \big)$ | (2) |
双基地角β满足:
| $\begin{aligned} \cos \beta = &\sin {\theta _{\rm{T}}}\cos {\varphi _{\rm{T}}}\sin {\theta _{\rm{R}}}\cos {\varphi _{\rm{R}}} + \sin {\theta _{\rm{T}}}\\ &\cdot \sin {\varphi _{\rm{T}}}\sin {\theta _{\rm{R}}}\sin {\varphi _{\rm{R}}} + \cos {\theta _{\rm{T}}}\cos {\theta _{\rm{R}}} \end{aligned}$ | (3) |
雷达目标在远场区的电磁散射是一个线性过程,入射波和目标散射波的各极化分量之间存在线性关系,并可由极化散射矩阵来描述,电磁波的Jones电场矢量是最为常用的极化描述子之一,设入射电磁波为${{E}_{\rm{T}}} = {\left( {{E_{{\rm{TH}}}},{E_{{\rm{TV}}}}} \right)^{\rm{T}}}$,散射电磁波为${{E}_{\rm{R}}} = {\left( {{{E}_{{\rm{RH}}}},{E_{{\rm{RV}}}}} \right)^{\rm{T}}}$,目标散射矩阵为${S} = $ $\left[{\begin{array}{*{20}{c}} {{S_{{\rm{HH}}}}}&{{S_{{\rm{HV}}}}}\\ {{S_{{\rm{VH}}}}}&{{S_{{\rm{VV}}}}} \end{array}} \right]$,则满足:
| ${{E}_{\rm{R}}} = {S} {\cdot} {{E}_{\rm{T}}}$ | (4) |
对于后向散射而言,通常情况下散射矩阵是对称的,但是对于非后向散射而言,散射矩阵通常不对称。${S_{{\rm{HV}}}}$物理意义上对应着以水平极化波照射目标时散射波的垂直极化分量,类似地可以解释其余3个元素的物理含义。且各个元素均与频率、当前入射角和散射角有关,因此可表示为${S_{ij}}\left( {f,{\theta _{\rm{T}}},{\varphi _{\rm{T}}},{\theta _{\rm{R}}},{\varphi _{\rm{R}}}} \right)$,则目标在确定频率、姿态、双基地几何配置的情况下,雷达散射截面积(RCS)和极化散射矩阵中的元素具有如下关系:
| $\begin{aligned} {\sigma _{ij}}\left( {f,{\theta _{\rm{T}}},{\varphi _{\rm{T}}},{\theta _{\rm{R}}},{\varphi _{\rm{R}}}} \right) = 4\pi &{\left| {{S_{ij}}\left( {f,{\theta _{\rm{T}}},{\varphi _{\rm{T}}},{\theta _{\rm{R}}},{\varphi _{\rm{R}}}} \right)} \right|^2},\\ &i,j = {\rm{H}},{\rm{V}} \end{aligned}$ | (5) |
|
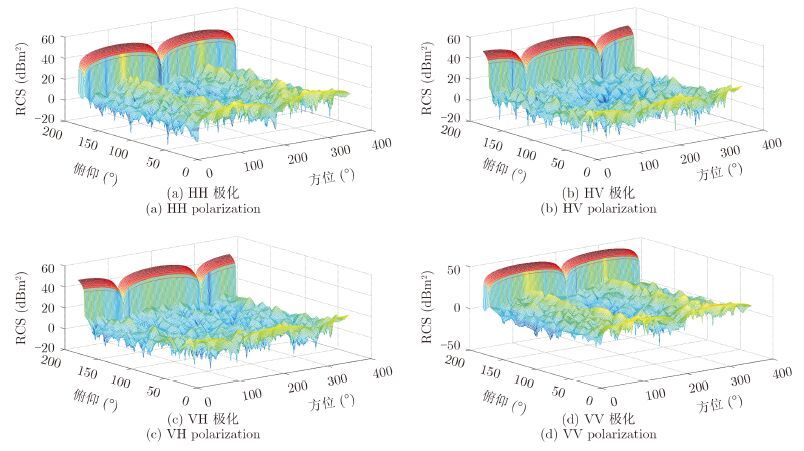
图 2 电磁计算数据结果 Fig.2 Electromagnetic computing results |
图中数据计算频率为682 MHz,从图中我们可以看到,随着接收方向的改变双基地RCS起伏较大;由于飞机的对称特性,4种极化RCS空间分布也对称;交叉极化RCS的空间分布相同,共极化的空间分布相同,均是俯仰角接近180°达到最大值,即前向散射,角度范围约为20°。
3 双基地散射特性分析 3.1 RCS起伏特性采用一些统计参数有助于直观描述雷达目标RCS 的统计特性。常用的统计参数包括均值、标准差、极大值、极小值和极差以及偏度系数、峰度系数等。区段均值是对给定频率范围和角扇形范围内的原始数据进行数学平均,设频率范围和角扇形范围内的数据长度为N,则区段均值定义为:
| $\bar \sigma = \frac{1}{N}\sum\limits_{n = 1}^N {{\sigma _n}} $ | (6) |
每一区段的标准差定义为:
| ${S_{{\rm{td}}}} = \sqrt {\frac{{\sum\limits_{n = 1}^N {{{\left( {{\sigma _n} - \bar \sigma } \right)}^2}} }}{{N - 1}}} $ | (7) |
而极大值σmax、极小值σmin和极差σL的定义分别为:
| ${\sigma _{\max }} = \max \left\{ {{\sigma _i}} \right\},\;i = 1,2,\cdots,N$ | (8) |
| ${\sigma _{\min }} = \min \left\{ {{\sigma _i}} \right\},\;i = 1,2,\cdots,N \ $ | (9) |
| ${\sigma _{\rm{L}}} = {\sigma _{\max }} - {\sigma _{\min }}$ | (10) |
偏度系数和峰度系数描述了RCS序列总体密度函数的图形特征,侧重表示了RCS序列密度函数的偏斜程度及相对参照分布的平坦程度。对长度为N、均值和标准差分别为$\bar \sigma $和${S_{{\rm{td}}}}$的RCS序列${\sigma _i}$(i=1,2,…,N),其数学定义分别为:
| ${g_1} = \frac{1}{{\sqrt {6N} }}{\sum\limits_{i = 1}^N {\left( {\frac{{{\sigma _i} - \bar \sigma }}{{{S_{{\rm{td}}}}}}} \right)} ^3}$ | (11) |
| ${g_2} = \frac{1}{{\sqrt {24N} }}\sum\limits_{i = 1}^N {\left[{{{\left( {\frac{{{\sigma _i} - \bar \sigma }}{{{S_{{\rm{td}}}}}}} \right)}^4} - 3N} \right]} $ | (12) |
由式(11),式(12)可见,当g1时,概率密度函数关于直线$x = \bar \sigma $对称;g1>0时,概率密度函数的峰相对参照分布偏左,右部拖尾较长,并且g1越大,峰越“瘦”,拖尾越长;反之,g1<0时,概率密度函数的峰相对参照分布偏右,左部拖尾较长,并且g1越小,峰越“瘦”,拖尾越长。g2越大,密度函数的峰值偏离参照分布的峰值越多,越陡峭,反之,越平坦。
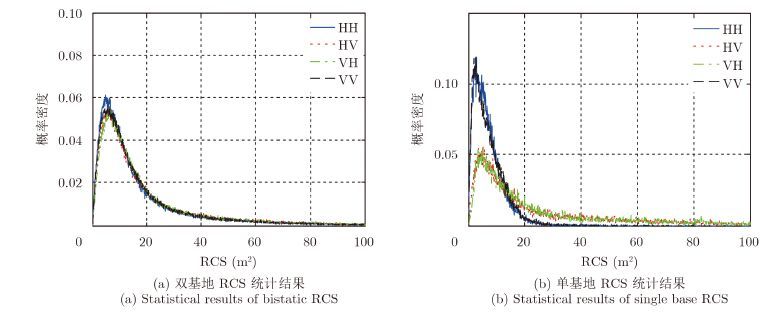
根据计算数据分别计算4个通道的均值、标准差、极大值、极小值和极差以及偏度系数、峰度系数,并统计得到直方图,进行归一化之后,得到近似的概率密度图,如图 3所示。从图中可以看到,双基地模式下,4种极化RCS的统计概率密度图基本一致,而单基地模式下,两种交叉极化RCS统计概率密度图一致,与两种共极化RCS统计概率密度图存在明显差异。
|
图 3 RCS统计分布 Fig.3 Statistical distribution of RCS |
统计的单/双基地4个极化分量的均值、标准差、极大值、极小值和极差以及偏度系数、峰度系数如表 1所示。从表 1可以看出,单/双基地RCS统计特性存在以下差异:
| 表 1 RCS统计参数 Tab.1 Statistical parameters of RCS |
(1) 4种极化双基地RCS极差达70 dB,而单基地RCS极差仅为40 dB,说明双基地模式下RCS的动态范围更大,为保证目标的探测能力,对接收机的动态范围要求更高;
(2) 4种极化双基地RCS均值约为26 dBm2,而单基地RCS均值仅为8~15 dBm2,说明双基地RCS普遍大于单基地RCS;
(3) 4种极化双基地RCS标准差约为37 dB,而单基地RCS标准差仅为8~17 dB,这再次说明双基地RCS的动态范围更大;
(4) 偏度系数均大于0,但双基地大于单基地,说明双基地RCS统计分布图的拖尾更长,即存在更多的大RCS值;
(5) 双基地RCS的峰度系数大于单基地RCS的峰度系数,说明双基地RCS峰值偏离参照分布的峰值更多。
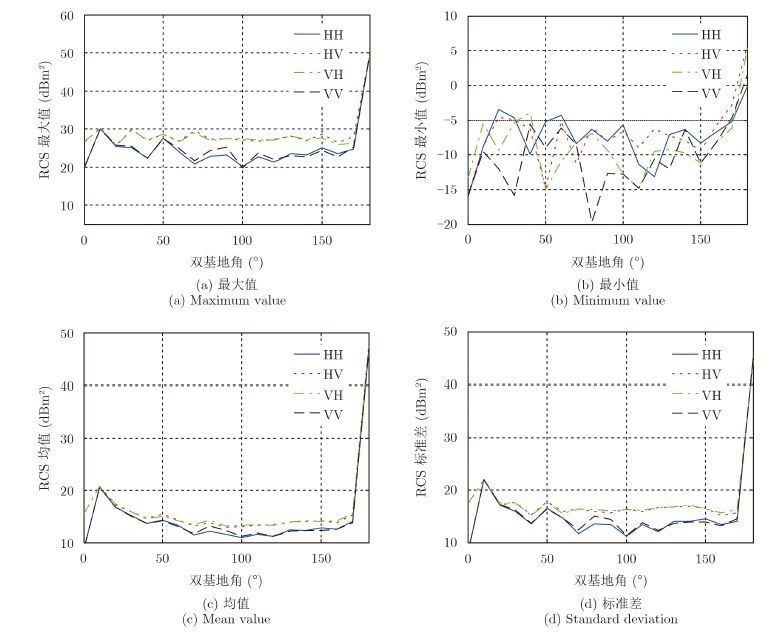
进一步我们统计了不同双基地角条件下双基地RCS的最大值、最小值、均值和标准差等参数,如图 4所示。从图中可以看出,双基地RCS最大值、最小值、均值、标准差在双基地角为零时(单基地模式),具有较小的值;在双基地角10°~150°范围内,RCS最大值比较变化不明显,而RCS最小值起伏较大,说明不同的视角与目标结构导致的结果,双基地角大于150°后,最小值随双基地角急剧增加;总体而言,交叉极化RCS的最大值、最小值、均值、标准差均大于共极化RCS。
|
图 4 不同双基地角RCS统计结果 Fig.4 RCS statistical results of different bistatic angles |
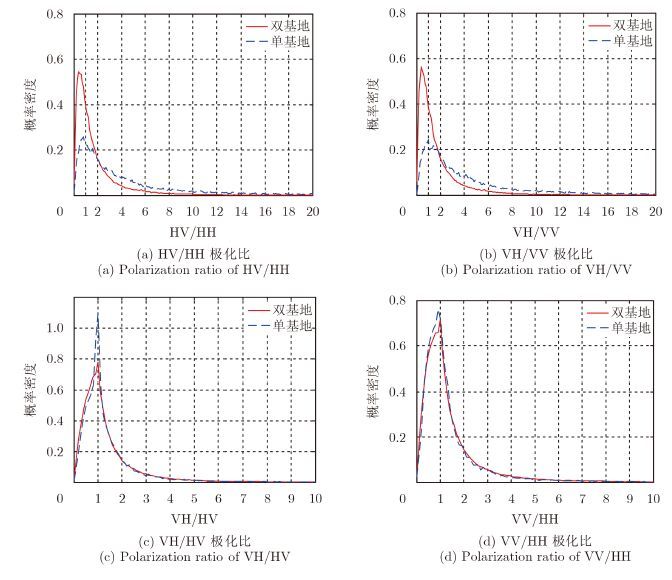
美国专利4035797 的作者认为,共极化和交叉极化信号幅度之比对简单目标而言是一个常数,而对于复杂目标而言,比值随着雷达和目标的距离不同而变化;由R.I.Dunn撰写的专利亦利用正交通道中回波幅度的比较进行军用机动交通车辆目标的识别,并与民用交通车辆予以区别。下面具体分析该目标不同观测角度下${S_{{\rm{HV}}}}/{S_{{\rm{HH}}}},{S_{{\rm{VH}}}}/{S_{{\rm{VV}}}},{S_{{\rm{VH}}}}/{S_{{\rm{HV}}}},$${S_{{\rm{VV}}}}/{S_{{\rm{HH}}}}$极化比的统计特性,统计结果如图 5所示。从图 5可以看到单/双基地交叉极化与共极化比统计分布图存在较大差异,而交叉极化比、共极化比统计分布图基本一致。
|
图 5 极化比统计结果 Fig.5 Statistical results of polarization ratio |
分别计算不同极化比大于1的所占整个分布的比例,如表 2所示。从表 2可以看出,单基地模式下,交叉极化与共极化之比大于1的比例达到0.80以上,存在交叉极化占优的现象,而共极化之比大于1的比例为0.52,说明两种共极化方式相当,交叉极化之比大于1的比例为0.42,说明SHV相比于SVH占优;而双基地模式下,交叉极化与共极化之比、共极化之比大于1的比例均接近0.50,说明各种极化对双基地雷达观测能力而言,均相当。也就是从统计意义上说,单基地雷达在设计接收极化方式时,为实现最佳观测,需结合目标特性选择极化方式;双基地雷达接收站可不需根据目标特性选择接收极化方式。
| 表 2 极化比大于1的比例 Tab.2 Proportion of polarization ratio (larger than one) |
统计的单/双基地4种极化比的均值、标准差、极大值、极小值和极差以及偏度系数、峰度系数如表 3所示。
| 表 3 极化比统计参数 Tab.3 Statistical results of polarization ratio |
从表 3可以看出,单/双基地RCS统计特性存在以下差异:
(1) 双基地交叉极化与共极化比极差达90 dB,而单基地交叉极化与共极化比极差为53 dB,说明双基地模式下交叉极化与共极化比的动态范围更大,双基地模式下要实现双极化通道信号的接收与检测、识别等能力,则对接收机性能要求更高;
(2) 双基地共极化比与单基地共极化的极差、均值、标准差、偏度系数、峰度系数较为接近,说明单/双基地共极化比的统计特性类似,与图 5(d)一致;
(3) 双基地交叉极化与共极化比均值与单基地交叉极化与共极化比均值接近;
(4) 双基地交叉极化与共极化比标准差大于单基地交叉极化与共极化比标准差,这再次说明双基地交叉极化与共极化比的动态范围更大;
(5) 偏度系数均大于0,但双基地大于单基地,说明双基地极化比统计分布图的拖尾更长,即存在更多的大比值;
(6) 双基地极化比的峰度系数大于单基地极化比的峰度系数,说明双基地极化比峰值偏离参照分布的峰值更多。
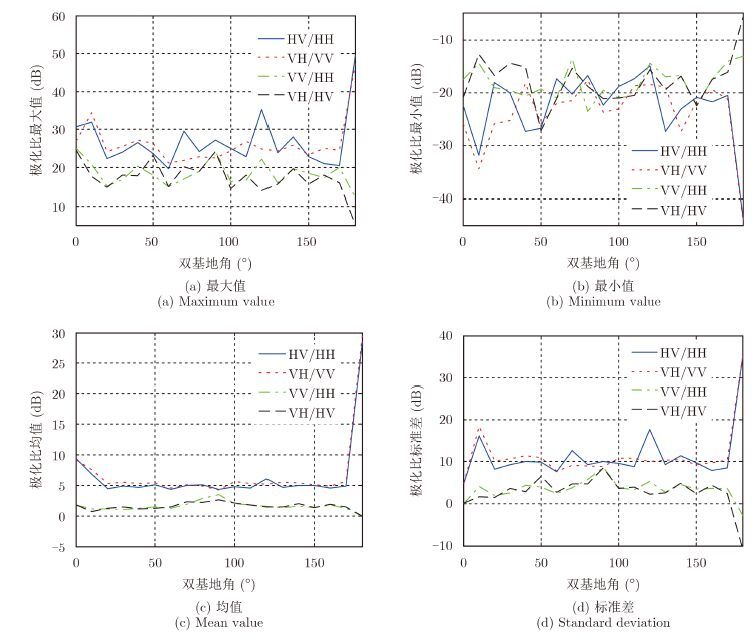
进一步,我们分析了不同双基地角条件下的极化比统计特性,图 6给出了不同双基地角条件下极化比统计的最大值、最小值、均值、标准差等参数,从图 6中可以看出交叉极化与共极化之比最大值、均值、标准差普遍大于共极化比、交叉极化比,交叉极化与共极化之比最小值普遍小于共极化比、交叉极化比,这说明交叉极化与共极化之比的动态大于共极化比、交叉极化比;交叉极化与共极化之比随双基地角变化规律基本一致,但起伏较为剧烈,共极化比、交叉极化比随双基地角变化规律基本一致,且均值和标准差保持稳定,说明不同的双基地角交叉极化与共极化散射变化不一致,两种交叉极化起伏特性一致,两种共极化起伏特性一致。
|
图 6 不同双基地角极化比统计结果 Fig.6 Statistical results of polarization ratio with different bistatic angles |
通过电磁计算数据分析了飞机目标单/双基地全极化RCS的统计特性以及极化比统计特性,结果表明双基地模式下4种极化RCS的统计特性近似,而单基地共极化和交叉极化RCS存在较大差异,双基地交叉极化与共极化比大于1的部分所占比例约为0.50,说明4种极化接收能够获得相近的观测能力,另一方面,如果双基地雷达采用双极化接收,则要求更大接收机动态。下一步将利用建立的无源雷达接收系统开展实测数据试验,并考虑综合利用两个极化通道的数据提升无源雷达系统的探测能力。另外,利用电磁计算数据结合典型目标运动和双基地雷达探测场景研究目标动态双基地极化特性也是值得关注的问题。
| [1] |
庄钊文, 肖顺平, 王雪松.
雷达极化信息处理及其应用[M]. 北京: 国防工业出版社, 1999 .
Zhuang Zhaowen, Xiao Shunping, and Wang Xuesong.
Radar Polarization Information Processing and Application[M]. Beijing: National Defence Industry Press, 1999 .
( 0) 0)
|
| [2] |
肖顺平, 王雪松, 代大海, 等.
极化雷达成像处理及应用[M]. 北京: 科学出版社, 2013 .
Xiao Shunping, Wang Xuesong, Dai Dahai, et al.
Polarimetric Radar Imaging Processing and Application[M]. Beijing: Science Press, 2013 .
( 0) 0)
|
| [3] |
李永祯, 李棉全, 程旭, 等. 雷达极化测量体制研究综述[J].
系统工程与电子技术 , 2013, 35 (9) : 1873-1877 Li Yongzhen, Li Mianquan, Cheng Xu, et al. Summarization of radar polarizarion measurement modes[J].
Systems Engineering and Electronics , 2013, 35 (9) : 1873-1877 ( 0) 0)
|
| [4] |
陈世春, 黄沛霖, 姬金祖. 典型隐身飞机的RCS起伏统计特性[J].
航空学报 , 2014, 35 (12) : 3304-3314 Chen Shichun, Huang Peilin, and Ji Jinzu. Radar cross section fluctuation charateristics of typical stealth aircraft[J].
Acta Aeronautica et Astronautica Sinica , 2014, 35 (12) : 3304-3314 ( 0) 0)
|
| [5] |
庄亚强, 张晨新, 张小宽, 等. 典型隐身飞机动态RCS仿真及统计分析[J].
微波学报 , 2014, 30 (5) : 17-21 Zhuang Yaqiang, Zhang Chenxin, Zhang Xiaokuan, et al. Statistical analysis and simulation of typical stealth aircraft dynamic RCS[J].
Journal of Microwaves , 2014, 30 (5) : 17-21 ( 0) 0)
|
| [6] |
施龙飞, 李盾, 王雪松, 等. 弹道导弹动态全极化一维像仿真研究[J].
宇航学报 , 2005, 26 (3) : 344-348 Shi Longfei, Li Dun, Wang Xuesong, et al. Study of simulation on the dynamic full-polarization range profiles of ballistic missile[J].
Journal of Astronautics , 2005, 26 (3) : 344-348 ( 0) 0)
|
| [7] |
马梁, 李永祯, 陈志杰, 等. 空间微动目标动态全极化回波仿真技术研究[J].
系统仿真学报 , 2012, 24 (3) : 628-637 Ma Liang, Li Yongzhen, Chen Zhijie, et al. Research on simulation of dynamic full-polarization radar echo for spatial targets[J].
Journal of System Simulation , 2012, 24 (3) : 628-637 ( 0) 0)
|
| [8] |
Cécile Titin-Schnaider. Power optimization for polarimetric bistatic random mechanisms[J].
IEEE Transactions on Geoscience and Remote Sensing , 2007, 45 (11) : 3646-3660 DOI:10.1109/TGRS.2007.903609 ( 0) 0)
|
| [9] |
Cécile Titin-Schnaider. Polarimetric characterization of bistatic coherent mechanisms[J].
IEEE Transactions on Geoscience and Remote Sensing , 2008, 46 (5) : 1535-1546 DOI:10.1109/TGRS.2008.916078 ( 0) 0)
|
| [10] |
Cécile Titin-Schnaider. Physical meaning of bistatic polarimetric parameters[J].
IEEE Transactions on Geoscience and Remote Sensing , 2010, 48 (5) : 2349-2356 DOI:10.1109/TGRS.2009.2038063 ( 0) 0)
|
| [11] |
Cécile Titin-Schnaide. Characterization and recognition of bistatic polarimetric mechanisms[J].
IEEE Transactions on Geoscience and Remote Sensing , 2013, 51 (3) : 1755-1774 DOI:10.1109/TGRS.2012.2208118 ( 0) 0)
|
| [12] |
万显荣. 基于低频段数字广播电视信号的外辐射源雷达发展现状与趋势[J].
雷达学报 , 2012, 1 (2) : 109-123 Wan Xianrong. An overview on development of passive radar based on the low frequency band digital broadcasting and TV signals[J].
Journal of Radars , 2012, 1 (2) : 109-123 DOI:10.3724/SP.J.1300.2012.20027 ( 0) 0)
|
| [13] |
You Jun, Wan Xianrong, Fu Yan, et al. Experimental study of polarization technique on multi-FM-based passive radar[J].
IET Radar, Sonar &1Navigation , 2015, 9 (7) : 763-771 ( 0) 0)
|
| [14] |
Bongioanni C, Colone F, Martelli T, et al.. Exploiting polarimetric diversity to mitigate the effect of interferences in FM-based passive radar[C]. 11th International Radar Symposium (IRS-2010), Vilnius, Lithuania, 2010.
( 0) 0)
|
| [15] |
Fabiola Colone and Pierfrancesco Lombardo. Polarimetric passive coherent location[J].
IEEE Transactions on Aerospace and Electronic Systems , 2015, 51 (2) : 1079-1097 DOI:10.1109/TAES.2014.130775 ( 0) 0)
|




