② (航天东方红卫星有限公司 北京 100094)
② (DFH Satellite Co., Ltd, Beijing 100094, China)
在雷达系统中,可以利用步进频信号获得合成距离高分辨[1]。步进频信号具有瞬时带宽低、合成带宽高的特点,因此,步进频信号避免了高速A/D采样和宽带接收等问题,降低了对硬件系统的要求和雷达系统的实现难度[2],是一种较为经济实用的高分辨信号形式。
步进频信号对目标的径向运动非常敏感[3, 4]。目标的径向运动会使合成距离像产生位置移动和发散,位置移动会引起测距偏差,发散会引起信噪比损失和分辨率降低。由于距离像的发散程度与单帧脉冲串的时间成正比,因此,在不影响雷达其它性能的情况下,可以通过提高PRF[5]或者减少子脉冲个数[6]的方法抑制发散,但当雷达和目标径向之间存在高速运动时,这种方法的抑制效果有限,难以满足需求。文献[3, 7-14]提出了一系列步进频信号运动补偿方法,这些方法可简单归结为两类:一类只对目标速度进行补偿,并没有考虑加速度的影响;另一类利用两帧或多帧脉冲串对目标速度和加速度同时进行补偿,数据率降低,增加了回波起伏特性和距离徙动对步进频雷达的影响。
当雷达和目标径向之间存在高速运动时,由于雷达和目标之间视角的影响,雷达和目标的径向上通常会产生较大的加速度分量,在步进频信号处理时必须考虑加速度的影响。为了不降低步进频雷达的数据率,需要采用一种基于单帧步进频脉冲串的对速度和加速度同时补偿的算法。目标运动会导致合成距离像聚焦效果变差,因此,可以将ISAR成像中的图像聚焦质量因子[4, 15-17]作为评价函数对速度和加速度进行遍历搜索,通过搜索评价函数的最优值实现运动补偿,而且这类方法只需要一帧脉冲串即可实现。文献[4, 15, 16]将对比度作为评价函数,但对比度在速度-加速度空间内的代价面存在起伏现象,严重影响了算法的效率。为此,本文深入研究了基于对比度的步进频运动补偿方法,并对算法效率进行了提升。
本文首先从步进频信号回波模型出发,详细分析了目标运动对合成高分辨距离像的影响;其次,介绍了基于对比度的步进频信号运动补偿算法,并指出了其中的不足;最后,提出了一种改进的基于对比度的运动补偿算法,大大提高了算法效率,通过公式推导证明了新方法可以消除由散射点群位置移动造成的对比度起伏现象,并通过MATLAB仿真给出了不同场景、不同信噪比下的补偿性能,验证了本文方法的有效性。
2 步进频信号合成距离像原理 2.1 回波模型及处理方法一帧步进频发射信号可以表示为:
| $u\left( t \right)=\sum\limits_{n=0}^{N-1}{p\left( t-n{{T}_{\text{r}}} \right)}\exp \left[ \text{j}2\text{ }\!\!π\!\!\text{ }\left( {{f}_{0}}+n\Delta f \right)t \right]\text{ }$ | (1) |
式(1)中,t表示时间,n表示子脉冲序号,N表示一帧步进频信号中的子脉冲个数,Tr表示脉冲重复时间,f0表示载频起始频率,△f 表示频率步进量,p(t)表示基带信号。
假设目标有K个散射点,则第n个子脉冲的总回波在混频后可以表示为:
| $\begin{array}{*{35}{l}} {{s}_{n}}\left( t \right)=\sum\limits_{i=1}^{K}{{{A}_{i}}}p\left[ t-n{{T}_{\text{r}}}-{{\tau }_{i}}\left( t \right) \right] \\ \qquad \quad \cdot \exp \left[ -\text{j}2\text{ }\!\!π\!\!\text{ }\left( {{f}_{0}}+n\Delta f \right){{\tau }_{i}}\left( t \right) \right] \\ \end{array}$ | (2) |
式(2)中,Ai表示第i个散射点的回波强度;
| ${R_i}\left( t \right) \cong {R_i}\left( 0 \right) + {v_{\rm r}}t + \frac{1}{2}{a_{\rm r}}{t^2}$ | (3) |
令
| $\begin{array}{l} {s_n}\left( t \right) = {s_{\rm R}}\left( {t',n{T_{\rm r}}} \right) = \sum\limits_{i = 1}^K {{A_i}} p\left[{t' - {\tau _i}\left( {n{T_{\rm r}}} \right)} \right]\\ \quad\quad\quad\quad\!\! \cdot \exp \left[{ - {\text{j}}2\text{π} \left( {{f_0} + n\Delta f} \right){\tau _i}\left( {n{T_{\rm r}} + t'} \right)} \right] \end{array}$ | (4) |
将式(3)代入式(4)得
| $\begin{align} & {{s}_{\text{R}}}\left( {t}',n{{T}_{\text{r}}} \right)=\sum\limits_{i=1}^{K}{{{A}_{i}}}p\left[ {t}'-{{\tau }_{i}}\left( n{{T}_{\text{r}}} \right) \right] \\ & \quad \quad \quad \quad \cdot \exp \left\{ -\text{j}2π \left( {{\text{f}}_{\text{0}}}\text{+n}\Delta \text{f} \right)\left[ {{\tau }_{i}}\left( n{{T}_{\text{r}}} \right) \right. \right. \\ & \quad \quad \quad \quad \left. \left. +\frac{2{{v}_{\text{r}}}{t}'+2{{a}_{\text{r}}}n{{T}_{\text{r}}}{t}'+{{a}_{\text{r}}}{{{{t}'}}^{2}}}{\text{c}} \right] \right\} \\ \end{align}$ | (5) |
式(5)中,含有
| $\begin{array}{l} {s_{\text{R}}}\left( {t',n{T_{\rm r}}} \right) = \sum\limits_{i = 1}^K {{A_i}} p\left[{t' - {\tau _i}\left( {n{T_{\rm r}}} \right)} \right]\exp \left( {{\text{j}}2\text{π} {f_{\text{dn}}}t'} \right)\\ \quad \quad \quad \quad \quad \quad\!\! \cdot\exp \left[{ - {\text{j}}2\text{π} \left( {{f_0} + n\Delta f} \right){\tau _i}\left( {n{T_{\rm r}}} \right)} \right] \end{array}$ | (6) |
式(6)中,
| $\begin{array}{l} {s_{\text{R}}}\left( {t',n{T_{\rm r}}} \right) \!=\! \sum\limits_{i = 1}^K {{A_i}} {\mathop{\rm rect}\nolimits} \left[{t' \!-\! {\tau _i}\left( {n{T_{\rm r}}} \right)} \right]\exp \left( {{\text{j}}2\text{π} {f_{\text{dn}}}t'} \right)\\ \quad \quad \quad \quad \quad \quad\!\!\!\! \cdot\exp \left[{ - {\text{j}}2\text{π} \left( {{f_0} + n\Delta f} \right){\tau _i}\left( {n{T_{\rm r}}} \right)} \right] \end{array}$ | (7) |
当目标为静止的理想单散射点时,对式(7)中各子脉冲回波进行离散采样,并对N个采样点进行IFFT,便可得到目标的无畸变的1维高分辨距离像,距离像的表达式具有式(8)形式:
| $h\left( k \right)=\left| \frac{\sin \left[ π \left( \text{k-}{{\text{l}}_{\text{0}}} \right) \right]}{\sin \left[ π \left( \text{k-}{{\text{l}}_{\text{0}}} \right)\text{ /}N \right]} \right|$ | (8) |
式(8)中,
目标运动对子脉冲回波复数包络的影响通常可忽略不计。目标运动会使脉间相位产生额外相位项,可表示为:
| $\left. \begin{array}{l} {\varphi _{v1}} = - \frac{{4\text{π} }}{\text{c}}{f_0}{v_{\rm r}}{T_{\rm r}}n\\ {\varphi _{v2}} = - \frac{{4\text{π} }}{\text{c}}\Delta f{v_{\rm r}}{T_{\rm r}}{n^2}\\ {\varphi _{a2}} = - \frac{{2\text{π} }}{\text{c}}{f_0}{a_{\rm r}}{T_{\rm r}}^2{n^2}\\ {\varphi _{a3}} = - \frac{{2\text{π} }}{\text{c}}{a_{\rm r}}\Delta f{T_{\rm r}}^2{n^3} \end{array} \right\}$ | (9) |
式(9)中,
| $\begin{array}{*{35}{l}} \Delta {{R}_{v1}}=v\left( {{f}_{0}}\text{ /}\Delta f \right){{T}_{\text{r}}} \\ \Delta {{R}_{v2}}=v\left( N-1 \right){{T}_{\text{r}}} \\ \Delta {{R}_{a2}}={{f}_{0}}a\left( N-1 \right){{T}_{\text{r}}}^{2}/\left( 2\Delta f \right) \\ \Delta {{R}_{a3}}=3a{{\left( N-1 \right)}^{2}}{{T}_{\text{r}}}^{2}/4 \\ \end{array}$ | (10) |
通常情况下,
当△Rv1不超过半个高分辨距离单元,
| $\begin{array}{*{35}{l}} \left| \Delta {{v}_{1}} \right| & <c/\left( 4{{f}_{0}}N{{T}_{\text{r}}} \right) \\ \left| \Delta {{v}_{2}} \right| & <c/\left[ 8{{\left( N-1 \right)}^{2}}\Delta f{{T}_{\text{r}}} \right] \\ \left| \Delta {{a}_{2}} \right| & <c/\left[ 4{{\left( N-1 \right)}^{2}}{{f}_{0}}{{T}_{\text{r}}}^{2} \right] \\ \left| \Delta {{a}_{3}} \right| & <c/\left[ 4{{\left( N-1 \right)}^{3}}\Delta f{{T}_{\text{r}}}^{2} \right] \\ \end{array}$ | (11) |
通常情况下,
估计出目标的运动参数后,对目标回波进行脉间相位补偿,再沿
对目标所在区域的基带回波进行等间隔采样,得到回波响应矩阵:
| ${\text{P}} = \left( \begin{array}{l} \;\;\;\;\tilde x\left( {0,0} \right)\;\;\;\;\;\;\;\;\;\tilde x\left( {0,1} \right)\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\tilde x\left( {0,M - 1} \right)\\ \;\;\;\;\tilde x\left( {1,0} \right)\;\;\;\;\;\;\;\;\;\tilde x\left( {1,1} \right)\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\tilde x\left( {1,M - 1} \right)\\ \;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ \tilde x\left( {N - 1,0} \right)\;\;\;\tilde x\left( {N - 1,1} \right)\;\;\; \cdots \;\;\;\tilde x\left( {N - 1,M - 1} \right) \end{array} \right)$ | (12) |
式(12)中,
| ${\text{H}} = \left( \begin{array}{l} \;\;\;\;\;\tilde I\left( {0,0} \right)\;\;\;\;\;\;\;\;\;\;\tilde I\left( {0,1} \right)\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\tilde I\left( {0,M - 1} \right)\\ \;\;\;\;\;\tilde I\left( {1,0} \right)\;\;\;\;\;\;\;\;\;\;\tilde I\left( {1,1} \right)\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\tilde I\left( {1,M - 1} \right)\\ \;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ \tilde I\left( {{N_{\rm r}} - 1,0} \right)\;\;\;\tilde I\left( {{N_{\rm r}} - 1,1} \right)\;\;\; \cdots \;\;\;\;\tilde I\left( {{N_{\rm r}} - 1,M - 1} \right) \end{array} \right)$ | (13) |
步进频高分辨距离像矩阵H的对比度定义为:
| $\begin{align} & C\left( v,a \right)=\sqrt{\frac{1}{M{{N}_{\text{r}}}}\sum\limits_{m=0}^{M-1}{\sum\limits_{k=0}^{{{N}_{\text{r}}}-1}{{{\left( {{\left| \tilde{I}\left( k,m \right) \right|}^{2}}-\frac{1}{M{{N}_{\text{r}}}}\sum\limits_{m=0}^{M-1}{\sum\limits_{k=0}^{{{N}_{\text{r}}}-1}{{{\left| \tilde{I}\left( k,m \right) \right|}^{2}}}} \right)}^{2}}}}}/ \\ & \left( \frac{1}{M{{N}_{\text{r}}}}\sum\limits_{m=0}^{M-1}{\sum\limits_{k=0}^{{{N}_{\text{r}}}-1}{{{\left| \tilde{I}\left( k,m \right) \right|}^{2}}}} \right) \\ \end{align}$ | (14) |
基于对比度的步进频雷达运动补偿算法的步骤如下:
步骤1 在速度-加速度平面内进行2维搜索,利用式(15)通过使对比度最大化得到速度和加速度的估计值
| $\left( {\hat v,\hat a} \right) = {\mathop{\rm argument}\nolimits} \left[{\mathop {\max }\limits_{v,a} C\left( {v,a} \right)} \right]$ | (15) |
步骤2 利用
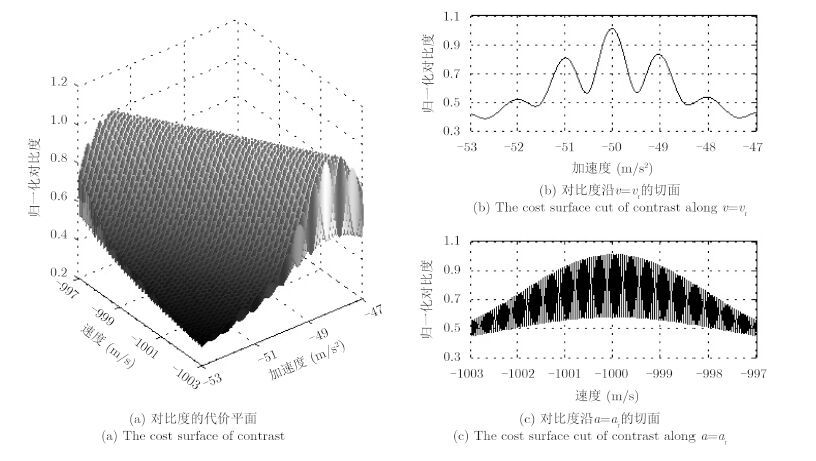
设目标与雷达之间的径向速度为vr=-1000 m/s,径向加速度为ar=-50 m/s2,雷达系统参数如表 1所示,图 1给出了利用Nr=N点IFFT合成距离像时理想单散射点目标的对比度代价面。
| 表 1 步进频雷达系统参数 Tab.1 Stepped-frequency radar system parameters |
|
图 1 Nr=N 时理想单散射点目标的对比度代价面 Fig.1 The contrast cost surface for a single ideal point scatterer target with Nr=N |
从图 1可以看出,对比度在真实运动参数附近取得全局最大值,因此,通过搜索对比度最大值估计目标的运动参数是合理的。但同时又注意到,对比度代价面出现剧烈起伏,存在许多局部极大值点,且起伏特性随搜索速度变化要比随搜索加速度变化显著得多。对比度代价面之所以出现起伏,是因为对比度不仅与距离像的发散程度有关,也与距离像的位置有关。由式(10)可知,运动参数补偿误差会使距离像位置产生移动,从而造成对比度代价面在速度-加速度空间内剧烈起伏。
代价面起伏问题通常难以保证寻优算法的收敛性,而且要求有较好的初始搜索值[17]。文献[4]以较小的固定间隔对速度-加速度空间上的所有可能位置进行遍历搜索,不存在寻优算法的收敛性问题,但运算量巨大,不利于工程应用。
4 改进的基于对比度的运动补偿算法 4.1 散射点群位置对对比度影响的消除
散射点群位置的移动等效为目标回波沿慢时间乘以一个一次相位项,由Parseval定理知,式(14)中
| $\tilde x\left( n \right) = x\left( n \right)W_N^{\alpha n},\,\,\ 0 \le n \le N - 1$ | (16) |
设
| ${\tilde x_2}\left( n \right) = \frac{1}{{{N_{\rm r}}}}\sum\limits_{l = 0}^{{N_{\rm r}} - 1} {{{\tilde x}^*}\left( l \right)\tilde x{{\left( {\left( {l + n} \right)} \right)}_{{N_{\rm r}}}}{R_{{N_{\rm r}}}}\left( n \right)} $ | (17) |
将式(16)代入式(17),并求模,可得:
(1) 当
| $\left| {{{\tilde x}_2}\left( n \right)} \right| = \left\{ \begin{array}{l} \frac{1}{{{N_{\rm r}}}}\left| {\sum\limits_{l = 0}^{N - 1 - n} {{x^*}\left( l \right)x\left( {l + n} \right)} } \right|,\quad \quad \quad \quad \quad \!\!\!\!0 \le n \le N - 1\\ 0,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \!\!N \le n \le {N_{\rm r}} - N\\ \frac{1}{{{N_{\rm r}}}}\left| {\sum\limits_{l = {N_{\rm r}} - n}^{N - 1} {{x^*}\left( l \right)x\left( {l + n - {N_{\rm r}}} \right)} } \right|,\quad \quad {N_{\rm r}} - N + 1 \le n \le {N_{\rm r}} - 1 \end{array} \right.$ | (18) |
(2) 当
| $\left| {{{\tilde{x}}}_{2}}\left( n \right) \right|=\left\{ \begin{array}{*{35}{l}} \frac{1}{{{N}_{\text{r}}}}\left| \sum\limits_{l=0}^{N-1-n}{{{x}^{*}}\left( l \right)}x\left( l+n \right) \right|,\quad \quad \quad \quad \quad \quad \quad \quad 0\le n\le {{N}_{\text{r}}}-N \\ \frac{1}{{{N}_{\text{r}}}}\left| \begin{align} & \sum\limits_{l=0}^{N-1-n}{{{x}^{*}}\left( l \right)x\left( l+n \right)}+ \\ & \sum\limits_{l={{N}_{\text{r}}}-n}^{N-1}{{{x}^{*}}\left( l \right)x\left( l+n-{{N}_{\text{r}}} \right)W_{N}^{-\alpha {{N}_{\text{r}}}}} \\ \end{align} \right|,{{N}_{\text{r}}}-N+1\le n\le N-1 \\ \frac{1}{{{N}_{\text{r}}}}\left| \sum\limits_{l={{N}_{\text{r}}}-n}^{N-1}{{{x}^{*}}\left( l \right)x\left( l+n-{{N}_{\text{r}}} \right)} \right|,\quad \quad \quad \quad \quad \quad N\le n\le {{N}_{\text{r}}}-1 \\ \end{array} \right.$ | (19) |
由Parseval定理可知,
(1) 当
(2) 当
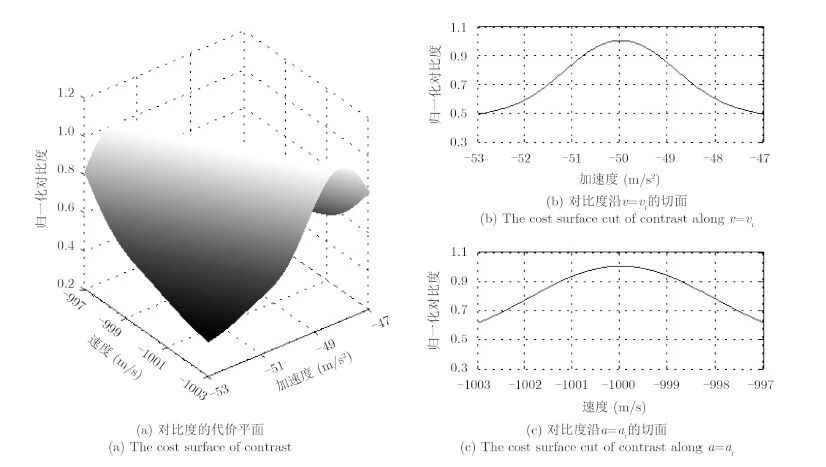
图 2给出了利用
|
图 2 Nr=2N 时理想单散射点目标的对比度代价面 Fig.2 The contrast cost surface for a single ideal point scatterer target with Nr=2N |
由于脉间一次相位项对对比度无影响,故只需考虑二次相位项和三次相位项。运动补偿后第n个子脉冲的目标回波的二次相位和三次相位之和可表示为:
| $\begin{align} & \Delta \phi \left( n{{T}_{\text{r}}},v,a \right)=\frac{2π }{\text{c}}{{T}_{\text{r}}}\left[ 2\Delta f\left( v-{{v}_{\text{r}}} \right)+{{f}_{0}}{{T}_{\text{r}}}\left( a-{{a}_{\text{r}}} \right) \right]{{n}^{2}} \\ & \text{ }+\frac{2π }{\text{c}}\Delta f{{T}_{\text{r}}}^{2}\left( a-{{a}_{\text{r}}} \right){{n}^{3}}n \\ \end{align}$ | (20) |
式(20)中,v和a分别表示补偿速度和补偿加速度。
| $\begin{align} & \Delta \phi \left( t,v,a \right)=\frac{2π }{\text{c}{{T}_{\text{r}}}}\left[ 2\Delta f\left( v-{{v}_{\text{r}}} \right)+{{f}_{0}}{{T}_{\text{r}}}\left( a-{{a}_{\text{r}}} \right) \right]{{t}^{2}} \\ & \text{ }+\frac{2π }{\text{c}{{T}_{\text{r}}}}\Delta f\left( a-{{a}_{\text{r}}} \right){{t}^{3}},t\in \left[ 0 \right.,\left. \left( N-1 \right){{T}_{\text{r}}} \right]\text{ } \\ \end{align}$ | (21) |
对
| ${f_{\Delta \phi }}\left( {t,v,a} \right) = \frac{1}{{2\text{π} }}\frac{{{\rm d}\left[{\Delta \phi \left( {t,v,a} \right)} \right]}}{{{\rm d}t}} = {\beta _1}{t^2} + {\beta _2}t$ | (22) |
式(22)中,
| $\begin{align} & {{\beta }_{1}}=\frac{3\Delta f\left( a-{{a}_{\text{r}}} \right)}{\text{c}{{T}_{\text{r}}}}, \\ & {{\beta }_{2}}=\frac{4\Delta f\left( v-{{v}_{\text{r}}} \right)+2{{f}_{0}}{{T}_{\text{r}}}\left( a-{{a}_{\text{r}}} \right)}{\text{c}{{T}_{\text{r}}}} \\ \end{align}$ | (23) |
设
| $\delta f\left( {v,a} \right) = \mathop {\max }\limits_t \left[{{f_{\Delta \phi }}\left( {t,v,a} \right)} \right] - \mathop {\min }\limits_t \left[{{f_{\Delta \phi }}\left( {t,v,a} \right)} \right]$ | (24) |
由式(22)和式(23)可知,对于一个固定的
| $\left. \begin{array}{l} - \frac{{{\beta _2}}}{{2{\beta _1}}} = \frac{{\left( {N - 1} \right){T_{\rm r}}}}{2},\ a \ne {a_{\rm r}}\\ v = {v_{\rm r}},\,\,a = {a_{\rm r}} \end{array} \right\}$ | (25) |
将式(23)代入式(25)得
| $v = - \frac{{\left[{2{f_0} + 3\left( {N - 1} \right)\Delta f} \right]{T_{\rm r}}}}{{4\Delta f}}\left( {a - {a_{\rm r}}} \right) + {v_{\rm r}}$ | (26) |
则此时对应的
| $\begin{array}{*{35}{l}} \delta {{f}_{\min }}\left( a \right)=\underset{v}{\mathop{\min }}\,\left[ \delta f\left( v,a \right) \right] \\ \quad \quad \quad \quad =\left| {{f}_{\Delta \phi }}\left( \left( N-1 \right){{T}_{\text{r}}}/2,v,a \right)-{{f}_{\Delta \phi }}\left( 0,v,a \right) \right| \\ \end{array}$ | (27) |
将式(22),式(23)和式(26)代入式(27)得
| $\delta {f_{\min }}\left( a \right) = \left| {\frac{{3{{\left( {N - 1} \right)}^2}\Delta f{T_{\rm r}}\left( {a - {a_{\rm r}}} \right)}}{{4{\rm c}}}} \right|$ | (28) |
由式(28)知,
对于理想的单散射点,对比度与
为了分析目标特性对对比度的影响,对表 2所列出的4种场景下的目标进行仿真,雷达系统参数如表 1所示。
| 表 2 4种场景下的目标参数 Tab.2 Target parameters in four different scenes |
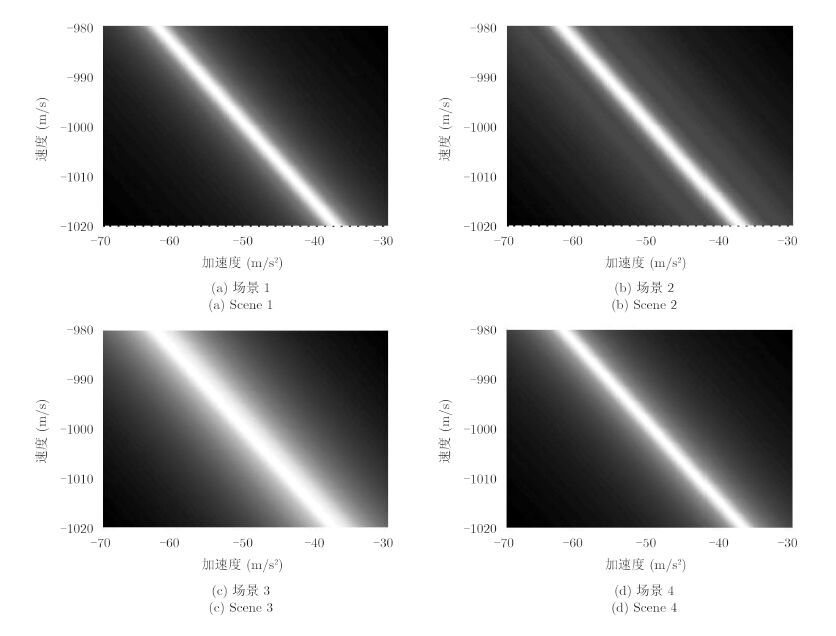
图 3给出了4种场景下的对比度代价面在速度-加速度面上的投影,对比度越大,投影越亮。可以看出,4种场景下的对比度代价面投影均出现一个光亮的条带,各条带的形状和斜率也基本一致,这与式(26)相对应;条带内部亮度变化不明显,这与式(28)相对应。
|
图 3 4种场景下的对比度代价面投影 Fig.3 The contrast cost surface projections in four different scenes |
为了定量分析目标特性对对比度的影响,通过MATLAB仿真得到4种场景下目标的对比度代价面内由对比度峰值确定的直线表达式:
| $\left. \begin{array}{l} {L_{{\rm m}1}}:v = - 1.597926a - 1079.896285\\ {L_{{\rm m}2}}:v = - 1.600474a - 1079.989844\\ {L_{{\rm m}3}}:v = - 1.601744a - 1080.449445\\ {L_{{\rm m}4}}:v = - 1.594944a - 1079.073461 \end{array} \right\}$ | (29) |
| ${L_{\rm m}}:v = - 1.597925a - 1079.896250$ | (30) |
比较式(29)和式(30)可知,目标特性会对由对比度峰值确定的直线表达式产生影响,但影响不大,特别是直线斜率几乎没有发生变化。
至此,对比度代价面的性质可总结如下:
(1) 在速度-加速度投影平面上存在一个条带,在条带内对比度取值较大且变化不明显,在条带外对比度取值较小。多散射点目标可能会引起条带的展宽,但条带的形状和斜率对目标特性并不敏感。
(2) 对比度峰值确定的直线包含在性质(1)所述的条带内。对于不同特性的目标,对比度峰值确定的直线斜率均可用式(26)给出的直线斜率近似表示。
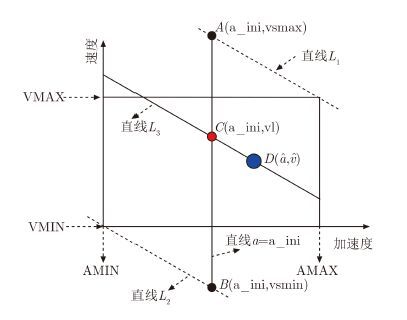
4.3 一种高效的搜索对比度最大值位置的方法在分析对比度代价面性质的基础上,本文提出一种高效的搜索对比度最大值位置的方法,将速度-加速度空间内的2维平面搜索问题简化为速度-加速度空间内的1维直线搜索问题,大大提高了搜索效率,降低了运算量。如图 4所示,该搜索方法的具体实现过程描述如下:
|
图 4 一种高效的搜索对比度最大值位置的方法示意图 Fig.4 The diagram of an efficient method of searching for the location corresponding to the max contrast |
步骤1 根据先验知识(如目标类型、窄带跟踪信息等)设置搜索速度区间[VMIN,VMAX]和搜索加速度区间[AMIN,AMAX]。
步骤2 取a_ini
步骤3 沿直线a=a_ini在速度区间[vsmin,vsmax]内搜索对比度最大值的位置,得到局部对比度最大值点C(a_ini,vl)。
步骤4 设经过点C(a_ini,vl),且与直线L1,L2平行的直线为L3。沿直线L3在搜索加速度区间[AMIN,AMAX]内搜索对比度最大值的位置,得到点
式(26)的推导过程表明,步骤2中a_ini的选取与真实径向加速度ar无关;仿真结果亦表明,步骤2中a_ini的取值非常宽松,即使在|a_ini
本文用搜索次数表征算法的运算量。对于本文算法,因为消除了由散射点群位置变化引起的对比度起伏,故可先用较大的搜索间隔进行粗搜索,再用较小的间隔进行精确搜索。设式(26)确定的直线斜率为km,则vsmax-vsmin=km(AMIN-AMAX)+VMAX-VMIN。步骤3中,取较大搜索间隔为
| $\begin{align} & {{n}_{\text{s1}}}=\frac{{{k}_{\text{m}}}\left( \text{AMIN-AMAX} \right)+\left( \text{VMAX-VMIN} \right)}{\left| \Delta {{v}_{2}} \right|} \\ & \quad \quad +\frac{\left( \text{AMAX-AMIN} \right)}{\left| \Delta {{a}_{2}} \right|}+2\frac{\left( \left| \Delta {{v}_{2}} \right|\text{+}\left| {{k}_{\text{m}}} \right|\left| \Delta {{a}_{2}} \right| \right)}{\left| \Delta {{v}_{1}} \right|} \\ \end{align}$ | (31) |
传统算法以固定间隔在速度-加速度2维平面内进行遍历搜索,寻找对比度最大值位置,速度搜索间隔为
| ${n_{\rm s2}} = \frac{{\left( {\rm VMAX - VMIN} \right)\left( {\rm AMAX - AMIN} \right)}}{{\left| {\Delta {v_1}} \right|\left| {\Delta {a_2}} \right|}}$ | (32) |
通常情况下,
仿真采用的雷达系统参数如表 1所示,目标参数如表 2所示,图 4中的参数设置为:VMIN=-1040 m/s,VMAX=-960 m/s,AMIN=-60 m/s2,AMAX=-40 m/s2。
将以上参数分别代入式(11),式(26),式(31)和式(32),可得ns1=414,ns2=246743,本文算法效率相对传统算法提高了近600倍。
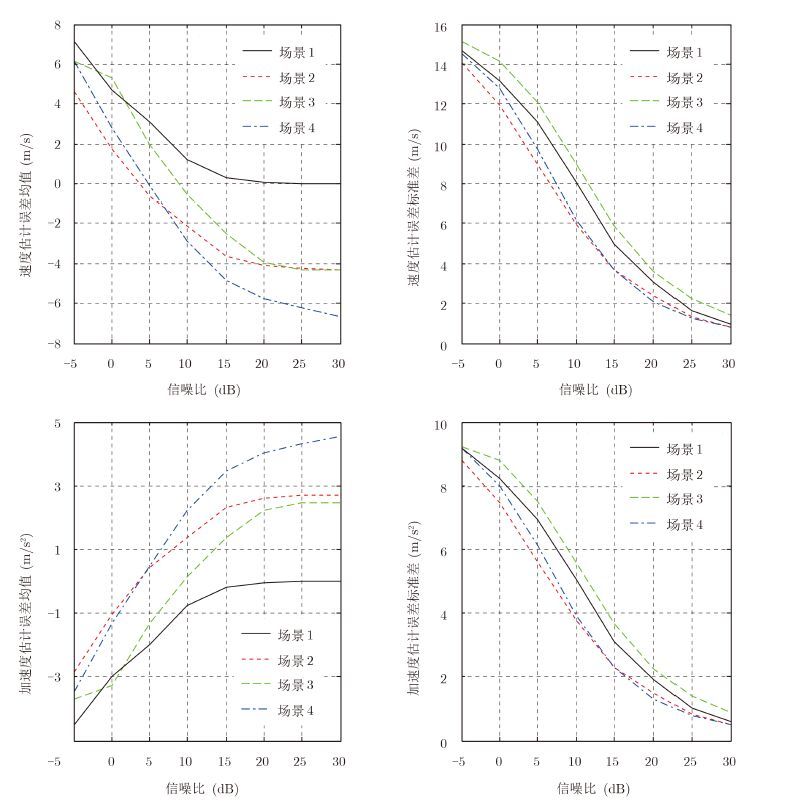
表 3给出了无背景噪声时4种场景下目标的运动参数估计误差。假设输入噪声为高斯白噪声,每种信噪比(利用IFFT合成距离像之前,目标最强散射点与噪声功率之比)运行1000次,图 5给出了4种场景下目标的运动参数估计误差随信噪比的变化关系。
| 表 3 无背景噪声时的运动参数估计误差 Tab.3 The estimation errors of motion parameters with no background noise |
|
图 5 运动参数估计误差与信噪比的关系 Fig.5 The relationship between estimation errors of motion parameters and SNR |
由表 3和图 5可以看出,速度估计误差和加速度估计误差对目标特性和信噪比非常敏感,只有当无噪声且目标为理想的单散射点时,基于对比度的步进频雷达运动补偿算法才可以实现对速度和加速度的精确估计,否则不能进行精确估计。
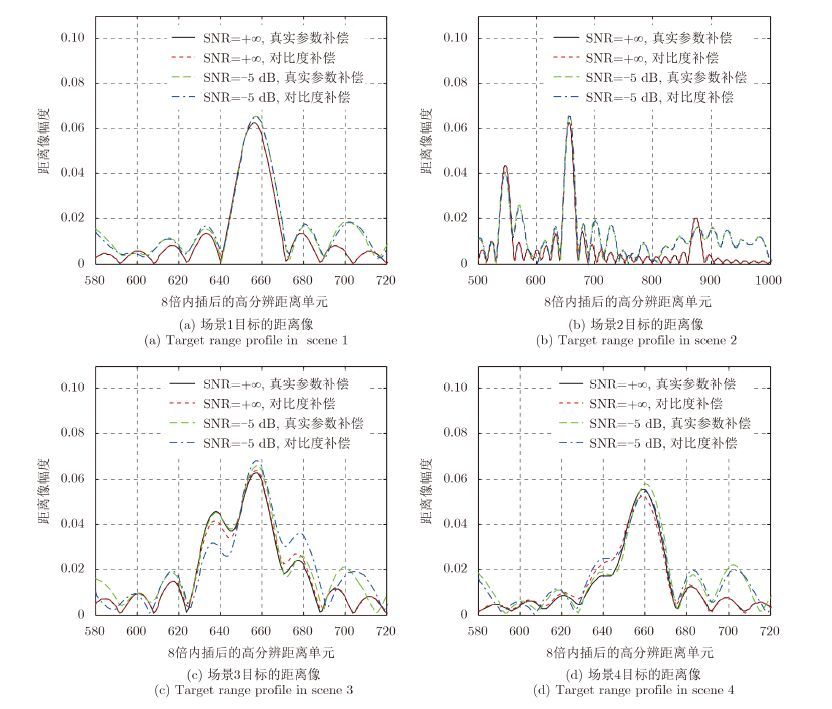
为了更直观地观察基于对比度的步进频雷达运动补偿算法的性能,图 6比较了4种场景下利用真实参数和基于对比度的方法补偿后的1维距离像,每个场景又分为无噪声(SNR=+∞)和SNR=-5 dB两种情况。为了便于从视觉上对距离像形状进行比较,图 6中对由运动参数估计误差造成的耦合时移进行了补偿。
|
图 6 利用不同补偿方法得到的1维距离像 Fig.6 One-dimension range profiles obtained by different compensation methods |
从图 6可以看出,在信噪比相同的情况下,两种补偿方法得到的距离像在峰值和副瓣处均吻合得很好,即便是对于吻合效果相对较差的场景3和场景4,两种补偿方法得到的距离像形状也基本一致。对于同一种补偿方法,不同信噪比下的距离像形状在峰值处一致性较好,但在副瓣处一致性无法保证,比如场景2中同一种补偿方法在不同信噪比下的距离像副瓣几乎看不出任何一致性。
基于对比度的步进频雷达运动补偿算法的性能可总结如下:
(1) 对于不同特性的目标,均能够抑制距离像的发散,基本保持目标距离像的固有形状,并且在低信噪比下依然适用。
(2) 实际工程中不能实现对速度和加速度的精确估计。其根本原因为运动目标回波的脉间相位中,速度产生的二次相位项和加速度产生的二次相位项存在耦合,且加速度产生的三次相位项通常很小,所以速度估计值和加速度估计值对目标特性和信噪比非常敏感,无法实现精确估计。
6 结论步进频雷达合成距离像的对比度代价面存在剧烈起伏,严重限制了算法的效率。为此,本文提出了一种改进的基于对比度的运动补偿算法。通过公式推导证明了沿慢时间利用
| [1] |
Wehner D R. High-Resolution Radar[M]. Norwood, MA, Artech House, Inc., 1995:200-209.
( 0) 0)
|
| [2] |
原浩娟. 米波雷达步进频信号处理理论及实现[D].[博士论文], 北京理工大学, 2009.
Yuan Haojuan. Stepped frequency signal processing theory and implementation for metrewave radar[D].[Ph.D. dissertation], Beijing Institute of Technology, 2009.
( 0) 0)
|
| [3] |
刘峥, 张守宏. 步进频率雷达目标的运动参数估计[J].
电子学报 , 2000, 28 (3) : 43-45 Liu Zheng and Zhang Shouhong. Estimation of target motion parameter in a stepped-frequency pulses radar[J].
Acta Electronica Sinica , 2000, 28 (3) : 43-45 ( 0) 0)
|
| [4] |
Berizzi F, Martorella M, Cacciamano A, et al. A contrast-based algorithm for synthetic range-profile motion compensation[J].
IEEE Transactions on Geoscience and Remote Sensing , 2008, 46 (10) : 3053-3062 ( 0) 0)
|
| [5] |
Wong S K, Duff G, and Riseborough E. Analysis of distortion in the high range resolution profile from a perturbed target[J].
IEE Processings-Radar, Sonar and Navigation , 2001, 148 (6) : 353-362 ( 0) 0)
|
| [6] |
Fukushima C and Hamada N. A study on stepped frequency radar by using intra-pulse phase coded modulation[C]. The World Congress on Engineering and Computer Science, San Francisco, USA, 2008:391-396.
( 0) 0)
|
| [7] |
Liu Yimin, Meng Huadong, Li Gang, et al. Velocity estimation and range shift compensation for high range resolution profiling in stepped-frequency radar[J].
IEEE Geoscience and Remote Sensing Letters , 2010, 7 (4) : 791-795 ( 0) 0)
|
| [8] |
Chen Hangyong, Liu Yongxiang, Jiang Weidong, et al. A new approach for synthesizing the range profile of moving targets via stepped-frequency waveforms[J].
IEEE Geoscience and Remote Sensing Letters , 2006, 3 (3) : 406-409 ( 0) 0)
|
| [9] |
Chen Hangyong, Liu Yongxiang, Jiang Weidong, et al.. Phase cancellation for synthesizing range profile of target with micro-motion[C]. 2006 CIE International Conference on Radar, Shanghai, China, 2006:817-820.
( 0) 0)
|
| [10] |
Hu Jiemin, Jiang Weidong, Fu Yaowen, et al.. A novel approach to synthesize the range profile via predesigned stepped-frequency waveforms[C]. 20102nd International Conference on Computer Engineering and Technology, Chengdu, China, 2010, 5:363-366.
( 0) 0)
|
| [11] |
胡杰民, 付耀文, 魏玺章, 等. 调频步进雷达高速运动目标距离像合成方法研究[J].
电子与信息学报 , 2011, 33 (7) : 1756-1760 Hu Jiemin, Fu Yaowen, Wei Xizhang, et al. Research on range profile synthesizing method for high speed moving target in stepped frequency modulated radar[J].
Journal of Electronics & Information Technology , 2011, 33 (7) : 1756-1760 ( 0) 0)
|
| [12] |
胡光, 曾大治, 龙腾. 基于变PRT步进频信号对运动目标同时测距和测速的方法研究[J].
信号处理 , 2010, 26 (11) : 1627-1631 Hu Guang, Zeng Da-zhi, and Long Teng. Research on method of simultaneously range and velocity measuring with variable PRT stepped-frequency waveform[J].
Signal Processing , 2010, 26 (11) : 1627-1631 ( 0) 0)
|
| [13] |
袁昊天, 文树梁, 程臻. 调频步进信号高速运动目标径向速度精确测量技术研究[J].
电子学报 , 2009, 37 (3) : 649-653 Yuan Haotian, Wen Shuliang, and Cheng Zhen. Accurate velocity measurement of high speed moving target about stepped-frequency chirp signal[J].
Acta Electronica Sinica , 2009, 37 (3) : 649-653 ( 0) 0)
|
| [14] |
吴亮, 魏玺章, 杨德贵, 等. 调频步进信号高速目标精确运动估计[J].
电子学报 , 2010, 38 (12) : 2832-2838 Wu Liang, Wei Xizhang, Yang Degui, et al. Accurate motion estimation of high speed moving target about stepped-frequency chirp signal[J].
Acta Electronica Sinica , 2010, 38 (12) : 2832-2838 ( 0) 0)
|
| [15] |
Berizzi F, Martorella M, and Cacciamano A. Synthetic range profile focusing via contrast optimization[C]. 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 2007:3563-3566.
( 0) 0)
|
| [16] |
Cacciamano A, Giusti E, Capria A, et al. Contrast-optimization-based range-profile autofocus for polarimetric stepped-frequency radar[J].
IEEE Transactions on Geoscience and Remote Sensing , 2010, 48 (4) : 2049-2056 ( 0) 0)
|
| [17] |
Kim K T. Focusing of high range resolution profiles of moving targets using stepped frequency waveforms[J].
IET Radar, Sonar & Navigation , 2010, 4 (4) : 564-575 ( 0) 0)
|


